Математическая теория игр
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
УРАЛЬСКИЙ
ГУМАНИТАРНЫЙ ИНСТИТУТ
Кафедра
«Бухгалтерский учет, анализ и аудит»
КОНТРОЛЬНАЯ
РАБОТА
по
предмету: «Теория экономического анализа»
Вариант
5
СОДЕРЖАНИЕ
I.
Теоретическая часть
1. Математическая теория игр
II. Практическая
часть
1. Задание № 1
. Задание № 2
. Задание № 3
. Задание № 4
. Задание № 5
Список использованных источников
I.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Методика экономического анализа
базируется на пересечении трех областей знаний: экономики, статистики и
математики.
Математические методы можно
разделить на три группы: экономические (матричные методы, теория
производственных функций, теория межотраслевого баланса); методы экономической
кибернетики и оптимального программирования (линейное, нелинейное, динамическое
программирование); методы исследования операций и принятия решений (теория
графов, теория игр, теория массового обслуживания).
Методы математического программирования - основное средство решения задач оптимизации
производственно-хозяйственной деятельности. По своей сути эти методы - средство
плановых расчетов. Ценность их для экономического анализа выполнения
бизнес-планов состоит в том, что они позволяют оценивать напряженность плановых
заданий, определять лимитирующие группы оборудования, виды сырья и материалов,
получать оценки дефицитности производственных ресурсов и т.п.
Значение экономико-математических
методов и их классификация.
Среди способов оптимизации
показателей наибольшее применение нашли экономико-математические методы:
программирование, теория массового обслуживания, теория игр, исследования
операций, экспертных оценок специалистов и др.
Экономико-математические методы
используются в анализе для решения задач, связанных с выбором оптимальных
вариантов по производственной программе отдельного предприятия, структуре
посевных площадей, рационов кормления скота и др. С помощью
экономико-математических методов можно решать задачи по наилучшему
использованию материальных и трудовых ресурсов.
Использование
экономико-математических методов повышает точность экономического анализа,
делает его более глубоким, сокращает сроки проведения аналитической работы и
повышает его оперативность.
Применение математических методов в
экономическом анализе деятельности предприятия требует:
• системного подхода к изучению
экономики предприятий, учета всего множества существенных взаимосвязей между
различными сторонами деятельности предприятий; в этих условиях анализ все более
приобретает черты системного в кибернетическом смысле слова;
• разработки комплекса
экономико-математических моделей, отражающих количественную характеристику
экономических процессов и задач, решаемых с помощью экономического анализа;
• совершенствования системы
экономической информации о работе предприятий;
• наличия технических средств (ЭВМ и
др.), осуществляющих хранение, обработку и передачу экономической информации в
целях экономического анализа;
• организации специального
коллектива аналитиков, состоящего из экономистов-производственников,
специалистов по экономико-математическому моделированию,
математиков-вычислителей, программистов-операторов и др.
Применение экономико-математических
методов в анализе предполагает использование методов элементарной математики,
классических методов математического анализа, методов математической
статистики, эконометрических методов, методов математического программирования
и др.
Методы элементарной математики
используются в обычных традиционных экономических расчетах при обосновании
потребностей в ресурсах, учете затрат на производство, разработке планов,
проектов, при балансовых расчетах и т.д.
Методы классической высшей
математики применяются в экономическом анализе как отдельно, так и в рамках
других методов (методов математической статистики, математического
программирования).
Наибольшее распространение из
математико-статистических методов в экономическом анализе получили методы
множественного и парного корреляционного анализа.
Эконометрические методы строятся на
синтезе трех областей знаний: экономики, математики и статистики. Основой
эконометрических методов является экономическая модель, под которой понимается
схематическое представление экономического явления или процесса с помощью
научной абстракции, отражения их характерных черт.
Наибольшее распространение в
современной экономике получил метод анализа экономики «затраты-выпуск». Это
матричные (балансовые) модели, строящиеся по шахматной схеме и позволяющие в
наиболее компактной форме представить взаимосвязь затрат и результатов
производства. Удобство расчетов и четкость экономической интерпретации-главные
особенности матричных моделей. Это важно при создании систем механизированной
обработки данных, при планировании производства продукции с использованием ЭВМ.
Математическое моделирование
экономических явлений и процессов дает возможность получить четкое
представление об исследуемом объекте, охарактеризовать и количественно описать
его внутреннюю структуру и внешние связи.
Экономико-математическое
моделирование работы предприятия должно быть основано на анализе его
деятельности и, в свою очередь, обогащать этот анализ результатами и выводами,
полученными после решения соответствующих задач.
Применение того или иного
математического метода в экономическом анализе опирается на методологию
экономико-математического моделирования хозяйственных процессов и научно
обоснованную классификацию методов и задач анализа.
По классификационному признаку
оптимальности все экономико-математические методы (задачи) подразделяются на
две группы: оптимизационные и неоптимизационные. Если метод или задача
позволяет искать решение по заданному критерию оптимальности, то этот метод
относят в группу оптимизационных методов. В случаях, когда поиск решения
ведется без критерия оптимальности, соответствующий метод относят к группе
неоптимизационных методов.
По признаку получение точного
решения все экономико-математические методы делятся на точные и приближенные.
Если алгоритм метода позволяет получить только единственное решение по
заданному критерию оптимальности или без него, то данный метод относят к группе
точных методов. В случае, когда при поиске решения используется стохастическая
информация и решение задачи можно получить с любой степенью точности,
используемый метод относят к группе приближенных методов. К группе приближенных
методов относят и такие, при применении которых не гарантируется получение
единственного решения по заданному критерию оптимальности.
Таким образом, используя только два
признака классификации, все экономико-математические методы делятся на четыре
группы:
) оптимизационные точные методы;
) оптимизационные приближенные
методы;
) неоптимизационные точные методы;
) неоптимизационные приближенные
методы.
Так, к оптимизационным точным
методам можно отнести методы теории оптимальных процессов, некоторые методы
математического программирования и методы исследования операций.
К оптимизационным приближенным
методам относятся отдельные методы математического программирования, методы
экономической кибернетики, методы математической теории планирования
экстремальных экспериментов, эвристические методы.
К неоптимизационным точным методам
относятся методы элементарной математики и классические методы математического
анализа, эконометрические методы.
К неоптимизационным приближенным
методам относятся метод статистических испытаний и другие методы математической
статистики.
Методы линейного программирования
применяются для решения многих экстремальных задач, с которыми довольно часто
приходится иметь дело в экономике. Решение таких задач сводится к нахождению
крайних значений (максимума и минимума) некоторых функций переменных величин.
Линейное программирование основано
на решении системы линейных уравнений (с преобразованием в уравнения и
неравенства), когда зависимость между изучаемыми явлениями строго
функциональна. Для него характерно математическое выражение переменных величин,
определенный порядок, последовательность расчетов (алгоритм), логический
анализ. Применять его можно только в тех случаях, когда изучаемые переменные
величины и факторы имеют математическую определенность и количественную
ограниченность, когда в результате известной последовательности расчетов
происходит взаимозаменяемость факторов, когда логика в расчетах, математическая
логика, совмещается с логически обоснованным пониманием сущности изучаемого
явления.
С помощью этого метода в промышленном
производстве, например, исчисляется оптимальная общая производительность машин,
агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных
величинах).
Методом линейного программирования
решается транспортная задача, т.е. задача рационального прикрепления
предприятий-потребителей к предприятиям-производителям.
В сельском хозяйстве метод линейного
программирования используется для определения минимальной стоимости кормовых
рационов при заданном количестве кормов (по видам и содержащимся в них
питательным веществам).
Все экономические задачи, решаемые с
применением линейного программирования, отличаются альтернативностью решения и
определенными ограничивающими условиями. Решить такую задачу - значит выбрать
из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный.
Важность и ценность использования в
экономике метода линейного программирования состоит в том, что оптимальный
вариант выбирается из значительного количества альтернативных вариантов. При
помощи других способов решать такие задачи практически невозможно.
Методы динамического
программирования применяются при решении оптимизационных задач, в которых
целевая функция или ограничения, или же и первое, и второе одновременно
характеризуются нелинейными зависимостями. Признаками нелинейности является, в
частности, наличие переменных, у которых показатель степени отличается от
единицы, а также наличие переменной в показателе степени, под корнем, под
знаком логарифма.
Примеры нелинейных зависимостей
достаточно обширны. Например, экономическая эффективность производства
возрастает или убывает непропорционально изменению масштабов производства.
Величина затрат на производство продукции возрастает в связи с увеличением
объема продукции, но не пропорционально.
Нелинейной связью характеризуется
величина износа производственного оборудования в зависимости от времени его
работы, удельный расход бензина (на 1 км пути) - от скорости движения
автотранспорта и многие другие хозяйственные ситуации. Например, себестоимость
с увеличением объема выпускаемой продукции понижается, но при нарушении
ритмичности производства она может и возрастать (за счет оплаты сверхурочных
работ в конце отчетного периода). Здесь затраты представляются нелинейной
функцией от объема производства.
Под исследованием операций
понимаются разработка методов целенаправленных действий (операций),
количественная оценка полученных решений и выбор из них наилучшего. Предметом
исследования операций являются экономические системы, в том числе
производственно-хозяйственная деятельность предприятий. Целью является такое
сочетание структурных взаимосвязанных элементов систем, которое в наибольшей
степени отвечает задаче получения наилучшего экономического показателя из ряда
возможных.
Теория игр как раздел исследования
операций - это теория математических моделей принятия оптимальных решений в
условиях неопределенности или конфликта нескольких сторон, имеющих различные
интересы. Теория игр исследует оптимальные стратегии в ситуациях игрового
характера. К ним относятся ситуации, связанные с выбором наивыгоднейших
производственных решений системы научных и хозяйственных экспериментов, с
организацией статистического контроля, хозяйственных взаимоотношений между
предприятиями промышленности и других отраслей. Формализуя конфликтные ситуации
математически, их можно представить как игру двух, трех и т.д. игроков, каждый
из которых преследует цель максимизации своей выгоды, своего выигрыша за счет
другого.
На промышленных предприятиях теория
игр может использоваться для выбора оптимального решения, например, при
создании рациональных запасов сырья, материалов, полуфабрикатов. В данном
случае противоборствуют две тенденции: увеличения запасов, в том числе и
страховых, гарантирующих бесперебойную работу производства, и сокращения запасов,
обеспечивающих минимизацию затрат на их хранение. В машиностроительном
производстве противоборствующими направлениями являются стремление к
максимальной экономии металла в конструкциях, с одной стороны, и обеспечение
необходимой прочности конструкций - с другой.
В сельском хозяйстве теория игр
может применяться при решении экономических задач, в которых оппозиционной
силой выступает природа, и когда вероятность наступления тех или иных событий
многовариантна или неизвестна.
Теория массового обслуживания исследует
на основе теории вероятностей математические методы количественной оценки
процессов массового обслуживания. Так, любое из структурных подразделений
промышленного предприятия можно представить как объект системы обслуживания.
Общей особенностью всех задач, связанных с массовым обслуживанием, является
случайный характер исследуемых явлений.
Матричные методы анализа, основанные
на линейной и векторно-матричной алгебре, применяются для изучения сложных и
высокоразмерных структур как на отраслевом уровне, так и на уровне предприятий
и объединений. Например, для выявления оптимального распределения продукции
между цехами предприятия, идущей на внутреннее потребление, и общим объемом
выпускаемой продукции при заданных параметрах прямых затрат и конечного продукта
(т.е. объемом реализации продукции).
Экономическая кибернетика
анализирует экономические явления и процессы в качестве очень сложных систем с
точки зрения законов и механизмов управления и движения информации в них.
Наибольшее распространение в экономическом анализе получили методы
моделирования и системного анализа.
Все перечисленные методы связаны с
достаточно трудоемкими вычислительными процедурами. В ряде случаев приходится
находить решение экстремальных задач при неполном знании механизма рассматриваемого
явления. Такое решение отыскивается экспериментально.
II.
ПРАКТИЧЕСКАЯ ЧАСТЬ
. С помощью методов анализа
количественного влияния факторов на изменение результативного показателя
определить влияние двух факторов (дневного товарооборота и количества дней
работы магазина) на обобщающий показатель - объём месячного товарооборота
План
|
Факт
|
|
1.
Объем дневной реализации, руб.
|
13000
|
14040
|
|
2.
Количество дневной работы за месяц, дн.
|
26
|
27
|
Q мес. = V
реал. х Дни
Метод цепных подстановок.
I. 1. Q
план = V реал. пл. х Дни
пл. = 13000 х 26 = 338000 руб.
. Q
усл. 1 = V реал. факт х Дни
пл. = 14040 х 26 = 365040 руб.
. Q
факт = V реал. факт х Дни
факт = 14040 х 27 = 379080 руб.
II. ∆ Q
(V реал.) = Q
усл. 1 - Q пл. = 365040 -
338000 = 27040 руб.
∆ Q
(Дни) = Q факт - Q
усл. 1 = 379080 - 365040 = 14040 руб.
III. ∆ Q
= ∆ Q (V
реал.) + ∆ Q (Дни) =
27040 + 14040 = 41080 руб.
∆ Q
= Q факт - Q
план = 379080 - 338000 = 41080 руб.
Метод абсолютных разниц.
I. Δ
V реал. = V
реал. факт - V реал. пл. = 14040
- 13000 = 1040 руб.
Δ Дни = Дни факт -
Дни пл. = 27 - 26 = 1 день.
II. ∆ Q
(V реал.)
= Δ V реал. х Дни пл. =
1040 х 26 = 27040 руб.
Δ Q
(Дни) = V реал. факт х Δ
Дни
= 14040 х 1 = 14040 руб.
III. ∆ Q
= ∆ Q (V
реал.) + ∆ Q (Дни) =
27040 + 14040 = 41080 руб.
Δ Q
= Q факт - Q
пл. = 379080 - 338000 = 41080 руб.
Метод относительных разниц.
I. Δ
V реал. % = V
реал. факт / V реал. пл. х 100% -
100%
Δ V
реал. % = 14040 / 13000 х 100% - 100% = 8%
Δ Дни % = Дни факт /
Дни пл. х 100% - 100%
Δ Дни % = 27 / 26 х
100% - 100% = 3,8462%
II. ∆ Q
(V реал.) = Q
пл. х Δ
V реал. % / 100%
∆ Q
(V реал.) = 338000 х
8% / 100% = 27040 руб.
Δ Q
(Дни) = (Q пл. + ∆ Q
(V реал.)) х Δ
Дни
% / 100%
Δ Q
(Дни) = (338000 + 27040) х 3,8462% / 100% = 14040 руб.
III. ∆ Q
= ∆ Q (V
реал.) + ∆ Q (Дни) =
27040 + 14040 = 41080 руб.
Δ Q
= Q факт - Q
пл. = 379080 - 338000 = 41080 руб.
Q
(V месячного
товарооборота)
+
41080 руб.
+
27040 (V реал.) + 14040
(Дни)
Вывод: За фактический период по сравнению с
плановым на предприятии объём месячного товарооборота вырос на 41080 руб., это
произошло в результате действия следующих факторов:
. Рост объёма дневной реализации привел к
увеличению к увеличению объёма месячного товарооборота на 27040 руб.
. Увеличение количества дней работы за месяц на
1 день привело за собой рост объёма дневной реализации на 14040 руб.
Таким образом, увеличение объёма месячного
товарооборота в первую очередь было связано с ростом объёма дневной реализации,
то есть с действием интенсивного фактора. Данная тенденция для предприятия
является положительной.
математический метод товарооборот
фонд
2. Определить влияние изменения
среднегодовой стоимости основных производственных фондов и фондоотдачи на
динамику объёма выпущенной продукции
|
Показатели
|
2002
год
|
2003
год
|
|
1.
Объем выпущенной продукции, тыс.руб.
|
105
000
|
105
500
|
|
2.
Среднегодовая стоимость основных фондов, тыс.руб.
|
205
000
|
209
000
|
|
3.
Фондоотдача, тыс.руб
|
0,5122
|
0,5048
|
Фо =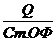
Метод цепных подстановок.
I. 1) Q 2002г. =  оф 2002г. х
Фо 2002г. = 205 000 х 0,5122 = 105 001 тыс.руб.
оф 2002г. х
Фо 2002г. = 205 000 х 0,5122 = 105 001 тыс.руб.
) Q усл.1 =  оф 2003г. х
Фо 2002г. = 209 000 х 0,5122 = 107049,8 тыс.руб.
оф 2003г. х
Фо 2002г. = 209 000 х 0,5122 = 107049,8 тыс.руб.
) Q 2003г. =  оф 2003г. х
Фо 2003г. = 209 000 х 0,5048 = 105 503,2 тыс.руб.
оф 2003г. х
Фо 2003г. = 209 000 х 0,5048 = 105 503,2 тыс.руб.
II. ∆Q ( оф) = Q усл.1 - Q 2002г. =
107 049,8 - 105 001 = 2048,8 тыс. руб.
оф) = Q усл.1 - Q 2002г. =
107 049,8 - 105 001 = 2048,8 тыс. руб.
∆Q (Фо) = Q 2003г. - Q усл.1 = 105
503, 2 - 107 049,8 = -1546,6 тыс.руб.
III. ∆Q = ∆Q ( оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
∆Q = Q 2003г. - Q 2002г. =
105 503,2 - 105 001 = 502,2 тыс.руб.
I. Δ оф =
оф =  оф 2003г. -
оф 2003г. -  оф 2002г. =
209000 - 205000 = 4000 тыс. руб.
оф 2002г. =
209000 - 205000 = 4000 тыс. руб.
Δ Фо = Фо 2003г. - Фо 2002г. =
0,5048 - 0,5122 = - 0,0074 тыс. руб.
II. ∆Q ( оф) = Δ
оф) = Δ оф х Фо
2002г. = 4000 х 0,5122 = 2048,8 тыс. руб.
оф х Фо
2002г. = 4000 х 0,5122 = 2048,8 тыс. руб.
∆Q (Фо) =  оф 2003г. х ΔФо = 209000
х (- 0,0074) = - 1546,6 тыс. руб.
оф 2003г. х ΔФо = 209000
х (- 0,0074) = - 1546,6 тыс. руб.
III. ∆Q = ∆Q ( оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
∆Q = Q 2003г. - Q 2002г. =
105 503,2 - 105 001 = 502,2 тыс.руб.
Метод относительных разниц.
I. Δ оф % =
оф % =  оф 2003г. /
оф 2003г. /  оф 2002г. х
100% - 100%
оф 2002г. х
100% - 100%
Δ оф % = 209000 / 205000 х 100% - 100%
= 1,9512%
оф % = 209000 / 205000 х 100% - 100%
= 1,9512%
Δ Фо % = Фо 2003г. /
Фо 2002г. х 100% - 100%
Δ Фо % = 0,5048 /
0,5122 х 100% - 100% = - 1,4447%
II. ∆Q ( оф) = Q 2002г. х Δ
оф) = Q 2002г. х Δ оф % / 100%
оф % / 100%
∆Q ( оф) = 105001
х 1,9512% / 100% = 2048,8 тыс. руб.
оф) = 105001
х 1,9512% / 100% = 2048,8 тыс. руб.
∆Q (Фо) = (Q 2002г. + ∆Q ( оф)) х Δ Фо % / 100%
оф)) х Δ Фо % / 100%
∆Q (Фо) =
(105001 + 2048,8) х (-1,4447) / 100% = - 1546,6 тыс. руб.
∆Q = ∆Q ( оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
оф) + ∆Q (Фо) =
2048,8 - 1546,6 = 502,2 тыс.руб.
∆Q = Q 2003г. - Q 2002г. =
105 503,2 - 105 001 = 502,2 тыс.руб.
Q
(V произ.)
+
502, 2 тыс. руб.
+
2048, 8 тыс. руб. - 1546,6 тыс. руб.
Вывод: За два года на предприятии объём
выпушенной продукции вырос на 502, 2 тыс. руб., это произошло в результате
действия двух факторов:
. Снижение фондоотдачи привело к уменьшению
объёма произведенной продукции на 1546, 6 тыс. руб.
. Увеличение стоимости ОФ повлекло за собой рост
объёма продукции на 2048,8 тыс. руб.
Таким образом, увеличение объёма выпушенной
продукции был связан с ростом среднегодовой стоимости основных фондов, то есть
с действием экстенсивного фактора. Данная тенденция для предприятия является
положительной.
3. Проанализировать выполнение
предприятием плана по реализации продукции в поквартальном разрезе, нарастающим
итогом и в целом за год
|
Квартал
|
План
|
Факт
|
Абсол.
откл.
|
Относит.
откл.
|
Нараст.
итогом план
|
Нараст.
итогом факт
|
Абсол.
откл.
|
Относит.
откл.
|
|
I.
|
5 300
|
4 800
|
- 500
|
- 9,4340
|
5
300
|
4
800
|
-
500
|
-
9,4340
|
|
II.
|
5 100
|
4 950
|
- 150
|
- 2, 9412
|
10
400
|
9
750
|
-
650
|
-
12,3752
|
|
III.
|
5 600
|
5 300
|
- 300
|
-
5, 3571
|
16
000
|
15
050
|
-
950
|
-
17,7323
|
|
IV.
|
5 450
|
5 300
|
- 150
|
-
2, 7523
|
21
450
|
20
350
|
-
1100
|
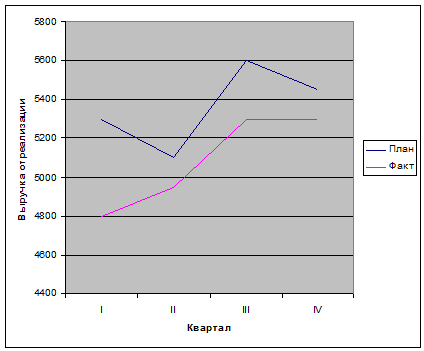
Вывод: За I
квартал фактическая выручка уменьшилась на 500 тыс. руб. или на 9,4340 %.по
сравнению с плановой.
За II
квартал фактическая выручка уменьшилась на 150 тыс. руб. или на 2,9412% по
сравнению с плановой.
За III
квартал фактическая выручка уменьшилась на 300 тыс. руб. или на 5,3571% по
сравнению с плановой.
За IV
квартал фактическая выручка уменьшилась на 150 тыс. руб. или на 2,7523% по
сравнению с плановой.
За I
полугодие фактическая выручка уменьшилась на 650 тыс. руб. или на 12,3752% по
сравнению с плановой.
За II
полугодие фактическая выручка уменьшилась на 450 тыс. руб. или на 8,1094% по
сравнению с плановой.
За год фактическая выручка уменьшилась на 1100
тыс. руб. или на 20,4846% по сравнению с плановой.
4. Рассчитать среднее число дней и
часов, отработанных одним работником предприятия за год, среднюю
продолжительность рабочего дня на предприятии за год, а также проанализировать
динамику этих показателей за два года (по абсолютному и относительному отклонению)
|
Показатели
|
Базисный
год
|
Отчетный
год
|
Абсолютное
отклонение
|
Относительное
отклонение
|
|
Среднесписочное
число работников, чел.
|
531
|
536
|
5
|
0,9416
|
|
Отработано
работниками за год, тыс. чел-дн.
|
153
|
158
|
5
|
3,2680
|
|
Отработано
работниками за год, тыс. чел-час.
|
1120
|
1128
|
8
|
0,7143
|
|
Среднее
число дней, отработанных одним работником, тыс. чел-дн.
|
0,2881
|
0,2948
|
0,0067
|
2,3256
|
|
Среднее
число часов, отработанных одним работником, тыс. чел-час.
|
2,109
|
2,104
|
-0,005
|
-0,2371
|
|
Средняя
продолжительность рабочего дня, час.
|
7,3204
|
7,1370
|
-0,1834
|
-2,5053
|
Вывод: Среднее число дней, отработанных одним
работником предприятия за базисный год составило 0,2881 тыс. чел.-дн., а за
отчетный год составило 0,2948 тыс. чел.-дн. Среднее число дней отработанных
одним работником предприятия за отчетный год превысило базисный год на 0,0064
тыс. чел.-дн., что в относительном выражении составило 2,3256%. Среднее число
часов, отработанных одним работником за базисный год составило 2,109 тыс.
чел.-час, а за отчетный год составило 2,104 тыс. чел.-час. Среднее число часов,
отработанных одним работником за отчетный год ниже базисного года на 0,005 тыс.
чел.-часов, что в относительном выражении составило 0,2371%. Средняя
продолжительность рабочего дня за базисный год составило 7,3204 часа, а за отчетный
год составило 7,1370 часа. Средняя продолжительность дня за отчетный период
ниже базисного на 0,1834, что в относительном выражении составило 2,5053% .
5. Проанализировать изменение
основных производственных фондов за год (сгруппировать по назначению, вычислить
удельный вес каждой группы на начало и конец года, рассчитать соотношение
активной и пассивной частей основных производственных фондов)
|
Производственные
фонды (актив)
|
|
Наименование
|
На
начало года
|
На
конце года
|
|
Холодильные
машины и устройства
|
210
|
218
|
|
Транспортные
средства
|
175
|
163
|
|
Кассовые
аппараты
|
23
|
31
|
|
Измерительные
приборы
|
142
|
143
|
|
Итого производственных фондов
|
550
|
555
|
|
Удельный
вес (%)
|
44,97
|
32,04
|
|
Непроизводственные
фонды (пассив)
|
|
Павильоны
|
476
|
|
Торговые
склады
|
273
|
275
|
|
Подъездные
пути
|
84
|
87
|
|
Передаточные
устройства
|
174
|
183
|
|
Инвентарь
|
142
|
156
|
|
Итого непроизводственных фондов
|
673
|
1177
|
|
Удельный
вес (%)
|
55,03
|
67,96
|
|
Итого основных фондов
|
1223
|
1732
|
|
Абсолютное
отклонение
|
-123
|
-622
|
|
Относительное
отклонение
|
-18,2764
|
-52,8462
|
Вывод: Удельный вес производственных фондов
составляет на начало года 44,97%, на конец года - 32,04%. Удельный вес
непроизводственных фондов составляет на начало года 55,03%, а на конец года
67,96. На начало года активная часть меньше чем пассивная на 123 тыс. руб., что
в относительном выражении составляет 18,2764%. На конец года активная часть
меньше пассивной на 622 тыс. руб., что в относительном выражении составляет
52,8462%.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.
Баканов М.И., Мельник М.В., Шеремет А.Д. Теория экономического анализа:
Учебник. - М.: Финансы и статистика, 2005. (Рек. Мин-вом обр-ния РФ).
.
Басовский Л.Е. Теория экономического анализа: Учебное пособие. - М.: Инфра-М,
2005. (Рек. Мин-вом обр-ния РФ).
3.
Шеремет А.Д. Теория экономического анализа: Учебник. - М.: Инфра-М, 2005. (Рек.
Мин-вом обр-ния РФ).