Теория игр и ценовые войны

Теория игр и ценовые войны

Содержание

Введение

.        Ценовые войны в теории игр.

.1 Сущность и сферы применения аппарата теории игр

.2 Понятие олигополии

.3 Понятие дуополии

.4 Ценовые войны дуополий

.5 Стратегии олигополий и теория игр

.6 Ценовая война и ее последствия в условиях олигополии.

. Поведение компаний в ценовой войне.

Заключение

Список источников

Введение

Существенные разработки связанные с применением теории игр в экономическом анализе принадлежат Дж. фон Нейману и О. Моргенштерну, которые проводили свои исследования в 70 -е гг. ХХ ст. С тех пор эту теорию с успехом применяют при решении самых различных экономических задач - при оптимизации ассортимента, при обосновании целесообразности проведения маркетинговых исследований, в теории массового обслуживания и т.п. Вместе с тем анализ литературных источников свидетельствует, что она практически не применяется для обоснования ценовых решений, хотя есть все основания считать условия, в которых они принимаются соответствующими условиям, на которых построена теория игр. Действительно принятия ценовых решений обычно требует выбора между различными стратегиями и осложнено тем, что лицо, принимающее эти решения должно предусмотреть будущие события которые могут повлиять на ожидаемый результат. Влияние не прогнозированных событий особенно усиливается в периоды экономических кризисов и посткризисной депрессии, что характерно для экономики. В таких условиях актуализируется проблема поиска и применения адекватных методов ценообразования которые учитывали бы последствия различных вариантов установления цены и позволяли выбрать оптимальный вариант. На мой взгляд, эта проблема может быть решена именно с помощью экономико-математических методов в частности теории игр.

Основная цель работы - изучить применение теории игр к ценовым войнам.

Основные задачи: изучить общие сведения теории игр и ее применения, определить понятия основных структур рынка в ценовых войнах (олигополия, дуополия), исследовать практическое применение аппарата теории игр для моделирования поведения компаний в ценовой войне.

1.      Ценовые войны в теории игр

Стратегическое поведение в ценовых войнах адекватно отражают модели теории игр. Ключевой особенностью любой игры является зависимость результата не только от собственных действий, но и от действий других участников. Поэтому, принимая решение, участники игры должны учитывать возможные ответы конкурентов.

1.1 Сущность и сферы применения аппарата теории игр

Среди всех формальных методов моделирования теория игр является наиболее конкретной. Она базируется на теории вероятности и предусматривает конструирование различных типов поведения субъектов.

Как математическая дисциплина теория игр зародилась в XVII в., но в течение 300 лет почти не развивалась. Впервые она была изложена Дж. фон Нейманом и О. Монгенштерном в 1944 в работе "Теория игр и экономическое поведение". С самого начала своего развития она была направлена на решение экономических задач. Позже ее начали применять в других отраслях, связанных с конфликтами. Теоретико-игровые методы принятия оптимальных решений имеют широкое применение в медицине, в экономическом и социальном планировании и прогнозировании, а также в других вопросах науки и техники.

В 1994 г. Нобелевскую премию по экономике получили Джон Нэш (США), Джон Харсаньи (США), Рейнхард Зелтен (Германия) за труды в области теории игр.

Игра представляет собой совокупность правил, описывающих формальную структуру ситуации соревнования и уточняющих: альтернативы (стратегии), из которых должны сделать выбор игроки; информацию доступную игроку при выборе им варианта; выигрыш, получаемый каждым игроком в конце игры. [3]

Игры классифицируют в зависимости от выбранного критерия: по количеству игроков, по количеству стратегий, по свойствам функций выигрыша и по возможностям предварительных переговоров между игроками.

В зависимости от количества игроков различают игры с двумя, тремя и более участниками. Теорию оптимизации, например, можно рассматривать как теорию игр с одним игроком. Можно исследовать также игры с бесконечным количеством игроков.

По количеству стратегий различают:

Конечные;

Бесконечные игры.

В конечных играх количество возможных стратегий отображаются конечным числом (подбрасывание монеты - две стратегии, подбрасывание кубика - шесть стратегий). Стратегии в конечных играх называют чистыми стратегиями. В бесконечных играх количество стратегий бесконечно. [2]

По свойствам функций выигрыша (платежных функций) теорию игр делят на три вида:

. Игра с нулевой суммой, или антагонистическая игра - игра, в которой выигрыш одного из игроков равен проигрышу другого;

. Игры с постоянной разницей - игра, когда игроки выигрывают и проигрывают одновременно и им выгодно действовать вместе;

. Игра с ненулевой суммой - это игра, в которой имеются конфликт и согласованное действие игроков.

По возможности предварительных переговоров между игроками различают кооперативные и некооперативных игры. Кооперативная игра - это игра, в которой до ее начала участники образуют коалиции и принимают соглашения о своих стратегиях. Некооперативное игра - игра, в которой игроки не могут координировать свои стратегии. Примером кооперативной игры может стать ситуация лоббирования в парламенте принятие решения заинтересованных в нем участников путем голосования [ 1].

Теория игр - раздел прикладной математики, который используется в социальных науках, биологии, политических науках, компьютерных науках (главным образом для искусственного интеллекта) и философии. В социальных науках аппарат теории игр применяется в психологии для анализа торговых соглашений и переговоров, а также для изучения принципов формирования коалиций и т.п..

Теория игр пытается математически зафиксировать поведение в стратегических ситуациях, в которых успех субъекта, делающего выбор, зависит от выбора других участников.

Основной задачей применения игр в человеческой деятельности является обучение. Считается, что первые серьезные игры взрослых людей были военными играми, в частности, военные маневры - это глобальные игры по особым правилам, а игра в шахматы является предком современных имитационных игр. Современные деловые игры берут начало с 1930- х годов, когда в СССР вводилась научная организация труда для решения сложных управленческих задач. В конце 50-х годов деловые игры получили новое рождение в США в связи с решением, опять же, военных проблем. [2]

Значение многих игр неожиданно приобретает глобальные масштабы и не позволяет игнорировать их социально-психологическое значение. Например, кубик Рубика, по мнению автора, дает серьезные уроки логики, учит людей быть более осторожными, бросив своеобразный вызов европейской традиции двухмерного мышления и общения, поскольку заставляет смотреть и думать трехмерно: мы должны постоянно учитывать, что происходит на обратной стороне.

Считается, что сочетание обучения и игры может быть основой новой методологии образования, благодаря которой "человек перестает быть каторжником, прикованным к парте", а Homo Ludens (человек играющий), живущий в каждом из нас. [3]

Поэтому среди наиболее употребляемых средств интерактивных технологий, которые используются в высшей школе, есть игровые технологии обучения. Рассматривая применение игровых технологий в учебном процессе, исследователи называют их "играми взрослых" и рассматривают как интерактивные методы обучения [3].

Теория игр - теория индивидуальных рациональных решений, принимаемых в условиях недостаточной информации относительно результатов этих решений. Теория исследует взаимодействие индивидуальных решений при некоторых предположениях, касающихся принятия решений в условиях риска, общих условий окружающей среды, кооперативного или некооперативного поведения других индивидов. В то время, как традиционная микроэкономическая теория предлагает теорию принятия решений в условиях определенности, очевидно, что рациональному индивиду приходится принимать решения в условиях неопределенности и взаимодействия.

Игра является универсальной формой, в которой происходят мощные процессы самоопределения, самовыражения, самоутверждения и самопроверки. Игры развивают сообразительность, логику, пространственное воображение, т.е. учат творчеству. Поэтому игры используются в различных областях общественной жизни, в частности, теория игр является разделом математики, в котором изучаются модели принятия оптимальных решений в условиях конфликта.

Теория игр является одним из математических инструментов. Поскольку дилемма характеризует такие ситуации, когда двум игрокам нужно сотрудничать, но при этом существует очень сильный стимул предать друг друга, то ее применение получает распространение в политике, при исследовании экономики и других социальных науках.

1.2 Понятие олигополии

Олигополия (oligopoly) - это структура рынка, в которой несколько продавцов доминируют в продаже продукта и где вход дополнительных продавцов или затруднен или невозможен [4]. Продукт, который продается на олигопольном рынке, может быть как стандартизированным, так и дифференцированным. Олигополистические рынки типично контролируются от 2 до10 фирмами, держат 50 % и более от объема продажи товаров. Примером для Соединенных Штатов является производство оборудования для фотографии.

На олигополистическом рынке фирма имеет возможность влиять на цены благодаря своей значительной части в общем объеме продаж товаров. Олигополисты знают, что любые вмешательства в цены или объемы приведут к нарушению равновесия на всем рынке. Это потому, что соперники начнут реагировать на изменения. В связи с этим индивидуальные продавцы при принятии решений на олигополистическом рынке должны иметь в виду реакцию своих соперников.

Во многих случаях олигопольний рынок защищен барьерами входа. Естественная олигополия (natural oligopoly) - существует, когда несколько фирм могут удовлетворять полностью рыночные потребности. В такой отрасли малые фирмы должны быть слитыми со своими соперниками. Однако более крупные фирмы будут применять возможность контроля над ценами для того, чтобы вытолкнуть малые фирмы с рынка. Например, в России к таким отраслям относятся переработка нефти, металлургия.

Картели (cartel) - группа фирм, действующих совместно для координации решений относительно объемов производства и контроля за ценами как будто они были единственной монополией. [4]

Главная проблема картелей - это координация решений между членами и применение ограничений к участникам (Евросоюз можно рассматривать как глобальный картель).

теория игра дуополия олигополия

1.3 Понятие дуополии

Дуополия (duopoly) - это рыночная структура, в которой есть два защищенных от входа продавца, которые являются единственными производителями стандартизированного продукта не имеющего близких заменителей [4]. Модель дуополии удобно использовать для объяснения, как рассуждения отдельного олигополиста, относительно возможной реакции соперника, влияют на состояние рынка. Классическая модель дуополии была исследована еще в 1838 году французским экономистом А. Курно (Augustin Cournot). Эта модель предполагает, что:

) каждый из двух продавцов делает предположение, что их соперники будут всегда поддерживать объем фиксированным на текущем уровне;

) продавцы не делают выводов из своих ошибок.

Современная демонстрация равновесия Курно происходит с помощью кривых реакции. Кривые реакции (reaction curves) - показывают максимизируемую прибыль от объема товаров, производимых одной фирмой при данном объеме производства ее соперника (рис. 1). Кривая реакции 1 показывает максимизируемую прибыль от объема продаж производителя В как функцию объема продаж производителя А. Если А принимает решение производить QA1, то рассчитывает, что В будет производить QB1. При объеме производства QB1 фирма А будет производить QA2 и т.д. Наконец фирмы достигнут в своих ожиданиях равновесия в точке Е с объемами QA3, QB2. Это и будет точка равновесия Курно. [4]

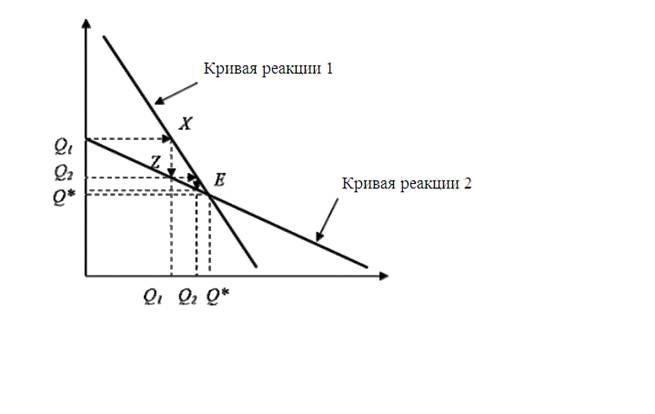
Рис. 1. Модель Курно в объяснении равновесия дуополии

1.4 Ценовые войны дуополий

Равновесие Курно предполагает, что каждая фирма верит, что их конкуренты всегда будут поддерживать текущий уровень производства. Любые другие предположения изменяют состояние равновесия. Если предположить, что соперники будут настойчиво поддерживать свои текущие цены, то оба соперника будут последовательно уменьшать цену продукта в попытке отобрать потребителей от своего конкурента. Равновесие достигается, когда ни одна из фирм не может уже выиграть от уменьшения цены, а экономическая прибыль равна 0. Поскольку каждая фирма предполагает, что соперник поддерживает текущую цену, оба теряют стимулы к любому изменению цены, даже к ее увеличению. В целом равновесие на олигопольном рынке зависит от того, какие предположения относительно поведения соперников делают фирмы олигополисты.

То, что приведено выше, фактически и есть ценовой войной - явление, которое довольно часто встречается в действительности. К сожалению для потребителей такие войны длятся недолго. Дуополист чаще договариваются относительно уровней цен и долей рынка для того, чтобы предотвратить ценовые войны и их негативное влияние на прибыль. [4]

1.5 Стратегии олигополий и теория игр

Поведение фирм на олигопольном рынке можно сравнить с поведением армий на войне. Они - соперники, их добыча - прибыль и оружие - это контроль над ценами, реклама и объемы предложения. Небольшое их количество побуждает фирмы к анализу реакций соперников на принимаемые решения. Они разрабатывают и внедряют определенные стратегии для того, чтобы увеличить долю рынка и прибыль. Ясно, что их интересы находятся в конфликте. Формальный инструмент для анализа поведения лиц и организаций с конфликтующими интересами дает теория игр.

Рассмотрим пример платежной матрицы для дуополии двух фирм А и В (табл. 1):

Таблица 1.

Анализ исходит из того, что менеджеры олигополий понимают, если они примут решение об уменьшении цены, их соперник может, либо оставить цену постоянной, или тоже пойти на ее уменьшение. Учитывая это, менеджеры вычисляют прибыль исходя из обоих случаев. Менеджеры обеих фирм считают прибыли, которые они могут получить, когда они уменьшат цену (1) или поддержат текущую цену (2). Они делают это для двух случаев: во-первых, когда их соперники тоже уменьшат цены, во-вторых, когда они оставят цены постоянными. В результате формируется матрица выигрыша (payoff matrix). Она показывает достижения и потери от каждой возможной стратегии для каждого типа реакции соперника. Менеджеры фирм могут преследовать различные стратегии в своих попытках максимизации прибыли. Можно представить, что каждая из стратегий - наихудшие возможные последствия. Для фирмы А это будет проигрыш в $ 10 000.

Стратегия, связанная с наименьшим уменьшением прибыли, называется стратегие1 максимина (maximin strategy). Она максимизирует минимально возможные достижения из всех возможных стратегий.

1.6 Ценовая война и ее последствия в условиях олигополии

Всеобщая взаимозависимость фирм на рынке олигополии проявляется и в условиях обострения конкурентной борьбы, и в условиях, когда достигается договоренность с другими олигополистами. Значительный вес олигополиста на рынке может вызвать его желание увеличить доходы путем увеличения своей доли на рынке. Поскольку кривая спроса фирмы олигополиста имеет отрицательный наклон, увеличить объем своих продаж можно только снизив цену продукции. Поэтому на рынке олигополии используют методы ценовой конкуренции, которые могут переходить в ценовые войны. [2] Ценовая война - это цикл постепенного снижения существующего уровня цен с целью вытеснения конкурентов с олигополистического рынка. Снижение цен имеет, однако, свои пределы. Оно будет продолжаться до тех пор, пока цена не упадет до уровня предельных издержек, а так как средние издержки постоянны, то

Р=МС=АТС,

где МС - предельные издержки, АТС - средние общие издержки. (рис. 2)

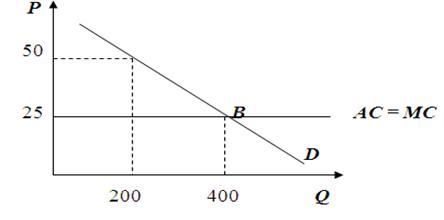
Рис. 2.

В точке В установится равновесие, потому что ни одна фирма не сможет снизить цену ниже, не понеся убытки. Цена фактически станет такой же, как и в условиях совершенной конкуренции, а экономическая прибыль в результате ценовой войны станет равной нулю. От ценовой войны выиграют потребители и проиграют производители. Поэтому ценовые войны быстротечны и в настоящее время бывают довольно редко. Конкурентная борьба одного олигополиста с другим чаще приводит к соглашениям, которые учитывают возможные действия других производителей. [4]

Ценовые войны не выгодны прежде всего самим олигополистам, и перед тем, как прибегнуть к ним, они должны учесть возможную реакцию конкурентов. Поэтому должны применяться определенные методики, которые позволяли бы разрабатывать поведение олигополиста с учетом возможной реакции конкурентов.

2. Поведение компаний в ценовой войне

Результаты действий участников в игре двух лиц отражаются в матрице выигрышей, которая показывает выигрыш каждого из участников при любой из возможных пар их стратегий.

Рассмотрим игру двух компаний Samsung и Apple . Будем считать, что в каждой из компаний есть два варианта решения (две возможные стратегии) - уменьшить цену с целью захватить дополнительную долю рынка или оставить цену без изменений. Для начала, предположим, что фирмы принимают решение одновременно и независимо друг от друга - то есть речь идет о разовой игре с одновременными ходами игроков.

Результат для каждой фирмы зависит не только от собственного решения, но и от того - какое решение примет конкурент. Если компания Samsung решит снизить цену (начать ценовую войну), она получит дополнительную прибыль (предположительно - 100 млн. дол.) при условии, что конкурент (компания Apple) оставит цену неизменной. Если конкурент также снизит цену, компания Samsung понесет убытки в размере 20 млн. дол. При условии, что компания Samsung оставит цену неизменной и так же поведет себя конкурент, прибыль не изменится. Наконец, если компания Samsung не изменит цену, а конкурент снизит цену, компания Samsung потеряет 50 млн. дол. прибыли. Предположим, что варианты и последствия решений для компании Apple аналогичны. Тогда условия игры можно представить в виде платежной матрицы:

Каждая клеточка платежной матрицы показывает размеры выигрышей участников при различных вариантах выбора стратегий. Первое число - выигрыш компании Samsung, второе число - выигрыш компании Apple.

Платежная матрица является удобным инструментом анализа возможных последствий игры. Если внимательно посмотреть на возможные стратегии компании Samsung и их последствия, можно увидеть, что выбор стратегии ценовой войны (уменьшить цену) является лучшим для компании Samsung независимо от того, какое решение выберет конкурент. Действительно, если компания Apple снизит цену, убытки компании Samsung при выборе уменьшения цены меньше, чем в случае неизменной цене. Если компания Apple решит оставить цену неизменной, то уменьшение цены принесет Samsung прибыль 100 млн. по сравнению с неизменной прибылью, если цена останется неизменной. Apple руководствуется аналогичными соображениями.

Стратегия, которая для игрока является лучшей по сравнению с другими независимо от того, какую стратегию выбрал оппонент, называется доминантной. Если все игроки имеют доминантные стратегии, результатом игры будет состояние, которое называют доминантной равновесием.

В рассматриваемой игре состояние доминантного равновесия для обеих фирм является худшим по сравнению со случаем, если бы обе фирмы оставили цену без изменений. Такой вариант был бы возможным, если бы фирмы договорились между собой (образовали бы картель). При независимом принятии решений, они окажутся в состоянии ценовой войны, которое является проигрышным для обоих.

Ситуация и состояние равновесия в играх может существенно измениться, если участники игры знают, что им придется играть с соперником не один, а много раз. Можно рассмотреть случай, когда в ситуации возможной ценовой войны сторонам удалось договориться между собой и образовать картель. Однако если игра одноразовая, у каждого участника есть стимул нарушить картельное соглашение и в конце концов стороны придут в состояние доминантного равновесия - то есть ценовой войны.

Все может измениться, если фирмы конкурируют постоянно, то есть игровая ситуация повторяется, причем, очень важно - повторяется неизвестное количество раз. Если одна из комапний нарушит картельное соглашение, то другая - в следующей партии, как минимум, также будет вести ценовую войну. Ситуацию можно представить следующим образом - выигрыш от нарушения картеля составляет 100 млн. дол., но во всех последующих играх компания будет нести потери в размере 20 млн. дол. Такие рассуждения (если наказание за нарушение договора является неотвратимым) могут заставить обе компании придерживаться картельного соглашения.

Более того, бесконечная повторяемость партий, может заставить конкурирующие компаний перейти от стратегии ценовых войн к завышению цен даже без явного сговора между собой. Следует отметить, что это справедливо только для случая, когда неизвестно - сколько еще партий придется сыграть. Если количество партий известно и ограничено, то результаты будут такими же, как и в разовых играх.

Заключение

Несовершенная конкуренция рынков несет в себе как элементы монополии, так и совершенной конкуренции. На таких рынках фирмы имеют некоторое влияние на цены. Они испытывают конкурентное движение со стороны существующих или потенциальных продавцов. На рынках монополистической конкуренции многие фирмы продают продукт, который отличается у каждого продавца. В таких ситуациях возможен свободный вход в рынок.

Олигополистические рынки имеют только несколько продавцов, и вход новых участников затруднен или вовсе невозможен. Продукт может быть стандартизированным, или дифференцированным между продавцами. Фирмы, которые работают в таких условиях, испытывают взаимозависимость с конкурентами. Эффект на олигопольном рынке проявляется в возможности для нескольких фирм обслуживать рынок в целом, при условии низких средних издержек по сравнению с этим показателем у большего числа небольших фирм.

Дуополия - это рыночная структура, в которой работает только два продавца, защищенных барьерами входа. Равновесие на дуопольном и олигопольном рынках зависит от решений, которые принимаются фирмами относительно того, какой будет реакция их соперников на изменения в ценах и объемах производства. Ценовая война на олигополистических рынках побуждает к уменьшению цен.

Для анализа олигополистического соперничества применяют теорию игр. Платежная матрица демонстрирует последствия любой стратегии, например, снижение цен для каждой возможной реакции конкурентов. Стратегия максимина является одним из средств предотвращения уменьшения возможных потерь.

Список источников

1.   Таха Х.А. Введение в исследование операций/Х.А. Таха. - М.: Вильямс, 2005. - 912 с.

2.      Фрейдина, Е.В. Исследование систем управления: учеб. пособие / Е.В. Фрейдина; под ред. Ю.В. Гусева. - М.: ОМЕГ А-Л, 2009. - 368 с.

3.         Грег Тейн, Джон Брэдли Торговые войны: Битва за успех на прилавках и онлайн. - М.: Альпина Паблишер, 2013. - 315 с.

4.      В. Бусыгин, Е. Желободько, С. Коковин, А. Цыплаков. Микроэкономический анализ несовершенных рынков. Режим доступа: <http://www.allmath.ru/appliedmath/micro/micro20/micro.htm>

.        Фелькер Р. Использование теории игр в практике управления. Режим доступа: <http://www.cfin.ru/management/game_theory.shtml>

.        Платежная матрица. Нижняя и верхняя цена игры. Режим доступа: http://matmetod-popova.narod.ru/themePO.htm

.        Элементы теории игр. Режим доступа: <http://emm.ostu.ru/lect/lect5_P.html>