Расчет вероятности событий
Контрольная
работа
по
курсу Теория вероятностей
Задача 1
Вероятность
появления поломок на каждой из 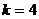 соединительных линий равна
соединительных линий равна 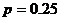 . Какова
вероятность того, что хотя бы две линии исправны?
. Какова
вероятность того, что хотя бы две линии исправны?
Решение: В данном
случае имеется последовательность испытаний по схеме Бернулли, т.к. испытания
независимы, и вероятность успеха (соединительная линия будет исправна) р=1-0,25=0,75 одинакова
во всех испытаниях. Тогда по формуле Бернулли при n=4, р=0,75,
q=1-p=1-0,75=0,25 найдем вероятности того, что исправны две, три и четыре
линии:
4(4) = pn
= 0.754 = 0.3164
По условию задачи
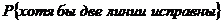 =
= 
Тогда найдем вероятность того, что
исправных линий будет не меньше двух (хотя бы две), по формуле:
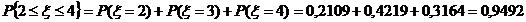
Задача 2
вероятность гипергеометрический
дискретный величина
В одной урне  белых шаров
и
белых шаров
и 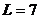 черных
шара, а в другой -
черных
шара, а в другой - 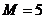 белых и
белых и 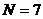 черных. Из
первой урны случайным образом вынимают
черных. Из
первой урны случайным образом вынимают 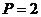 шара и опускают во вторую урну.
После этого из второй урны также случайно вынимают
шара и опускают во вторую урну.
После этого из второй урны также случайно вынимают 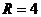 шара. Найти
вероятность того, что все шары, вынутые из второй урны, белые.
шара. Найти
вероятность того, что все шары, вынутые из второй урны, белые.
Решение:
Введем следующие обозначения для
событий:
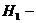 из первой урны переложили два белых
шара
из первой урны переложили два белых
шара
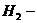 из первой урны переложили один белый
шар и один черный
из первой урны переложили один белый
шар и один черный
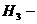 из первой урны переложили два черных
шара
из первой урны переложили два черных
шара
Так как других вариантов вытащить из
первой урны два шара нет, эти события составляют полную группу событий, и они
несовместны. Найдем вероятности этих событий по формуле гипергеометрической
вероятности:
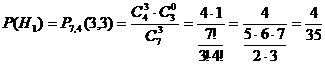
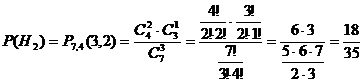
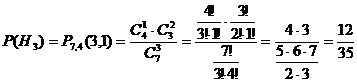
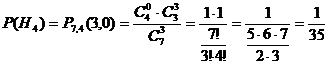
Введем событие А - после
перекладывания из второй урны вытащили 2 белых шара. Вероятность этого события
зависит от того, что во вторую урну переложили из первой. Найдем условные
вероятности:
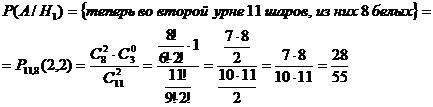
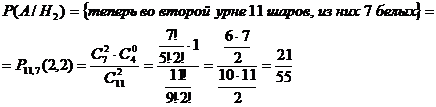
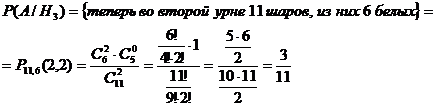
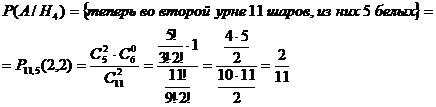
Теперь найдем вероятность события А
по формуле полной вероятности:
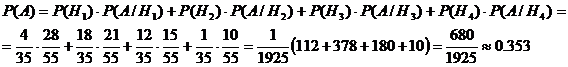
Задача 3
В типографии имеется 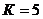 печатных
машин. Для каждой машины вероятность того, что она работает в данный момент,
равна
печатных
машин. Для каждой машины вероятность того, что она работает в данный момент,
равна 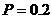 . Построить
ряд распределения числа работающих машин, построить функцию распределения этой
случайной величины, найти математическое ожидание, дисперсию, а также
вероятность того, что число работающих машин будет не больше
. Построить
ряд распределения числа работающих машин, построить функцию распределения этой
случайной величины, найти математическое ожидание, дисперсию, а также
вероятность того, что число работающих машин будет не больше 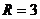 .
.
Решение:
В этой задаче x - дискретная
случайная величина, принимающая значения 0,1,2,3,4,5. Чтобы построить ряд
распределения х, требуется найти вероятности, с которыми она принимает эти
значения. В данном случае имеется последовательность испытаний по схеме
Бернулли, т.к. испытания независимы, и вероятность успеха р=0,2 одинакова во
всех испытаниях (успех - печатная машина работающая). Тогда по формуле Бернулли
при n=5, р=0,2, q=1-p=1-0.2=0.8:
5(0) = (1-p)n
= (1-0.2)5 = 0.32775(1) = np(1-p)n-1 =
5(1-0.2)5-1 = 0.4096
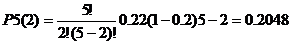
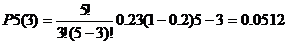
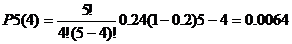 5(5) = pn
= 0.25 = 0.00032
5(5) = pn
= 0.25 = 0.00032
Теперь построим ряд распределения:
|
Значения
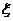 012345 012345
|
|
|
|
|
|
|
|
вероятность
|
0,3277
|
0,4096
|
0,2048
|
0,0512
|
0,0064
|
0,00032
|
Найдем математическое ожидание по формуле:
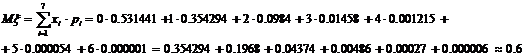
Найдем дисперсию:
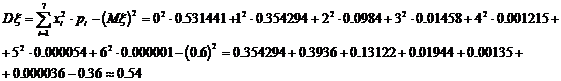
Выпишем в аналитическом виде функцию
распределения:
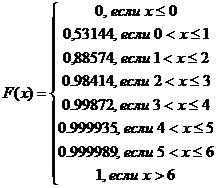
Найдем вероятность того, что число
работающих машин будет не больше 3:
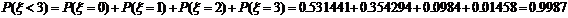
Задача 4
Непрерывная случайная величина
задана ее функцией распределения:
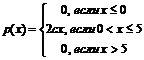 .
.
Найти параметр С, функцию
распределения, математическое ожидание, дисперсию, а также вероятность попадания
случайной величины в интервал 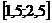 и квантиль порядка
и квантиль порядка 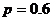
Решение:
Найдем параметр С из уравнения  . Так как
плотность на разных интервалах задана разными функциями, разбиваем область
интегрирования на соответствующее количество интервалов.
. Так как
плотность на разных интервалах задана разными функциями, разбиваем область
интегрирования на соответствующее количество интервалов.
 , тогда
, тогда 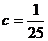
Найдем функцию распределения по
формуле: 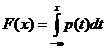 . Так как
плотность распределения задается разными выражениями в зависимости от
интервала, функция распределения так же будет задаваться разными выражениями на
этих интервалах:
. Так как
плотность распределения задается разными выражениями в зависимости от
интервала, функция распределения так же будет задаваться разными выражениями на
этих интервалах:
если 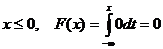
если 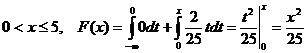
если 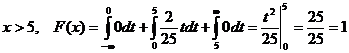 .
.
Таким образом, можно записать
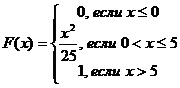
Найдем математическое ожидание по
формуле:
 .
.

Дисперсию находим по формуле:
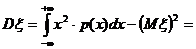
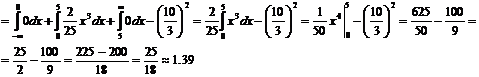
Вероятность попадания случайной
величины в интервал 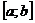 найдем по
формуле
найдем по
формуле
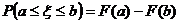 .
.
В нашем случае
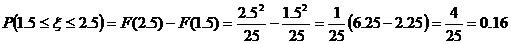
Найдем квантиль порядка 0,6: это
решение уравнения 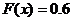 :
:  этот корень
не попадает в интервал, где функция распределения принимает значения от 0 до 1.
Квантиль один:
этот корень
не попадает в интервал, где функция распределения принимает значения от 0 до 1.
Квантиль один: 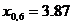
Задача 5
Суточное потребление электроэнергии
исправной печью является случайной величиной, распределенной по нормальному
закону со средним 1000 кВт/ч и СКО 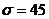 . Если суточное потребление превысит
1100 кВт, то по инструкции печь отключают и ремонтируют. Найти вероятность
ремонта печи. Каким должно быть превышение по инструкции, чтобы вероятность
ремонта печи была равна 0,02?
. Если суточное потребление превысит
1100 кВт, то по инструкции печь отключают и ремонтируют. Найти вероятность
ремонта печи. Каким должно быть превышение по инструкции, чтобы вероятность
ремонта печи была равна 0,02?
Решение:
Пусть 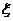 - суточное потребление
электроэнергии исправной печью. По условию задачи надо найти
- суточное потребление
электроэнергии исправной печью. По условию задачи надо найти 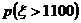 .
.
Сначала найдем вероятность того, что
суточное потребление не превысит 1100 кВт. Вероятность того, что Х примет
значение, принадлежащее интервалу 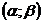 , найдем по формуле
, найдем по формуле
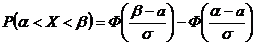 .
.
Тогда
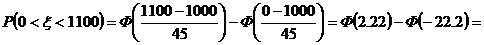
т.к. функция Ф - нечетная
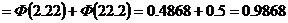
Тогда вероятность того, что суточное
потребление превысит 1100 кВт, и печь отключат, и будут ремонтировать, равна 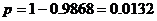
Для решения второй части задачи
обозначим переменной t величину превышения суточного потребления электроэнергии
по инструкции, чтобы вероятность ремонта печи была равна 0,02.
Тогда вероятность того, что суточное
потребление электроэнергии не превысит величину (1000+t) равна 1- 0,02=0,98.
Для нахождения t нам надо решить
уравнения вида:
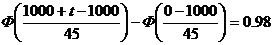
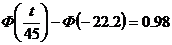
т.к. функция Ф(х) - нечетная
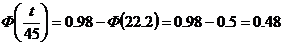
найдя значение функции Лапласа в
таблице, имеем:
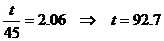
Таким образом, чтобы вероятность
ремонта печи была равна 0,02, суточное потребление должно превысить 1092,7 кВт.