Применение математических моделей в логистике
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
"Курганский
государственный университет"
Кафедра
математического анализа
Специальность
математика 010101
Дипломная
работа
Применение
математических моделей в логистике
Студент
группы № М-5318
Дахина
Л.Р.
Руководитель:
канд. физ.- мат. наук, доцент
Ионин
Л.Д.
Заведующий
кафедрой математического анализа
канд.
физ.- мат. наук, доцент
Гаврильчик
М.В.
Курган 2013
г.
Содержание
Введение
. Развитие логистики как науки и её
практическая реализация
. Математические модели в логистике
.1 Математический анализ в логистике
.1.1 Модель, определяющая
оптимальный размер партии поставки
.1.2 Модель, определяющая
оптимальный размер партии поставки при периодическом поступлении и равномерном
расходе ресурсов
2.1.3 Модель определения места
дислокации базы снабжения
.1.4 Модель межотраслевого баланса
.2 Гармонический анализ в логистике
.3 Теория вероятностей в логистике
.3.1 Нормальный закон распределения
вероятностей
.3.2 Экспоненциальный закон
распределения вероятностей
.3.3 Биномиальный закон
распределения вероятностей
.3.4 Сравнение законов распределения
вероятностей. Критерий согласия
.4 Математическая статистика в
логистике
. Применение математических моделей
в логистических задачах
Заключение
Список использованных источников
Приложения
Введение
Логистика как наука и практическая деятельность
стала неотъемлемой частью и инструментом современной экономики. По своей
сущности логистика носит универсальный характер, т.к. все субъекты
интегрированного рынка занимаются логистикой и используют логистические методы
управления производством и торговлей.
Для того, чтобы грамотно принимать
управленческие решения, необходимо знать приемы и методы получения основы для
выбора решений. Часто опыт и, так называемый, здравый смысл недостаточны для
принятия рациональных решений. Следует использовать научный подход к проблеме.
В большинстве случаев на помощь приходит прикладная математика, знание которой
для специалиста-менеджера или специалиста-логистика просто необходимо.
Управление есть тот инструмент, который
обеспечивает системность логистических процессов и их результативность, а
вместе с этим - результативность производственно-коммерческой деятельности.
Результативность в логистике выражается количественно, и вследствие этого
управление включает математические модели.
Таким образом, при рассмотрении математических
моделей в логистике исходным положением являются теория и практика управления.
При этом следует иметь в виду, что в числе величин, которыми оперирует
математика в логистике, важное место занимают стоимостные, т. е. экономические,
параметры:
) стоимость выполнения заказа (поставки);
2) стоимость содержания единицы запаса за
определенный период;
) постоянные (условно-постоянные)
расходы;
) стоимость перевозки единицы груза;
) убытки от отказа в обслуживании;
) убытки от простоя транспортных или иных
технических средств;
) потери от дефицитов товаров.
Перечисленные параметры конкретизируются в
зависимости от моделируемых ситуаций. Кроме того, в ряде моделей, прежде всего
динамических, присутствуют временные параметры (интервалы поставок, время
хранения запаса, время транспортировки и т. п.), которые в свою очередь также
определяют стоимостные характеристики логистических процессов.
В логистике требуется обеспечить прохождение
материального потока от начальной до конечной точки его траектории с
наименьшими затратами живого и овеществленного труда. Однако для принятия
управленческого решения требуется модель управляемого процесса. Таким образом,
модель представляет собой отображение управляемого процесса или отображение
процесса или объекта в целях управления или изучения.
Качество модели характеризуется ее адекватностью,
т. е. степенью приближения к реальному процессу или объекту. Максимальной
адекватностью обладают математические модели, т. е. модели, построенные с
помощью математического языка. В данном случае математический язык объективно
является точным и лаконичным. Математические модели отображают процесс или
объект с помощью математической символики.
В современных условиях логистические процессы
могут быть также выражены с помощью массива цифр при использовании компьютерных
технологий. Цифровые компьютерные модели также входят в разряд математических
моделей, поскольку отражают количественную сторону логистических процессов.
Большинство логистических задач опирается на расчетные модели, являющиеся по
своей сущности оптимизационными, поскольку данные модели имеют цель получения
оптимального результата.
Математическая модель предопределяет и методы
решения. Любая модель в той или иной форме содержит целевую функцию и
ограничения.
Поэтому модель может интерпретироваться как
задача, в которой даны исходные данные и требуется определить значение искомых
величин. Нахождение этих величин и определяет метод решения задачи для
построенной модели.
Цель работы: изучение информации по теме
"Применение математических моделей в логистике" и применение
математических моделей при решении логистических задач.
Для реализации цели были выдвинуты следующие
задачи:
. Изучить материал по логистике и
логистическим задачам;
2. Проанализировать литературу по теме
исследования;
. Отобрать и систематизировать
необходимый материал;
. Рассмотреть различные математические
модели для решения логистических задач;
Дипломная работа состоит из введения, трёх
разделов, заключения, списка использованных источников, приложений.
Во введении обоснована актуальность темы
исследования.
В первой главе рассмотрено определение
логистики, её возникновение и развитие.
Во второй главе рассматриваются разделы
математики: математический анализ, гармонический анализ, теория вероятностей и
математическая статистика. С помощью данных разделов математики, рассмотрены такие
логистические задачи, как: определение оптимального размера партии поставки,
определение оптимального размера партии поставки при периодическом поступлении
и равномерном расходе ресурсов, определение места дислокации базы снабжения,
определение межотраслевого баланса, определение периодичности потребления
электроэнергии, построение распределения вероятностей величины спроса на
определённый товар, определить уровень издержек от величины товарооборота при
помощи.
В третьей главе приведено решение логистических
задач, с использованием математических методов.
В заключении подводится итог работы.
1. Развитие логистики как науки и её
практическая реализация
Логистика как наука и как сфера практических
знаний вызывает в последнее время всё более возрастающий интерес. Менеджеры по
логистике являются одной из наиболее востребованных позиций на рынке труда и
являются целью для любой компании.
Логистика - это наука о планировании,
организации управлении и контроле движения материальных и информационных
потоков в пространстве и во времени от их первичного источника до первичного
потребителя.
Логистика сравнительно молодая наука, хотя и
имеет глубокие исторические корни. Активно развиваться она стала в период
Второй мировой войны, когда была применена для решения стратегических задач и
чёткого взаимодействия оборонной промышленности, тыловых снабженческих баз и
транспорта, с целью своевременного обеспечения армии вооружением,
горюче-смазочными материалами и продовольствием. Постепенно понятия и методы
логистики стали переносить из военной области в гражданскую.
Расширение сферы применения логистики, которое
наблюдается в 80-е особенно 90-е года, объясняется в первую очередь, развитием
оптимальных методов управления материальными потоками. Логистика позволяет
существенно сократить временной интервал между приобретением сырья и
полуфабрикатов, и поставкой готового продукта потребителю, способствует резкому
сокращению материальных запасов, ускоряет процесс получения информации,
повышает уровень сервиса.
Логистика включает следующие логистические
научные дисциплины:
. Коммерческая логистика
2. Производственная
(внутрипроизводственная) логистика.
. Транспортная логистика.
. Складская логистика.
Перечисленные логистики являются наиболее
распространенными.
В приложении 1 приведено сведение, которое
показывает охват разделами математики совокупности основных логистических
научных дисциплин.
Деятельность в области логистики многогранна.
Она включает управление транспортом, складским хозяйством, запасами, кадрами,
организацию информационных систем, коммерческую деятельность и многое другое. логистика математический снабжение товарооборот
Принципиальная новизна логистического подхода -
органичная взаимная связь, интеграция выше перечисленных областей в единую
материалопроводящую систему. Иными словами, цель логистического подхода -
сквозное управление материальными потоками.
Опыт промышленно развитых стран и передовых
компаний показывает, что логистике принадлежит стратегически важная роль и в
современном бизнесе. Внедрение методов логистического менеджмента в практику
бизнеса позволяли фирмам значительно сократить товарные запасы, ускорить
оборачиваемость оборотного капитала, снизить себестоимость продукции,
обеспечивать наиболее полное удовлетворение потребностей покупателей в отношении
качества товара и сопутствующего сервиса.
Большинство исследователей сходится на том, что
семантика слова "логистика" восходит к Древней Греции, где
"logistike" обозначало "счетное искусство" или
"искусство рассуждения, вычисления". В период Римской империи
существовали служители, которые носили титул "логисты" или
"логистики"; они занимались распределением продуктов питания.
По мнению ряда западных учёных логистика
возросла в науку благодаря военному делу. Создателем первых научных трудов по
логистике принято считать французского военного специалиста начала XIX в.
барона А.А. Жомини, который утверждал, что логистика включает такой широкий
круг вопросов, как планирование, управление, снабжение, определение мест
дислокации войск, а так же строительство мостов, дорог и т.д.
Существует так же математическое направление в
логистике. Так в 1904 г. на философском конгрессе в Женеве термин
"логистика" был закреплён за математической логикой. Данный термин в
значении математической логики использовался в работах знаменитого немецкого
математика Г. Лейбница (1646-1716). Логистика развивалась и в России. Ещё в
начале XX в.
петербургские профессора путей сообщения издали труд "Транспортная
логистика". На его основе были построены модели перевозки войск, их
обеспечения и снабжения. Эти модели получили практическое применение при
планировании и проведении ряда компаний русской армии в ходе Первой мировой
войны.
В 60-е гг. XX
века начинает развиваться экономическое направление логистики, когда была
сформулирована так называемая концепция бизнес-логистики как интегрального
инструмента менеджмента. Основное содержание концепции сводилось к следующему:
"Логистика - это менеджмент всех видов деятельности, которые способствуют
движению и координации спроса и предложения на товары в определенном месте и в
заданное время".
К началу 1970-х годов были сформулированы
фундаментальные принципы бизнес-логистики, и некоторые западные фирмы начали их
успешно применять на практике. Кроме того, попытки внедрить логистическую
координацию натолкнулись на многих западных фирмах на противодействие среднего
и даже высшего звена менеджмента.
Период с 1980-х до середины 1990-х гг.
характеризуется стремительным развитием современных маркетинговой и
интегральной концепций логистики в индустриальных странах Запада. Определяющей
идеей развития логистики в это время была максимальная интеграция логистических
функций фирмы и ее логистических партнеров в так называемой полной
логистической цепи: "закупки - производство - дистрибьюция - продажи"
для достижения конечной цели бизнеса с минимальными затратами. В
рассматриваемый период произошли существенные изменения в мировой экономике,
которые объясняют феномен логистического "взлета".
Развитие интеграции мировой экономики и
глобализация бизнеса способствовали созданию международных логистических
систем. Крупные западные фирмы стремились развивать глобальные стратегии, т. е.
производить продукцию для мирового рынка и в тех местах, где можно было найти
наиболее дешевые сырье, компоненты, трудовые ресурсы. Ликвидация традиционных
национальных, торговых, таможенных, транспортных и других барьеров, как это
произошло в странах ЕС и между США и Канадой, сделала возможным свободное
перемещение товаров, услуг и людей через границы и в то же время усилила
значимость международной логистической координации.
На международной арене логистическая
деятельность стала более комплексной, а такие проблемы, как размещение
производства и центров дистрибьюции, выбор видов транспорта, типов сервиса,
методов управления запасами, проектирование адекватных коммуникационных и
информационных систем, потребовали новых навыков логистического менеджмента. С
начала 1990-х годов стали активно разрабатываться и внедряться международные
программы и проекты, в которых логистике отводилась ведущая роль.
Эволюция логистики за рубежом показывает, что
она становится одним из важнейших стратегических инструментов в конкурентной
борьбе для многих организаций бизнеса, и те фирмы, которые использовали
концепции интегрированной логистики, как правило, упрочили свои позиции на
рынке.
2. Математические модели в логистике
.1 Математический анализ в логистике
Предметом изучения в математическом анализе
являются переменные величины и их взаимозависимости. Важным понятием
математического анализа является функция. С помощью функций математически
выражается многообразие количественных закономерностей в логистических
процессах движения материальных ресурсов. Необходимым условием для применения
методов математического анализа являются установление функциональных
зависимостей, после чего полученная функция исследуется на экстремум и
подвергается всестороннему анализу.
В управлении логистическими процессами довольно
часто встречаются ситуации, когда та или иная величина увеличивается в
зависимости от увеличения данного фактора.
.1.1 Модель, определяющая
оптимальный размер партии поставки
Представленной моделью описывается обширный
класс задач по управлению запасами. Запасы являются ключевой категорией в
логистике. С точки зрения логистики запасы - это материальный поток с нулевой
скоростью физического перемещения. Запасы обладают двойственной природой: с
одной стороны, они имеют положительное значение, а с другой стороны, они
обладают отрицательным качеством.
Положительное значение запасов заключается в
том, что с ростом величины запаса возрастает надежность функционирования
системы, т. е. обеспечивается надежное, бесперебойное обеспечение материальными
ресурсами производства или надежность реализации товара. Но запасы обладают и
отрицательным свойством, которое заключается в том, что в запасах
иммобилизируются материальные и финансовые ресурсы. Отсюда и возникают проблемы
оптимизации запаса, т. е. определение того уровня запаса, при котором общие
издержки при управлении запасом будут минимальными.
Оптимизация уровня запасов выполняется исходя из
того, что имеет место две группы затрат: это затраты на хранение запаса и
затраты на доставку продукции и совершение заказа, отсюда проблема: поставлять
продукцию большими или малыми партиями. При поставках крупными партиями сокращаются
транспортные расходы, но увеличиваются затраты на хранение. При поставках
малыми партиями - уменьшаются затраты на хранение запаса, но возрастают
транспортные расходы. Следовательно, проблема оптимизации запасов сводится к
проблеме оптимизации партии поставки.
Общие издержки управления запасами (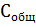
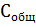 ) складываются из стоимости доставки
продукции - выполнения поставки (
) складываются из стоимости доставки
продукции - выполнения поставки (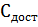
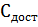 ) и затрат на хранение запаса (
) и затрат на хранение запаса (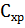
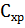 ). Тогда стоимость доставки -
выполнения поставки, можно представить в следующем виде:
). Тогда стоимость доставки -
выполнения поставки, можно представить в следующем виде:
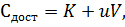
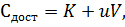 (1)
(1)
где 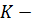
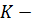 условно-постоянная часть на
транспортировку;
условно-постоянная часть на
транспортировку;
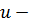
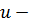 затраты, зависящие от величины
партии поставки.
затраты, зависящие от величины
партии поставки.
Затраты на хранение запаса:
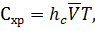
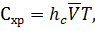 (2)
(2)
где 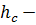
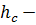 стоимость хранения единицы запаса в
сутки;
стоимость хранения единицы запаса в
сутки;
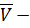
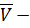 средний запас;
средний запас;
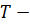
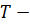 время хранения запаса.
время хранения запаса.
Для определения затрат на хранение
необходимо вычислить средний запас. Средний запас вычисляется с помощью
среднего в интегральном исчислении, т. е. по формуле:
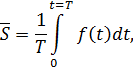
где 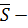
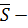 средняя величина запаса;
средняя величина запаса;
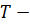
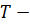
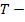 длительность расхода запаса;
длительность расхода запаса;
Функция изменения запаса выглядит
следующим образом:
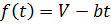
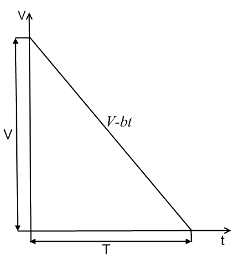
Рисунок 1
Вычисляется средний
запас:
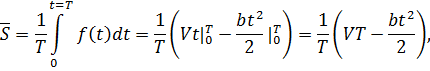
при
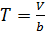
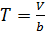
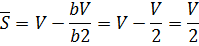
Таким образом, в логистике запасов при линейном
потреблении материальных ресурсов средний запас равняется половине партии
поставки.
Получаем выражение общих затрат:
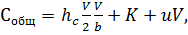
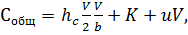 (3)
(3)
Полученные общие затраты относятся
на единицу хранимого запаса, т. е. 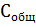
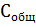
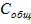 делится на V:
делится на V:
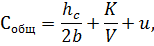
Далее находится производная, которая
приравнивается к нулю:
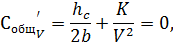
Отсюда оптимальный размер поставки:
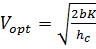
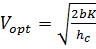 ,
,
Полученная формула называется формулой
Уилсона.
В логистической деятельности
используется также и такой вывод формулы Уилсона:
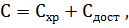
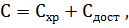 (4)
(4)
где 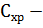
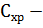
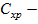 издержки хранения запаса;
издержки хранения запаса;
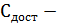
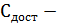 издержки доставки;
издержки доставки;
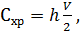
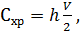 (5)
(5)
где 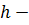
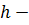
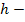 издержки хранения единицы запасов в
год.
издержки хранения единицы запасов в
год.
Издержки доставки - это издержки, независящие от
величины партии поставки, но зависящие от количества поставок в год:
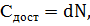
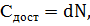 (6)
(6)
где 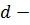
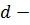 стоимость выполнения одной
поставки;
стоимость выполнения одной
поставки;
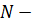
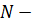 кол-во поставок за год.
кол-во поставок за год.
В свою очередь количество поставок
за год равно:
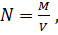
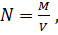 (7)
(7)
где 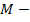
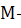 годовая потребность в материальных
ресурсах;
годовая потребность в материальных
ресурсах;
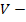
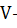 размер партии поставки;
размер партии поставки;
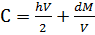
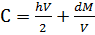 (8)
(8)
Найдём первую производную от этого
выражения и приравняем к нулю:
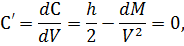
отсюда оптимальный размер поставки:
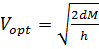
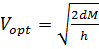 (9)
(9)
Пример: потребность предприятия в
стальном прокате равна 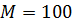
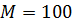
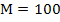 тонн в год. Выполнение заказа, т.
е. независящие расходы равны
тонн в год. Выполнение заказа, т.
е. независящие расходы равны 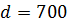
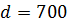
 рублей, а содержание единицы запаса
рублей, а содержание единицы запаса


 рублей. Определяется оптимальный
размер партии поставки.
рублей. Определяется оптимальный
размер партии поставки.
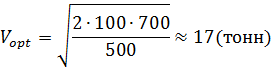
В годовом исчислении оптимальный размер партии
поставки используется в производственно-коммерческой деятельности предприятия.
При этом издержки хранения определяются путем непосредственной калькуляции, а
стоимость выполнения заказа определяется как совокупность транзакционных
издержек. В данном случае транзакционные издержки включают издержки на поиск
поставщиков, на ведение деловых переговоров, на организацию транспортировки
продукции. Формулы Уилсона для определения оптимального размера партии поставки
как в суточном, так и в годовом исчислении дают один и тот же результат.
В первом случае в качестве основных параметров
используется суточное потребление продукции - b и издержки содержания
единицы запаса в одни сутки. Во втором случае используется годовая потребность
и издержки содержания единицы запаса в год, т. е. имеет место следующее
тождество:
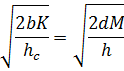
В обеих формулах параметры  K и
K и 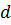
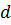
 равны, так как выражают
затраты на одну поставку, т. е. независящие от количества продукции в поставке.
Относительно предыдущих параметров имеют место следующие равенства:
равны, так как выражают
затраты на одну поставку, т. е. независящие от количества продукции в поставке.
Относительно предыдущих параметров имеют место следующие равенства:
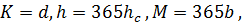
где 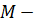
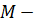
 это расход данного материального
ресурса за год.
это расход данного материального
ресурса за год.
По условию задачи за год расходуются все
материальные ресурсы, поставляемые на предприятие, а поэтому получаем, что:
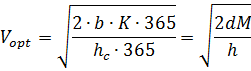
На практике в основном применяется формула
Уилсона в годовом исчислении.
2.1.2 Модель, определяющая
оптимальный размер партии поставки при периодическом поступлении и равномерном
расходе материальных ресурсов
Ситуация 1:
Рассматриваемая ситуация иллюстрируется графиком
на рисунке 2:
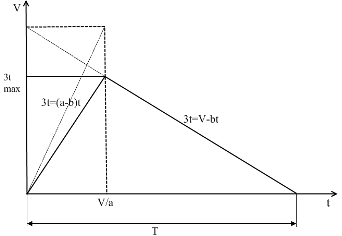
Рисунок 2
Из графика следует, что материальные ресурсы
поступают на предприятие и расходуются предприятием одновременно.
Следовательно, имеется запас:
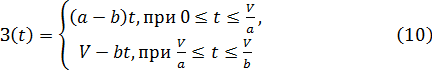
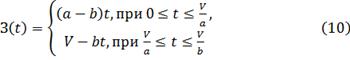
Рассмотрим равенство:
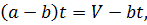
отсюда
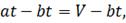
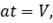
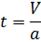
Согласно общему правилу для
определения партии поставки необходимо вычислить средний запас за период Т,
где 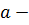
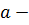 среднесуточное поступление
материальных ресурсов,
среднесуточное поступление
материальных ресурсов,
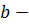
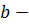 среднесуточный расход материальных
ресурсов на предприятии.
среднесуточный расход материальных
ресурсов на предприятии.
Вычислим средний запас:
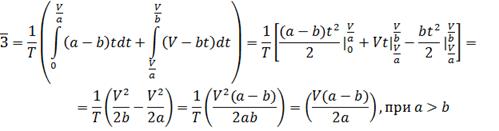
Далее определим общие издержки как
сумму издержек по хранению и доставке:
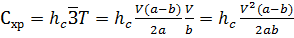
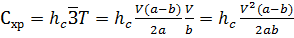 (11)
(11)
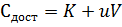
Выражение общих издержек примет вид:
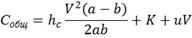 (12)
(12)
Общие издержки относятся на единицу продукции,
тогда
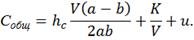 (13)
(13)
Полученную функцию исследуем на экстремум:
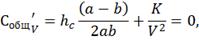
отсюда оптимальный размер партии поставки:
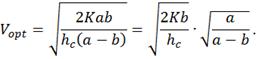 (14)
(14)
Таим образом, при определении
оптимального размера партии поставки к стандартной формуле Уилсона добавляется
поправочный коэффициент 
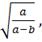 этот поправочный коэффициент
применяется и для формулы Уилсона в годовом исчислении.
этот поправочный коэффициент
применяется и для формулы Уилсона в годовом исчислении.
Ситуация 2:
Рассмотрим ситуацию на рисунке 3:
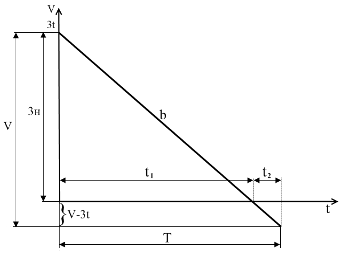
Рисунок 3
Обозначения на графике:

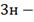 начальный запас;
начальный запас;

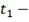 период наличия запаса на складе;
период наличия запаса на складе;

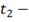 период отсутствия запаса на складе,
при этом
период отсутствия запаса на складе,
при этом
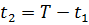
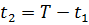
Задача сводится к количественному определению
размера снижения и установления величины начального запаса. Таким образом,
следует минимизировать сумму следующих издержек:
) расходы по доставке;
2) расходы по хранению запаса;
) потери от дефицита.
Все эти издержки рассчитываются на единицу
продукции:
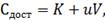
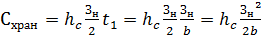
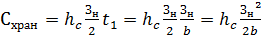 (15)
(15)
Потери от дефицита - это
дополнительные затраты от дефицита в период 
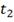 , к таким потерям относятся: простой
оборудования, простой персонала, упущенная выручка и др.
, к таким потерям относятся: простой
оборудования, простой персонала, упущенная выручка и др.
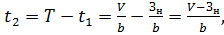
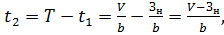 (16)
(16)
отсюда издержки вследствие дефицита:
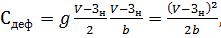
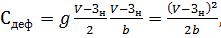 (17)
(17)
где 
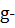 стоимостная оценка дефицита
(издержки вследствие дефицита на
стоимостная оценка дефицита
(издержки вследствие дефицита на
единицу),

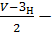
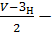 средний объём дефицита;
средний объём дефицита;
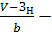
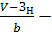 длительность дефицита.
длительность дефицита.
Общие затраты составят:
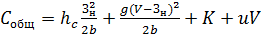
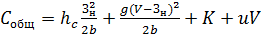 (18)
(18)
Издержки на единицу продукции примут
вид:
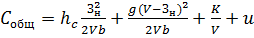
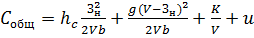 (19)
(19)
После преобразования получим:
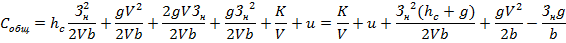
Далее определим:

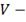 размер поставки;
размер поставки;

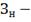 начальный размер запаса, для этого
решается следующая система дифференциальных уравнений:
начальный размер запаса, для этого
решается следующая система дифференциальных уравнений:
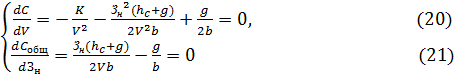
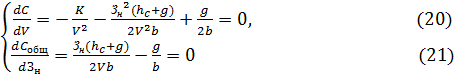
Из уравнения (21) данной системы
получаем:


отсюда


после преобразования уравнения (20)
системы, получаем:


Подставляя в уравнение (24) отношение начального
запаса к объему партии поставки (23), получаем:
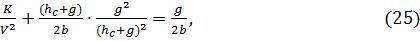
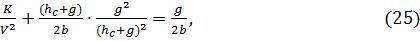
отсюда оптимальный размер партии
поставки:
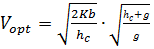
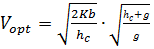 (26)
(26)
Оптимальное значение начального
запаса следует из формулы (23):
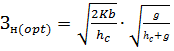
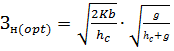 (27)
(27)
Таким образом, при допущении
дефицита в базисную модель Уилсона вносится коэффициент, равный 
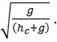
2.1.3 Модель определения места
дислокации базы снабжения
Рассматривается следующая логистическая
задача: снабжение острова А осуществляется через железнодорожную станцию

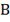 . От береговой линии остров удален
по прямой на расстояние
. От береговой линии остров удален
по прямой на расстояние 
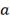 км, а железнодорожная станция
- на расстояние
км, а железнодорожная станция
- на расстояние 
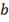 км. Расстояние между
основаниями перпендикуляров, проведенных к береговой линии через точки
км. Расстояние между
основаниями перпендикуляров, проведенных к береговой линии через точки 
 и
и 
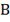 , равно
, равно 
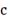 км. Стоимость перевозки одной тонны
груза на расстояние в 1 км: по суше -
км. Стоимость перевозки одной тонны
груза на расстояние в 1 км: по суше - 
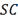 , по морю -
, по морю - 
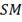 . Определить, где разместить
перевалочную базу
. Определить, где разместить
перевалочную базу 
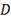 , чтобы стоимость перевозки была
минимальна.
, чтобы стоимость перевозки была
минимальна.
Решение задачи представлено в приложении 2.
2.1.4 Модель межотраслевого баланса
Межотраслевые потоки на макрологистическом
уровне, то есть материальные потоки между отраслями экономики, отображаются с
помощью модели межотраслевого баланса.
Межотраслевой баланс показывает объемы
производства и их распределение между отраслями и конечными потребителями.
Межотраслевые потоки - материальные потоки в групповой (укреплённой)
номенклатуре. Согласно межотраслевому балансу вся производимая продукция данной
отрасли направляется к другим отраслям на производственное потребление и на
конечное потребление.
Конечное потребление включает:
) экспорт;
2) государственный резерв;
) личное потребление граждан.
Часть продукции отрасль оставляет себе, для
своих нужд. Например, для дальнейшего передела, для контроля и испытаний,
сертификации, для рекламы и др. Таким образом, можно составить систему
уравнений, показывающих объем производства и его распределение.
В межотраслевом балансе отрасли-производители
одновременно являются отраслями потребителями:
1, 2…i…m−отрасли-производители
продукции;
1,2…j…n−отрасли-потребители
продукции, при этом:
i=j,
m=n
Система уравнений, описывающая производство и
потребление, имеет следующий вид:

 (28)
(28)
Полученная система уравнений может
быть выражена в компактной форме:
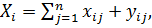
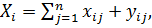 (29)
(29)
где 
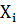 − объёмы производства i-й отрасли;
− объёмы производства i-й отрасли;

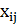 − объёмы поставок из i-й отрасли в
j-ю отрасль,
т. е. объемы
− объёмы поставок из i-й отрасли в
j-ю отрасль,
т. е. объемы
межотраслевых поставок;

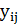 − объёмы конечного
потребления.
− объёмы конечного
потребления.
В межотраслевом балансе объемы производства и
потребления исчисляются в групповой (укрупнённой) номенклатуре. Например,
черные металлы, цветные металлы, цемент, строительные материалы, пиломатериалы
и т. п. Такой перечень охватывает наименования всех видов продукции
производимых в стране. Однако полученная система уравнений не имеет решений,
так как количество неизвестных больше числа уравнений.
Для того чтобы система имела решение, вводится
величина, которая называется коэффициентом прямых затрат:
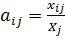
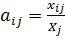 (30)
(30)
где 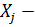
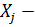 валовая продукция потребляющих
отраслей.
валовая продукция потребляющих
отраслей.
Коэффициент прямых затрат
показывает, какое количество продукции i-й отрасли
необходимо затратить для получения единицы продукции j-й отрасли.
По своему экономическому смыслу
коэффициент прямых затрат представляет собой нормы расходов, a норма
расхода - это расход данного материала для производства единицы продукции.
Отсюда получаем значения межотраслевых поставок:
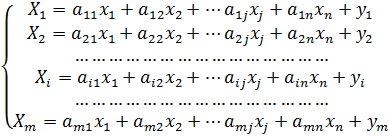
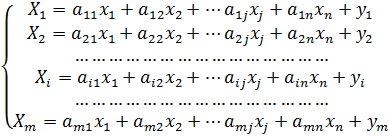 (31)
(31)
Полученная система уравнений имеет
решения, так как количество неизвестных равно количеству уравнений в системе.
Такая система уравнений именуется моделью межотраслевого баланса. Эту модель
ещё именуют как модель "затраты - выпуск" (input - output).
Так же в межотраслевом балансе
вычисляются коэффициенты полных затрат:
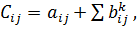
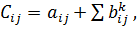 (32)
(32)
где 
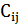 - коэффициент полных затрат;
- коэффициент полных затрат;

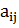 - коэффициент прямых затрат;
- коэффициент прямых затрат;
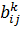
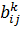 - коэффициент косвенных затрат k-го порядка.
- коэффициент косвенных затрат k-го порядка.
Прямые затраты определяются
материальной субстанцией данного товара. Полные затраты учитывают косвенные
затраты материальных ресурсов, израсходованных на предыдущих стадиях
изготовления продукции. В каждой продукции или в каждом товаре имеют место
затраты всех прочих товаров. Вследствие всеобщего характера косвенного
потребления сдвиги в ценах даже самых отдаленных товаров могут повлиять на стоимость
данной продукции.
В рыночной экономике межотраслевой
баланс составляется государственными органами статистики по отчетным данным
предприятия, как исполнительный баланс. В таком балансе исчисляются прямые и
полные затраты в рублях на 1 тысячу рублей произведенной продукции.
По величине прямых затрат каждое
предприятие оценивает свой уровень материалопотребления.
Таким образом, межотраслевой баланс
адекватно отражает систему межотраслевых потоков на макрологистическом уровне.
2.2 Гармонический анализ в логистике
Гармонический анализ - это раздел
математики. Часть периодической функции может быть точно или приближённо
разложена в тригонометрический ряд:
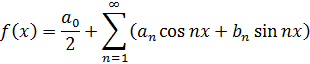
С помощью гармонического анализа
изучается влияние сезонности или иных факторов периодичности на величину спроса
и потребления материальных ресурсов, что необходимо для прогнозирования
конъюнктуры рынка.
Изучаемую фактическую периодическую
зависимость можно представить в таком виде:

 (33)
(33)
где 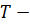
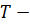 полный период;
полный период;
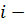
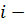 номер гармоники (синусоиды или
косинусоиды);
номер гармоники (синусоиды или
косинусоиды);

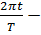
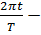 переменная в радианной или градусной
мере
переменная в радианной или градусной
мере 
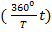 ;
;

 ,
, 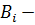
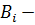 коэффициенты гармоник.
коэффициенты гармоник.
Для получения значений 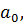
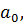

 ,
,

 можно воспользоваться этими
формулами:
можно воспользоваться этими
формулами:
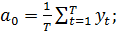
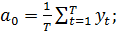 (34)
(34)
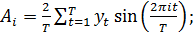
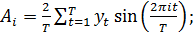 (35)
(35)
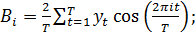
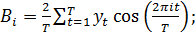 (36)
(36)
где 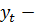
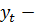
 фактические данные об удельном
расходе электроэнергии (на 1 тонну погруженного груза на базе оптово- торгового
предприятия), кВт.ч/т.
фактические данные об удельном
расходе электроэнергии (на 1 тонну погруженного груза на базе оптово- торгового
предприятия), кВт.ч/т.
Пример: Определить периодичность потребления
электроэнергии на базе оптово- торгового предприятия. В таблице 1 приводятся
фактические данные удельного расхода электроэнергии.
Таблица 1
|
№
п/п
|
Месяцы
|
Удельный
расход кВт.ч/т
|
|
1
|
Январь
|
15,5
|
|
2
|
Февраль
|
14,3
|
|
3
|
Март
|
15,2
|
|
4
|
Апрель
|
14,6
|
|
5
|
Май
|
11,2
|
|
6
|
Июнь
|
8,4
|
|
7
|
Июль
|
8,0
|
|
8
|
Август
|
8,2
|
|
9
|
Сентябрь
|
8,7
|
|
10
|
Октябрь
|
14,0
|
|
11
|
Ноябрь
|
14,5
|
|
12
|
Декабрь
|
15,0
|
|
Итого:
|
147,6
|
Решение задачи представлено в приложении 3.
Уровень соответствия фактических и расчётных
данных, полученных с помощью гармонического анализа, оценивается методами
математической статистики.
.3 Теория вероятностей в логистике
Случайные отклонения сопутствуют любому
закономерному процессу, а тем более логистическим процессам в рыночной
экономике. Практика ставит такие задачи, в которых различные факторы играют
существенную роль в рассматриваемых процессах, однако число этих факторов столь
велико, что проследить причинно-следственные связи между ними не всегда
представляется возможным. Элементы неопределенности, сложности, множества
причин, присущи случайным явлениям и процессам в логистике, и соответственно требуются
специальные методы для их исследования, изучения и управления. Такие методы и
разрабатывает теория вероятностей.
Таким образом, теория вероятностей в логистике
рассматривает случайные величины, обусловленные логистическими процессами и
операциями.
В логистике имеют место следующие стохастические
случайные величины:
. Спрос (платежеспособность).
2. Объем реализации (объем продаж).
. Длительность (период реализации).
. Выручка от реализации продукции
. Издержки (общие, логистичекие,
транзакционные)
. Время погрузки-выгрузки транспортных
средств
. Время доставки (перемещения продукции)
. Время обслуживания покупателей
(потребителей)
. Товарооборот торгового предприятия
. Оборот оптово-торговой базы
. Поток потребителей (поток заявок на
обслуживание)
. Время занятости средств обслуживания
. Движение товарного запаса
. Объем партии отгрузки реализуемой
продукции
. Распределение продукции по группам АВС
. Процесс поставки - надежность поставок
и другие
Если изучаемое явление
представляется в виде полной группы событий, которые несовместны и
равновозможны, то вероятность данного события равна отношению числа 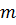
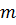 благоприятствующих этому событию
случаев к общему числу
благоприятствующих этому событию
случаев к общему числу 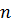
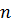 возможных случаев, т. е.
вероятность равна:
возможных случаев, т. е.
вероятность равна:
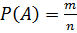
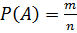 (38)
(38)
На практике обычно рассматривают
статистическую вероятность, в результате накопленных статистических данных о
благоприятствующих событиях 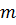
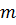 и общего числа событий
и общего числа событий 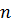
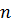 .
.
Так, например, в логистике
используется такая величина, как надежность снабжения. Надежность снабжения в
большинстве случаев величина случайная и определяется за определенный период
времени как отношение числа поставок, выполненных согласно договору поставки, к
общему числу поставок.
Допустим, за рассматриваемый период
было выполнено поставщиком 24 поставки, из них 18 поставок соответствуют
параметрам, предусмотренным договором поставки. Отсюда надежность равняется:
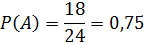
Поставка соответствующей надежности
определяется следующими параметрами: количество, качество, сроки поставок.
Случайные величины характеризуются законом распределения или плотностью
распределения вероятностей.
Таблица 2
|
х
|
х1
|
х2
|
…
|
хn
|
|
p
|
p1
|
p2
|
…
|
pn
|
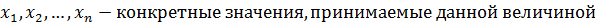
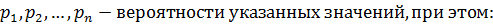
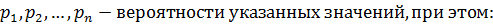
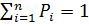
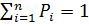

В логистике наиболее распространенными являются
следующие законы распределения вероятностей: нормальное, экспоненциальное,
биноминальное, Пуассона.
2.3.1
Нормальный
закон распределения вероятностей
Плотность нормального распределения имеет
следующий вид:
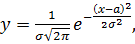
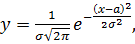 (39)
(39)
где a - центр
распределения вероятностей или математическое ожидание данной случайной
величины, т. е. 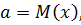
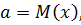
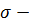
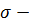 среднеквадратическое отклонение
данной случайной величины.
среднеквадратическое отклонение
данной случайной величины.
На практике исчисляются
соответствующие статистические оценки. Так, оценкой для математического
ожидания будет средняя величина:
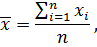
где 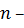
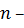 количество данных в рассматриваемом
статистическом массиве.
количество данных в рассматриваемом
статистическом массиве.
Математическое ожидание есть то
теоретическое значение данной случайной величины, к которому стремится средняя
величина при неограниченном увеличении количества данных.
Среднеквадратичное отклонение:
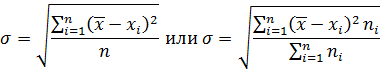
В логистике то или иное значение
величины оценивается значением
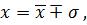
при этом оценивается коэффициент
вариации:
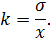
На рисунке 4 представлен график
нормального распределения вероятностей.
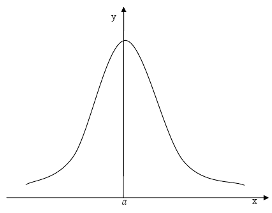
Рисунок 4- Нормальный закон распределения
вероятностей
2.3.2
Экспоненциальный закон распределения вероятностей
Плотность экспоненциального закона распределения
вероятностей имеет следующий вид:
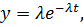
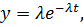 (40)
(40)
где 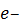
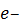 основание натурального логарифма.
основание натурального логарифма.
Экспоненциальный закон описывает
временные параметры случайных логистических процессов. Под экспоненциальный
закон попадают следующие случайные величины:
) время обслуживания покупателей;
) время погрузки-выгрузки
транспортных средств;
) время, затрачиваемое на выполнение
прочих логистических операций
) интервал между заявками,
приходящими на обслуживание.
Особенностью экспоненциального
закона является то, что он определяется одним параметром 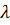
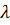 . При этом
. При этом
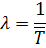
где 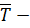
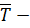
 среднее значение исследуемого
временного параметра.
среднее значение исследуемого
временного параметра.
Для величин, подчиняющихся экспоненциальному
закону, математическое ожидание М и среднеквадратическое значение равны между
собой:
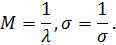
На рисунке 5 представлен график
экспоненциального закона.
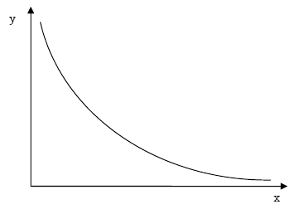
Рисунок 5- Экспоненциальный закон распределения
вероятностей
2.3.3 Биномиальный
закон распределения вероятностей
Биноминальный закон распределения вероятностей
выражается формулой:
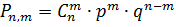
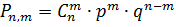 (41)
(41)
Данный закон определяет вероятности
наступления 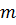
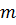 событий из общего числа событий
событий из общего числа событий 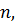
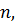
где 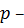
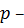 вероятность наступления одного
события из данной группы событий;
вероятность наступления одного
события из данной группы событий;
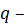
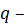 вероятность ненаступления указанного
события,
вероятность ненаступления указанного
события,
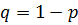
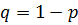
 .
.
Величина 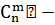
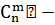 количество сочетаний из
количество сочетаний из 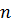
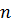 по
по 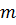
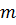 , определяется по формуле:
, определяется по формуле:
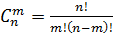
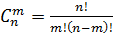 (42)
(42)
Для вычисления числа сочетаний
используется равенство:
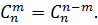
При биноминальном распределении
наивероятнейшее число событий равно 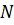
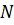 :
:

 .
.
2.3.4 Сравнение законов
распределения вероятностей. Критерий согласия
В теории вероятностей существуют
методы, позволяющие оценивать степень соответствия фактических распределений
вероятностей их теоретическим значениям. С этой целью используются так называемые
критерии согласия, наиболее известным из которых является критерий 
 . Данный критерий позволяет
сравнивать между собой эмпирические законы распределения, полученные по одним и
тем же фактическим данным.
. Данный критерий позволяет
сравнивать между собой эмпирические законы распределения, полученные по одним и
тем же фактическим данным.
Чем меньше значение 
 , тем лучше данный эмпирический
закон согласуется с теоретическим. Для сравнения эмпирических законов
распределения вероятностей вычисляются значения
, тем лучше данный эмпирический
закон согласуется с теоретическим. Для сравнения эмпирических законов
распределения вероятностей вычисляются значения 
 по следующей формуле:
по следующей формуле:
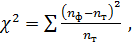
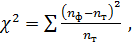 (43)
(43)
Где 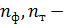
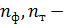 соответственно фактические и
теоретические значения частот исследуемых законов распределения.
соответственно фактические и
теоретические значения частот исследуемых законов распределения.
Величина 
 так же является случайной, а
поэтому подчиняется своему закону распределения. Подход к сравнению
эмпирических законов распределения можно показать на примере.
так же является случайной, а
поэтому подчиняется своему закону распределения. Подход к сравнению
эмпирических законов распределения можно показать на примере.
Установим, какой закон распределения
вероятностей- нормальный или экспоненциальный- лучше отражает распределение
данной величины, т.е. осуществим проверку гипотез. В качестве исследуемой
величины берём объём реализации определённого товара. Исходные данные
представлены в таблице 3:
Таблица 3. Сведения о
реализации товара
|
Дата
|
Реализация
(тыс.руб.)
|
|
1
|
3,5
|
|
2
|
3,8
|
|
3
|
2,7
|
|
4
|
14,5
|
|
5
|
18,3
|
|
6
|
13,4
|
|
7
|
7,5
|
|
8
|
24,8
|
|
9
|
16,5
|
|
10
|
12,4
|
|
11
|
34,5
|
|
12
|
41,2
|
|
13
|
27,4
|
|
14
|
24,5
|
|
15
|
25,5
|
|
16
|
27
|
|
17
|
29,5
|
|
18
|
22,1
|
|
19
|
48,3
|
|
20
|
64,5
|
|
21
|
18,5
|
|
22
|
19,5
|
|
23
|
27,4
|
|
24
|
35
|
|
25
|
42
|
|
26
|
54
|
|
27
|
32,1
|
|
28
|
14,5
|
|
29
|
9,4
|
|
30
|
10
|
Задача формулируется следующим образом:
построить распределение вероятностей величины спроса на данный товар, если в
результате проведённого исследования получены результаты о реализации, в тыс.
руб. в день.
Решение задачи представлено в приложении 4.
В общем случае ряд логистических процессов, а
именно: продажи, отгрузка продукции с оптово-торговых предприятий, движение
запасов, оказание услуг при поставках продукции, расходование материальных
ресурсов и т.п. описывается нормальным законом распределения вероятностей.
Отличительный признак данного распределения- наличие выраженной симметрии
случайных величин относительно их среднего значения. Для указанных процессов нормальный
закон применим для всей продукции, определённых ассортиментных групп или
отдельных наименований товаров.
При ABC-анализе
структуры логистических процессов, получаемые характеристики в стоимостном или
натуральном выражениях подчинены экспоненциальному распределению.
Тот факт, что реализация продукции соответствует
нормальному закону, имеет важное значение для логистики, поскольку позволяет
определять величину товарного запаса, для чего рекомендуется следующая формула:
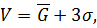
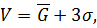 (44)
(44)
где 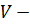
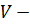
 необходимая величина товарного
запаса на неопределённый период,
необходимая величина товарного
запаса на неопределённый период,
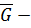
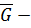
 средняя реализация в единицу
времени(день, неделя, месяц),
средняя реализация в единицу
времени(день, неделя, месяц),

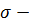
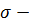 среднеквадратическое отклонение.
среднеквадратическое отклонение.
Для рассмотренного примера товарный запас равен:
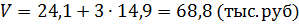
Данная модель показывает, что любое
требование покупателя на то или иное качество товара должно быть удовлетворено
с вероятностью близкой к 1. В этой модели используется правило "трёх
сигм". В нормальном законе 
 соответствует вероятности 0,99.
соответствует вероятности 0,99.
В современных условиях компьютерные
технологии позволяют отслеживать в текущем режиме времени среднюю реализацию и
среднеквадратические отклонения, а так же корректировать величину товарного
запаса.
Предоставленная модель определения
товарного запаса может быть использована как для розничной, так и для оптовой
торговли.
2.4 Математическая
статистика в логистике
Модели математической статистики позволяют
выявить характер действия факторов - причин на следствия. Эти модели дают
возможность по одним величинам вычислять другие, недоступные или малодоступные.
Методы математической статистики позволяют предвидеть течение и развитие
логистических процессов. При помощи методов математической статистики решаются
такие вопросы, как построение кривых распределения вероятностей и оценка
степени согласия фактических характеристик с теоретическими, позволяют
определять эмпирические зависимости, оценивать тесноту связи между изучаемыми
величинами.
Наиболее часто в логистике применяется корреляционно-регрессионный
анализ, при помощи которого выявляются качественные и количественные влияния
различных факторов на показатели логистической деятельности.
Данный анализ позволяет измерять
тесноту связи между величинами и строить теоретические зависимости влияния
одной величины на другую. Теснота связи при линейной зависимости изменяется
коэффициентом корреляции 
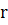 , а теснота связи при нелинейной
зависимости измеряется корреляционным отношением
, а теснота связи при нелинейной
зависимости измеряется корреляционным отношением 
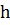 .
.
В логистических задачах целесообразно
использовать линейные зависимости и измерять тесноту связи с помощью
коэффициента корреляции. В этом случае предполагается линеаризовать
зависимости.
Коэффициент линейной корреляции
будет изменяться в пределах от 0 до 1, 
 . Чем ближе значение показателя
тесноты связи, тем сильнее влияние одной величины на другую, а значение близкое
к нулю говорит об ослаблении тесноты связи.
. Чем ближе значение показателя
тесноты связи, тем сильнее влияние одной величины на другую, а значение близкое
к нулю говорит об ослаблении тесноты связи.
Относительно логистики используется
шкала тесноты связи.
Таблица 4/ Шкала
тесноты связи
|
Значения
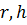 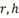  Характеристика степени тесноты
связи Характеристика степени тесноты
связи
|
|
|
0,9-1
|
Очень
сильная зависимость
|
|
0,75-0,9
|
Сильная
зависимость
|
|
0,5-0,75
|
Средняя
зависимость
|
|
0,3-0,5
|
Слабая
зависимость
|
|
Менее
0,3
|
Очень
слабая зависимость
|
Линейный коэффициент корреляции определяется по
следующей формуле:
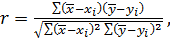
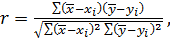 (45)
(45)
где 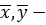
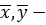
 средние значения исследуемых
величин.
средние значения исследуемых
величин.
Расчёт коэффициента корреляции можно вести в
табличной форме.
Другой составляющей корреляционно-регрессионного
анализа является установление вида уравнения регрессии. В этих целях в
мат.статистике используется метод наименьших квадратов. Согласно этому методу,
сумма квадратов отклонений фактических данных от теоретических значений
соответствующих величин, полученных по уравнению регрессии, должна быть
наименьшей.
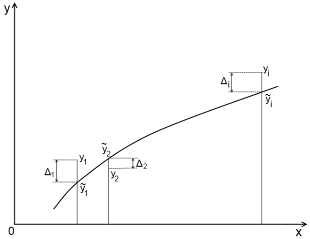
Рисунок 6- График метода "наименьших
квадратов"
На графике фактическое значение
величины обозначим через 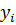
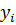 , а теоретическое значение,
полученное из уравнения регрессии обозначим через
, а теоретическое значение,
полученное из уравнения регрессии обозначим через 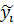
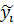 , отсюда разность отклонений
, отсюда разность отклонений
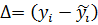
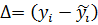 .
.
Уравнение регрессии должно
удовлетворять условию:
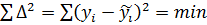
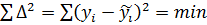 (46)
(46)
Для использования метода наименьших
квадратов решаются системы нормальных уравнений. Для каждой зависимости система
нормальных уравнений будет принимать определённый вид.
Различают линейные и нелинейные
регрессии.
Нелинейные регрессии делятся на два
класса: регрессии нелинейные, относительно включённых в анализ объясняющих
переменных, но линейные по оцениваемым параметрам, и регрессии нелинейные, по
оцениваемым параметрам.
1) для линейной зависимости
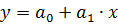
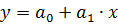 ;
;
2) регрессии нелинейные, по объясняющим
переменным:
· полиномы разных степеней
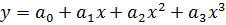
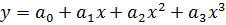
· равносторонняя гипербола
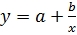
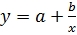

3) регрессии нелинейные, по оцениваемым параметрам:
· степенная
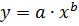
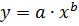
· показательная
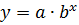
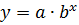
· экспоненциальная
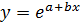
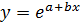
При вычислении параметров уравнения
регрессии исходными данными являются попарно упорядоченные фактические значения
исследуемых величин 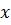
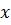 и
и 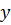
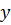 . В нормальных уравнениях
неизвестными являются параметры
. В нормальных уравнениях
неизвестными являются параметры 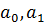
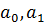 .
.
Для линейных и нелинейных уравнений,
приводимых к линейным, решается следующая система, относительно 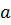
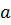 и
и 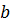
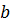 :
:
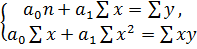
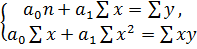 (47)
(47)
Пример: Имеются данные о
товарообороте торгового предприятия за определённый период в млн.руб. и
соответствующих издержках обращения:
Таблица 5
|
Товарооборот,
млн.
руб
|
x
|
1
|
3
|
5
|
8
|
12
|
|
Издержки,
%
|
y
|
10
|
5
|
7
|
3
|
1
|
Решение задачи представлено в приложении 5.
В корреляционно-регрессионном анализе уравнение
регрессии лучше всего вычислять через коэффициент корреляции. Получаемое таким
образом уравнение регрессии идентично уравнению, параметры которого
определяются по методу наименьших квадратов с помощью нормальных уравнений.
Уравнение регрессии для величин, связанных
прямой линейной зависимостью, можно определить по следующей формуле:
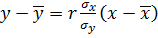
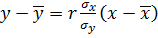 (48)
(48)
где 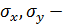
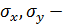
 соответственно среднеквадратические
отклонения величин
соответственно среднеквадратические
отклонения величин 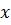
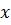 и
и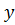
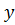 , т.е.
, т.е.
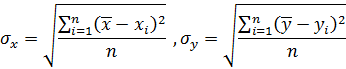
где 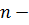
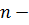 количество данных в исследуемом
статистическом ряду.
количество данных в исследуемом
статистическом ряду.
Выражение
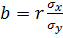
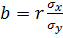
есть коэффициент регрессии.
При положительном значении
коэффициента корреляции с увеличением одной величины 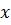
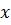 , увеличивается и зависимая от неё
величина
, увеличивается и зависимая от неё
величина 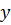
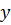 , а при
, а при 
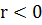 с увеличением величины
с увеличением величины 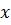
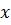 , величина
, величина 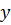
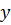 уменьшается. Так же положительные и
отрицательные значения могут принимать коэффициенты регрессии.
уменьшается. Так же положительные и
отрицательные значения могут принимать коэффициенты регрессии.
В логистике
корреляционно-регрессионному анализу подвергается совокупность пар величин- 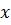
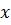 и
и 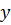
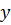
 , но возможны и другие варианты
логистических величин для расчёта парной регрессии и корреляции. Примером из
них является многофакторный корреляционно-регрессионный анализ. Отличие
многофакторного корреляционно-регрессионного анализа от парного заключается в
основном в том, что в многофакторном анализе используется более одной величины
, но возможны и другие варианты
логистических величин для расчёта парной регрессии и корреляции. Примером из
них является многофакторный корреляционно-регрессионный анализ. Отличие
многофакторного корреляционно-регрессионного анализа от парного заключается в
основном в том, что в многофакторном анализе используется более одной величины 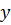
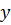 .
.
Результаты корреляционно-регрессионного анализа
в логистике служат действенным инструментом планирования и прогнозирования
производственно-коммерческой деятельности.
3. Применение математических моделей
в логистических задачах
Задача 1:
(использование методов математического анализа)
Есть сеть магазинов некоторой фирмы. Известно,
что в центральном магазине продаётся А количество товара. В радиусе одного
километра от этого магазина в торговых точках этой же фирмы продаётся В
количество товара. Известно так же, что объём реализуемых товаров
пропорционален площади территории распространения товара, а затраты на
перевозку единицы товара пропорционально расстоянию, причём коэффициент
пропорциональности- D. Необходимо
определить радиус распространения товара, при котором прибыль от продаж будет
максимальной, если единица товара продаётся за C
денежных единиц.
Решение: Из поставленной задачи следует, что
необходимо найти такой радиус распространения товаров, при котором прибыль от
продажи товаров будет максимальной, т.е. нужно найти прибыль как функцию,
зависимую от радиуса R
и определить максимум этой функции.
Из условия следует, что количество продаваемых
товаров- линейная функция площади или иначе:
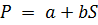
где P-
количество продаваемых товаров,
S- площадь
распространения товаров,
a, b-
неизвестные коэффициенты
Определим коэффициенты a и b. При 
 и
и 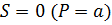
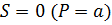 , поэтому
, поэтому 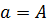
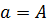 . Так же известно, что в радиусе
одного километра от центрального магазина продаётся В товаров. Это условие даёт
возможность определить величину b.
. Так же известно, что в радиусе
одного километра от центрального магазина продаётся В товаров. Это условие даёт
возможность определить величину b.
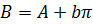
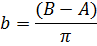
Тогда количество продаваемых товаров
как функция, зависимая от радиуса, будет выглядеть так:
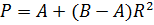
Прибыль от продажи товаров без учёта
на транспортировку L равна:
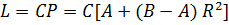
Чтобы найти расходы на перевозку
товаров, сначала определим прирост товарооборота 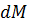
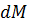 при предельно малом приращении
радиуса
при предельно малом приращении
радиуса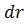
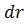 :
:
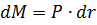
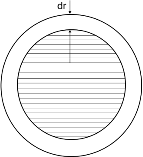
Рисунок 7
Тогда
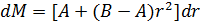
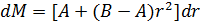
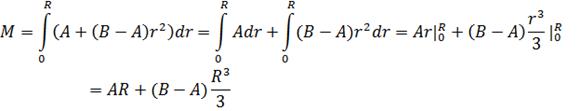
Тогда расходы на транспортировку(T) буду
равны:
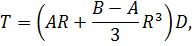
и прибыль с учётом расходов на
транспортировку- 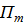
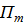 :
:
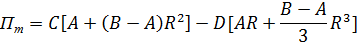
Для нахождения точек экстремума
продифференцируем это выражение и приравняем производную к нулю.
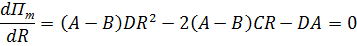
Получили квадратное уравнение:

 (*)
(*)
Найдём корни уравнения:
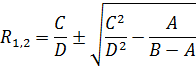
График левой части выражения (*)
является параболой и поскольку коэффициент перед 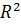
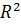 с положительным знаком, то ветви
направлены вверх (рисунок 8):
с положительным знаком, то ветви
направлены вверх (рисунок 8):
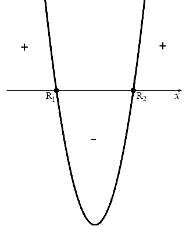
Рисунок 8
В точке 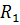
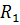 функция меняет знак с плюса на
минус, соответственно,
функция меняет знак с плюса на
минус, соответственно, 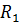
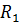 является точкой максимума.
является точкой максимума.
Таким образом, при значении радиуса
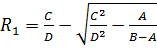
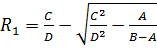
распространения товара, прибыль
будет максимальной.
Задача 2: (на
основании модели регрессионного анализа)
Выполнить регрессионный анализ по
следующим данным:
x- стоимость
товара, тыс.руб./ед.;
y- скорость
реализации, часы.
Таблица 6
|
x
|
6,0
|
7,1
|
12,1
|
15,3
|
16,2
|
18,0
|
18,8
|
|
y
|
292,8
|
275,2
|
246,8
|
220,3
|
215,6
|
220,4
|
204,3
|
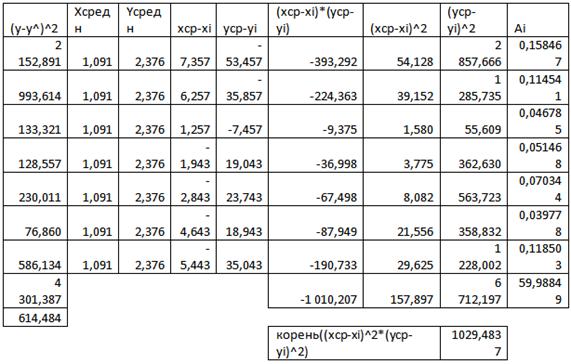
Произведём расчёты:
Для решения задачи регрессионного анализа в MS
Excel было выбрано в меню Сервис "Пакет анализа" и инструмент анализа
"Регрессия". Задаем входные интервалы X и Y. Входной интервал Y - это
диапазон зависимых анализируемых данных. Входной интервал X - это диапазон
независимых данных, которые необходимо проанализировать. На выходе процедуры в
выходном диапазоне получаем отчет, приведенный в таблицах.
Таблица вывода итогов представлена в приложении
6.
Таблица расчёта величин и коэффициентов
представлена в приложении 7.
Получили уравнение регрессии:
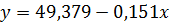
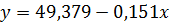 .
.
Построим график уравнения регрессии.
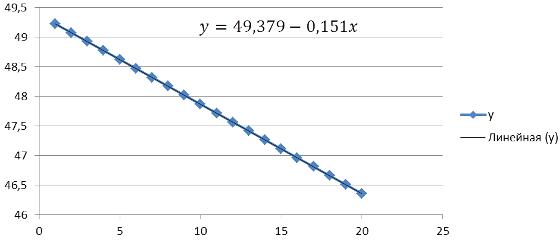
Отрицательный наклон (убывающая линейная
регрессия) - означает, что продажи происходят при значениях индикатора,
больших, чем ноль. Это можно увидеть из фрагмента:
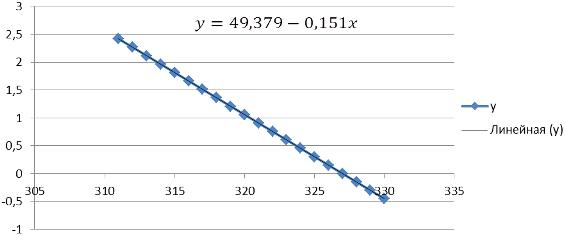
При значении 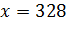
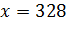 , значение
, значение 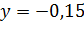
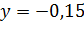 , произойдёт остановка продаж. То
есть если стоимость товара будет иметь значение равное
, произойдёт остановка продаж. То
есть если стоимость товара будет иметь значение равное 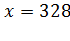
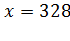 (тыс. руб.) потребители перестанут
покупать этот товар. Так же об этом говорит и скорость реализации товара
(тыс. руб.) потребители перестанут
покупать этот товар. Так же об этом говорит и скорость реализации товара 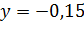
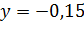 . Пока
. Пока 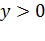
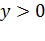 продажа будет осуществляться, но
уже с меньшим успехом. Таким образом, чем меньше цена, тем быстрее реализуется
продукция.
продажа будет осуществляться, но
уже с меньшим успехом. Таким образом, чем меньше цена, тем быстрее реализуется
продукция.
Проверку значимости уравнения регрессии
произведём на основе вычисление F-критерия
Фишера:
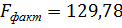
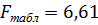
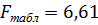 (при уровне значимости
(при уровне значимости 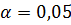
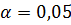 )
)

 , следовательно уравнение регрессии
следует признать адекватным.
, следовательно уравнение регрессии
следует признать адекватным.
Величина R-квадрат, которую
называют также мерой определенности, характеризует качество полученной
регрессионной прямой. Это качество выражается степенью соответствия между
исходными данными и регрессионной моделью. Значение 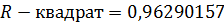
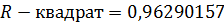 - близко к единице, это говорит о
хорошем качестве построенной модели.
- близко к единице, это говорит о
хорошем качестве построенной модели.
Коэффициент корреляции выражает
степень зависимости независимых переменных и зависимой переменной, 
 связь между переменными сильная.
связь между переменными сильная.
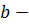
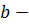 коэффициент регрессии, показывает
на сколько процентов уменьшится результативный показатель
коэффициент регрессии, показывает
на сколько процентов уменьшится результативный показатель 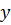
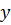 при изменении фактора
при изменении фактора 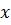
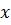 на
на 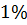
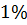 . В нашем случае
. В нашем случае 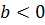
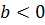 , следовательно с увеличением
, следовательно с увеличением 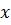
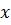 , снижается
, снижается 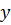
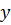 .
.
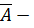
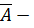 средняя ошибка аппроксимации,
показывает насколько расчётные значения отклоняются от фактических.
средняя ошибка аппроксимации,
показывает насколько расчётные значения отклоняются от фактических.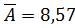
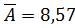 , а т.к. допустимый предел значений
, а т.к. допустимый предел значений 
 не более
не более 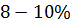
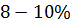 , качество модели по данному
показателю удовлетворительное. Однако средняя ошибка аппроксимации не является
главным критерием оценки значимости модели.
, качество модели по данному
показателю удовлетворительное. Однако средняя ошибка аппроксимации не является
главным критерием оценки значимости модели.
Таким образом, в результате использования
регрессионного анализа в пакете Microsoft Excel:
построено уравнение регрессии;
установлена форма зависимости и
направление связи между переменными
определена форма уравнения:
отрицательная линейная регрессия, которая выражается в равномерном убывании
функции;
установлено направление связи между
переменными;
оценено качество полученной модели;
подсчитано отклонение расчетных
данных от исходных данных;
Можно считать, что построенная
модель и прогнозные значения обладают достаточной надежностью.
Прогнозные значения, полученные
таким способом, являются средними значениями, которые можно ожидать.
Анализируя данные и показатели,
можно сказать, что связь между стоимостью товара и скоростью реализации
существует, и она высокая.
Задача 3:
(использование модели построения нормального и экспоненциального законов
распределения вероятностей).
Имеются данные о рентабельности
организаций (без субъектов малого бизнеса) РФ, в % (таблица 7). Необходимо
вычислить параметры нормального и экспоненциального законов распределения
вероятностей, построить графики законов распределения вероятностей.
Таблица 7
|
Год
|
Рентабельность
|
|
1995
|
15,8
|
|
1996
|
4,8
|
|
1997
|
6,3
|
|
1998
|
8,1
|
|
1999
|
18,5
|
|
2000
|
18,9
|
14,4
|
|
2002
|
10,9
|
|
2003
|
10,2
|
|
2004
|
13,2
|
|
2005
|
13,5
|
|
2006
|
13,2
|
|
2007
|
13,1
|
|
2008
|
13
|
|
2009
|
10,8
|
|
2010
|
10
|
|
2011
|
9,6
|
Вычисления:
. Построим интервальный ряд статистического
распределения для рентабельности организаций.
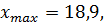
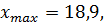


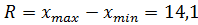
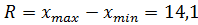
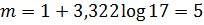
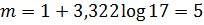
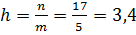
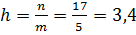
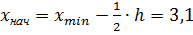
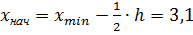
Таблица 8
|
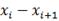
|
[3,1; 6,5)
|
[6,5; 9,9)
|
[9,9; 13,3)
|
[13,3; 16,7)
|
[16,7; 20,1)
|
|
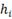
|
2
|
2
|
8
|
3
|
2
|
|

|
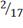
|
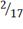
|
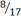
|
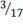
|
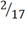
|
2. Определим параметры для нормального и
экспоненциального распределений. Расчёт данных произведён в программе Microsoft
Excel.
Таблица 9
|
№
|
Xi
|
Хср-Xi
|
(Хср-Xi)^2
|
|
1
|
15,8
|
-3,7824
|
14,306194
|
|
2
|
4,8
|
7,21765
|
52,094429
|
|
3
|
6,3
|
5,71765
|
32,691488
|
|
4
|
8,1
|
3,91765
|
15,347958
|
|
5
|
18,5
|
-6,4824
|
42,0209
|
|
6
|
18,9
|
-6,8824
|
47,366782
|
|
7
|
14,4
|
-2,3824
|
5,6756055
|
|
8
|
10,9
|
1,11765
|
1,2491349
|
|
9
|
10,2
|
1,81765
|
3,3038408
|
|
10
|
13,2
|
-1,1824
|
1,3979585
|
|
11
|
13,5
|
-1,4824
|
2,1973702
|
|
12
|
13,2
|
-1,1824
|
1,3979585
|
|
13
|
13,1
|
-1,0824
|
1,1714879
|
|
14
|
13
|
-0,9824
|
0,9650173
|
|
15
|
10,8
|
1,21765
|
1,4826644
|
|
16
|
10
|
2,01765
|
4,0708997
|
|
17
|
9,6
|
2,41765
|
5,8450173
|
|
Сумма
|
17
|
204,3
|
0
|
232,58471
|
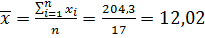
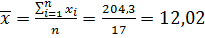
среднеквадратическое
отклонение:
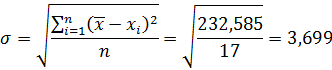
параметр экспоненциального
распределения:
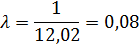
вид нормального закона:
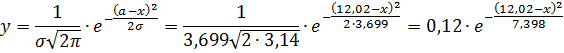
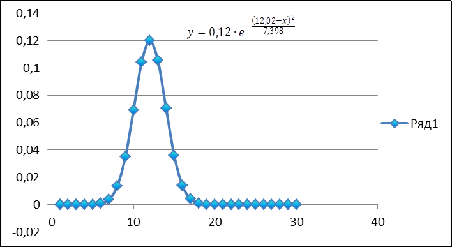
вид экспоненциального закона:
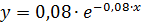
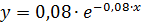

3. Рассчитаем вероятности (для нормального
распределения) для каждого из интервалов:

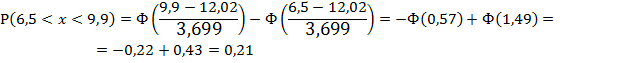
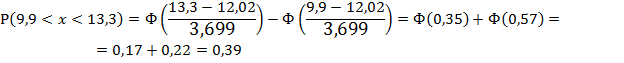
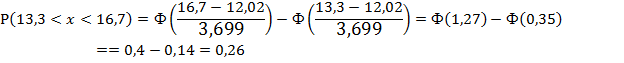
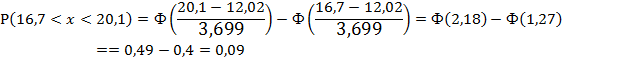
Рассчитаем 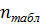
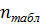 для каждого интервала:
для каждого интервала:
1) 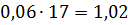
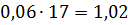
) 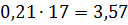
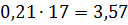
) 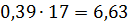
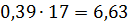
) 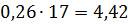
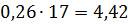
) 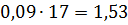
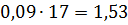
Рассчитаем значения
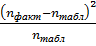
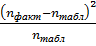
для каждого интервала:
) 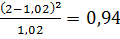
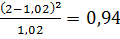
) 

) 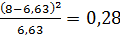
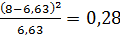
) 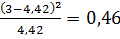
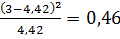
) 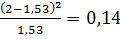
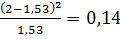
Запишем значение 
 при нормальном распределении:
при нормальном распределении:

4. Рассчитаем значение 
 при экспоненциальном распределении:
при экспоненциальном распределении:
Таблица 10
|
Середина
инт.
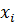 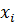 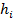 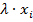 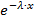 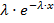 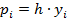 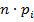 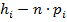 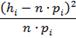
|
|
|
|
|
|
|
|
|
|
4,8
|
2
|
0,384
|
0,681
|
0,054
|
0,185
|
3,15
|
-1,15
|
0,42
|
|
8,2
|
2
|
0,656
|
0,519
|
0,042
|
0,141
|
2,4
|
-0,4
|
0,07
|
|
11,6
|
8
|
0,928
|
0,395
|
0,032
|
0,108
|
1,8
|
6,17
|
20,84
|
|
15
|
3
|
1,2
|
0,301
|
0,024
|
0,082
|
1,4
|
1,61
|
1,85
|
|
18,4
|
2
|
1,472
|
0,229
|
0,018
|
0,062
|
1,06
|
0,92
|
0,83
|
Запишем значение 
 :
:
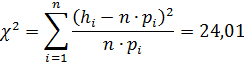
Сравним полученные результаты:
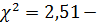
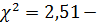 при нормальном распределении,
при нормальном распределении,
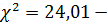
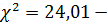 при экспоненциальном распределении.
при экспоненциальном распределении.
Следовательно, теоретическое
нормальное распределение в большей степени соответствует фактическому, чем
экспоненциальное.
Задача 4: (использование
модели биномиального распределения вероятностей)
База снабжает 10 магазинов.
Вероятность наступления заявки от одного магазина - 0,4. Определить
наивероятнейшее число заявок, вероятность поступления наивероятнейшего числа
наступления заявок, вероятность поступления заявок от 5 магазинов.
Вычисления:
1) 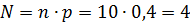
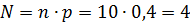
2) Вероятность поступления наивероятнейшего
числа заявок определяется по формуле Бернулли:
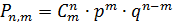
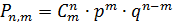
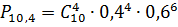
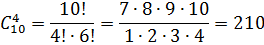
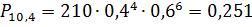
) Вероятность поступления заявок от 5
магазинов:
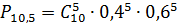
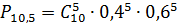
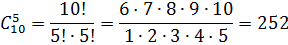
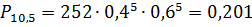
Теперь построим график распределения
вероятностей, для этого нужно рассчитать остальные вероятности поступления
заявок от магазинов:
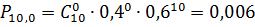
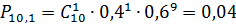
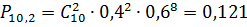
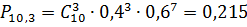
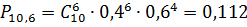
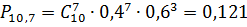
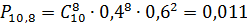
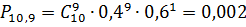
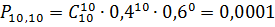
Занесём данные в таблицу(11), и на основании
вычисленных значений построим график:
Таблица 11
|
m
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
P(10,m)
|
0,006
|
0,04
|
0,121
|
0,215
|
0,251
|
0,201
|
0,112
|
0,052
|
0,011
|
0,002
|
0,0001
|
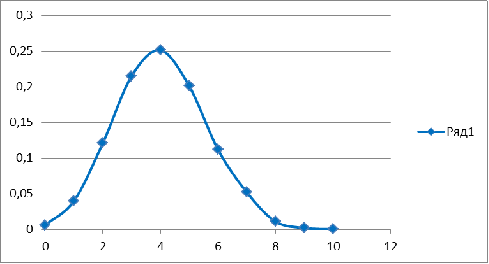
Выполнив вычисления, было определено
наивероятнейшее число заявок 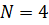
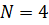 . Это говорит о том, что на базу
придёт 4 заявки. Вероятность поступления наивероятнейшего числа наступления
заявок
. Это говорит о том, что на базу
придёт 4 заявки. Вероятность поступления наивероятнейшего числа наступления
заявок 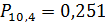
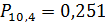 . Из вычисленных вероятностей
поступления заявок на базу, вероятность
. Из вычисленных вероятностей
поступления заявок на базу, вероятность 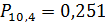
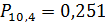 является большей из всех остальных,
так же это можно увидеть на графике распределения вероятностей. До
является большей из всех остальных,
так же это можно увидеть на графике распределения вероятностей. До 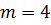
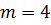 вероятность поступления заявок на
базу возрастает, после чего убывает. Вероятность поступления заявок от 5
магазинов
вероятность поступления заявок на
базу возрастает, после чего убывает. Вероятность поступления заявок от 5
магазинов 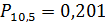
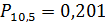 и
и 
 .
.
Задача 5:
(Использование модели межотраслевого баланса)
Даны коэффициенты прямых затрат и
значение величины конечного потребителя (таблица 12). Требуется:
) Найти матрицу коэффициентов прямых
затрат
) Составить баланс производства и
распределения продукции;
) Найти конечный продукт каждой
отрасли для новых значений валовых продуктов отраслей
) Найти валовой продукт каждой
отрасли для новых значений конечных продуктов отраслей
Таблица 12
|
Отрасли
производства
|
Потребляющие
отрасли
|
Конечный
продукт
|
Валовой
продукт
|
|
1
|
2
|
3
|
|
|
|
А
|
6
|
36
|
20
|
40
|
102
|
|
B
|
12
|
12
|
20
|
50
|
94
|
|
C
|
22
|
12
|
12
|
10
|
56
|
Решение:
1. Найдем матрицу коэффициентов прямых затрат.
Используя значения из таблицы 12, вычислим
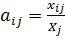
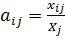 .
.
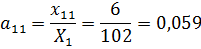
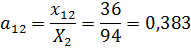
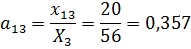
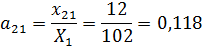
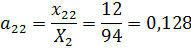
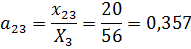
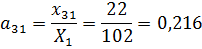
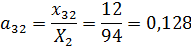
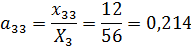
Получим следующую матрицу прямых затрат:
Таблица 13
|
1
|
2
|
3
|
|
A
|
0,059
|
0,383
|
0,357
|
|
B
|
0,118
|
0,128
|
0,357
|
|
C
|
0,216
|
0,128
|
0,214
|
Составим баланс производства и распределения
продукции. Модель баланса производства и распределения продукции отрасли можно
представить следующей системой уравнений:
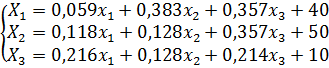
Найдем матрицу полных затрат
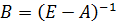
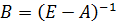 .
.
Вычисления проводятся в программе MathCad.
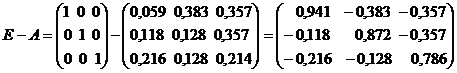
Элементы матрицы B
рассчитываются по формуле
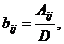
 ;
;  ,
,
где 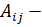
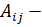 алгебраические дополнения элементов
матрицы
алгебраические дополнения элементов
матрицы 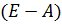
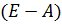 ;
;
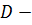
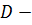 определитель матрицы
определитель матрицы 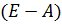
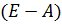 .
.
Определитель матрицы 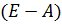
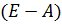 :
:
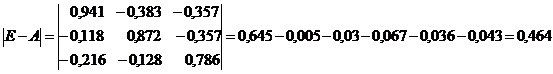
Расчет алгебраических дополнений
матрицы 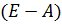
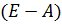 дает следующие результаты:
дает следующие результаты:

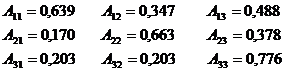
Составим матрицу 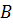
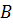 :
:

Вычисление нового конечного продукта
при измененном валовом выпуске:
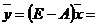
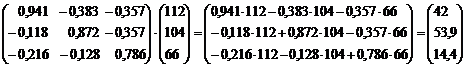
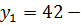
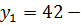 конечный продукт
конечный продукт 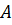
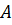 ,
,
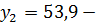
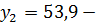 конечный продукт B,
конечный продукт B,
Вычисление нового валового продукта
при измененном конечном потреблении
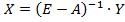
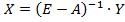
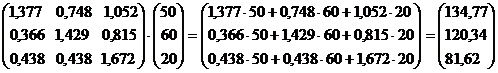
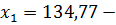
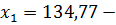 валовая продукция A,
валовая продукция A,

 валовая продукция B,
валовая продукция B,
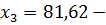
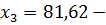 валовая продукция C.
валовая продукция C.
Задача 6:
(использование модели, определяющей оптимальный размер партии поставки)
Дано: Потребность предприятия в
продукции- 600(тонн/год), издержки содержания запаса- 15(руб./ тонн в год),
условно- постоянные расходы- 45(руб).
Необходимо определить:
1) Оптимальный размер партии поставки
2) Общие затраты содержания запаса и
выполнения поставок
3) Составить таблицу, которая
показывает влияние величины партий поставок на общие издержки 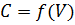
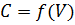 , при размерах партий в тоннах: 20,
40, 60, 80, 100, 120.
, при размерах партий в тоннах: 20,
40, 60, 80, 100, 120.
) Составить таблицу
показывающую влияние стоимости запаса на оптимальный размер партии поставки при
таких издержках хранения, руб/тонн в год: 5, 10, 15, 20, 25, 30.
Решение: 1)Запишем условие задачи с помощью
обозначений:
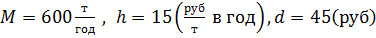
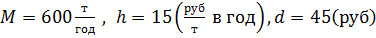
Найдём оптимальный размер партии
поставки по формуле (9):
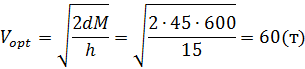
2) Общие затраты содержания запаса и
выполнения поставок найдём по формулам (6), (7), (5), (4) соответственно:
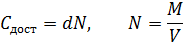
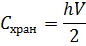
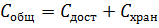
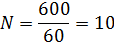
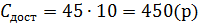
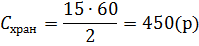
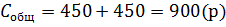
3) Чтобы выявить влияние величины партий
поставок на общие издержки, воспользуемся формулой (4):
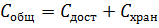
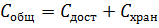
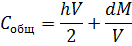
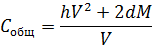
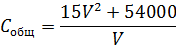
Таблица 14
|
V
|
20
|
40
|
60
|
80
|
100
|
120
|
|
C
|
3000
|
1950
|
1800
|
1875
|
2040
|
2250
|
Из расчёта видим, что общие издержки
уменьшаются до 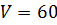
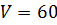 , после
, после 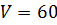
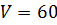 издержки начинают возрастать. Это
означает то, что если брать величину партий более 60 единиц, то придётся больше
расходов на хранений партий. Оптимальным решением будет являться величина
партий равная
издержки начинают возрастать. Это
означает то, что если брать величину партий более 60 единиц, то придётся больше
расходов на хранений партий. Оптимальным решением будет являться величина
партий равная 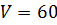
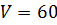 , при этом будут самые минимальные
расходы на её хранение.
, при этом будут самые минимальные
расходы на её хранение.
4) Для выявления влияния стоимости запаса на
оптимальный размер партии поставки, воспользуемся формулой (5):
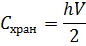
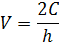
Стоимость запаса хранения (С) прямо
пропорциональна размеру партии поставки, т.е. 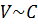
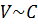 , следовательно, при увеличении C, будет
увеличиваться V. Так же это
можно увидеть из таблицы (15):
, следовательно, при увеличении C, будет
увеличиваться V. Так же это
можно увидеть из таблицы (15):
Таблица 15
|
С
|
5
|
10
|
15
|
20
|
25
|
30
|
|
V
|
0,667
|
1,334
|
2
|
2,667
|
3,334
|
4
|
Заключение
На данном этапе работы удалось достаточно
подробно рассмотреть применение математических методов в логистике.
В ходе наших исследований были решены все
поставленные задачи, а именно:
. Изучен материал по логистике, методам
решения логистических задач;
2. Проанализирована литература по данной
теме;
. Отобран и систематизирован необходимый
теоретический материал;
. Изучены методы решения логистических
задач;
. Рассмотрены следующие модели: модель,
определяющая оптимальный размер партии поставки, модель определения места
дислокации, модель межотраслевого баланса, а так же такие логистические задачи
как: определение периодичности потребления электроэнергии, построение
распределения вероятностей величины спроса на определённый товар, определение
уровня издержек от величины товарооборота;
. Приведено решение логистических задач,
с использованием математических моделей.
Список использованных источников
1. Лукинский В.С. Модели и методы
теории логистики: учебное пособие. СПб.: Питер, 2007. - 448 с.
2. Щербакова В.В. Основы
логистики. - СПб.: Питер, 2009. - 432 с.
. Н.Г. Филонов. Логистика:
учебное пособие. Томск: Издательство
томского педагогического
университета, 2008.- 250 с.
. Плоткин Б.К.
Экономико-математические методы и модели в управлении материальными ресурсами.
- СПб.: Издательство СПбУЭФ, 1992. - 64 с.
5. Фомин Г.П. Математические
методы и модели в коммерческой деятельности. - М.: Финансы и статистика, 2005.
- 616 с.
. Экланд И. Элементы
математической экономики / Перевод с англ. - М.:
Мир, 1983. - 248 с.
. Экономико-математические
методы в снабжении. Под общей редакцией профессора В.М. Лагуткина. - М.:
Экономика, 1971. -367 с.
8. Кантрович Л.В.
Математические методы организации и планирования производства. - Л.:
Издательство ЛГУ, 1939.
. Леонтьев В.В. Экономические
эссе. Теории, исследования, факты и политика: Перевод с англ. М.: Политиздат,
1990. - 415 с.
. Плоткин Б.К., Делюкин Л.А.,
Экономико-математические методы и модели в логистике: Учебное пособие. СПб.:
Изд-во СПбГУЭФ, 2010. - 96 с.
. Хазанова Л.Э. Логистика:
Методы и модели управления материальными потоками: Учебник. М.: Изд-во БЕК,
2003. - 120 с.
. Елисеева И.И., Курышева
С.В., Гордеенко Н.М. и др. Практикум по эконометрике: Учебное пособие. Под
редакцией И.И. Елисеевой. М.:Финансы и статистика, 2002.-192 с.
. Лубенцова В.С.
Математические модели и методы в логистике. Учебное пособие. Под редакцией В.П.
Радченко. - Самара. Самар. гос. техн. ун-т. 2008. - 157 с.
. Гмурман В.Е. Теория
вероятностей и математическая статистика. Учебник для вузов. 9-е издание, стер.
- М.: Высшая школа, 2003.- 479 с.
. Аникин Б.А. Логистика:
тренинг и практикум: учебное пособие. М.:Проспект, 2007. - 439с.
. #"663002.files/image401.gif">
Рисунок 9
Решение:
Обозначим расстояние 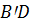
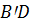 через
через 
 . Тогда
. Тогда
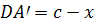
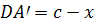
 ,
,
отсюда получаем длину пути:
по суше:
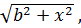
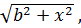
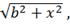
по морю:
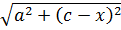
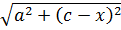
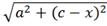 .
.
Стоимость перевозки одной тонны
груза из B в A
в A выразится
следующим образом:
выразится
следующим образом:
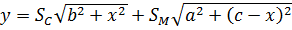
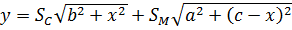
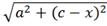
Определим минимум полученной
функции, для чего найдем первую производную и приравняем ее к нулю:
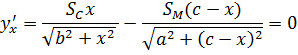
из чего следует:
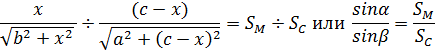
Таким образом перевалочную базу 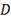
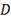 следует расположить так, чтобы
выполнялось равенство:
следует расположить так, чтобы
выполнялось равенство:
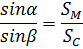
Приложение 3. Определение
периодичности потребления электроэнергии
Решение: Рассчитаем периодическую
функцию с четырьмя гармониками.
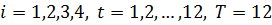
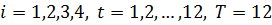
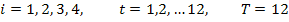
Определим коэффициент:
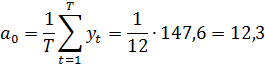
Получаем, что 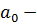
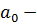
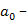 есть средняя величина из исходных
данных, т.е. в нашем случае средний удельный расход электроэнергии.
есть средняя величина из исходных
данных, т.е. в нашем случае средний удельный расход электроэнергии.
Расчёт коэффициентов 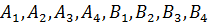
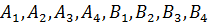
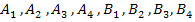 произведём с помощью таблицы 16:
произведём с помощью таблицы 16:
Таблица 16. 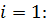
|
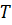
|
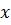
|
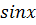
|
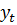
|
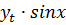
|
|
1
|
30
|
0,5
|
15,5
|
7,75
|
|
2
|
60
|
0,866
|
14,3
|
12,38
|
|
3
|
90
|
1
|
15,2
|
15.2
|
|
4
|
120
|
0,866
|
14,6
|
12,64
|
|
5
|
150
|
0,5
|
11,2
|
5,6
|
|
6
|
180
|
0
|
8,4
|
0
|
|
7
|
210
|
-0,5
|
8,0
|
-4
|
|
8
|
240
|
-0,866
|
8,2
|
-7,1
|
|
9
|
270
|
-1
|
8,7
|
-8,7
|
|
10
|
300
|
-0,866
|
14,0
|
-12,12
|
|
11
|
330
|
-0,5
|
14,5
|
-7,25
|
|
12
|
360
|
0
|
15,0
|
0
|
|
Итого:
|
14,4
|
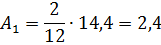
Таким же образом можно рассчитать остальные
коэффициенты, тогда получим теоретическую периодичность удельного расхода
электроэнергии, которая выражается следующей функцией:
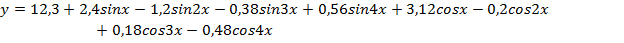
В таблице 17 приведено сравнение фактических
данных с расчётными.
Таблица 17
|
Месяца
|
Фактические
данные
|
Расчётные
данные
|
Отклонения
|
|
1
|
15,5
|
15,41
|
0,09
|
|
2
|
14,3
|
14,57
|
0,27
|
|
3
|
15,2
|
14,8
|
0,4
|
|
4
|
14,6
|
14,86
|
0,26
|
|
5
|
11,2
|
11,11
|
0,09
|
|
6
|
8,4
|
8,32
|
0,08
|
|
7
|
8,0
|
8,36
|
0,36
|
|
8
|
8,2
|
7,66
|
0,54
|
|
9
|
8,7
|
9,24
|
1,04
|
|
10
|
14,0
|
13,47
|
0,53
|
|
11
|
14,5
|
14,88
|
0,38
|
|
12
|
15,0
|
14,92
|
0,08
|
Приложение 4. Распределение
вероятностей величины спроса на данный товар
Для построения нормального и
экспоненциального законов распределения вероятностей вычислим среднее значение
реализации товара в день 

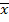 , среднеквадратическое отклонение σ, а так же
параметр экспоненциального закона λ. Для расчёта указанных величин
ряд фактических данных упорядочивается от
, среднеквадратическое отклонение σ, а так же
параметр экспоненциального закона λ. Для расчёта указанных величин
ряд фактических данных упорядочивается от 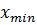
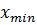
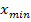 до
до 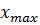
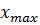
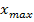 .
.
Вычисления:
1) среднее значение реализации:
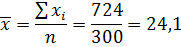
2) среднеквадратическое отклонение:
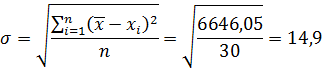
3) параметр экспоненциального распределения:
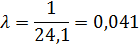
4) вид нормального закона:
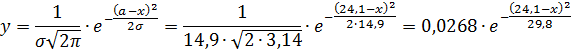
5) вид экспоненциального закона:
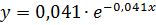
Таблица 18. Расчёт средней реализации и
среднеквадратического отклонения
|
№
|
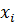
|
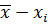
|
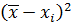
|
|
1
|
3,5
|
20,64333333
|
426,1472111
|
|
2
|
3,8
|
20,34333333
|
413,8512111
|
|
3
|
2,7
|
21,44333333
|
459,8165444
|
|
4
|
14,5
|
9,643333333
|
92,99387778
|
|
5
|
18,3
|
5,843333333
|
34,14454444
|
|
6
|
13,4
|
10,74333333
|
115,4192111
|
|
7
|
7,5
|
16,64333333
|
277,0005444
|
|
8
|
24,8
|
-0,656666667
|
0,431211111
|
|
9
|
16,5
|
7,643333333
|
58,42054444
|
|
10
|
12,4
|
11,74333333
|
137,9058778
|
|
11
|
34,5
|
-10,35666667
|
107,2605444
|
|
12
|
41,2
|
-17,05666667
|
290,9298778
|
|
13
|
27,4
|
-3,256666667
|
10,60587778
|
|
14
|
24,5
|
-0,356666667
|
0,127211111
|
|
15
|
25,5
|
-1,356666667
|
1,840544444
|
|
16
|
27
|
-2,856666667
|
8,160544444
|
|
17
|
29,5
|
-5,356666667
|
28,69387778
|
|
18
|
22,1
|
2,043333333
|
4,175211111
|
|
19
|
48,3
|
-24,15666667
|
583,5445444
|
|
20
|
64,5
|
-40,35666667
|
1628,660544
|
|
21
|
18,5
|
5,643333333
|
31,84721111
|
|
22
|
19,5
|
4,643333333
|
|
23
|
27,4
|
-3,256666667
|
10,60587778
|
|
24
|
35
|
-10,85666667
|
117,8672111
|
|
25
|
42
|
-17,85666667
|
318,8605444
|
|
26
|
54
|
-29,85666667
|
891,4205444
|
|
27
|
32,1
|
-7,956666667
|
63,30854444
|
|
28
|
14,5
|
9,643333333
|
92,99387778
|
|
29
|
9,4
|
14,74333333
|
217,3658778
|
|
30
|
10
|
14,14333333
|
200,0338778
|
|
Итого:30
|
724,3
|
0
|
6645,994
|
Установим интервалы значений и вычислим
фактические частоты двумя способами:) через нормальное
распределение
Таблица 19
|
№
п/п
|
Интервал
|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|
50-60
|
Свыше
60
|
Итого
|
|
1
|
Кол-во
случаев
|
6
|
8
|
8
|
3
|
3
|
1
|
1
|
30
|
|
2
|
Частоты
|
0,2
|
0,27
|
0,27
|
0,1
|
0,1
|
0,03
|
0,03
|
1
|
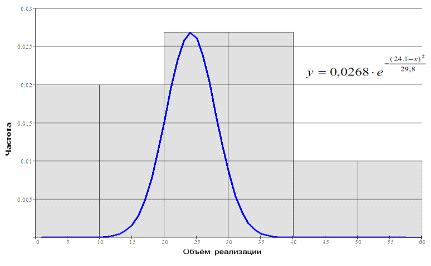
Рисунок 10
- Нормальный
закон распределения
b) через экспоненциальное распределение:
Таблица 20
|
№
п/п
|
Интервал
|
0-20
|
20-40
|
40-60
|
Свыше
60
|
Итого
|
|
1
|
Кол-во
случаев
|
14
|
11
|
4
|
1
|
30
|
|
2
|
Частоты
|
0,47
|
0,37
|
0,13
|
0,03
|
1
|
На основании полученного выражения для
экспоненциального закона определяются его теоретические значения:
Таблица 21. Построение теоретического
распределения реализации продукции по экспоненциальному распределению
|
№
|
Показатели
|
0
|
20
|
40
|
60
|
|
1
|
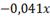
|
0
|
-0,82
|
-1,64
|
-2,46
|
|
2
|
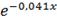
|
1
|
0,44
|
0,194
|
0,0085
|
|
3
|
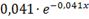
|
0,041
|
0,018
|
0,008
|
0,003
|
|
4
|
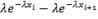
|
0,023
|
0,01
|
0,005
|
0,038
|
|
5
|
Частота
теоретическая
|
0,61
|
0,26
|
0,13
|
1
|
Вероятности по гипотезе нормального закона для
каждого интервала определяются с помощью функции Лапласа:
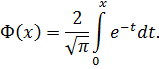
Вероятность в интервале [a;
b]:
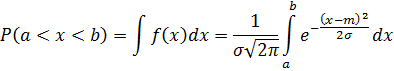
Введём обозначения:
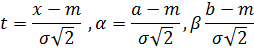
Тогда:
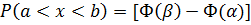
Функция Лапласа табулирована и при вычислении
вероятностей конкретных значений интервалов используются её конкретные
значения.
Чтобы проверить, насколько
соответствует теоретическое распределение фактическому, необходимо использовать
критерий согласия. Рассчитаем значение 

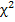 для экспоненциального и нормального
распределений. Чем меньше будет значение
для экспоненциального и нормального
распределений. Чем меньше будет значение 

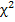 , тем больше будет уровень соответствия
данного теоретического распределения фактическому.
, тем больше будет уровень соответствия
данного теоретического распределения фактическому.
Таблица 22. Расчёты для
экспоненциального распределения
|
№
п/п
|
Величины
|
0-20
|
20-40
|
40-60
|
Свыше
60
|
Итого
|
|
1
|
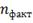
|
47
|
37
|
13
|
3
|
100
|
|
2
|
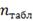
|
61
|
26
|
13
|
-
|
100
|
|
3
|
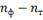
|
-14
|
11
|
0
|
3
|
0
|
|
4
|
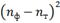
|
196
|
121
|
0
|
9
|
3
|
|
5
|
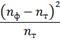
|
3,21
|
4,65
|
0
|
-
|
7,86
|
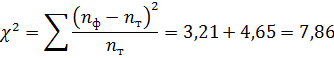
Расчёты для нормального распределения:) рассчитываются
вероятности для каждого из интервалов (с помощью табличных значений функции
Лапласа):
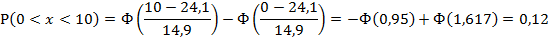
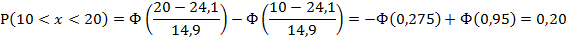
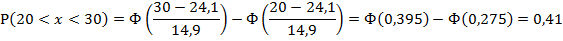
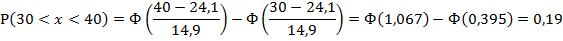
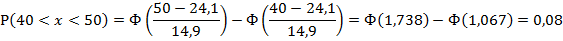
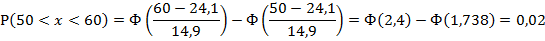
b) Рассчитываем 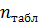
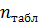
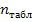 для каждого интервала:
для каждого интервала:
) 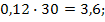
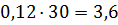
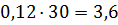
) 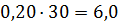
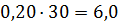
) 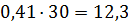
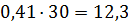
) 

) 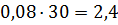
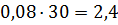
) 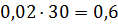
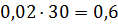
c) Рассчитываем значения
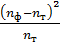
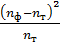
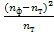
для
каждого интервала:
1) 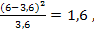
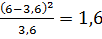
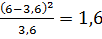
) 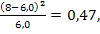
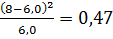
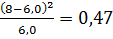
) 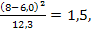
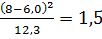
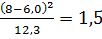
) 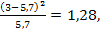


) 
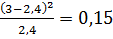
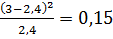
) 
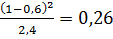
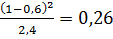
Отсюда запишем значение 
 :
:
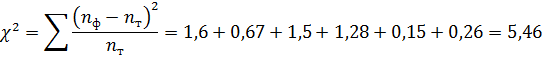
При вычислении значения 
 в качестве фактических частот
принято количество случаев.
в качестве фактических частот
принято количество случаев.
Сравним полученные результаты:
) 
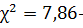 при экспоненциальном распределении
при экспоненциальном распределении
) 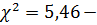
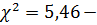
 при нормальном распределении
при нормальном распределении

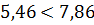 следовательно, теоретическое нормальное
распределение в большей степени соответствует фактическому, чем
экспоненциальное.
следовательно, теоретическое нормальное
распределение в большей степени соответствует фактическому, чем
экспоненциальное.
Приложение 5. Уровень издержек от
величины товарооборота
Решение: Введём данные в таблицу 23, чтобы далее
составить систему нормальных уравнений.
Таблица 23
|
№
п/п
|
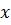
|
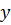
|
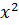
|
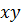
|
|
1
|
1
|
10
|
1
|
10
|
|
2
|
3
|
5
|
9
|
15
|
|
3
|
5
|
7
|
25
|
35
|
|
4
|
8
|
3
|
64
|
24
|
|
5
|
12
|
1
|
144
|
12
|
|
Всего
|
29
|
26
|
243
|
96
|
Теперь по итогам таблицы составим систему
нормальных уравнений:
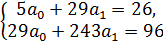
Решив эту систему, получили результат:
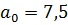
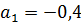
Отсюда получили уровень издержек 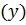
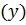
 от величины товарооборота
от величины товарооборота 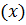
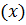
 :
:
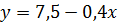
Приложение 6. Вывод итогов
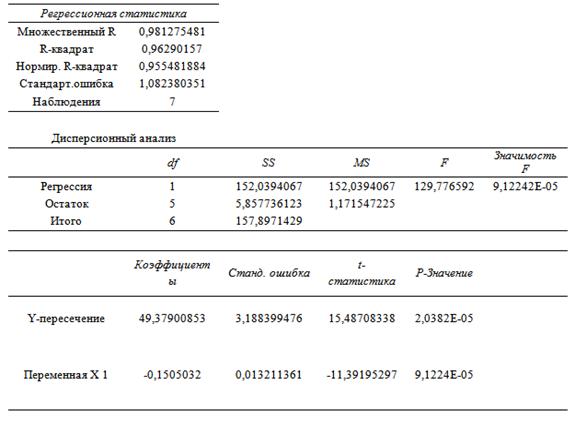
Приложение 7. Расчёт данных
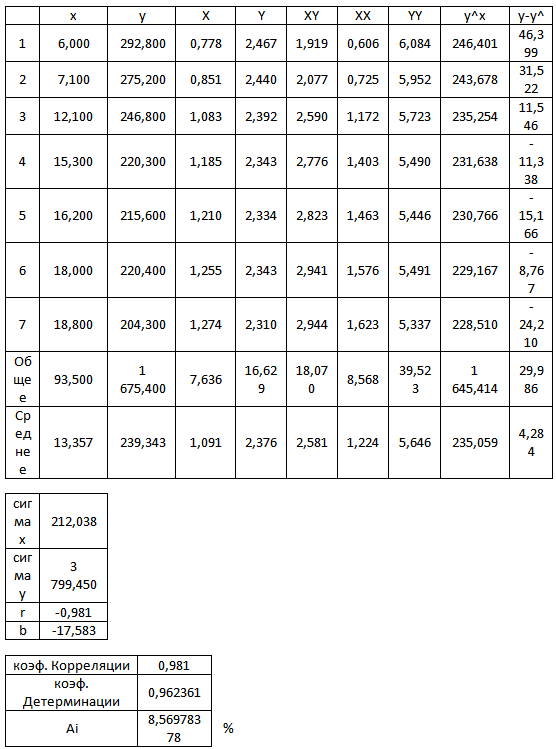
Приложение 7. Расчёт данных
(продолжение)