Метод Монте-Карло

Метод Монте-Карло

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева»

Финансово - экономический факультет

Кафедра Логистика

КУРСОВАЯ РАБОТА

по дисциплине

«Экономико-математические методы и модели в логистике»

на тему:

«Метод Монте- Карло»

Вариант 10

Выполнила студентка группы Л-92

Очной формы обучения

Домишева Елена

Руководитель:

Товстоношенко В.Н

Красноярск 2012 г.

Содержание

Введение

.                   Алгоритм Бюффона для определения числа Пи

1.1     Связь стохастических процессов и дифференциальных уравнений

.        Рождение метода Монте- Карло. Дальнейшее развитие и современность

.1 Обычный метод Монте-Карло интегрирования

.2 Интегрирование методом Монте-Карло

.3 Геометрический алгоритм Монте-Карло интегрирования

.4 Алгоритм Метрополиса

.5 Квантовый метод Монте-Карло

. Применение метода Монте-Карло в логистике

Расчетная часть

Заключение

Список используемых источников

Введение

Целью данной курсовой работы является закрепление теоретической основы по дисциплине «Экономико-математические методы и модели в логистике», тщательно научиться разбираться в дисциплине экономико-математические методы и модели, а именно: научиться определять оптимальный размер заказа комплектующих изделий для производства продукции промышленного предприятия и делать прогнозы объема продаж готовой продукции со склада промышленного предприятия за определенный период. Кроме того, приобрести навыки практического применения экономико-математических методов для моделирования реальных экономических ситуаций, возникающих в различных логистических системах, что способствует повышению эффективного управления логистическими цепями поставок и является условием успешной деятельности предприятия.

Объектом работы являются логистические товаропотоки промышленного предприятия.

Предмет работы - экономико-математические методы и модели.

Основная задача курсовой работы заключается в возможности применения различных экономико-математических методов и моделей для совершенствования показателей логистической деятельности предприятия.

Метод Монте-Карло (методы Монте-Карло, ММК) - общее название группы численных методов, основанных на получении большого числа реализаций стохастического <#"704084.files/image001.gif"> на плоскость, расчерченную параллельными прямыми, расположенными на расстоянии  друг от друга. Вероятность того, что отрезок пересечет прямую, связана с числом Пи:

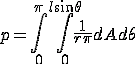, где

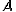- расстояние от начала иглы до ближайшей к ней прямой;

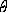- угол иглы относительно прямых.

Этот интеграл просто взять: 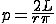 (при условии, что 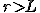), поэтому подсчитав долю отрезков, пересекающих прямые, можно приближенно определить это число. При увеличении количества попыток точность получаемого результата будет увеличиваться.

В 1864 году капитан Фокс, выздоравливая после ранения, чтобы как-то занять себя, реализовал эксперимент по бросанию иглы. Результаты представлены в следующей таблице:

Комментарии:

В третьей попытке длина иглы была больше расстояния между линиями, что позволило не увеличивая числа бросаний эффективно увеличить число событий и повысить точность.

.1 Связь стохастических процессов и дифференциальных уравнений

Создание математического аппарата стохастических методов началось в конце XIX века. В 1899 году лорд Релей показал, что одномерное случайное блуждание на бесконечной решётке может давать приближенное решение параболического дифференциального уравнения. Андрей Николаевич Колмогоров в 1931 году дал большой толчок развитию стохастических подходов к решению различных математических задач, поскольку он сумел доказать, что цепи Маркова связаны с некоторыми интегро-дифференциальными уравнениями. В 1933 году Иван Петровский показал, что случайное блуждание, образующее Марковскую цепь, асимптотически связано с решением эллиптического дифференциального уравнения в частных производных. После этих открытий стало понятно, что стохастические процессы можно описывать дифференциальными уравнениями и, соответственно, исследовать при помощи хорошо на тот момент разработанных математических методов решения этих уравнений.

.       
Рождение метода Монте-Карло

Сначала Энрико Ферми <#"704084.files/image008.gif">

Рассмотрим случайную величину 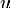, равномерно распределённую на отрезке интегрирования 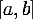. Тогда  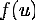так же будет случайной величиной, причём её математическое ожидание <#"704084.files/image012.gif">,

где 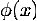 - плотность распределения случайной величины 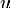, равная  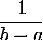на участке .

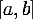Таким образом, искомый интеграл выражается как

.

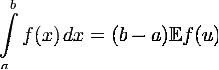Но матожидание случайной величины 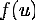 можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее.

Итак, бросаем 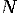 точек, равномерно распределённых на 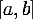, для каждой точки  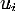вычисляем 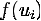. Затем вычисляем выборочное среднее:

.

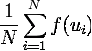В итоге получаем оценку интеграла:

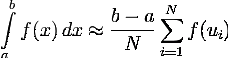
Точность оценки зависит только от количества точек .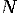

Этот метод имеет и геометрическую интерпретацию. Он очень похож на описанный выше детерминистический метод, с той разницей, что вместо равномерного разделения области интегрирования на маленькие интервалы и суммирования площадей получившихся «столбиков» мы забрасываем область интегрирования случайными точками, на каждой из которых строим такой же «столбик», определяя его ширину как 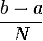, и суммируем их площади.

.2 Интегрирование методом Монте-Карло

Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла <#"704084.files/image022.gif"> <#"704084.files/image023.gif"> частиц описываемой функцией гамильтониана 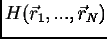, где 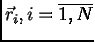 задает все степени свободы одной частицы (например 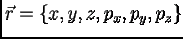). Вектор  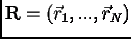задает одно состояние системы. Множество состояний системы составляет доступное ей фазовое пространство 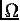. Тогда среднее значение величины 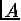, являющейся функцией состояния системы, дается интегралом

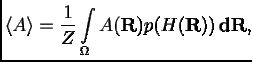                                                          (1.1)

где 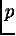 -- функция распределения, а в знаменателе находится статистическая сумма

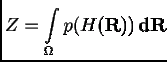                                                                           (1.2)

Если система состоит из небольшого числа частиц и размерность пространства 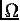 мала, то интеграл (1.1) можно вычислить, используя обычные формулы для приближенного численного вычисления интегралов с заданной точностью. Однако при большом 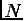, когда кратность интеграла становится большой, такой подход малопродуктивен, т.к. затраты на вычисления зависят экспоненциально от .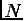

Другой способ, носящий имя метода Монте Карло^1.1, основан на стохастическом переборе точек в фазовом пространстве с предпочтительной выборкой тех областей из 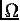, которые дают существенный вклад в интеграл (1.1).

Таким образом, в соответствии с функцией распределения 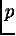 генерируется цепь состояний в фазовом пространстве, вдоль которой и вычисляется интеграл (1.1). При количестве элементов в цепи, стремящемся к бесконечности, мы получаем точное значение среднего. При конечной же длине цепи погрешность такого способа вычисления интеграла гораздо меньше погрешности получаемой обычными методами при тех же затратах.

Обычно генерируется марковская цепь, т.е. такая последовательность, в которой последующее состояние зависит только от настоящего состояния и не зависит «от прошлого». Математически это означает, что условная вероятность 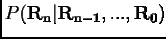 появления состояния 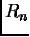 после последовательности 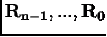 равна вероятности .

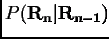Один из возможных способов реализации марковского процесса, обладающего заданной функцией распределения, излагается ниже в параграфе 1.2.1. А сейчас мы конкретизируем вид распределения.

Для классической системы в тепловом равновесии при температуре 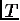 функция распределения дается законом Больцмана:

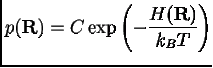                                                                  (1.3)

Если часть 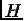, зависящая от импульсов, отделяется от координатной части, и энергия взаимодействия частиц не зависит от импульсов, как имеет место для пылевой плазмы (см. главу <#"704084.files/image029.gif"> не зависит от импульсов частиц (например, конфигурации минимумов, корреляционные функции), то интеграл по импульсам в формуле (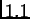) выносится из числителя и знаменателя и сокращается. Тем самым достаточно рассмотреть не все фазовое пространство, а только его конфигурационную часть.

Для квантовой системы среднее от величин, операторы которых диагональны в координатном представлении, описывается все той же формулой (1.1 <#"704084.files/image041.gif">                                                                                  (1.4)

Однако для квантовой системы возможен и другой подход, использующий матрицу плотности 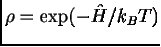. Тогда математическое ожидание величины 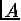, которой соответствует оператор 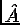, при любом значении температуры 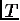 может быть вычислено по формуле

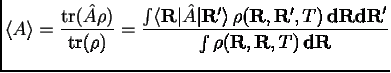                                   (1.5)

Этот интеграл можно взять при помощи метода Монте- Карло интегрирования по траекториям.

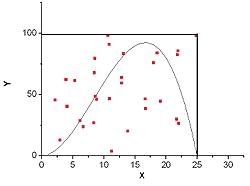
.3 Геометрический алгоритм Монте-Карло интегрирования

 <#"704084.files/image046.gif">

Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

.4 Алгоритм Метрополиса

В алгоритме Метрополиса на каждом шаге марковского процесса по имеющейся конфигурации строится следующая изменением одной из степеней свободы (переворотом одного спина). Новая конфигурация принимается (т.е. спин переворачивается) с вероятностью, равной отношению гиббсовских весов новой и старой конфигураций₁₂ = exp[(E₁-E₂)/T]при E₁ < E₂ ; W₁₂ = 1при E₁ > E₂

где E₁, E₂ - энергии старой и новой конфигураций спинов соответственно. Если новая конфигурация отбрасывается, то старая используется в усреднении еще один раз. В асимптотическом пределе частота прохождения через данное состояние оказывается пропорциональной его вероятностному (гиббсовскому) весу. Средние вычисляются с использованием полученных конфигураций (более подробное описание алгоритма можно посмотреть у Казакова или Гулда и Тобочника). Алгоритм Метрополиса может быть легко применен для моделирования фазового перехода в XY модели.

Далее мы убедимся, что выбирать W₁₂ можно различными способами. Для того, чтобы итерационный процесс в асимптотическом пределе приводил к распределению Гиббса достаточно, чтобы вероятности перехода удовлетворяли принципу детального равновесия

₁₂ exp(-E₁/T) = W₂₁ exp(-E₂ /T) или W₁₂ / W₂₁ = exp[(E₁-E₂ )/T].

Используемое Java приложение основывается на программах приведенных в книге Гулда и Тобочника. Алгоритм Метрополиса (случайный переворот спина) последовательно применяется ко всем ячейкам решетки после чего выводятся "мгновенные" значения E_t, M_t и вычисляются средние по "марковскому" времени

<M>_M = 1/T ∑_t=1,T M_t , <E>_M = 1/T ∑_t=1,T E_t .

Теплоемкость C и магнитная восприимчивость χ системы могут быть определены по величине флуктуаций энергии и намагниченности из формул

= d<E>/dT = n/T² (<E²> - <E>²) ,

χ = lim_{H→ 0} d<M>/dT = n/T (<M²> - <M>²) .

Прямое моделирование методом Монте-Карло

Прямое моделирование методом Монте-Карло какого-либо физического процесса подразумевает моделирование поведения отдельных элементарных частей физической системы. По сути это прямое моделирование близко к решению задачи из первых принципов <#"704084.files/image047.gif">                   (1),

где J-обменное взаимодействие, h-внешнее магнитное поле. В соответствии с формулой Зазуки-Троттера статсумма преобразуется следующим образом:

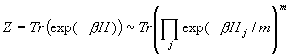                 (2),

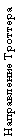
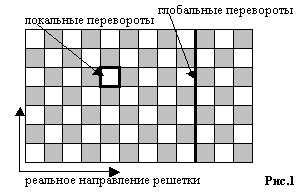
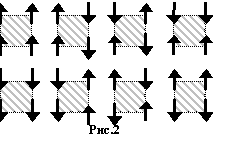
где Hj-локальные взаимодействия, такие что H=SjHj, а m - целое положительное число, называемое числом Троттера. Таким образом, система переходит в двухмерную модель с шахматным расположением четырех спинов. Графическое представление дано на Рис.1, где затемненные квадратики означают взаимодействия четырех спинов. На Рис.2 видно четырехспиновые конфигурации позволенные для S=1/2. Обычно такие конфигурации называют <плакетами>. Таким образом, в системе L´m плакетов. При обновлении системы необходимо перевернуть все спины в плакете в силу закона сохранения. Преобразуя гамильтониан (1) с помощью спиноров

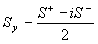
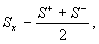                 (3)

и принимая J_x=J_y=J^{^} получаем

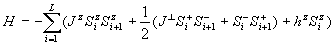                 (4).

Матричные элементы гамильтониана (4) имеют следующий вид:

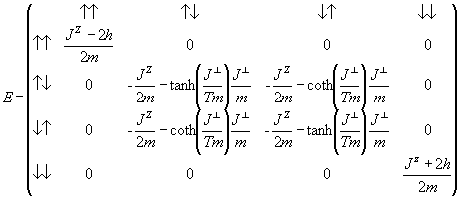           (5)

а также вычисляется матрица вероятностей участвующих в статсумме (2):

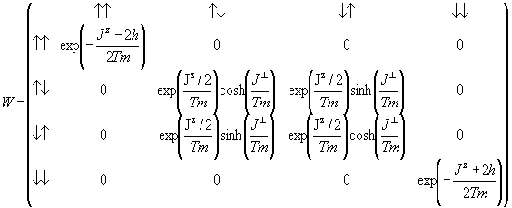(6)

Теперь известно, с какой вероятностью четырехспиновая конфигурация (плакет) может перейти в другую конфигурацию при перевороте всех четырех спинов.

В процедуре Монте-Карло используются два типа переворотов: локальные и глобальные (Рис.1). Локальные перевороты происходят следующим образом: вычисляется произведение (WOld) матричных элементов W четырех затемненных плакетов вокруг локального переворота (незакрашенный плакет), затем переворачиваем четыре спина в этом незакрашенном плакете и снова считаем произведение (WNew) матричных элементов W, выбирается случайное число x в интервале [0..1] и сравнивается с WNew/WOld. Если x меньше этого значения то принимается новая конфигурация плакета, иначе остается старая. Таким образом мы проходим всю решетку. Глобальные перевороты: вычисляется произведение вероятностей затемненных плакетов находящихся по обе стороны от вертикальной линии (Рис.1 жирная вертикальная линия), затем переворачиваются все спины которые находятся на вертикальной линии и снова считается произведение вероятностей плакетов вдоль линии, дальше та же процедура как и с локальными переворотами. В вычислениях по методу Монте-Карло используются периодические граничные условия по троттеровскому и реальному направлению решетки. Один шаг Монте-Карло определяется поворотом всех спинов на решетке (решетка L´2m). Размер решетки выбирается по возможностям компьютера и зависит от оптимизации алгоритма вычислений. Из-за конечности размеров решетки, чтобы добиться большей достоверности результатов, обычно приходится проделывать большое количество шагов Монте-Карло, обычно это 3000-10000.

В процессе Монте-Карло могут вычисляются следующие термодинамические характеристики: энергия E, намагниченность M, восприимчивость, теплоемкость C, корреляционные функции: спин-спиновая R и четырехспиновая R⁴, корреляционный радиус взаимодействия спинов x.

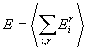
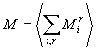
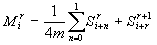
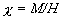
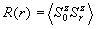
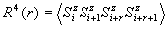
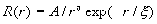                         (7),

где i=1..L, r=1..m.

Обычно метод Монте-Карло реализуют в виде программы на универсальной ЭВМ. Ранее применялись механич. устройства, ныне всё чаще используют спец. моделирующие устройства с применением микропроцессоров. С помощью таких устройств получен ряд результатов в статистич. физике и квантовой теории поля.

Для реализации случайной величины в традиционно используют датчики, генерирующие случайную последовательность чисел, равномерно распределённых на интервале (0,1). Различают три типа случайных чисел. Истинно случайные числа можно вырабатывать, напр., преобразуя случайные сигналы от радиоактивного источника или от шумового диода. Таким способом можно достаточно быстро получать большие последовательности некоррелированных случайных чисел. В расчётах на ЭВМ используют псевдослучайные числа, полученные с помощью некоторого алгоритма. Назначение такого алгоритма - генерировать числа, которые похожи на случайные, хотя, строго говоря, они детерминированы. Необходимы спец. исследования и тесты, чтобы убедиться в достаточной случайности таких чисел (равномерность распределения, отсутствие корреляций и пр.). Квазислучайные числа также получают при помощи нек-рого алгоритма, причём в основу алгоритма закладывают требование равномерного заполнения точками заданного многомерного объёма. Известен ряд алгоритмов, дающих точки, распределённые в гиперкубе более равномерно, чем случайные и псевдослучайные. Следствием лучшей равномерности является более быстрая сходимость результата. Использование M.-К. м. в физике базируется гл. обр. на возможности его применения для вычисления интегралов, решения интегральных ур-ний и др.

В нейтронной физике основными задачами являются моделирование прохождения потока нейтронов в среде, расчёт коэффициента размножения нейтронов в ядерном реакторе, расчёт защиты реактора и др. Используют как прямое, так и косвенное моделирование. В первом случае в объёме реактора моделируют набор некоторого числа нейтронов с заданными скоростями (первое поколение). Для каждого нейтрона прослеживают его судьбу (поглощение <#"704084.files/image064.gif">,

где: Со - затраты на выполнение одного заказа (руб.);

А - потребность в заказываемом товаре в течение периода (шт.);

Cn - цена за единицу3 товара, хранимого на складе (руб.);

i - доля от цены, приходящаяся на затраты по хранению;

Sо - оптимальный размер заказа (шт.).

Sо =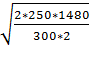 = 49,66 (ед)

Во избежание дефицита комплектующего изделия можно округлить оптимальный размер заказа в большую сторону, т.е.   Sо = 50 ед.

.        Рассчитываем параметры системы управления запасами:

Таблица 2 - Расчет параметров управления запасами

.        По полученным данным строим графики движения запаса.

По полученным данным строится график движения запасов в системе координат: «Х» - время, «У» - объем запаса.

Объем        запаса (ед)                            Максимальный желательный запас

Пороговый запас

Гарантийный запас

                4       6                    10                12 время (дн)

Рисунок 1 - Построение графика движения запасов

Задание №2. Прогнозирование объема продаж готовой продукции со склада промышленного предприятия

Условие:

За период с 2005 по 2010 годы известен объем продаж готовой продукции со склада промышленного предприятия. Сделать прогноз объема продаж 2015 года.

Исходные данные:

Таблица 3 - Объем продаж за 2005 - 2010 гг.

Решение:

По исходным данным выравнивания и прогнозирования первоначально строим график:

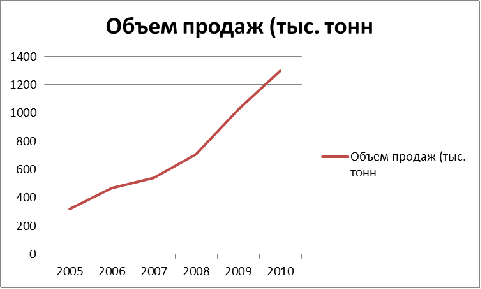
Рисунок 2 - Динамика изменения объема продаж за период 2005 - 2010гг

Ух = а + в ^. х, где

Ух - объем продаж готовой продукции (тыс.тонн);

х - период рассматриваемый (год);

а, в - параметры.

Для определения параметров а и в, расчет ведем в табличной форме:

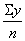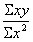Полученные значения подставим в формулы а =и в =, найдем параметры а и в:

а = 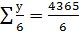=728 тыс.тонн

Уравнение прямой примет вид:

Ух = 728 + 96 ^. х

Подсчитаем теоретические уровни ряда для каждого года.

Сопоставляя у = 37705 тыс.тонн и теоретическое значение Ух = 13288 тыс.тонн, видим весьма незначительные отклонения расчетных уровней от фактических, что подтверждает правильность выбора математического уравнения.

Для прогнозирования объема продаж готовой продукции промышленного предприятия продолжим графу 5 числами, следующими за указанным числом, т.е. далее рассматриваемый период будет 7, 9, 11.,13,15.

На 2011 год:

Х = 7, тогда Ух = 728+96 ^. 7 = 1400 тыс.тонн

На 2012 год:

Х = 9, тогда Ух = 728+96 ^. 9= 1592 тыс.тонн

На 2013 год:

Х=11,тогда Ух = 728+96 ^. 11= 1784 тыс.тонн

На 2014:

Х=13, тогда Ух=728+96 ^. 13=1976 тыс.тонн

На 2015:

Х=15, тогда Ух=728+96 ^. 15=2168 тыс.тонн

Заключение

По окончанию выполнения курсовой работы по дисциплине « Экономико- математические методы и модели в логистике» была дастигнута поставленная цель, а именно: научились определять оптимальный размер заказа комплектующих изделий для производства продукции промышленного предприятия и делать прогнозы объема продаж готовой продукции со склада промышленного предприятия за определенный период. Были приобретены навыки практического применения экономико-математических методов для моделирования реальных экономических ситуаций, возникающих в различных логистических системах, что способствует повышению эффективного управления логистическими цепями поставок и является условием успешной деятельности предприятия.

Список использованных источников

1.       Бродецкий, Г.Л. Экономико-математические методы и модели в логистике: потоки событий и системы обслуживания: учеб. пособие / Г.Л. Бродецкий. - М.: Академия, 2009. - 272 с.

.        Владимирова, Л. П. Прогнозирование и планирование в условиях

.        рынка : учеб. пособие / Л. П. Владимирова. - М. : Дашков и К, 2001. - 400 с.

.        Гаджинский, А. М. Логистика : учебник / А. М. Гаджинский. -

.        11-е изд., перераб. и доп. - М. : Дашков и К, 2005. - 432 с.

.        Дж.Гласс, Дж.Стенли. Статистические методы в прогнозировании. М.: Прогресс, 2006.

.        Логинов, В.Н. Управленческие решения: модели и методы: учеб. пособие. / В.Н. Логинов - М.: Альфа- Пресс, 2011. - 310 с.

.        Модели и методы теории логистики: Учебное пособие.- 2-е изд. /под ред. В.С.Лукинского. - СПб.: Питер, 2008. - 448 с.

.        Николайчук, В.Е. Логистический менеджмент: учебник / В.Е. Николайчук. -М.: Издательско-торговая корпорация «Дашков и К», 2010. - 980 с.

.        Плоткин Б.К., Экономико-математические методы и модели в логистике: Учебное пособие / Б.К. Плоткин, Л.А. Делюкин - СПб.: Изд-во СПбГУЭФ, 2010. - 96 с.

.        Товстоношенко, В.Н. Экономико-математические методы и модели в логистике: учеб. пособие / В.Н. Товстоношенко. - Красноярск: Сиб. гос. аэрокосмич. ун-т., 2010. - 80 с.