Подставляя в данное уравнение фактические значения х, получаем
теоретические значения результата ŷх. По ним рассчитаем
показатели: тесноты связи - индекс корреляции ρху и среднюю ошибку аппроксимации Āi:
Характеристики степенной модели указывают, что она несколько лучше
линейной функции описывает взаимосвязь.
|
Y
|
x
|
Y2
|
X2
|
ŷx
|
y-ŷx
|
(y-ŷx)
2
|
Ai
|
|
1
|
1,8376
|
45,1
|
82,8758
|
3,3768
|
2034,01
|
60,7
|
8,1
|
65,61
|
11,8
|
|
2
|
1,7868
|
59,0
|
105,4212
|
3, 1927
|
3481,00
|
56,4
|
4,8
|
23,04
|
7,8
|
|
3
|
1,7774
|
57,2
|
101,6673
|
3,1592
|
3271,84
|
56,9
|
3,0
|
9,00
|
5,0
|
|
4
|
1,7536
|
61,8
|
108,3725
|
3,0751
|
3819,24
|
55,5
|
1,2
|
1,44
|
2,1
|
|
5
|
1,7404
|
58,8
|
102,3355
|
3,0290
|
3457,44
|
56,4
|
-1,4
|
1,96
|
2,5
|
|
6
|
1,7348
|
47,2
|
81,8826
|
3,0095
|
2227,84
|
60,0
|
-5,7
|
32,49
|
10,5
|
|
7
|
1,6928
|
55,2
|
93,4426
|
2,8656
|
3047,04
|
57,5
|
-8,2
|
67,24
|
16,6
|
|
Итого
|
12,3234
|
384,3
|
675,9974
|
21,7078
|
21338,41
|
403,4
|
-1,8
|
200,78
|
56,3
|
|
Среднее
значение
|
1,7605
|
54,9
|
96,5711
|
3,1011
|
3048,34
|
х
|
х
|
28,68
|
8,0
|
|
σ
|
0,0425
|
5,86
|
х
|
х
|
Х
|
х
|
х
|
х
|
х
|
|
σ2
|
0,0018
|
34,3396
|
х
|
х
|
Х
|
х
|
х
|
х
|
х
|
Значения параметров регрессии А и В составили:
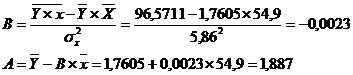
Получено линейное уравнение: 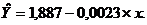
Произведем потенцирование полученного уравнения и запишем его в
обычной форме:
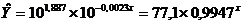
Тесноту связи оценим через индекс корреляции ρху:
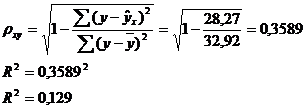
Связь умеренная.
Показательная функция чуть хуже, чем степенная, она описывает
изучаемую зависимость.
г) Уравнение равносторонней гиперболы 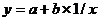 линеаризуется при замене z=1/х. Тогда
линеаризуется при замене z=1/х. Тогда 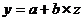 .
.
Для расчетов используем данные таблицы 1.5
Таблица 1.5
|
y
|
z
|
yz
|
z2
|
y2
|
ŷx
|
y-ŷx
|
(y-ŷx)
2
|
Ai
|
|
1
|
68,8
|
0,0222
|
1,5255
|
0,000492
|
4733,44
|
61,8
|
7,0
|
49,00
|
10,2
|
|
2
|
61,2
|
0,0169
|
1,0373
|
0,000287
|
3745,44
|
56,3
|
4,9
|
24,01
|
8,0
|
|
3
|
59,9
|
0,0175
|
1,0472
|
0,000306
|
3588,01
|
56,9
|
3,0
|
9,00
|
5,0
|
|
4
|
56,7
|
0,0162
|
0,9175
|
0,000262
|
3214,89
|
55,5
|
1,2
|
1,44
|
2,1
|
|
5
|
55
|
0,0170
|
0,9354
|
0,000289
|
3025,00
|
56,4
|
-1,4
|
1,96
|
2,5
|
|
6
|
54,3
|
0,0212
|
1,1504
|
0,000449
|
2948,49
|
60,8
|
-6,5
|
42,25
|
12,0
|
|
7
|
49,3
|
0,0181
|
0,8931
|
0,000328
|
2430,49
|
57,5
|
-8,2
|
67,24
|
16,6
|
|
Итого
|
405,2
|
0,1291
|
7,5064
|
0,002413
|
23685,76
|
405,2
|
0,0
|
194,90
|
56,5
|
|
Среднее
значение
|
57,9
|
0,0184
|
1,0723
|
0,000345
|
3383,68
|
х
|
х
|
27,84
|
8,1
|
|
σ
|
5,74
|
0,002145
|
х
|
х
|
Х
|
х
|
х
|
х
|
х
|
|
σ2
|
32,9476
|
0,00005
|
х
|
х
|
Х
|
х
|
х
|
х
|
х
|
Значения параметров регрессии а и b составили:
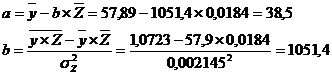
Получено уравнение: 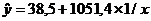
Индекс корреляции:
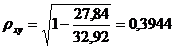
Коэффициент детерминации:
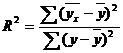
Оценку качества построенной модели даст коэффициент детерминации: 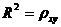 ,
, 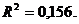 Вариация результата на 15,6% объясняется вариацией фактора х.
Вариация результата на 15,6% объясняется вариацией фактора х.
а) 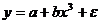 - функция линейна по параметрам;
- функция линейна по параметрам;
б) 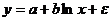 - функция линейна по параметрам;
- функция линейна по параметрам;
в) 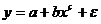 - функция линейна по параметрам;
- функция линейна по параметрам;
г) 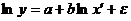 - нелинейна ни по переменным, ни по
параметрам;
- нелинейна ни по переменным, ни по
параметрам;
д) 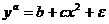 - нелинейна ни по переменным, ни по
параметрам;
- нелинейна ни по переменным, ни по
параметрам;
е) 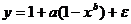 - линейна по параметрам;
- линейна по параметрам;
ж) 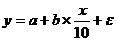 - линейна по переменным.
- линейна по переменным.
Тема 3.
Регрессионные модели с переменной структурой
1. МНК позволяет получить такие оценки параметров, при
которых сумма квадратов отклонений фактических значений результативного
признака у от теоретических ŷх минимальная, т.е.
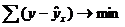
. Для применения МНК требуется, чтобы дисперсия остатков была
гомоскедастичной.
Для каждого значения фактора хj остатки εi имеют одинаковую дисперсию.
. 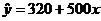 частное уравнение регрессии для домов
типа "хрущевка".
частное уравнение регрессии для домов
типа "хрущевка".
. 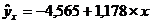 ,
, 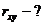
Таблица 1.6
|
Районы города
|
xi
|
yi
|
ŷx
|
y-ŷx
|
(y-ŷx) 2
|
|
1. Павловский
|
3,3
|
4,4
|
-0,6776
|
5,0776
|
25,7820
|
|
2. Кронштадт
|
6,2
|
8,1
|
2,7386
|
5,3614
|
28,7446
|
|
3.
Ломоносовский
|
8,1
|
12,9
|
4,9768
|
7,9232
|
62,7771
|
|
4. Курортный
|
18,3
|
20,8
|
16,9924
|
3,8076
|
14,4978
|
|
5. Петродворец
|
20,2
|
15,5
|
19,2306
|
-3,7306
|
13,9173
|
|
6. Пушкинский
|
23,1
|
28,8
|
22,6468
|
6,1532
|
37,8619
|
|
7. Красносельский
|
39,0
|
37,5
|
41,377
|
-3,877
|
|
|
8. Приморский
|
49,1
|
48,7
|
53,2748
|
-4,5748
|
|
|
9. Колпинский
|
60,1
|
68,6
|
66,2328
|
2,3672
|
|
|
10. Фрунзенский
|
74,2
|
104,6
|
82,8426
|
21,1574
|
|
|
11.
Красногвардейск.
|
79,0
|
90,5
|
88,497
|
2,003
|
|
|
12.
Василеостровск.
|
95,0
|
88,3
|
107,345
|
-19,045
|
|
|
13. Невский
|
106,0
|
132,4
|
120,303
|
12,097
|
|
|
14.
Петроградский
|
112,2
|
122,0
|
127,6066
|
|
|
15. Калининский
|
115,0
|
99,1
|
130,905
|
-31,805
|
1011,5580
|
|
16. Выборгский
|
125,1
|
114,2
|
142,8082
|
-28,8028
|
829,6013
|
|
17. Кировский
|
132,0
|
150,6
|
150,931
|
-0,331
|
0,10956
|
|
18. Московский
|
149,0
|
156,1
|
170,957
|
-14,857
|
220,7304
|
|
19.
Адмиралтейский
|
157,0
|
209,5
|
180,381
|
29,119
|
847,91616
|
|
20. Центральный
|
282,0
|
342,9
|
327,631
|
15,269
|
233,1424
|
|
Итого
|
1653
|
1855,5
|
1856,9942
|
0
|
|
|
Среднее
значение
|
82,695
|
92,775
|
|
|
|
|
σ
|
92,84971
|
104,72395
|
|
|
|
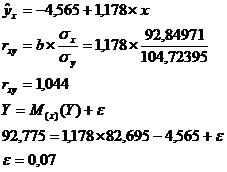
Отклонение фактических значений от теоретических минимально.
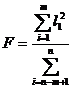 F2
F2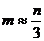 m=6
m=6
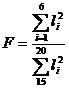
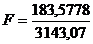 Fфакт. ≈0,06 L=0,05
Fфакт. ≈0,06 L=0,05
Fтабл. =
0,05: 20=0,6Fфакт < Fтабл.
Тема 4.
Обобщенный метод наименьших квадратов
1. В классе линейных несмещенных оценок вектора β для обобщений регрессионной модели оценка
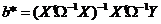 имеет наименьшую ковариационную матрицу.
имеет наименьшую ковариационную матрицу.
Х - неслучайная матрица
Ω положительно определенная матрица
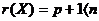
р - число объясняющих переменных- число наблюдений
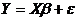 - обобщенная линейная модель множественной регрессии.
- обобщенная линейная модель множественной регрессии.
Сравнивая обобщенную модель с классической видим, что она
отличается от классической только видом ковариационной матрицы: для обобщенной
имеем:  ∑ε=Ω.
∑ε=Ω.
В отличие от классической, в обобщенной модели ковариации и
дисперсии объясняющих переменных могут быть произвольными.
В этом состоит суть обобщения регрессионной модели.
Оценка b* обобщенного метода наименьших квадратов для параметра β при известной матрице Ω совпадает с его оценкой, полученной
методом максимального правдоподобия.
Оценка b* обобщенного метода наименьших квадратов может быть
определена как точка минимума обобщенного критерия 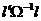 .
.
. Обобщенный метод наименьших квадратов для модели с
гетероскедастичностью, когда ковариационная матрица возмущенной ∑ε=Ω есть диагональная матрица, называется
взвешенным методом наименьших квадратов. Применяя этот метод, минимизируем:
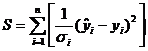
"Взвешивая" каждый остаток 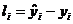 с помощью коэффициента 1/σi, мы добиваемся равномерного вклада остатков в общую сумму, что
приводит в конечном счете к получению наиболее эффектных оценок параметров
модели.
с помощью коэффициента 1/σi, мы добиваемся равномерного вклада остатков в общую сумму, что
приводит в конечном счете к получению наиболее эффектных оценок параметров
модели.
Оценка параметров регрессионной модели:
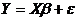
Сначала применить обычный метод наименьших квадратов, затем найти
регрессию квадратов остатков на квадратичные функции регрессоров, т.е. найти
уравнение аргументами которой являются квадраты значений регрессоров и их попарные
произведения:
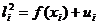
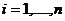
где 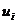 - случайный член.
- случайный член.
После чего следует вычислить прогнозные значения 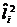 по полученному уравнению регрессии и
получить набор весов:
по полученному уравнению регрессии и
получить набор весов: 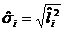 . Затем надо ввести новые переменные.
. Затем надо ввести новые переменные.
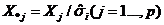 ,
, 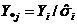 и найти уравнение:
и найти уравнение: 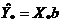 .
.
Полученная при этом оценка b* и есть оценка взвешенного метода
наименьших квадратов исходного уравнения 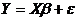 .
.
Тема 5.
Нелинейные модели регрессии
Соотношение между социально-экономическими явлениями и
процессами далеко не всегда можно выразить линейными функциями, т.к. при этом
могут возникнуть неоправданно большие ошибки.
Нелинейными оказываются производственные функции (зависимости
между объемом произведенной продукции и основными факторами производства -
трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары
или услуги и их ценами или доходом) и другие.
Для оценки параметров нелинейных моделей используются 2
подхода.
Первый подход основан на линеаризации модели. Исследуемую
зависимость представляют в виде линейного соотношения. Когда подобрать
соответствующее линеаризующее преобразование не удается, применяются методы
нелинейной оптимизации на основе исходных переменных.
Виды уравнений регрессии, нелинейные относительно включенных
в анализ объясняющих переменных, но линейные по параметрам:
1. парабола II порядка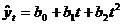
. кубическая парабола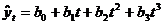
. показательная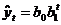
. экспонециальная 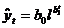
. модифицированная экспонента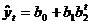
. кривая Гомперца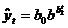
. логическая кривая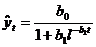
. логарифмическая парабола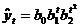
. гиперболическая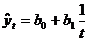 .
.
. Средние коэффициенты эластичности для линейной регрессии
рассчитываются по формуле:
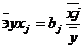
Для расчета частных коэффициентов эластичности применяется
следующая формула:
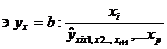
где 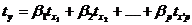 - уравнение регрессии в стандартизованном
масштабе:
- уравнение регрессии в стандартизованном
масштабе:
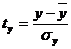
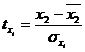
βi - стандартизованные коэффициенты
регрессии.
Связь коэффициентов множественной регрессии bi со
стандартизованными коэффициентами βi описывается соотношением:
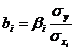
. 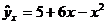 - парабола второго порядка, нелинейная по
объясняющим переменным.
- парабола второго порядка, нелинейная по
объясняющим переменным.
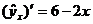
- 2х=0
х=3 тыс. руб., потребление товара А - максимальное, величина
потребления товара А с увеличением дохода семьи уменьшается.
Таблица 7
|
Ц-на на 1 га
|
Урожайность,
ц-на 1 га, у
|
|
1
|
6,1
|
|
2
|
9,0
|
|
3
|
10,2
|
|
4
|
12,3
|
|
5
|
13,1
|
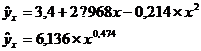
- регрессия нелинейная по объясняющим переменным, полином второй
степени;
- регрессия, нелинейная по оцениваемым параметрам, степенная.
. 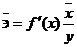
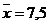 ;
; 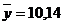
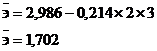 .
. 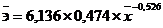
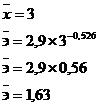
-ое уравнение регрессии лучше описывает зависимость урожайности
озимой пшеницы от количества внесенных минеральных удобрений.
Тема 6.
Множественная регрессия в экономических исследованиях
1. 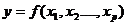
у - зависимая переменная
х1, х2, х3…хр -
независимые переменные (факторы)
Для построения уравнения множественной регрессии чаще используются
следующие функции:
линейная - 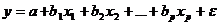
степенная - 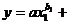
экспонента -  y=la+b1+x1+. bpxp+ε
y=la+b1+x1+. bpxp+ε
гипербола - 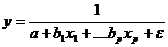
Уравнение регрессии в стандартизованном масштабе:
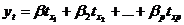
где 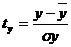
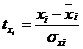 - стандартизованные переменныеi - стандартизованные
коэффициенты регрессии.
- стандартизованные переменныеi - стандартизованные
коэффициенты регрессии.
. Тесноту совместного влияния факторов на результат оценивает
индекс множественной корреляции:
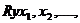
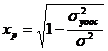
Значение индекса множественной корреляции лежит в пределах от 0 до
1 и должно быть больше или равно максимальному парному индексу корреляции:
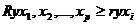
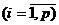
Индекс множественной корреляции для уравнения в стандартизованном
масштабе можно записать в виде:
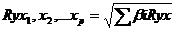
При линейной зависимости коэффициент множественной корреляции
можно определить через матрицу парных коэффициентов корреляции:
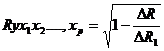
Δr 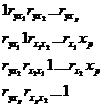 определитель матрицы парных коэффициентов корреляции.
определитель матрицы парных коэффициентов корреляции.
Δr1 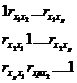 определитель матрицы межфакторной
корреляции.
определитель матрицы межфакторной
корреляции.
|
Признак
|
Среднее
значение
|
Среднее
квадратич. отклонение
|
линейный
коэффициент парной корреляции
|
|
среднедневной
душевой доход у
|
86,8
|
11,4
|
-
|
|
среднедневная
з/плата одного работающего, руб.
|
54,9
|
5,86
|
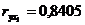
|
|
средний возраст
безработного, лет, х2
|
33,5
|
0,58
|
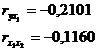
|
Решение:
Линейное уравнение имеет вид:
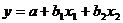
Применим метод стандартизации переменных и построим уравнение в
стандартизованном масштабе:
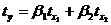
Расчет β -
коэффициентов:
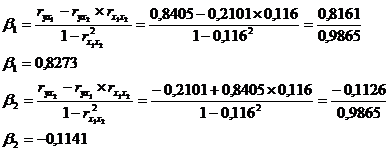
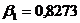
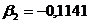
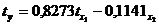
Рассчитываем b1 и b2:
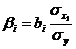 ;
; 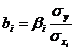

Расчет линейного коэффициента множественной корреляции выполним с
использованием коэффициентов ryxj и βj:
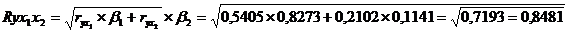
Зависимость у от х1 и х2
характеризуется как тесная, в которой 72% вариации среднего душевого дохода
определяется вариацией учетных в модели факторов: средней заработной платы и
среднего возраста безработного. Прочие факторы составляют 28% от общей вариации
у.
Таблица 5
|
Признак
|
Среднее
значение
|
Среднеквадрат.
отклонение
|
Коэффициент
парной корреляции
|
|
у
|
12,0
|
2,0
|
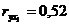
|
|
х1
|
4,3
|
0,5
|
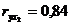
|
|
х2
|
10,0
|
1,8
|
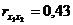
|
. Линейное уравнение множественной регрессии имеет вид:
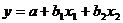
Искомое уравнение в стандартизованном масштабе: 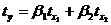
Расчет β-коэффициентов
выполним по формулам:
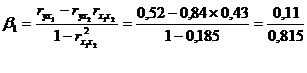
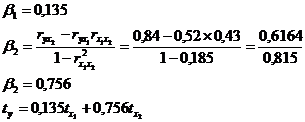
Рассчитываем b1 и b2:
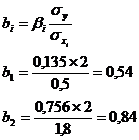
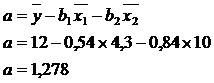
Уравнение множественной регрессии:
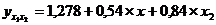
Оно показывает, что при увеличении х1 на 1 кВт/ч на
одного рабочего (при неизменном х2) У увеличивается в среднем
на 0,54 т. При увеличении х2 (на 1 тыс. ед. произведенной
продукции), потребление материалов У (Т) увеличивается в среднем на
0,84т.
Коэффициент множественной корреляции:
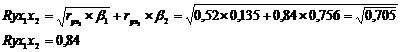
Зависимость у от х1 и х2 характеризуется
как тесная, в которой 70% вариации потребления материалов определяются
вариацией учтенных в модели факторов х1 и х2.
Тема 7.
Моделирование одномерных временных рядов
. Каждый уровень временного ряда формируется из трендовой
(Т), циклической (S) и случайной (Е) компонентов.
Модели, в которых временной ряд представлен как сумма
перечисленных компонент, - аддитивные модели, как произведение -
мультипликативные модели временного ряда.
Аддитивная модель имеет вид:
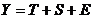 .
.
Мультипликативная модель:
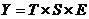
Построение аддитивной и мультипликативной моделей сводится к
расчету значений Т, S и Е для каждого уровня ряда.
Построение модели включает следующие шаги:
1) выравнивание ряда методом скользящей средней;
2) расчет значений сезонной компоненты S;
) устранение сезонной компоненты из исходных уровней
ряда и получение выровненных данных в аддитивной (Т+Е) или в мультипликативной
(Т х Е) модели;
) аналитическое выравнивание уровней (Т+Е) или (Т х Е)
и расчет значений Т с использованием полученного уравнения тренда;
) расчет полученных по модели значений (Т+S) или (Т х
S)
) расчет абсолютных и/или относительных ошибок
2. Автокорреляция уровней ряда - это корреляционная
зависимость между последовательными уровнями временного ряда:
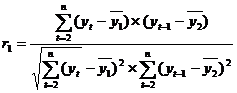
где 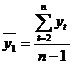 ;
; 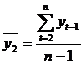 - коэффициент автокорреляции уровней ряда первого порядка.
- коэффициент автокорреляции уровней ряда первого порядка.
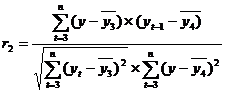
где
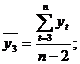
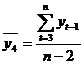 - коэффициент автокорреляции уровней ряда второго порядка.
- коэффициент автокорреляции уровней ряда второго порядка.
. Построение аналитической функции для моделирования тенденции
(тренда) временного ряда называют аналитическим выравниванием временного ряда.
Таблица 6
|
Показатель
|
1997
|
1998
|
1999
|
2000
|
2001
|
2001
|
|
Расходы на
товар А, руб.
|
30
|
35
|
39
|
44
|
50
|
53
|
|
Доход на 1
члена семьи, % 1997г.
|
100
|
103
|
105
|
109
|
115
|
118
|
Решение:
. Пусть расходы на товар А будет у, а доходы одного члена
семьи - х. Ежегодные абсолютные приросты:
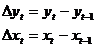
Расчеты оформим в виде таблицы:
|
yt
|
Δyt
|
xt
|
Δxt
|
|
30
|
-
|
100
|
-
|
|
35
|
5
|
103
|
3
|
|
39
|
4
|
105
|
2
|
|
44
|
5
|
109
|
4
|
|
50
|
6
|
115
|
6
|
|
53
|
3
|
118
|
3
|
Значения Δу не имеют четко
выраженной тенденции, они варьируют вокруг среднего уровня, что означает
наличие в ряде динамики линейного тренда. Аналогичный вывод можно сделать и по
ряду х: абсолютные приросты не имеют систематической направленности, они
примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией.
Модель имеет вид:
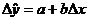
Для определения параметров а и b применяется МНК. Система
нормальных уравнений следующая:
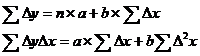
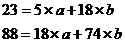
Решая эту систему, получим:
а=2,565=0,565
Модель имеет вид:
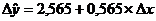
Включим фактор времени:
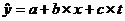
Применяя МНК, получим систему нормальных уравнений:
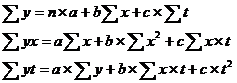
|
t
|
Y
|
x
|
yx
|
yt
|
xt
|
x2
|
t2
|
|
1
|
30
|
100
|
3000
|
30
|
100
|
10000
|
1
|
|
2
|
35
|
103
|
3605
|
70
|
206
|
10609
|
4
|
|
3
|
39
|
105
|
4095
|
117
|
315
|
11025
|
9
|
|
4
|
44
|
109
|
4796
|
176
|
436
|
11881
|
16
|
|
5
|
50
|
115
|
5750
|
250
|
575
|
13225
|
25
|
|
6
|
53
|
118
|
6254
|
318
|
708
|
13924
|
36
|
|
21
|
251
|
27500
|
961
|
2340
|
70664
|
91
|
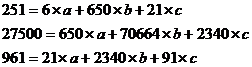
Решая, получаем:
а=-5,42; b=0,322; с=3,516
Уравнение регрессии имеет вид:
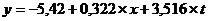
Параметр b=0,322 фиксирует силу связи у и х. Его величина
означает, что с ростом дохода на одного члена семьи на 1% -ный пункт при
условии неизменной тенденции расходы на товар А возрастают в среднем на 0,322
руб.
Параметр с=3,516 характеризует среднегодовой абсолютный прирост
расходов на товар А под воздействием прочих факторов при условии неизменного
дохода.
.
Таблица 7
|
Год
|
Выпуск
продукции, млн. долл
|
Год
|
Выпуск
продукции, млн. долл.
|
|
1967
|
1513
|
1985
|
13617
|
|
1969
|
1987
|
1987
|
20037
|
|
1971
|
2367
|
1989
|
23298
|
|
1973
|
3837
|
1991
|
23080
|
|
1975
|
5502
|
1993
|
23446
|
|
1977
|
7665
|
1995
|
39573
|
|
1979
|
11172
|
1997
|
39200
|
|
1981
|
14004
|
1999
|
43100
|
|
1983
|
12518
|
2001
|
45320
|
. Для определения параметров линейного тренда по методу
наименьших квадратов используется статистическая функция ЛИНЕЙН, для
определения экспоненциального тренда - ЛГРФПРИБЛ.
В качестве зависимой переменной выступает время (t=1,2,…. n).
Результат вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ.
Уравнения линейного и экспоненциального тренда
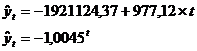
. Построение графиков осуществляется с помощью Мастера диаграмм
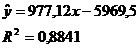
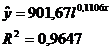
Сравним значения R2 по разным уровням трендов:
экспоненциальный 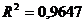
линейный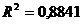
Исходные данные лучше всего описывает экспоненциальный тренд.
В примере для расчета прогнозных значений следует использовать
экспоненциальное уравнение.
Тема 8.
Моделирование тенденции временного ряда при наличии структурных изменений
1. При аналитическом выравнивании ряда динамики закономерно
изменяющийся уровень изучаемого показателя оценивается как функция времени 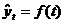 , где
, где 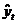 - уровни динамического ряда, вычисленные по соответствующему
аналитическому уравнению на момент времени t.
- уровни динамического ряда, вычисленные по соответствующему
аналитическому уравнению на момент времени t.
|
Название
функции
|
Описание
функции
|
|
1. Линейная
|
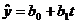
|
|
2. Парабола
второго ряда
|
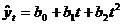
|
|
3. Кубическая
парабола
|
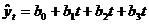
|
|
4.
Показательная
|
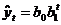
|
|
5.
Экспоненциальная
|
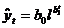
|
|
6.
Модифицированная экспонента
|
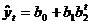
|
|
7. Кривая
Гомперца
|
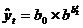
|
|
8.
Гиперболическая
|
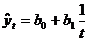
|
Применяется для выравнивания линейная функция, если любые три
равностоящие уровня имеют нулевую вторую разность.
. Критерием отбора наилучшей формы тренда является R2
- коэффициент детерминации, его наибольшее значение.
4. 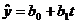 - линейное уравнение тренда- порядковый
номер периодов;0 и b1 - рассчитываем по МНК
- линейное уравнение тренда- порядковый
номер периодов;0 и b1 - рассчитываем по МНК
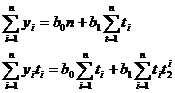
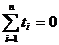
Уровень, находящийся в середине ряда принимается за условное
начало отсчета времени.
Даты времени, стоящие выше этого уровня, обозначаются натуральными
числами со знаком минус (-1; - 2; - 3; и т.д.).
При условии 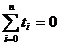 система нормальных уравнений
преобразуется следующим образом:
система нормальных уравнений
преобразуется следующим образом:
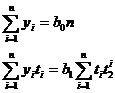
откуда 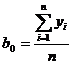
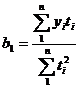
Используя итоги графиков, 2,4,5 определим параметры уравнения
прямой:
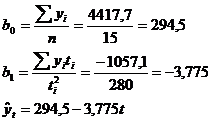
Таблица 8
|
Год
|
Цена yi
|
ti
|
уiti
|
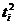 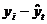
|
|
|
1973
|
296,6
|
-7
|
-2076,2
|
49
|
|
|
1975
|
363,2
|
-6
|
-2179,2
|
36
|
|
|
1977
|
272,4
|
-5
|
-1362
|
25
|
|
|
1979
|
334,3
|
-4
|
-1337,2
|
16
|
|
|
1981
|
482,8
|
-3
|
-1448,4
|
9
|
|
|
1983
|
276,8
|
-2
|
-553,6
|
4
|
|
|
1985
|
217,4
|
-1
|
-217,4
|
1
|
|
|
1987
|
229,8
|
0
|
0
|
0
|
|
|
1989
|
241,3
|
1
|
241,3
|
1
|
|
|
1991
|
253,8
|
3
|
507,6
|
4
|
|
|
1993
|
265,7
|
3
|
797,1
|
9
|
|
|
1995
|
277,6
|
4
|
110,4
|
16
|
|
|
1997
|
289,8
|
5
|
1449
|
25
|
|
|
1999
|
301,9
|
6
|
1811,4
|
36
|
|
|
2001
|
314,3
|
7
|
2200,1
|
49
|
|
|
Итого
|
4417,7
|
|
-1057,1
|
280
|
|
Рассчитаем для 1983 г.:
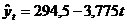
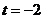
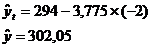
Правильность расчета уровней выравниваемого ряда динамики м. б.
проверена следующим образом:
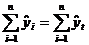 (итоги граф 2 и 6).
(итоги граф 2 и 6).
Целесообразность моделирования: можно подсчитать примерную цену на
рис и на несколько лет вперед (составить прогноз). Прогнозирование на основе
развития изучаемого процесса.
Тема 9.
Системы экономических уравнений
Сложные экономические процессы описывают с помощью системы
взаимосвязанных (одновременных уравнений).
Различают несколько видов систем уравнений:
система независимых уравнений - когда каждая зависимая
переменная рассматривается как функция одного и того же набора факторов х:
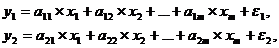

Для решения этой системы и нахождения ее параметров используется
метод наименьших квадратов;
система рекурсивных уравнений - когда зависимая переменная у
одного уравнения выступает в виде фактора х в другом уравнении:
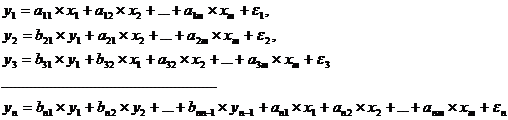
Для решения этой системы и нахождения ее параметров используется
метод наименьших квадратов;
система взаимосвязанных (совместных) уравнений - когда одни и те
же зависимые переменные в одних уравнениях входят в левую часть, а в других - в
правую:
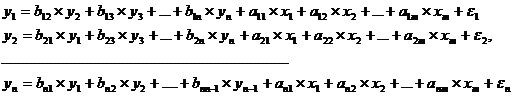
Такая система уравнений называется структурной формой модели.
Эндогенные переменные - взаимосвязанные переменные, которые
определяются внутри модели (системы) у.
Экзогенные переменные - независимые переменные, которые определяются
вне системы х.
Предопределенные переменные - экзогенные и лаговые (за предыдущие
моменты времени) эндогенные переменные системы.
Коэффициенты а и b при переменных - структурные
коэффициенты модели.
Система линейных функций эндогенных переменных от всех
предопределенных переменных системы - приведенная форма модели:
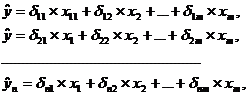
где δ -
коэффициенты приведенной формы модели.
Необходимое условие идентификации - выполнение счетного
правила:+1=Н - уравнение идентифицируемо;+1<Н - уравнение
неидентифицируемо;+1>Н - уравнение сверхиндентифицируемо,
где Н - число эндогенных переменных в уравнении,- число
предопределенных переменных, отсутствующих в уравнении, но присутствующих в
системе.
Достаточное условие идентификации - определитель матрицы,
составленной из коэффициентов при переменных, отсутствующих в исследуемом
уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных
переменных системы без единицы.
Оценить следующую структурную модель на идентификацию уравнений.
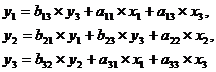
Исходя из приведенной формы модели уравнений:
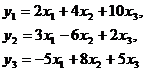
Найти структурные коэффициенты модели.
Решение:
. Модель имеет три эндогенные (у1, у2, у3)
и три экзогенные (х1, х2, х3) переменные.
Проверим каждое уравнение системы на необходимое (Н) и достаточное
(Д) условия идентификации.
Первое уравнение:
Н: эндогенных переменных - 2 (у1, у3)
отсутствующих экзогенных - 1 (х2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение
точно идентифицируемо.
Д: в первом уравнении отсутствуют у2 и х2.
Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение
|
Отсутствующие
переменные
|
|
у2
|
х2
|
|
Второе
|
-1
|
а22
|
|
Третье
|
b32
|
0
|
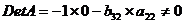
Определитель матрицы не равен 0, ранг матрицы равен 2;
следовательно, выполняется достаточное условие идентификации, и первое
уравнение точно идентифицируемо.
Второе уравнение.
Н: эндогенных переменных - 3 (у1, у2, у3)
отсутствующих экзогенных - 2 (х1, х3).
Выполняется необходимое равенство: 3=2+1, следовательно, уравнение
точно идентифицируемо.
Д: во втором уравнении отсутствуют х1 и х3.
Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение
|
Отсутствующие
переменные
|
|
х1
|
х3
|
|
Первое
|
а11
|
а13
|
|
Третье
|
а31
|
а33
|
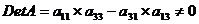
Определитель матрицы не равен 0, ранг матрицы равен 2,
следовательно, выполняется достаточное условие идентификации, и второе
уравнение точно идентифицируемо.
Третье уравнение.
Н: эндогенных переменных - 2 (у2, у3),
отсутствующих экзогенных - 1 (х2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение
точно идентифицируемо.
Д: в третьем уравнении отсутствуют у1 и х2.
Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение
|
Отсутствующие
переменные
|
|
у1
|
х2
|
|
Первое
|
-1
|
0
|
|
Второе
|
b21
|
а22
|
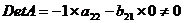
Определитель матрицы не равен 0, ранг матрицы равен 2,
следовательно, выполняется достаточное условие идентификации, и третье
уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может
быть решена косвенным методом наименьших квадратов.
. Вычислим структурные коэффициенты модели:
) из третьего уравнения приведенной формы выразим х2
(так как его нет в первом уравнении структурной формы):
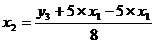
Данное выражение содержит переменные у3, х1
и х3, которые нужны для первого уравнения структурной формы модели
(СФМ). Подставим полученное выражение х2 в первое уравнение
приведенной формы модели (ПФМ):

- первое уравнение СФМ;
) во втором уравнении СФМ нет переменных х1 и х3.
Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим х1 в данном случае из первого или
третьего уравнения ПФМ. Например, из первого уравнения:
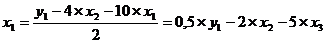
Подстановка данного выражения во второе уравнение ПФМ не решило бы
задачу до конца, так как в выражении присутствует х3, которого нет в
СФМ.
Выразим х3 из третьего уравнения ПФМ:
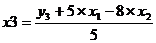
Подставив его в выражение х1:
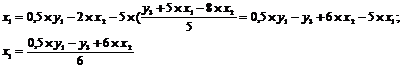
Второй этап: аналогично, чтобы выразить х3 через
искомые у1, у3 и х2, заменим в выражении х3
значение х1 на полученное из первого уравнения ПФМ:
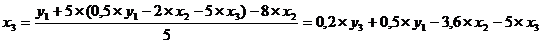
Следовательно:
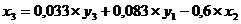
Подставим полученные х1 и х3 во второе
уравнение ПФМ:
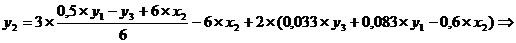
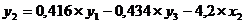 - второе уравнение СФМ.
- второе уравнение СФМ.
Это уравнение можно получить из ПФМ иным путем.
Суммируя все уравнения, получим:
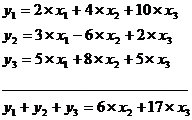
Далее из первого и второго уравнений ПФМ исключим х1,
домножив первое уравнение на 3, а второе - на (-2) и просуммировав их:
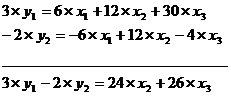
Затем аналогичным путем из полученных уравнений исключаем х3,
а именно:
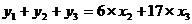 - 26
- 26
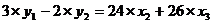 17
17
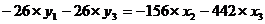
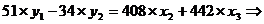
____________________________________________
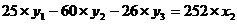
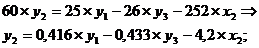
) из второго уравнения ПФМ выразим х2, так как его нет
в третьем уравнении СФМ:
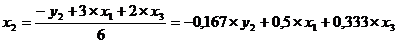
Подставим полученное выражение в третье уравнение ПФМ:
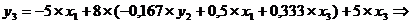
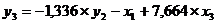 - третье уравнение СФМ.
- третье уравнение СФМ.
Таким образом СФМ примет вид:
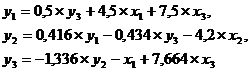
Тема 10.
Оценивание параметров структурной модели косвенным методом наименьших квадратов
Приведенная форма модели - это система линейных функций
эндогенных переменных от всех предопределенных переменных системы:
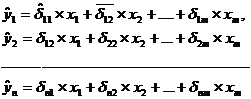
где δ -
коэффициенты приведенной формы модели.
Для решения идентифицируемого уравнения применяется косвенный
метод наименьших квадратов, для решения сверхидентифицированных - двухшаговый
метод наименьших квадратов.
Косвенный МНК состоит в следующем:
- составляют приведенную форму модели и определяют
численные значения параметров каждого ее уравнения обычным МНК;
- путем алгебраических преобразований переходят от
приведенной формы к уравнениям структурной формы модели, получая тем самым
численные оценки структурных параметров.
Пример:
Имеются статистические данные за 1998 - 2002гг.,
характеризующие потребление мяса в Австралии.
|
Год
|
Годовое
потребление свинины на душу населения, фунты, у1
|
Оптовая цена за
фунт, долл., у2
|
Доход на душа
населения, долл., х1
|
Расходы по
обработке мяса, % к цене, х2
|
|
1998
|
60
|
5б0
|
1300
|
60
|
|
1999
|
62
|
4,0
|
1300
|
56
|
|
2000
|
65
|
4,2
|
1500
|
56
|
|
2001
|
62
|
5,0
|
1600
|
63
|
|
2002
|
66
|
3,8
|
1800
|
50
|
Требуется:
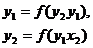
рассчитав соответствующие структурные коэффициенты.
Система одновременных уравнений с двумя эндогенными и двумя
экзогенными переменными имеет вид:
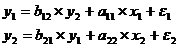
В каждом уравнении две эндогенные и одна отсутствующая экзогенная
переменная из имеющихся в системе. Для каждого уравнения данной системы
действует счетное правило 2=1+1, это означает, что каждое уравнение и система в
целом идентифицированы.
Для определения параметров такой системы применяется косвенный
метод наименьших квадратов.
С этой целью структурная форма модели преобразуется в приведенную
форму:
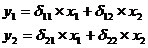
в которой коэффициенты при х определяются методом
наименьших квадратов.
Для нахождения значений δ11 и δ12 запишем систему нормальных уравнений:
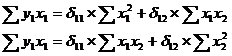
При решении предполагается, что х и у выражены через
отклонения от средних уровней, т.е. матрица исходных данных составит:
у1у2х1х2
,6-2003
-0,4-200-1
-0, 20-1
,61006
-0,6300-7
________________________________________
∑00,000
Применительно к ней необходимые суммы оказываются следующими:
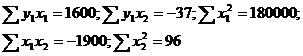
Система нормальных уравнений составит:
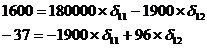
Решая ее, получим:
δ11=0,00609; δ12=-0,26481.
Итак, имеем 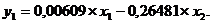
Аналогично строим систему нормальных уравнений для определения
коэффициента δ21 и δ22:
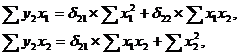
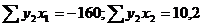
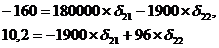
Следовательно,
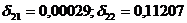
Тогда второе уравнение примет вид
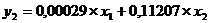
Из приведенной формы модели определяем коэффициенты структурной
модели:
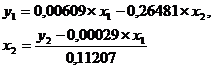
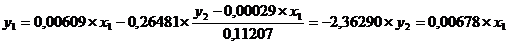
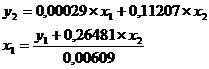
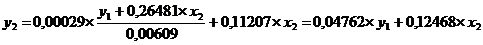
Итак, структурная форма модели имеет вид:
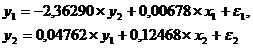
Тема
11. Оценивание параметров структурной модели двухшаговым и трехшаговым методами
наименьших квадратов
. Параметр называется сверхидентифицируемым, если косвенный
метод наименьших квадратов дает несколько различных его оценок.
. В приведенной форме уравнения:
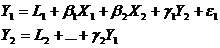
Три коэффициента не могут быть найдены из 2-х уравнений: β1; β2; β3 (коэффициенты). Это значит, существует бесконечное множество их
возможных значений.
. Изучается модель вида
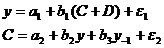
Информация за девять лет о приросте всех показателей дана в
таблице 12.
Таблица 12.
|
Год
|
Д
|
у-1
|
у
|
с
|
Год
|
Д
|
у-1
|
у
|
с
|
|
1
|
-6,8
|
46,7
|
3,1
|
7,4
|
6
|
44,7
|
17,8
|
37,2
|
8,6
|
|
2
|
22,4
|
3,1
|
22,8
|
30,4
|
7
|
23,1
|
37,2
|
35,7
|
30,0
|
|
3
|
-17,3
|
22,8
|
7,8
|
1,3
|
8
|
51,2
|
35,7
|
46,6
|
31,4
|
|
4
|
12,0
|
7,8
|
21,4
|
8,7
|
9
|
32,3
|
46,6
|
56,0
|
39,1
|
|
5
|
5,9
|
21,4
|
17,8
|
25,8
|
∑
|
167,5
|
239,1
|
248,4
|
182,7
|
Система приведенных уравнений:
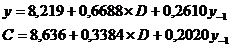
Решение:
В модели две эндогенные переменные (у и с) и две экзогенные
переменные (D и у-1). Для второго уравнения имеем по счетному
правилу идентификации равенство: 2=1+1.
Первое уравнение сверхидентифицировано, т.к. в нем на параметры
при С и D наложено ограничение: они должны быть равны.
В этом уравнении содержится одна эндогенная переменная у.
Переменная С в данном уравнении не рассматривается как эндогенная, так как она
участвует в уравнении не самостоятельно, а вместе с переменной D. В данном
уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По
счетному правилу идентификации получаем: 1+1=2; D+1>Н это больше, чем число
эндогенных переменных в данном уравнении, → система
сверхидентифицирована.
Рассчитайте параметры первого уравнения структурной модели.
Используем двухшаговый метод наименьших квадратов. Шаг 1.
Определим теоретические значения эндогенной переменной С. В
приведенное уравнение
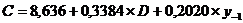 подставим D и у-1 (из условия).
подставим D и у-1 (из условия).
Ĉ1=15,8Ĉ2=16,8Ĉ3=7,4Ĉ4=14,3Ĉ5=15,0
Ĉ6=27,4Ĉ7=24,0Ĉ8=33,2Ĉ9=29,0
Шаг 2. По сверхидентифицированному уравнению структурной формы
модели заменяем фактические значения С на теоретические Ĉ и рассчитываем
новую переменную Ĉ+D.
|
Год
|
D
|
Ĉ
|
Ĉ+D
|
Год
|
D
|
Ĉ
|
Ĉ+D
|
|
1
|
-6,8
|
15,8
|
9,0
|
6
|
44,7
|
27,4
|
72,1
|
|
2
|
22,4
|
16,8
|
39,2
|
7
|
23,1
|
24,0
|
47,1
|
|
3
|
-17,3
|
7,4
|
-9,9
|
8
|
51,2
|
33,2
|
84,4
|
|
4
|
12,0
|
14,3
|
26,3
|
9
|
32,3
|
29,0
|
61,3
|
|
5
|
5,9
|
15,0
|
20,9
|
∑
|
167,5
|
182,9
|
350,4
|
К сверхидентифицированному уравнению применим МНК. Обозначим новую
переменную Ĉ+D через Z. Решаем уравнение: 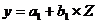 .
.
Система нормальных уравнений составит:
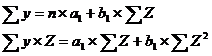
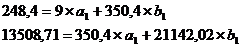
а1=7,678; b1=0,512
Первое уравнение структурной модели:
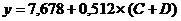
. Рассматривается следующая модель:
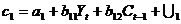 - (функция потребления)
- (функция потребления)
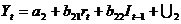 - (функция инвестиций)
- (функция инвестиций)
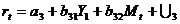 - (функция денежного рынка)
- (функция денежного рынка)
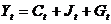 - (тождество дохода)
- (тождество дохода)
где Сt - расходы на потребление в период t;
Уt - совокупный доход в период t;t -
инвестиции в период t;t - процентная ставка в период t;
Мt - денежная масса в период t;t -
государственные расходы в период t;t-1 - расходы на потребление в
период t-1;t-1 - инвестиции в период t-1;1 U2
U3 - случайные ошибки.
Решение:
Модель представляет собой систему одновременных уравнений.
Проверим каждое ее уравнение на идентификацию.
Модель включает 4 эндогенные переменные (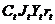 ) и 4 предопределенные Мt и Gt
и две лаговые эндогенные переменные - Сt-1 и Jt-1.
) и 4 предопределенные Мt и Gt
и две лаговые эндогенные переменные - Сt-1 и Jt-1.
Необходимое условие идентификации для уравнений модели.
уравнение.
Это уравнение включает две эндогенные переменные (Сt и
Jt) и одну предопределенную переменную (Сt-1). Число
предопределенных переменных не входящих в это уравнение, плюс 1, больше числа
эндогенных переменных, входящих в уравнение: 3+1>1. Уравнение
сверхидентифицировано.
уравнение.
Уравнение 2 включает две эндогенные переменные (Jt и rt)
и не включает три предопределенные переменные. Как и 1 уравнение, оно
сверхидентифицировано.
уравнение.
Уравнение 3 тоже включает две эндогенные переменные (Yt
и rt) и не включает три предопределенные переменные. Это уравнение
сверхидентифицировано.
уравнение.
Уравнение 4 представляет собой тождество, параметры которого
известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие
идентификации.
Составим матрицу коэффициентов при переменных модели:
|
Ct
|
Yt
|
Ct-1
|
Jt
|
rt
|
Jt-1
|
Mt
|
Gt
|
|
1 уравнение
|
-1
|
b11
|
b12
|
0
|
0
|
0
|
0
|
0
|
|
2 уравнение
|
0
|
0
|
0
|
-1
|
b12
|
b22
|
0
|
0
|
|
3 уравнение
|
0
|
b31
|
0
|
0
|
-1
|
0
|
b32
|
0
|
|
4 уравнение
|
1
|
-1
|
0
|
1
|
0
|
0
|
0
|
1
|
Достаточное условие идентификации: определитель матрицы
коэффициентов при переменных, не входящих в исследуемое уравнение, не должен
быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных
модели минут 1, т.е.4-1=3.
уравнение. Матрица коэффициентов при переменных не входящих в
уравнение, имеет вид:
b21b2200
А0-10b320
Ранг равен 3, т.к. определитель квадратной подматрицы 3 х 3
этой матрицы не равен нулю:
b210
Det A*=0-10 70
Достаточное условие идентификации для первого уравнения.
уравнение. Матрица коэффициентов, не входящих в уравнение:
b11b1200
А=0b310b320
-1001
Ранг равен 3.
Det A*=0b320  0
0
Достаточное условие идентификации для 2-ого уравнения выполняется.
Все уравнения модели сверхидентифицированы.
Применим двухшаговый МНК.
Шаг 1. Приведенная форма модели в общем виде:
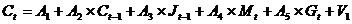
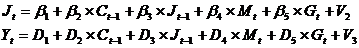
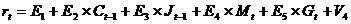 1, V2,
V3, V4 - случайные ошибки.
1, V2,
V3, V4 - случайные ошибки.
Шаг 2
В структурных уравнениях заменим эндогенные переменные,
выступающие в качестве факторных признаков, их расчетными значениями:
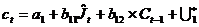
где 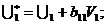
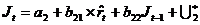
где 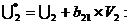
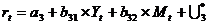
где 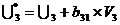
Применяя обычный МНК, определим структурные параметры a1, b11, b12, a2, b21, b22,a3, b31 и b32.
Литература
1. Доугерти
К. Введение в эконометрику. - М.: Финансы и статистика, 2009.
2. Эконометрика:
Учебник/ под ред.Н. Н. Елисеевой. - М.: Финансы и статистика, 2010.
. Экономическая
статистика: Учебник/ под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 2008.
. Иванова
В.М. Основы эконометрики. - М.: МЭСИ, 2011.
. Чавкин
А.М. Методы и модели рационального управления в рыночной экономике: Учеб.
пособие. - М.: Финансы и статистика, 2011.
. Шмойлова
Р.А. Теория статистики: Учебник. - 3-е изд., перераб. и доп. - М.: Финансы и
статистика, 2011