Кривые Евклидова пространства
Содержание
1. Кривые Евклидова пространства
.1 Касательная прямая и нормальная
плоскость кривой. Практическая часть нахождения касательной прямой и нормальной
плоскости кривой
.2 Соприкасающаяся плоскость в
произвольной и в выбранной точке. Практическая часть нахождения соприкасающейся
плоскости в произвольной и в выбранной точке
.3 Кривизна и кручение в выбранной и
произвольной точке. Практическая часть вычисления кривизны и кручения в
произвольной и выбранной точке
.4 Построение кривой
. Поверхности Евклидова пространства
.1 Касательная плоскость и нормаль
поверхности. Нахождение касательной плоскости и нормали в произвольной и
выбранной точке
.2 Первая квадратичная форма в
выбранной и произвольной точке. Вычисление первой квадратичной формы в
произвольной и выбранной точке
.3 Вторая квадратичная форма в
выбранной и произвольной точке. Вычисление второй квадратичной формы
поверхности в произвольной и выбранной точке
.4 Полная и средняя кривизна
поверхности. Вычисление полной и средней кривизны поверхности
.5 Изображение поверхности
Список использованной литературы
касательная нормаль плоскость
кривизна
1. Кривые Евклидова пространства
Нам даны параметрические координаты
кривой: x= , y=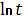
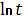 , z=-
, z=-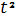
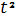 . Найдем на ее примере касательную
прямую, нормальную плоскость, кривизну и кручение в произвольной и выбранной
точке. Построим кривую.
. Найдем на ее примере касательную
прямую, нормальную плоскость, кривизну и кручение в произвольной и выбранной
точке. Построим кривую.
.1 Касательная прямая и нормальная
плоскость прямой в произвольной и в выбранной точке. Практическая часть
нахождения касательной прямой и нормальной плоскости кривой
Вектор 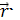
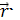 (
(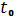
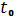 ) является вектором касательной
кривой
) является вектором касательной
кривой 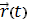
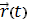 в точке
в точке 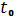
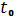 . Обозначим точку кривой
. Обозначим точку кривой 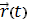
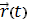 , соответствующую значению параметра
, соответствующую значению параметра
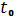
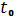 , через P, т.е. P=P
, через P, т.е. P=P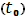
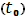 . Плоскость, проходящая через точку P
. Плоскость, проходящая через точку P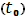
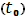 кривой и перпендикулярная вектору
кривой и перпендикулярная вектору 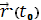
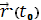 , называется нормальной плоскостью
кривой в точке
, называется нормальной плоскостью
кривой в точке 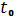
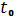 . По вектору
. По вектору 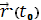
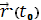 =
= 
 и точке P
и точке P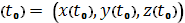
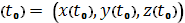 запишем уравнения касательной
прямой и нормальной плоскости кривой
запишем уравнения касательной
прямой и нормальной плоскости кривой 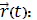
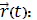
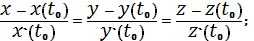
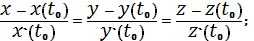
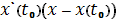
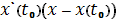 +
+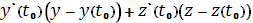
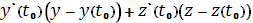 =0.
=0.
Практическая часть нахождения касательной
прямой и нормальной плоскости кривой
Применим все вышесказанное к нашей
кривой: найдем касательную прямую и нормальную плоскость в произвольной и
выбранной точке.
В уравнение касательной прямой:
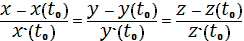
подставим наши координаты: x, y и z вместо 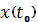
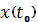 ,
, 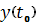
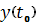 и
и 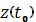
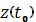 соответственно, и производные
соответственно, и производные 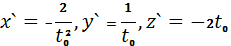
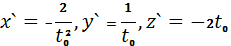 вместо
вместо 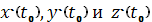
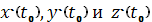 , получим:
, получим:
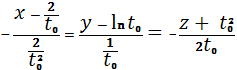
Мы получили уравнение касательной
прямой в общем виде, теперь найдем уравнение прямой в выбранной точке, приняв 
 :
:
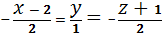
Нами получено уравнение касательной
прямой в выбранной точке. Теперь найдем уравнение нормальной плоскости кривой,
по аналогии с нахождением уравнения касательной прямой, подставив в формулу:
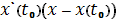
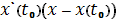 +
+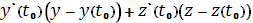
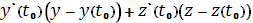 =0
=0
наши координаты:
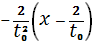
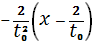 +=0.
+=0.
Уравнение нормальной плоскости
кривой в произвольной точке найдено. Напишем уравнение в выбранной точке,
напомню, что 
 . В итоге получаем:
. В итоге получаем:
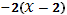
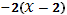 +
+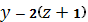
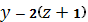 =0.
=0.
Нами получено уравнение нормальной
плоскости кривой в выбранной точке.
.2 Соприкасающаяся плоскость в произвольной
и выбранной точке. Практическая часть нахождения соприкасающейся плоскости в
произвольной и в выбранной точке
Рассмотрим плоскости, проходящие
через касательную кривой  (t) в точке
Р=Р (t0) кривой.
При изменении параметра t получаем вектор
(t) в точке
Р=Р (t0) кривой.
При изменении параметра t получаем вектор 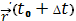
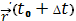 . Для вектора
. Для вектора 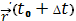
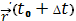 имеет место формула Тейлора:
имеет место формула Тейлора:
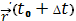
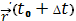 =
=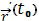
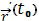 +
+ 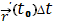
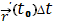 +
+ 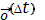
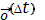 ,
, 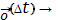
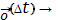 0.
0.
Точка М(t0+∆t) кривой и
касательная 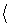 P,
P,  Δ(t0)
Δ(t0)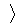 определяют
плоскость
определяют
плоскость
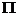 =
=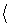 P,
P,  Δ(t0),
Δ(t0),  Δ (t0+∆t)
Δ (t0+∆t)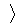 .
.
Нормальный вектор плоскости есть  Δ (t0)
Δ (t0)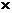
 Δ(t0+∆t).
Δ(t0+∆t).
Плоскость 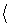 P ,
P ,  Δ(t0),
Δ(t0),  Δ(t0)
Δ(t0)  называется
соприкасающейся плоскостью кривой в точке t0 .
называется
соприкасающейся плоскостью кривой в точке t0 .
Уравнение соприкасающейся плоскости:
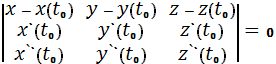
Практическая часть нахождения
соприкасающейся плоскости в произвольной и в выбранной точке
Найдем формулу соприкасающейся плоскости
в произвольной и выбранной точке:
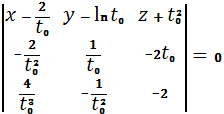
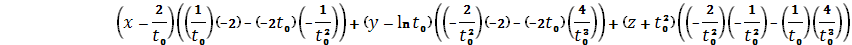
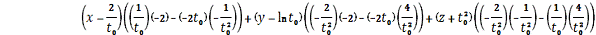 =
=
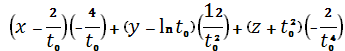
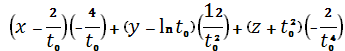 =0.
=0.
Мы нашли формулу соприкасающейся
плоскости в произвольной точке. Теперь найдем в произвольной точке, которую мы
ранее приняли равной 
 :
:
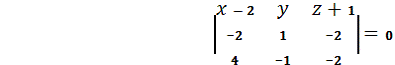
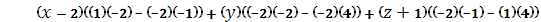
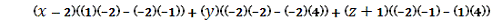 =
= 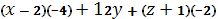
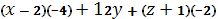 =0.
=0.
Соприкасающаяся плоскость в
выбранной точке найдена.
.3 Кривизна и кручение кривой.
Вычислительные формулы для кривизны и кручения. Практическая часть вычисления
кривизны и кручения в произвольной и выбранной точке
Величина k1 называется
кривизной или первой кривизной кривой r(s) в точке Р;
функция k1 = k1(s) называется
функцией кривизны кривой r(s), k1 ≥ 0,
 (s) -вектор
кривизны кривой
(s) -вектор
кривизны кривой  (s).
(s).
Величина k2 называется
кручением кривой  ꞌ(s) или второй
кривизной кривой
ꞌ(s) или второй
кривизной кривой  (s) в точке Р.
При движении точки Р по кривой
(s) в точке Р.
При движении точки Р по кривой  (s), т.е. с
изменением параметра s, имеем функцию k2= k2(s) - функцию
кручения. Знак величины k2 может быть и
положительным, и отрицательным
(s), т.е. с
изменением параметра s, имеем функцию k2= k2(s) - функцию
кручения. Знак величины k2 может быть и
положительным, и отрицательным
k1=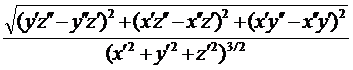 (1);
(1);
k2 = 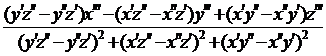
 (2).
(2).
Практическая часть вычисления
кривизны и кручения в произвольной и выбранной точке
Вычислим, имея компоненты нашей
кривой: кривизну и кручение в произвольной и выбранной точке.
Кривизна кривой (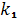
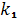 ) в произвольной точке вычисляется
согласно формуле (1).Подставляем наши координаты в эту формулу, получаем:
) в произвольной точке вычисляется
согласно формуле (1).Подставляем наши координаты в эту формулу, получаем:
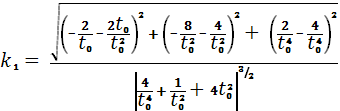
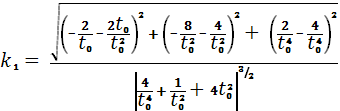
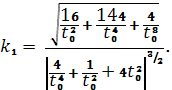
Мы нашли кривизну кривой в
произвольной точке. Найдем кривизну выбранной точке, подставив вместо 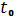
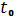 значение равное 1, которое мы
выбрали ранее.
значение равное 1, которое мы
выбрали ранее.
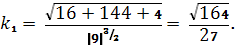
Кривизна кривой в выбранной точке
найдена.
Кручение кривой (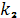
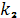 ) в произвольной точке вычисляется
согласно формуле (2).Подставляем наши координаты в эту формулу, получаем:
) в произвольной точке вычисляется
согласно формуле (2).Подставляем наши координаты в эту формулу, получаем:

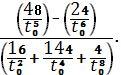
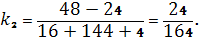
Кручение кривой в выбранной точке
найдена.
.4 Построение кривой
Изобразим нашу кривую; она будет
иметь следующий вид:

2. Поверхности евклидова пространства
Нам даны компоненты поверхности: x=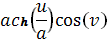
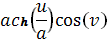 , y=
, y=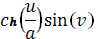
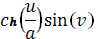 , z=
, z=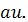
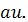 Найдем на ее примере уравнение
касательной плоскости и нормали, первую и вторую квадратичные формы в произвольной
и выбранной точке. Вычислим полную и среднюю кривизны поверхности. Изобразим
поверхность.
Найдем на ее примере уравнение
касательной плоскости и нормали, первую и вторую квадратичные формы в произвольной
и выбранной точке. Вычислим полную и среднюю кривизны поверхности. Изобразим
поверхность.
.1 Касательная плоскость и нормаль
поверхности. Нахождение касательной плоскости и нормали в произвольной и
выбранной точке
Пусть P - точка
регулярной поверхности  (u,v). В этой
точке имеем неколлинеарные векторы
(u,v). В этой
точке имеем неколлинеарные векторы 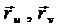 . Для любой линии
. Для любой линии  (t) =
(t) =  (u(t),v(t))
выполняется
(u(t),v(t))
выполняется 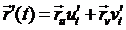 .
.
Касательная прямая 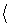 P ,
P ,  ꞌ(t)
ꞌ(t)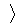 всякой
кривой
всякой
кривой  (t) =
(t) =  (u(t),v(t))
поверхности
(u(t),v(t))
поверхности  (u,v) лежит в
плоскости
(u,v) лежит в
плоскости 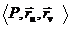 .
Касательные всех линий поверхности
.
Касательные всех линий поверхности  (u,v)
,проходящих через точку Р, образуют плоскость.
(u,v)
,проходящих через точку Р, образуют плоскость.
Пусть Р=(x0,y0,z0) и
производные 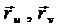 вычислены в
точке Р.
вычислены в
точке Р.
Тогда уравнение касательной
плоскости таково
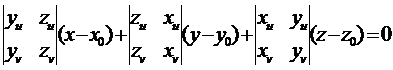 .
.
Прямая 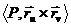 называется
нормалью поверхности
называется
нормалью поверхности  (u,v) в точке Р.
Ее уравнение
(u,v) в точке Р.
Ее уравнение
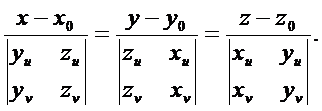
Нахождение касательной плоскости и
нормали в произвольной и выбранной точке
Вычислим производные по u и v. Получим
следующее:
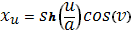
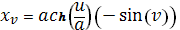
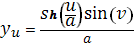
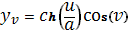
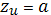
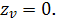
Возьмем точки 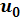
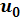 =
=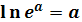
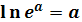 ,
, 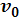
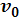 =
=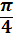
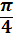 .
.
Найдем касательную плоскость в
произвольной точке:

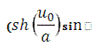
Уравнение касательной плоскости в
произвольной точке найдено.
Найдем в выбранной точке, подставив
значения 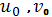
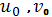 и расписав
и расписав
sh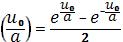
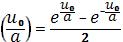 и ch
и ch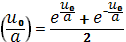
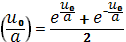 :
:
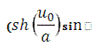
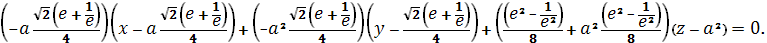
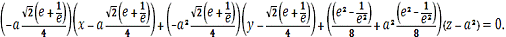
Мы нашли уравнение касательной плоскости
в выбранной точке.
Теперь найдем уравнение нормали в
произвольной и выбранной точке, используя теоретическую часть нашего вопроса,
получим:
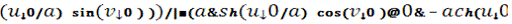

Получено уравнение нормали в произвольной точке.
Найдем в выбранной:
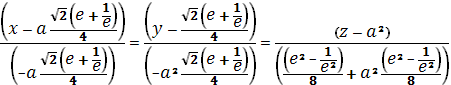
Уравнение нормали в выбранной точке найдено.
.2 Первая основная квадратичная форма
поверхности. Вычисление первой квадратичной формы в произвольной и выбранной
точке
В произвольной точке Р поверхности  (u,v) зададим направление, выбрав u=u(t), v=v(t). Отношение дифференциалов
(u,v) зададим направление, выбрав u=u(t), v=v(t). Отношение дифференциалов
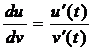
определяет
направление на поверхности , имеем
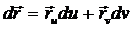 .
.
Производная от  (u,v) по направлению du: dv имеет вид:
(u,v) по направлению du: dv имеет вид:
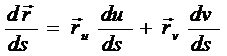 .
.
Малое смещение ds по кривой  (u(t),v(t)) на поверхности вычисляется на основании равенств
(u(t),v(t)) на поверхности вычисляется на основании равенств
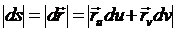 .
.
Отсюда
получаем ,вычисляя скалярный квадрат
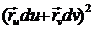 =
=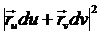 ,
,
ds2=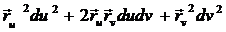 .
.
Введем
обозначения
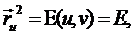
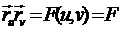 ,
,  .
.
Значения
этих скалярных произведений зависят от выбора точки Р поверхности . Выражение:
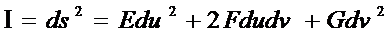
называется
первой квадратичной формой поверхности  (u,v).
(u,v).
Вычисление первой квадратичной формы в
произвольной и выбранной точке.
Вычислим первую квадратичную форму в выбранной
точке.
Найдем
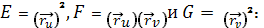
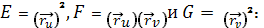
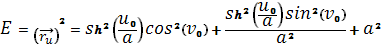
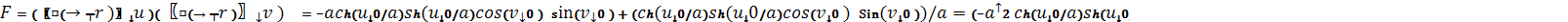
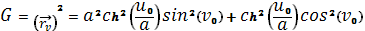
Теперь, когда найдены значения E,F и G, напишем
формулу первой квадратичной формы в произвольной точке:
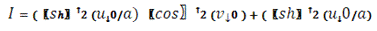
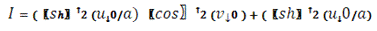
Нами получена формула первой
квадратичной формы в произвольной точке.
Теперь, подставив наши значения 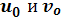
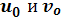 в формулу первой квадратичной
формы, найдем ее значение в выбранной точке:
в формулу первой квадратичной
формы, найдем ее значение в выбранной точке:
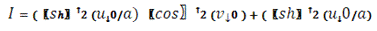
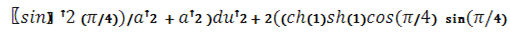
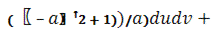 )
)
.3 Вторая квадратичная форма поверхности.
Вычисление второй квадратичной формы поверхности в произвольной и выбранной
точке
На поверхности  (u,v) рассмотрим
линию u=u(s), v=v(s) в
естественной параметризации :
(u,v) рассмотрим
линию u=u(s), v=v(s) в
естественной параметризации :
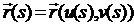 .
.
Кривизна кривой :
 (s) =
(s) =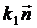 ,
,
где k1 кривизна
кривой, 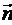 - единичный
вектор главной нормали кривой. Обозначим
- единичный
вектор главной нормали кривой. Обозначим 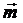 - единичный вектор нормали
поверхности
- единичный вектор нормали
поверхности
 (u,v) , это
вектор
(u,v) , это
вектор
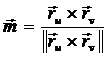 .
.
Умножим скалярно 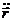 и
и 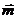 :
:
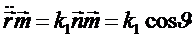 ,
,
если 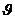 - угол между
- угол между 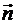 и
и 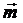 . Величина
. Величина
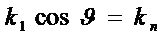
Называется нормальной кривизной  (s) на
поверхности
(s) на
поверхности  (u,v) или
нормальной кривизной поверхности
(u,v) или
нормальной кривизной поверхности
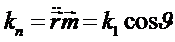 .
.
Вычислим kn в
окрестности точки Р=(x0,y0,z0) . Находим
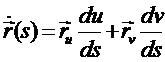 ,
,
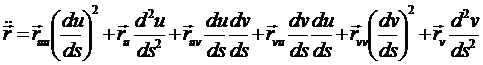 ,
,
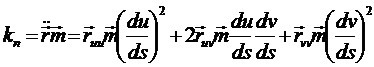 ,
,
здесь 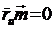 и
и 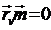 , так как
, так как 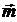
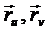 . Обозначим
. Обозначим
 ,
, 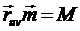 ,
, 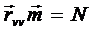 .
.
На основании формул:
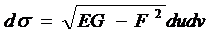 и
и 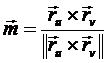 имеем
имеем
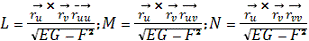
Коэффициенты L,M,N вычислены в
точке Р поверхности .Выражение для нормальной кривизны линии на поверхности
таково:
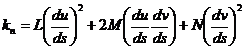 .
.
Отсюда получаем
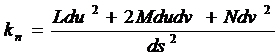 .
.
Воспользуемся значением ds2 из первой
квадратичной формы поверхности
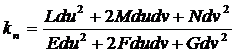 .
.
Квадратичная форма
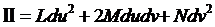
Называется второй квадратичной
формой поверхности.
Вычисление второй квадратичной формы
поверхности в произвольной и выбранной точке.
Найдем вторую квадратичную форму в
произвольной точке:
Вычислим, для начала чему равен 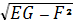
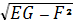 , подставив ранее полученные
значения E, G и F для первой
квадратичной формы:
, подставив ранее полученные
значения E, G и F для первой
квадратичной формы:

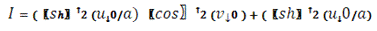
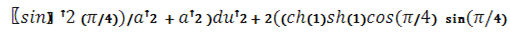
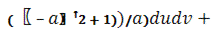 )
)
Найдем векторное произведение 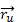
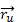 и
и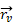
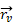 :
:
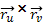
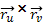 =
= 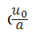 )
)
Затем вычислим
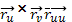
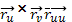 ,
, 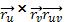
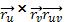 и
и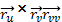
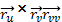 :
:
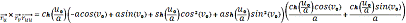
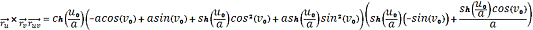
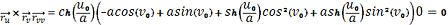
Найдем коэффициенты второй
квадратичной формы, подставив в формулы
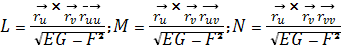
наши значения:
L=
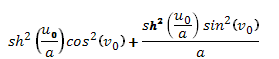
M=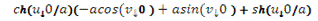

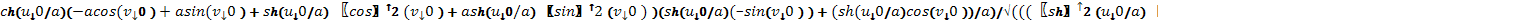
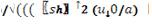
N=0
Теперь напишем формулу второй
квадратичной формы поверхности в произвольной точке
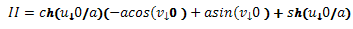


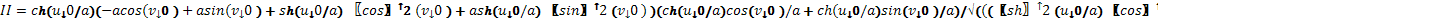
Вторая квадратичная форма в
произвольной точке найдена.
Подставив значения 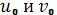
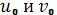 в нашу формулу, получим уравнение
второй квадратичной формы в выбранной точке:
в нашу формулу, получим уравнение
второй квадратичной формы в выбранной точке:
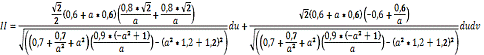
Уравнение второй квадратичной формы
в выбранной точке найдено.
2.4 Полная и средняя кривизны поверхности.
Вычисление полной и средней кривизны поверхности
Рассмотрим регулярную  (u,v) в
окрестности точки Р.
(u,v) в
окрестности точки Р.
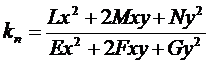 .
.
Отсюда получаем
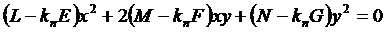 .
.
Дифференцируем это неравенство по x и по y
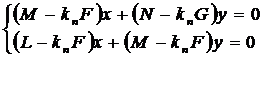
Главные направления в касательной
плоскости определяются этой системой уравнений, если она имеет ненулевые
решения, т.е. в случае ∆=0
Значение определителя
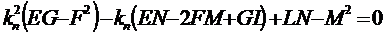 .
.
Главные кривизны 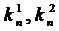 есть корни
выписанного уравнения. Воспользуемся теоремой Виета
есть корни
выписанного уравнения. Воспользуемся теоремой Виета
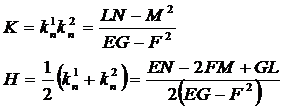 ,
,
где К- полная кривизна поверхности
(Гауссова кривизна),
Н- средняя кривизна поверхности.
Вычисление полной и средней кривизны поверхности
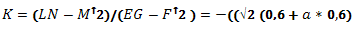
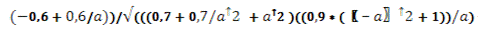
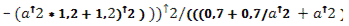
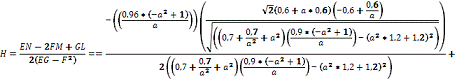
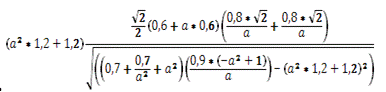
Мы вычислили полную и среднюю кривизну
поверхности.
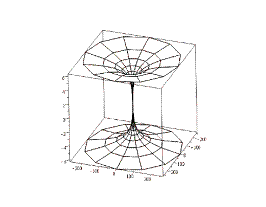
2.5 Изображение поверхности
Изобразим нашу поверхность; она будет иметь
следующий вид:
Список
использованной литературы
.Долгарев А.И.
Элементы дифференциальной галилеевой геометрии и одуль галилеевых
преобразований. - Саранск: Средневолжское математическое общество, 2003(препринт
63). - 116 с.
.Долгарев А.И.
Классические методы в дифференциальной геометрии одулярных пространств. -
Пенза: Инф.-изд. Центр Пенз. гос. ун-та, 2004. - 306 с.
.Позняк Э.Г.
Дифференциальная геометрия. Первое знакомство / Э.Г. Позняк, Е.В. Шикин. - М.:
Изд-во МГУ, 1990.-384 с.
.Долгарев А.И.
Одулярное описание афинных преобразований плоскости: Деп. В ВИНИТИ 07.02.97,
№369 - В97. - 59 с.