Реализация амплитудной модуляции
СОДЕРЖАНИЕ
НОРМАТИВНЫЕ ССЫЛКИ
ВВЕДЕНИЕ
. Амплитудная модуляция
.1 Понятие и сущность амплитудной модуляции
.2 Амплитудно-модулированные колебания и их спектры
.3 Амплитудная модуляция как нелинейный процесс
. Реализация амплитудной модуляции
.1 Построение модулирующего сигнала
.2 Амплитудно-частотная характеристика
.3 Метод суперпозиции
.4 Оцифровка сигнала
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
ПРИЛОЖЕНИЕ А - Код подпрограммы «Построение модулирующего
сигнала»
ПРИЛОЖЕНИЕ Б - Код подпрограммы «Амплитудно-частотная
характеристика»
ПРИЛОЖЕНИЕ В - Код подпрограммы «Метод суперпозиции»
ПРИЛОЖЕНИЕ Г - Код подпрограммы «Оцифровка сигнала»
НОРМАТИВНЫЕ
ССЫЛКИ
В настоящем пособии использованы ссылки на следующие стандарты:
ГОСТ 2.105-95. Общие требования к текстовым документам
ГОСТ Р 50739-95. Государственный стандарт РФ. Средства вычислительной
техники. Защита от несанкционированного доступа к информации. Общие технические
требования
ГОСТ 7.32-2001. СИБИД. Отчет о НИР. Структура и правила оформления
ГОСТ 7.1-84 СИБИД. Библиографическое описание
документа. Общие требования и правила составления»
ГОСТ 7.80-2000 Библиографическая запись. Заголовок.
Общие требования и правила составления
ГОСТ 19.701-90 (ИСО 5807-85) ЕСПД. Схемы алгоритмов, программ, данных и систем.
Обозначения условные и правила выполнения
ГОСТ 34.601-90 Информационная технология. Комплекс
стандартов на автоматизированные системы. Автоматизированные системы. Стадии
создания
ВВЕДЕНИЕ
Курсовая работа выполняется с целью закрепления пройденного материала по
амплитудной модуляции сигналов, а также для углубления знаний по данной
проблеме. В работе необходимо дать определение амплитудной модуляции, раскрыть
её сущность, описать основные формы. После этого преступить к рассмотрению
алгоритмов задания данного вида модуляции. Затем написать программу,
демонстрирующую наглядное представление амплитудной модуляции сигналов.
Полученные сигналы необходимо оцифровать и вывести результаты на экран.
Программирование будет выполняться в Microsoft Visual Studio 2010 в Win Forms
на языке C#. В конце работы сформулировать выводы.
1. Амплитудная модуляция
.1 Понятие и сущность амплитудной модуляции
Амплитудная модуляция - вид модуляции, при которой изменяемым параметром
несущего сигнала является его амплитуда.
Первый опыт передачи речи и музыки по радио методом амплитудной модуляции
произвёл в 1906 году американский инженер Р. Фессенден. Несущая частота 50 кГц
радиопередатчика вырабатывалась машинным генератором (альтернатором), для её
модуляции между генератором и антенной включался угольный микрофон, изменяющий
затухание сигнала в цепи. С 1920 года вместо альтернаторов стали использоваться
генераторы на электронных лампах. Во второй половине 1930-х годов, по мере
освоения ультракоротких волн, амплитудная модуляция постепенно начала
вытесняться из радиовещания и радиосвязи на УКВ частотной модуляцией. С
середины XX века в служебной и любительской радиосвязи на всех частотах
внедряется модуляция с одной боковой полосой (ОБП), которая имеет ряд важных
преимуществ перед АМ. Поднимался вопрос о переводе на ОБП и радиовещания,
однако это потребовало бы замены всех радиовещательных приёмников на более
сложные и дорогие, поэтому не было осуществлено. В конце XX века начался
переход к цифровому радиовещанию с использованием сигналов с амплитудной
манипуляцией.
Определение
Пусть
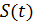 - информационный сигнал,
- информационный сигнал, 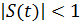 ,
,
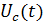 - несущее колебание.
- несущее колебание.
Тогда амплитудно-модулированный сигнал 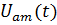 может быть записан следующим
образом:
может быть записан следующим
образом:
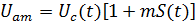
Здесь 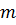 - некоторая константа, называемая коэффициентом модуляции.
Формула (1) описывает несущий сигнал
- некоторая константа, называемая коэффициентом модуляции.
Формула (1) описывает несущий сигнал 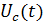 , модулированный по амплитуде
сигналом
, модулированный по амплитуде
сигналом 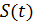 с коэффициентом модуляции
с коэффициентом модуляции 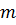 . Предполагается также, что выполнены
условия:
. Предполагается также, что выполнены
условия:
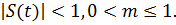
Выполнение условий (2) необходимо для того, чтобы выражение в квадратных
скобках в (1) всегда было положительным. Если оно может принимать отрицательные
значения в какой-то момент времени, то происходит так называемая перемодуляция
(избыточная модуляция). Простые демодуляторы (типа квадратичного детектора)
демодулируют такой сигнал с сильными искажениями.
1.2 Амплитудно-модулированные колебания и их спектры
Пусть гармоническое колебание 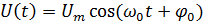 используется в качестве несущего, а
модулирующий сигнал
используется в качестве несущего, а
модулирующий сигнал 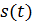 является гармоническим (однотональным) колебанием
является гармоническим (однотональным) колебанием 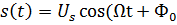 и выполняется условие
и выполняется условие 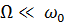 . Тогда AM-колебание называется
однотональным. При
. Тогда AM-колебание называется
однотональным. При 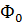 имеем:
имеем:
 , (1)
, (1)
где 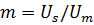 - коэффициент амплитудной модуляции.
- коэффициент амплитудной модуляции.
Спектральный состав сигнала можно получить, представляя произведение
функций (1) в виду суммы гармонических колебаний. Тогда
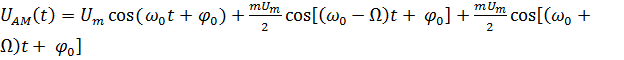 .
.
Спектр однотонального AM колебания линейчатый эквидистантный. Он состоит
из трех гармонических колебаний с близкими частотами.
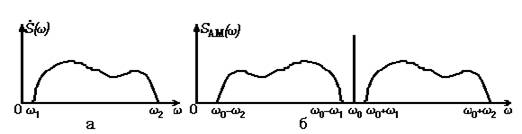
Рисунок 1 - Спектр однотонального AM колебания
Амплитудная модуляция гармонического колебания произвольным сигналом,
обладающим сплошным спектром в области низких частот, сопровождается
формированием в окрестности несущего колебания двух групп боковых колебаний
(Рисунок 1). Верхняя группа колебаний (от ( ) до (
) до ( )) является точной копией спектра
модулирующего сигнала, сдвинутой в область радиочастот, а нижняя группа
колебаний представляется зеркальное отражение спектра модулирующего сигнала
относительно
)) является точной копией спектра
модулирующего сигнала, сдвинутой в область радиочастот, а нижняя группа
колебаний представляется зеркальное отражение спектра модулирующего сигнала
относительно 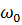 , а также смещенное в область радиочастот. Колебания с
комбинационными частотами (
, а также смещенное в область радиочастот. Колебания с
комбинационными частотами (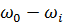 ) и (
) и (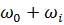 ) располагаются попарно-симметрично относительно частоты
несущего колебания. Полная ширина спектра AM-процесса равняется удвоенной
ширине спектра модулирующего сигнала.
) располагаются попарно-симметрично относительно частоты
несущего колебания. Полная ширина спектра AM-процесса равняется удвоенной
ширине спектра модулирующего сигнала.
Частным случаем многотонального AM-сигнала является высокочастотное
колебание, промодулированное по амплитуде последовательностью прямоугольных
импульсов.
1.3 Амплитудная модуляция как нелинейный процесс
При амплитудной модуляции сигналов происходит перемножение двух функций:
высокочастотного колебания с частотой 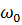 и модулирующего гармонического или
полигармонического сигнала. Эту процедуру можно осуществить в нелинейной
системе при задании на вход суммы несущего и модулирующего сигналов и выделении
на выходе их произведения. Спектр выходного сигнала содержит составляющие с
частотами, отсутствовавшими у исходных колебаний. Количество и частоты новых
составляющих зависят от вида нелинейного элемента и его вольт-амперной
характеристики (ВАХ).
и модулирующего гармонического или
полигармонического сигнала. Эту процедуру можно осуществить в нелинейной
системе при задании на вход суммы несущего и модулирующего сигналов и выделении
на выходе их произведения. Спектр выходного сигнала содержит составляющие с
частотами, отсутствовавшими у исходных колебаний. Количество и частоты новых
составляющих зависят от вида нелинейного элемента и его вольт-амперной
характеристики (ВАХ).
ВАХ нелинейных элементов (НЭ), получаемые экспериментально и
представляемые в виде графиков или таблиц, неудобно использовать в расчетах, и
для теоритического анализа их аппроксимируют аналитическими функциями.
Наибольшее распространение в радиоэлектронике получили аппроксимации степенным
многочленом и ломаной линией.
2. Реализация амплитудной модуляции
.1 Построение модулирующего сигнала
Амплитудная модуляция характеризуется изменением амплитуды 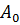 переносчика
переносчика 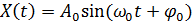 по закону сигнала передаваемого
сообщения
по закону сигнала передаваемого
сообщения
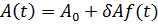 ,
,
где 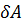 - наибольшее изменение амплитуды при модуляции,
- наибольшее изменение амплитуды при модуляции,
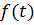 - функция, выражающая закон изменения во времени передаваемого
сообщения.
- функция, выражающая закон изменения во времени передаваемого
сообщения.
Тогда амплитудно-модулированный гармонический сигнал (Рисунок 2.1) будет
иметь следующий вид:
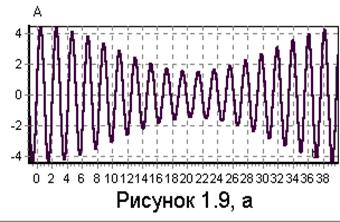
Рисунок 2.1.1 - Амплитудно-модулированный гармонический сигнал
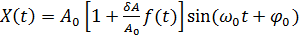 ,
,
где 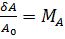 - глубина амплитудной модуляции.
- глубина амплитудной модуляции.
В том случае, когда 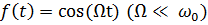 ,
,
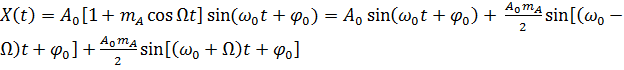 .
.
Как видно из выражения (Рисунок 2.1), спектр сигнала состоит из трех
гармонических составляющих: несущей с частотой  и двух частот - нижней
и двух частот - нижней  и верхней -
и верхней - 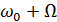 . Ширина спектра сигнала
. Ширина спектра сигнала 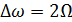 .
.
В рассмотренном примере А0=13, w0 =20, W=4, А0mА=10.
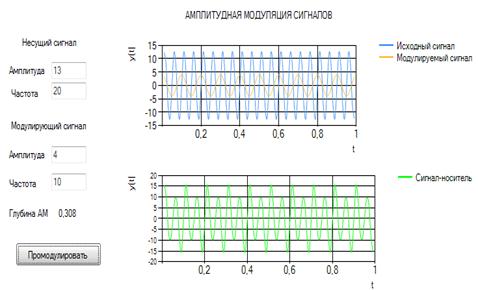
Рисунок 2.1.2 - Графики сигналов
На рисунке 2.1.2 на верхней оси координат изображены 2 функции: исходный
сигнал (синий) с входными параметрами: амплитуда 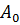 =13 и частотой
=13 и частотой 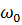 =20; и модулируемый сигнал (оранжевый)
с параметрами на входе: амплитуда
=20; и модулируемый сигнал (оранжевый)
с параметрами на входе: амплитуда 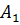 =4 и частотой
=4 и частотой 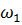 =10.
=10.
На нижней оси координат представлен сигнал-носитель, который строится по
следующей формуле:
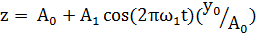 ,
,
где 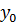 =
= 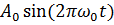 .
.
 изменяется от 0,01 до 1 с шагом 0,01.
изменяется от 0,01 до 1 с шагом 0,01.
Амплитудно-частотная характеристика (АЧХ) - функция, показывающая
зависимость модуля некоторой комплекснозначной функции от частоты. Также может
рассматриваться АЧХ других комплекснозначных функций частоты, например,
спектральной плотности мощности сигнала.
АЧХ в теории линейных стационарных систем означает зависимость модуля
передаточной функции системы от частоты. АЧХ показывает, во сколько раз
амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на
всём диапазоне частот.
На графике АЧХ по оси абсцисс откладывается частота, а по оси ординат
отношение амплитуд выходного и входного сигналов системы. Обычно для частоты
используется логарифмический масштаб, так как исследуемый диапазон частот может
изменяться в достаточно широких пределах (от единиц до миллионов Гц или рад/с).
В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ
превращается в логарифмическую амплитудно-частотную характеристику. ЛАЧХ
получила широкое распространение в теории автоматического управления в связи с
простотой построения и наглядностью при исследовании систем управления.
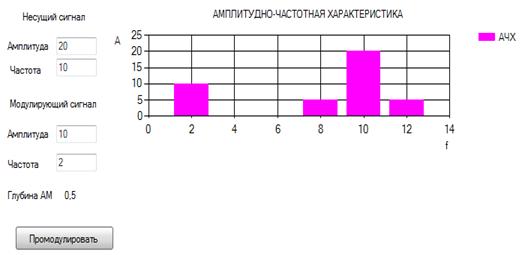
Рисунок 2.2 - Программная реализация амплитудно-частотной характеристики
2.3 Метод суперпозиции
Непосредственный анализ воздействия сигналов сложной формы на
радиотехнические цепи весьма затруднителен и вообще не всегда возможен. Поэтому
сложные сигналы имеет смысл представлять как сумму некоторых простых
элементарных сигналов. Принцип суперпозиции обосновывает возможность такого
представления, утверждая, что в линейных цепях воздействие суммарного сигнала
равносильно сумме воздействий соответствующих сигналов по отдельности.
В качестве элементарных сигналов часто применяют гармоники. Такой выбор
имеет ряд достоинств:
) Разложение на гармоники реализуется достаточно легко путем
использования преобразования Фурье.
) При воздействии гармонического сигнала на любую линейную цепь его форма
не изменяется (остается гармонической). Сохраняется также частота сигнала.
Амплитуда и фаза, конечно, изменяются; их можно сравнительно просто
рассчитывать, применяя метод комплексных амплитуд.
) В технике широко используются резонансные системы, позволяющие
экспериментально выделять одну гармонику из сложного сигнала.
Представление сигнала суммой гармоник, заданных частотой, амплитудой и
фазой, называется разложением сигнала в спектр.
Гармоники, входящие в состав сигнала, задаются в тригонометрической или
мнимопоказательной форме.
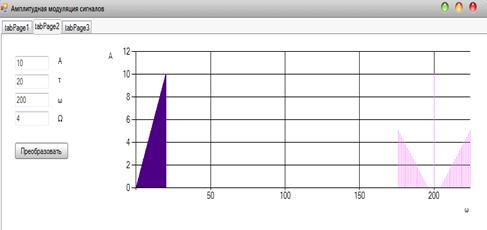
Рисунок 3.3 - Программная реализация принципа суперпозиции
На рисунке 3.3 показано, что исходный сигнал с амплитудой (A) = 10 и
длиной (τ)
= 20 может быть
представлен двумя другими сигналами, которые размещены от исходного сигнала на
указанном расстоянии  ) = 200 и отступом (Ω) = 4 от
) = 200 и отступом (Ω) = 4 от  в обе стороны.
в обе стороны.
2.4 Оцифровка сигнала
Для более удобной передачи данных сигналы следует оцифровывать. Следующая
программа оцифровывает случайный сигнал. Входные параметры: Максимальная
амплитуда A. Шаг оцифровки: чем он больше, тем крупнее шаги и меньше значений
будет обработано и переведено в двоичную систему счисления.
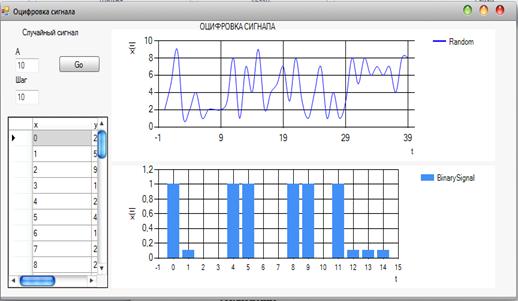
Рисунок 3.4.1 - Результат выполнения оцифровки сигнала
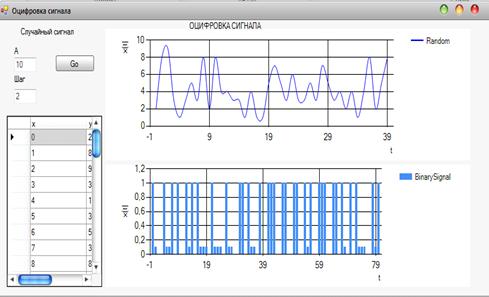
Рисунок 3.4.2 - Результат выполнения оцифровки сигнала
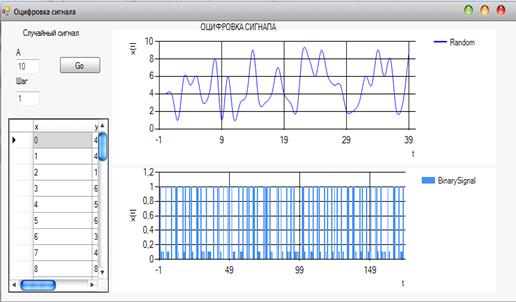
Рисунок 3.4.3 - Результат выполнения оцифровки сигнала
На рисунках 3.4.1 - 3.4.2 показаны результаты выполнения программы, которая
оцифровывает сигнал. Из рисунков видно как с изменением параметра «Шаг»
меняется нижний график (бинарный сигнал). Чем меньше шаг, тем больше точек
сигнала обработчик переводит из десятичной системы счисления в двоичную систему
счисления.
ЗАКЛЮЧЕНИЕ
В курсовой работе дано определение амплитудной модуляции, представлены
амплитудно-модулированные колебания и их спектры, описан технический смысл
амплитудной модуляции сигналов. Рассмотрен принцип суперпозиции. Построены
сигналы по входным данным. Построена амплитудно-частотная характеристика этих
сигналов. Реализован алгоритм бинарной (двоичной) оцифровки сигнала, а также
определено, от какого параметра зависит точность получаемых результатов при
оцифровке данного вида. В итоге написана программа, которая разбита на
несколько подпрограмм, наглядно демонстрирующие все вышеперечисленное.
СПИСОК
ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Власенко
А.В., Ключко В.И. Теория информации и сигналов. Учебное пособие / Краснодар:
Изд-во КубГТУ, 2003.- 97 с.
. Теория
передачи сигналов: Учебник для вузов / А.Г.Зюко, Д.Д.Кловский,
М.В.Назаров,
Л.М.Финк. - 2-е изд., перераб. и доп. - М.: Радио и связь, 1986. - 304 с.: ил.
3. Прокис Дж.
Цифровая связь. Пер. с англ./ Под ред. Д.Д. Кловского. - М.: Радио и связь.
2000. - 800 с.
4. А.В. Хохлов,
Г.А. Окрокверцхов, В.С. Маляев - Исследование амплитудной модуляции и
детектирования сигналов в нелинейных радиосистемах: Учебное пособие для
спецпрактикума по курсу «Теоретические основы радиоэлектроники».
ПРИЛОЖЕНИЕ А - Код подпрограммы «Построение модулирующего сигнала»
(double t = 0.01; t <= 1; t = t + 0.01)
{y1 = A1 * Math.Sin(2 * Math.PI * f1 * t);y2 = A2 * Math.Cos(2 * Math.PI
* f2 * t);.Series[0].Points.AddXY(t, y1);.Series[1].Points.AddXY(t, y2);z = (A1
+ A2 * Math.Cos(2 * Math.PI * f2 * t)) * (y1 / A1);.Series[0].Points.AddXY(t,
z);
}
ПРИЛОЖЕНИЕ Б - Код подпрограммы «Амплитудно-частотная
характеристика»
A1 = Convert.ToDouble(textBox4.Text);f1 =
Convert.ToDouble(textBox6.Text);A2 = Convert.ToDouble(textBox7.Text);f2 =
Convert.ToDouble(textBox8.Text);.Series[0].Points.AddXY(f1,
A1);.Series[0].Points.AddXY(f2, A2);.Series[0].Points.AddXY(f1 + f2, A2 /
2);.Series[0].Points.AddXY(f1 - f2, A2 / 2);
ПРИЛОЖЕНИЕ В - Код подпрограммы «Метод суперпозиции»
void button2_Click(object sender, EventArgs e)
{.Series[0].Points.Clear();.Series[1].Points.Clear();.Series[2].Points.Clear();A1
= Convert.ToDouble(textBox1.Text); // Амплитудаt =
Convert.ToDouble(textBox2.Text); // Длительность импульсаw =
Convert.ToDouble(textBox3.Text);(double xx = 0.01; xx < t; xx = xx + 0.01)
{y = Math.Abs((A1 / t) * xx);.Series[2].Points.AddXY(xx, y);
}
//f = Convert.ToDouble(textBox5.Text);(double xx = 0.01; xx < t; xx =
xx + 0.01)
{y = Math.Abs((A1 / t) * xx);.Series[0].Points.AddXY(Math.Ceiling(xx) + f
+ w, y / 2);
}(int i = 0; i < t; i++)
{(double xx = 0.01; xx > -t; xx = xx - 0.01)
{y = Math.Abs((A1 / t) * xx);.Series[1].Points.AddXY(Math.Ceiling(xx) + f
- 1 - w, y / 2);
}
}.Series[1].Points.AddXY(f, A1);
}
ПРИЛОЖЕНИЕ Г - Код подпрограммы «Оцифровка сигнала»
void button1_Click(object sender, EventArgs e)
{.Series[0].Points.Clear();.Series[0].Points.Clear();.Rows.Clear();shagkv
= int.Parse(textBox4.Text);A = int.Parse(textBox3.Text);int n = 40;[] y = new
int[1000000];[] binary = new double[10000000];r = new Random();(int i = 0; i
< n; i = i + 1)
{[i] = r.Next(1, A);.Series[0].Points.AddXY(i, y[i]);.Rows.Add(i, y[i]);
}
//////////////////////////////////////////////////////////kk = 0;(int i =
0; i < n; i=i+shagkv)
{l = 0;= Math.Ceiling(Math.Log(y[i], 2)) + 1;(int j = 1; j <= l; j++)
{[j] = y[i] % 2;(y[i] == 1) binary[j] = 1;(binary[j] == 0) binary[j] =
binary[j] + 0.1;.Series[0].Points.AddXY(l - j + kk, binary[j]);(y[i] == 1)
break;(binary[j] == 1)
{[i] = (y[i] - 1) / 2;
}y[i] = y[i] / 2;
}= kk + l + 1;
}