Моделирование динамических биологических систем

Моделирование динамических биологических систем

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «КубГУ»)

Физико-технический факультет Кафедра физики и информационных систем

КУРСОВАЯ РАБОТА

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ БИОЛОГИЧЕСКИХ СИСТЕМ

Работу выполнил

Литвинов Николай Александрович

Научный руководитель

канд. физ.-мат. наук, доцент В. В. Супрунов

Краснодар 2012

СОДЕРЖАНИЕ

Введение

. Исследование устойчивости бистабильных систем

.1 Условие устойчивости бистабильной системы

.2 Результаты выполнения

. Моделирование системы в пакете Model Vision Studium

.1 Условие устойчивости динамической системы

.2 Результаты выполнения

Заключение

Список используемых источников

РЕФЕРАТ

Литвинов Н.А. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ БИОЛОГИЧЕСКИХ СИСТЕМ.

Курсовая работа: 25 страниц, 14 рисунков, 0 таблиц, 8 источников

БИСТАБИЛЬНЫЕ СИСТЕМЫ, УСТОЙЧИВОСТЬ, ФАЗОВЫЙ ПОРТРЕТ, ДОМЕН, MVS, КАРТА ПОВЕДЕНИЯ, ЭКЗЕМПЛЯР КЛАССА, ПОВЕДЕНИЕ СИСТЕМЫ.

Целью курсовой работы является более подробное, углубленное и в некоторой степени исследовательское изучение наиболее важных разделов курса с помощью программного обеспечения персональных ЭВМ (математические инструментальные среды MathCAD, пакет моделирования систем Model Vision Studium).

ВВЕДЕНИЕ

В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования.

Компьютерное моделирование используют для исследования системы до того, как она спроектирована, с целью определения чувствительности ее характеристик к изменениям структуры и параметров объекта моделирования и внешней среды. На этом этапе проектирования системы компьютерное моделирование используют для анализа и синтеза различных вариантов и выбора максимально эффективного при принятых ограничениях.

Программный комплекс Model Vision Studium (MVS) предназначен для моделирования сложных динамических систем. MVS является представителем подхода к решению проблемы моделирования сложных динамических систем, основанного на использовании схемы гибридного автомата. Использование карты поведения при описании переключений состояний, а также непосредственное описание непрерывных поведений системы системами алгебро-дифференциальных уравнений предоставляет большие возможности в описании гибридного поведения со сложной логикой переключений.

Сложные по внутренним связям и большие по количеству элементов системы экономически трудно поддаются прямым способам моделирования и зачастую для построения и изучения переходят к имитационным методам. Появление новейших информационных технологий увеличивает не только возможности моделирующих систем, но и позволяет применять большее многообразие моделей и способов его реализации. Совершенствование вычислительной и телекоммуникационной техники привело к дальнейшему развитию методов машинного моделирования, без которых невозможно изучение процессов и явлений, а также построение больших и сложных систем.

Вычислительная техника облегчает задачи исследователей, связанных с математическими расчетами. Построение математической и компьютерной моделей системы, работать в этой области стало проще, поскольку математические расчеты и выкладки без применения ЭВМ занимают много времени.

Передо мной была поставлена задача: исследовать модели устойчивости бистабильной и динамической систем.

1. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ БИСТАБИЛЬНЫХ СИСТЕМ

.1 Условие устойчивости бистабильной системы

Бистабильная система - это система с двумя положениями устойчивого равновесия. Бистабильный элемент обладает двумя стационарными состояниями (1 и 2), в каждом из которых он может находиться неограниченно долго ( Рисунок 1). Внешние воздействия могут приводить к переходам из одного состояния в другое. Чтобы вызвать переход, интенсивность воздействия должна превысить некоторый пороговый уровень.

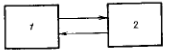
Рисунок 1 - Стационарные состояния

Простейший бистабильный элемент описывается дифферинциальным уравнением:

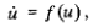
в котором нелинейная функция f(u) имеет характерный вид, изображенный на рисунке . Поведение малых отклонений подчиняется линеаризованному уравнению:

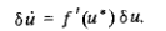
Следовательно, значение u = u` отвечает устойчивому стационарному состоянию элемента, лишь если производная f`(u) в этой точке отрицательна. Поэтому для функции f(u), изображенной на рисунке, значения u=u1, u=u3 соответствуют устойчивым состояниям, тогда как стационарное состояние со значение u=u2 абсолютно не устойчиво. [2]

Приведем несколько примеров различных систем, поведение которых действительно характеризуется уравнением вида (1) с двумя устойчивыми состояниями.

Пусть элемент представляет собой ячейку, внутри которой может протекать процесс горения. При этом будем считать, что имеющийся запас горючей смеси в этой ячейке поддерживается постоянным за счет непрерывного притока от внешнего источника либо он настолько велик, что его расходом в ходе реакции можно пренебречь.

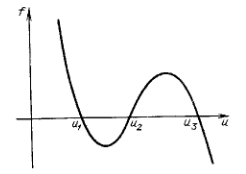
Рисунок 2 - Типичный вид функции f(u)

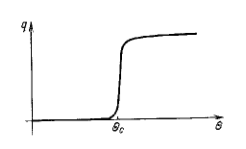
Рисунок 3 - Зависимость количества теплоты от температуры

Предположим, что при горении в единицу времени выделяется количество теплоты q(Q), которое зависит от температуры Q, при которой происходит горение. Ясно, что зависимость имеет ступенчатый характер.

Если элемент изолирован от внешней среды, то вся выделяющаяся при горении теплота расходуется на его нагрев, т.е.

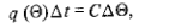
где 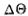 - приращение температуры за время 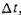 а С - теплоемкость элемента. Поэтому изменение температуры со временем подчиняется уравнению

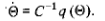
Поскольку функция 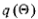 неотрицательна, то температура элемента неограниченно возрастает с течением времени.

В данном случае устойчивые по отношению к малым возмещениям стационарные состояния имеют особенно простую интерпретацию (Рисунок 4): состояние Q=Q1 отвечает отсутствию горения, так что температура элемента совпадает с температурой окружающей среды, а состояние Q=Q3 соответствует установившемуся стационарному режиму, когда выделяющаяся при горении теплота полностью отводится в окружающую среду.

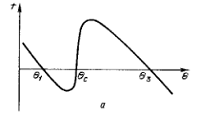
Рисунок 4 - Бистабильный режим

Оба состояния устойчивы по отношению к малым возмещениям, однако воздействия достаточно большой интенсивности могут приводить к переходам между двумя состояниями - элемент можно «зажечь» или «погасить».

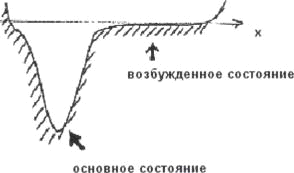
До этого шла речь только о бистабильных системах. Однако недавно было осознанно, что это явление совершенно общего плана,и оно может возникать и в системах, отличных от бистабильных. Главное требование - это наличие какого-либо порога. Примеров такой системы может служить потенциал, изображенный на(рисунок 5). В этом случае перескоки происходят не между двумя устойчивыми положениями равновесия,а между «основным» и «возбужденным» состояниями системы [4]

Рисунок 5 - Потенциал бистабильной системы

Еще одним механическим примером бистабильной системы может являться движение материальной точки в потенциале с двумя минимумами. Если на частицу действует еще и сила трения, то какие бы мы не выбрали начальные условия, колебания затухнут, частица упадет в одну и потенциальных ям и будет находится там неограниченно долго.

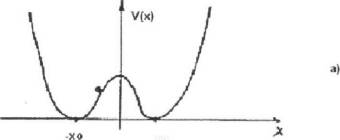
б)

Рисунок 6 - Бистабильная система и перескок под действием внешней силы

Для того, чтобы частица все-таки попала в другую потенциальную яму, надо приложить внешнюю силу. Если эта сила достаточно велика, то она "вытащит" частицу из первой ямы и перекинет ее во вторую.

Если V(x) - бистабильный потенциал, то внешняя сила должна превосходить величину F₀ = |V'(x)|, взятой в точке перегиба, т.е. там, где возвращающая сила, создаваемая потенциалом, самая большая. Тогда суммарный потенциал модифицируется так, как показано на рисунке, и частица скатится во вторую яму.

Имеется система «нагреватель - охлаждающая жидкость». Дано дифференциальное уравнение температурного поля этой системы:

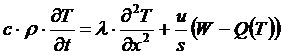, (1)

где W - тепловая нагрузка;, s - периметр и площадь сечения нагревателя;, r, l - теплоемкость, плотность, теплопроводность нагревателя;(T) - плотность теплового потока в охладитель;

а).Найти соответствующие температуру и размер домена: Tmax, ∆L и построить профиль «горячего» домена.

б).Построить фазовый портрет стационарных решений уравнения.

в).Для случая W не const, а прямой, имеющей уравнение W=a×(T-T₀), (система «сверхпроводник- жидкий гелий») найти значение коэффициента теплоотдачи a.

Данные по варианту: a = 1, λ = 1, c = 1, ρ = 1.

Номер моего варианта - 5, следовательно:=5, T2=9, Т3 =21

1.2 Результаты выполнения

Для того, чтобы выполнить эту задачу, во-первых, нужно решить задачу Коши для дифференциального уравнения второго порядка:

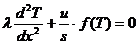 (2)

Во-вторых, изменяя начальные условия необходимо наблюдать за графиком решения, отслеживая качественное изменение его фазового портрета.

 (3)

Окончательный результат выглядит следующим образом (Рисунок 7):

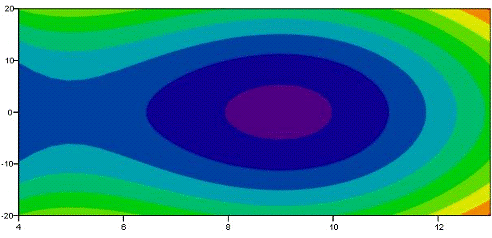
Рисунок 7 - фазовый портрет

Температура в центре домена: Т0 := 10.9

Тепловой поток в центре домена нулевой: Т(0)=0

В результате получим следующий график (Рисунок 8 )

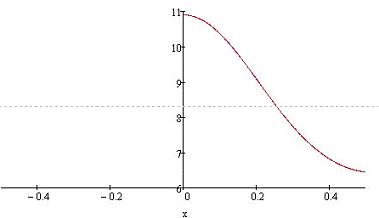
Рисунок 8 - График функции

Анализируя полученный фазовый портрет стационарных состояний нагревателя и график, получим следующее:

температура домена T_max = 10.9;

размер домена ∆L = 0.5

2. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ СИСТЕМЫ В ПАКЕТЕ MODEL VISION STUDIUM

2.1  Условие устойчивости динамической системы

Model Vision Studium - это интегрированная графическая оболочка для быстрого создания интерактивных визуальных моделей сложных динамических систем и проведения вычислительных экспериментов с ними.[2]

Пакет предназначен для численного моделирования гибридных систем. Гибридная система - это специальная математическая модель реальных объектов, обладающих одновременно "непрерывными" и "дискретными" свойствами. Такие системы достаточно трудно формализовать, так как необходим единый язык для описания как непрерывных и так и дискретных аспектов поведения, но еще труднее корректно численно решить возникающую при этом математическую задачу.[2.1]

Моделирование является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, используемым для принятия решений в различных сферах инженерной деятельности. [1]

Карта поведения - это ориентированный граф, в котором узлам приписываются некоторые локальные поведения, а дуги интерпретируются как переходы от одного поведения к другому. В каждый момент времени один из узлов является текущим. Один из узлов должен быть помечен как начальный, он становится текущим при создании карты состояний. Смена текущего узла происходит в результате срабатывания переходов. Локальные поведения являются экземплярами соответствующих классов. Когда узел становится текущим, создается экземпляр приписанного ему локального поведения, который уничтожается, когда узел перестает быть текущим. Начальное поведение проявляется при создании экземпляра блока.[6]

Карта поведения представляет собой простую и наглядную форму визуального представления смены поведений. В частном случае элемента с чисто дискретным поведением (рисунок 11), его карта поведения, всем узлам которой приписаны пустые поведения, вырождается в обычную карту состояний с некоторыми упрощениями. Упрощения связаны с запретом перехода в локальную карту поведения . Это связано с трактовкой поведения как параметризованного класса, конкретный экземпляр которого создается при входе в узел карты поведения и уничтожается при выходе. Элемент с чисто непрерывным поведением трактуется как гибридный с картой поведения, состоящей из единственного узла, которому приписано непрерывное поведение.[6.1]

С картой поведения связан гибридный интерпретатор поведений, объединяющий интерпретатор карт состояний, интерпретатор интерактивных воздействий и менеджер численных методов. В MVSTUDIUM имеется достаточно богатый набор численных методов предназначенных для воспроизведения поведения гибридных систем. Это программные реализации методов решения нелинейных алгебраических уравнений, систем обыкновенных дифференциальных уравнений и систем алгебро-дифференциальных уравнений. Для каждой группы задач имеется свой автоматический решатель, цель которого обеспечивать получение решения на заданном временном участке, любыми доступными, из числа имеющихся в пакете, методами. Любой автоматический решать начинает решать каждую новую задачу наименее трудоемких методом, а если при этом возникают какие-либо сложности, пытается подобрать метод, способный их преодолеть. Каждая смена поведения рассматривается как новая численная задача. Автоматический решатель может не справится с поставленной задачей, и тогда пользователь может попытаться управлять выбором метода самостоятельно. Пользователю доступны те же программные реализации численных методов, что и автоматическому решателю. Для отладки или первоначального решения задач в форме обыкновенных дифференциальных уравнений, когда у пользователя нет отчетливого представления о свойствах решаемой задачи или в описании поведения допущена ошибка, которую и надо найти, предусмотрена группа отладочных численных методов.[2]

Для описания модели разработан специальный язык - Model Vision Language (MVL). Он имеет как графическую, так и текстовую формы. Все переменные это языка должны быть явно описаны. В MVL существуют следующие типы данных: скалярные, регулярные и комбинированные типы, а также типы, определяемые пользователем. Скалярные типы это - вещественные, целые, булевский, перечислимые, символьный и строковый типы. Регулярные типы представлены одномерными и двумерными массивами с произвольными элементами, матрицами и векторами с вещественными элементами, а также списками. К комбинированным типам относятся записи с полями различных типов.

Пакет MVSTUDIUM относится к компилирующим средам моделирования, т.е. выполняемая модель создается как некоторый исполняемый модуль операционной среды, который может запускаться и без интегрированной оболочки пакета. Возможны два вида выполняемой модели:

) визуальная интерактивная модель с отладочными возможностями;

) "скрытая" модель с максимальным быстродействием.[1]

Визуальная модель является имитацией некоторого виртуального испытательного стенда, где все можно посмотреть и все изменить. Пользователь может наблюдать динамику процессов на временных и фазовых диаграммах в ходе моделирования, в окнах карт поведения, где отображаются текущий узел и срабатывающие переходы, в окнах структурных схем, где отображается прохождение сигналов по связям, в окнах фазового вектора, где динамически выводятся текущие значения переменных, а также с помощью типовых 2D и 3D-анимационных элементов и анимационных окон, которые он сам может создать. Пользователь может в любой момент изменить значение любой переменной модели. а также менять значение непрерывно с помощью интерактивных анимационных элементов. Можно задать план прогона модели, в котором указывается последовательность изменений значений переменных и подач сигналов во времени. Можно задать останов по времени, по истинности логического условия, по срабатыванию перехода, по входу в указанный узел. При появлении ошибки в ходе вычислений диагностируется блок и поведение, где произошла ошибка, а в случае, если при создании выполняемой модели были установлены отладочные опции, то и выводится текст соответствующего уравнения или оператора. Имеется встроенный калькулятор, в котором можно задавать любые выражения с именами переменных модели.[8]

Таким образом, дискретные аспекты поведения отражаются с помощью хорошо знакомого языка карт состояния, а непрерывные аспекты - с помощью привычного языка систем уравнений и формул.

Наиболее конструктивным средством решения инженерных задач на базе моделирования в настоящее время стали ЭВМ. Компьютерное моделирование используют для реализации различных имитационных моделей. При использовании компьютерного моделирования разрабатывается алгоритм расчета характеристик, в соответствии с которыми составляются программы, дающие возможность осуществлять расчеты по требуемым аналитическим соотношениям. Основная задача исследователя заключается в том, чтобы попытаться описать поведение реального объекта одной из известных математических моделей.[7]

Объектно-ориентированный подход к моделированию сложных динамических систем был предложен авторами языка SIMULA-67. Именно они стали использовать специальные модели - классы, описывающие сразу все множество близких по своим свойствам объектов, обладающих внутренней структурой и поведением. Разрабатываемая программная система сначала моделируется с помощью специального объектно-ориентированного языка моделирования, а только затем превращается в реальный программный комплекс. Наиболее известным является унифицированный язык моделирования (UML). Модификации объектно-ориентированной технологии применительно к моделированию сложных динамических систем возникли сравнительно недавно и называются объектно-ориентированным моделированием. Они представлены языком моделирования Modelica, реализованы в явном виде в пакетах AnyLogic, MvStudium, Ptolemy II, неявно - в Simulink, Stateflow и других компонентах пакета Mathlab.[8]

Динамическая система - системы, под действием внешних и внутренних сил изменяющие во времени свои состояния. Представления о динамических системах возникли как обобщение понятия механической системы, поведение которой описывается законами динамики Ньютона. В современной науке понятие динамической системы охватывает системы практически любой природы-физические, химические, биологические, экономические, социальные и др. При этом системы характеризуются различной внутренней организацией-жестко-детерминированные, стохастические, нелинейные, системы с элементами самоорганизации, самоорганизующиеся.[4]

Важнейшим свойством динамических систем является их устойчивость, т. е. сохранение системой своей базовой структуры и основных выполняемых функций в течение определенного времени и при относительно небольших и разнообразных внешних воздействях и внутренних возмущениях. Устойчивость есть внутреннее свойство систем, а не результат внешнего воздействия. Представления же о развитии этих систем отражают такие изменения их структурной организации, которые ведут к более эффективному выполнению системой своих основных функций. Качественные перестройки систем анализируются в теории катастроф, которая рассматривается как ветвь общей теории динамических систем.

Развитие представлений о динамических системах связано с переходом к познанию все более сложных систем. При этом особую роль приобретает изучение динамики внутренних свойств систем. В случае механических систем действие внутренних факторов сводилось к силам инерции. По мере усложнения систем возрастает значение внутренних факторов. На первый план выходят проблемы изучения источников внутренней активности систем и природы их целенаправленного функционирования и поведения.[4.1]        

Среди всех динамических систем, прежде всего, можно выделить такие, которые в процессе своего движения не изменяют свою динамическую симметрию. Это консервативные системы не способные к развитию. Отличительной чертой таких систем является их замкнутость и изолированность.

Создадим в пакете MVS модель следующей системы:

Дана система из двух тел с массами m₁ и m₂, соединенных двумя пружинами, жёсткости которых равны c₁ и с₂ (Рисунок 9):

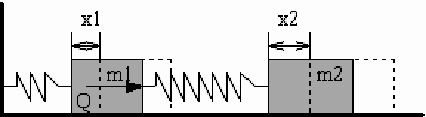
Рисунок 9 - Колебания грузов

компьютерное моделирование бистабильная система

Пусть m₁ = 1кг, m₂ = 1кг, c₁ = 1кг/с², с₂ = 1кг/с².

На левый груз системы действует гармоническая возмущающая сила Q, задаваемая с интервалом в 10 секунд то законом (1), то законом (2):

Q = H₁×Sin(w×t) (4)

Q = H₂×Cos(w×t) (5)

где H₁ и H₂ - амплитуды колебаний, w - частота колебаний.

Пусть H₁ = 1м, H₂ = 1,5м, w = 2с^-1. Частота колебаний вне зависимости от закона колебаний каждые 15 секунд то уменьшается на 50%, то возвращается к прежнему значению.

Пусть x₁ и x₂ - горизонтальное отклонение грузов от положения равновесия (в начальный момент времени отсутствующее). Тогда уравнениями движения будут:

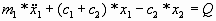 (6)

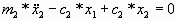 (7)

Построить модель данной системы, а также модель системы, состоящей из двух систем типа "два груза", несвязанных друг с другом. Вторая система "два груза" идентична первой, за исключением того, что в ней левый груз имеет другую массу (между m₂ и m₁), а правая пружина имеет другую жёсткость (выше с₂).

2.2 Результаты выполнения

Для решения задачи №2 в MVS был создан один класс Class_1 (рисунок 10).

Рисунок 10 - Класс Class_1

Начальные значения объявим в разделе Параметры. Все переменные, которые используются в процессе вычислений, описаны в разделе Внутренние переменные. Также были созданы локальная карта поведения Карта_поведения_1 и 2 системы уравнений.

После описания всех переменных и констант проект kursovik выглядит следующим образом (рисунок 11):

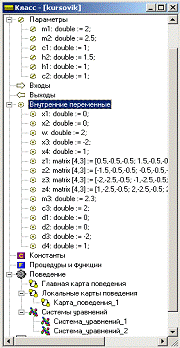
Рисунок 11 - Проект kursovik

Алгоритм поведения системы я отобразил на Карте поведения (Рисунок 11). Система имеет 11 состояний:

Состояние, в котором вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₁×Sin(w×t) (Node_1)

Состояние, в котором происходит уменьшение частоты колебаний на 50% (Node_4)

Состояние, в котором вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₁×Sin(w×t) (Node_5)

Состояние, в котором происходит увеличение частоты колебаний на 50%. А также вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₂×Cos(w×t) (Node_7)

Состояние, в котором вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₁×Sin(w×t) (Node_8).

Состояние, в котором происходит уменьшение частоты колебаний на 50% (Node_9)

Состояние, в котором вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₂×Cos(w×t) (Node_10)

Состояние, в котором происходит увеличение частоты колебаний на 50%. А также вычисляется горизонтальное отклонение грузов от положения равновесия, при действии на левый груз системы гармонической возмущающей силы Q, задаваемая с интервалом в 20 секунд то законом Q = H₁×Sin(w×t) (Node_11)

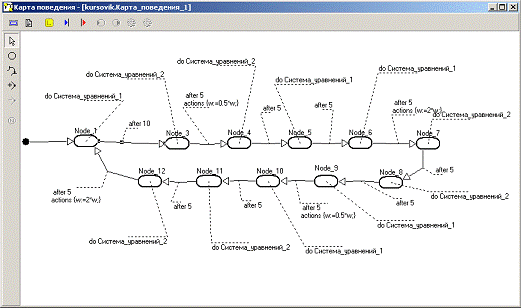
Рисунок 12 - Карта поведения системы

Переход в каждое из состояний происходит через каждые 5 секунд. При этом по условию задачи каждые 10 секунд на левый груз системы действует гармоническая возмущающая сила Q, задаваемая то законом (1), то законом (2):

Q = H₁×Sin(w×t) (8)

Q = H₂×Cos(w×t) (9)

Частота колебаний вне зависимости от закона колебаний каждые 15 секунд то уменьшается на 50%, то возвращается к прежнему значению.

Для каждого состояния описана своя система уравнений, по которым происходит изменение переменных системы (рисунок 13).

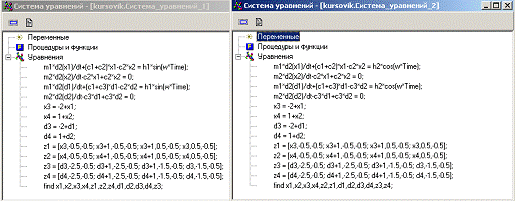
Рисунок 13 - Системы уравнений состояний класса Class_1

Графически эту модель можно представить в виде 3D-анимации (рисунок 14), которая будет включать в себя 4 бруска, прикрепленных к пружинам.

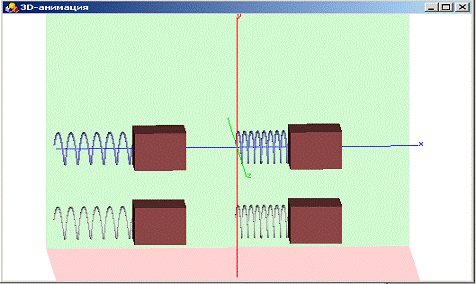
Рисунок 14 - 3D-анимация системы kursovik

ЗАКЛЮЧЕНИЕ

Процесс проектирования информационных систем, реализующих новую информационную технологию, непрерывно совершенствуется. В центре внимания инженеров оказываются все более сложные системы, что затрудняет использование физических моделей и повышает значимость математических моделей и машинного моделирования систем. Машинное моделирование стало эффективным инструментом исследования и проектирования сложных систем. Актуальность математических моделей непрерывно возрастает из-за их гибкости, адекватности реальным процессам, невысокой стоимости реализации на базе современных ЭВМ.

Современные вычислительные средства позволили существенно увеличить сложность используемых моделей при изучении систем, появилась возможность построения комбинированных моделей, учитывающих все многообразие факторов, имеющих место в реальных системах.

В результате выполнения курсовой работы были созданы математическая модель бистабильной системы «нагреватель - охлаждающая жидкость» и компьютерная модель

В первой задаче изучено поведение стационарных решений уравнения теплопроводности в характерных точках внутри диапазона бистабильности, построены фазовые портреты, найден коэффициент α в уравнении тепловой нагрузки.

Во второй задаче изучено компьютерное построение модели системы, представление системы в виде 3D-анимации.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Советов Б.Я., Яковлев С.А. Моделирование систем (учебник). - М.: Высш.шк., 2007. - 343с.

. Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. - М.: Наука, 1990. - 272с.3. Бенькович Е.С., Колесов Ю.Б., Сениченков Ю.Б.

. Абрамычев А.Ю., Зельдович Я.Б. Биофизика. М.: 1990г. - 100с.

. Бенькович Е.С., Колесов Ю.Б., Сениченков Ю.Б. Практическое моделирование сложных динамических систем. - СПб.: БХВ, 2001. - 441с.

. Арансон И.С., Гапонов-Грехов А.В. Решеточные модели в нелинейной динамике неравновесных сред: Предпринт ИПФ, 1997. - 200сю

.Практическое моделирование сложных динамических систем. - СПб.: БХВ, 2001. - 441с.

. Методические указания по выполнению курсовых и дипломных работ для студ. спец. 220400 - Программное обеспечение ВТ и АС / Сост. И.Д.Никитенко, С.В. Усатиков, А.Б.Боровский 2004. 56с.

. Петров Г.Н. Использование пакета “Model Vision” для создания компьютерных лабораторных работ.: Изд-во СПбГТУ, 2001. 8-12с