Устойчивости продольно сжатых стержней
Контрольная работа
Тема 7
Устойчивости продольно сжатых
стержней
Содержание
1. Основные положения и определения
. Задача Эйлера
. Влияние граничных условий на величину критической силы при
потере устойчивости
. Пределы применимости формулы Эйлера
. Расчет продольно-сжатых стержней с использованием
коэффициента снижения допускаемых напряжений
. Использование коэффициента в поверочных расчетах
. Использование коэффициента в проектировочных расчетах
Литература
1. Основные положения и определения
Для упругого тела, так же как и для жесткого, можно говорить об
устойчивом и неустойчивом положениях равновесия.
Представим себе, что некоторой упругой системе сообщено малое отклонение
от положения равновесия (Рис. 7.1). Если система после снятия внешнего
воздействия возвращается к исходному положению, то такое положение называется
устойчивым (положение 1). Если же система к первоначальному состоянию не
возвращается, то оно называется неустойчивым (положение 2). В технических
приложениях существует и нейтральное равновесие (положение 3).
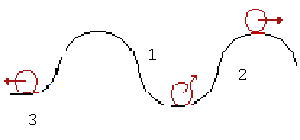
Рис. 1 Основные виды равновесия в технике
Аналогичная
картина наблюдается и при продольном сжатии стержней
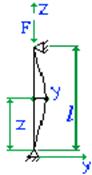
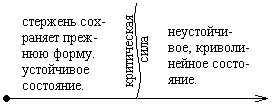
Рис.2. Поведение сжатых стержней
Первые исследования в области устойчивости сжатых стержней были Леонардом
Эйлером (1707-1783).
К задачам устойчивости стержней примыкают задачи об устойчивости
оболочек. Практическое приложение: несущие колонны, железнодорожные мосты (низ
растягивается, верх - сжимается), шест для прыжков в высоту.
. Задача Эйлера
Задачей
Эйлера называется задача о равновесии стержня сжатого центральными силами 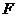 . Поэтому, когда говорят об устойчивости сжатого
стержня, употребляют выражения: “задача Эйлера“ или “устойчивость стержня по
Эйлеру “. Введем текущую точку S.
. Поэтому, когда говорят об устойчивости сжатого
стержня, употребляют выражения: “задача Эйлера“ или “устойчивость стержня по
Эйлеру “. Введем текущую точку S.
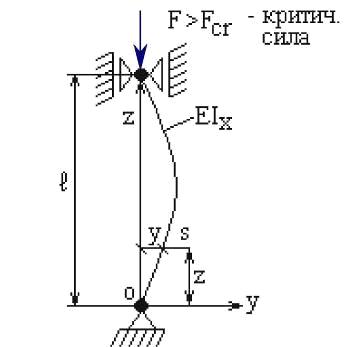
Рис.
3. Расчетная схема к задаче Эйлера
Продольная
сила 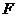 создает относительно точки
создает относительно точки 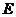 изгибающий момент в плоскости минимальной жесткости
стержня
изгибающий момент в плоскости минимальной жесткости
стержня
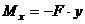 .
.
В
разделе 5 получена следующая зависимость
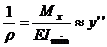
и
после подстановки можно записать
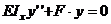 (7.1)
(7.1)
Зависимость
(7.1) представляет собой дифференциальное уравнение второго порядка
относительно упругой линии продольно сжатого стержня при потере устойчивости.
Уравнение (7.1) можно привести к известной в курсе высшая математика форме
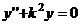 (7.2)
(7.2)
где 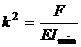
Общее
решение (7.2) имеет вид
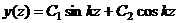 (7.3)
(7.3)
Для
определения постоянных интегрирования 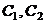 необходимо
использовать граничные условия
необходимо
использовать граничные условия
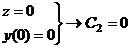
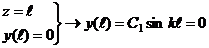
Если
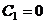 , то потеря устойчивости не наступает, так как прогиб
любой точки будет равен нулю.
, то потеря устойчивости не наступает, так как прогиб
любой точки будет равен нулю.
Второе
граничное условие 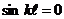 выполняется, если
выполняется, если 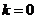 . Однако,
условие
. Однако,
условие 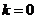 соответствует отсутствию внешних нагрузок и
бесконечно большой изгибной жесткости.
соответствует отсутствию внешних нагрузок и
бесконечно большой изгибной жесткости.
Таким
образом, второе граничное условие 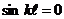 выполняется,
если
выполняется,
если
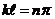 ,
, 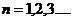
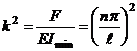 -
условие потери устойчивости.
-
условие потери устойчивости.
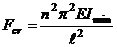
При
n=2, 3, 4 и т.д. критическая сила, при которой
наступает потеря устойчивости, возрастает в 4, 9, 16 . . . раз. Однако, с
позиций технического приложения необходима наименьшая сила. При n=1
имеем
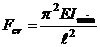 (7.4)
(7.4)
Эта
зависимость известна, как формула Эйлера.
На
рис. 7.4. показаны формы потери устойчивости при различных значениях
коэффициента n.
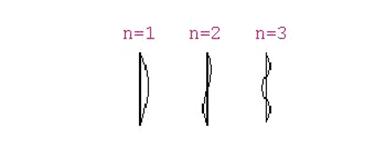
Рис.
4. Формы потери устойчивости при различных значениях
коэффициента n
В
практических приложениях формы потери устойчивости при значениях коэффициента n=2 и
n=3 могут быть реализованы за счет установки
промежуточных шарнирно подвижных опор.
3. Влияние граничных условий на величину критической силы при потере
устойчивости
На практике концы стержня закрепляются различным способом. Некоторые
варианты граничных условий показаны на рис. 7.5. Первый способ - шарнирное
закрепление обоих концов - рассмотрен в разделе 7.2. при выводе формулы Эйлера.
Для других способов закрепления обобщенная формула Эйлера для определения
критической силы имеет вид
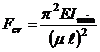 (7.5)
(7.5)
где
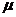 - коэффициент приведения длины стержня.
- коэффициент приведения длины стержня.
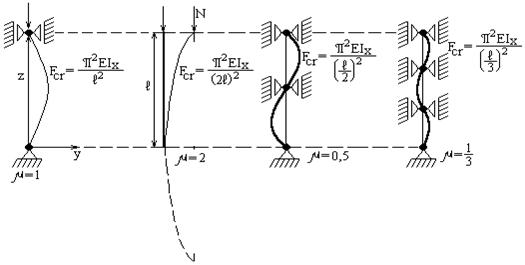
Рис 5. Влияние граничных условий на величину критической силы при потере
устойчивости
Значение коэффициента приведения длины для других вариантов закрепления
можно найти в справочниках.
Как
видно из формулы (7.5), чем меньше 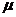 , тем
больше критическая сила, а следовательно, и допускаемая нагрузка стержня.
Например, нагрузка стержня, заделанного двумя концами, может быть в 16 раз
больше нагрузки стержня, заделанного одним концом. Поэтому там, где возможно,
следует осуществлять жесткую заделку обоих концов стержня. Однако это не всегда
можно осуществить на практике. Элементы, к которым прикрепляются концы рассматриваемого
стержня, всегда более или менее упруги, податливы, что вносит некоторую
неопределенность в расчет. Поэтому весьма часто даже при жестком соединении
концов стержня с другими элементами расчет в запас прочности ведут, предполагая
шарнирное закрепление обоих концов.
, тем
больше критическая сила, а следовательно, и допускаемая нагрузка стержня.
Например, нагрузка стержня, заделанного двумя концами, может быть в 16 раз
больше нагрузки стержня, заделанного одним концом. Поэтому там, где возможно,
следует осуществлять жесткую заделку обоих концов стержня. Однако это не всегда
можно осуществить на практике. Элементы, к которым прикрепляются концы рассматриваемого
стержня, всегда более или менее упруги, податливы, что вносит некоторую
неопределенность в расчет. Поэтому весьма часто даже при жестком соединении
концов стержня с другими элементами расчет в запас прочности ведут, предполагая
шарнирное закрепление обоих концов.
4. Пределы применимости формулы Эйлера
Потеря устойчивости наступает для достаточно гибких длинных стержней. Для
относительно коротких стержней потеря работоспособности может наступить как за
счет пластического деформирования, так и за счет хрупкого разрушения.
Таким образом, формулой Эйлера не всегда можно пользоваться. При выводе
этой зависимости было использовано дифференциальное уравнение упругой линии,
вывод которого основан на использовании закона Гука. В свою очередь закон Гука
справедлив лишь при напряжениях меньших предела пропорциональности.
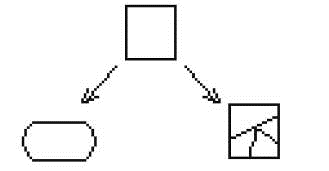
Рис. 6. Потеря работоспособности относительно коротких стержней
при сжатии
Определим
критическое напряжение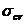 , то есть напряжение, возникающее в поперечном сечении
стержня критической силы:
, то есть напряжение, возникающее в поперечном сечении
стержня критической силы:
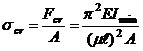
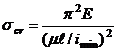 (7.6)
(7.6)
где
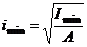 - наименьший радиус инерции поперечного сечения
стержня. При одинаковых значениях площадей поперечного сечения стержней
большему
- наименьший радиус инерции поперечного сечения
стержня. При одинаковых значениях площадей поперечного сечения стержней
большему 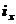 соответствует большая изгибная жесткость (рис. 7. 7).
соответствует большая изгибная жесткость (рис. 7. 7).
Рис. 7.
Сопоставление двух поперечных сечений с одинаковыми площадями
Величина
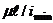 характеризует влияние размеров стержня и способа
закрепления концов; она называется гибкостью стержня
характеризует влияние размеров стержня и способа
закрепления концов; она называется гибкостью стержня 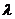 . Гибкость является величиной безразмерной. С учетом
сделанных обозначений выражение (7.7) можно записать в следующем виде:
. Гибкость является величиной безразмерной. С учетом
сделанных обозначений выражение (7.7) можно записать в следующем виде:
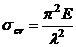 (7.7)
(7.7)
Для
того чтобы можно было использовать формулу Эйлера, необходимо удовлетворить
следующему условию
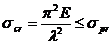 (7.8)
(7.8)
где
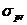 - предел пропорциональности материала стержня.
Выражая из формулы (7.8) гибкость стержня, можно получить условие
применимости формулы Эйлера в следующем виде:
- предел пропорциональности материала стержня.
Выражая из формулы (7.8) гибкость стержня, можно получить условие
применимости формулы Эйлера в следующем виде:
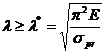 (7.9)
(7.9)
Например,
для стали Ст. 3 предел пропорциональности 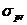 =200 МПа
после подстановки в (7.9) получаем
=200 МПа
после подстановки в (7.9) получаем
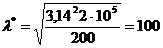
Таким
образом, формула Эйлера для стержней из малоуглеродистой стали может быть
использована в тех случаях, когда их гибкость оказывается больше 100 (рис.
7.8). Аналогичным образом получим условия применения формулы Эйлера для чугуна 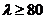 . Для средне- и высокоуглеродистых сталей формула
Эйлера применима и при гибкости, меньше указанной. Так, для стержней из
хромомолибденовой стали формула Эйлера применима в тех случаях, когда гибкость
стержня
. Для средне- и высокоуглеродистых сталей формула
Эйлера применима и при гибкости, меньше указанной. Так, для стержней из
хромомолибденовой стали формула Эйлера применима в тех случаях, когда гибкость
стержня 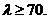
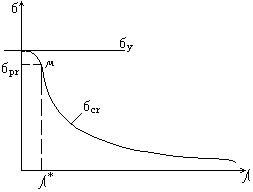
Рис 8.
Зависимость критических напряжений от гибкости стержня
устойчивость сила стержень напряжение
При
гибкости 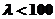 , существует несколько гипотез, приближенно
описывающих поведение продольно сжатых стержней при потере устойчивости в
неупругой стадии деформирования. В этих случаях обычно пользуются следующей
эмпирической формулой Тетмаейра-Ясинского, которая была получена на основании
многочисленных опытов:
, существует несколько гипотез, приближенно
описывающих поведение продольно сжатых стержней при потере устойчивости в
неупругой стадии деформирования. В этих случаях обычно пользуются следующей
эмпирической формулой Тетмаейра-Ясинского, которая была получена на основании
многочисленных опытов:
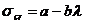 . (7.10)
. (7.10)
здесь
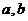 - коэффициенты, зависящие от материала стержня.
Для стали Ст3 при гибкости
- коэффициенты, зависящие от материала стержня.
Для стали Ст3 при гибкости 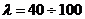 эти
коэффициенты могут быть приняты равными:
эти
коэффициенты могут быть приняты равными: 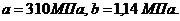
Для
относительно коротких стержней при гибкости 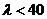 расчеты
на прочность можно проводить без учета опасности
расчеты
на прочность можно проводить без учета опасности
5
Расчет продольно-сжатых стержней с использованием коэффициента снижения
допускаемых напряжений
Коэффициентом снижения допускаемых напряжений называется отношение
действительных фактических напряжений к пределу текучести при сжатии (рис.7.9).
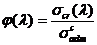 (7.11)
(7.11)
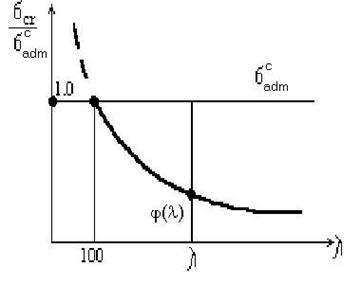
Рис.9.
График функции 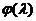
Как
следует из названия коэффициент 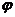 , он
непосредственно используется для определения допускаемых напряжений с учетом
влияния опасности потери устойчивости
, он
непосредственно используется для определения допускаемых напряжений с учетом
влияния опасности потери устойчивости
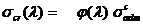
и
для нахождения критической силы
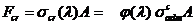 .
.
Значения
коэффициента 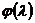 зависят как от материала, так и от гибкости стержня и
приведены в таблице 7.1.
зависят как от материала, так и от гибкости стержня и
приведены в таблице 7.1.
Таблица 7.1
|
Гибкость 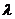 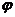 для для
|
|
|
сталей Ст1, Ст2, Ст3, Ст4
|
Стали Ст5
|
стали повышенного качества 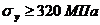 чугундерево чугундерево
|
|
|
|
0
|
1,00
|
1,00
|
1,00
|
1,0.
|
1,00
|
|
10
|
0,99
|
0,98
|
0,97
|
0,97
|
0,99
|
|
20
|
0,96
|
0,95
|
0,95
|
0,91
|
0,97
|
|
30
|
0,94
|
0,92
|
0,91
|
0,81
|
0,93
|
|
40
|
0,92
|
0,89
|
0,87
|
0,69
|
0,87
|
|
50
|
0,89
|
0,86
|
0,83
|
0,57
|
0,80
|
|
60
|
0,86
|
0,82
|
0,79
|
0,44
|
|
70
|
0,81
|
0,76
|
0,72
|
0,34
|
0,60
|
|
80
|
0,75
|
0,70
|
0,65
|
0,26
|
0,48
|
|
90
|
0,69
|
0,62
|
0,55
|
0,20
|
0,38
|
|
100
|
0,60
|
0,51
|
0,43
|
0,16
|
0,31
|
|
110
|
0,52
|
0,43
|
0,35
|
-
|
0,25
|
|
120
|
0,45
|
0,37
|
0,30
|
-
|
0,22
|
|
130
|
0,40
|
0,33
|
0,26
|
-
|
0,18
|
|
140
|
0,36
|
0,29
|
0,23
|
-
|
0,16
|
|
150
|
0,32
|
0,26
|
0,21
|
-
|
0,14
|
|
160
|
0,29
|
0,24
|
0,19
|
-
|
0,12
|
|
170
|
0,26
|
0,21
|
0,17
|
-
|
0,11
|
|
180
|
0,23
|
0,19
|
0,15
|
0,10
|
|
190
|
0,21
|
0,17
|
0,14
|
-
|
0,09
|
|
200
|
0,19
|
0,16
|
0,13
|
-
|
0,08
|
Промежуточное
значение 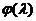 может быть найдено с помощью по линейной
интерполяции. Например, найдем коэффициент снижения допускаемых напряжений для
стержня, выполненного из стали Ст3, при
может быть найдено с помощью по линейной
интерполяции. Например, найдем коэффициент снижения допускаемых напряжений для
стержня, выполненного из стали Ст3, при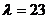
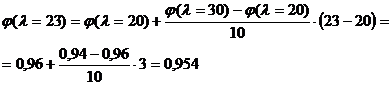 (7.12)
(7.12)
При
значениях гибкости 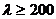 можно безо всяких опасений вести расчет по формуле
Эйлера.
можно безо всяких опасений вести расчет по формуле
Эйлера.
.
Использование коэффициента 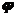 в
поверочных расчетах
в
поверочных расчетах
Дано:
1. Условия закрепления стержня.
2. Геометрические размеры.
Физические
и механические характеристики металла 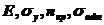 .
.
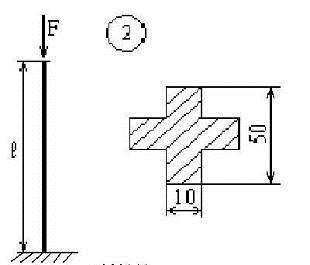
Рис 10. Расчетная схема для проверочного расчета
1 Вычисляем гибкость данного стержня.
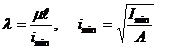
.
С помощью таблицы 7.1 и линейной интерполяции определяем 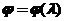 .
.
.
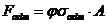
.
Использование коэффициента 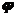 в
проектировочных расчетах
в
проектировочных расчетах
Дано:
.
Граничные условия.
.
Сила (F)
.
Физико-механические характеристики материала стержня 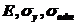 .
.
.
Задан тип поперечного сечения.
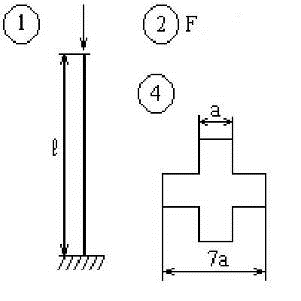
Рис
11. Расчетная схема для проектировочного расчета
1.
В первом приближении задается 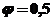
2.
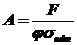
.
Определяем характерный размер поперечного сечения заданного типа
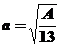
Далее
выполним проверочный расчет по методике, изложенной в предыдущем параграфе
.
Определяем гибкость 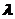
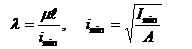
.
Определяем 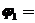
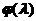 по
таблице 7.1.
по
таблице 7.1.
.
Находим критическую силу для первого приближения
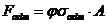
и
после сопоставления с заданной нагрузкой определяем погрешность первого приближения.
Если погрешность меньше 3%,то найденное приближение является достаточным. В
противном случае продолжаем вычисление с помощью метода последовательных
приближений.
Для
ускорения сходимостей на следующем шаге метода последовательных приближений
определяем 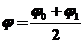
7. Переходим к пункту 2
Для получения достаточной точности необходимо выполнить 3-5 итераций.
см. п.3 задачи 1 DF>3%
. Пример расчета прямого бруса на продольный изгиб.
Задача 1.


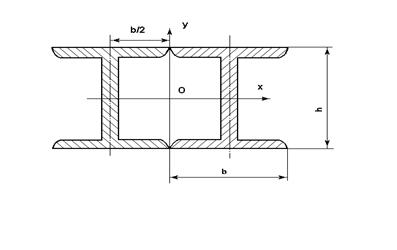
Рис. Расчетная схема и поперечное сечение стержня
.Определим осевые моменты инерции.

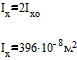
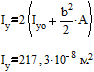
Минимальный осевой момент инерции
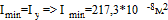
.Определим гибкость стержня и радиус инерции данного сечения.
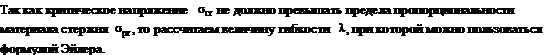
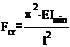 (1)
(1)

Находим критические напряжения
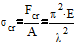 ( 2 )
( 2 )
,где
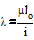
гибкость стержня, характеризующая склонность стержня к продольному
изгибу;
минимальный радиус инерции поперечного сечения стержня.
. Проверим возможность использования формулы Эйлера.
Формулу Эйлера ( 1 ) можно использовать при условии:
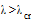
где
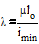
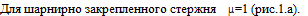
Подставив численные значения в формулу ( 3 ), получим:
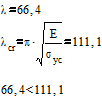
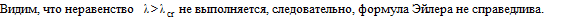
. Определяем допускаемую силу

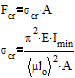 ( 4 )
( 4 )
Подставив численные значения в формулу ( 4 ), получим:
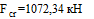
Допустимая нагрузка на данный стержень составляет 1072, 34 кН.
Задача 2

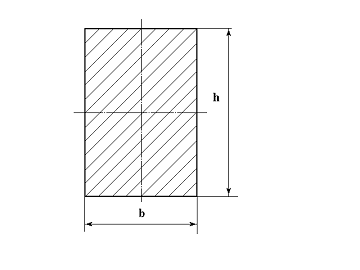
Рис.
7.13. Поперечное сечение для проектировочного расчета

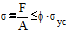

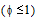 ,
,

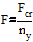 (5)
(5)
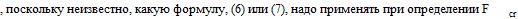
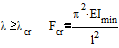 (6)
(6)
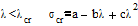 (7)
(7)
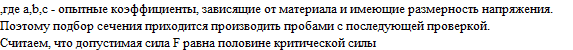
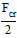
Расчет сечения будем осуществлять по следующему алгоритму:
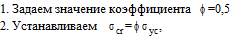
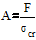
,подбираем размеры сечения или номер профиля (если стержень прокатная
сталь).



Первая итерация.
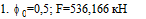
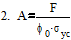
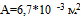
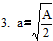
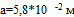
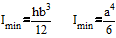
соответственно
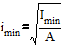
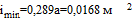
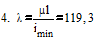
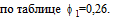
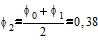
Вторая итерация.
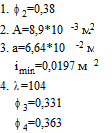
Третья итерация.
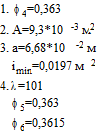

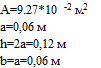
Литература
1.
Александров Анатолий Васильевич и др. Сопротивление материалов: Учебник для
ст-тов вузов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В.
Александрова. - 2-е изд., испр. - М.: Высшая школа, 2000. - 559 с.
.Гафаров
Радик Хайдарович. Что нужно знать о сопротивлении материалов: Учебное пособие
для вузов обуч. по направлениям подгот. и спец. в области техники и технологии/
Р.Х. Гафаров, В.С. Жернаков; под ред. В.С. Жернакова. - М.: Машиностроение,
2001. - 275 с.
.Феодосьев
Всеволод Иванович. Сопротивление материалов: Учебник для студ-ов
высш.техн.учеб.зав./ В.И.Феодосьев. - 10-е изд., перераб. и доп. - М.: Изд-во
МГТУ им. Н.Э. Баумана, 2001. - 588 с.