Исследование возможностей пакета MathCAD

Исследование возможностей пакета MathCAD

Исследование возможностей пакета Mathcad для решения дифференциальных уравнений и систем дифференциальных уравнений

Введение

Решение дифференциальных уравнений является актуальной проблемой, т. к. они встречаются во многих отраслях человеческой деятельности: экономике, программировании, физике и т.д.

Решить аналитически данные задачи не всегда представляется возможным или решение представляет собой очень сложный процесс. В помощь решению выступают численные методы, применение которых и рассматривается в данной работе.

Рассматривается следующий численный метод для решения конкретных задачи: решение однородного дифференциального уравнения первого порядка методом Эйлера.

Решение производится в математическом пакете MathCAD с помощью средств программирования.

1. Теоретическая часть

1.1 Основные теоретические сведения

Пусть необходимо найти решение уравнения

     (1)

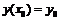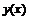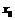с начальным условием . Такая задача называется задачей Коши. Разложим искомую функцию в ряд вблизи точки и ограничимся первыми двумя членами разложения 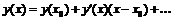. Учтя уравнение (1) и обозначив 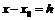, получаем 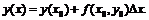 Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.

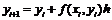      (2)

Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера - метод первого порядка, то есть его точность растет линейно с уменьшением шага h.

Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале. Среднее значение производной можно получить (конечно же только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала 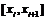 и использовать его для аппроксимации решения на всем интервале

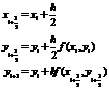
Можно также оценить среднее значение производной на интервале

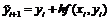
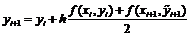
Такие модификации метода Эйлера имеет уже точность второго порядка.

Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутта следующие

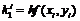
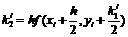
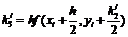
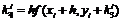
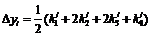
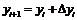
Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.

Еще один тип задач, часто встречающихся на практике, - краевые задачи. Пусть имеется дифференциальное уравнение второго порядка 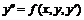. Решение уравнения требуется найти на интервале 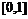, причем известно, что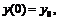 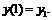 Понятно, что произвольный интервал 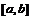заменой переменных 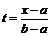 может быть сведен к единичному. Для решения краевой задачи обычно применяют метод стрельб. Пусть 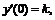где k - некоторый параметр. Для некоторого пробного значения k может быть решена задача Коши, например, методом Рунге-Кутта. Полученное решение будет зависеть от значения параметра 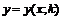. Мы хотим найти такое значение параметра, чтобы выполнялось условие 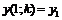. Фактически мы свели исходную задачу к задаче решения трансцендентного уравнения с таблично заданной функцией. Если найдены такие значения параметра k₁ и k₂, что 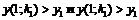, то дальнейшее уточнение значения параметра можно проводить методом деления отрезка пополам.

1.2 Метод Эйлера для дифференциальных уравнений первого порядка

Решим задачу Коши для дифференциального уравнения первого порядка  методом Эйлера.

Пусть правая часть уравнения равна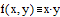

Зададим границы изменения x: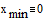     

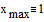
Зададим число точек и величину шага: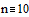    

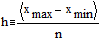
Вычислим x и y по формулам Эйлера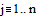

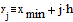
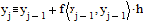
Представим результат графически и сравним его с аналитическим решением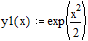

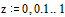
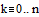
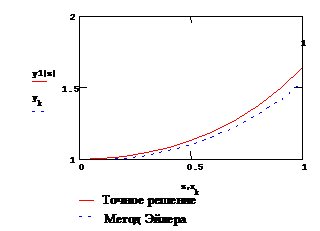
Точное аналитическое решение и решение, полученное численно, отличаются в точке x=1 на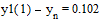

То есть относительная ошибка составляет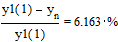

1.3 Решение систем дифференциальных уравнений

Для решения дифференциальных уравнений Mathcad имеет ряд встроенных функций, в частности, функцию rkfixed, реализующую метод Рунге-Кутты четвертого порядка с фиксированным шагом. Фактически эта функция предназначена для решения систем дифференциальных уравнений первого порядка.

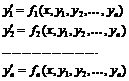
Функция rkfixed (y, x1, x2, npoints, D) возвращает матрицу. Первый столбец этой матрицы содержит точки, в которых получено решение, а остальные столбцы - решения и его первые 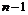 производные.

Аргументы функции:

·   y - вектор начальных значений (n элементов).

·   x1 и x2 - границы интервала, на котором ищется решение дифференциального уравнения.

·   npoints - число точек внутри интервала (x1, x2), в которых ищется решение. Функция rkfixed возвращает матрицу, состоящую из 1+npoints строк.

·   D - вектор, состоящий из n элементов, который содержит первые производные искомой функции.

В качестве примера рассмотрим решение системы Вольтерры-Лотки. Эта система описывает динамику численности хищников и жертв на замкнутом ареале и является одной из базовых моделей экологии.

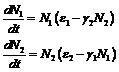
Для решения систем дифференциальных уравнений используются функция rkfixed.

В этом примере установлено значение ORIGIN=1, то есть нумерация элементов массива начинается с 1, а не с 0, как это принято в Mathcad'е по умолчанию.

Пусть в начальный момент времени число хищников 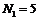и число жертв .

Задаем вектор начальных значений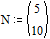

параметры системы  

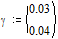
интервал времени и количество точек, в которых будет вычислено решение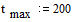    

и вектор правых частей системы. (Поскольку исходная система не зависит явно от времени t, функция D так же не зависит от времени явно хотя и содержит его в числе своих аргументов).

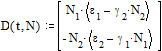
Решаем систему с помощью встроенной функции

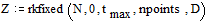
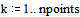
Представим на графике результаты расчета - зависимость численности популяций от времени

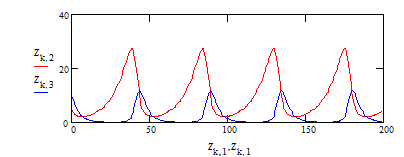
и зависимость числа жертв от числа хищников

Можно использовать обозначения 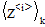 или 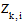 - это одно и то же.

Поскольку дифференциальное уравнение порядка выше первого может быть преобразовано к системе дифференциальных уравнений первого порядка, функция rkfixed может быть использована и для решения дифференциальных уравнений.

1.4 Решение дифференциальных уравнений методом Рунге-Кутта

Зададим границы изменения x: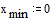   

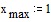
Зададим число точек внутри интервала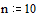

Зададим начальные условия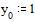

Поскольку мы решаем только одно дифференциальное уравнение первого порядка, а не систему дифференциальных уравнений, матрица y содержит только один элемент, однако запись y=1 была бы неправильной. Необходимо явно указывать на то, что величина y - матрица, то есть писать индекс.

Определим теперь матрицу производных. Эта матрица тоже состоит только из одного элемента. Этот элемент с точностью до обозначений совпадает с правой частью исходного дифференциального уравнения:

Решаем дифференциальное уравнение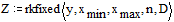

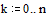
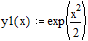
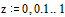
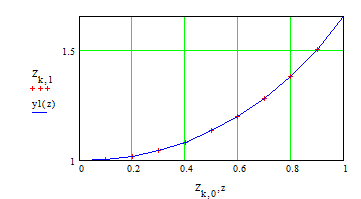
Точное аналитическое решение и решение, полученное численно отличаются в точке 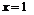на

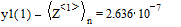
Относительная ошибка составляет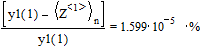

1.5 Решение дифференциальных уравнений второго порядка

В качестве примера решим задачу о гармоническом осцилляторе, для которого известно аналитическое решение, и легко может быть оценена точность вычислений. Дифференциальное уравнение второго порядка

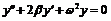
преобразуем к системе из двух дифференциальных уравнений первого порядка

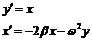
Пусть декремент затухания

Пусть циклическая частота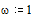

Зададим начальные условия 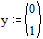 соответствует начальной координате, а y1 - начальной скорости. Зададим теперь матрицу D. С учетом того, что искомая величина соответствует нулевому элементу массива y, ее первая производная - первому, а вторая - второму, имеем

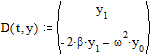
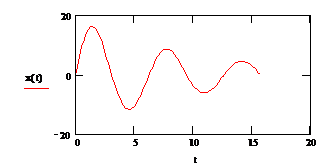
Представим результаты расчета на графике и сравним их с аналитическим решением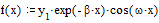

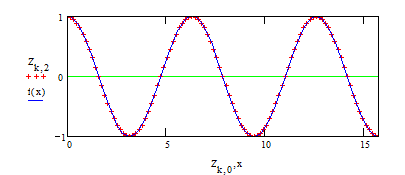
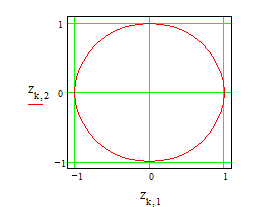
Для контроля точности вычислений нарисуем фазовую траекторию (зависимость смещения от скорости). Для гармонического осциллятора фазовая траектория должна иметь вид эллипса.

Mathcad имеет еще две функции для решения задачи Коши. Это функции Rkadapt и Bulstoer. Эти функции имеют те же самые аргументы и возвращают решения в такой же форме, что и функция rkfixed. Первая из этих функций использует метод Рунге-Кутты с переменным шагом, что позволяет повысить точность вычислений и сократить их объем, если искомое решение имеет области, где ее значения меняются быстро, и области плавного изменения. Функция Rkadapt будет варьировать величину шага в зависимости от скорости изменения решения.

Функция Bulstoer реализует иной численный метод - метод Булирша-Штёра. Ее следует применять, если известно, что решение является гладкой функцией.

1.6 Решение краевой задачи

Пусть требуется найти решение дифференциального уравнения 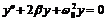при условиях  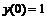и .

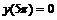При значениях параметров            

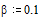
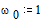
Для решения краевой задачи имеется встроенная функция sbval, реализующая метод стрельб и позволяющая свести краевую задачу к задаче Коши. Функция sbval имеет следующие параметры:

·   v - вектор, содержащий начальные приближения для недостающих начальных условий,

·   xmin, xmax - границы интервала, на котором ищется решение,

·   D (x, y) - вектор-функция, содержащий правые части системы дифференциальных уравнений первого порядка, эквивалентной исходному уравнению, размер вектора n совпадает со степенью старшей производной дифференциального уравнения

·   load (xmin, v) - вектор-функция, элементы которой соответствуют n значениям функций на левой границе интервала. Часть этих значений известна, а для части заданы начальные приближения в векторе v. Их уточненные значения будут найдены в процессе вычисления

·   score (xmax, y) - вектор-функция, имеющая то же число элементов, что и v. Каждое значение является разностью между начальными значениями в конечной точке интервала и соответствующей оценки для решения. Этот вектор показывает, на сколько близко найденное решение к истинному.

Наша задача сводится к системе двух дифференциальных уравнений первого порядка:

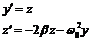
Поэтому функция D имеет вид

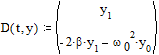
Задаем граничные условия:

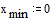
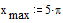
Задача Коши для дифференциального уравнения второго порядка содержит два начальных условия. Нам известно только одно. Начальное приближение для недостающего значения задаем в векторе v, который в нашем случае состоит только из одного элемента. Несмотря на это, индекс о должен быть обязательно указан, чтобы подчеркнуть векторный характер этой величины: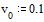

На левой границе интервала нам известно значение 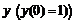и задано начальное приближение для 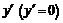. Это значение записано в . Задаем вектор-функцию load. Ее нулевой элемент - начальное значение для 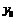, первый - для .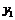

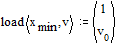
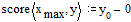
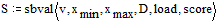
Теперь, когда нам стало известно недостающее начальное условие в задаче Коши, можно воспользоваться, например, функцией rkfixed

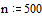
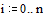
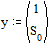
1.7 Решение обыкновенных дифференциальных уравнений в Mathcad

предлагает новый способ для решения обыкновенных дифференциальных уравнений, разрешенных относительно старшей производной. Для этих целей служит уже известный нам блок given совместно с функцией odesolve. Дифференциальное уравнение совместно с начальными или граничными условиями записывается в блоке given. Производные можно обозначать как штрихами (Ctrl+F7), так и с помощью знака производной 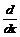. Пример использования функции для решения задачи Коши приведен ниже.

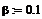
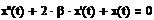
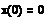
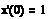
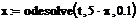
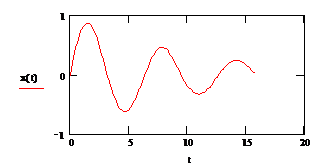
У искомой функции явно указан аргумент, знак производной стоит перед скобкой.

Функция odesolve имеет три аргумента. Первый аргумент - независимая переменная, вторая - граница интервала, на котором ищется решение, последний аргумент - шаг, с которым ищется решение. Последний аргумент может быть опущен.

Следующий пример демонстрирует решение краевой задачи. Использован другой способ записи производных, используется odesolve функция с двумя аргументами.

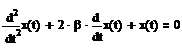
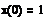
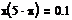
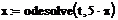
Одним из методов решения дифференциальных уравнений в частных производных является метод сеток. Идея метода заключается в следующем. Для простоты, ограничимся случаем только функции двух переменных, и будем полагать, что решение уравнения ищется на квадратной области единичного размера. Разобьем область сеткой. Шаг сетки по оси x и по оси y, вообще говоря, может быть разный. По определению частная производная равна

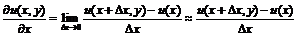
Если рассматривать функцию только в узлах сетки, то частную производную можно записать в форме

где узел 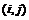 соответствует точке 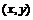. Полученное выражение называется правой конечной разностью. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.

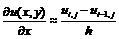
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.

Теперь получим выражения для вторых производных.

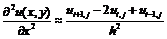
В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.

. Уравнения гиперболического типа

В качестве примера рассмотрим решение волнового уравнения (уравнения гиперболического типа).

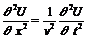
Уравнение будем решать методом сеток. Запишем уравнение в конечных разностях

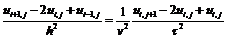
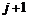Полученное уравнение позволяет выразить значение функции u в момент времени через значения функции в предыдущие моменты времени.

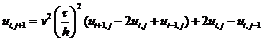
Такая разностная схема называется явной, так как искомая величина получается в явном виде. Она устойчива, если.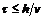

Зададим начальные условия: смещение струны U в начальный и последующий моменты времени описывается синусоидальной функцией.

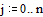
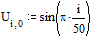
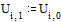
(Совпадение смещений при j=0 и j=1 соответствует нулевой начальной скорости).

Зададим граничные условия: на концах струны смещение равно 0 в любой момент времени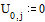    

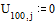
Будем полагать коэффициент          

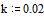
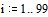
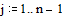
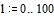
Записываем уравнение в конечных разностях, разрешенное относительно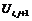

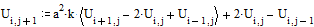
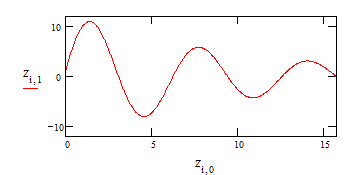
Представляем результат на графике

2. Уравнения параболического типа

Еще один пример использования конечных разностей - уравнение диффузии.

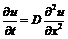
Это уравнение параболического типа. Явная разностная схема для этого уравнения имеет вид

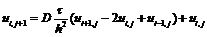      (3)

Эта разностная схема устойчива, если 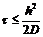. Для краткости в дальнейшем мы будем обозначать весь множитель, стоящий перед скобкой, как k.

Задаем коэффициент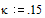  

и диапазон изменения пространственной и временной координат:

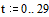
Задаем начальные и граничные условия

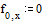
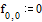
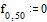
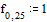
Уравнение в конечных разностях имеет вид

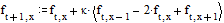
Представляем результаты на графике. (Для большей наглядности изображена только центральная часть)

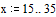
Основное достоинство явных методов - их простота - зачастую сводится на нет достаточно жесткими ограничениями на величину шага. Явные схемы обычно устойчивы при столь малых шагах по времени, что они становятся непригодными для практических расчетов. Этого существенного недостатка позволяют избежать неявные схемы. Свое название они получили потому, что значения искомой функции на очередном временном шаге не могут быть явно выражены через значения функции на предыдущем шаге.

Рассмотрим применение неявной схемы на примере уравнения теплопроводности

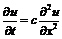      (4)

Запишем неявную разностную схему для этого уравнения

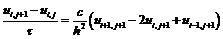  (5)

Здесь первый индекс соответствует пространственной, а второй - временной координате. В отличие от явной схемы, для вычисления в правой части уравнения используются значения функции на том же самом временном шаге. Вводя обозначение 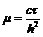, уравнение (5) можно переписать в виде

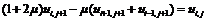      (6)

или в матричной форме

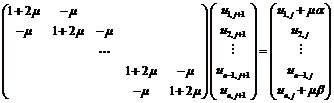
где .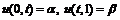

Задаем количество узлов сетки (в данном случае оно одинаково для обеих переменных)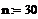

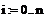
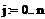
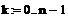
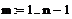
Задаем значения параметров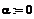             

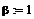
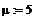
и начальное распределение температуры в области

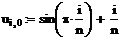
Формируем матрицы уравнения (7)

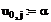
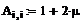
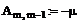
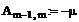
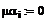
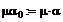
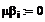
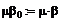
Находим решение системы

3. Решение уравнений Лапласа и Пуассона

Для решения уравнений Пуассона 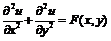 и Лапласа (частный случай, когда 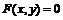) - уравнений эллиптического типа - предназначена функция relax (a, b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического уравнения общего вида

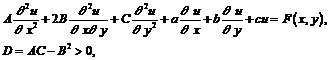
которое может быть сведено к уравнению в конечных разностях

В частности, для уравнения Пуассона коэффициенты .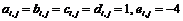

Идея метода релаксации заключается в следующем. Если нет источников (уравнение Лапласа), то значение функции в данном узле на текущем шаге 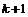 определяется как среднее значение функции в ближайших узлах на предыдущем шаге k

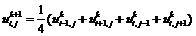        (8)

При наличии источников разностная схема имеет вид

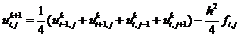        (9)

Метод релаксации сходится достаточно медленно, так как фактически он использует разностную схему (3) с максимально возможным для двумерного случая шагом .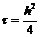

В методе релаксации необходимо задать начальное приближение, то есть значения функции во всех узлах области, а так же граничные условия.

Функция relax возвращает квадратную матрицу, в которой:

1)   расположение элемента в матрице соответствует его положению внутри квадратной области,

2)   это значение приближает решение в этой точке.

Эта функция использует метод релаксации для приближения к решению.

Вы должны использовать функцию relax, если Вы знаете значения искомой функции u (x, y) на всех четырех сторонах квадратной области.

Аргументы:

a, b, c, d, e - квадратные матрицы одного и того же размера, содержащие коэффициенты дифференциального уравнения.

f - квадратная матрица, содержащая значения правой части уравнения в каждой точке внутри квадрата

u - квадратная матрица, содержащая граничные значения функции на краях области, а также начальное приближение решения во внутренних точках области.

rjac - Параметр, управляющий сходимостью процесса релаксации. Он может быть в диапазоне от 0 до 1, но оптимальное значение зависит от деталей задачи.

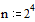
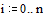
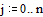
Задаем правую часть уравнения Пуассона - два точечных источника

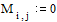
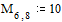
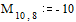
Задаем значения параметров функции relax

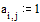
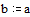
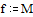
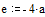
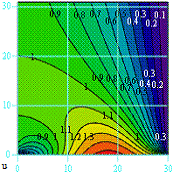
Задаем граничные условия и начальное приближение - нули во всех внутренних точках области

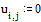
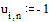
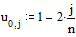
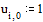
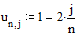
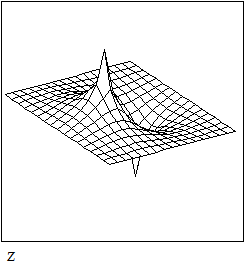
Находим решение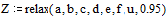

и представляем его графически в виде поверхности и линий уровней.

Если граничные условия равны нулю на всех четырех сторонах квадрата, можно использовать функцию multigrid.

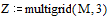
Алгоритм метода достаточно громоздкий, поэтому рассматривать его мы не будем.

Заключение

В процессе выполнения работы была создана программа в среде MathCAD с помощью средств программирования данного математического пакета. Это позволяет использовать данную программу для решения задач, аналогичного содержания.

Использование пакета MathCAD позволяет решать очень широкий круг задач. Преимуществами этого пакета являются простота задания сложных вычислений, быстрота решения и дружественный интерфейс.

Вывод: полученные результаты говорят о том, что при уменьшении шага разбиения отрезка решение уточняется и погрешность вычисления становится меньше.

дифференциальный уравнение mathcad лаплас

Список литературы

1.   Заварыкин В.М. и др. Численные методы: Учеб. Пособие для студентов пед. ин-в./ В.М. Заварыкин, В.Г. Житомирский, М.П. Лапчик. - М.: Просвещение, 1990.

2.      Вычислительная математика: Учеб. Пособие для техникумов/ Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л. - М.: Высш. шк., 1985.

.        Амосов А.А., Дубянский Ю.А., Копченов Н.В. Вычислительные методы для инженеров: Учеб. пособие. - М.: Высш. шк., 1994.

.        Кирьянов Д.В. Самоучитель MathCAD 2001. - СПб.: БХВ - Петербург, 2001.

.        Макаров Е.Г. Инженерные расчеты в MathCAD. Учебный курс. - СПб.: Питер, 2005.

.        Дьяконов В.П. MathCAD 2001. Специальный справочник. - СПб.: Питер, 2002.