Особенности применения программного пакета MathCAD
Содержание
1. Основные элементы системы MathCAD
Введение
Обзор возможностей системы
Интерфейс системы
Концепция построения документа системы
Типы данных. Входной язык системы
Формат вывода числовых данных
Структурированные данные
Стандартные и пользовательские функции
2. Стандартные функции
Классификация стандартных функций
Основные элементарные математические функции
Основные функции работы с векторами и матрицами
Типовые статистические функции
Функции с условиями сравнения
Функции доступа к внешним данным
3. Графические возможности системы MathCAD
Построение графиков в декартовой системе координат
Построение графиков в полярной системе координат
Построение трехмерных графиков
Установка форматов двумерной графики
4. Решение уравнений и систем
Решение линейных и трансцендентных уравнений
Решение систем уравнений и неравенств
Решение дифференциальных уравнений и систем
5. Программирование в пакете Mathcad
6. Апроксимация функций
Регрессия функций
Интерполирование функций
Встроенные операторы
Литература
1. Основные
элементы системы MathCAD
Введение
Одной из основных областей применения ПК являются
математические и научно-технические расчеты. Сложные вычислительные задачи,
возникающие при моделировании технических устройств и процессов, можно разбить
на ряд элементарных: вычисление интегралов, решение уравнений, решение
дифференциальных уравнений и т.д. Для решения таких задач имеется целый ряд
различных математических пакетов, реализующих разнообразные численные методы,
способных так же производить аналитические математические преобразования.
Наиболее известными сегодня являются следующие пакеты: Mathematica (фирма
Wolfram Research), Maple (фирма Waterloo Maple Inc), Matlab (фирма The
MathWorks), MathCAD (фирма MathSoft Inc).
Пакет Mathcad популярен, пожалуй, более в инженерной, чем в
научной среде. Характерной особенностью пакета является использование привычных
стандартных математических обозначений, то есть документ на экране выглядит
точно так же как обычный математический расчет. Для использования пакета не
требуется изучать какую-либо систему команд, как, например, в случае пакетов
Mathematica или Maple. Пакет ориентирован в первую очередь на проведение
численных расчетов, но имеет встроенный символический процессор Maple, что
позволяет выполнять аналитические преобразования. В отличие от упомянутых выше
пакетов, Mathcad является средой визуального программирования, то есть не
требует знания специфического набора команд, имеет чрезвычайно удобный
математико-ориентированный интерфейс и прекрасные средства научной графики.
Система MathCAD существует в нескольких основных вариантах:
·
MathCAD
Standard
- идеальная система для повседневных технических вычислений. Предназначена для
массовой аудитории и широкого использования в учебном процессе;
·
MathCAD
Professional - промышленный стандарт прикладного использования математики в
технических приложениях. Ориентирована на математиков и научных работников,
проводящих сложные и трудоемкие расчеты.
·
MathCAD
Professional Academic - пакет программ для профессионального использования
математического аппарата с электронными учебниками и ресурсами.
Обзор
возможностей системы
объединяет в себе простой текстовый редактор, математический
интерпретатор и графический процессор. Весь функциональный набор возможностей
системы можно классифицировать следующим образом:
1.
вычислительные
функции;
2.
графические
функции;
3.
программирование;
4.
сервисные
функции;
5.
аналитические
вычисления.
Вычислительные возможности системы могут, применяются для
решения разнообразных задач из области математики, физики, экономики,
инженерных расчетов, статистики, научных исследований и т.д. К основным
вычислительным функциям можно отнести следующие:
1.
вычисление
арифметических выражений с различной точностью;
2.
вычисление
производных (обычных и частных), интегралов (обычных, многомерных и контурных);
3.
вычисление
суммы и произведения;
4.
выполнение
операций с размерными величинами и переменными;
5.
решение
уравнений и неравенств и их систем;
6.
решение
дифференциальных уравнений и систем дифференциальных уравнений;
7.
обработка
матриц, векторов и ранжированных переменных;
8.
использование
встроенных математических функций;
9.
создание
пользовательских функций;
10.использование символьных преобразований и вычислений.
Графические возможности системы применяются для визуализации
результатов вычислений и включают построение двумерных графиков, поверхностей,
карт линий уровня, трехместных гистограмм, точечных графиков и графиков
векторных полей.
Система позволяет продемонстрировать процесс движения или
изменения каких-либо результатов в виде анимационного клипа. Возможно также
внесение графических файлов определенного формата из других систем в документ,
создавать программы MathCAD.
Система позволяет создавать программы, представляющие собой
выражения, состоящие из программных конструкций, подобных конструкциям языков
программирования. Программные выражения позволяют успешно решать в системе те
задачи, которые невозможно вычислить с помощью имеющихся встроенных функций.
К основным сервисным функция программы MathCAD можно отнести
следующие.
1.
ведение
диалога с пользователем посредством меню, пиктограмм или команд;
2.
размещение
на экране и редактирование математических, графических и текстовых конструкций;
3.
вывод
документа или его части на принтер;
4.
форматирование
различных конструкций документа, изменение локальных и глобальных форматов;
5.
поддержка
файловой структуры документа;
6.
создание
и использование файлов данных на диске;
7.
обработка
текстовой информации.
Пакет MathCAD позволяет выполнять аналитические (символьные)
преобразования. Символьные операции можно разделить на шесть разделов:
. символьная алгебра (упрощения, раскрытие скобок, разложение
на множители, приведение подобных, ряды и т.д.);
1.
символьные
действия анализа (производные, интегралы, пределы);
2.
символьное
решение уравнений (решение уравнений и систем уравнений);
3.
символьные
действия с матрицами (матричная алгебра, транспонирование, обращение,
определитель);
4.
способы
отображения символьных результатов;
5.
символьные
преобразования (преобразования Фурье, Лапласа, z-преобразования).
Интерфейс
системы
Система MathCAD имеет три режима работы: режим набора и
редактирования документа, командный режим и режим помощи. Это разделение
режимов носит условный характер, так как переход в тот или иной режим не
вызывает полного изменения вида экрана и области:
·
строка
заголовка (первая строка, содержащая имя рабочего документа и стандартные
кнопки управления окном)
·
основное
меню команд системы (вторая строка, включающая пункты иерархического меню,
которое содержит полный набор команд работы с системой)
·
наборная
панель (третья строка, содержащая набор кнопок или пиктограмм для удобного
набора документа в MathCAD)
·
панель
инструментов (четвертая строка, содержащая кнопки или пиктограммы, дублирующие
наиболее важные функции основного меню)
·
панель
управления шрифтами (пятая строка, содержащая кнопки переключения типа
символов, типа вида и размера шрифтов, расположения букв в строке)
·
окно
набора и редактирования документа (основная часть экрана, предназначенная для
обработки документа в системе MathCAD).
Основную часть экрана занимает окно набора и редактирования.
За один сеанс работы с системой можно организовать несколько окон набора и
редактирования.
Окно снабжено нижней и правой полосами прокрутки,
предназначенными для перемещения изображения на экране по горизонтали и
вертикали.
Верхняя строка окна содержит наименование документа, номер
окна и кнопки, функции которых типичны для всех приложений в самой системе
Windows.
Основное меню команд имеет иерархическую структуру и содержит
полный набор команд, обеспечивающих выполнение основных функций системы.
Некоторые часто используемые команды выведены в виде
пиктограмм или кнопок на панель инструментария.
Меню File
New (Создать) - создание нового документа с очисткой окна
редактирования;(Открыть) - загрузка ранее созданного документа из диалогового
окна;(Сохранить) - запись текущего документа с его именем;Setup - параметров
страницы;(Печать) - распечатка документа на принтере;Preview (Просмотр) -
предварительный просмотр документа;
Меню Edit
Cut (Вырезать) - перенос выделенной части документа в буфер
обмена;(Копировать) - копирование выделенной части документа в буфер;(Вставить)
- перенос содержимого буфера обмена в окно редактирования на указанное
место;(Отменить) - отмена предшествующей операции редактирования
Меню Insert
Graph - выбор типа графика и его вставка графика в документ;-
вставка матрицы с выбором размерности;- вставка функции из списка,
появляющегося в диалоговом окне;- вставка единиц измерения;Region - вставка
текстового блока;Break - вставка разрыва страницы;
Меню Format
Number - установка локального и глобального цифрового формата
отображения;Regions - Across (Выровнять по горизонтали) - блоки выравниваются
по горизонтали;Regions - Down (Выровнять вниз) - блоки выравниваются по
вертикали, располагаясь сверху вниз.
Меню Math
Calculate - вычисление выражений по желанию пользователя
расположенных ниже курсора;Worksheet - вычисление всего документа;Calculation -
включение/отключение автоматического режима вычисления;- включение/отключение
оптимизации вычислений;
программный пакет mathcad
Options - установка системных переменных, выбор системы
единиц измерения.
Меню Symbolics
Меню управления символьными преобразованиями.
Меню Window
Меню управления многооконным режимом работы.
Меню Help
Меню вызова справочной системы, примеров.
В системе действует, в зависимости от режима работы,
несколько типов курсоров:
·
курсор
в виде диагональной белой стрелки, управляемый устройством типа
"мышь", в дальнейшем - курсор мыши
·
курсор
в виде маленького красного крестика, определяющий начало формирования новой
области на свободном поле документа, в дальнейшем - курсор ввода
·
курсор
в виде синей вертикальной линии, используемый внутри формульной области или
графической области при наборе и редактировании, в дальнейшем - курсор
редактирования
·
курсор
в виде тонкой красной вертикальной линии, используемый внутри текстовой области
при наборе и редактировании, в дальнейшем - текстовый курсор
·
курсор
в виде рамки синего цвета, заключающей внутри себя часть области или область
целиком для выполнения над ней операций по редактированию, в дальнейшем - рамка
объекта
·
курсор
в виде большого черного перекрестья, используемый внутри области, выделенной
пунктирной рамкой, в дальнейшем - курсор области
·
курсор
в виде маленького квадрата с указывающей на него диагональной стрелкой,
применяемый для копирования и переноса выделенных объектов, в дальнейшем -
курсор переноса
·
курсоры
в виде двойных вертикальных, горизонтальных, диагональных стрелок, применяемых
при редактировании размеров области, выделенной пунктирной рамкой, в дальнейшем
- размерные курсоры.
Концепция
построения документа системы
Документ системы MathCAD строится из областей, которые
делятся на вычислительные, графические, текстовые и обрабатываются
соответственно тремя различными процессорами системы: вычислительным
(математическим), графическим и текстовым. Области создаются средствами
формульного, текстового и графического редакторов пакета. Общение пользователя
с системой происходит на промежуточном математически ориентированном языке
визуального программирования - входном языке системы. Этот язык максимально
приближен к обычному математическому языку, что практически не требует
программирования, нужно лишь точное описание алгоритма решения задачи.
Подготовка вычислительных блоков облегчается благодаря вводу
шаблонов. Для этого служат панели (палитры) с набором шаблонов различных
математических символов.
В системе действует, в зависимости от режима работы,
несколько типов курсоров:
·
курсор
мыши;
·
курсор
в виде маленького красного крестика, определяющий начало формирования новой
области - курсор ввода;
·
курсор
в виде синей вертикальной линии, используемый внутри формульной области или
графической области при наборе и редактировании, в дальнейшем - курсор
редактирования;
·
курсор
в виде тонкой красной вертикальной линии, используемый внутри текстовой области
при наборе и редактировании, в дальнейшем - текстовый курсор;
·
курсор
в виде рамки синего цвета, заключающей внутри себя часть области или область
целиком для выполнения над ней операций по редактированию, в дальнейшем - рамка
объекта;
·
курсор
в виде большого черного перекрестья, используемый внутри области, выделенной
пунктирной рамкой, в дальнейшем - курсор области;
·
курсор
в виде маленького квадрата с указывающей на него диагональной стрелкой,
применяемый для копирования и переноса выделенных объектов, в дальнейшем -
курсор переноса;
·
курсоры
в виде двойных вертикальных, горизонтальных, диагональных стрелок, применяемых
при редактировании размеров области, выделенной пунктирной рамкой, в дальнейшем
- размерные курсоры.
При наборе выражений, следует придерживаться следующих
рекомендаций:
·
с
помощью курсора редактирования (синий уголок), можно вставлять и удалять
отдельные символы в выражениях, для появления курсора редактирования нужно
указать курсором мыши на нужный символ в математическом выражении, расширение
области редактирования выполняется клавишей "пробел";
·
в
формульной области рамка объекта может быть правосторонней и левосторонней в
зависимости от того, справа или слева срезан верхний угол рамки, изменение вида
рамки выполняется с помощью клавиши Insert;
Для ввода и редактирования текстов в системе существует
специальный текстовый редактор. Он обрабатывает два вида текстовой информации -
текстовые области и текстовые параграфы.
Текстовая область создается выбором команды Create Text
Region из Insert или нажатием клавиши " (двойные кавычки). На поле документа
появляется черная текстовая рамка и текстовый курсор, с помощью которого можно
вводить и редактировать текстовую информацию. Длина текстовой области
ограничена длиной наибольшей строки, каждая из которых заканчивается нажатием
клавиши Enter. Над текстовой областью можно выполнять такие операции
редактирования, как удаление, копирование, перемещение, вставка, причем
выделение области может выполняться как с помощью пунктирной рамки, так и
построчного выделения мышью.
Создание текстового параграфа выполняется с помощью команды
Text Region меню Insert из меню работы с текстами. Над текстовым параграфом
выполняются операции выделения, копирования, удаления и вставки, причем
выделение той части текстовой информации над которой нужно сделать
преобразование, выполняется долговременным нажатием левой кнопки мыши и
перемещением текстового курсора от начальной к конечной точке выделения. Для
текстового параграфа можно выполнять ряд установок, таких как установка полей,
установка абзацев, тип выравнивания строки и т.д.
По мере того, как пользователь создает различные типы
объектов - выражения, формулы, тексты, графики система сама составляет
программу, которая хранится в памяти компьютера и сохраняется на диск в виде
файла с расширением mcd. Именно эта программа обрабатывается системой для
получения результатов вычислений.
В MathCAD решена проблема сквозной передачи данных от одного
объекта к другому, например, от одного выражения к другому, к матрицам и
графикам и т.д. Поэтому изменение в любой формуле или исходных данных ведет к
пересчету результатов всего документа по цепи взаимодействия объектов.
Объектами в системе MathCAD называют элементы, которые можно
выделить курсором (матрицы, графики выражения, текстовые области) и их
отдельные элементы этих областей.
Конструирование выражений облегчается средствами выделения
отдельных фрагментов выражений. Все, что попадает в ходе выделения в уголки
курсора, оказывается операндом для следующего вводимого оператора. Как правило,
удобно сочетать отметку начала выделения мышью, поскольку она позволяет сразу и
точно указать место выделения, с последующим расширением или сужением места
выделения с помощью управляющих клавиш.
В процессе работы с документом используется ручной и
автоматический режим вычислений. В автоматическом режиме вычисляются все
видимые на экране области документа. При просмотре документа вновь появившиеся
области вычисляются автоматически, что не всегда удобно при выполнении
громоздких расчетов. В ручном режиме вычисления производятся нажатием кнопки со
знаком = на панели инструментов или клавиши F9.
Типы данных.
Входной язык системы
Входной язык системы MathCAD - интерпретирующего типа.
Документ обрабатывается сверху вниз, а в пределах строки слева направо, как
только система распознает объект, автоматически запускается внутренняя
подпрограмма, выполняющая необходимые действия. Например, вычисление выражения,
вывод таблицы и т.д.прежде всего требует от пользователя корректного описания
алгоритма решения математической задачи на входном языке, очень напоминающем
общепринятый язык описания математических и научно-технических расчетов.
Рассматривая входной язык системы как язык программирования, мы можем выделить
в нем типичные понятия и объекты, такие, как идентификаторы, константы,
переменные, массивы и другие типы данных, операторы и функции, управляющие
структуры и т.д.
Алфавит входного языка системы определяет совокупность
символов и слов, которые используются при задании команд. Алфавит системы
MathCAD содержит:
·
строчные
и прописные буквы латинского и греческого алфавитов;
·
арабские
цифры от 0 до 9;
·
системные
переменные;
·
операторы;
·
имена
встроенных функций;
·
спецзнаки;
К укрупненным элементам языка относятся типы данных,
операторы, функции пользователя и управляющие структуры.
Типы данных системы MathCAD.
|
Простые
|
Структурированные
|
|
константы
|
переменные
|
дискретные
|
массивы
|
файлы
|
|
целые
|
пользовательские
|
|
матрицы
|
|
|
вещественные
(от 10-307 до 10307)
|
стандартные
|
|
вектора
|
|
|
комплексные
(5+2.3i)
|
|
|
|
|
|
восьмеричные
(от 0 до 7 437о)
|
|
|
|
|
|
шестнадцатиричные
(от 0 до 15 43h)
|
|
|
|
|
|
зарезервированные
(e, π, % -
константы; TOL,ORIGIN - системные переменные; единицы измерения)
|
|
|
|
|
|
строковые
констаны ("пример")
|
|
|
|
|
Константы - поименованные объекты, хранящие
некоторые значения, которые не могут быть изменены. Переменные - поименованные
объекты, имеющие некоторое значение, которое может изменяться по ходу
выполнения программы. В MathCAD тип переменной определяется значением и
предварительно не задается. Переменные могут быть числовыми, строковыми,
символьные и т.д. Имена констант, переменных и иных объектов называют
идентификаторами. Идентификаторы в системе MathCAD могут иметь
практически любую длину, и в них могут входить любые латинские и греческие
буквы, а также цифры. Однако начинаться идентификатор может только с буквы.
Кроме того, идентификатор не должен содержать пробелов. Некоторые спецсимволы
(например, знак объединения _) могут входить в состав идентификаторов -
недопустимы. Нельзя использовать для идентификаторов буквы русского языка.
Строчные и прописные буквы в идентификаторах различаются. Идентификаторы должны
быть уникальными, т.е. они не должны совпадать с именами встроенных или
определенных пользователем функций.
В MathCAD содержится небольшая группа особых объектов
значения которых определены сразу после запуска программы. Их правильнее
считать системными переменными. Изменение значений системных
переменных производят во вкладке Built-In Variables диалогового окна Math -
Options. Обычные переменные отличаются от системных тем, что они должны
быть предварительно определены пользователем, т.е. им необходимо присвоить
значение.
К базовым операторам системы относятся:: = - локальное
присваивание, = - оператор вычисления, º - глобальное
присваивание. Локальное присваивание (: =) распространяет свое действие на
область документа расположенную ниже места присваивания. Пример - значение
переменной b на момент вычисления с неопределенно.
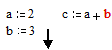
Глобальное присваивание (º) не зависит от места присвоения и распространяет свое действие на
весь документ.
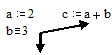
Переменные могут быть размерными, т.е. характеризоваться не только
своим значением, но и указанием физической величины, значение которой они
хранят. Для присваивания значений таким переменным используется знак º. Проведение расчетов с размерными
величинами и переменными особенно удобно при решении различных физических
задач.

В версии MathCAD 7.0 допустимо при первом присваивании переменной
вводить знак = (например, х=123), при этом система сама заменит его на знак на:
=.
Формат вывода
числовых данных
При работе с вычислительными областями с помощью команды
Format - Number, возможно установить формат вывода числовых данных. Это окно
содержит три выделенные части В первой - Radix - устанавливается тип основания
чисел Decimal, Hex или Octal.
Вторая часть Precision (точность) - задает погрешность
вычислений в виде показателя степени n для числа 10 в этой степени. Задаются
число отображаемых знаков Displayed (точность вывода), границы представления
чисел в экспоненциальной форме Exponential Threshold (диапазон
показателя), допустимая граница для комплексных чисел Complex Tolerance
(комплексная точность) и допустимая граница для действительных чисел Zero
Tolerance (точность нуля).
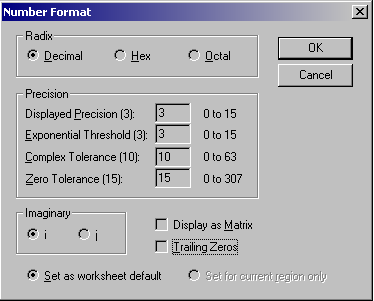
Окно для установки формата чисел
В третьей части - Imaginary (мнимая единица) - задается знак
мнимой единицы для комплексных чисел i или j. Если Re (Z) /Im (Z) >10n, то
комплексное число Z выводится как действительное, а если Im (Z) /Re (Z) >10n,
то число Z выводится как мнимое. Значения n для этих представлений задает
параметр Complex Tolerance. Если действительное число больше
числа 10 в степени п или меньше, чем 10 в степени - n, где n - значение
параметра Exponencial Threshold, то число представляется в экспоненциальной
форме. Если значения чисел по модулю меньше указанных параметром Zero
Tolerance, числа представляются в виде нулей. Все это особенно важно при
научно-технических расчетах, когда излишняя точность представления чисел ни к
чему хорошему не ведет
С помощью диалогового окна можно сделать формат глобальным
(Global) или локальным (Local). Глобальный формат задает
представление для всех числовых данных документа, а локальный - только для
текучего блока.
Для массивов чисел их вывод задается в виде матрицы - включением
опции Display as Matrix (отображение в виде матрицы). Однако для больших
массивов это может быть неприемлемо, так как такая матрица выходит за пределы
экрана. Если опция отключена, то большие массивы отображаются как электронные
таблицы. Trailig Zeros - включает отображение нулевых младших разрядов.
Структурированные
данные
. Дискретные переменные
Дискретной называется переменная, содержащая несколько
значений, каждое из которых отличается от предыдущего на величину постоянного
шага и имеющая начальное и конечное значение. Эти переменные имеют два способа
определения:
1.
Name: = Nbegin. Nend;
2.
Name: = Nbegin, (Nbegin + Step). Nend.
где Name - имя переменной, Nbegin - ее начальное
значение, Nend - конечное значение,. (; на клавиатуре,
либо m. n - в арифметической палитре) - символ, указывающий на изменение переменной
в заданных пределах (вводится клавишей;). Step - шаг изменения
переменной (он должен быть положительным, если Nbegin < Nend, или
отрицательным в обратном случае).
Если шаг не указывается (1 способ), то он выбирается равным
единице. Если Nbegin < Nend, то шаг переменной будет равен +1, иначе
- 1.
Дискретные аргументы значительно расширяют возможности
MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися
вычислениями, формировать векторы и матрицы. Параметрами могут быть константы,
переменные, выражения.
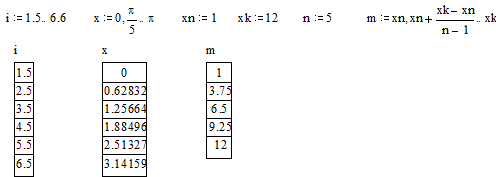
Функция дискретного аргумента имеет множество значений, каждое из
которых соответствует соответствующему значению дискретного аргумента.
Дискретная переменная может являться аргументом функции пользователя или
индексом для организации одномерных и двумерных массивов.
. Векторы и массивы
Массив - имеющая уникальное имя совокупность конечного числа
числовых или символьных элементов, упорядоченных некоторым образом и имеющих
определенные адреса. В пакете MathCAD используются массивы двух наиболее
распространенных типов: одномерные (векторы), двумерные (матрицы).
Порядковый номер элемента, который является его адресом,
называется индексом. Индексы могут иметь только целочисленные значения. Они
могут начинаться с нуля или другого целого числа, в соответствии со значением
системной переменной ORIGIN. Значение этой переменной может быть
переопределено непосредственно в документе, либо с помощью меню Math-Options.
векторы и матрицы можно задавать различными способами: с помощью
команды Insert - Matrix, комбинации клавиш Ctrl + M, щелчком на
кнопке  панели Matrix. В появившемся окне
задают размерность массива (Columns - столбцы, Rows - строки). Пустые поля
заполняют, перемещаясь между ними клавишей Tab. Максимальный
размер вводимых таким способом матриц - 10х10, поэтому большие матрицы задают с
помощью компоненты Insert - Component - Input Table. Данный компонент вставляет
в рабочий документ лист электронной таблицы (подобный листу в Excel). При таком
способе ввода матрицы не существует ограничений на ее размер, а использование
функций табличного процессора облегчает ввод и просмотр больших массивов,
целиком не помещающихся в рабочей области;
панели Matrix. В появившемся окне
задают размерность массива (Columns - столбцы, Rows - строки). Пустые поля
заполняют, перемещаясь между ними клавишей Tab. Максимальный
размер вводимых таким способом матриц - 10х10, поэтому большие матрицы задают с
помощью компоненты Insert - Component - Input Table. Данный компонент вставляет
в рабочий документ лист электронной таблицы (подобный листу в Excel). При таком
способе ввода матрицы не существует ограничений на ее размер, а использование
функций табличного процессора облегчает ввод и просмотр больших массивов,
целиком не помещающихся в рабочей области;
1.
как
переменные с индексами (номер элемента в массиве). Нижний индекс вводится
нажатием клавиши [, либо щелчком на кнопке Xn панели Arithmetic.
Незаданные элементы по умолчанию задаются нулевыми.;
2.
как
переменная с индексом, а элементы в массив заносятся перечислением, через
запятую;
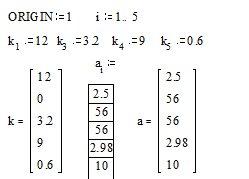
1.
с
использованием дискретного аргумента, когда имеется некоторая явная зависимость
для вычисления элементов массива через их индексы.

Для удобства отображения, громоздкие массивы выводятся в виде
электронной таблицы с номерами строк и столбцов и полосами прокрутки. Формат
представления данных в таблицах может быть изменен с помощью команды
Format-Number - Display as Matrix.
3. Обращение к элементам массива
Массивы могут использоваться в выражениях целиком или
поэлементно. Для обращения к элементам массивов нужно указать числовые значения
индексов элементов. Также можно обращаться к конкретной строке или столбцу
матрицы с помощью верхнего индекса (выделения столбца CTRL+^) или нижних
индексов.
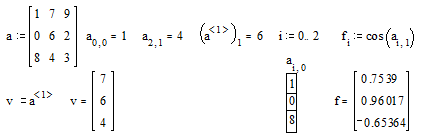
4. Параллельные вычисления, векторизация.
Большинство вычислений с дискретными переменными и массивами
строятся на принципе параллельных (поэлементных) вычислений. Точно такая же
операция может быть выполнена с помощью векторизации. Векторизация - проведение
некоторой операции над всеми элементами вектора или матрицы.
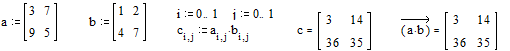
Операция векторизации позволяет применить математические операции
и функции к каждому элементу массива поочередно. Система позволяет выполнять
рекуррентные вычисления, когда последующий элемент массива вычисляется через
предыдущий по какому либо закону.
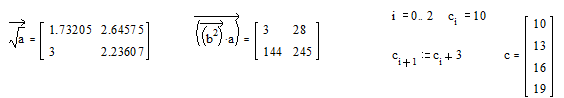
Стандартные и
пользовательские функции
Функция - выражение, согласно которому проводятся некоторые
вычисления с аргументами и определяется её числовое значение.
Следует особо отметить разницу между аргументами и
параметрами функции. Переменные, указанные в скобках после имени функции,
являются ее аргументами и заменяются при вычислении функции значениями из
скобок. Переменные в правой части определения функции, не указанные скобках в
левой части, являются параметрами и должны задаваться до определения функции.
Главным признаком функции является возврат значения, т.е.
функция в ответ на обращение к ней по имени с указанием ее аргументов должна
возвратить свое значение.
Функции в пакете MathCAD могут быть встроенные (cos, sin,
ln), т.е. заблаговременно введенные разработчиками, и определенные
пользователем.
Способы вставки встроенной функции:
. Выбрать пункт меню Insert -
Function.
2. Нажать комбинацию клавиш Ctrl + F.
3. Щелкнуть на кнопке  .
.
Пакет MathCAD позволяет расширить систему новыми функциями
представляющими интерес для пользователя. Функция пользователя в общем случае
имеет вид: Имя_функции (Список аргументов): =Выражение. Имя
функции задается как любой идентификатор. Список аргументов функции разделяется
запятыми. Аргументы функции являются локальными для неё переменными, поэтому
они могут, не определятся до задания функции. Локальные переменные действуют
только в выражении, описывающем функцию. При этом их имена могут совпадать с
именами глобальных переменных, но при выходе из блока функции значения этих
переменных сохраняют ранее заданные значения.
Функции пользователя также могут описываться как локальные,
так и глобальные. К сожалению функции пользователя нельзя применять в составе
выражений, над которыми осуществляются символьные операции.
2.
Стандартные функции
Классификация
стандартных функций
Пакет MathCAD является мощной вычислительной системой за счет
наличия огромного количества стандартных функций, которые можно
классифицировать следующим образом:
1.
математические
(арифметические, тригонометрические, гиперболические, комплексные,
специальные);
2.
векторные
и матричные (создания, объединения, работы со строками и столбцами, матричная
алгебра, специальные функции);
3.
статистические
(вероятности, гистограммные, распределения);
4.
аппроксимация
и интерполяция (интерполяция, аппроксимация, регрессия, сплайны, линейное
предсказание);
5.
решение
линейных, нелинейных, дифференциальных уравнений и систем;
6.
доступа
к внешним данным (ввод/вывод структурированных и неструктурированных файлов).
Основные
элементарные математические функции
Основные элементарные математические функции можно разделить
на 6 групп:
1.
тригонометрические - sin (z), cos (z), tan (z), cot (z), csc (z),
sec (z);
2.
гиперболические - sinh (z), cosh (z), tanh (z), coth
(z), csch (z), sech (z);
3.
обратные - asin (z), acos (z), atan (z);
4.
обратные гиперболические - asinh (z), acosh (z), atanh (z);
5.
показательные и логарифмические - exp (z), ln (z),
log (z);
6.
функции комплексного аргумента - Re (z), Im (z), arg (z),
CTRL+"-комплексно сопряженное.
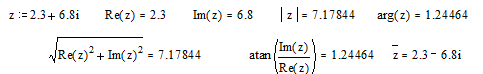
Во всех тригонометрических функция аргумент (z) должен быть в
радианах, скалярным и безразмерным. Для перевода из градусов в радианы и
обратно удобно использовать встроенную переменную deg. Обратные
тригонометрические функции возвращают результат в радианах.
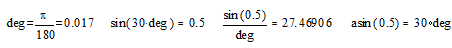
Основные
функции работы с векторами и матрицами
Существует ряд встроенных векторных и матричных функций.
Рассмотрим основные, введя следующие обозначения: V - для векторов, M - для
матриц.
|
Функция
|
Назначение
|
|
length (V)
|
число элементов
вектора
|
|
last (V)
|
индекс
последнего элемента
|
|
max
(M), min (M)
|
максимум,
минимум матрицы
|
|
Re
(M), Im (M)
|
действительная
и мнимая части матрицы
|
|
augment
(M1,M2)
|
объединяет в
одну матрицу матрицы М1 и М2, имеющие одинаковое число строк (объединение бок
о бок)
|
|
identity (n)
|
создает
единичную матрицу размером n´n
|
|
stack
(M1,M2)
|
объединяет две
матрицы М1 и М2 имеющие одинаковое количество столбцов, располагая М1 над М2
|
|
diag (V)
|
создает диагональную
квадратную матрицу, элементами главной диагонали являются V
|
|
submatrix
(A, ir,jr, ic,jc)
|
возвращает
подматрицу состоящую из элементов расположенных в строках от ir до jr и
столбцах от ic до jc
|
|
matrix
(m,n,f)
|
создает матрицу
в которой (i, j) - элемент равен f (i, j)
|
|
cols
(M), rows (M)
|
число столбцов
и строк матрицы
|
|
rank (M)
|
ранг матрицы
|
|
tr (M)
|
след квадратной
матрицы (сумма диагональных элементов),
|
|
sort (V)
|
сортировка
вектора по возрастанию
|
|
reverse (V)
|
сортировка
вектора по убыванию
|
|
csort
(M,n)
|
перестановка
строк матрицы так, чтобы отсортированным оказался n-й столбец
|
|
rsort
(M,n
|
перестановка
столбцов матрицы так, чтобы отсортированной оказалась n-я строка
|
Типовые
статистические функции
В системе MathCAD можно проводить наиболее распространенные
статистические расчеты.
|
ФункцияНазначение
|
|
|
rnd (x)
|
генерация
случайных чисел
|
|
corr
(VX,VY)
|
коэффициент
корреляции двух векторов VX, VY
|
|
cvar
(X,Y)
|
коэффициент
ковариации X и Y
|
|
mean (M)
|
среднее
значение элементов массива
|
|
var (V)
|
дисперсия
элементов вектора V
|
|
side (V)
|
среднеквадратичная
погрешность (корень из дисперсии)
|
|
stdev (V)
|
задает
стандартное отклонение элементов вектора V
|
|
hist
(int,V)
|
возвращает
вектор частот попадания элементов вектора V в заданные интервалы int (для
построения гистограмм). Вектор int должен содержать значения границ. Число
элементов этого вектора на один больше количества интервалов.
|
Функции с
условиями сравнения
Существует ряд встроенных функций, результат работы которых
зависят от знака или значения аргумента. К таким функциям относятся:
|
Функция
|
Назначение
|
|
ceil (x)
|
наименьшее
целое, большее или равное х
|
|
floor (x)
|
наибольшее
целое, меньшее или равное х
|
|
mod
(x,y)
|
остаток от
деления x/y со знаком х
|
|
angel
(x,y)
|
положительный
угол между осью х и радиус вектором с координатами (x, y)
|
|
Ф (x) (фи)
|
функция
Хевисайда (0 - при х<0 и 1 в остальных случаях)
|
|
d (m,n)
|
функция
Кронекера (1 при m=n и 0 в остальных случаях). Аргументы целые числа.
|
|
if (усл, выр1,
выр2)
|
функция
создания условных выражений
|
|
until
(x, z)
|
функция
возвращает z пока x не станет отрицательным.
|
Пример:

Функции
доступа к внешним данным
Для работы с внешними данными система MathCAD имеет
специальный тип данных - файловые данные. Фактически, это те же вектора и
матрицы, но с элементами, которые записываются в виде простых текстовых файлов.
Значения элементов считываются последовательно слева направо и сверху вниз и по
мере обработки преобразуются в соответствующие им ASCII - коды.
|
Функция
|
Назначение
|
|
READ
("путь, имя файла")
|
Считывает
данные в вектор.
|
|
WRITE
("путь, имя файла")
|
Записывает
вектор в файл.
|
|
APPEND
("путь, имя файла")
|
Добавление
данных в конец файла.
|
|
READPRN
("путь, имя файла")
|
Считывает
данные в матрицу.
|
|
WRITEPRN
("путь, имя файла")
|
Записывает
матрицу в файл.
|
|
APPENDPRN
("путь, имя файла")
|
Добавление
данных в конец файла.
|
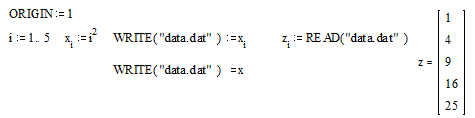
Содержимое файла "data. dat" - 1 4 9 16 25.
3.
Графические возможности системы MathCAD
Пакет MathCAD позволяет строить самые разнообразные графики -
в декартовой и полярной системе координат, трехмерные поверхности, графики
уровней и т.д. Графические области делятся на три основных типа - двумерные
графики, трехмерные графики и импортированные графические образы. Для
построения графиков используются шаблоны. Их перечень содержится в меню Insert
- Graph:
1.
X-Y
Plot [@] - декартова система координат;
2.
Polar
Plot [Ctrl+7] - график в полярной системе координат;
3.
Surface
Plot [Ctrl+2] - трехмерный график (график поверхности);
4.
Contour
Plot [Ctrl+5] - контурный график трехмерной поверхности (карта линий уровня);
5.
3D
Scatter Plot - график в виде точек в трехмерном пространстве (точечный график
фигур);
6.
3D
Bar Chart - гистограмма в трехмерном пространстве;
7.
Vector
Field Plot - график векторного поля на плоскости (векторное поле).
Построение
графиков в декартовой системе координат
В шаблоне графика по вертикали задается через запятую
функции, а по горизонтали - переменные. График строится по точкам соединяющихся
между собой разнообразными линиями (сплошной, пунктирной и т.д.). Исходные
(узловые) точки могут быть показаны в виде жирных точек, квадратиков, кружков и
т.д. Крайние шаблоны данных служат для указания предельных значений абсцисс и
ординат, т.е. они задают масштабы графика. Если оставить эти шаблоны
незаполненными, то масштабы по осям графика будут устанавливаться
автоматически.
1.
упрощенный
способ построения без предварительного задания дискретной переменной (изменение
переменной по умолчанию от - 10 до +10);
2.
с
заданием дискретной переменной.
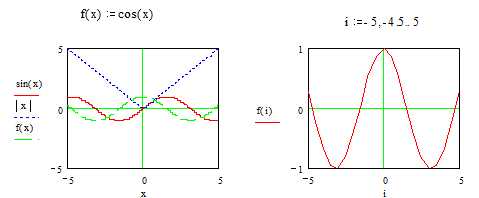
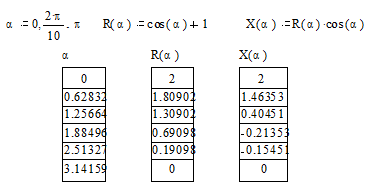
Построение
графиков в полярной системе координат
В полярной системе координат каждая точка задается углом (а),
радиусом и длиной радиус - вектора R (а). График функции обычно строится при
изменении угла (а) в определенных пределах, чаще всего от 0 до 2p. При построении графика
в полярной системе координат с использованием шаблона графика в прямоугольной
системе координат надо по оси Х установить R (а) ×cos (а), а по оси Y - R
(а) ×sin (а).
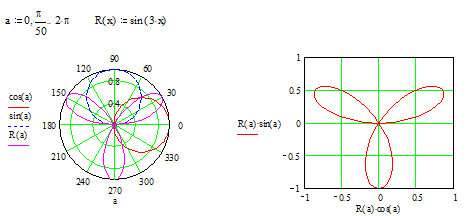
Построение
трехмерных графиков
Трехмерные, или 3D-графики, отображают
функции двух переменных вида Z (X, Y). Для построения трехмерная поверхность Z
(X, Y), предварительно представленной матрицей (М) ординат (Z). Шаблон содержит
единственный - темный прямоугольник, в который заносится имя матрицы со
значениями ординат.
Большие возможности дает способ задания трехмерных
поверхностей - в параметрическом виде. При этом приходится формировать три
матрицы - X, Y и Z - и указывать их в шаблоне в виде X, Y, Z
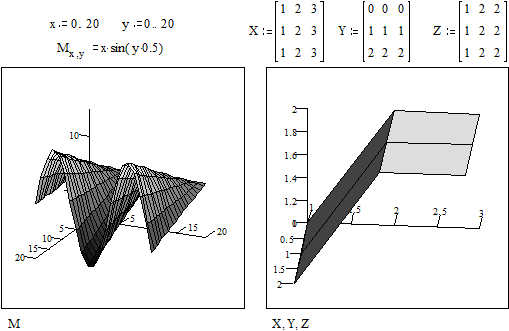
Установка
форматов двумерной графики
Диалоговое окно установки формата отображения графика
вызывается из меню Format - Graph, либо двойным нажатием левой клавиши мыши на
графике.
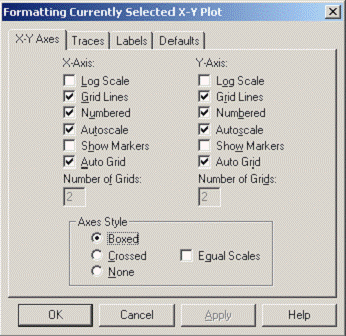
Как видно из рисунка диалоговое окно формата имеет четыре
закладки:
1.
X-Y
Axes (X-Y Оси) - управление опциями осей;
2.
Traces
(Графики) - управление линиями графика;
3.
Labels
(Надписи) - управление метками (надписями) у осей;
4.
Defaults
(По умолчанию) - задание опций по умолчанию.
Форматирование осей графика
В панели X-Y Axes содержатся следующие основные опции,
относящиеся к осям Х и Y (Axis X и Axis Y):Scale (Лог. масштаб) - установка
логарифмического масштаба;
1.
Crid
Lines (Линии сетки) - установка линий масштабной сетки;
2.
Numbered
(Пронумеровать) - установка цифровых данных по осям;
3.
Autoscale
(Автомасштаб) - автоматическое масштабирование графика;
4.
Show
Markers (Нанести риски) - установка маркеров по осям;
5.
Auto
Grid (Автосетка) - автоматическая установка масштабных линий;
6.
Nunber
of Grids (Число интервалов) - установка заданного числа масштабных линий.
Возможна также установка следующих опций координатных осей
(Axes Style):
1.
Boxed
(Рамка) - оси в виде прямоугольника;
2.
Crossed
(Репер) - оси в виде креста;
3.
None
(Ничего) - отсутствие осей;
4.
Equal
Scales (Равные деления) - установка равенства масштабов по осям графика.
Форматирование линий графиков
Следующая панель, Traces (Графики), служит для управления
отображением линий, которыми строится график. С помощью опций этой панели можно
управлять следующими параметрами линий графика:
1.
Legend
Label (Имя кривой) - указание типа линий у оси ординат;
2.
Symbol
(Маркер) - установка символа отметки базовых точек графика;
3.
Line
(Линия) - установка типа линий;
4.
Color
(Цвет) - установка цвета линии и базовых точек;
5.
Type
(Тип) - тип графиков;
6.
Weight
(Толщина) - толщина линий.
Узловые точки графиков (для которых вычисляются координаты)
часто требуется выделить какой-либо фигурой кружком, крестиком, прямоугольником
и т.д. Опция Symbol позволяет задать следующие отметки базовых точек графика
каждой из функции: none - без отметки, x's - наклонный крестик, +'х - прямой
крестик, box - квадрат, dmnd ромбик, o's - окружность.
Графики отдельных функций можно также выделять, используя для
их построения линии различного типа: none - линия не строится, solid -
непрерывная линия, dash - пунктирная линия, dadot - штрих-пунктирная линия
Опция Color (Цвет) задает следующие основные цвета линии и
базовых точек red - красный, blu - синий, gm - зеленый, суа - голубой, bm -
коричневый, blc - черный.
Опция Туре (Тип) задает следующие типы графика:
1.
line
- построение линиями;
2.
points
- построение точками;
3.
err -
построение вертикальными черточками с оценкой интервала погрешностей;
4.
bar -
построение в виде столбцов гистограмм;
5.
step
- построение ступенчатой линией step;
6.
draw
- построение протяжкой от точки до точки.
Возможные конфликты с отметкой символами и типами линий
автоматически устраняются. При этом приоритет отдается опции Type (Тип), а
конфликтные типы линий или точек отмечаются тремя звездочками.
Еще две опции связаны с возможностью удаления с графика
вспомогательных надписей:
1.
Hide
Argument - прячет обозначения математических выражений по осям графика;
2.
Hide
Legend - прячет обозначения имен кривых графика.
Задание надписей в графиках
Панель меток Label (Надписи) позволяет вводить в рисунок
дополнительные надписи. Эта панель появляется, если уже создан текущий график.
Для установки надписей служат небольшие окошки:
1.
Title
- установка титульной надписи к рисунку;
2.
X-Axis
- установка надписи по оси X;
3.
Y-Axis
- установка надписи по оси Y.
В разделе Title содержатся опции Above (Сверху) и Below
(Снизу) для установки титульной надписи либо над рисунком, либо под ним. Кроме
того, опция Show Title (Показать заголовок) позволяет включать или выключать
отображение титульной надписи.
Графические установки по умолчанию
Панель Defaults (По умолчанию), служит для установки опций
графиков Change to Defaults (Вернуть значения по умолчанию) и Use for Defaults
(Использовать для значений по умолчанию).
4. Решение
уравнений и систем
Как известно, многие уравнения и системы уравнений не имеют
аналитических решений. В первую очередь это относится к большинству
трансцендентных уравнений. Доказано также, что нельзя построить формулу, по
которой можно было бы решить произвольное алгебраическое уравнение степени выше
четвертой. Однако такие уравнения могут решаться численными методами с заданной
точностью (не более значения заданного системной переменной TOL).

Рис. Классификация уравнений
Выбор подходящего метода для решения уравнений зависит от
характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и
трансцендентных уравнений, можно классифицировать по числу уравнений и в
зависимости от предлагаемого характера и числа решений. Одно уравнение будем
называть линейным, алгебраическим или трансцендентным в зависимости от
того, имеет ли оно одно решение, n решений или неопределенное число
решений.
Решение
линейных и трансцендентных уравнений
Для простейших уравнений вида f (x) =0 решение в MathCad
находится с помощью функции root.(f (х1, x2, …), х1), где(х1, x2, …) - функция
описывающая левую часть выражения вида f (x) =0. Выражение должно возвращать
скалярные значения;
х1 - имя переменной, относительно которой решается уравнение.
Функция реализует вычисления итерационными методами и требует
предварительного задания начального приближения искомой переменной (х1). Эта
переменная называется варьируемой. Функция позволяет найти как вещественные
корни, так и комплексные. В этом случае начальное приближение нужно задать как
комплексное число.
Приближенные значения корней (начальные приближения) могут
быть:
1.
Известны
из физического смысла задачи;
2.
Известны
из решения аналогичной задачи при других исходных данных;
3.
Найдены
графическим способом.
Наиболее распространен графический способ определения начальных
приближений. В этом случае достаточно построить график функции f (x) и отметить
точки пересечения f (x) с осью Ох, или отметить на оси Ох отрезки, содержащие
по одному корню. Построение графиков часто удается сильно упростить, заменив
уравнение f (x) = 0 равносильным ему уравнением 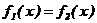 , где функции f1 (x) и f2 (x) - более
простые, чем функция f (x). Тогда, построив графики функций у = f1 (x) и у = f2
(x), искомые корни получим как абсциссы точек пересечения этих графиков. Для
решения уравнений вида
, где функции f1 (x) и f2 (x) - более
простые, чем функция f (x). Тогда, построив графики функций у = f1 (x) и у = f2
(x), искомые корни получим как абсциссы точек пересечения этих графиков. Для
решения уравнений вида 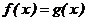 его необходимо привести к виду
его необходимо привести к виду 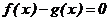 .
.
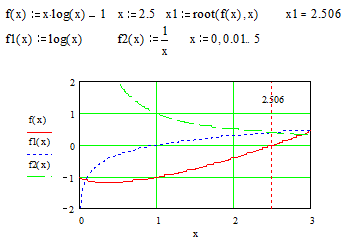
Часто возникает необходимость многократного решения уравнения при
изменении одного из параметров.
Отсутствие сходимости функции root
Если после многих итераций Mathcad не находит подходящего
приближения, то появится сообщение  (отсутствует сходимость). Эта ошибка может быть вызвана следующими
причинами:
(отсутствует сходимость). Эта ошибка может быть вызвана следующими
причинами:
1.
Уравнение
не имеет корней.
2.
Корни
уравнения расположены далеко от начального приближения.
3.
Выражение
имеет локальные max и min между начальным приближением и корнями.
4.
Выражение
имеет разрывы между начальными приближениями и корнями.
5.
Выражение
имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки, исследуйте график f (x). Он
поможет выяснить наличие корней уравнения f (x) = 0 и, если они есть, то
определить приблизительно их значения. Чем точнее выбрано начальное приближение
корня, тем быстрее будет root сходиться.
Рекомендации по использованию функции root
Для изменения точности, с которой функция root ищет
корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается,
функция root будет сходиться быстрее, но ответ будет менее точен. Если значение
TOL уменьшается, то функция root будет сходиться медленнее, но ответ
будет более точен. Значение TOL можно определить непосредственно в рабочем
документе, либо в меню Math - Option. Если два корня расположены близко друг от
друга, следует уменьшить TOL, чтобы различить их.
Если функция f (x) имеет малый наклон около искомого корня,
функция root (f (x), x) может сходиться к значению, отстоящему от корня
достаточно далеко. В таких случаях для нахождения более точного значения корня
необходимо уменьшить значение TOL. Другой вариант заключается в замене
уравнения f (x) = 0 на g (x) = 0 где 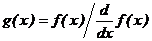 .
.
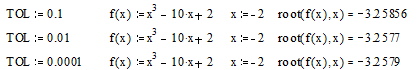
Для выражения f (x) с известным корнем (а) нахождение
дополнительных корней f (x) эквивалентно поиску корней уравнения h (x) =f (x) /
(x-a). Подобный прием полезен для нахождения корней, расположенных близко друг
к другу. Проще искать корень выражения h (x), чем пробовать искать другой
корень уравнения f (x) = 0, выбирая различные начальные приближения.
Нахождение корней полинома
Для нахождения корней выражения, вида 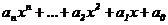 используется функция polyroots. В
отличие от функции root, polyroots не требует начального
приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Общий вид polyroots (v), где v - вектор коэффициентов полинома длины
используется функция polyroots. В
отличие от функции root, polyroots не требует начального
приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Общий вид polyroots (v), где v - вектор коэффициентов полинома длины 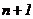 , n - степень полинома. Возвращает вектор
длины n, состоящий из корней полинома. Вектор v удобно создавать
использую команду меню Symbolics - Polynomial Cofficients.
, n - степень полинома. Возвращает вектор
длины n, состоящий из корней полинома. Вектор v удобно создавать
использую команду меню Symbolics - Polynomial Cofficients.
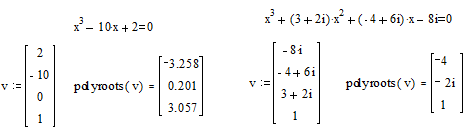
Решение
систем уравнений и неравенств
MathCAD дает возможность решать также и системы уравнений.
Максимальное число уравнений и переменных равно 50. Результатом решения системы
будет численное значение искомого корня.
Наиболее распространенным является блочный метод. Mathcad
решает систему с помощью итерационных методов. Для решения системы этим методом
необходимо выполнить следующее:
1.
Задать
начальное приближение для всех неизвестных, входящих в систему уравнений;
2.
Напечатать
ключевое слово Given. Оно указывает, что далее следует система уравнений;
3.
Введите
уравнения и неравенства в любом порядке. Используйте [Ctrl] + = либо палитру,
для печати символа =. Между левыми и правыми частями неравенств может стоять
любой из символов <, >, ³ и £;
Введите любое выражение, которое включает функцию Find, например: 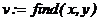 .
.
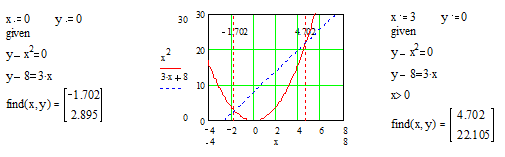
возвращает точное решение системы уравнений. Число аргументов
должно быть равно числу неизвестных. Решающим блоком - называется часть
документа, расположенная между ключевыми словами Given и Find. Внутри блока
недопустимы следующие символы: ¹,
дискретные переменные или выражения, содержащие дискретный аргумент в любой
форме, неравенства вида a<b<c, вложенные блоки решения уравнений.
Функция, Find может возвращать результат следующими способами:
1.
Find (var1, var2,…) =.
2.
a: = Find (x) - скаляр, var: = Find (var1, var2,…) - вектор. Удобно при использовании
решения системы в другом месте рабочего документа.
3.
f (a, b, c, …): = Find (x, y, z, …). Определить другую функцию
с помощью Find. Эта конструкция удобна для многократного решения системы
уравнений для различных значений некоторых параметров a, b, c,…,
непосредственно входящих в систему уравнений;
4.
f (x, y, z, …): = Find (x, y, z, …). Если необходимо найти
решение при различных начальных приближениях, имеет смысл определить новую
функцию.

Последние два способа можно комбинировать.
Отсутствие сходимости решения
Сообщение об ошибке  (Решение не найдено) при решении уравнений появляется, когда:
(Решение не найдено) при решении уравнений появляется, когда:
1.
система
не имеет решения;
2.
для
уравнения, которое не имеет вещественных решений, в качестве начального
приближения взято вещественное число и наоборот;
3.
в
процессе поиска решения последовательность приближений попала в точку
локального минимума невязки. Для поиска искомого решения нужно задать различные
начальные приближения;
4.
возможно,
поставленная задача не может быть решена с заданной точностью. Попробуйте
увеличить значение TOL.
Приближенные решения
Функция Minerr очень похожа на функцию Find (использует тот
же алгоритм). Если в результате поиска не может быть получено дальнейшее
уточнение текущего приближения к решению, Minerr возвращает это приближение.
Функция Find в этом случае возвращает сообщение об ошибке. Правила
использования функции Minerr такие же, как и функции Find. Общий вид Minerr Minerr
(z1, z2,.). Число
аргументов должно быть равно числу неизвестных. При использовании Minerr
используется в блоке решения уравнений, необходимо всегда включать дополнительную
проверку достоверности результатов.
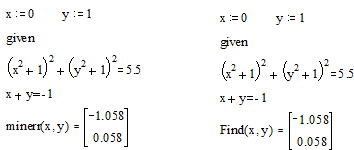
Решение матричных уравнений
Система n линейных алгебраических уравнений относительно n
неизвестных х1, х2, …, хn может быть записана в матричном виде ах=b где:
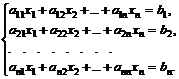

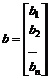 .
.
Если матрица а - неособенная, то есть det (а) ¹ 0 то система, имеет единственное решение.
Для решения систем линейных уравнений можно использовать общепринятые математические
методы: метод Крамера, матричный метод и т.д.
Системы линейных уравнений удобно решать с помощью функции lsolve
(а, b) - где а - матрица коэффициентов (не сингулярная), b - вектор свободных
членов.
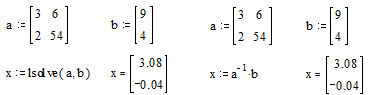
Решение
дифференциальных уравнений и систем
Основные функции
Для решения дифференциальных однородных дифференциальных уравнений
(ОДУ) - 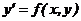 с начальными условиями
с начальными условиями 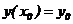 пакет Mathcad имеет ряд встроенных
функций:
пакет Mathcad имеет ряд встроенных
функций:
1.
rkfixed
- функция решения ОДУ и систем ОДУ методом Рунге-Кутта четвертого порядка с
постоянным шагом;
2.
Rkadapt
- функция решения ОДУ и систем ОДУ методом Рунге-Кутта с переменным шагом;
3.
Bulstoer
- функция решения ОДУ и систем ОДУ методом - метод Булирша-Штёра если заранее
известно, что решением является гладкая функция.
Рассмотрим подробнее каждую из этих функций:
1.
rkfixed
(y, x1, x2, p, D) - возвращает матрицу первый столбец которой содержит точки, в
которых получено решение, а остальные столбцы - решения, первые n-1
производные. Функция возвращает матрицу, состоящую из 1+n строк. Аргументы
функции: y - вектор начальных условий (k элементов); x1 и x2 - границы
интервала, на котором ищется решение ОДУ; p - число точек внутри интервала (x1,
x2), в которых ищется решение; D - вектор, состоящий из k элементов, который
содержит первые производные искомой функции.
2.
Rkadapt
(y, x1, x2, p, D) - назначение параметров то же, что и для функции rkfixed.
Существует несколько модифицированная функция rkadapt (y,x1,x2, acc,p,D,k,s) -
где добавлены параметры k - максимальное число промежуточных точек решения; s -
минимально допустимый интервал между точками; acc - погрешность решения
(рекомендуется порядка 0.001).
3.
Bulstoer
(y, x1, x2, p, D) - назначение параметров то же, что и для функции rkfixed.
Рекомендации по использованию
Обычно функция Rkadapt благодаря автоматическому изменению
шага решения дает более точный результат, но по скорости вычислений она
проигрывает функции rkfixed, хотя если решение меняется медленно, она может
привести к заметному уменьшению числа вычислений. Поэтому функция Rkadapt
наиболее пригодна для решения ОДУ дающих медленно меняющееся решения.
Примеры решения дифференциальных уравнений 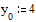
1. Решим ОДУ 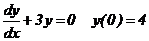 .
.
1.1. Задаем вектор начальных условий:
1.2. Задаем вектор - функцию первой производной неизвестной
функции:
.3. Для решения воспользуемся функцией rkfixed:
. Решим дифференциальное уравнение второго порядка:
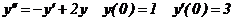 .
.
Преобразуем уравнение в систему ОДУ первого порядка, решенных
относительно первой производной:
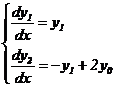
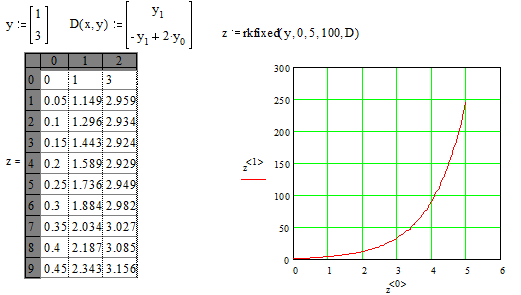
3. Решим систему линейных уравнений первого порядка:
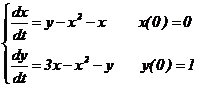 .
.
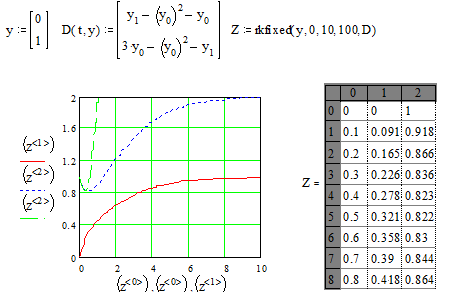
. Решим систему двух линейных уравнений второго порядка:
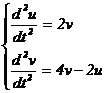 с начальными условиями
с начальными условиями  .
.
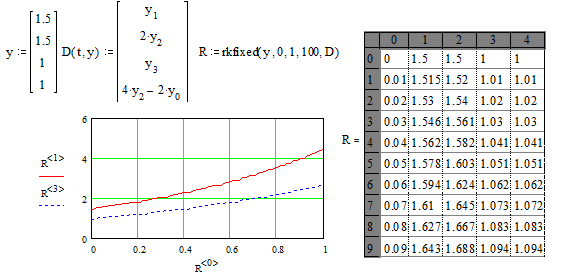
5.
Программирование в пакете Mathcad
Система Mathcad позволяет задавать функции пользователя
используя встроенный язык программирования, что позволяет значительно расширить
область применения пакета. Перед тем как использовать программу-функцию нужно
ее задать - выполнить описание.
Порядок описания программы-функции Mathcad:
. ввести имя программы-функции и список формальных
параметров.
имя_программы (формальные параметры: =);
. в панели Programming, выбрать Add line. На экране появится вертикальная черта и
вертикальный столбец с двумя полями ввода для ввода операторов, образующих тело
программы-функции;
3. в поле 1 (щелкнув на нем мышью или нажав клавишу
[Tab]) ввести первый оператор тела программы-функции. Для вставки
дополнительных полей ввода нажать на кнопке Add line;
. в последнем поле (поле 2), определить возвращаемое
через имя программы-функции значение (см. рис.).
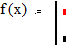
Рис. Структура программы-функции
В качестве примера определим функцию перевода из радиан в градусы:
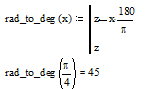
Для выполнения программы-функции необходимо обратиться к её имени
с указанием списка фактических параметров. Фактические параметры указывают при
каких конкретных значениях осуществляются вычисления в теле программы. Между
фактическими и формальными параметрами должно быть соответствие по количеству,
порядку следования и типу. Программный модуль может вести себя и как функция
без имени и параметров, но обязательно возвращающий результат.
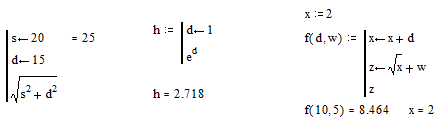
Переменные определенные в функции являются локальными. Как видно
из последнего примера локальное изменение переменной х в программе-функции, не
привело к изменению внешней переменной х.
Основные программные операторы
Для создания программных модулей используются следующие
основные элементы:
|
Название
|
Описание
|
|
Add Line
|
Создание и
расширение программного модуля;
|
|
¬
|
Внутреннее
локальное присваивание.
|
|
if
|
Оператор
условного выражения. Общий вид: выражение if условие. В случаи выполнения
условия возвращается значение выражения. Совместно с этим оператором
часто используются break и otherwise.
|
|
for
|
Циклов с заданным
числом повторений. Общий вид: for Var ÎNmin. Nmax. Цикл можно задать диапазоном, множеством, вектором,
возможна их комбинация. Переменную цикла Var можно использовать в программе.
|
|
while
|
Цикл с
предусловием, действующий пока условие истинно. Общий вид: while условие.
Тело цикла записывается на месте шаблона.
|
|
otherwise
|
Оператор
"иначе", обычно используется совместно с if для выполнения действий
в случаи не выполнения условия.
|
|
break
|
Вызывает
прерывание работы программного блока. Обычно используется с операторами
циклов и условия, для досрочного выхода из цикла или программного блока.
|
|
continue
|
Используется
для продолжения работы цикла после прерывания. Обычно используется совместно
с операторами задания циклов, обеспечивает прерывание и возврат в начало
цикла.
|
|
return
|
Прерывает
выполнение программы и возвращает значение своего операнда.
|
|
on error
|
Оператор
обработки ошибок. Общий вид: выражение1 on error выражение2. Если при
выполнении выражения1 возникла ошибка, то выполняется выражение2. Для обработки
ошибок полезна функция error (S), которая выдает текстовое сообщение (S) и
прерывает работу программного блока.
|
Логические операции и выражения отношений
Логическим выражением называется конструкция, составленная из
выражений отношений, знаков логических операций и круглых скобок. Значение
логического выражения вычисляется слева направо с учетом приоритетов операций.
Список приоритетов (по их убыванию):
. круглые скобки;
2. логическая операция И;
. логическая операция ИЛИ.
Выражения отношений - используются для сравнения двух
арифметических выражений между собой. Общий вид: выражения знак отношения
выражение
Допустимые знаки отношений представлены в таблице:
|
Знак отношения
|
Вводимые
символы
|
|
=
|
Ctrl + =
|
|
<
|
<
|
|
>
|
>
|
|
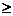 Ctrl + 0 Ctrl + 0
|
|
|
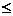 Ctrl + 9 Ctrl + 9
|
|
|
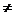 Ctrl + 3 Ctrl + 3
|
|
Логические операции ставятся между выражениями отношений.
Определены две логические операции - логическое ИЛИ (+) и логическое И (×)
Примеры программных модулей

Определим программу-функцию для вычисление корней квадратного
уравнения 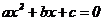 .
.
1)
Примеры
цикла for.
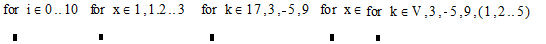
В первых двух случаях цикл задается с помощью дискретной
переменной, в третьем - списком принимаемых значений. В четвертом, переменная
цикла принимает значения элемента вектора V. Последний способ комбинирует
приведенные выше способы.
3)
Составим
программу-функцию для определения позиций заданного элемента в векторе.

3)
Составим
программу-функцию для зануления нечетных элементов вектора.

3)
Составим
программу-функцию для определения позиции первого нулевого элемента матрицы.
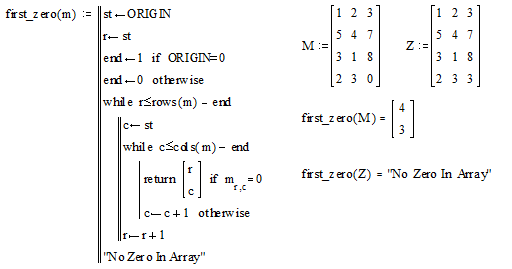
Составим программу-функцию для определения максимального элемента
массива и его позиции.

) Составим программу-функцию для определения произведения
элементов массива.
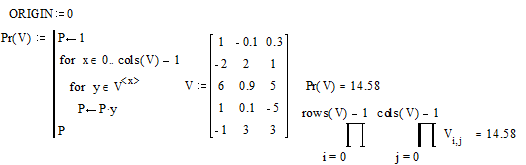
6.
Апроксимация функций
Аппроксимацией (приближением) функции 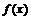 называется нахождение такой функции
называется нахождение такой функции  (аппроксимирующей функции), которая была
бы близка заданной. Критерии близости функций
(аппроксимирующей функции), которая была
бы близка заданной. Критерии близости функций 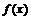 и
и  могут быть различные.
могут быть различные.
В том случае, когда приближение строится на дискретном наборе
точек, аппроксимацию называют точечной или дискретной.
В том случае, когда аппроксимация проводится на непрерывном
множестве точек (отрезке), аппроксимация называется непрерывной или
интегральной. Примером такой аппроксимации может служить разложение функции в
ряд Тейлора, то есть замена некоторой функции степенным многочленом.
Наиболее часто встречающим видом точечной аппроксимации является
интерполяция (в широком смысле).
В том случае, когда полином един для всей области интерполяции,
говорят, что интерполяция глобальная.
В тех случаях, когда между различными узлами полиномы различны,
говорят о кусочной или локальной интерполяции.
Найдя интерполяционный полином, мы можем вычислить значения
функции 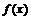 между узлами (провести интерполяцию в
узком смысле слова), а также определить значение функции
между узлами (провести интерполяцию в
узком смысле слова), а также определить значение функции 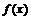 даже за пределами заданного интервала
(провести экстраполяцию).
даже за пределами заданного интервала
(провести экстраполяцию).
Следует иметь в виду, что точность экстраполяции обычно очень
невелика.
Регрессия
функций
Регрессия - представление совокупности данных некоторой
функцией f (x). Задачей регрессии является вычисление параметров функции f (x)
таким образом, чтобы функция приближала "облако" исходных точек с
наименьшей погрешностью. При этом функция f (x) называется уравнением
регрессии. При регрессии не требуется чтобы функция проходила через все
заданные точки, что особенно важно при аппроксимации данных, заведомо
содержащих ошибки.
Линейная регрессия
Линейная регрессия является простейшим видом регрессии.
Классическим алгоритмом линейной регрессии является метод наименьших квадратов.
В котором критерием является минимизация суммы квадратов отклонений аппроксимирующей
функции от заданных точек:
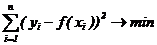 .
.
Существуют и другие алгоритмы определения коэффициентов линейной
регрессии - метод медиан.
В общем виде аппроксимирующею функцию можно представить как 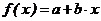 . Задачей линейной регрессии является
вычисление параметров a и b. Для этого в MathCad существует ряд встроенных
функций (где VX, VY - вектора узловых точек):
. Задачей линейной регрессии является
вычисление параметров a и b. Для этого в MathCad существует ряд встроенных
функций (где VX, VY - вектора узловых точек):
1.
corr
(VX, VY) - возврящает скаляр - коэффициент корреляции Пирсона. Чем ближе коэффициент
к 1 тем точнее исходная зависимость приближается к линейной;
2.
intercept
(VX, VY) - возвращает значение параметра а (свободный член) рассчитанного
методом наименьших квадратов;
3.
slope
(VX, VY) - определяет значение параметра b (угловой коэффициент) рассчитанного
методом наименьших квадратов;
4.
line
(VX, VY) - [MathCAD 2000] возвращает вектор первый элемент которого параметр а,
второй b рассчитанные по методу наименьших квадратов;
5.
medfit
(VX, VY) - [MathCAD 2000] возвращает вектор первый элемент которого параметр а,
второй b рассчитанные по методу медиан.
Как видно из примера при аппроксимации линейной регрессией
прямая проходит через "облако" точек.
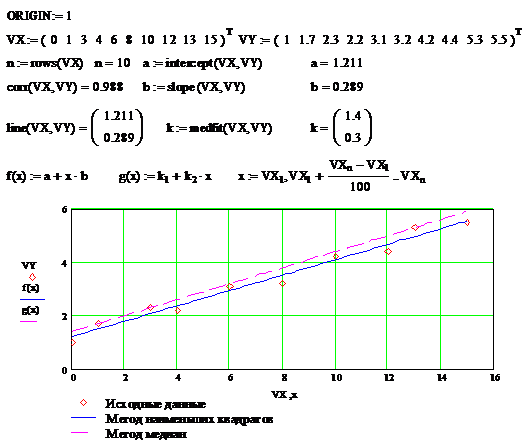
Используя встроенные функции можно рассчитывать регрессию не
только для линейных, но и для экспоненциальных функций 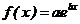 . Для этого f (x) с помощью
логарифмирования по натуральному основанию приводится к линейной. Рассчитанный
коэффициент а, полученный в логарифмической форме, затем пересчитывается.
. Для этого f (x) с помощью
логарифмирования по натуральному основанию приводится к линейной. Рассчитанный
коэффициент а, полученный в логарифмической форме, затем пересчитывается.
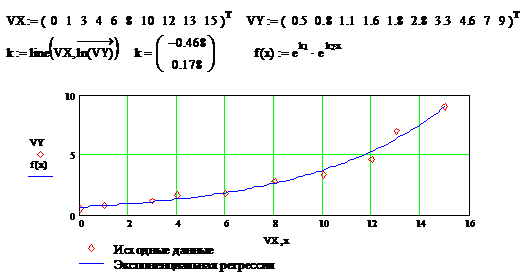
Линейная регрессия общего вида
MathCAD позволяет проводить линейную регрессию общего вида, в
которой аппроксимирующая функция задается линейной комбинацией функций, причем
сами фикции fi (x) могут быть не линейными:
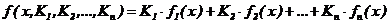 .
.
Линейная регрессия общего вида реализуется с помощью функции
linfit (VX, VY,F) - возвращающей вектор коэффициентов К, при котором
среднеквадратичная погрешность приближения "облака" исходных точек с
координатами VX, VY, минимальна. Вектор F содержит функции fi (x)
записанные в символьном виде. Вектор VX должен быть возрастающим.

Полиномиальная регрессия
Полиномиальная регрессия позволяет аппроксимировать зависимость
полиномом произвольной степени. Вычисление коэффициентов полинома
осуществляется с помощью встроенной функции regress (VX, VY,n), где VX, VY -
вектора с координатами исходных данных, n - порядок полинома (первые три
возвращаемые коэффициенты служебные, а далее искомые значения расположенные по
возрастанию степени полинома). Для построения аппроксимирующей зависимости
можно воспользоваться либо встроенной функцией interp (VK,VX, VY,x), либо
функцией 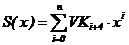 , где VK - вектор коэффициентов
расчитанных функцией regress; x - рассчитываемая точка. Для проведения
регрессии необходимо что бы вектор VX был
возрастающим и его количество его элементов было больше степени полинома на 1.
, где VK - вектор коэффициентов
расчитанных функцией regress; x - рассчитываемая точка. Для проведения
регрессии необходимо что бы вектор VX был
возрастающим и его количество его элементов было больше степени полинома на 1.
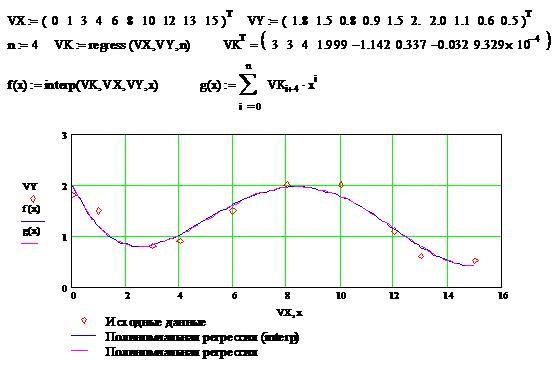
Функция regress определяет единственный приближающий полином,
элементы которого вычисляются по всей совокупности точек. Для проведения
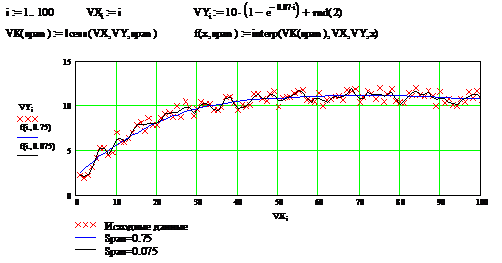
локальной регрессии используется функция loess (VX, VY,span) - дающая приближение отрезками полиномов второй степени, где
span - величина задающая длину отрезков. Чем больше величина span>0, тем
сильнее сглаживаются данные. Чем меньше шаг между точками VX, тем меньше должно
быть span. При больших значениях span функция приближается к regress (VX,
VY,2). Рекомендуемое значение 0.75, однако оно подходит далеко не всегда и
требует уточнения.
Нелинейная регрессия общего вида
Для выполнения нелинейной регрессии общего вида необходимо
определить параметры произвольной аппроксимирующей функции 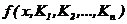 , при которой обеспечивается минимальная
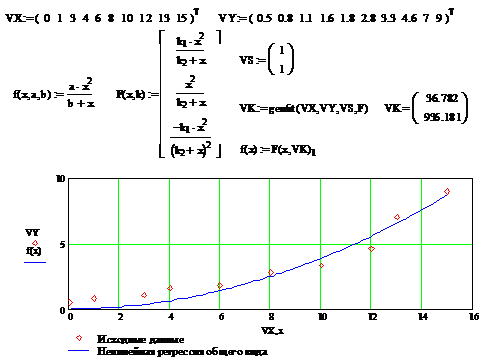
среднеквадратичная ошибка. Для этого используется встроенная функция genfit
(VX,VY,VS,F) -
которая возвращает вектор K параметров функции
, при которой обеспечивается минимальная
среднеквадратичная ошибка. Для этого используется встроенная функция genfit
(VX,VY,VS,F) -
которая возвращает вектор K параметров функции 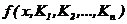 . Вектор VS - задает начальные приближения элементов вектора K
рассчитываемых итерационным способом, вектор F содержит искомую функцию и ее
частные производные по параметрам Ki в аналитическом виде:
. Вектор VS - задает начальные приближения элементов вектора K
рассчитываемых итерационным способом, вектор F содержит искомую функцию и ее
частные производные по параметрам Ki в аналитическом виде:
 .
.
Интерполирование
функций
Интерполирование - способ приближенного или точного нахождения,
какой либо величины по известным отдельным значениям, её или других величин,
связанных с ней. Задача интерполирования состоит в том, чтобы подобрать
многочлен f (x) с действительными коэффициентами проходящий через все узлы
интерполяции yi. Критерием близости функции является 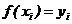 . Дискретный набор значений
. Дискретный набор значений 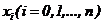 - называют узлами интерполяции, а
многочлен f (x) интерполяционным полиномом. Для выполнения интерполяции
средствами MathCAD необходимо, что бы точки xi были возрастающими и
не совпадающими, а также были заданы значения yi для всех точек.
- называют узлами интерполяции, а
многочлен f (x) интерполяционным полиномом. Для выполнения интерполяции
средствами MathCAD необходимо, что бы точки xi были возрастающими и
не совпадающими, а также были заданы значения yi для всех точек.
Кусочная линейная интерполяция
Кусочная линейная интерполяция является простейшим случаем
локальной. Интерполяционной функцией является полином первой степени, то есть
узловые точки соединяются прямой. Линейная интерполяция осуществляется с
помощью встроенной функции linterp (VX,VY,x), где VX, VY - вектора узловых
точек; x - рассчитываемая точка.

Сплайновая интерполяция
Среди методов локальной интерполяции наибольшее
распространение получила интерполяция сплайнами (от англ. spline - гибкая линейка).
Идея сплайн - интерполяции в том, что полином высокой степени проходящий через
все опорные точки заменяется фрагментами полиномов малых порядков. В MathCAD
используются кубические полиномы. При таком способе приближения не появляется
множества не связанных со значениями узловых точек экстремумов, и
аппроксимирующая функция точно проходит через все узлы и имеет непрерывную
первую и вторую производные.
На каждом интервале 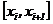 интерполирующую функцию можно представить как полином 3-ей
степени
интерполирующую функцию можно представить как полином 3-ей
степени 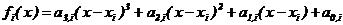 удовлетворяющий условию
удовлетворяющий условию 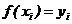 . Коэффициенты полиномов
. Коэффициенты полиномов 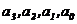 рассчитываются из условия непрерывности
первой и второй производных.
рассчитываются из условия непрерывности
первой и второй производных.
Встроенные
операторы
В таблице, приведенной ниже, используются следующие
обозначения: X и Y - переменные или выражения любого типа; x и y - вещественные
числа; z и w - вещественные или комплексные числа; m и n - целые числа; A и B -
массивы (векторы или матрицы); i - дискретный аргумент; t - любая переменная; f
- любая функция.
|
Оператор
|
Клавиши
|
Назначение
оператора
|
|
X: = Y
|
X: Y
|
Локальное
присваивание X значения Y
|
|
X ºY
|
X ~ Y
|
Глобальное
присваивание X значения Y
|
|
X =
|
X =
|
Вывод значения X
|
|
X + Y
|
X + Y
|
Сложение X
с Y
|
|
X + Y
|
X [Ctrl] [¿] Y
|
То же, что и
сложение. Перенос чисто косметический.
|
|
X - Y
|
X - Y
|
Вычитание из X
значения Y
|
|
X × Y
|
X * Y
|
Умножение X
на Y
|
|
 X / zДеление X на z X / zДеление X на z
|
|
|
|
zw
|
z ^ w
|
Возведение z
в степень w
|
|
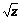 z \Вычисление квадратного корня из z z \Вычисление квадратного корня из z
|
|
|
|
 n [Ctrl] \ zВычисление корня n-ой степени из z n [Ctrl] \ zВычисление корня n-ой степени из z
|
|
|
|
n!
|
n!
|
Вычисление
факториала
|
|
Bn
|
B
[n
|
Ввод нижнего
индекса n
|
|
An,m
|
A
[n, m
|
Ввод двойного
индекса
|
|
A<n>
|
A
[Ctrl] 6 n
|
Ввод верхнего
индекса
|
|
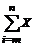 [Ctrl] [Shift] 4Суммирование Х
по i = m, m + 1,. n [Ctrl] [Shift] 4Суммирование Х
по i = m, m + 1,. n
|
|
|
|
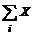 $Суммирование Х по дискретному
аргументу i $Суммирование Х по дискретному
аргументу i
|
|
|
|
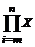 [Ctrl] [Shift] 3Перемножение Х
по i = m, m + 1,. n [Ctrl] [Shift] 3Перемножение Х
по i = m, m + 1,. n
|
|
|
|
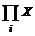 #Перемножение Х по дискретному
аргументу i #Перемножение Х по дискретному
аргументу i
|
|
|
|
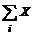 $Суммирование Х по дискретному
аргументу i $Суммирование Х по дискретному
аргументу i
|
|
|
|
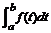 &Вычисление определенного интеграла f
(t) на интервале [a, b] &Вычисление определенного интеграла f
(t) на интервале [a, b]
|
|
|
|
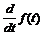 ?Вычисление производной f (t) по t ?Вычисление производной f (t) по t
|
|
|
|
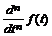 [Ctrl] ?Вычисление производной n-го порядка функции f (t) по
t [Ctrl] ?Вычисление производной n-го порядка функции f (t) по
t
|
|
|
|
(§)
|
‘
|
Ввод пары
круглых скобок с шаблоном
|
|
x
> y
|
x
> y
|
Больше чем
|
|
x < y
|
x < y
|
Меньше чем
|
|
x
³ y
|
x
[Ctrl] 0 y
|
Больше либо
равно
|
|
x
£ y
|
x
[Ctrl] 9 y
|
Меньше либо
равно
|
|
z
= w
|
z
[Ctrl] = w
|
Булево
равенство возвращает 1, если операнды равны, иначе 0
|
|
z
¹ w
|
z
[Ctrl] 3 w
|
Не равно
|
|
|z|
|
| z
|
Вычисление
модуля комплексного z
|
Литература
1. Дьяконов
В.П. Справочник по
MathCAD PLUS 6.0 PRO. - М.: "СК Пресс”, 1997. - 336 с.: ил.
2. Дьяконов
В.П., Абраменкова И.В. MathCAD 8 PRO в"Нолидж”, 2000. - 512 с.: ил.
3. Кудрявцев математике, физике и Internet. - М.:
Е.М. MathCAD 2000 Pro. - М.: ДМК Пресс, 2001. - 576 с.: ил.
4. Очков
В.Ф. Mathcad 7 Pro
для студентов и инженеров. - М.: КомпьютерПресс, 1998. - 384 с.: ил.
5. Плис
А.И., Сливина Н.А. Mathcad
2000. Лабораторный практикум по высшей математике. - М.: Высш. шк., 2000. - 716
с.: ил.
. Новиков
А.А. Практическое пособие к лабораторным и контрольным работам по теме
"Решение инженерно-экономических задач в среде MathCad for Windows" курса "Информатика" для студентов
заочного отделения. - Гомель.: ГГТУ, 2000. - 45с. (м. ук № 2774)
. Токочаков
В.И. Практическое пособие по теме " Решение систем алгебраических и
дифференциальных уравнений в среде MathCad for Windows" для студентов всех
специальностей дневного и заочного отделений. - Гомель.: ГГТУ, 2000. - 25с. (м.
ук № 2453)
. Трохова
Т.А. Практическое пособие по теме " Основные приемы работы в системе MathCad, версия 6.0" курса "Вт и
программирование" для студентов всех специальностей дневного и заочного
отделений. - Гомель.: ГГТУ, 1998. - 42с. (м. ук № 2286)