Теория автоматического управления
Некоммерческое
акционерное общество
«АЛМАТИНСКИЙ
УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра
Промышленной теплоэнергетики
РАСЧЕТНО
- ГРАФИЧЕСКАЯ РАБОТА № 2
Дисциплина:
Теория автоматического управления
Вариант
38
Выполнил
Икласов И.М.
Группа
ТЭС-09-3
Руководитель
преподаватель
Джаманкулова Н.О.
Алматы
2012
Введение
Теория автоматического управления (ТАУ)
появилась во второй половине ХІХ
века сначала как теория регулирования. Широкое применение паровых машин вызвало
потребность в регуляторах, то есть в специальных устройствах, поддерживающих
устойчивый режим работы паровой машины. Это дало начало научным исследованиям в
области управления техническими объектами. Оказалось, что результаты и выводы
данной теории могут быть применимы к управлению объектами различной природы с
различными принципами действия. В настоящее время сфера ее влияния расширилась
на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому
прежнее название “Теория автоматического регулирования” заменено на более
широкое - “Теория автоматического управления”.
В данной работе необходимо ознакомиться с
теорией получения сигналов со звеньями, также решить задачу, получить
дифференциальное уравнение, передаточную функцию, и частотные характеристики.
Задание 1
Пояснить метод построения области устойчивости в
пространстве параметров настройки регулятора (Д-разбиение). Привести пример
построения области устойчивости простейшей АСР. Теоретическое обоснование
метода D-разбиений
Изменение параметров САУ, например, с целью
оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется
ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего
не говорят. Рассмотрим метод определения границ допустимых изменений
параметров, при которых САУ не теряет устойчивости.
Приведем характеристическое уравнение замкнутой
САУ к виду:
D(p) = pn + c1
pn -1 + c2 pn-2 +... +
cn = 0,
где c0 = a0 /a0
= 1, c1 = a1 /a0 и т.д. При
некоторых конкретных значениях c1 ,c2 ,...,cn
уравнение имеет единственное решение, то есть единственный набор корней (p1,p2
,...,pn ). По их расположению на комплексной плоскости можно
судить об устойчивости САУ при заданных параметрах.
Если изменить какой-либо параметр САУ, например
коэффициента передачи, то изменятся и коэффициенты характеристического
уравнения D(p) = 0 и станут равными cн1 ,cн2
,...,cнn. Уравнение примет вид:
н(p)
= pn + cн1 pn -1 + cн2 pn -2
+... + cнn = 0.
Это уже другое уравнение и оно также имеет
единственное решение (pн1 ,pн2 ,...,pнn ),
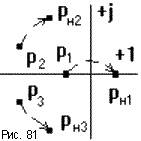
отличающееся от (p1 ,p2 ,...,pn ). Если
плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут
плавно изменяться, а его корни будут перемещаться по комплексной плоскости
(рис.81).
Каждый уникальный набору коэффициентов c1
,c2 ,...,cn можно изобразить точкой в пространстве
коэффициентов, по осям которого откладываются значения коэффициентов c1
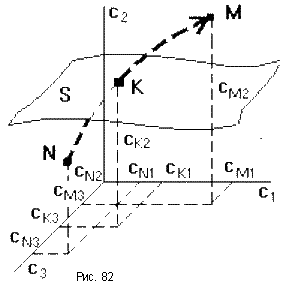
,c2 ,...,cn. Так уравнению третьей степени
соответствует трехмерное пространство коэффициентов (рис.82).
Пусть точка N с координатами (cN1
,cN2,cN3) соответствует уравнению, имеющему решение (pN1,pN2,pN3),
точка M с координатами (cM1 ,cM2 ,cM3)
соответствует уравнению, имеющему решение (pM1 ,pM2 ,pM3).
При изменении какого-либо параметра САУ коэффициенты характеристического
уравнения будут изменяться, при этом точка в пространстве коэффициентов,
соответствующая данному уравнению будет перемещаться по некоторой траектории,
например из положения N в положение M. Этому перемещению будет
соответствовать и перемещение корней (pN1,pN2,pN3)
на комплексной плоскости в положение (pM1 ,pM2 ,pM3)
(аналогично рис.81).
При этом движении некоторые корни будут
переходить через мнимую ось комплексной плоскости из левой полуплоскости в
правую и наоборот. В момент перехода такой k-й корень примет значение pK
= j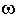 K,
а коэффициенты уравнения будут иметь определенные значения cK1,cK2,cK3,
определяющие в пространстве коэффициентов точку K. Подставим корень pK
в характеристическое уравнение, получим тождество:
K,
а коэффициенты уравнения будут иметь определенные значения cK1,cK2,cK3,
определяющие в пространстве коэффициентов точку K. Подставим корень pK
в характеристическое уравнение, получим тождество:
D(pK
) = (j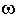 K)3
+ cK1(j
K)3
+ cK1(j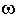 K)2
+ cK2
(jK
) + cK3
= 0
K)2
+ cK2
(jK
) + cK3
= 0
Меняя w от - до +
до +  ,
и находя при каждой частоте все возможные сочетания коэффициентов c1
,c2 ,...,cn,удовлетворяющих уравнению
,
и находя при каждой частоте все возможные сочетания коэффициентов c1
,c2 ,...,cn,удовлетворяющих уравнению
D(j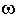 )
= (j
)
= (j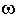 )n
+ c1 (j
)n
+ c1 (j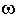 )n-1 + c2
(j
)n-1 + c2
(j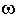 )n-2
+... + cn = 0,
)n-2
+... + cn = 0,
можно построить в n-мерном пространстве
коэффициентов сложную поверхность S, разделяющую его на области,
называемое D-областями. Полученное уравнение называется уравнением
границы D-разбиения.
Переход из одной D-области в другую через
поверхность S соответствует переходу одного или нескольких корней через
мнимую ось в плоскости корней. То есть каждая точка внутри определенной D-области
соответствует уравнению с определенным количеством левых и правых корней.
Поэтому области обозначают D(m) по числу m правых корней.
Достаточно взять любую точку в пространстве
коэффициентов и найти для нее число правых корней. Затем, двигаясь по
пространству коэффициентов через границу S, можно выявить обозначения
всех других областей. Особый интерес представляет область D(0), которой
соответствуют уравнения с полным отсутствием правых корней, называемая областью
устойчивости. Описанный метод определения областей устойчивости называется методом
D-разбиений.
Не обязательно строить сложную n-мерную
картину D-разбиения, можно изменять значения, например, только двух
коэффициентов, оставляя другие коэффициенты постоянными. Границу D-разбиения
S можно строить не только также и в пространстве конкретных параметров
системы, от которых зависят данные коэффициенты.
D-разбиение по одному параметру
Пусть необходимо выявить влияние на устойчивоять
САУ, например, коэффициента усиления K. Приведем характеристическое
уравнение к виду D(p) = S(p) + K N(p),
выделив члены, не зависящие от K в полином S(p), а в остальных
членах, линейно зависящих от K, вынесем его за скобки. Граница D-разбиения
задается уравнением
N(p),
выделив члены, не зависящие от K в полином S(p), а в остальных
членах, линейно зависящих от K, вынесем его за скобки. Граница D-разбиения
задается уравнением
D(j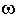 )
= S(j
)
= S(j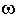 )
+ K
)
+ K N(j
N(j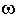 )
= 0, => K = -S(j
)
= 0, => K = -S(j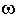 )/N(j
)/N(j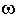 )
= X(
)
= X(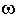 )
+ jY(
)
+ jY(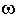 ).
).
Изменяя w от - до +
до +  ,
будем вычислять X(
,
будем вычислять X(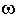 )
и Y(
)
и Y(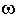 )
и по ним строить точки границы D-разбиения. Пространство коэффициентов
представляется системой координат X-Y (рис.83а). Обычно строят только
половину кривой (
)
и по ним строить точки границы D-разбиения. Пространство коэффициентов
представляется системой координат X-Y (рис.83а). Обычно строят только
половину кривой (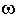 = [0, +
= [0, +  ),
другую половину достраивают симметрично относительно вещественной оси.
),
другую половину достраивают симметрично относительно вещественной оси.
Если в плоскости корней двигаться вдоль мнимой
оси от - до +
до +  и
штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль
линии D-разбиения при изменении w от -
и
штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль
линии D-разбиения при изменении w от - до +
до +  и
штриховке ее также слева. Переходу корня в плоскости корней из штрихованной
полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный
переход через границу D-разбиения вдоль стрелки 1, и наоборот.
Если пересекается область с двойной штриховкой (точки A, В, C), то в
плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.
и
штриховке ее также слева. Переходу корня в плоскости корней из штрихованной
полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный
переход через границу D-разбиения вдоль стрелки 1, и наоборот.
Если пересекается область с двойной штриховкой (точки A, В, C), то в
плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.
Если известно количество правых корней,
соответствующее хотя бы одной D-области, то двигаясь от нее через
границы с учетом штриховок, можно обозначить все остальные области. Область с
наибольшим количеством штриховок является претендентом на область устойчивости.
Нужно взять любую точку из этой области и при соответствующем значении K
проверить систему на устойчивость любым методом.
Есть одна особенность. Так как K -
вещественное число, то Y(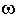 ) = 0,
поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной
оси в этой области, то есть K = X(
) = 0,
поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной
оси в этой области, то есть K = X(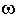 ).
).
Задание 2
Пояснить метод приближенной оценки вида
переходного процесса по вещественной частотной характеристике.
Оценки качества переходного процесса по
вещественной частотной характеристике
Такие оценки оказываются особенно
удобными в случае, когда для исследования системы применяются частотные методы
<#"606861.files/image007.gif">
Риc.5.12. Иллюстрация 1-ой и 2-ой оценок
· Оценка 3. Если для
частотных характеристик двух систем справедливо выражение
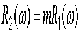 или
или 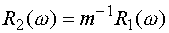 ,
,
то аналогичное соотношение будет связывать и
переходные характеристики:
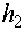 (t) = m
(t) = m 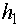 (t)
или
(t)
или 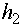 (t)
=
(t)
= 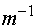
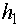 (t).
(t).
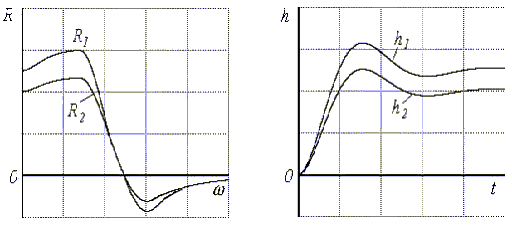
Рис.5.13. Иллюстрация 3-ей оценки
· Оценка 4. В случае, когда
частотные характеристики двух систем связаны соотношением
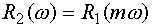 ,
,
для переходных характеристик справедливо
равенство
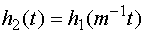 .
.
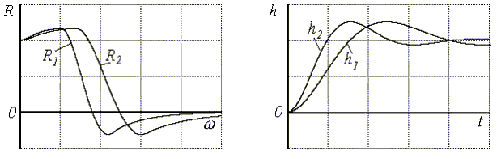
Рис.5.14. Иллюстрация 4-ой оценки
· Оценка 5. Если R( ) является
положительной невозрастающей функцией, то перерегулирование
<#"606861.files/image019.gif">представляет собой отрицательную,
убывающую по модулю непрерывную функцию.
) является
положительной невозрастающей функцией, то перерегулирование
<#"606861.files/image019.gif">представляет собой отрицательную,
убывающую по модулю непрерывную функцию.
· Оценка 7. В случае,
когда R (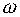 ) есть
локально возрастающая функция, перерегулирование можно оценить по формуле:
) есть
локально возрастающая функция, перерегулирование можно оценить по формуле:
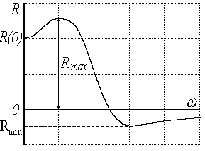
Рис.5.15. Иллюстрация 7-ой оценки
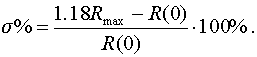
· Оценка 8. Если на
какой-то частоте R(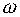 ) терпит разрыв, то
переходная характеристика будет иметь незатухающие колебания этой частоты.
) терпит разрыв, то
переходная характеристика будет иметь незатухающие колебания этой частоты.
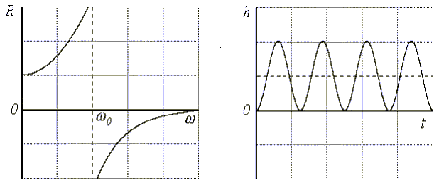
Рис.5.16. Иллюстрация 8-ой оценки
· Оценка 9. Для монотонных
процессов время переходного процесса можно приближенно оценить по формуле:
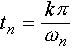 ,
, 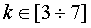 .
.
Если частотная характеристика R ( 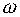 )
всегда положительна, то в качестве
)
всегда положительна, то в качестве 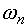 выбирается
частота, на которой
выбирается
частота, на которой 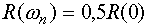 .
.
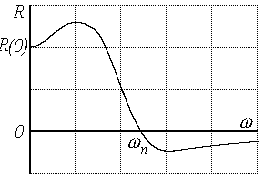
<="" p="">
Рис.5.17. Иллюстрация 9-ой оценки
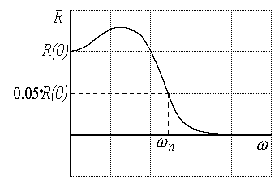
Рис.5.18. Определение частоты
Таким образом, с помощью приведенных оценок
можно приближенно (без вычислений) оценить качество переходного процесса по
виду вещественной частотной характеристики.
Задание 3
Дать определение понятиям: запас устойчивости по
модулю и запас устойчивости по фазе. Указать и пояснить основные приемы
повышения качества процесса регулирования.
Понятие запаса устойчивости
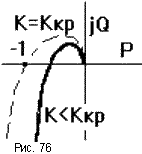
В условиях эксплуатации параметры системы по тем
или иным причинам могут меняться в определенных пределах (старение,
температурные колебания и т.п.). Эти колебания параметров могут привести к
потере устойчивости системы, если она работает вблизи границы устойчивости.
Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы
устойчивости.
Степень этого удаления называют запасом
устойчивости.
Согласно критерия Найквиста, чем дальше АФЧХ от
критической точки (-1, j0), тем больше запас устойчивости. Различают
запасы устойчивости по модулю и по фазе.
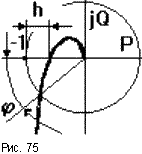
Запас устойчивости по модулю
характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в
направлении вещественной оси и определяется расстоянием h от критической
точки до точки пересечения годографом оси абсцисс (рис.75).

Запас устойчивости по фазе характеризует
удаление годографа от критической точки по дуге окружности единичного радиуса и
определяется углом 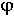 между отрицательным
направлением вещественной полуоси и лучом, проведенным из начала координат в
точку пересечения годографа с единичной окружностью.
между отрицательным
направлением вещественной полуоси и лучом, проведенным из начала координат в
точку пересечения годографа с единичной окружностью.
Как уже отмечалось, с ростом коэффициента
передачи разомкнутой САУ растет модуль каждой точки АФЧХ и при некотором
значении K = Kкр АФЧХ пройдет через критическую точку
(рис.76) и попадет на границу устойчивости, а при K > Kкр замкнутая
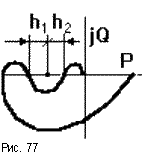
САУ станет неустойчива. Однако в случае “клювообразных” АФЧХ (получаются из-за
наличия внутренних обратных связей) не только увеличение, но и уменьшение K
может привести к потере устойчивости замкнутых САУ (рис.77). В этом случае
запас устойчивости определяется двумя отрезками h1 и h2,
заключенными между критической точкой и АФЧХ.
Обычно при создании САУ задаются требуемыми
запасами устойчивости h и 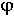 ,
за пределы которых она выходить не должна. Эти пределы выставляются в виде
сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой
САУ входить не должна (рис.78).
,
за пределы которых она выходить не должна. Эти пределы выставляются в виде
сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой
САУ входить не должна (рис.78).
Заключение
Управление каким-либо объектом
(объект управления будем обозначать ОУ) есть воздействие на него в целях
достижения требуемых состояний или процессов. В качестве ОУ может служить
самолет, станок, электродвигатель и т.п. Управление объектом с помощью
технических средств без участия человека называется автоматическим
управлением. Совокупность ОУ и средств автоматического управления
называется системой автоматического управления (САУ).
Основной задачей автоматического
управления является поддержание определенного закона
изменения одной или нескольких физических величин, характеризующих процессы,
протекающие в ОУ, без непосредственного участия человека. Эти величины
называются управляемыми величинами. Если в качестве ОУ рассматривается
хлебопекарная печь, то управляемой величиной будет температура, которая должна
изменяться по заданной программе в соответствии с требованиями технологического
процесса.
И так основная задача студента понять процесс
поддержания определенного сигнала, и уменьшить внешнее воздействие на него, для
этого разбираем схемы, рассматримваем простейшие звенья, и для конечного
результата решаем задачу, имеем схему, описываем законом Кирхгофа, и находим
дифференциальное уравнение, передаточную функцию, и частотные характиристики,
для более глубого понимания я бы предложил провести эксперимент по схеме, и
сравнить с теорией.
Список использованной литературы
регулирование устойчивость паровая
машина
1) Н.К.
Бекалай, Н.О. Джаманкулова. Теория автоматического управления. Методические
указания к выполнению расчетно-графических работ и контрольные задания для
студентов всех форм обучения специальности 5В071700 - Теплоэнергетика. - Алматы:
АУЭС, 2010.- 15 с.
2) Стефани
Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. -М.:
Энергия, 1972. - 376 с.