Критерий сходимости Коши
Введение
сравнение ряд критерий
математический
В данной работе рассмотрены следующие источники:
Архипов Г. И. Лекции по математическому анализу.
- М.: Высш. шк., 1999, 347-366с.
Фихтенгольц Г. М. Курс дифференциального
исчисления. Том 2. - М.: Лань,2002 ,11-32c.
Запорожец Г. И. Руководство к решению задач по
математическому анализу. - М.: Высш. шк. 1966. 342с.
Харди Г. Х. Курс чистой математики. - М.: Гос.
изд. иностр. лит.1949. 341 с.
Кудрявцев Л. Д. Курс математического анализа.
Том 2. - М.: Высш. шк.,1988.25-27с.
В первом источнике подробно расписана вся тема,
но нет определения знакопеременных рядов и геометрического смысла интегрального
признака. Во втором источнике можно найти основные теоремы и определения, а
также определение знакопеременного ряда и геометрический смысл интегрального
признака, которые и представлены в работе. Геометрический смысл можно найти в
пятом источнике, но в нем скудно раскрыты аспекты рассматриваемой темы. Третий
источник дает лишь поверхностное представление о числовых рядах, рассматривая
основные определения и теоремы. В четвертом источнике очень мало можно найти
нужной информации, но можно рассмотреть признак сравнения рядов.
Исходя из анализа представленной литературы,
основой для написания работы я посчитала целесообразнее использовать материал
из первого источника, так как в нем более подробно и удобнее изложен материал.
Сходимость и сумма числового ряда
Определение 1. Пусть {
Пусть {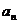 } -
произвольная числовая последовательность. Числовым рядом или просто рядом
называется формальная бесконечная сумма S вида
} -
произвольная числовая последовательность. Числовым рядом или просто рядом
называется формальная бесконечная сумма S вида
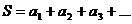 .
.
Обычно используется следующая
сокращенная запись:
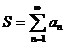 ,
,
Или просто  .
.
Рассмотрим новую последовательность
{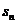 },
задаваемое равенством
},
задаваемое равенством
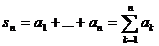 .
.
Определение 2. Последовательность {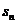 } называется
последовательностью частичных (или частных) сумм ряда
} называется
последовательностью частичных (или частных) сумм ряда  , а ее n-й член
называется n-й частичной
суммой этого ряда.
, а ее n-й член
называется n-й частичной
суммой этого ряда.
Определение 3. Если
последовательностью {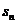 } частичных
сумм ряда
} частичных
сумм ряда  сходится к
числу
сходится к
числу 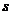 , т.е. если
, т.е. если 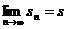 , то ряд
, то ряд  называется
сходящимися (к
называется
сходящимися (к 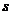 ), а число
), а число 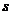 - его
суммой. В это случае пишут
- его
суммой. В это случае пишут
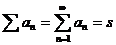 .
.
Если же последовательность {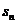 } не имеет
предела, то говорят, что ряд
} не имеет
предела, то говорят, что ряд  расходиться.
расходиться.
В основном нас будут интересовать
сходящиеся ряды.
Определение 4. Если ряд  сходится к
числу
сходится к
числу 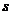 , то
последовательность
, то
последовательность 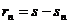 называется
остаточным членом или остатком ряда.
называется
остаточным членом или остатком ряда.
Заметим, что так как 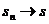 при
при 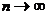 , то
, то 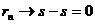 при
при 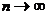 .
.
Несколько модифицируем введенные
определения и обозначения. Если в числовой последовательности {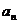 } отбросить
несколько начальных членов, например, в количестве
} отбросить
несколько начальных членов, например, в количестве 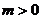 , то
оставшиеся члены
, то
оставшиеся члены 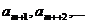 в
совокупности можно снова рассматривать как некую новую последовательность {
в
совокупности можно снова рассматривать как некую новую последовательность {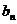 },
задаваемую равенством
},
задаваемую равенством 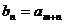 .
.
Рассматривая {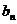 } как общий
член ряда
} как общий
член ряда 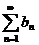 для его
частичных сумм
для его
частичных сумм 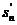 получим
равенство
получим
равенство
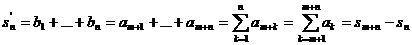 .
.
Кроме того, ряд 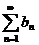 как
формальную бесконечную сумму можно записать в виде
как
формальную бесконечную сумму можно записать в виде
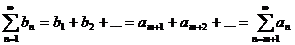 .
.
Таким образом, бесконечную сумму 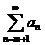 тоже можно
рассматривать как ряд [1], [2], [3], [5].
тоже можно
рассматривать как ряд [1], [2], [3], [5].
Далее будем рассматривать также
формальные ряды вида 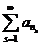 , где ns -
какая-либо последовательность натуральных чисел, и исследовать их на
сходимость.
, где ns -
какая-либо последовательность натуральных чисел, и исследовать их на
сходимость.
Утверждение 1. Остаточный член rn ряда 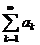 можно
представить в виде ряда
можно
представить в виде ряда 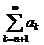 в том
смысле, что:
в том
смысле, что:
. его сумма равна rn , когда
исходный ряд 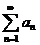 сходится
сходится
. это представление
принимается как формальное равенство, когда оба равенства расходятся;
. другие случаи не имеют
места.
Доказательство начнем с п.3. При 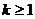 для
частичных сумм
для
частичных сумм 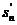 ряда
ряда 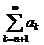 и sk+n ряда
и sk+n ряда 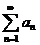 имеет место
равенство
имеет место
равенство 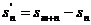 .
.
Ясно, что при фиксированном n сходимость
и расходимость последовательностей {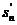 } и {sk+n } имеют
место одновременно, что и означает справедливость утверждения п.3.
} и {sk+n } имеют
место одновременно, что и означает справедливость утверждения п.3.
В случае 1, т.е. когда оба ряда
сходятся, можно перейти к пределу при 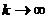 в равенстве
в равенстве 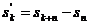 . Тогда
получим
. Тогда
получим
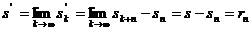 ;
;
тем самым утверждение п. 1 доказано
[1].
Относительно утверждения п. 2
следует заметить, что формальное равенство
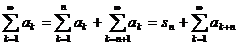
Можно рассматривать как определение
одной из возможных операций над формальными числовыми рядами. Приведении
подобных операций необходимо только требовать, чтобы правые и левые части
равенств переходили бы в равенство между числами в случае наличия сходимости
хотя бы для одной из частей равенства, что действительно имеет место в нашем
случае. Доказательство закончено.
Утверждение 2. Отбрасывание любого
конечного числа членов в бесконечной сумме или прибавление к ней любого
конечного числа новых слагаемых не влияет на сходимость ряда.
Доказательство. Рассмотрим случай
отбрасывания слагаемых, так как второй случай разбирается аналогично. Итак,
пусть мы отбросили члены ряда  с номерами
с номерами 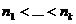 . Оставшиеся
слагаемые переномеруем в порядке возрастания их прежних номеров. Общий член
получившейся таким образом последовательности обозначим
. Оставшиеся
слагаемые переномеруем в порядке возрастания их прежних номеров. Общий член
получившейся таким образом последовательности обозначим 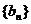 . Тогда при
любом
. Тогда при
любом 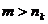 имеем
имеем
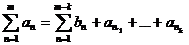 .
.
Отсюда следует, что
последовательности частичных сумм этих рядов 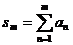 и
и 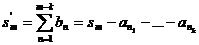 сходятся и расходятся одновременно.
Утверждение доказано.[1].
сходятся и расходятся одновременно.
Утверждение доказано.[1].
Утверждение 3. Если 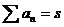 и
и 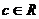 , то
, то 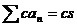
Утверждение 4. Если 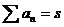 и
и 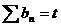 , то
, то 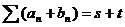 .
.
Доказательство утверждений 3 и 4
есть прямое следствие определения суммы ряда и арифметических свойств
сходящихся последовательностей {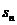 } и {
} и {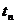 } как частичных сумм рядов
} как частичных сумм рядов  и
и 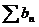 .
Доказательство закончено.
.
Доказательство закончено.
Утверждение 5. (необходимый признак
сходимости ряда). Если ряд  сходится, то
сходится, то 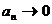 при
при 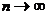 . Другими
словами, {
. Другими
словами, {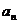 } есть
бесконечно малая последовательность.
} есть
бесконечно малая последовательность.
Доказательство. Имеем 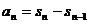 . Отсюда при
. Отсюда при
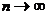 получим
получим 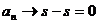 , что и
требовалось доказать.[1], [2], [5].
, что и
требовалось доказать.[1], [2], [5].
Примеры.
. Ряд 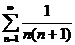 сходится, и его сумма равна 1.
сходится, и его сумма равна 1.
Действительно, имеем
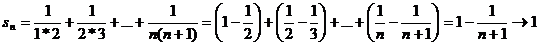
при 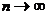 , т.е.
, т.е. 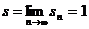 .[1].
.[1].
. Сумма членов бесконечной
геометрической прогрессии вида
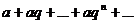 , при
, при 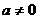 .
.
В случае 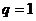 имеем
имеем 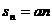 , и ряд
расходится. При
, и ряд
расходится. При 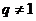 справедливо
равенство
справедливо
равенство
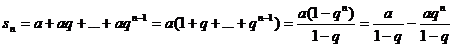 .
.
Известно, что 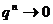 при
при 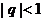 и {
и {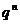 } расходится
при
} расходится
при 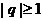 .
.
Таким образом, указанный ряд
сходится к сумме 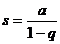 при
при 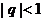 и
расходится при
и
расходится при 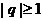 ,
, 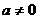 .[1].
.[1].
.Гармонический ряд 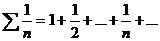 расходится,
а ряд
расходится,
а ряд 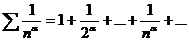 сходится
при
сходится
при 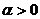 .
.
Применим теорему 2. При всех 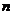 и
и 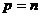 имеем
имеем
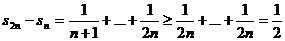 .
.
Таким образом условия теоремы 2
будут выполнены, если положить 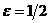 и при любом
и при любом 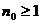 в качестве
в качестве 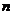 и
и 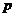 взять числа
взять числа
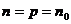 . Тем самым
расходимость ряда установлена. Для доказательства сходимости ряда
. Тем самым
расходимость ряда установлена. Для доказательства сходимости ряда 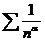 по теореме
Вейерштрасса достаточно доказать ограниченность его частичных сумм
по теореме
Вейерштрасса достаточно доказать ограниченность его частичных сумм 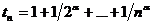 , поскольку
они монотонно возрастают. Рассмотрим какое-либо
, поскольку
они монотонно возрастают. Рассмотрим какое-либо 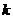 с условием
с условием 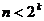 . Тогда
справедлива следующая оценка
. Тогда
справедлива следующая оценка
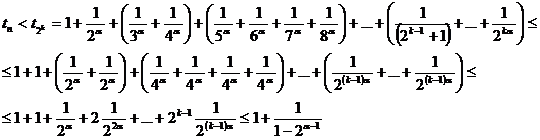
Таким образом, частичные суммы {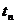 } ограничены
в совокупности, что и означает сходимость искомого ряда.[1].
} ограничены
в совокупности, что и означает сходимость искомого ряда.[1].
Теорема 1 (критерий Коши). Для
сходимости ряда 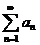 необходимо
и достаточно, чтобы для любого
необходимо
и достаточно, чтобы для любого 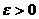 существовал номер
существовал номер 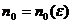 такой, что
при всяком натуральном
такой, что
при всяком натуральном 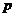 и всех
и всех 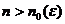 имело место
равенство
имело место
равенство
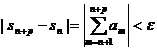 .
.
Доказательство. Утверждение теоремы
равносильно критерию Коши для сходимости {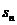 } частичных сумм ряда, что согласно
определению и есть сходимость его самого. Теорема доказана.[1], [2], [5].
} частичных сумм ряда, что согласно
определению и есть сходимость его самого. Теорема доказана.[1], [2], [5].
Теорему 1 можно переформулировать
таким образом, чтобы иметь критерий расходимости ряда 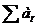 в прямом
виде.
в прямом
виде.
Теорема 2 (критерий Коши для
расходимости ряда). Для расходимости ряда 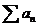 необходимо и достаточно, чтобы
существовало хотя бы одно
необходимо и достаточно, чтобы
существовало хотя бы одно 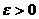 с условием,
что для любого номер
с условием,
что для любого номер 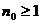 найдутся
натуральные
найдутся
натуральные 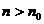 и
и 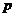 , для
которых справедливо равенство
, для
которых справедливо равенство
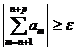 .[1].
.[1].
Знакопостоянные ряды
Определение 5. Всякое выражение вида
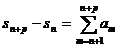 называется
отрезком ряда.[1].
называется
отрезком ряда.[1].
Определение 6. Знакопеременными
называются ряды, члены которых имеют то положительный, то отрицательный знаки[2].
Определение 7. Ряд 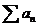 называется
рядом с неотрицательными членами, если при всех n имеем
называется
рядом с неотрицательными членами, если при всех n имеем 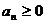 .[1], [2].
.[1], [2].
Теорема 2. Для сходимости ряда  , где
, где 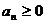 при всех n, необходима
и достаточна ограниченность последовательности его частичных сумм.
при всех n, необходима
и достаточна ограниченность последовательности его частичных сумм.
Доказательство. Пусть 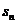 - n-я частичная
сумма ряда
- n-я частичная
сумма ряда  . Поскольку
. Поскольку 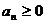 , имеем, что
{
, имеем, что
{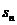 } не
убывает. Теперь требуемый результат вытекает из критерия Вейерштрасса для
сходимости монотонной последовательности. Доказательство закончено.[1].
} не
убывает. Теперь требуемый результат вытекает из критерия Вейерштрасса для
сходимости монотонной последовательности. Доказательство закончено.[1].
Пример. Пусть 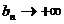 и
и 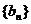 не убывает
и положительна. Тогда ряд
не убывает
и положительна. Тогда ряд 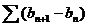 расходится,
а ряд
расходится,
а ряд 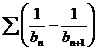 сходится.
сходится.
Действительно, для частичных сумм 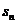 и
и 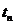 этих рядов
имеем
этих рядов
имеем
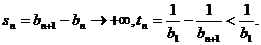 [1].
[1].
Сравнение рядов
Теорема 3 (признак сравнения). Пусть
 и
и 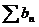 - два ряда
с неотрицательными членами и пусть, начиная с некоторого
- два ряда
с неотрицательными членами и пусть, начиная с некоторого 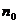 , для всех
, для всех 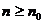 имеем
имеем 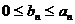 . Тогда:
. Тогда:
. сходимость ряда  влечет за
собой сходимость ряда
влечет за
собой сходимость ряда 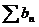 ;
;
. из расходимости ряда 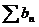 следует
расходимость ряда
следует
расходимость ряда  .
.
Доказательство. Без нарушения
сходимости можно отбросить первые 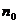 членов каждого ряда. При всех
членов каждого ряда. При всех 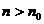 полагаем
полагаем
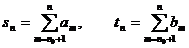 .
.
Тогда для любого 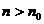 имеем
имеем 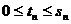 . В случае
1. последовательность {
. В случае
1. последовательность {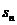 }
ограничена, следовательно, и {
}
ограничена, следовательно, и {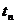 } тоже ограничена и ряд
} тоже ограничена и ряд 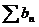 сходится. В
случае 2. последовательность
сходится. В
случае 2. последовательность 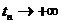 , поэтому
, поэтому 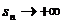 , т. е. ряд
, т. е. ряд  расходится.
Теорема доказана.[1], [4], [5].
расходится.
Теорема доказана.[1], [4], [5].
Замечание. Говорят, что ряд  мажорирует
ряд
мажорирует
ряд 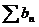 , а
последний, в свою очередь, его минорирует.
, а
последний, в свою очередь, его минорирует.
Теорема 4 (обобщенный признак
сравнения). Если в условии теоремы 3 неравенство 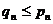 заменить
неравенством
заменить
неравенством 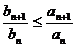 , то ее
утверждение также будет иметь место.
, то ее
утверждение также будет иметь место.
Доказательств. Поскольку
отбрасывание нескольких первых членов ряда не влияет на его сходимость, с
самого начала можно считать, что 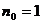 . Перемножая все неравенства из
условия теоремы до номера
. Перемножая все неравенства из
условия теоремы до номера 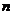 включительно,
приходим к неравенствам вида
включительно,
приходим к неравенствам вида
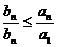 ,
, 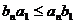 .
.
Применяя теорему 3, получаем
требуемый результат относительно рядов 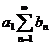 и
и 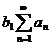 , а так как умножение всех членов
ряда на одно и то же число, отличное от нуля, не влияет на сходимость, теорема
доказана.[1].
, а так как умножение всех членов
ряда на одно и то же число, отличное от нуля, не влияет на сходимость, теорема
доказана.[1].
Признаки сходимости Даламбера, Коши,
интегральный признак сходимости
Теорема 5 (признак Даламбера). Пусть
для членов ряда  ,начиная с
некоторого номера
,начиная с
некоторого номера 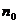 , выполнены
условия:
, выполнены
условия:
. 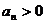 ;
;
. 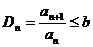 , где
, где 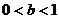 .
.
Тогда ряд  сходится.
Если же при всех
сходится.
Если же при всех 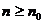 вместо
неравенства 2 имеем
вместо
неравенства 2 имеем 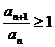 , то ряд
, то ряд 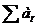 расходится.
расходится.
Доказательство. Сравним ряд  со
сходящимся рядом
со
сходящимся рядом 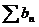 , где
, где  . При
. При 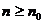 имеем
имеем
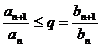 .
.
Поэтому первое утверждение теоремы 5
вытекает из теоремы 4.
Во втором случае надо положить 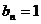 для всех
для всех 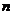 . Тогда
ввиду расходимости ряда
. Тогда
ввиду расходимости ряда 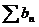 и
неравенств
и
неравенств
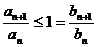
из той же теоремы 4 следует
расходимость ряда  . Теорема
доказана.[1], [2], [5].
. Теорема
доказана.[1], [2], [5].
Теорема 6 (признак Даламбера в
предельной форме). Рассмотрим ряд  с условием
с условием 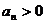 для всех
для всех 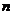 . Положим
. Положим
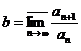 ,
, 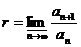 .
.
Тогда при всех 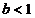 ряд
ряд  сходится, а
при
сходится, а
при 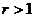 -
расходится.
-
расходится.
Доказательство. Рассмотрим сначала
первый случай. Положим 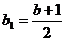 . Тогда
. Тогда 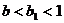 . Поскольку
. Поскольку 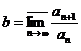 , при
некотором
, при
некотором 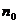 имеем
имеем
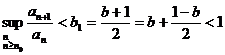 .
.
Следовательно, ряд  сходится в
силу первого утверждения теоремы 5.
сходится в
силу первого утверждения теоремы 5.
Рассмотрим теперь второй случай.
Положим 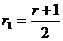 . Тогда
имеем
. Тогда
имеем 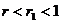 . Поскольку
. Поскольку 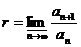 , при
некотором
, при
некотором 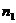 имеем
оценку
имеем
оценку
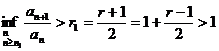 .
.
Тем самым ряд  расходится
по второму утверждению теоремы 5. Теорема доказана. [1].
расходится
по второму утверждению теоремы 5. Теорема доказана. [1].
Замечание. При 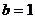 вопрос о
сходимости ряда
вопрос о
сходимости ряда  в теоремах
5 и 6 остается открытым. Для примера можно указать на ряды
в теоремах
5 и 6 остается открытым. Для примера можно указать на ряды 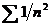 и
и 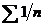 , один из
которых сходится, а другой - расходится, но в обоих случаях имеем
, один из
которых сходится, а другой - расходится, но в обоих случаях имеем 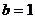 . Для
исследования сходимости подобных рядов требуются более «тонкие» признаки,
которые будут рассмотрены позже.
. Для
исследования сходимости подобных рядов требуются более «тонкие» признаки,
которые будут рассмотрены позже.
Несколько тонкий признак дает
следующая теорема.
Теорема 7 (признак Коши). Если для
членов ряда  с условием
с условием 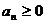 , начиная с
некоторого номера
, начиная с
некоторого номера 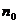 , имеет
место неравенство
, имеет
место неравенство 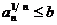 , где число
, где число 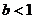 и
фиксировано, то ряд
и
фиксировано, то ряд  сходится.
сходится.
Если же для бесконечно многих 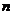 имеем
имеем 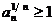 , то этот
ряд расходится.
, то этот
ряд расходится.
Доказательство. Рассмотрим сначала
первый случай. Последовательно имеем 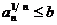 ,
, 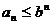 , и так как
, и так как 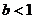 , то ряд
, то ряд  сходится по
признаку сравнения вместе с рядом
сходится по
признаку сравнения вместе с рядом 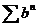 .
.
Во втором случае для бесконечного
количества значений 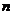 имеем
имеем 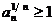 ,
, 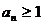 . Это
значит, что
. Это
значит, что 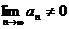 и ряд
и ряд  расходится,
поскольку условие необходимого признака сходимости ряда (
расходится,
поскольку условие необходимого признака сходимости ряда (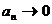 при
при 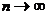 ) не
выполняется. Теорема доказана.[1], [2], [5].
) не
выполняется. Теорема доказана.[1], [2], [5].
Теорема 8 (признак Коши в предельной
форме). Пусть
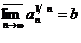 ,
,
где 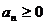 при всех
при всех 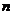 .
.
Тогда при 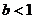 ряд
ряд  сходится, а
при
сходится, а
при 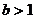 -
расходится.
-
расходится.
Доказательство. Положим сначала 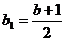 и допустим,
что
и допустим,
что 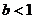 . Тогда при
некотором
. Тогда при
некотором 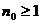 имеем
имеем
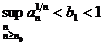 .
.
Поэтому по первому случаю признака
Коши ряд  сходится.
сходится.
Если же 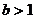 , то при
всех
, то при
всех 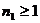 имеем
оценку
имеем
оценку
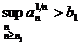 .
.
Это означает существование бесконечного
множества значений 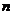 , для
которых справедливо неравенство
, для
которых справедливо неравенство 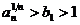 . Следовательно, ряд
. Следовательно, ряд  расходится
по второму случаю признака Коши. Теорема доказана.[1].
расходится
по второму случаю признака Коши. Теорема доказана.[1].
Признак Коши, как и признак
Даламбера, является довольно грубым. Он, например, тоже не позволят решить
вопрос о сходимости рядов 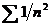 и
и 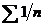 .
.
Теорема 9 (интегральный признак Коши
- Маклорена). Пусть функция 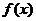 определена на промежутке
определена на промежутке 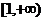 и
и 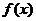 убывает на
нем. Тогда:
убывает на
нем. Тогда:
. если 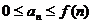 при всех
при всех 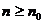 и
несобственный интеграл
и
несобственный интеграл 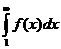 сходится,
то ряд
сходится,
то ряд  тоже
сходится;
тоже
сходится;
. если 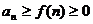 при всех
при всех 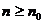 и
несобственный интеграл
и
несобственный интеграл 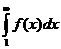 расходится,
то расходится и ряд
расходится,
то расходится и ряд  .
.
Доказательство. Как и выше, без
ограничения общности будем считать, что 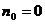 . Далее, поскольку
. Далее, поскольку 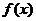 монотонно
убывает, при всяком натуральном
монотонно
убывает, при всяком натуральном 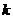 и
и 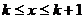 имеем
имеем
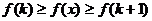 .
.
Интегрируя это неравенство по
указанному промежутку, получим
При всяком 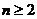 просуммируем
эти неравенства по
просуммируем
эти неравенства по 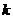 от 1 до
от 1 до 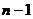 . Получим
. Получим
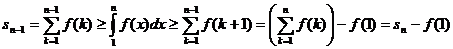 .
.
Далее каждый из двух случаев будем
рассматривать отдельно.
. В этом случае интеграл 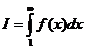 сходится,
поэтому при всех
сходится,
поэтому при всех  для
частичных сумм
для
частичных сумм 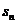 ряда
ряда 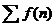 имеет место
единообразная оценка вида
имеет место
единообразная оценка вида 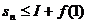 , и
поскольку
, и
поскольку 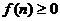 для всех
натуральных
для всех
натуральных 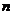 , ряд
, ряд 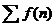 сходится, а
вместе с ним сходится и мажорируемый им ряд
сходится, а
вместе с ним сходится и мажорируемый им ряд  , что и требовалось доказать.
, что и требовалось доказать.
. Поскольку в этом случае
интеграл 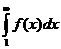 расходится,
расходится,
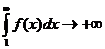 при
при 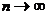 . Но так как
. Но так как
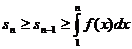 ,
,
то и 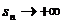 при
при 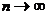 . А это означает, что ряд
. А это означает, что ряд 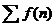 расходится
вместе с рядом
расходится
вместе с рядом  , для
которого первый ряд по условию является минорантой. Теорема доказана.[1], [2].
, для
которого первый ряд по условию является минорантой. Теорема доказана.[1], [2].
Геометрическая интерпретация
интегрального признака
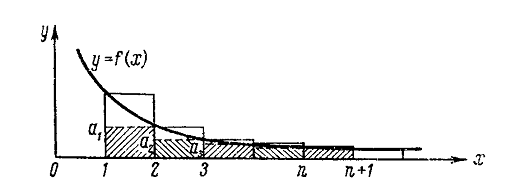
Рис.
Интегральный признак допускает
простое геометрическое истолкование. Если изобразить функцию 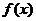 кривой
(рис. 1), то интеграл
кривой
(рис. 1), то интеграл 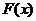 выражать
площадь фигуры, ограниченной этой кривой, осью
выражать
площадь фигуры, ограниченной этой кривой, осью 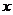 и двумя ординатами; интеграл же
и двумя ординатами; интеграл же 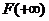 , в
некотором смысле, можно рассматривать для площади всей бесконечно
простирающейся направо фигуры под кривой. С другой же стороны, члены
, в
некотором смысле, можно рассматривать для площади всей бесконечно
простирающейся направо фигуры под кривой. С другой же стороны, члены 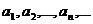 ряда
ряда  выражают
величины ординат в точках
выражают
величины ординат в точках 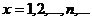 или, что то
же, площади прямоугольников с основаниями 1 и с высотами, равными упомянутым
ординатам.
или, что то
же, площади прямоугольников с основаниями 1 и с высотами, равными упомянутым
ординатам.
Таким образом, сумма ряда  есть не что
иное, как сумма площадей, выходящих прямоугольников, и лишь первым членом
отличается от суммы площадей входящих прямоугольников. Это делает наглядным
установленный выше результат: если площадь криволинейной фигуры конечна, то и
подавно конечна площадь заключенной в ней ступенчатой фигуры. И предположенный
ряд сходится; если же площадь криволинейной фигуры бесконечна, то бесконечна и
площадь содержащей ее ступенчатой фигуры, так что в этом случае ряд расходится
[2], [5].
есть не что
иное, как сумма площадей, выходящих прямоугольников, и лишь первым членом
отличается от суммы площадей входящих прямоугольников. Это делает наглядным
установленный выше результат: если площадь криволинейной фигуры конечна, то и
подавно конечна площадь заключенной в ней ступенчатой фигуры. И предположенный
ряд сходится; если же площадь криволинейной фигуры бесконечна, то бесконечна и
площадь содержащей ее ступенчатой фигуры, так что в этом случае ряд расходится
[2], [5].
Литература
.Архипов
Г. И. Лекции по математическому анализу. - М.: Высш. шк., 1999, 347-366с.
.Фихтенгольц
Г. М. Курс дифференциального исчисления. Том 2. - М.: Лань,2002 ,11-32c.
.Запорожец
Г. И. Руководство к решению задач по математическому анализу. - М.: Высш. шк.
1966. 342с.
.Харди
Г. Х. Курс чистой математики. - М.: Гос. изд. иностр. лит.1949. 341 с.
.Кудрявцев
Л. Д. Курс математического анализа. Том 2. - М.: Высш. шк.,1988.25-27с.