Решение систем уравнений

Решение систем уравнений

Задача 1

Найти базисное решение для системы уравнений (одна из свободных

переменных - х₄.

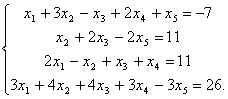
уравнение линия кривая вероятность вектор объём

Решение

Запишем расширенную матрицу системы и преобразуем ее.

.

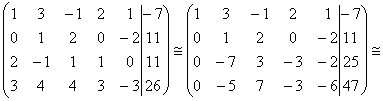
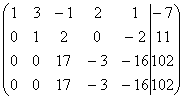
Ранг этой матрицы равен 3, следовательно, одно из уравнений системы можно отбросить, например, четвертое.

.

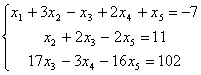Пусть х₄ и х₅ - свободные переменные. Выясним, могут ли переменные х₁, х₂, х₃ быть основными. Найдем определитель матрицы из коэффициентов при этих переменных, т.е. базисный минор:

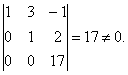
Значит переменные х₁, х₂, х₃ могут быть базисными, а х₄ и х₅ свободными. Приравняем свободные переменные к нулю, т.е. х₄ = х₅ = 0, получим систему уравнений в виде:

, .

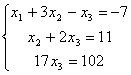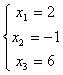Тогда базисное решение (2; -1; 6; 0; 0).

Ответ: (2; -1; 6; 0; 0).

Задача 2

Составить уравнение линии, для каждой точки которой ее расстояние до точки А(2;-1) равно расстоянию до прямой у = 1. Полученное уравнение привести к каноническому виду и построить кривую.

Решение

Пусть М(х;у) - текущая точка искомого геометрического места точек. Опустим перпендикуляр МВ на прямую у = 1. Тогда В(х;1). По условию задачи МА = МВ

 ;  ;

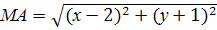
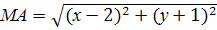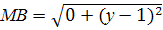
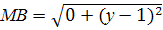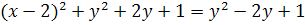
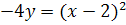
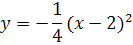
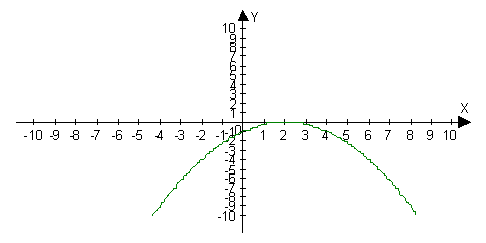
Полученное уравнение представляет параболу вида

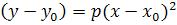
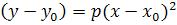
, где 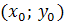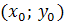- вершина параболы, р - параметр параболы. Парабола имеет вершину в точке (2; 0), ветви направлены вверх.

Задача 3

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей

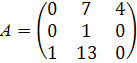
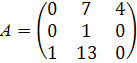
Решение

Составим характеристическое уравнение матрицы А

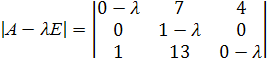
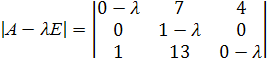=0 или

 .

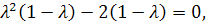
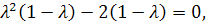
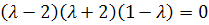
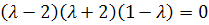Откуда собственные значения линейного оператора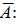

.

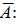
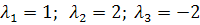
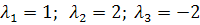Найдем собственный вектор 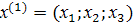 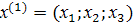соответствующий собственному значению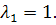

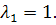
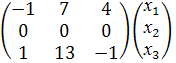
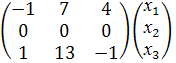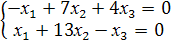
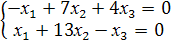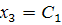
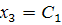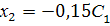
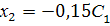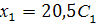
= 0, откуда находим . Пусть , тогда  , , 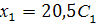т.е. .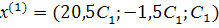

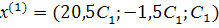Аналогично для 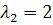 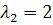найдем

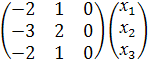
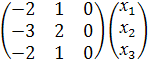 = 0 откуда .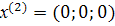

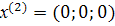Аналогично для 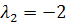 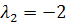найдем

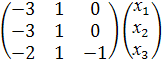
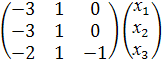 = 0 откуда .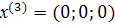

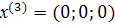Задача 4

Из квадратного листа картона со стороной а вырезаются по углам одинаковые квадраты, а из остальной части склеивается прямоугольная коробка. Какова должна быть сторона вырезаемых квадратов, чтобы объем коробки был наибольшим?

Решение

Площадь основания коробки

.

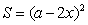Высота Н = х.

Объем коробки

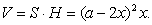 Исследуем эту функцию.

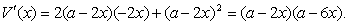
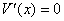
при .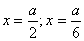

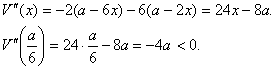
В точке 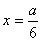функция имеет максимум. Из условия задачи видно, что значение 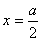 для данной задачи не имеет смысла. Следовательно, при 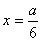 объем коробки будет наибольшим

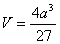
Ответ: ,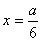

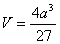
Задача 5

Вычислить предел функции по правилу Лопиталя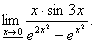

Решение

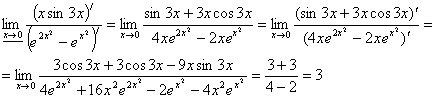
Ответ: 3

Задача 6

Исследовать функцию и построить ее график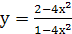

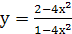
Решение

1)      Область определения функции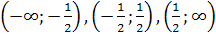

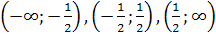
)        Функция четная

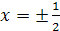
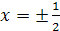)        - вертикальные асимптоты функции

)        Исследуем поведение функции в бесконечности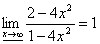

значит у=1 горизонтальная асимптота графика функции, других асимптот график функции не имеет

)        Найдем экстремумы функции и интервалы монотонности. Найдем

Поскольку при 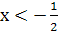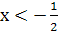у΄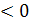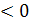, функция на этом интервале убывает,

при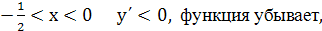

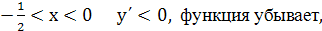
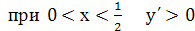
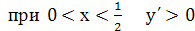, функция возрастает и х = 0 точка минимума,

при .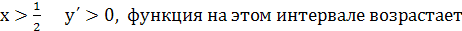

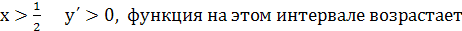6)      Найдем интервалы выпуклости и точки перегиба. Для этого найдем

 =.

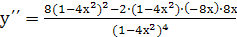
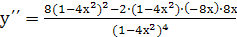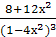
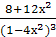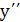
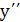 не обращается в нуль ни при каких х, т.е точек перегиба функция не имеет. Очевидно, что 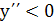 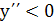на интервалах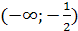 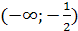и (;2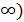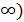, и на этих интервалах функция выпукла вверх, 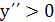 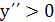на интервале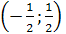 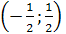 и на этом интервале функция выпукла вниз.

7)      Строим график функции

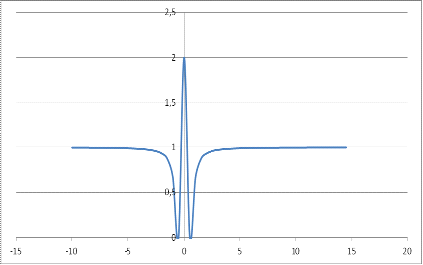
Задача 7

Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями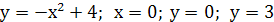

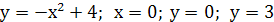
Решение

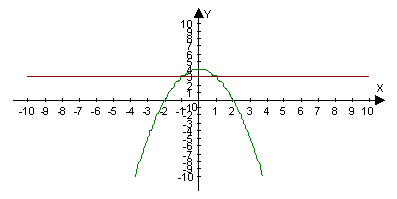
Построим фигуру, ограниченную заданными линиями. Искомый объем найдем по формуле

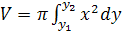
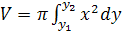
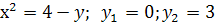
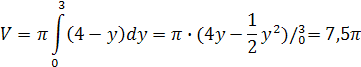
Ответ: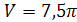

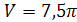
Задача 8

Найти область сходимости степенного ряда .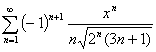

Решение

Для решения данной задачи применим признак Даламбера: :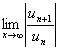

.

.

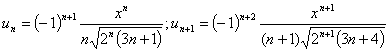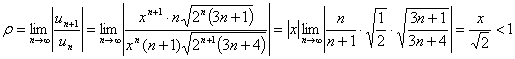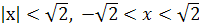
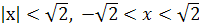. Граничные точки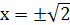 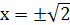 исследуем особо.

При 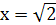 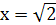получим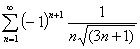

Согласно признаку Лейбница, знакочередующийся ряд сходится, т.к. его члены убывают по абсолютному значению и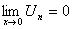

При 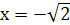 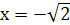получим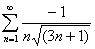

Применим предельный признак сравнения, сравнив ряд из абсолютных величин данного ряда со сходящимся гармоническим рядом ,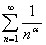

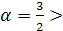
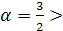 и так как предел отношения общих членов двух рядов

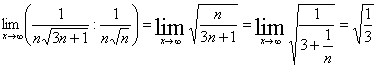 есть конечное число,

не равное нулю, то данный ряд сходится.

Ответ: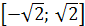

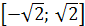
Задача 9

Из партии телевизоров, состоящей из 20 штук, из которых 5 неисправных, случайным образом отбираются для проверки 3 телевизора. Найти вероятность того, что, в число отобранных, войдут только исправные телевизоры.

Решение

Пусть событие А - отобраны три исправных телевизора. Общее число способов, которыми можно выбрать 3 телевизора из 20 равно: .

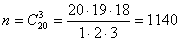Три исправных телевизора из 15 исправных можно выбрать 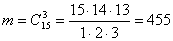способами.

Искомая вероятность Р(А) = .

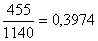Ответ: Р = 0,3974.

Задача 10

Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго 0,6. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, сто в мишень попал второй стрелок.

Решение

Пусть событие А - мишень поражена. Можно сделать два предположения: В₁ - мишень поразил первый стрелок, B₂ - мишень поразил второй стрелок. Так как мишень поражена, то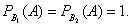  

;

.

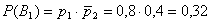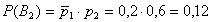
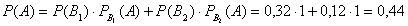Искомая вероятность того, что мишень поражена вторым стрелком, по формуле Бейеса равна

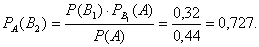
Ответ: Р = 0,727