Решение систем линейных уравнений
Федеральное
агентство связи
Сибирский
Государственный Университет Телекоммуникаций и Информатики
Контрольная
работа
По
дисциплине: Линейная алгебра
Новосибирск,
2014г
1. Формулы Крамера для решения систем линейных уравнений
Система линейных уравнений порядка n имеет вид:
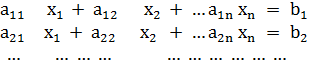
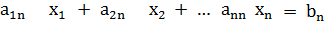
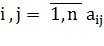 При этом числа -называются коэффициентами при неизвестных
При этом числа -называются коэффициентами при неизвестных
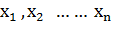
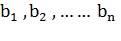 -свободные члены
-свободные члены
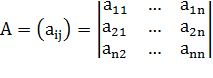
Матрица называется матрицей системы
Числа 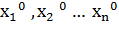 - решение системы если
- решение системы если
при подстановке этих чисел в систему каждое из уравнений системы
превращается в верное числовое тождество.
Система линейных уравнений называется совместной, если она имеет по
крайней мере одно решение.
Если система линейных уравнений не имеет решений, то система называется
несовместной.
Формулы Крамера. Рассмотрим систему уравнений (*). И пусть А- матрица
системы

Если i -столбец заменим свободными членами , то соответствующую матрицу
обозначим
Если система линейных уравнений (*) такова, что определитель системы
отличен от нуля, то система линейных уравнений имеет единственное решение ,
которое находится по формуле:
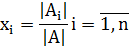
2. Найти проекцию точки М0 (-8;12) на прямую, проходящую
через точки А (2;-3), В(-5; 1)
Решение:
Напишем уравнение прямой проходящий через точки А(2;-3) и В (-5; 1)
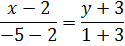
Или
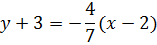
Отметим что угловой коэффициент равен 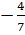 . Поэтому у прямой, которая
перпендикулярна данной, угловой коэффициент будет равен
. Поэтому у прямой, которая
перпендикулярна данной, угловой коэффициент будет равен  , и уравнение этого перпендикуляра ,
проходящего через точку М0 (-8;12) имеет вид:
, и уравнение этого перпендикуляра ,
проходящего через точку М0 (-8;12) имеет вид:
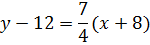
Осталось найти точку пересечения перпендикуляра и исходной прямой. Так
найдем нужную проекцию. Другими словами надо решить систему уравнений:
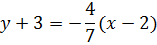
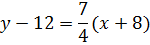
Слегка преобразив получим:
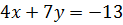
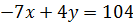
Выразив одну переменную через другую из первого уравнения и подставив это
выражение во второе уравнение, найдем сначала одно, а потом и второе .
Ответ: х=-12; y=5.
. Исследовать и найти решение системы
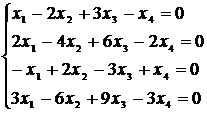
точка
линейный уравнение матричный
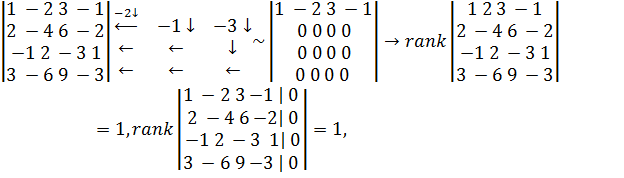
Т.к. добавление столбца из нулей 9 свободных членов) не может повысить
ранг матрицы. Ранг расширенной матрицы равен рангу матрицы, но меньше числа
неизвестных (4=4, 1<4) следовательно (согласно теоремы Кронекера-Капелли)
система совместна и имеет бесконечное множество решений, в том числе и нулевое
решение: (0,0,0,0).
Общее решение системы имеет вид:
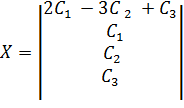
Базисные решения:
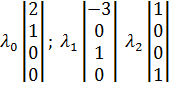
Фундаментальная система решений
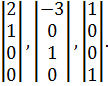
Ответ:
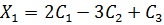
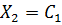
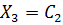
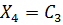
Примечание: Решить методом Крамера и методом обратной матрицы нельзя,
т.к. необходимо чтобы 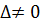 (а у данной матрицы
(а у данной матрицы 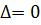 ).
).