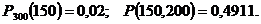Решение систем линейных уравнений. Теория вероятности
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РФ
ОМСКИЙ
ИНСТИТУТ (ФИЛИАЛ) РОССИЙСКОГО
ГОСУДАРСТВЕННОГО
ТОРГОВО-ЭКОНОМИЧЕСКОГО УНИВЕРСИТЕТА
Контрольная
работа по дисциплине «Математика»
Вариант
6
Омск,
2011 г.
ЗАДАЧА 1
уравнение матрица квадратическое
отклонение
В декартовой прямоугольной системе координат
даны вершины пирамиды А1В1С1D1. Найдите:
а) длину ребра А1В1;
б) косинус угла между векторами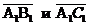 ;
;
в) уравнение ребра А1В1;
г) уравнение грани А1В1С1;
д) уравнение высоты, опущенной из
вершины D1 на грань А1В1С1;
е) координаты векторов 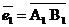 ,
, 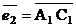 ,
, 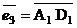 , и
докажите, что они образуют линейно независимую систему;
, и
докажите, что они образуют линейно независимую систему;
ж) координаты вектора 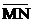 , где
, где 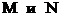 - середины
ребер А1D1 и В1С1, соответственно;
- середины
ребер А1D1 и В1С1, соответственно;
з) разложение вектора 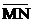 по базису
по базису 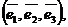
если A1(3, 0, -1), B1(-1, -2, -4),
C1(-1, 2, 4), D1(7, -3, 1).
Решение.
а) найдем координаты вектора 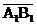 по формуле:
по формуле:
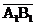 =
=  XВ
XВ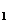 - XА
- XА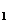 ; YВ
; YВ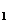 - YА
- YА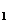 ; ZВ
; ZВ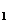 - ZА
- ZА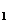
 , где (ХА
, где (ХА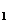 , YА
, YА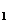 , ZА
, ZА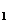 ) -
координаты точки А1, (ХВ
) -
координаты точки А1, (ХВ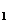 , YВ
, YВ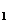 , ZВ
, ZВ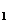 ) -
координаты точки В1.
) -
координаты точки В1.
Итак, 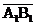 =
= 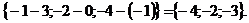
Тогда 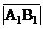 =
= 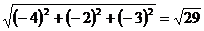 .
.
Итак, длина отрезка 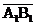 (или длина
вектора
(или длина
вектора 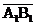 ) равна
) равна 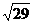 . Это и есть
искомая длина ребра.
. Это и есть
искомая длина ребра.
б) координаты вектора 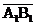 =
= 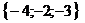 уже
известны, осталось определить координаты вектора
уже
известны, осталось определить координаты вектора 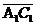 :
: 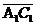 =
=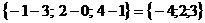 .
.
Угол между векторами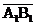 и
и 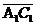 вычислим по
формуле:
вычислим по
формуле: =
=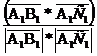 ,
,
где скалярное произведение векторов 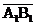 и
и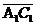 равно
равно
(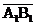 ,
,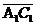 )=(-4)´(-4)+(-2)´2+(-3)´3=16+(-4)+(-9)=16-4-9=3,
)=(-4)´(-4)+(-2)´2+(-3)´3=16+(-4)+(-9)=16-4-9=3,
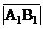 =
=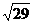 ,
, 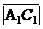 =
= 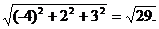
Итак, cos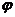 =
=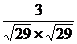 =
=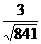 .
.
в) координаты точки А1(3,0,-1)
обозначим соответственно Х0 = 3, У0 = 0, Z0=-1, а координаты точки В1
(-1,-2,-4) через Х1=-1, У1 = -2, Z1=-4 и воспользуемся уравнением прямой в
пространстве, проходящей через две точки:
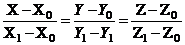 .
.
Следовательно, уравнение ребра А1В1
имеет вид
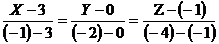 или
или 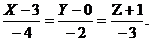
г) обозначим координаты векторов 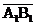 и
и 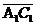 через
Х1=-4,У1= -2,
через
Х1=-4,У1= -2, 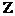 1=-3 и
Х2=-4, У2=2,
1=-3 и
Х2=-4, У2=2, 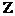 2=3,
соответственно. Векторное произведение данных векторов определяется формулой
2=3,
соответственно. Векторное произведение данных векторов определяется формулой
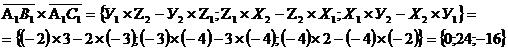
Так как данный вектор
перпендикулярен грани А1 В1 С1, то можно воспользоваться уравнением плоскости,
проходящей через точку (Х0, У0, 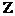 0) перпендикулярно вектору
0) перпендикулярно вектору 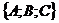 , которое
имеет вид:
, которое
имеет вид:
А 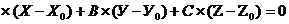 .
.
Подставим координаты точки А1 (Х0=3,
У0=0, 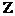 0=-1) и
координаты перпендикулярного вектора А=0, В=24, С=-16 в это уравнение:
0=-1) и
координаты перпендикулярного вектора А=0, В=24, С=-16 в это уравнение:
(Х-3)+24(У-0)-16(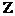 +16) = 0.
Раскроем скобки и приведем подобные члены 24Y-16Z-256=0. Итак, уравнение грани
А1 В1 С1 имеет вид:
+16) = 0.
Раскроем скобки и приведем подобные члены 24Y-16Z-256=0. Итак, уравнение грани
А1 В1 С1 имеет вид:
Y-16Z-256=0 или 3Y-2Z-32=0.
д) вектор 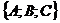 является
направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1.
Воспользуемся уравнением прямой в пространстве, проходящей через точку
является
направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1.
Воспользуемся уравнением прямой в пространстве, проходящей через точку 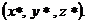 с заданным
направляющим вектором:
с заданным
направляющим вектором: 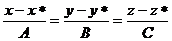 , где
, где 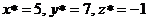 -
координаты точки D1. Отсюда искомое уравнение:
-
координаты точки D1. Отсюда искомое уравнение: 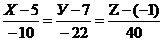 или
или 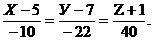
е) координаты вектора 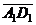 =
=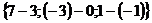 =
=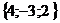 .
.
Обозначим 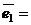
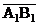 =
=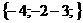 ,
,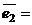
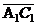 =
=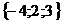 ,
, 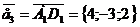 .
.
Чтобы доказать, что векторы 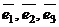 образуют
линейно независимую систему векторов необходимо убедиться, что определитель
третьего порядка, составленный из координат этих векторов,
образуют
линейно независимую систему векторов необходимо убедиться, что определитель
третьего порядка, составленный из координат этих векторов,
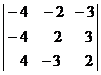 отличен от 0. Определитель третьего
порядка равен
отличен от 0. Определитель третьего
порядка равен
 =
=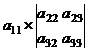 -
- 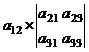 +
+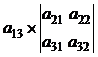 =
=
=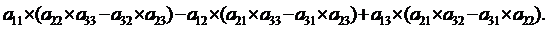
Вычислим определитель
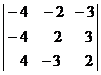 =-4
=-4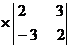 - (-2)
- (-2)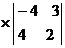 +(-3)
+(-3)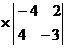 =
=
=-4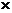 (2*2 -
(2*2 - )+2
)+2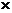 (2
(2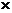 (-4) -4
(-4) -4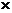 3) -3
3) -3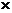 ((-4)
((-4)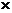 (-3) -4
(-3) -4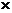 2) =
2) =
=-4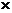 13+2
13+2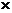 (-20) - 3
(-20) - 3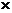 4=-52 - 40-
12 = -104.
4=-52 - 40-
12 = -104.
Так как данный определитель отличен
от 0, то вектора 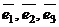 образуют
линейно независимую систему.
образуют
линейно независимую систему.
ж) сначала найдем координаты точек М
и N, соответственно. Координаты точки
М =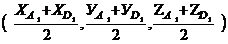 =
= 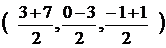 =
= 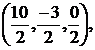 =
=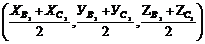 =
=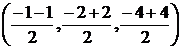 =
=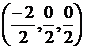 .
.
Получаем вектор 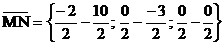 =
=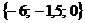 .
.
з) обозначим через 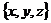 координаты
вектора
координаты
вектора  в базе
в базе 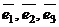 .
.
Тогда  =
=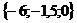 =
= 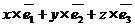 .
.
Так как: 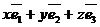 =
=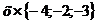 +
+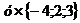 +
+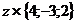 =
=
=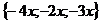 +
+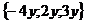 +
+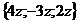 =
=
=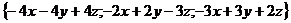 ,
,
то приравнивая соответствующие координаты,
получим систему трех линейных уравнений с тремя неизвестными:
(1)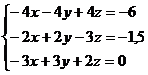
Решим данную систему уравнений с
помощью формул Крамера. Рассмотрим произвольную систему трех линейных уравнений
с тремя неизвестными:
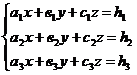
Тогда 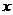 =
=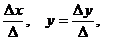 z
z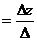 , где:
, где:
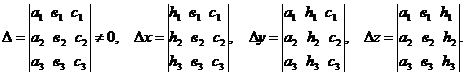
Для системы (1) определитель:
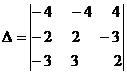 =(-4)
=(-4)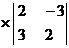 -(-4)
-(-4)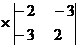 +4
+4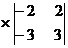 =
=
=(-4)*13+4*(-13)+4*0=-52-52+0=-104;
=(-6)*13+4*(-3)+4*(-4.5)=-78-12-18=-108;
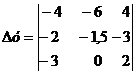 =(-4)
=(-4)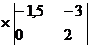 - (-6)
- (-6) +4
+4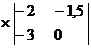 =
=
=(-4)*
(-3)+6*(-13)+4*(-4.5)=12-78-18=-84;
 =(-4)
=(-4)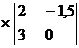 - (-4)
- (-4) + (-6)
+ (-6)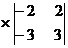 =
=
=(-4)*4.5+4*(-4.5)-6*0=-18-18-0=-36.
По формулам Крамера 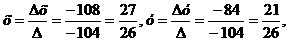
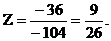
Итак, разложение вектора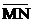 по базису (
по базису (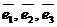 ) имеет вид
) имеет вид
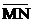 =
= 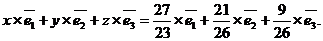
ЗАДАЧА 2
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
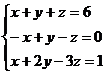
Решение.
а) Метод Крамера состоит в решении
системы линейных уравнений по формулам Крамера 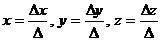 ,
,
где 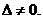 (Подробности смотрите в пункте з)
задачи 1.
(Подробности смотрите в пункте з)
задачи 1.
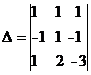 =1
=1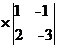 -1
-1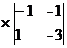 +1
+1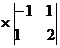 =1*(-3+2)-1(3+1)+1(-2-1)=
=1*(-3+2)-1(3+1)+1(-2-1)=
=1*(-1)-1*4+1(-3)=-1-4-3=-8
 =6
=6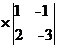 -1
-1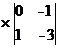 +1
+1 =6*(-3+2)-1(0+1)+1(0-1)=
=6*(-3+2)-1(0+1)+1(0-1)=
=6*(-1)-1*1+1(-1)=-6-1-1=-8
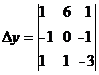 =1
=1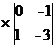 -6
-6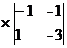 +1
+1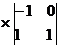 =1*(0+1)-6(3+1)+1(-1-0)=
=1*(0+1)-6(3+1)+1(-1-0)=
=1*1-6*4+1(-1)=1-24-1=-24
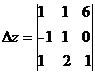 =1
=1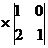 -1
-1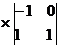 +6
+6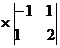 =1*(1-2)-1(-1-1)+6(-2-1)=
=1*(1-2)-1(-1-1)+6(-2-1)=
=1*(-1)-1*(-2)+6(-3)=-1+2-18=-17
Так как 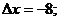
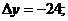
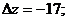
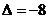 ; то
; то 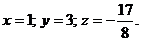
Ответ: 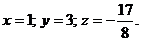
б) Найдем определитель главной
матрицы, составленной из коэффициентов при X1 - n:
|
1
1 1 -1 1 -1 1 2 -3
|
=
-8
|
|
Определитель главной матрицы системы уравнений
не равен нулю, следовательно данная система уравнений имеет единственное
решение. Найдем его.
Достроим главный определитель системы уравнений
еще одним столбцом, в который вставим значения за знаком равенства.
|
1
1 1 6 -1 1 -1 0 1 2 -3 1
|
|
Теперь последовательно, при помощи элементарных
преобразований преобразуем левую часть матрицы (3 ×
3) до
треугольного вида (обнулим все коэффициенты находящиеся не на главной
диагонали, а коэффициенты на главной диагонали преобразуем до единиц).
Вычтем 1 - ую строку из всех строк, которые
находятся ниже нее. Это действие не противоречит элементарным преобразованиям
матрицы.
|
1
1 1 6 0 2 0 6 0 1 -4 -5
|
|
|
Вычтем 2 - ую строку из всех строк, которые
находятся ниже нее. Это действие не противоречит элементарным преобразованиям
матрицы.
|
1
1 1 6 0 2 0 6 0 0 -4 -8
|
|
|
Вычтем 3 - ую строку из всех строк, которые
находятся выше нее. Это действие не противоречит элементарным преобразованиям
матрицы.
|
1
1 0 4 0 2 0 6 0 0 -4 -8
|
|
|
Вычтем 2 - ую строку из всех строк, которые
находятся выше нее. Это действие не противоречит элементарным преобразованиям
матрицы.
|
1
0 0 1 0 2 0 6 0 0 -4 -8
|
|
|
Приведем все коэффициенты на главной диагонали
матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки
находящийся на главной диагонали, если он не равен 1.
|
Числа
получившиеся правее единичной матрицы и будут решением системы уравнений.
Ответ: X=1; Y=3; Z=2.
|
в) решение системы в этом случае
равно 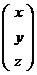 =
=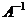
 , где
, где 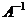 =
= 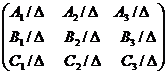 - обратная матрица для матрицы
- обратная матрица для матрицы 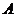 =
=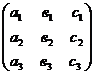 ,
, 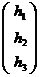 - столбец
свободных членов,
- столбец
свободных членов, 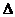 -
определитель этой матрицы.
-
определитель этой матрицы.
Составим матрицу состоящую из
коэффициентов при неизвестных данной системы:
А = 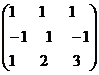 .
.
Вычислим ее определитель
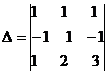 =1
=1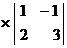 -1
-1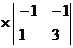 +1
+1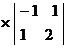 =
=
=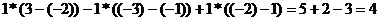 .
.
Вычислим алгебраические дополнения
для всех элементов матрицы А:
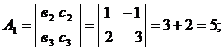
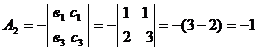
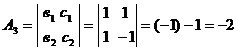
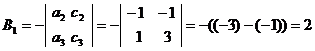
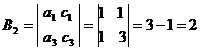
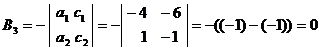
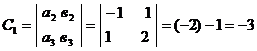
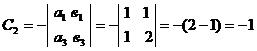
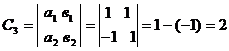
Тогда
 =
=  и
и 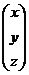 =
=
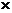
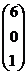 =
=
=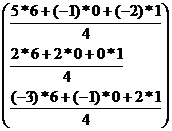 =
= =
= 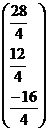 =
=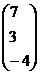 .
.
Ответ: 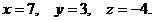
ЗАДАЧА 3
В ящике 18 одинаковых бутылок пива
без этикеток. Известно, что треть из них «Жигулевское». Случайным образом
выбирают 3 бутылки. Вычислите вероятность того, что среди них :
а) только пиво сорта «Жигулевское»;
б) ровно одна бутылка этого сорта.
Решение. Общее число возможных
элементарных исходов для данных испытаний равно числу способов, которыми можно
извлечь 3 бутылки Жигулевского из 18 бутылок, то есть 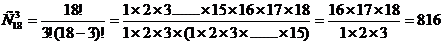 - число
сочетаний из 18 элементов по 3.
- число
сочетаний из 18 элементов по 3.
а) подсчитаем число исходов,
благоприятствующих интересующему нас событию. Это число исходов ровно числу
способов, которыми можно извлечь 3 бутылки Жигулевского из 12 бутылок, то есть
искомая вероятность равна отношению
числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
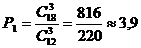
б) подсчитаем число исходов,
благоприятствующих данному событию: две бутылки Жигулевского можно выбрать из
18 бутылок: 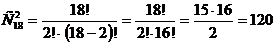 способами,
при этом одну бутылку нужно выбирать из четырех:
способами,
при этом одну бутылку нужно выбирать из четырех: 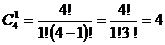 способами. Следовательно, число
благоприятствующих исходов равно
способами. Следовательно, число
благоприятствующих исходов равно 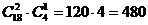
Искомая вероятность равна отношению
числа исходов, благоприятствующих данному событию, к числу всех элементарных
исходов
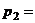
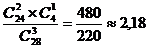 .
.
Ответ: а) 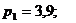 б)
б) 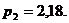
ЗАДАЧА 4
В двух одинаковых коробках находятся
карандаши «Конструктор». Известно, что ⅓ карандашей в первой коробке и ¼ во второй
имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один
карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен
из первой коробки?
Решение: Обозначим через А событие -
«карандаш имеет твердость ТМ». Возможны следующие гипотезы о происхождении
этого карандаша: 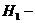 «карандаш
из первой коробки»,
«карандаш
из первой коробки», 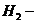 «карандаш
из второй коробки». Так как доля первой коробки составляет ⅓, то
вероятности этих гипотез равны соответственно:
«карандаш
из второй коробки». Так как доля первой коробки составляет ⅓, то
вероятности этих гипотез равны соответственно: 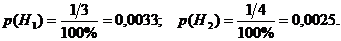
Искомую вероятность того, что взяли
карандаш с твердостью ТМ, находим по формуле полной вероятности:
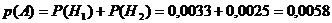 .
.
Ответ: 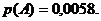
ЗАДАЧА 5
Задан закон распределения дискретной
случайной величины X:
|
X
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
p
|
0,16
|
0,25
|
0,25
|
0,16
|
0,10
|
p
|
0,03
|
Найдите:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и
среднее квадратическое отклонение s данной случайной
величины;
в) функцию распределения F(x) и построить её
график;
г) закон распределения случайной величины Y,
если её значения заданы функциональной зависимостью y = 4½x½
- 1.
Решение:
а) так как сумма всех вероятностей
должна равняться единице, то получим уравнение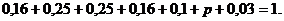
Отсюда 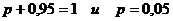 ;
;
б) математическое ожидание М это
сумма всех произведений значений случайной величины на их вероятности:
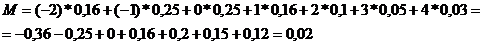
Дисперсия D=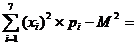
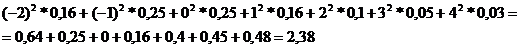
Среднее квадратическое отклонение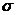 =
=  ;
;
в) если 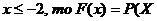 <
<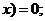
если - 2<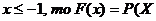 <
<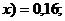
если - 1<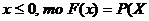 <
<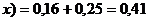
если 0<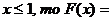 0,41+0,25=0,66
0,41+0,25=0,66
если 1<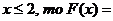 0,66+0,16=0,82
0,66+0,16=0,82
если 2<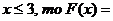 0,82+0,10=0,92
0,82+0,10=0,92
если 3<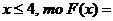 0,92+0,05=0,97
0,92+0,05=0,97
если х >4, то F(x)=Р( Х < х )=0,97+0,03=1
Итак, функция распределения может
быть записана так: (x) = 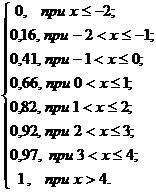
График этой функции приведен на
рисунке:
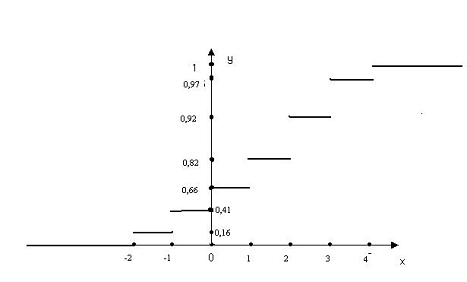
г) сначала найдем значения случайной
величины Y.
По условиям задачи 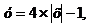
Поэтому
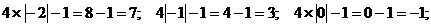
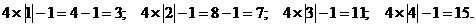
Составим таблицу вида.
|
Y
|
7
|
3
|
-1
|
3
|
7
|
11
|
15
|
|
P
|
0,25
|
0,25
|
0,16
|
0,10
|
0,05
|
0,03
|
Чтобы получить закон распределения случайной
величины Y, необходимо:
) рассмотреть ее значение в порядке возрастания;
) сложить вероятности, соответствующие
совпадающим значениям данной таблицы.
Итак, закон распределения случайной величины Y :
|
Y
|
-1
|
3
|
7
|
11
|
15
|
|
Р
|
0,12
|
0,41
|
0,26
|
0,14
|
0,04
|
ЗАДАЧА 6
Известно, что вероятность рождения мальчика
равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных
окажется:
а) 150 мальчиков;
б) от 150 до 200 мальчиков?
Решение:
а) воспользуемся локальной теоремой
Лапласа. Вероятность того, что в n =300 испытаниях, в каждом из которых
вероятность появления события равна 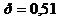 равна к=150 раз (безразлично, в
какой последовательности) приближенно равна
равна к=150 раз (безразлично, в
какой последовательности) приближенно равна
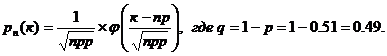
Так как 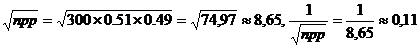
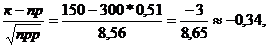 то
то 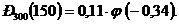
Значение функции  находим в
таблице Брадиса:
находим в
таблице Брадиса: 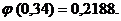
Итак, 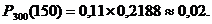
Отметим, что таблица функции 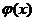 приведена
только для положительных значений. Если же значение
приведена
только для положительных значений. Если же значение 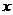 получилось
отрицательным, то знак минус можно просто опустить в силу четности функции
получилось
отрицательным, то знак минус можно просто опустить в силу четности функции 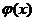 ;
;
б) воспользуемся интегральной
теоремой Лапласа. Вероятность того, что в n =300 независимых испытаниях событие
наступит от К1=150 до К2 =200 раз приближенно равна:
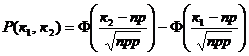
Так как 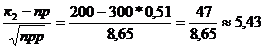 ,
,
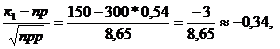 то
то 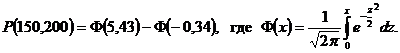
Значение функции 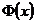 также
находим в специальной таблице Брадиса. В таблице
также
находим в специальной таблице Брадиса. В таблице 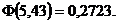 Для отрицательных значений х
используют эту же таблицу, учитывая, что
Для отрицательных значений х
используют эту же таблицу, учитывая, что 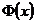 является нечетной функцией, то есть
является нечетной функцией, то есть 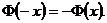 Итак,
Итак,  . Отсюда
. Отсюда 
Ответ: