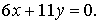Решение систем уравнений
Задание 1.
Проверить совместность системы
уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы
(матричным методом);
в) методом Гаусса.
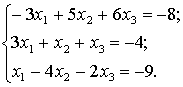
Совместность данной
системы проверим по теореме Кронекера-Капелли. С помощью элементарных
преобразований расширенную матрицу 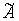 приведем к
трапециевидной форме
приведем к
трапециевидной форме
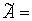

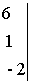
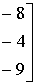 ~
~ 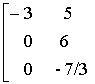
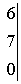
 .
.
Следовательно, 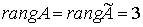 (числу
неизвестных системы). Значит, исходная система совместна и имеет единственное
решение.
(числу
неизвестных системы). Значит, исходная система совместна и имеет единственное
решение.
а) По формулам Крамера: 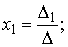
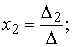
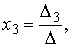 где
где
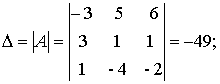
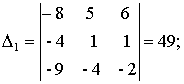
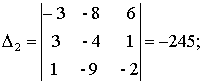
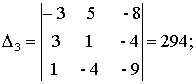 .
.
Находим 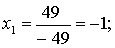
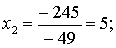
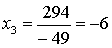 .
.
б) С помощью обратной
матрицы 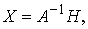 где
где
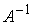 -
обратная матрица к
-
обратная матрица к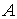 ,
,
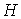 -
столбец правых частей.
-
столбец правых частей.
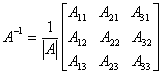 .
.
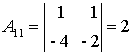 ;
; 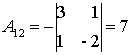 ;
;
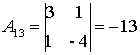 ;
;
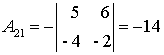 ;
; 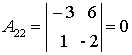 ;
;
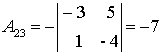 ;
;
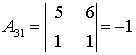 ;
; 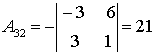 ;
;
 .
.
Решение системы
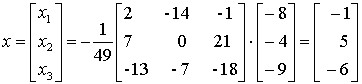 ,
,
т.е. 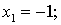
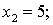
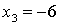 .
.
в) Наша система
эквивалентна
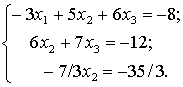
(прямой ход Гаусса
совершен при нахождении рангов матриц 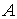 и
и 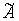 ).
).
Тогда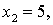
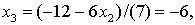
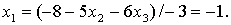
Задание 2.
Решить однородную систему линейных
алгебраических уравнений.
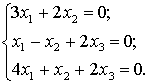
С помощью элементарных
преобразований матрицу 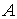 приведем
к трапециевидной форме
приведем
к трапециевидной форме
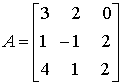 ~
~ 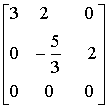 .
.
Следовательно,  2<3
и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной
постоянной. Исходная система эквивалентна
2<3
и система имеет бесконечное множество решений, зависящих от 3-2=1 произвольной
постоянной. Исходная система эквивалентна
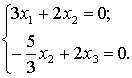
Откуда 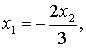
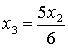 .
.
Полагая 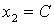 (произвольной
постоянной), имеем
(произвольной
постоянной), имеем
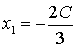 ,
, 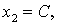
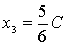 .
.
Задание 3.
По координатам точек 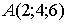 ,
,
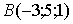 ,
,
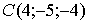 найти:
найти:
а) Модуль вектора 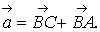
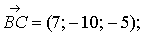
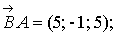
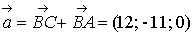 ;
;
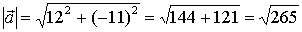 .
.
б) Скалярное
произведение векторов 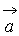 и
и
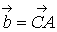 .
.
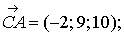
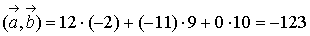 .
.
в) Проекцию вектора 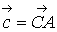 на
вектор
на
вектор 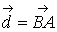 .
.
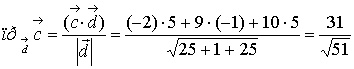 .
.
г) Координаты точки 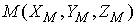 ,
делящей отрезок
,
делящей отрезок 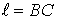 в
отношении 1:3;
в
отношении 1:3; 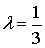 .
Следовательно:
.
Следовательно:
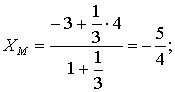
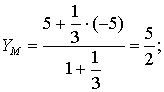
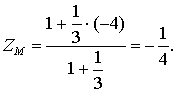
Задание 4.
Даны векторы 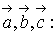
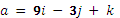
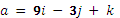 ,
,
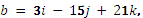
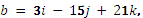 c
= i - 5j + 7k Необходимо:
c
= i - 5j + 7k Необходимо:
а) Найти модуль
векторного произведения 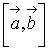 .
.
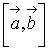 =
=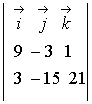
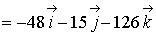 ;
;
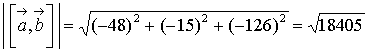 .
.
б) Проверить, будут ли
коллинеарны или ортогональны два вектора 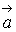 и
и 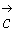 .
.
Условие коллинеарности
двух векторов 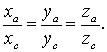
Т.к. 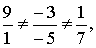 то
вектора
то
вектора 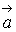 и
и
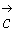 неколлинеарны.
неколлинеарны.
Условие ортогональности
двух векторов 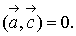
Т.к. 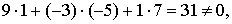 то
вектора неортогональны.
то
вектора неортогональны.
в) Вычислить смешанное
произведение трех векторов
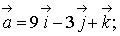
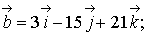
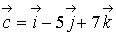 .
.
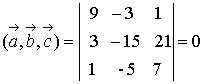 .
.
г) Проверить, будут ли
компланарны три вектора 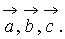
Вектора 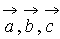 компланарны,
если
компланарны,
если 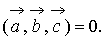
Из пункта в) 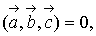 следовательно,
эти векторы компланарны.
следовательно,
эти векторы компланарны.
Задание 5.
Даны четыре точки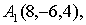
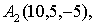
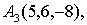
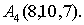
Составить уравнения:
а) Плоскости 
Уравнение плоскости по
трем точкам имеет вид
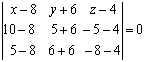 , откуда
, откуда 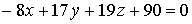 .
.
Уравнение прямой по двум
точкам
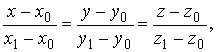 откуда
откуда 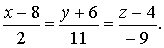
в) Прямой 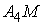 ,
перпендикулярной к плоскости
,
перпендикулярной к плоскости 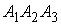 .
.
Из уравнения плоскости 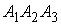 следует,
что вектор
следует,
что вектор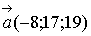 ||
|| откуда уравнение
откуда уравнение 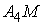 имеет
вид
имеет
вид 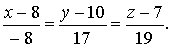
г) Прямой 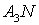 ,
параллельной
,
параллельной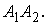 Значит, вектор
Значит, вектор 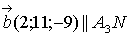 и
уравнение этой прямой имеет вид
и
уравнение этой прямой имеет вид 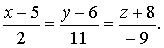
д) Плоскости, проходящей
через точку 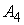 перпендикулярно
к прямой
перпендикулярно
к прямой 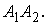
Вектор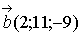 перпендикулярен искомой плоскости.
перпендикулярен искомой плоскости.
Значит, 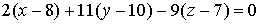 -
ее уравнение, которое приводится к виду
-
ее уравнение, которое приводится к виду 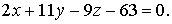
е) Вычислить 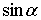 -
угла между прямой
-
угла между прямой 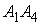 и
плоскостью
и
плоскостью 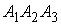 .
.
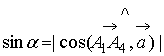 ;
; 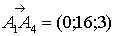 ;
;
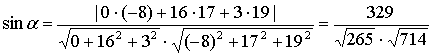 .
.
ж) Косинус угла между
координатной плоскостью 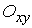 и
плоскостью
и
плоскостью 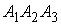 .
.
Вектор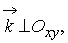 а вектор
а вектор 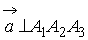 .
Поэтому
.
Поэтому
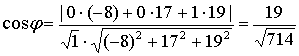 .
.
Задание 6.
Показать, что прямая 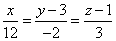 параллельна
плоскости
параллельна
плоскости
х
+ 3у - 2z + 1 = 0, а прямаях = t + 7, у = t
- 2, z = 2t + 1 лежит в этой плоскости.
В общем виде уравнение
плоскости имеет вид 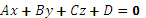
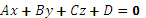 , а каноническое
уравнение прямой:
, а каноническое
уравнение прямой: 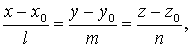
Параметрическое
уравнение прямой:
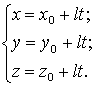
Если прямая параллельна
плоскости, то 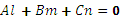
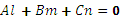
Значит, из условия
задачи, 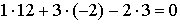 .
Следовательно, прямая параллельна плоскости.
.
Следовательно, прямая параллельна плоскости.
Если прямая лежит в
плоскости, то 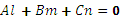
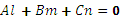 ,
,
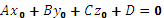
Значит, из условия
задачи, 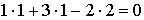 ,
,
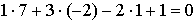 Следовательно,
прямая лежит в плоскости.
Следовательно,
прямая лежит в плоскости.
Задание 7.
Составить уравнение
прямой, проходящей через начало координат и точку пересечения прямых 2х
+ 5у - 8 = 0 и 2х + 3у + 4 = 0.
Найдем точку пересечения
прямых:
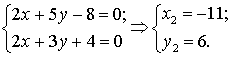
Уравнение прямой,
проходящей через две точки и:
уравнение прямая система вектор
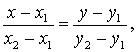
Поэтому ее уравнение
запишем как 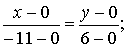 оно
приводится к виду
оно
приводится к виду