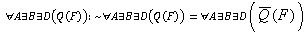|
x1
|
x2
|
x3
|
f (x1,x2,x3)
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
15 . Пусть P1 и P2 обозначают
высказывания:
P1 –эти прямые
перпендикулярны,
P2 –эти прямые имеют
точку пересечения.
Записать, как читаются следующие символические
выражения:
а) Ø P1
б) P1 Ú P2
в) P1 & P2
г) P1 Þ P2
д) P1 Û P2
е) P1 Å P2
Определить истинность выражения, если это возможно.
16. Следующие сложные высказывания расчленить на
простые и записать с помощью математической символики:
а) на улице идет дождь, значит надо взять зонт
б) на каникулы Лена поедет либо в Испанию, либо в
Италию,
в) кот Вася любит есть рыбу и играть в мячик.
17. Связать свободную переменную квантором так, что бы
получить истинное высказывание (предметная область – множество действительных
чисел):
18. Пусть P(x, y) – двухместный предикат «окружность x вписана в треугольник y».
Записать высказывания, определить значения их истинности, построить отрицания
данных высказываний:
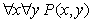
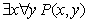
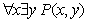
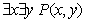 .
.
19. Записать высказывания в предикатной форме,
используя кванторы. Построить отрицания, а затем перевести обратно в
литературное высказывание так, что бы отрицание не начиналось со слов «не» или
«неверно, что»:
В каждом городе хотя бы одна улица застроена только
такими домами, в которых есть однокомнатные квартиры.
РЕШЕНИЕ
1. а) Трапеция - четырехугольник, у
которого одна пара противолежащих сторон параллельна. Параллельные стороны
называются основаниями трапеции, две другие стороны называются боковыми.
Трапеция, у которой боковые стороны равны, называются равнобедренными или
равнобокими. Трапеция, имеющая прямые углы называется прямоугольной.
С
помощью данной математической модели решаются задачи построения крыш домов, где
необходимо знать размер основания, боковых сторон и высоты.
б) Тетрадь
– четырехугольник, у которого все углы прямые и противолежащие стороны попарно
параллельны. Данную модель используют в магазинах канцтоваров. Необходимо знать
количество листов, в клетку или линию, с толстым или тонким переплетом.
2. Инвариантная модель решения задачи:
Дано: матрица А (3,3)
Найти: Ʃ четных чисел S:S+A[I, J] mod2 = 0
Аналитическая модель: Алгоритмическая
модель:
S=S+A[i,j] mod 2=0
Присвоим: S=0;
Задаем цикл:
for i=1 to 3 do
for j=1 to 3
do
If
A[I, J] mod2 = 0,
S=S+A[I, J]
Схемная модель:
3. Перечислением: M = {2, 4, 8, 16,
..., 300} 28 = 256, т.е. больше 300
Порождающей процедурой: а) 2nÎM; б) если nÎN, то 2n; в) n
≤ 8;
Характеристическим свойством
элементов: M = {n:n – целое положительное число, не превышающее 8} или M = {n:nÎN и 2nÎN, n
≤ 8}
4. U = {a1,a2,a3,a4}
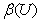 = {Æ, {a1},
{a2}, {a3}, {a4}, {a1,a2},
{a1,a3}, {a1,a4}, {a2,a3},
{a2,a4}, {a3,a4}, {a1,a2,a3},
{a1,a2,a4}, {a2,a3,a4},
{a1,a3,a4}, {a1,a2,a3,a4}}
= {Æ, {a1},
{a2}, {a3}, {a4}, {a1,a2},
{a1,a3}, {a1,a4}, {a2,a3},
{a2,a4}, {a3,a4}, {a1,a2,a3},
{a1,a2,a4}, {a2,a3,a4},
{a1,a3,a4}, {a1,a2,a3,a4}}
|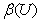 | =24=16
| =24=16
5. U = {1, 2, 3, 4, 5, 6}, A = {1, 3, 4},
B = {2, 3}, C = {1, 4, 6}.
а) A È B = {1,2,3,4};
б) A Ç B = {3};
в) A \ B = {1,4};
г) B \ A = {2};
д)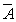 =
U \ A = {2,5,6};
=
U \ A = {2,5,6};
е) 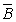 =
U \ B = {1,4,5,6};
=
U \ B = {1,4,5,6};
ж)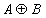 = (A \ B) È (B \ A) = {1,4}È {2}= {1,2,4};
= (A \ B) È (B \ A) = {1,4}È {2}= {1,2,4};
з) 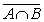 =
U \ (A Ç B) =
{1,2,3,4,5,6} \ {3} = {1,2,4,5,6,};
=
U \ (A Ç B) =
{1,2,3,4,5,6} \ {3} = {1,2,4,5,6,};
и) АÇ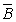 =
A Ç (U \ B) = {1,3,4} Ç {1,4,5,6} = {1,4};
=
A Ç (U \ B) = {1,3,4} Ç {1,4,5,6} = {1,4};
к) (B\A)È 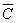 = (B
\ A) È (U
\ C) = {2} È {2,3,6} = {2,3,6}.
= (B
\ A) È (U
\ C) = {2} È {2,3,6} = {2,3,6}.
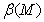 = {a,b}, {a,a}, {a,c}, {b,b}, {c,c}, {b,c}
= {a,b}, {a,a}, {a,c}, {b,b}, {c,c}, {b,c}
|
R
|
a
|
b
|
c
|
|
a
|
1
|
1
|
1
|
|
b
|
0
|
1
|
1
|
|
c
|
0
|
0
|
1
|
D (R) = {a,b,c}
Q (R) = {a,b,c}
7. R – «быть больше». M = {3, 7, 8, 12, 15, 16}
R 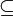 M × M
M × M
R = {{a,b}: a, bÎM; a > b} – антирефлексивно,
транзитивно
R = {(7,3), (8,3), (8,7), (12,3),
(12,7), (12,8), (15,3), (15,7), (15,8), (15,12), (16,3), (16,7), (16,8), (16,12),
(16,15)}
8. R1
= {(a, b): b = a + 1; a, b Î N}
R2 = {(a, b):
b = a2 + 1; a, b Î N}
R1°R2 =
{(a,b): (a,c) ÎR1; (c,b) ÎR2; a,b,c Î N} = {(a,b): c = a+1; c2+1=b;
a,b,c ÎN} = {(a,b):
(a+1)2+1=b; a,b ÎN} = {(1,5), (2,10), (3,17),..}
R1(2) =R1°R1 = {(a,b): a+1=b;
a,b ÎN} = {(1,2), (2,3), (3,4), (4,5),..}
R2(2)=R2°R2 = {(a,b): a4+1=b;
a,b ÎN} = {(1,2), (2,17), (3,82),..}
9. ( x1 Ú ( x2 => x1 )) & (x1 => x2)
|
x1
|
0
|
0
|
1
|
1
|
|
x2
|
0
|
1
|
1
|
0
|
|
x2 => x1
|
1
|
0
|
1
|
1
|
|
( x1 Ú
( x2 => x1 ))
|
1
|
0
|
1
|
1
|
|
x1 => x2
|
1
|
1
|
1
|
0
|
|
( x1 Ú
( x2 => x1 )) & (x1 => x2)
|
1
|
0
|
1
|
0
|
10. 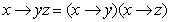
Доказать равносильность можно с помощью равносильных
преобразований. Для этого упрощают правую и левую части равенства отдельно.

 Левая часть. x® yz=x Ú (y
˄ z)
Левая часть. x® yz=x Ú (y
˄ z)




 Правая часть. ( x®y)( x®y)=(
x ˅y) ˄ ( x
˅ z) = x ˅ (y
˄ z)
Правая часть. ( x®y)( x®y)=(
x ˅y) ˄ ( x
˅ z) = x ˅ (y
˄ z)
Равносильность доказана
11. (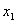 Ú
Ú 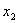
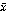 3)(
3)(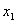 Ú
Ú 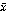 3) =
3) = 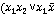 3)
3)
Для того, чтобы получить СДНФ функции,
требуется составить её таблицу истинности.
|
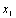
|
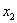
|
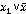 3 3
|
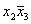
|
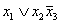
|
(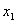 Ú Ú 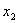 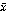 3)( 3)(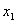 Ú Ú 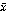 3) 3)
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
Далее, рассматриваются значения переменных,
при которых функция равна 1. Если значение переменной равно 0, то она
записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Т.о. СДНФ
запишется в виде:. 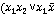 3)=
3)=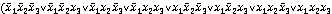
12. 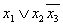 =(
=(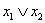 )(
)(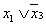 )
)
|
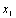
|
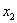
|
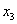
|
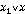 2 2
|
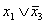
|
(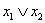 )( )(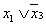 ) )
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
0
|
|
1
|
0
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
1
|
1
|
1
|
|
1
|
1
|
0
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
1
|
1
|
СКНФ запишем в виде:
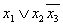 =
= 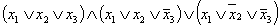
13. (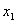 Ú
Ú 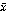 2
2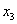 )(
)(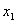 Ú
Ú 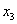 ) =
) = 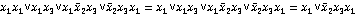
(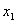 Ú
Ú 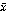 2
2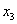 )(
)(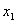 Ú
Ú 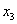 ) =
) =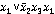 .
.
Левая часть
равенства – форма, записанная в КНФ, а правая – в ДНФ
14.
|
x1
|
x2
|
x3
|
f (x1,x2,x3)
|
|
|
0
|
0
|
0
|
0
|
|
|
0
|
0
|
1
|
1
|
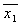 , ,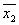 ,x3 ,x3
|
|
0
|
1
|
0
|
|
|
0
|
1
|
1
|
1
|
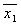 , x2, x3 , x2, x3
|
|
1
|
0
|
0
|
0
|
|
|
1
|
0
|
1
|
1
|
x1,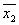 , x3 , x3
|
|
1
|
1
|
0
|
0
|
|
|
1
|
1
|
1
|
1
|
x1, x2, x3
|
f (x1, x2, x3) = (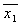 ,
,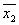 ,x3
) Ú (
,x3
) Ú (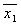 , x2, x3) Ú (x1,
, x2, x3) Ú (x1,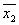 , x3) Ú (x1, x2, x3) – CДНФ
, x3) Ú (x1, x2, x3) – CДНФ
f (x1, x2, x3) = (x1, x2, x3)( x1,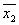 , x3)(
, x3)(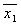 , x2, x3)(
, x2, x3)(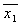 ,
,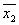 ,x3) – СКНФ
,x3) – СКНФ
15. а) эти прямые не перпендикулярны
б) прямые перпендикулярны или
имеют точку пересечения
в) эти прямые перпендикулярны
и имеют точку пересечения
г) если прямые
перпендикулярны, то прямые имеют точку пересечения
д) эти прямые перпендикулярны
тогда и только тогда, когда имеют точку пересечения
е) если эти прямые
перпендикулярны, то они не имеют общую точку. Если эти прямые не
перпендикулярны, то они имеют точку пересечения.
16. а) на улице идет дождь, значит надо взять зонт.
А
– на улице идет дождь;
В
– надо взять зонт;
А
Þ В
б)
на каникулы Лена поедет либо в Испанию, либо в Италию.
А –
На каникулы Лена поедет;
В –
Либо в Испанию;
С
- Либо в Италию.
А
® (B Å C)
в)
кот Вася любит есть рыбу и играть в мячик.
А –
кот Вася любит;
В –
есть рыбу;
С –
играть в мячик.
А
® (В & С)
17.
а) |x| = x ;
(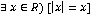 – Данное высказывание истинно.
– Данное высказывание истинно.
б) 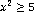 ;
; 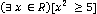 – Данное высказывание является истинным. [
– Данное высказывание является истинным. [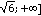 – область значения.
– область значения.
в) 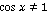 ;
; 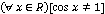 – Данное высказывание верно.[
– Данное высказывание верно.[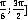 - область значения.
- область значения.
г) 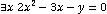 ;
; 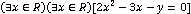 - Данное высказывание является истинным.
- Данное высказывание является истинным.
18.
а)
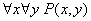 - для любой окружности
- для любой окружности 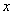 и
треугольника
и
треугольника 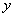 , окружность
, окружность 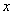 вписана
в треугольник
вписана
в треугольник 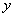 . Данное высказывание ложно.
Построим отрицание:
. Данное высказывание ложно.
Построим отрицание:
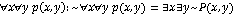
б) 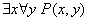 - есть такая окружность
- есть такая окружность 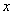 , которая вписана в
любой треугольник
, которая вписана в
любой треугольник 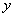 . Данное высказывание ложно.
Построим отрицание:
. Данное высказывание ложно.
Построим отрицание:
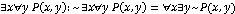
в) 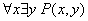 - для любой
окружности
- для любой
окружности 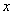 , существует треугольник
, существует треугольник 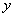 , описанный около него. Данное высказывание
является истинным. Построим отрицание:
, описанный около него. Данное высказывание
является истинным. Построим отрицание:
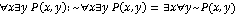
г) 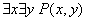 - существует
такая окружность
- существует
такая окружность 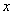 и треугольник
и треугольник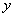 , что окружность
, что окружность 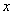 вписана
в треугольник
вписана
в треугольник 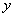 . Данное высказывание
является истинным.
. Данное высказывание
является истинным.
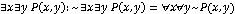
19. В каждом городе хотя бы одна улица застроена только
такими домами, в которых есть однокомнатные квартиры.
A –
город; B – улица; D – дом; Q(F) –
однокомнатные квартиры.
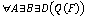 –
высказывание, удовлетворяющее нашему условию.
–
высказывание, удовлетворяющее нашему условию.
Построим
отрицание: