Конечные сверхразрешимые группы
Содержание
Введение
Глава
1. Вспомогательные определения и утверждения
Глава
2. Конечные сверхразрешимые группы
Глава
3. Примеры
Заключение
Список
использованной литературы
Введение
Теория групп имеет большую и содержательную
историю. Возникшая в связи с теорией Галуа и для нужд этой теории, она
развивалась сперва в качестве теории конечных групп подстановок (Коши, Жордан,
Силов). Довольно скоро обнаружилось, однако, что для большинства вопросов,
интересовавших эту теорию, не является существенным тот специальный
материал-подстановки,-который использовался для построения групп, и что на
самом деле речь идет об изучении свойств одной только алгебраической операции,
определенной в множестве, состоящем из конечного числа элементов произвольной
природы. Это открытие, представляющееся в настоящее время тривиалным, оказалось
в действительности весьма плодотворным и привело к созданию общей теории
конечных групп. Правда, переход от групп подстановок к произвольным конечным
группам не называл по существу расширения запаса изучаемых объектов, однако он
перевел теорию на аксиоматические основы, придав ей стройность и прозрачность и
облегчив этим ее дальнейшее развитие.
Старейшей и по-прежнему интенсивно развивающейся
ветвью теории групп является теория конечных групп. Достаточно хорошо изученным
в теории конечных групп является класс всех абелевых групп. Разрешимые группы
представляют собой очень широкое обобщение абелевых групп и лишь весьма
немногие нетривиальные свойства последних удается распространить на разрешимые
группы. Групповым свойством, качественно более сильным, чем разрешимость,
является сверхразрешимость.
Целью данной курсовой работы является изучение
конечных сверхразрешимых групп.
Для достижения поставленной цели предполагается
решить следующие задачи:
) изучить замкнутость класса всех конечных
сверхразрешимых групп относительно подгрупп, фактор-групп и прямых
произведений;
) изучить свойства подгрупп конечной
сверхразрешимой группы;
) привести примеры конечных сверхразрешимых
групп.
Работа состоит из трех глав. В первой главе
содержатся вспомогательные определения и утверждения, используемые в основном
тексте курсовой работы. Вторая глава посвящена изучению конечных
сверхразрешимых групп. В третьей главе приведены примеры конечных
сверхразрешимых групп.
Глава 1. Вспомогательные определения
и утверждения
Все используемые в дальнейшем обозначения и
определения можно найти в [1-5].
Определение 1.1.
Группой называется непустое множество G
с бинарной алгебраической операцией (умножением), удовлетворяющей следующим
требованиям:
(1) операция определена на G, то есть 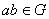 , для всех
, для всех  .
.
(2) операция ассоциативна, то
есть 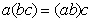 , для любых
, для любых 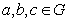 .
.
(3) в G существует
единичный элемент, то есть такой элемент 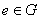 , что
, что 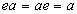 для всех
для всех 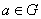 .
.
(4) каждый элемент обладает
обратным, то есть для любого 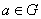 существует такой элемент
существует такой элемент 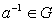 , что
, что  .
.
Определение 1.2. Абелева
группа - группа с коммутативной операцией.
Определение 1.3. Если  -конечное
множество, являющееся группой, то
-конечное
множество, являющееся группой, то  называют конечной группой, а число
называют конечной группой, а число 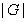 элементов в
элементов в
 -порядком
группы
-порядком
группы  .
.
Определение 1.4. Подмножество
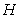 группы
группы  называется
подгруппой, если
называется
подгруппой, если 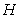 - группа
относительно той же операции, которая определена на группе
- группа
относительно той же операции, которая определена на группе  . Для
подгруппы используется следующие обозначение:
. Для
подгруппы используется следующие обозначение: 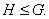 Запись
Запись 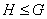 читается
так:
читается
так: 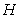 - подгруппа
группы
- подгруппа
группы 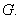
Определение 1.5.
Максимальная подгруппа - такая подгруппа, что не существует других подгрупп её
содержащих (не совпадающих с самой подгруппой).
Определение 1.6. Пусть 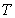 - непустое
подмножество группы
- непустое
подмножество группы  .
Совокупность всех элементов группы
.
Совокупность всех элементов группы  , перестановочных с каждым элементом
множества
, перестановочных с каждым элементом
множества 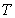 , называется
централизатором множества
, называется
централизатором множества 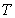 в группе
в группе  и
обозначается через
и
обозначается через 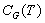 . Таким
образом,
. Таким
образом,
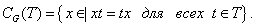
Определение 1.7. Центром
группы  называется
совокупность всех элементов группы
называется
совокупность всех элементов группы  , перестановочных с каждым элементом
группы
, перестановочных с каждым элементом
группы  . Центр
группы
. Центр
группы  обозначается
через
обозначается
через  Ясно, что
Ясно, что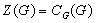 , т.е. центр
группы
, т.е. центр
группы совпадает с
центролизатором подмножества
совпадает с
центролизатором подмножества  в группе
в группе  . Кроме
того,
. Кроме
того, 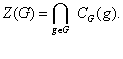
Определение 1.8. Зафиксируем
элемент  в группе
в группе  . Пересечение
всех подгрупп группы
. Пересечение
всех подгрупп группы  , содержащих
элемент
, содержащих
элемент  , назовем
циклической подгруппой, порожденной элементом
, назовем
циклической подгруппой, порожденной элементом  , и обозначим через
, и обозначим через 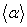 . Таким
образом,
. Таким
образом, 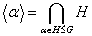 .
.
Определение 1.9. Пусть 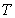 -
подмножество группы
-
подмножество группы  и
и 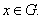 через
через  обозначим
подмножество всех элементов группы
обозначим
подмножество всех элементов группы  вида
вида  , где
, где 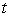 пробегает все элементы множества
пробегает все элементы множества 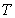 .
Подмножество
.
Подмножество 
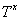 называется подмножеством,
сопряженным подмножеству
называется подмножеством,
сопряженным подмножеству 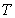 посредством
элемента
посредством
элемента 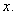
Пусть H - подгруппа
группы G. Подгруппа  называется
подгруппой, сопряженной подгруппе
называется
подгруппой, сопряженной подгруппе 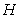 посредством элемента
посредством элемента 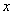 .
.
Определение 1.10. Совокупность
всех элементов группы  ,
перестановочных с подмножеством
,
перестановочных с подмножеством 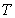 называется нормализатором
подмножества
называется нормализатором
подмножества 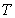 в группе
в группе  и обозначается
через
и обозначается
через 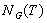 . Итак,
. Итак,
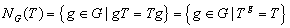 .
.
Определение 1.11. Подгруппа 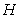 называется
нормальной подгруппой группы
называется
нормальной подгруппой группы  , если
, если 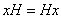 для всех
для всех 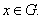 Запись
Запись 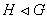 читается
так:
читается
так: 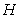 -нормальная
подгруппа группы
-нормальная
подгруппа группы  . Равенство
. Равенство 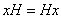 означает,
что для любого элемента
означает,
что для любого элемента 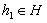 существует
элемент
существует
элемент 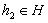 такой, что
такой, что 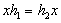 .
.
Лемма 1.1.
[1, лемма 6.4.] Пусть Н - нормальная подгруппа группы G.
Тогда:
(1) 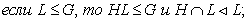
(2) 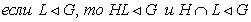
(3) 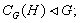
(4) 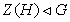 .
.
Определение 1.12. Пусть  - группа,
- группа, 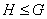 и
и 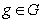 . Правым
смежным классом группы
. Правым
смежным классом группы  по
подгруппе
по
подгруппе 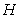 называется
множество
называется
множество 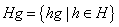 всех
элементов группы
всех
элементов группы  вида
вида 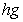 , где
, где 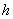 пробегает
все элементы подгруппы
пробегает
все элементы подгруппы 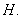 Аналогично
определяется левый смежный класс
Аналогично
определяется левый смежный класс 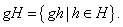
Определение 1.13. Индекс
подгруппы - число смежных классов в каждом (правом или левом) из разложений
группы в данной подгруппе.
Определение 1.14. Группа 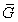 называется
фактор-группой группы
называется
фактор-группой группы  по группе
по группе 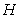 и
обозначается через
и
обозначается через 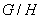 .
.
Теорема 1.1. [1, теорема
6.10 ]. (Теорема о соответствии) Пусть H -
нормальная подгруппа группы G. Тогда:
(1) если U - подгруппа
группы G и 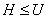 , то
, то  - подгруппа
фактор-группы
- подгруппа
фактор-группы 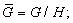
(2) каждая подгруппа
фактор-группы 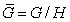 имеет вид
имеет вид 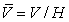 , где V - подгруппа
группы G и
, где V - подгруппа
группы G и 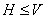 ;
;
(3) отображение 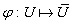 является
биекцией множества S(G,H) на
множество S(
является
биекцией множества S(G,H) на
множество S(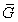 );
);
(4) если 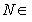 S(G,H), то N -
нормальная подгруппа группы G тогда и только тогда, когда
S(G,H), то N -
нормальная подгруппа группы G тогда и только тогда, когда 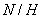 - нормальная
подгруппа фактор-группы
- нормальная
подгруппа фактор-группы 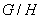 .
.
Определение 1.15. Пусть
р-простое число. р-Группой называют конечную группу, порядок которой есть
степень числа р. Конечная группа называется примарной, если она является p-группой
для некоторого простого р.
Определение 1.16. Силовской
р-подгруппой конечной группы  называют такую р-подгруппу, индекс
которой не делится на р.
называют такую р-подгруппу, индекс
которой не делится на р.
Определение 1.17. Группа
называется нильпотентной, если все ее силовские подгруппы нормальны.
Определение 1.18. Две группы  и
и 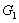 называются
изоморфными, если существует биекция
называются
изоморфными, если существует биекция 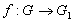 такая, что
такая, что 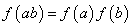 для всех
для всех  Факт
изоморфизма записывают так:
Факт
изоморфизма записывают так: 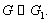
Теорема 1.2.[1, теорема
8.4.]. Пусть H -
нормальная подгруппа группы G. Тогда для любой подгруппы A пересечение
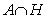 является
нормальной подгруппой в подгруппе А, а отображение
является
нормальной подгруппой в подгруппе А, а отображение 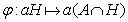 является
изоморфизмом групп
является
изоморфизмом групп 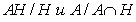 .
.
Теорема 1.3. .[1, теорема
8.5.] Если N и H -
нормальные подгруппы группы G, причём 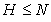 , то
, то 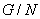 изоморфна
изоморфна 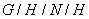 .
.
Определение 1.19. Положив  в
определении изоморфизма, получим изоморфное отображение группы G на себя,
которое называют автоморфизмом группы G.
Совокупность всех автоморфизмов группы G обозначим
через AutG.
в
определении изоморфизма, получим изоморфное отображение группы G на себя,
которое называют автоморфизмом группы G.
Совокупность всех автоморфизмов группы G обозначим
через AutG.
Теорема 1.4.
Совокупность AutG всех
автоморфизмов группы G является группой.
Теорема 1.5. Пусть G - группа и H - её
подгруппа. Тогда 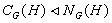 и
и  изоморфна
подгруппе группы автоморфизмов H.
изоморфна
подгруппе группы автоморфизмов H.
Теoрема 1.6.
(1) Если 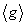 -
бесконечная циклическая группа, то
-
бесконечная циклическая группа, то 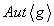 - группа порядка 2.
- группа порядка 2.
(2) Если 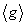 - конечная
циклическая группа порядка n, то
- конечная
циклическая группа порядка n, то 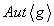 изоморфна группу всех обратимых
элементов полугруппы
изоморфна группу всех обратимых
элементов полугруппы 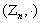 .
.
(3) Группа автоморфизмов
циклической группы абелева.
(4) Группа автоморфизмов группы
простого порядка p является циклической группой
порядка p-1.
Определение 1.20. Пусть 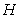 -подгруппа
группы
-подгруппа
группы  и
и  -автоморфизм
группы
-автоморфизм
группы  . Если
. Если 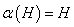 для всех
для всех 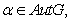 то
то 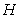 называют
характеристической подгруппой группы
называют
характеристической подгруппой группы  и пишут
и пишут  В каждой
группе
В каждой
группе  единичная
подгруппа и вся группа являются характеристическими подгруппами. Если в группе
единичная
подгруппа и вся группа являются характеристическими подгруппами. Если в группе  не других
(отличной от единичной подгруппы и всей группы) характеристических подгрупп, то
группа называется характеристически простой.
не других
(отличной от единичной подгруппы и всей группы) характеристических подгрупп, то
группа называется характеристически простой.
Лемма 1.2. [1, лемма
9.7]. Каждая подгруппа конечной циклической группы характеристическая.
Лемма 1.3. [1, лемма
9.10]. Пусть 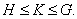 Тогда:
Тогда:
(1) если H
char K,
K char
G, то H
char G;
(2) если H char K, 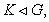 то
то 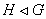 .
.
Определение 1.21. Цепочка
подгрупп
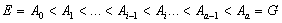
Определение 1.22. Ряд 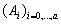 называется
нормальным, если
называется
нормальным, если 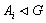 для всех i.
для всех i.
Определение 1.23. Ряд 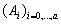 называется
субнормальным, если
называется
субнормальным, если 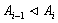 для всех i.
для всех i.
Определение 1.24. Пусть 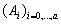 -
субнормальный ряд конечной группы G.
Фактор-группы
-
субнормальный ряд конечной группы G.
Фактор-группы 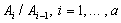 называются
факторами ряда.
называются
факторами ряда.
Определение 1.25. Числа 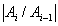 - индексы
ряда.
- индексы
ряда.
Определение 1.26. Нормальный
ряд 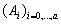 конечной
группы G называется
главным, если подгруппа
конечной
группы G называется
главным, если подгруппа 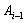 является
максимальной нормальной подгруппой группы G,
содержащейся в
является
максимальной нормальной подгруппой группы G,
содержащейся в 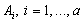 .
.
Определение 1.27. Пусть теперь
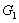 и
и 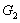 -
произвольные группы. На множестве
-
произвольные группы. На множестве  определим операцию (умножение)
следующим образом:
определим операцию (умножение)
следующим образом: 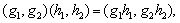 где
где 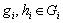 . Множество
. Множество 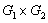 превращается
в группу с единичным элементом
превращается
в группу с единичным элементом  , где
, где 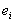 - единичный элемент группы
- единичный элемент группы 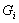 , и обратным
элементом
, и обратным
элементом 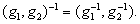
Группу 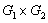 называют
прямым произведением групп
называют
прямым произведением групп 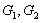 .
.
Определение 1.28. Минимальной
нормальной подгруппой группы G называют такую нормальную подгруппу
N группы G, что 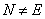 и в N нет
нетривиальных нормальных подгрупп группы G.
и в N нет
нетривиальных нормальных подгрупп группы G.
Лемма 1.4. [1, лемма
13.1]. Пусть 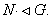 Тогда:
Тогда:
(1) если 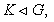 то либо
то либо 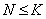 , либо
, либо
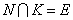 и
и 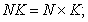
(2) если N абелева и NH=G для
некоторой собственной подгруппы H группы G, то 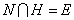 ;
;
(3) если 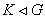 и
и 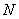
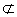
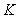 , то
, то 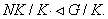
Определение 1.29. Коммутатором
элементов a и b называют
элемент 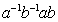 , который
обозначают через
, который
обозначают через 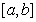 . Ясно, что
. Ясно, что 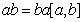 .
.
Определение 1.30. Подгруппа,
порождённая коммутаторами всех элементов группы G, называется
коммутантом группы G и обозначается через 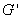 . Таким
образом,
. Таким
образом,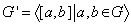 .
.
Определение 1.31. Для любой
неединичной группы G можно построить целую цепочку
коммутантов
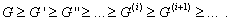
Если существует номер n такой, что 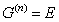 , то группа G называется
разрешимой.
, то группа G называется
разрешимой.
Лемма 1.5. [1, лемма
21.2.].
(1) Подгруппы и фактор-группы
разрешимой группы разрешимы;
(2) Если 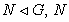 и
и 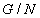 разрешимы,
то G разрешима;
разрешимы,
то G разрешима;
(3) Прямое произведение разрешимых
групп является разрешимой группой.
Глава 2. Конечные сверхразрешимые
группы
сверхразрешимый группа лемма
Определение 2.1. Группа
называется сверхразрешимой, если она обладает нормальным рядом с циклическими
факторами.
Лемма 2.1
[1, Лемма 26.1].
(1) Каждая подгруппа и каждая фактор-группа
сверхразрешимой группы сверхразрешимы.
(2) Прямое произведение сверхразрешимых
групп является сверхразрешимой группой.
(3) Сверхразрешимая группа разрешима.
Доказательство:
(1) Пусть группа G
сверхразрешима. Тогда группа G
обладает нормальным рядом с циклическими факторами:
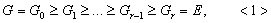
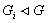 и фактор-группы
и фактор-группы 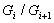 циклические
для всех i. Пусть
циклические
для всех i. Пусть 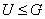 и
и 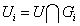 Тогда
подгруппа U имеет ряд
Тогда
подгруппа U имеет ряд

причём 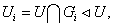 для вех i. Далее
для вех i. Далее
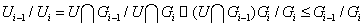
и фактор-группа 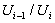 циклическая.
Итак, ряд <2> нормальный и его факторы циклические. Поэтому подгруппа U
сверхразрешима.
циклическая.
Итак, ряд <2> нормальный и его факторы циклические. Поэтому подгруппа U
сверхразрешима.
Пусть 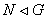 . Рассмотрим ряд
. Рассмотрим ряд
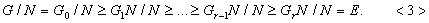
Ясно, что 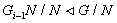 для всех
для всех 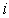 , поэтому
ряд <3> нормальный.
, поэтому
ряд <3> нормальный.
Далее,
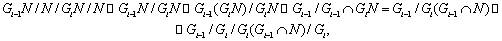
поэтому факторы ряда <3>
циклические и фактор-группа 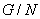 сверхразрешима.
сверхразрешима.
(2) Пусть G и H - сверхразрешимые группы.
Тогда группы G и H обладают нормальными рядам
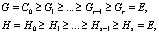
с циклическими факторами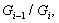
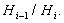 Рассмотрим прямое произведение
Рассмотрим прямое произведение 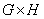 и построим
ряд
и построим
ряд
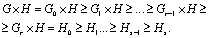
Этот ряд нормальный и его факторы
циклические.
(3) Пусть группа  сверхразрешима.
Тогда группа
сверхразрешима.
Тогда группа  обладает
нормальным рядом <1> с циклическими факторами. Так как
обладает
нормальным рядом <1> с циклическими факторами. Так как 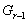 циклическая,
то
циклическая,
то 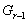 разрешима.
Так как
разрешима.
Так как 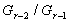 и
и 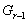 циклические,
то они разрешимы, поэтому
циклические,
то они разрешимы, поэтому 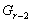 разрешима
по лемме 1.2. Теперь
разрешима
по лемме 1.2. Теперь 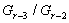 и
и 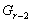 разрешимы,
значит и
разрешимы,
значит и 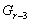 разрешима
по лемме 1.2, и т.д. Через конечное число шагов получаем, что группа
разрешима
по лемме 1.2, и т.д. Через конечное число шагов получаем, что группа  разрешима.
разрешима. 
Лемма 2.2 [1, Лемма
26.2]. (1) Если группа G содержит нормальную циклическую
подгруппу K и
фактор-группа G/K
сверхразрешима, то группа G сверхразрешима.
(2) Если фактор-группа G/Z(G)
сверхразрешима, то группа G
сверхразрешима.
(3) Нильпотентная группа сверхразрешима.
Доказательство.
(1) Так как G/Kсверхразрешима,
то имеется нормальный ряд
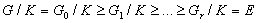
с циклическими факторами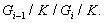 Рассмотрим
ряд
Рассмотрим
ряд
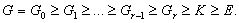 <4>
<4>
Так как 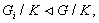 то
то 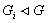 и ряд
<4> нормальный.
и ряд
<4> нормальный.
Кроме того, факторы 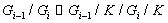 циклические
для
циклические
для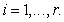 Далее,
Далее,  -
циклическая группа. Значит ряд <4> нормальный с циклическими факторами и
группа
-
циклическая группа. Значит ряд <4> нормальный с циклическими факторами и
группа  сверхразрешима.
сверхразрешима.
(2) Пусть 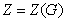 . Так как
. Так как 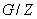 сверхразрешима,
то имеется нормальный ряд
сверхразрешима,
то имеется нормальный ряд
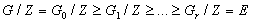
с циклическими факторами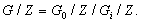 Поскольку в
абелевой группе максимальные подгруппы имеют простые индексы, то группа
Поскольку в
абелевой группе максимальные подгруппы имеют простые индексы, то группа 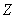 обладает
рядом
обладает
рядом
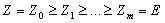
с факторами 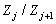 простых
порядков. Рассмотрим ряд
простых
порядков. Рассмотрим ряд
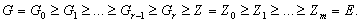 <5>
<5>
Так как 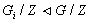 , то
, то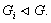 Поскольку
все подгруппы из центра группы нормальны в группе, то ряд <5> нормальный.
Кроме того, факторы
Поскольку
все подгруппы из центра группы нормальны в группе, то ряд <5> нормальный.
Кроме того, факторы
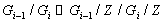
циклические для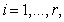 а факторы
а факторы
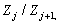
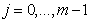
имеют простые порядки. Значит ряд
<5> нормальный с циклическими факторами и группа  сверхразрешима.
сверхразрешима.
Лемма 2.3
[1, Лемма 26.3]:
Группа сверхразрешима тогда и только тогда,
когда она обладает главным рядом с факторами простых порядков.
Доказательство.
Пусть G
сверхразрешима. Тогда она имеет нормальный ряд <1> с циклическими
факторами  . Так как
. Так как 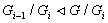 и
и  циклическая,
то по лемме 1.2, все подгруппы в
циклическая,
то по лемме 1.2, все подгруппы в  характеристические. Пусть
характеристические. Пусть 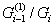 - подгруппа
простого индекса в
- подгруппа
простого индекса в  . Тогда
. Тогда
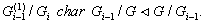
следовательно 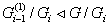 по лемме
1.3, и ряд
по лемме
1.3, и ряд
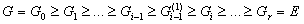
нормальный с циклическим фактором 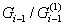 простого
порядка. Повторяя эти действия, через конечное число шагов придём к главному
ряду с факторами простых порядков.
простого
порядка. Повторяя эти действия, через конечное число шагов придём к главному
ряду с факторами простых порядков.
Обратно, если группа G имеет
главный ряд с факторами простых порядков, то этот ряд будет нормальным, а его
факторы циклическими. Значит группа G будет
сверхразрешимой.
Теорема 2.1. [1, теорема
26.4]. (1) Максимальные подгруппы сверхразрешимой группы имеют простые индексы
(2) В сверхразрешимой группе каждая минимальная
нормальная подгруппа имеет простой порядок.
Доказательство.
(1) Пусть G -
сверхразрешимая группа и 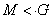 . По лемме
2.3 группа G имеет
главный ряд
. По лемме
2.3 группа G имеет
главный ряд
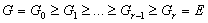 <6>
<6>
с факторами простых порядков.
Зафиксируем число i такое что 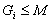 , но
, но 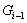
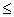
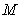 . Поскольку
. Поскольку 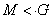 и
и 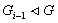 , то
, то 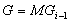 и
и 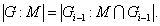
Но  и
и  , поэтому либо
, поэтому либо 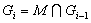 , либо
, либо 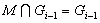 . Поскольку,
. Поскольку,
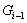

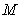 , то
, то 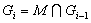 и
и 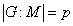 .
.
(2) Воспользуемся индукцией по
порядку группы. Пусть 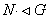 . По лемме
2.3 в группе G существует
минимальная нормальная подгруппа K простого порядка. Если
. По лемме
2.3 в группе G существует
минимальная нормальная подгруппа K простого порядка. Если 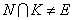 , то N=K и
утверждение справедливо. Пусть
, то N=K и
утверждение справедливо. Пусть 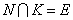 . По лемме 1.4, подгруппа
. По лемме 1.4, подгруппа 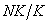 -
минимальная нормальная подгруппа фактор-группы
-
минимальная нормальная подгруппа фактор-группы 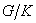 . По индукции
. По индукции 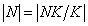 - простое
число.
- простое
число. 
Лемма 2.4
[1, Лемма 26.5]. Если G
- сверхразрешимая группа и p-наибольший
простой делитель порядка G,
то силовская p-подгруппа группы G
нормальна.
Доказательство.
Воспользуемся индукцией по порядку
группы G. Пусть 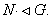 Тогда
Тогда 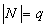 - простое
число теореме 2.1. Фактор-группа
- простое
число теореме 2.1. Фактор-группа 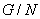 сверхразрешима. По индукции,
сверхразрешима. По индукции, 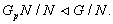 т.е.
т.е. 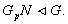 Если
Если 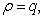 то
то 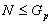 и
и 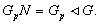 Пусть
Пусть 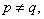 тогда
тогда 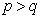 . Так как
фактор-группа
. Так как
фактор-группа  по теореме
1.6, является циклической группой порядка
по теореме
1.6, является циклической группой порядка 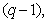 то
то 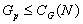 и
и 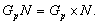 Но теперь,
Но теперь, 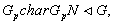 следовательно
следовательно
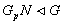 .
. 
Глава 3. Примеры
Заметим, что можно привести пример конечной
неабелевой группы, которая является сверхразрешимой.
Пример 3.1. Группа
кватернионов Q сверхразрешима, но
не абелева.
Пусть Q=<A,B|A4=B4=E,
A2=B2,
B-1AB=A-1>
- группа кватернионов, порожденная матрицами A=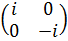 и B=
и B= .
.
Элементами группы Q
являются матрицы:
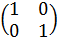 ,
, 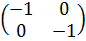 ,
,
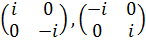 ,
,
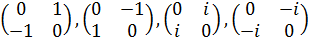 .
.
Таким образом, 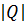 =8=23.
Следовательно, в силу примера 3.1 группа кватернионов Q
сверхразрешима.
=8=23.
Следовательно, в силу примера 3.1 группа кватернионов Q
сверхразрешима.
Однако группа Q
не является абелевой.
Действительно,
A×B=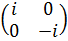 ×
× =
= 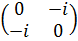 ≠
≠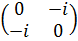 =
=  ×
×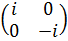 = B×A.
= B×A.
Согласно пункту (3) леммы 2.2. каждая
нильпотентная группа сверхразрешима. Обратное утверждение в общем случае не
верно. Приведем соответствующий пример.
Пример 3.2.
Симметрическая группа S3
степени 3 сверхразрешима, но не нильпотентна.
Пусть S3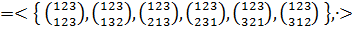 -
симметрическая группа степени 3. Найдем все ее собственные подгруппы.
-
симметрическая группа степени 3. Найдем все ее собственные подгруппы.
Н1 = <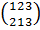 >
= <{
>
= <{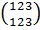 ,
, },
},
Н2 = <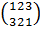 >
= <{
>
= <{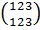 ,
,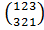 },
},
Н3 = <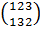 >
= <{
>
= <{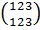 ,
, },
}, ,
,
Н4 = <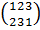 >
= <{
>
= <{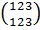 ,
,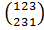 ,
,
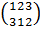 },
}, .
.
Подгруппа Н1 не является нормальной
подгруппой группы S3.
Действительно, выберем 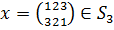 . Пусть
. Пусть 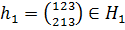 .
Тогда
.
Тогда 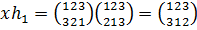 и
и
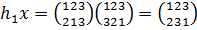 ,
,
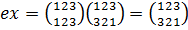 .
Следовательно,
.
Следовательно, 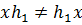 и
и 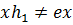 .
Таким образом, для
.
Таким образом, для 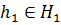 не существует
элемента
не существует
элемента 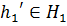 такого,
что
такого,
что 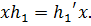 Значит,
по определению
Значит,
по определению 
Подгруппа Н2 не является нормальной
подгруппой группы S3.
Действительно, выберем 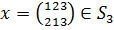 . Пусть
. Пусть 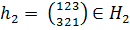 .
Тогда
.
Тогда 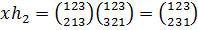 и
и
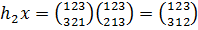 ,
,
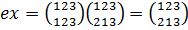 .
Следовательно,
.
Следовательно, 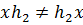 и
и  .
Таким образом, для
.
Таким образом, для  не существует
элемента
не существует
элемента 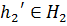 такого,
что
такого,
что  Значит,
по определению
Значит,
по определению 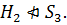
Подгруппа Н3 не является нормальной
подгруппой группы S3.
Действительно, выберем 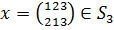 . Пусть
. Пусть 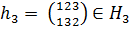 .
Тогда
.
Тогда 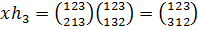 и
и
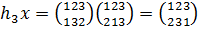 ,
,
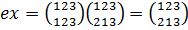 .
Следовательно,
.
Следовательно, 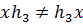 и
и  .
Таким образом, для
.
Таким образом, для 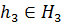 не существует
элемента
не существует
элемента 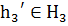 такого,
что
такого,
что 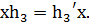 Значит,
по определению
Значит,
по определению 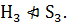
Рассмотрим подгруппу Н4. Ее порядок 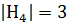 .
Следовательно, она является силовской 3-подгруппой группы S3.
Поскольку Н4 - единственная силовская 3-подгруппа группы S3,
то
.
Следовательно, она является силовской 3-подгруппой группы S3.
Поскольку Н4 - единственная силовская 3-подгруппа группы S3,
то 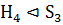 .
.
Таким образом, группа S3 обладает
нормальным рядом 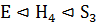 , факторы которого
, факторы которого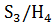 и
и 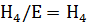 имеют
порядки 2 и 3 соответственно, значит, являются циклическими группами.
Следовательно, по определению, группа S3 сверхразрешима.
имеют
порядки 2 и 3 соответственно, значит, являются циклическими группами.
Следовательно, по определению, группа S3 сверхразрешима.
То, что группа S3 не является
нильпотентной, следует из того, что она обладает только одной силовской
3-подгруппой 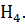
Заключение
В данной курсовой работе были приведены
некоторые результаты касающиеся вопроса сверхразрешимости конечных групп,
обладающих нормальным рядом с циклическими факторами. Рассмотрены и доказаны
некоторые свойства сверхразхрешимых групп в виде лемм во второй главе. В главе
три приведены и рассмотрены примеры.
Список используемой литературы
1. Монахов
В. С. Введение в теорию конечных групп и их классов. - Гомель: УО «ГГУ им. Ф.
Скорины», 2003. - 320 с.;
. Каргаполов
М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982. - 288 с.;
. Холл
М. Теория групп. - М.: Издательство иностранной литературы, 1962. - 468 с.;
. Курош
А. Г. Теория групп. - М.: Наука, 1967. - 648 с.;
. Ленг
С. Алгебра. - М.: Мир, 1986. - 564 с.