Векторы линейного преобразования
Контрольная работа
Векторы линейного преобразования
71-80. Найти собственные значения и
собственные векторы линейного преобразования, заданного в некотором базисе
матрицей А.
Задание 74.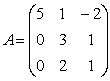 
Решение:
Для нахождения
собственных значений составим характеристическое уравнение:
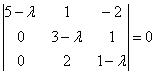
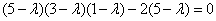
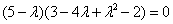
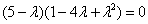
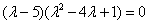
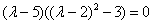
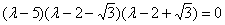
Корни характеристического уравнения
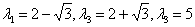
Подставим полученные
собственные значения и вычислим собственные векторы:
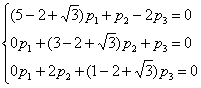
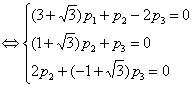
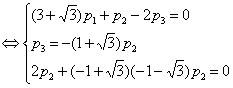
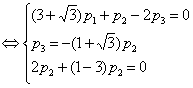
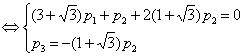
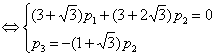
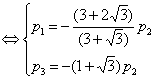
Аналогично,
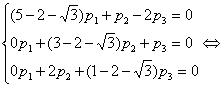
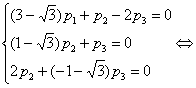
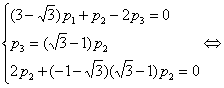
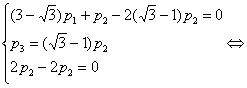
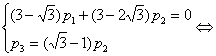
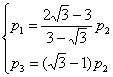
Подставив вместо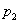 
любое
значение, например 
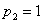получаем
.
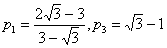Последнее
значение:
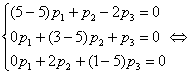
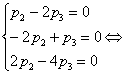
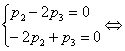
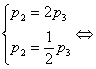
Следовательно, параметр 
может быть любым, а 
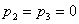
Собственный вектор имеет вид, например (1,0,0).
вектор базис матрица
Ответ: собственные значения
.
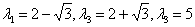Собственные вектора:
, 
,
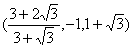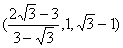(1,0,0)