Сущность уравнений квадратичной формы и их приведение к каноническому виду
Сущность
уравнений квадратичной формы и их приведение к каноническому виду
Введение
квадратичная форма канонический вид
уравнение
Первоначально теория квадратичных
форм использовалась для исследования кривых и поверхностей, задаваемых уравнениями
второго порядка, содержащими две или три переменные. Позднее эта теория нашла и
другие приложения. В частности, при математическом моделировании экономических
процессов целевые функции могут содержать квадратичные слагаемые.
Многочисленные приложения квадратичных форм потребовали построения общей
теории, когда число переменных равно любому 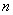 , а коэффициенты квадратичной формы
не всегда являются вещественными числами.
, а коэффициенты квадратичной формы
не всегда являются вещественными числами.
Теория квадратичных форм впервые
была развита французским математиком Лагранжем, которому принадлежат многие
идеи в этой теории, в частности, он ввел важное понятие приведенной формы, с
помощью которого им была доказана конечность числа классов бинарных
квадратичных форм заданного дискриминанта. Затем эта теория значительно была
расширенна Гауссом, который ввел много новых понятий, на основе которых ему
удалось получить доказательства трудных и глубоких теорем теории чисел,
ускользавших от его предшественников в этой области.
Целью работы является изучение видов
квадратичных форм и способов приведения квадратичных форм к каноническому виду.
В данной работе поставлены следующие задачи:
выбрать необходимую литературу, рассмотреть определения и основные теоремы,
решить ряд задач по данной теме.
§1. Приведение квадратичной формы к
каноническому виду
Истоки теории квадратичных форм лежат в
аналитической геометрии, а именно в теории кривых (и поверхностей) второго
порядка. Известно, что уравнение центральной кривой второго порядка на
плоскости, после перенесения начала прямоугольных координат в центр этой
кривой, имеет вид

Известно, далее, что можно совершить
такой поворот осей координат на некоторый угол 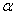 , т.е. такой переход от координат
, т.е. такой переход от координат 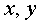 к
координатам
к
координатам 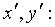
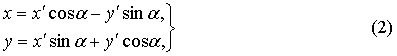
что в новых координатах уравнение
нашей кривой будет иметь «канонический» вид

в этом уравнении коэффициент при
произведении неизвестных 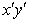 равен,
следовательно, нулю. Преобразование координат (2) можно толковать, очевидно,
как линейное преобразование неизвестных, притом невырожденное, так как
определитель из его коэффициентов равен единице. Это преобразование применяется
к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения
(1) невырожденным линейным преобразованием (2) превращается в левую часть
уравнения (3).
равен,
следовательно, нулю. Преобразование координат (2) можно толковать, очевидно,
как линейное преобразование неизвестных, притом невырожденное, так как
определитель из его коэффициентов равен единице. Это преобразование применяется
к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения
(1) невырожденным линейным преобразованием (2) превращается в левую часть
уравнения (3).
Многочисленные приложения
потребовали построения аналогичной теории для случая, когда число неизвестных
вместо двух равно любому 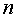 , а
коэффициенты являются или действительными, или же любыми комплексными числами.
, а
коэффициенты являются или действительными, или же любыми комплексными числами.
Обобщая выражение, стоящее в левой
части уравнения (1), мы приходим к следующему понятию.
Квадратичной формой  от
от 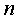 неизвестных
неизвестных
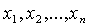 называется
сумма, каждый член которой является или квадратом одного из этих неизвестных,
или произведением двух разных неизвестных. Квадратичная форма называется
действительной или комплексной в зависимости от того, являются ли ее
коэффициенты действительными или же могут быть любыми комплексными числами.
называется
сумма, каждый член которой является или квадратом одного из этих неизвестных,
или произведением двух разных неизвестных. Квадратичная форма называется
действительной или комплексной в зависимости от того, являются ли ее
коэффициенты действительными или же могут быть любыми комплексными числами.
Считая, что в квадратичной форме 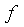 уже сделано
приведение подобных членов, введем следующие обозначения для коэффициентов этой
формы: коэффициент при
уже сделано
приведение подобных членов, введем следующие обозначения для коэффициентов этой
формы: коэффициент при 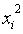 обозначим
через
обозначим
через 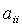 , а
коэффициент при произведении
, а
коэффициент при произведении 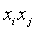 для
для 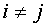 - через
- через 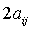 (сравнить с
(1)!).
(сравнить с
(1)!).
Так как, однако, 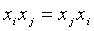 , то
коэффициент при этом произведении мог бы быть обозначен и через
, то
коэффициент при этом произведении мог бы быть обозначен и через 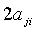 , т.е.
введенные нами обозначения предполагают справедливость равенства
, т.е.
введенные нами обозначения предполагают справедливость равенства

Член  можно записать теперь в виде
можно записать теперь в виде
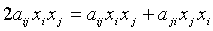 ,
,
а всю квадратичную форму 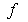 - в виде суммы
всевозможных членов
- в виде суммы
всевозможных членов 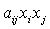 , где
, где 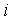 и
и 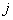 уже
независимо друг от друга принимают значения от 1 до
уже
независимо друг от друга принимают значения от 1 до 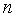 :
:

в частности, при 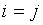 получается
член
получается
член 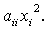
Из коэффициентов 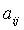 можно
составить, очевидно, квадратную матрицу
можно
составить, очевидно, квадратную матрицу 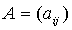 порядка
порядка 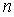 ; она
называется матрицей квадратичной формы
; она
называется матрицей квадратичной формы  , а ее ранг
, а ее ранг 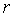 - рангом
этой квадратичной формы.
- рангом
этой квадратичной формы.
Если, в частности, 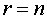 , т.е.
матрица - невырожденная, то и квадратичная форма
, т.е.
матрица - невырожденная, то и квадратичная форма  называется невырожденной. Ввиду
равенства (4) элементы матрицы А, симметричные относительно главной диагонали,
равны между собой, т.е. матрица А - симметрическая. Обратно, для любой
симметрической матрицы А
называется невырожденной. Ввиду
равенства (4) элементы матрицы А, симметричные относительно главной диагонали,
равны между собой, т.е. матрица А - симметрическая. Обратно, для любой
симметрической матрицы А 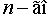 порядка
можно указать вполне определенную квадратичную форму (5) от
порядка
можно указать вполне определенную квадратичную форму (5) от 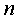 неизвестных,
имеющую элементы матрицы А своими коэффициентами.
неизвестных,
имеющую элементы матрицы А своими коэффициентами.
Квадратичную форму (5) можно
записать в ином виде, используя умножение прямоугольных матриц. Условимся
сначала о следующем обозначении: если дана квадратная или вообще прямоугольная
матрица А, то через 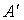 будет
обозначаться матрица, полученная из матрицы А транспонированием. Если матрицы А
и В таковы, что их произведение определено, то имеет место равенство:
будет
обозначаться матрица, полученная из матрицы А транспонированием. Если матрицы А
и В таковы, что их произведение определено, то имеет место равенство:
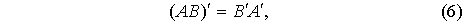
т.е. матрица, полученная
транспонированием произведения, равна произведению матриц, получающихся
транспонированием сомножителей, притом взятых в обратном порядке.
В самом деле, если произведение АВ
определено, то будет определено, как легко проверить, и произведение 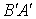 : число
столбцов матрицы
: число
столбцов матрицы 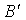 равно числу
строк матрицы
равно числу
строк матрицы 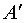 . Элемент
матрицы
. Элемент
матрицы 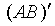 , стоящий в
ее
, стоящий в
ее 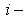 й строке и
й строке и 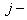 м столбце, в
матрице АВ расположен в
м столбце, в
матрице АВ расположен в 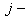 й строке и
й строке и 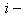 м столбце.
Он равен поэтому сумме произведений соответственных элементов
м столбце.
Он равен поэтому сумме произведений соответственных элементов 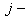 й строки
матрицы А и
й строки
матрицы А и 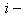 го столбца
матрицы В, т.е. равен сумме произведений соответственных элементов
го столбца
матрицы В, т.е. равен сумме произведений соответственных элементов 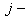 го столбца
матрицы
го столбца
матрицы 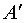 и
и 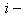 й строки
матрицы
й строки
матрицы 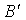 . Этим
равенство (6) доказано.
. Этим
равенство (6) доказано.
Заметим, что матрица А тогда и
только тогда будет симметрической, если она совпадает со своей
транспонированной, т.е. если
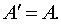
Обозначим теперь через 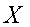 столбец,
составленный из неизвестных.
столбец,
составленный из неизвестных.
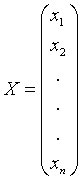 .
.
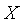 является матрицей, имеющей
является матрицей, имеющей 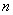 строк и
один столбец. Транспонируя эту матрицу, получим матрицу
строк и
один столбец. Транспонируя эту матрицу, получим матрицу
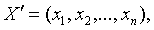
Составленную из одной строки.
Квадратичная форма (5) с матрицей 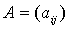 может быть
записана теперь в виде следующего произведения:
может быть
записана теперь в виде следующего произведения:
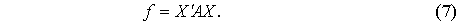
Действительно, произведение 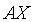 будет
матрицей, состоящей из одного столбца:
будет
матрицей, состоящей из одного столбца:
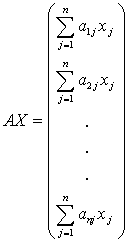 .
.
Умножая эту матрицу слева на матрицу
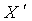 , мы получим
«матрицу», состоящую из одной строки и одного столбца, а именно правую часть
равенства (5).
, мы получим
«матрицу», состоящую из одной строки и одного столбца, а именно правую часть
равенства (5).
Что произойдет с квадратичной формой
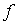 , если
входящие в нее неизвестные
, если
входящие в нее неизвестные 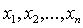 будут подвергнуты линейному
преобразованию
будут подвергнуты линейному
преобразованию
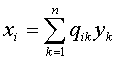 ,
, 
с матрицей 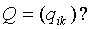 Будем
считать при этом, что если форма
Будем
считать при этом, что если форма 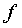 действительная, то и элементы
матрицы
действительная, то и элементы
матрицы 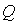 должны быть
действительными. Обозначая через Y столбец из неизвестных
должны быть
действительными. Обозначая через Y столбец из неизвестных 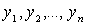 , запишем
линейное преобразование (8) в виде матричного равенства:
, запишем
линейное преобразование (8) в виде матричного равенства:
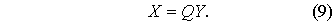
Отсюда по (6)
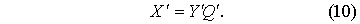
Подставляя (9) и (10) в запись (7)
формы 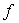 , получаем:
, получаем:
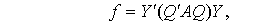
Или
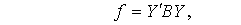
где
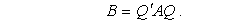
Матрица В будет симметрической, так
как ввиду равенства (6), справедливого, очевидно, для любого числа множителей,
и равенства 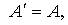 равносильного
симметричности матрицы
равносильного
симметричности матрицы 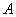 , имеем:
, имеем:
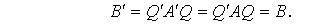
Таким образом, доказана следующая
теорема:
Квадратичная форма от 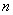 неизвестных,
имеющая матрицу
неизвестных,
имеющая матрицу 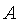 , после
выполнения линейного преобразования неизвестных с матрицей
, после
выполнения линейного преобразования неизвестных с матрицей 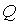 превращается
в квадратичную форму от новых неизвестных, причем матрицей этой формы служит
произведение
превращается
в квадратичную форму от новых неизвестных, причем матрицей этой формы служит
произведение 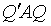 .
.
Предположим теперь, что мы выполняем
невырожденное линейное преобразование, т.е. 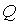 , а поэтому и
, а поэтому и 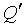 - матрицы
невырожденные. Произведение
- матрицы
невырожденные. Произведение 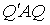 получается в этом случае умножением
матрицы
получается в этом случае умножением
матрицы 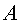 на
невырожденные матрицы и поэтому, ранг этого произведения равен рангу матрицы
на
невырожденные матрицы и поэтому, ранг этого произведения равен рангу матрицы 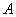 . Таким
образом, ранг квадратичной формы не меняется при выполнении невырожденного
линейного преобразования.
. Таким
образом, ранг квадратичной формы не меняется при выполнении невырожденного
линейного преобразования.
Рассмотрим теперь, по аналогии с
указанной в начале параграфа геометрической задачей приведения уравнения
центральной кривой второго порядка к каноническому виду (3), вопрос о
приведении произвольной квадратичной формы некоторым невырожденным линейным
преобразованием к виду суммы квадратов неизвестных, т.е. к такому виду, когда
все коэффициенты при произведениях различных неизвестных равны нулю; этот
специальный вид квадратичной формы называется каноническим. Предположим
сначала, что квадратичная форма 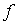 от
от  неизвестных
неизвестных 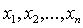 уже
приведена невырожденным линейным преобразованием к каноническому виду
уже
приведена невырожденным линейным преобразованием к каноническому виду
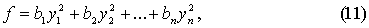
где 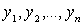 - новые неизвестные. Некоторые из
коэффициентов
- новые неизвестные. Некоторые из
коэффициентов 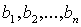 могут.
Конечно, быть нулями. Докажем, что число отличных от нуля коэффициентов в (11)
непременно равно рангу
могут.
Конечно, быть нулями. Докажем, что число отличных от нуля коэффициентов в (11)
непременно равно рангу 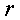 формы
формы 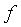 .
.
В самом деле, так как мы пришли к
(11) при помощи невырожденного преобразования, то квадратичная форма, стоящая в
правой части равенства (11), также должна быть ранга 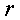 .
.
Однако матрица этой квадратичной
формы имеет диагональный вид
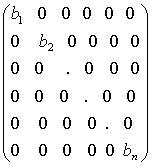
и требование, чтобы эта матрица
имела ранг 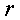 ,
равносильно предположению, что на ее главной диагонали стоит ровно
,
равносильно предположению, что на ее главной диагонали стоит ровно 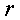 отличных от
нуля элементов.
отличных от
нуля элементов.
Перейдем к доказательству следующей
основной теоремы о квадратичных формах.
Всякая квадратичная форма может быть
приведена некоторым невырожденным линейным преобразованием к каноническому
виду. Если при этом рассматривается действительная квадратичная форма, то все
коэффициенты указанного линейного преобразования можно считать действительными.
Пуст дана квадратичная форма
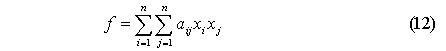
от n неизвестных
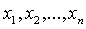 . Мы
постараемся найти такое невырожденное линейное преобразование, которое выделило
бы из
. Мы
постараемся найти такое невырожденное линейное преобразование, которое выделило
бы из 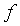 квадрат
одного из неизвестных, т.е. привело бы
квадрат
одного из неизвестных, т.е. привело бы 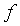 к виду суммы этого квадрата и
некоторой квадратичной формы от остальных неизвестных. Эта цель легко достигается
в том случае, если среди коэффициентов
к виду суммы этого квадрата и
некоторой квадратичной формы от остальных неизвестных. Эта цель легко достигается
в том случае, если среди коэффициентов 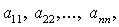 стоящих в матрице формы
стоящих в матрице формы 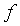 на главной
диагонали, есть отличные от нуля, т.е. если в (12) входит с отличием от нуля
коэффициентов квадрат хотя бы одного из неизвестных
на главной
диагонали, есть отличные от нуля, т.е. если в (12) входит с отличием от нуля
коэффициентов квадрат хотя бы одного из неизвестных 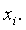
Пусть, например, 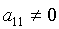 . Тогда, как
легко проверить, выражение
. Тогда, как
легко проверить, выражение 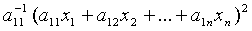 , являющееся квадратичной формой,
содержит такие же члены с неизвестным
, являющееся квадратичной формой,
содержит такие же члены с неизвестным 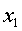 , как и наша форма
, как и наша форма 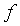 , а поэтому
разность
, а поэтому
разность
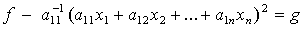
будет квадратичной формой,
содержащей лишь неизвестные 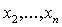 , но не
, но не 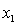 . Отсюда
. Отсюда
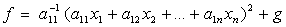
Если мы введем обозначения
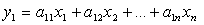
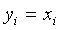 при
при 
то получим

где 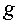 будет теперь квадратичной формой о
неизвестных
будет теперь квадратичной формой о
неизвестных 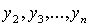 . Выражение
(14) есть искомое выражение для формы
. Выражение
(14) есть искомое выражение для формы 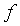 , так как оно получено из (12)
невырожденным линейным преобразованием, а именно преобразованием, обратным
линейному преобразованию (13), которое имеет своим определителем
, так как оно получено из (12)
невырожденным линейным преобразованием, а именно преобразованием, обратным
линейному преобразованию (13), которое имеет своим определителем 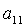 и поэтому
не вырождено.
и поэтому
не вырождено.
Если же имеют место равенства 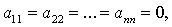 то
предварительно нужно совершить вспомогательное линейное преобразование,
приводящее к появлению в нашей форме
то
предварительно нужно совершить вспомогательное линейное преобразование,
приводящее к появлению в нашей форме 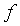 квадратов неизвестных. Так как среди
коэффициентов в записи (12) этой формы должны быть отличные от нуля, - иначе
нечего было бы доказывать, - то пусть, например,
квадратов неизвестных. Так как среди
коэффициентов в записи (12) этой формы должны быть отличные от нуля, - иначе
нечего было бы доказывать, - то пусть, например, 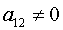 , т.е.
, т.е. 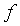 является
суммой члена
является
суммой члена 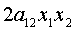 и членов, в
каждый из которых входит хотя бы одно из неизвестных
и членов, в
каждый из которых входит хотя бы одно из неизвестных  .
.
Совершим теперь линейное
преобразование
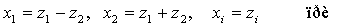

Оно будет невырожденным, так как
имеет определитель
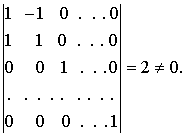
В результате этого преобразования
член 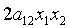 нашей формы
примет вид
нашей формы
примет вид
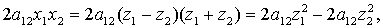
т.е. в форме 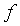 появятся, с
отличными от нуля коэффициентами, квадраты сразу двух неизвестных, причем они
не могут сократиться ни с одним из остальных членов, так как в каждый их этих
последних входит хотя бы одно из неизвестных
появятся, с
отличными от нуля коэффициентами, квадраты сразу двух неизвестных, причем они
не могут сократиться ни с одним из остальных членов, так как в каждый их этих
последних входит хотя бы одно из неизвестных  теперь мы находимся в условиях уже
рассмотренного выше случая , т.е. еще одним невырожденным линейным
преобразованием можем привести форму
теперь мы находимся в условиях уже
рассмотренного выше случая , т.е. еще одним невырожденным линейным
преобразованием можем привести форму 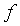 к виду (14).
к виду (14).
Для окончания доказательства
остается отметить, что квадратичная форма  зависит от меньшего, чем
зависит от меньшего, чем 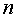 , числа
неизвестных и поэтому, по предположению индукции, некоторым невырожденным
преобразованием неизвестных
, числа
неизвестных и поэтому, по предположению индукции, некоторым невырожденным
преобразованием неизвестных 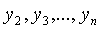 приводится к каноническому виду.
Это преобразование, рассматриваемое как (невырожденное, как легко видеть)
преобразование всех
приводится к каноническому виду.
Это преобразование, рассматриваемое как (невырожденное, как легко видеть)
преобразование всех 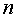 неизвестных,
при котором
неизвестных,
при котором 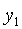 остается
без изменения, приводит, следовательно, (14) к каноническому виду. Таким
образом, квадратичная форма
остается
без изменения, приводит, следовательно, (14) к каноническому виду. Таким
образом, квадратичная форма 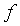 двумя или тремя невырожденными
линейными преобразованиями, которые можно заменить одним невырожденным
преобразованием - их произведением, приводится к виду суммы квадратов
неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы
знаем, рангу формы
двумя или тремя невырожденными
линейными преобразованиями, которые можно заменить одним невырожденным
преобразованием - их произведением, приводится к виду суммы квадратов
неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы
знаем, рангу формы 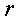 . Если,
сверх того, квадратичная форма
. Если,
сверх того, квадратичная форма 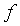 действительная , то коэффициенты
как в каноническом виде формы
действительная , то коэффициенты
как в каноническом виде формы 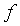 , так и в линейном преобразовании,
приводящем
, так и в линейном преобразовании,
приводящем 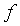 к этому
виду, будут действительными; в самом деле, и линейное преобразование, обратное
(13), и линейное преобразование (15) имеют действительные коэффициенты.
к этому
виду, будут действительными; в самом деле, и линейное преобразование, обратное
(13), и линейное преобразование (15) имеют действительные коэффициенты.
Доказательство основной теоремы
закончено. Метод, использованный в этом доказательстве, может быть применен в
конкретных примерах для действительного приведения квадратичной формы к
каноническому виду. Нужно лишь вместо индукции, которую мы использовали в
доказательстве, последовательно выделять изложенным выше методом квадраты
неизвестных.
Пример 1. Привести к каноническому
виду квадратичную форму

Ввиду отсутствия в этой форме
квадратов неизвестных мы выполним сначала невырожденное линейное преобразование
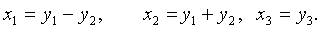
с матрицей
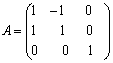 ,
,
после чего получим:
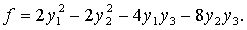
Теперь коэффициенты при 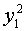 отличен от
нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного.
Полагая
отличен от
нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного.
Полагая
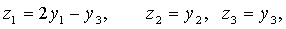
т.е. совершая линейное
преобразование, для которого обратное будет иметь матрицу
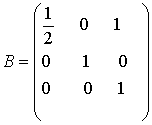
мы приведем 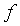 к виду
к виду
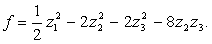
Пока выделился лишь квадрат
неизвестного 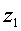 , так как
форма еще содержит произведение двух других неизвестных. Используя неравенство
нулю коэффициента при
, так как
форма еще содержит произведение двух других неизвестных. Используя неравенство
нулю коэффициента при 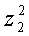 , еще раз
применим изложенный выше метод. Совершая линейное преобразование
, еще раз
применим изложенный выше метод. Совершая линейное преобразование
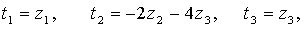
для которого обратное имеет матрицу
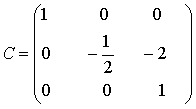 ,
,
мы приведем, наконец, форму 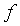 к
каноническому виду
к
каноническому виду

Линейное преобразование, приводящее
(16) сразу к виду (17), будет иметь своей матрицей произведение
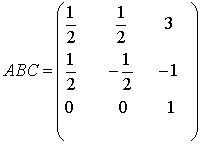 .
.
Можно и непосредственной
подстановкой проверить, что невырожденное ( так как определитель равен 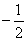 ) линейное
преобразование
) линейное
преобразование
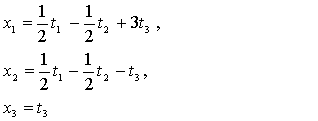
превращает (16) в (17).
Теория приведения квадратичной формы
к каноническому виду построена по аналогии с геометрической теорией центральных
кривых второго порядка, но не может считаться обобщением этой последней теории.
В самом деле, в нашей теории допускается использование любых невырожденных
линейных преобразований, в то время как приведение кривой второго порядка к
каноническому виду достигается применением линейных преобразований весьма
специального вида ,
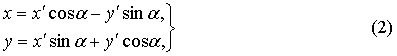
являющихся вращением плоскости. Эта
геометрическая теория может быть, однако, обобщена на случай квадратичных форм
от 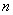 неизвестных
с действительными коэффициентами. Изложение этого обобщения, называемого
приведением квадратичных форм к главным осям, будет дано ниже.
неизвестных
с действительными коэффициентами. Изложение этого обобщения, называемого
приведением квадратичных форм к главным осям, будет дано ниже.
§2.1 Закон инерции
Канонический вид, к которому
приводится данная квадратичная форма, вовсе не является для нее однозначно
определенным: всякая квадратичная форма может быть приведена к каноническому
многими различными способами. Так, рассмотренная в предшествующем параграфе
квадратичная форма 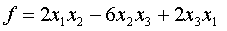 невырожденным
линейным преобразованием
невырожденным
линейным преобразованием
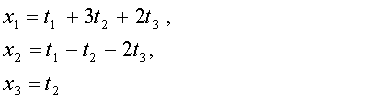
приводится к каноническому виду
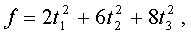
отличному от полученного ранее.
Возникает вопрос, что общего у тех
различных канонических квадратичных форм, к которым приводится данная форма  ? Этот
вопрос тесно связан, как мы видим, с таким вопросом: при каком условии одна из
двух данных квадратичных форм может быть переведена в другую невырожденным
линейным преобразованием? Ответ на эти вопросы зависит, однако, от того,
рассматриваются ли комплексные или действительные квадратичные формы.
? Этот
вопрос тесно связан, как мы видим, с таким вопросом: при каком условии одна из
двух данных квадратичных форм может быть переведена в другую невырожденным
линейным преобразованием? Ответ на эти вопросы зависит, однако, от того,
рассматриваются ли комплексные или действительные квадратичные формы.
Предположим сначала, что
рассматриваются произвольные комплексные квадратичные формы и, вместе с тем,
допускается употребление невырожденных линейных преобразований также с
произвольными комплексными коэффициентами. Мы знаем, что всякая квадратичная
форма  от
от 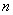 неизвестных,
имеющая ранг
неизвестных,
имеющая ранг 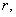 приводится к
каноническому виду
приводится к
каноническому виду
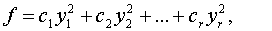
где все коэффициенты 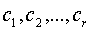 отличны от
нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный
корень, выполним следующее невырожденное линейное преобразование:
отличны от
нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный
корень, выполним следующее невырожденное линейное преобразование:
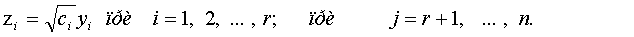
Оно приводит форму  к виду
к виду
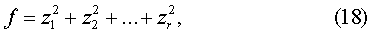
называемому нормальным; это - просто
сумма квадратов 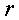 неизвестных
с коэффициентами, равными единице.
неизвестных
с коэффициентами, равными единице.
Нормальный вид зависит лишь от ранга
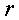 формы
формы 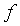 , т.е. все
квадратичные формы ранга
, т.е. все
квадратичные формы ранга 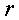 приводятся
к одному и тому же нормальному виду (18). Если, следовательно, формы
приводятся
к одному и тому же нормальному виду (18). Если, следовательно, формы 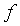 и
и 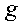 от
от 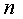 неизвестных
имеют одинаковый ранг
неизвестных
имеют одинаковый ранг 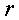 , то можно
перевести
, то можно
перевести 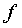 в (18), а
затем (18) в
в (18), а
затем (18) в  , т.е.
существует невырожденное линейное преобразование , переводящее
, т.е.
существует невырожденное линейное преобразование , переводящее 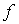 в
в  . Так как, с
другой стороны, никакое невырожденное линейное преобразование не изменяет ранга
формы, то мы приходим к следующему результату.
. Так как, с
другой стороны, никакое невырожденное линейное преобразование не изменяет ранга
формы, то мы приходим к следующему результату.
Теорема:
Две комплексные квадратичные формы
от n неизвестных
тогда и только тогда переводятся друг в друга невырожденными линейными
преобразованиями с комплексными коэффициентами, если эти формы имеют один тот
же ранг.
Из этой теоремы без труда вытекает,
что каноническим видом комплексной квадратичной формы ранга r может
служить всякая сумма квадратов r неизвестных с любыми отличными от
нуля комплексными коэффициентами.
Положение несколько более сложно в
том случае, если рассматриваются действительные квадратичные формы и, что
особенно важно, допускаются лишь линейные преобразования с действительными
коэффициентами. В этом случае уже не всякую форму можно привести к виду (18),
так как это могло бы потребовать извлечения квадратного корня из отрицательного
числа. Если, однако, мы назовем теперь нормальным видом квадратичной формы
сумму квадратов нескольких неизвестных с коэффициентами +1 или -1, то легко
показать, что всякую действительную квадратичную форму 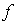 можно
привести невырожденным линейным преобразованием с действительными
коэффициентами к нормальному виду.
можно
привести невырожденным линейным преобразованием с действительными
коэффициентами к нормальному виду.
Форма 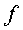 ранга
ранга 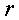 от
от 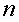 неизвестных
приводится к каноническому виду, который можно записать следующим образом:
неизвестных
приводится к каноническому виду, который можно записать следующим образом:
где все числа 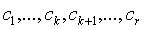 отличны от
нуля и положительны. Тогда невырожденное линейное преобразование с
действительными коэффициентами
отличны от
нуля и положительны. Тогда невырожденное линейное преобразование с
действительными коэффициентами 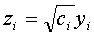 при
при 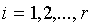 ;
; 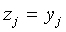 при
при 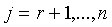 , приводит
, приводит 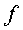 к
нормальному виду,
к
нормальному виду, 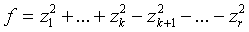 . Общее
число входящих сюда квадратов будет равно рангу формы.
. Общее
число входящих сюда квадратов будет равно рангу формы.
Действительная квадратичная форма
может быть приведена к нормальному виду многими различными преобразованиями,
однако с точностью до нумерации неизвестных она приводится лишь к одному
нормальному виду. Это показывает следующая важная теорема, называемая законом
инерции действительных квадратичных форм.
Теорема. Число положительных и число
отрицательных квадратов в нормальном виде, к которому данная квадратичная форма
с действительными коэффициентами действительным невырожденным линейным
преобразованием, не зависят от выбора этого преобразования.
Доказательство. Пусть квадратичная
форма 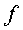 ранга
ранга 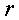 от
от 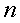 неизвестных
неизвестных
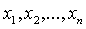 двумя
способами приведена к нормальному виду:
двумя
способами приведена к нормальному виду:
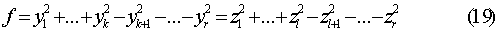
Так как переход от неизвестных 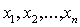 к
неизвестным
к
неизвестным 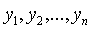 был
невырожденным линейным преобразованием, то, обратно, вторые неизвестные также
будут линейно выражаться через первые с отличным от нуля определителем:
был
невырожденным линейным преобразованием, то, обратно, вторые неизвестные также
будут линейно выражаться через первые с отличным от нуля определителем:
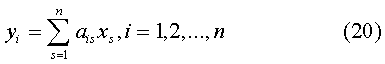 .
.
Аналогично,
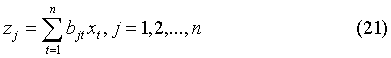 ,
,
причем определитель из коэффициентов
снова отличен от нуля. Коэффициенты же как в (20), так и в (21) -
действительные числа.
Можно предположить, что 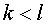 , и написать
систему равенств
, и написать
систему равенств
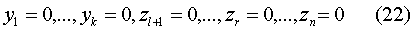
Если левые части этих равенств будут
заменены их выражениями из (20), и (21), получится система 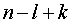 линейных
однородных уравнений с
линейных
однородных уравнений с 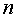 неизвестными
неизвестными
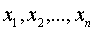 . Число
уравнений в этой системе равно меньше числа неизвестных, поэтому система
обладает ненулевым действительным решением
. Число
уравнений в этой системе равно меньше числа неизвестных, поэтому система
обладает ненулевым действительным решением 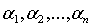 .
.
Необходимо заменить в равенстве (19)
все 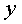 и все
и все 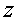 их
выражениями (20) и (21), а затем подставить вместо неизвестных числа
их
выражениями (20) и (21), а затем подставить вместо неизвестных числа 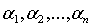 . Если через
. Если через
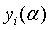 и
и 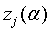 будут
обозначены значения неизвестных
будут
обозначены значения неизвестных 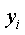 и
и 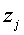 , получающиеся после такой
подстановке, то (19) превращается в равенство
, получающиеся после такой
подстановке, то (19) превращается в равенство
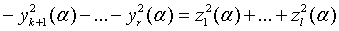 (23)
(23)
Так как все коэффициенты в (20) и
(21) действительные, то все квадраты, входящие в равенство (23),положительны, а
поэтому (23) влечет за собой равенство всех этих квадратов; отсюда следует
равенства
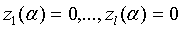 (24)
(24)
С другой стороны, по самому выбору
чисел 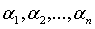
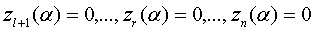 (25)
(25)
Таким образом, система 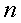 линейных
однородных уравнений
линейных
однородных уравнений 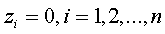 , с
, с 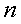 неизвестными
неизвестными
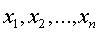 обладает,
ввиду (24) и (25), ненулевым решением
обладает,
ввиду (24) и (25), ненулевым решением 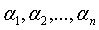 , то есть определитель этой системы
должен быть равен нулю. Это противоречит, однако, тому, что преобразование (21)
предполагалась невырожденным. Такое же противоречие будет, если
, то есть определитель этой системы
должен быть равен нулю. Это противоречит, однако, тому, что преобразование (21)
предполагалась невырожденным. Такое же противоречие будет, если 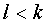 . Отсюда следует
равенство
. Отсюда следует
равенство 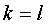 ,
доказывающее теорему.
,
доказывающее теорему.
Число положительных квадратов в той
нормальной форме, к которой приводится данная действительная квадратичная форма
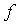 , называется
положительным индексом инерции этой формы, число отрицательных квадратов -
отрицательным индексом инерции, а разность между положительным и отрицательным
индексами инерции - сигнатурой формы
, называется
положительным индексом инерции этой формы, число отрицательных квадратов -
отрицательным индексом инерции, а разность между положительным и отрицательным
индексами инерции - сигнатурой формы 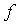 .
.
Теорема. Две квадратичные формы от 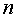 неизвестных
с действительными коэффициентами тогда и только тогда переводятся друг в друга
невырожденными действительными линейными преобразованиями, если эти формы имеют
одинаковые ранги и одинаковые сигнатуры.
неизвестных
с действительными коэффициентами тогда и только тогда переводятся друг в друга
невырожденными действительными линейными преобразованиями, если эти формы имеют
одинаковые ранги и одинаковые сигнатуры.
Доказательство. Пусть форма 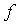 переводится
в форму
переводится
в форму  невырожденным
действительным преобразованием. Уже известно, что преобразование не меняет
ранга формы. Оно и не может менять сигнатуры, так как противном случае
невырожденным
действительным преобразованием. Уже известно, что преобразование не меняет
ранга формы. Оно и не может менять сигнатуры, так как противном случае 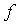 и
и  приводились
бы к различным нормальным видам, а тогда и форма
приводились
бы к различным нормальным видам, а тогда и форма 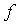 приводилась бы, в противоречие с
законом инерции, к этим обоим нормальным видам. Обратно, если формы
приводилась бы, в противоречие с
законом инерции, к этим обоим нормальным видам. Обратно, если формы 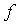 и
и  имеют
одинаковые ранги и одинаковые сигнатуры, то они приводятся к одному и тому же
нормальному виду и поэтому могут быть переведены друг в друга.
имеют
одинаковые ранги и одинаковые сигнатуры, то они приводятся к одному и тому же
нормальному виду и поэтому могут быть переведены друг в друга.
Если дана квадратичная форма  в
каноническом виде,
в
каноническом виде,
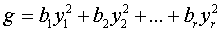 , (26)
, (26)
с неравными нулю действительными
коэффициентами, то ранг этой формы равен 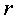 . Если приводить такую форму к
нормальному виду, то можно увидеть, что положительный индекс инерции формы
. Если приводить такую форму к
нормальному виду, то можно увидеть, что положительный индекс инерции формы  равен числу
положительных коэффициентов в правой части равенства (3.9). Отсюда и вытекает
такой результат:
равен числу
положительных коэффициентов в правой части равенства (3.9). Отсюда и вытекает
такой результат:
Квадратичная форма 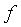 тогда и
только тогда будет иметь форму (26) своим каноническим видом, если ранг формы
тогда и
только тогда будет иметь форму (26) своим каноническим видом, если ранг формы 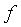 равен
равен 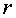 , а
положительный индекс инерции этой формы совпадает с числом положительных
коэффициентов в (26).
, а
положительный индекс инерции этой формы совпадает с числом положительных
коэффициентов в (26).
§2.2 Распадающиеся квадратичные
формы
Перемножая любые две линейные формы
от 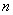 неизвестных,
неизвестных,
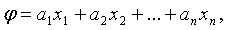
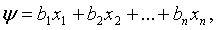
мы получим, очевидно, некоторую
квадратичную форму. Не всякая квадратичная форма может быть представлена в виде
произведения двух линейных форм, и для этого необходимо ввести условие, при
которых это имеет место, то есть при которых квадратичная форма является
распадающейся.
Комплексная квадратичная форма
распадается тогда и только тогда, если ее ранг меньше или равен двум.
Действительная квадратичная форма 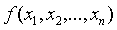 распадается тогда и только тогда,
если ее ранг не больше единицы, или же он равен нулю, а сигнатура равна нулю.
распадается тогда и только тогда,
если ее ранг не больше единицы, или же он равен нулю, а сигнатура равна нулю.
Для начала необходимо рассмотреть
произведение линейных форм 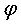 и
и 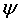 . Если хотя бы одна из этих форм
нулевая, то их произведение будет квадратичной формой с нулевыми
коэффициентами, то есть оно имеет ранг 0. Если линейные формы
. Если хотя бы одна из этих форм
нулевая, то их произведение будет квадратичной формой с нулевыми
коэффициентами, то есть оно имеет ранг 0. Если линейные формы 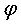 и
и 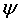 пропорциональны,
пропорциональны,
 , причем
, причем 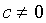 и форма
и форма 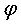 ненулевая,
то пусть, например, коэффициент
ненулевая,
то пусть, например, коэффициент 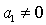 . Тогда невырожденное линейное
преобразование
. Тогда невырожденное линейное
преобразование
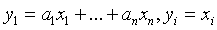 при
при 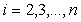
приводит квадратичную форму 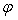
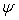 к виду
к виду
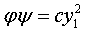 .
.
Справа стоит квадратичная форма
ранга 1, а поэтому и квадратичная форма 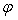
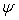 имеют ранг 1. Если же, линейные
формы
имеют ранг 1. Если же, линейные
формы 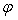 и
и 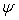 не являются
пропорциональными, то пусть, например,
не являются
пропорциональными, то пусть, например, .
.
Тогда линейное преобразование
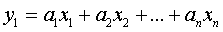 ,
,
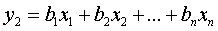 ,
,
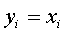 при
при 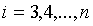
будет невырожденным; оно приводит
квадратичную форму 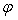
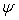 к виду
к виду
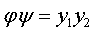 .
.
Справа стоит квадратичная форма
ранга 2, имеющая в случае действительных коэффициентов сигнатуру 0.
Необходимо перейти к доказательству
обратного утверждения. Квадратичная форма ранга 0 может, конечно,
рассматриваться как произведение двух линейных форм, одна из которых нулевая.
Далее, квадратичная форма 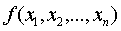 ранга 1
невырожденная линейным преобразованием приводится к виду
ранга 1
невырожденная линейным преобразованием приводится к виду
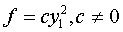 ,
,
то есть к виду
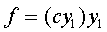 .
.
Выражая 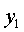 линейно
через
линейно
через 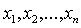 , получится
представление формы
, получится
представление формы 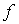 в виде
произведения двух линейных форм. Тогда действительная квадратичная форма
в виде
произведения двух линейных форм. Тогда действительная квадратичная форма 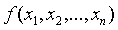 ранга 2 и
сигнатуры 0 приводится невырожденным линейным преобразованием к виду
ранга 2 и
сигнатуры 0 приводится невырожденным линейным преобразованием к виду 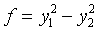 .
.
К этому же виду может быть приведена
любая комплексная квадратичная форма ранга 2. Однако
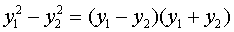 ,
,
но справа, после замены 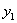 и
и 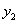 их
линейными выражениями через
их
линейными выражениями через 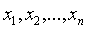 , будет стоять произведение двух
линейных форм. Теорема доказана.
, будет стоять произведение двух
линейных форм. Теорема доказана.
§3. Положительно определенные формы
Квадратичная форма 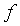 от
от 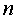 неизвестных
с действительными коэффициентами называется положительно определенной, если она
приводится к нормальному виду, состоящему из
неизвестных
с действительными коэффициентами называется положительно определенной, если она
приводится к нормальному виду, состоящему из 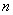 положительных квадратов, то есть
если и ранг, и положительный индекс инерции этой формы равны числу неизвестных.
положительных квадратов, то есть
если и ранг, и положительный индекс инерции этой формы равны числу неизвестных.
Теорема. Квадратичная форма 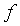 от
от 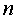 неизвестных
неизвестных
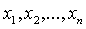 с
действительными коэффициентами тогда и только тогда будет положительно
определенной, если при всяких действительных значениях этих неизвестных, хотя
бы одно из которых отлично от нуля, эта форма получает положительные значения.
с
действительными коэффициентами тогда и только тогда будет положительно
определенной, если при всяких действительных значениях этих неизвестных, хотя
бы одно из которых отлично от нуля, эта форма получает положительные значения.
Доказательство. Пусть форма 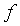 положительно
определенная, то есть приводится к нормальному виду
положительно
определенная, то есть приводится к нормальному виду
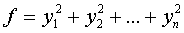 , (27)
, (27)
причем
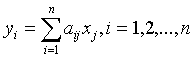 , (28)
, (28)
с отличным от нуля определителем из
действительных коэффициентов 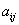 . Если подставить в
. Если подставить в  произвольные
действительные значения неизвестных
произвольные
действительные значения неизвестных 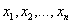 , хотя бы одно из которых отлично от
нуля, то можно подставить их сначала в (28), а затем значения полученные, для
всех
, хотя бы одно из которых отлично от
нуля, то можно подставить их сначала в (28), а затем значения полученные, для
всех 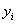 , - в (27).
Значения, полученные для
, - в (27).
Значения, полученные для 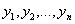 из (28), не
могут все сразу равняться нулю, так как иначе получилось бы, что система
линейных однородных уравнений
из (28), не
могут все сразу равняться нулю, так как иначе получилось бы, что система
линейных однородных уравнений 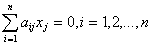 обладает ненулевым решением, хотя
ее определитель отличен от нуля. Подставляя найденные для
обладает ненулевым решением, хотя
ее определитель отличен от нуля. Подставляя найденные для 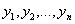 значения в
(27), получатся значения формы
значения в
(27), получатся значения формы  , равное сумме квадратов
, равное сумме квадратов 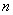 действительных
чисел, которые не все равны нулю; это значение будет строго положительным.
действительных
чисел, которые не все равны нулю; это значение будет строго положительным.
Обратно, пусть форма  не является
положительно определенной, то есть или ранг, или положительный индекс инерции
меньше
не является
положительно определенной, то есть или ранг, или положительный индекс инерции
меньше 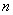 . Это
означает, что в нормальном виде этой формы, к которому она приводится,
невырожденным линейным преобразованием (28), квадрат хотя бы одного из новых
неизвестных, например
. Это
означает, что в нормальном виде этой формы, к которому она приводится,
невырожденным линейным преобразованием (28), квадрат хотя бы одного из новых
неизвестных, например 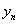 , или
отсутствует совсем, или же содержится со знаком минус. В этом случае можно
подобрать такие действительные значения для неизвестных
, или
отсутствует совсем, или же содержится со знаком минус. В этом случае можно
подобрать такие действительные значения для неизвестных 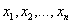 , которые не
все равны нулю, что значения формы
, которые не
все равны нулю, что значения формы  при этих значениях неизвестных
равно нулю или даже отрицательно. Такими будут, например, те значения для
при этих значениях неизвестных
равно нулю или даже отрицательно. Такими будут, например, те значения для 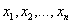 , которые мы
получим, решая по правилу Крамера систему линейных уравнений, получающихся из
(28) при
, которые мы
получим, решая по правилу Крамера систему линейных уравнений, получающихся из
(28) при 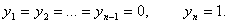 Действительно,
при этих значениях неизвестных
Действительно,
при этих значениях неизвестных 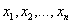 форма
форма  равна нулю,
если
равна нулю,
если 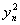 не входит в
нормальный вид этой формы, и равна -1, если
не входит в
нормальный вид этой формы, и равна -1, если 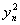 входит в нормальный вид со знаком
минус.
входит в нормальный вид со знаком
минус.
Пусть дана квадратичная форма  от
от 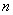 неизвестных
с матрицей
неизвестных
с матрицей 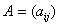 . Миноры
порядка
. Миноры
порядка 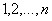 этой
матрицы, расположенные в ее левом углу, то есть миноры
этой
матрицы, расположенные в ее левом углу, то есть миноры
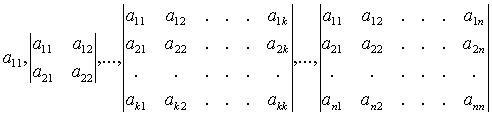 ,
,
из которых последний совпадает с
определителем матрицы 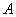 , называются
главными минорами формы
, называются
главными минорами формы  .
.
Теорема. Квадратичная форма  от
от 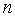 неизвестных
с действительными коэффициентами тогда и только тогда будет положительно
определенной, если все главные миноры строго положительны.
неизвестных
с действительными коэффициентами тогда и только тогда будет положительно
определенной, если все главные миноры строго положительны.
Доказательство. При 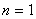 теорема
верна, так как форма имеет в этом случае вид
теорема
верна, так как форма имеет в этом случае вид 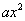 и поэтому она положительно
определенная тогда и только тогда, когда
и поэтому она положительно
определенная тогда и только тогда, когда 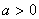 . Поэтому необходимо доказывать
теорему для случая
. Поэтому необходимо доказывать
теорему для случая 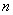 неизвестных,
предполагая, что для квадратичных форм от
неизвестных,
предполагая, что для квадратичных форм от 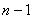 неизвестных она уже доказана.
неизвестных она уже доказана.
Сделаем сначала следующее замечание:
Если квадратичная форма  с
действительными коэффициентами, составляющими матрицу
с
действительными коэффициентами, составляющими матрицу 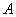 ,
подвергается невырожденному линейному преобразованию с действительной матрицей
,
подвергается невырожденному линейному преобразованию с действительной матрицей 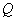 , то знак
определителя формы ( т.е. определителя ее матрицы) не меняется.
, то знак
определителя формы ( т.е. определителя ее матрицы) не меняется.
После преобразования получается
квадратичная форма с матрицей 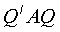 , однако, ввиду
, однако, ввиду 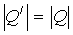 ,
, 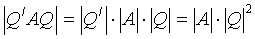 , то есть
определитель
, то есть
определитель 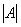 умножается
на положительное число.
умножается
на положительное число.
Пусть дана квадратичная форма
Ее можно записать в виде
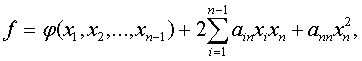 (29)
(29)
где 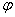 будет квадратичной формой от
будет квадратичной формой от 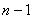 неизвестных,
составленной из тех членов формы
неизвестных,
составленной из тех членов формы  , в которые не входит неизвестное
, в которые не входит неизвестное 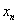 . Главные
миноры формы
. Главные
миноры формы 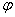 совпадают,
очевидно, со всеми, кроме последнего, главными минорами формы
совпадают,
очевидно, со всеми, кроме последнего, главными минорами формы  .
.
Пусть форма  положительно
определенная. Форма
положительно
определенная. Форма 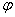 также будет
положительно определенной: если бы существовали такие значения неизвестных
также будет
положительно определенной: если бы существовали такие значения неизвестных 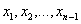 , не все
равны нулю, при которых форма
, не все
равны нулю, при которых форма 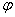 получает не строго положительное
значение, то полагая дополнительно
получает не строго положительное
значение, то полагая дополнительно 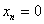 , то получилось бы (29), также не
строго положительное значение формы
, то получилось бы (29), также не
строго положительное значение формы  , хотя не все значения неизвестных
, хотя не все значения неизвестных 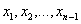 ,
, 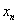 равны нулю.
Поэтому, по индуктивному предложению, все главные миноры формы
равны нулю.
Поэтому, по индуктивному предложению, все главные миноры формы  , кроме
последнего, строго положительны. Что же касается последнего главного минора
формы
, кроме
последнего, строго положительны. Что же касается последнего главного минора
формы  , то есть
определителя самой матрицы
, то есть
определителя самой матрицы 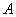 , то его положительность вытекает из
следующих соображений: форма
, то его положительность вытекает из
следующих соображений: форма  , которая положительно определенная
с линейным невырожденным преобразованием приводится к нормальному виду,
состоящей из
, которая положительно определенная
с линейным невырожденным преобразованием приводится к нормальному виду,
состоящей из 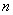 положительных
квадратов. Определитель этого нормального вида строго положителен, а поэтому
ввиду сделанного выше замечания положителен и определитель самой формы
положительных
квадратов. Определитель этого нормального вида строго положителен, а поэтому
ввиду сделанного выше замечания положителен и определитель самой формы  .
.
Пусть теперь строго положительны
главные миноры формы  . Отсюда
вытекает положительность всех главных миноров
. Отсюда
вытекает положительность всех главных миноров 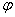 , то есть, по индуктивному,
предположению, положительная определенность этой формы. Следовательно,
существует, такое невырожденное линейное преобразование неизвестных
, то есть, по индуктивному,
предположению, положительная определенность этой формы. Следовательно,
существует, такое невырожденное линейное преобразование неизвестных 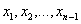 , которое
приводит форму
, которое
приводит форму 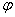 к виду
суммы
к виду
суммы 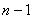 положительных
квадратов от новых неизвестных
положительных
квадратов от новых неизвестных 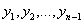 , то линейное преобразование можно
дополнить до невырожденного линейного преобразования всех неизвестных
, то линейное преобразование можно
дополнить до невырожденного линейного преобразования всех неизвестных 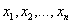 , полагая
, полагая 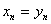 . Ввиду (29)
форма
. Ввиду (29)
форма  приводится
к указанным преобразованием к виду:
приводится
к указанным преобразованием к виду:
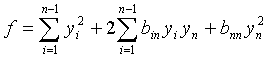 ; (30)
; (30)
точные выражения коэффициентов 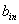 несущественны.
Так как
несущественны.
Так как 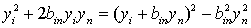 , то невырожденное
линейное преобразование
, то невырожденное
линейное преобразование 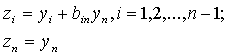 приводит
форму
приводит
форму  к
каноническому виду
к
каноническому виду
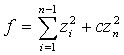 . (31)
. (31)
Для доказательства положительной
определенности формы  необходимо
доказать положительность числа
необходимо
доказать положительность числа 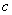 . Определитель формы, стоящий в
правой части равенства (31), равен
. Определитель формы, стоящий в
правой части равенства (31), равен 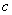 . Этот определитель должен быть
положительным, так как правая часть равенства (31) получена из формы
. Этот определитель должен быть
положительным, так как правая часть равенства (31) получена из формы  двумя
невырожденными линейными преобразованиями, а определитель формы
двумя
невырожденными линейными преобразованиями, а определитель формы  был
последний из главных миноров этой формы, положительным. Теорема доказана .
был
последний из главных миноров этой формы, положительным. Теорема доказана .
Пример 2. Является ли квадратичная
форма положительно определенной 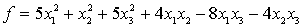 ?
?
Решение
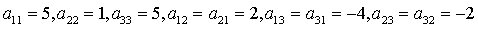 .
.
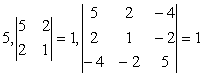 .
.
Квадратичная форма является
положительно определенной, так как все ее главные миноры положительны.
Пример 3. Является ли квадратичная
форма положительно определенной 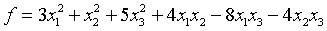 ?
?
Решение
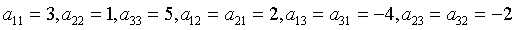 .
.
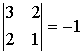 .
.
Квадратичная форма не является
положительно определенной, так как ее главный минор отрицателен.
§4.Примеры решения задач
квадратичных форм
Задача № 1. Написать матрицу
квадратичной формы 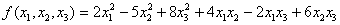 .
.
Решение
Здесь 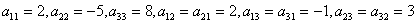
Следовательно: 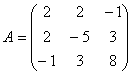
Задача № 2. Привести к каноническому
виду квадратичную форму 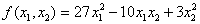 .
.
Решение
Коэффициенты: 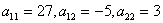 .
.
Составим характеристическое
уравнение 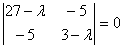 ;
;
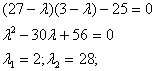
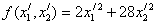
Задача № 3. Привести к каноническому
виду уравнение второго порядка: 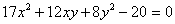 .
.
Решение
Коэффициенты 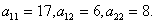
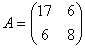 .
.
Составим характеристическое
уравнение: 
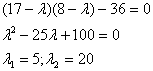
Итого: 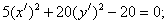
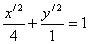 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Задача № 4. Привести к каноническому
виду уравнение второго порядка: 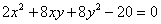
Решение
Коэффициенты 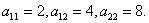
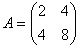 .
.
Составим характеристическое
уравнение: 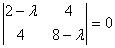
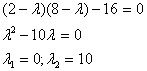
Итого: 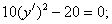
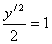 - каноническое уравнение параболы.
- каноническое уравнение параболы.
Задача № 5. Привести к каноническому
виду уравнение второго порядка: 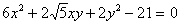 .
.
Решение
Коэффициенты 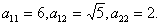
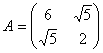 .
.
Составим характеристическое
уравнение: 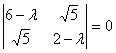
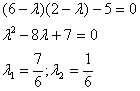
Итого: 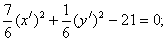
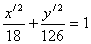 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Задача № 6 Привести к каноническому
виду уравнение второго порядка: 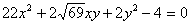 .
.
Решение
Коэффициенты 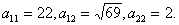
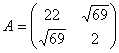 .
.
Составим характеристическое
уравнение: 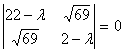
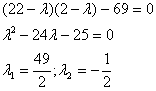
Итого: 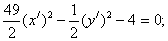
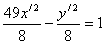 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 7. Привести к каноническому
виду уравнение второго порядка: 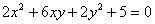 .
.
Решение
Коэффициенты 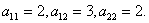
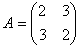 .
.
Составим характеристическое
уравнение: 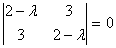
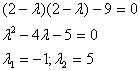
Итого: 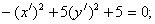
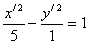 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 8. Привести к каноническому
виду уравнение второго порядка: 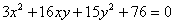 .
.
Решение
Коэффициенты 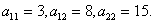
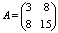 .
.
Составим характеристическое
уравнение: 
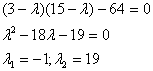
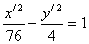 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 9. Привести к каноническому
виду уравнение второго порядка: 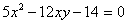
Решение
Коэффициенты 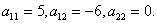
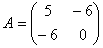 .
.
Составим характеристическое
уравнение: 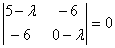
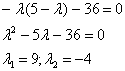
Итого: 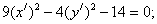
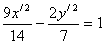 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 10. Привести к
каноническому виду уравнение второго порядка: 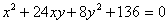 .
.
Решение
Коэффициенты 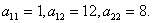
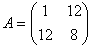 .
.
Составим характеристическое
уравнение: 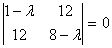
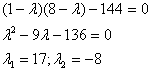
Итого: 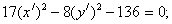
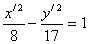 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 11. Привести к
каноническому виду уравнение второго порядка: 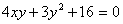 .
.
Решение
Коэффициенты 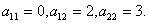
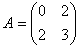 .
.
Составим характеристическое
уравнение: 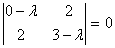
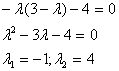
Итого: 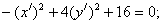
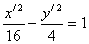 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 12. Привести к
каноническому виду уравнение второго порядка: 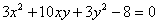 .
.
Решение
Коэффициенты 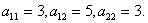
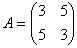 .
.
Составим характеристическое
уравнение: 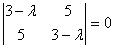
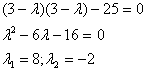
Итого: 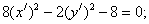
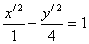 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 13. Привести к
каноническому виду уравнение второго порядка: 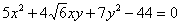 .
.
Решение
Коэффициенты 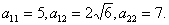
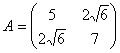 .
.
Составим характеристическое
уравнение: 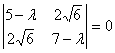
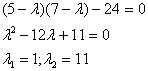
Итого: 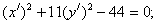
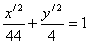 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Задача № 14. Привести к
каноническому виду уравнение второго порядка: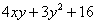 .
.
Решение
Коэффициенты: 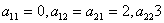 .
.
Составим характеристическое
уравнение: 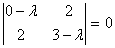 ;
;
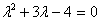
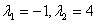 .
.
Итого: 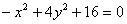
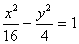 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
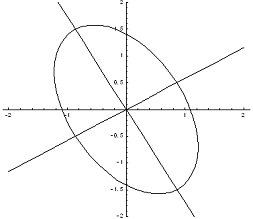
Задача № 15. Используя теорию
квадратичных форм, привести к каноническому виду уравнение линии второго
порядка. Схематично изобразить график 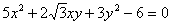 .
.
Решение
Составим характеристическое
уравнение квадратичной формы. Коэффициенты 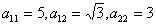 .
.
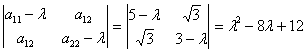
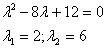
Найдем координаты собственных
векторов:
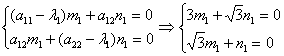 ,пологая что
,пологая что 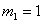 , тогда
, тогда 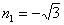 ;
;
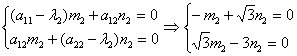 ,пологая что
,пологая что 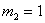 , тогда
, тогда 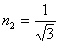 .
.
Собственные векторы: 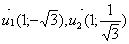
 .
.
Находим координаты единичных
векторов нового базиса
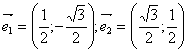 .
.
Имеем следующее уравнение линии в
новой системе координат:
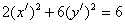 .
.
Каноническое уравнение линии в новой
системе координат будет иметь вид:
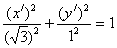 .
.
Задание № 16. Является ли
квадратичная форма положительно определенной 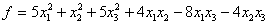 ?
?
Решение
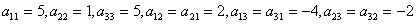 .
.
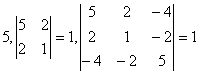 .
.
Квадратичная форма является
положительно определенной, так как все ее главные миноры положительны.
Задание № 17. Является ли
квадратичная форма положительно определенной 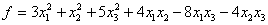 ?
?
Решение
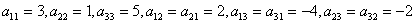 .
.
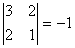 . Квадратичная форма не является
положительно определенной, так как ее главный минор отрицателен.
. Квадратичная форма не является
положительно определенной, так как ее главный минор отрицателен.
Решение
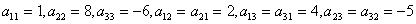 .
.
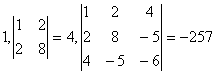 . Квадратичная форма является не
положительно определенной, так как не все ее главные миноры положительны.
. Квадратичная форма является не
положительно определенной, так как не все ее главные миноры положительны.
Задание № 19. Дана квадратичная
форма 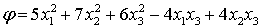 . Привести
её к каноническому виду.
. Привести
её к каноническому виду.
Решение
Составим характеристическое
уравнение
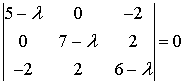
или 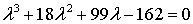 . Корни этого уравнения
. Корни этого уравнения 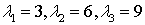 .
Собственные векторы, определяющие главные направления квадратичной формы найдём
из системы:
.
Собственные векторы, определяющие главные направления квадратичной формы найдём
из системы:
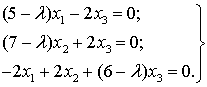 (1)
(1)
Подставляя сюда поочередно значения 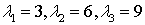 и беря
каждый раз нормированное решение системы (1), получаем:
и беря
каждый раз нормированное решение системы (1), получаем:
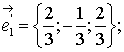
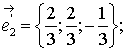
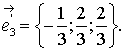
Формулы преобразования координат при
переходе к этому базису:
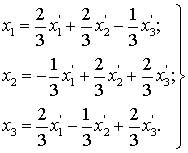
В базисе 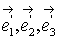 квадратичная
форма имеет канонический вид
квадратичная
форма имеет канонический вид
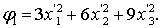
Задание № 20. Привести к
каноническому виду квадратичную форму
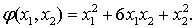
Решение
Составим уравнение

или 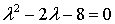 . Отсюда
. Отсюда 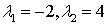 .
Канонический вид данной квадратичной формы
.
Канонический вид данной квадратичной формы 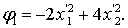
Для того чтобы найти базис, в
котором форма имеет вид, необходима найти собственные векторы симметрического
линейного преобразования с матрицей
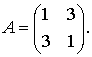
Запишем систему уравнений,
определяющую искомые собственные векторы:
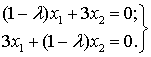 (1)
(1)
Подставляя сюда 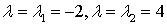 и беря
каждый раз нормированное решение системы (1), найдем векторы, определяющие
главные направления квадратичной формы:
и беря
каждый раз нормированное решение системы (1), найдем векторы, определяющие
главные направления квадратичной формы:
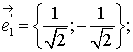
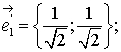
Они составляют нужный базис.
При переходе к базису 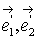 координаты
всех векторов преобразуются по формулам:
координаты
всех векторов преобразуются по формулам:
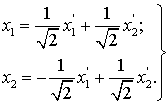
Задание № 21. Найти для квадратичной
формы
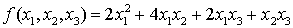
её матрицу.
Решение
Для данной квадратичной формы
запишем
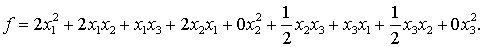
Следовательно её матрица равна
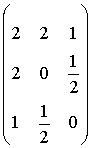 .
.
Задание № 22. С помощью линейных
преобразований переменных преобразуем квадратичную форму 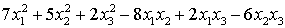 в
канонический вид.
в
канонический вид.
После преобразования
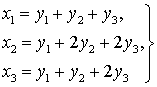
Перейдёт в форму с матрицей
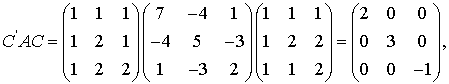
т.е в форму 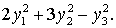
Квадратная матрица вида
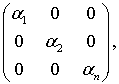
у которой все элементы вне главной
диагонали равны нулю, называется диагональной (канонической) матрицей.
Заключение
В выполненной работе рассмотрены
математические постановки для изучения материала: приведение квадратичной формы
к каноническому виду, законы инерции, положительно определенные формы.
Для того чтобы использовать
квадратичные формы на практике, вначале необходимо привести ее к каноническому
виду. Всякая квадратичная форма может быть приведена некоторым невырожденным
линейным преобразованием к каноническому виду. Любую действительную
квадратичную форму можно привести невырожденным линейным преобразованием с
действительными коэффициентами к нормальному виду. Если две квадратичные формы
с действительными коэффициентами имеют одинаковые ранги и одинаковые сигнатуры,
то эти формы могут быть переведены друг в друга невырожденными действительными
линейными преобразованиями. Квадратичная форма с действительными коэффициентами
будет положительно определенной, если все главные миноры строго положительны,
или если при всяких действительных значениях неизвестных, хотя бы одно из
которых отлично от нуля.
В процессе выполнения работы была рассмотрена не
только теоретическая часть, но и практическая, в которой решены задачи по
данным подтемам.
Список использованной литературы
1. Александров
П.С., Лекции по аналитической геометрии, пополненные необходимыми сведениями из
алгебры, «Наука», 1968.
2. Высшая
математика в упражнениях и задачах/Данко П.Е., Попов А.Г., Кожевникова Т.Я.-М.,
1986;
. Задачник
по линейной алгебре/ Икрамов Х.Д. - М., 1975;
4. Курс
высшей алгебры/ Курош А.Г.- М., 1968;
. Элементы
линейной алгебры и аналитической геометрии/ Бугров Я.С., Никольский
С.М.-М.,1980.