Расчет напряженно-деформированного состояния тела в потоке воздуха

К вопросу расчета напряженно деформированного состояния тела в потоке воздуха

Рассматриваются особенности расчета напряженно-деформированного состояния воздухоопорной оболочки методами теории открытых систем (OST) и методами безмоментной теории оболочек (MTS). Результаты расчета сравниваются с экспериментальными данными взаимодействия оболочки с потоком воздуха.

Исходные данные:

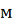
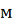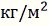
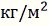Масштабы: линейные (); углов (рад); модулей, давлений и нагрузок (); сил (кг/м); перемещения- безразмерные (доли R). Система координат - сферическая. Неподвижная

На оболочку действует поток воздуха переменной скоростью. Результатом эксперимента являются:

- начальное распределени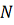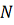е  частиц системы в 6-мерном пространстве .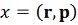

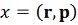За начальное распределение принимается выборка координат и импульсов .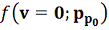

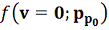конечное распределени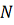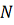е  частиц системы в 6-мерном пространстве .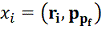

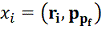Данные распределения координат и импульсов и форма оболочки начальная и в потоке воздуха получены экспериментальным путем. Погрешность измерений мне более 0,2%

За конечное распределение принимается выборка координат и импульсов соответствующая, например, скорости потока .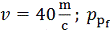

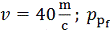Для краткости приводим сравнения только для главного меридиана оболочки.

Расчеты методами OSP предполагают: изменение формы тела в потоке, необратимые по времени процессы в виде учета трения и диффузии воздуха через материал.

В общем виде в открытых системах для описания неравновесных процессов используется кинетическое уравнение движения частиц :

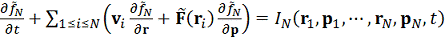
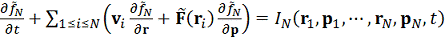
где: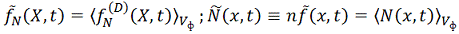

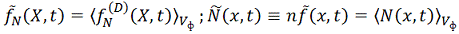
сглаженное распределение координат и импульсов. Распределени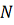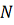е  частиц в 6-мерном фазовом пространстве .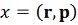

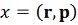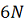
Рассмотрим 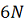- мерное фазовое пространство 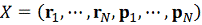 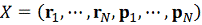с динамическим распределением

.

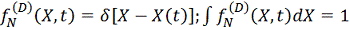
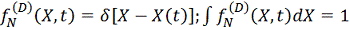С учетом усреднения по ансамблю Гиббса можно записать:

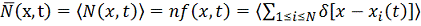
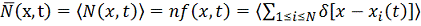
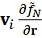
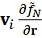 - зависимость скорости движения и изменения функции распределения частицы по координатам;

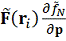
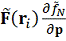 - зависимость внешних сил, приведенных к срединной линии и изменения функции распределения по импульсам;

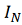
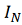 - интеграл взаимодействия, определяет изменения координат и импульсов частицы (внутренние силы), вызванные изменением функции распределений и корреляции функций распределения частиц и сил.

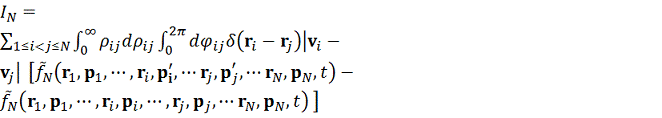
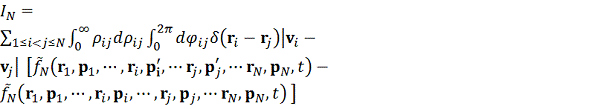
Уравнение учитывает взаимодействия (столкновения) всех пар частиц 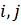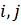. Импульсы 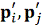 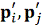связаны с импульсами 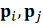 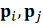законами сохранения импульса и кинетической энергии пары частиц.

Функция распределения 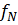 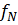определяется в виде: .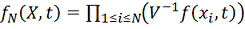

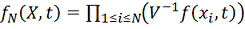Равновесным решением уравнения Леонтовича в отсутствии внешних сил является распределение Максвелла: 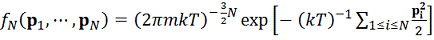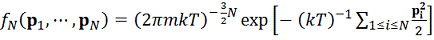. Распределение Максвелла делает функцию распределения зависимой только от импульсов. Этот прием используется в механике сплошной среды для уравнений равновесия.

Для статистического распределения 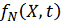 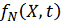уравнение движения записывается в виде:

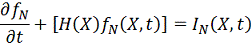
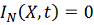
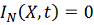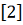
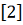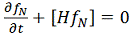
Если положить , то получим уравнение  Лиувилля 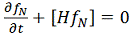. Уравнение описывает движение частиц консервативной системы (обмен только энергией).

Наряду с этим уравнением можно использовать уравнения Гамильтона .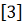

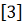Решением уравнения Леонтовича для известной функции распределения (экспериментальные значения) является определение интеграла взаимодействий, затем определение внутренних сил в безразмерном виде и определение перемещений.

В настоящее время расчеты напряженно-деформированного состояния сооружений (например, оболочек) под внешними воздействиями определяется методами механики сплошной среды, в частности для тонких тел уравнениями равновесия безмоментной теории оболочек . Основные гипотезы (приближения), используемые для решения задач методами классической механики.

Гипотезы сплошной среды формулируются в виде: сплошности среды, метрического эвклидова пространства, макроскопичности механических свойств материалов. Гипотезы приводят к рассмотрению движения методами механики сплошной среды. Методы сплошной среды рассматривают обратимые процессы по времени, для частиц в состоянии равновесия и отсутствия обмена веществом и информацией. Для методов механики сплошной среды характерным является соблюдение условий теории возмущений. Форма оболочки считается квазистационарной, изменения внутреннего давления малыми.

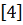
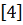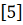
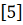Для рассмотрения напряженно-деформированного состояния объекта в условиях равновесия методами  MTS используется гипотезы: Кирхгофа - Лява, Тимошенко и отсутствия взаимодействия между слоями. Дальнейшие приближения в виде физической гипотезы и распределения деформаций по толщине приводят к теории тонких упругих оболочек и, в частности безмоментной теории . Следующие гипотезы  об отсутствии учета некомпенсированных сжимающих сил приводят к теориям мягких оболочек .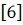

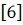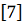
Нормами , стандартами  и специальной литературой  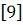предлагаются различные эпюры распределения коэффициентов давлений по поверхности сооружений. Эпюры описывают модельное распределение давлений, составленное из максимальных величин коэффициентов, фактическое распределение давлений не учитывается. Для расчета напряженно-деформированного состояния сооружения воспользуемся данными экспериментальных  исследований оболочки в потоке воздуха в аэродинамической трубе Т101 ЦАГИ 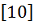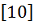, выполненными с участием автора.

Рассмотрим взаимодействие мягкой оболочки с потоком воздуха .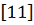

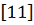Экспериментальными исследованиями установлено:

существенное отличие формы оболочки при больших скоростях потока от проектной формы (сферическая поверхность);

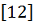
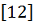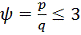
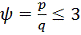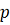
наличие в зоне активного действия потока областей складок в кольцевом направлении  и наличие складки у контура в меридиональном направлении для диапазонов  (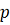- избыточное давление в оболочке, 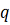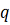- скоростной напор потока).

Наличие складчатых зон не позволяет для расчетов напряженно-деформированного состояния использовать теорию мягких оболочек. Компенсация сжимающих усилий в кольцевом направлении ведет к изменению объема, росту 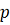 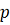и поточной формы оболочки, далекой от проектной, сферической.

Дискретные значения распределения нагрузок в расчетах тонких оболочек по безмоментной теории 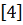 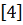, а также значения усилий и перемещений приводятся к безразмерному виду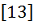

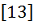
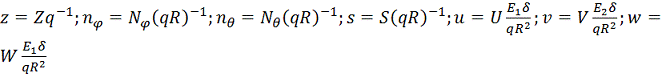
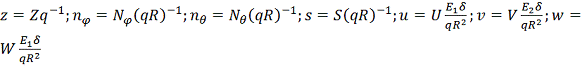
Из экспериментальных исследований получаем распределение безразмерных коэффициентов .

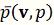
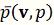В качестве примера рассмотрим распределение коэффициентов 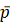 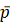для главного меридиана сферической оболочки при скорости потока 40м/с. Распределение представлено Рис.1

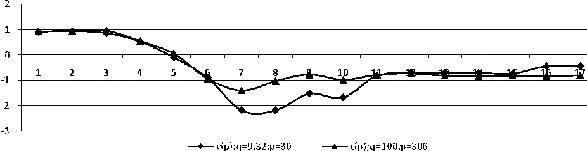
Рис.1. Распределение 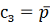 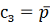 по главному меридиану оболочки

Ось абсцисс дренажные точки главного меридиана, ось ординат коэффициенты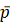

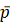
Нормальная нагрузка от потока аппроксимируется рядом:

.

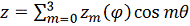
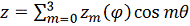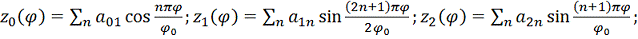
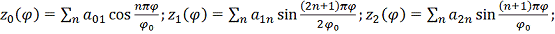
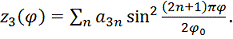
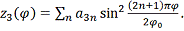
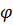
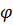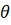
где: - широта; 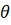- долгота,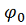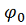- широта края оболочки;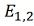 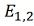- модули упругости.

Уравнения равновесия по методу MTS записываются в виде:

;

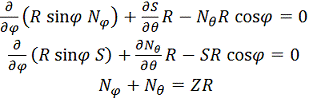
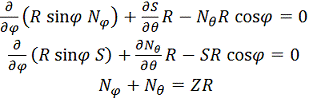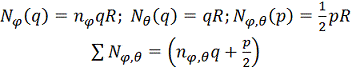
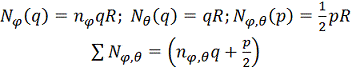
Уравнения перемещений записываются в виде:

;

;

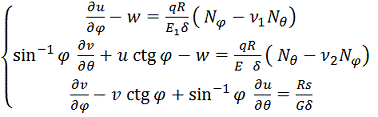
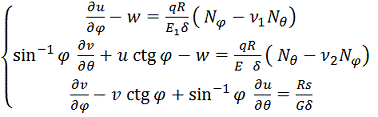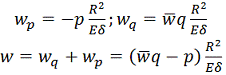
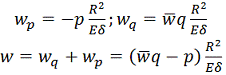Уравнения для усилий и перемещений после представления в нормальной форме Коши решаются методом Рунге-Кутта. Решение по безмоментной теории не удовлетворяет краевым условиям в отношени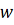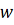и  и 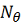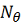. Для краевой зоны необходимо использовать нелинейные уравнения 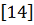 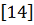для уточнения значений 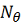 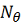в ви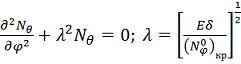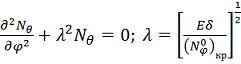де:  , где 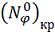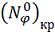- значение усилия на краю.

В результате решения уравнений равновесия для точек, лежащих на главном меридиане, получаем распределение коэффициентов усили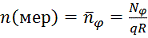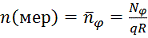й  и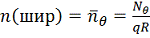

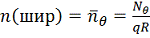
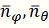
Распределениям  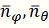соответствует распределение нормальных перемещений ,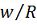

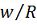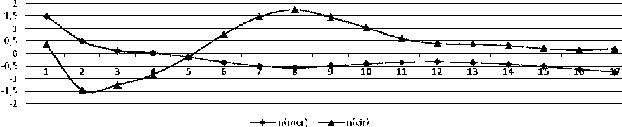
Рис. 2. Распределение коэффициентов усилий по главному меридиану (MTS)

Распределению усилий соответствуют перемещения 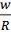 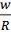точек меридиана Рис.3 (без учета избыточного давления). На диаграмме перемещений приводятся экспериментальные значения перемещений, измеренные инструментально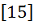

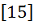
Рис.3. Теоретическое и экспериментальное (фактическое) распределения перемещений 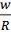 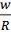(без учета действия внутреннего давления) на нормальные перемещения

Из диаграммы следует, что безмоментная теория оболочек (МТS) даже без учета влияния избыточного давления, дает значения перемещений в активной зоне существенно меньшее экспериментальных значений. Данные MTS применимы только для недеформируемых тел и/или как средство методологического обучения. Практически любые виды объектов, связанные с упругими изменениями формы, должны учитывать изменения коэффициентов давлений, изменения формы и изменения избыточного давления. Расчета открытых систем с использованием уравнений Леонтовича или закрытых систем с использованием уравнений Лиувилля (ангармоническая модель твердого тела)  приводят к существенным отличиям распределения перемещений Рис.4.

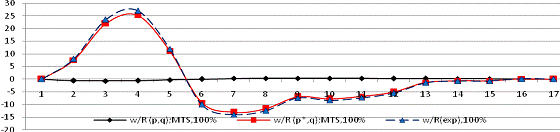
Рис. 4. Диаграммы коэффициентов нормальных перемещений 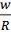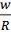, полученных по MTS, OST и experiment

Условия q=100; ; ,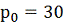

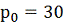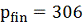
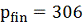В расчетах методом MTS считаются: форма тела квазистационарная, R-const.

В расчетах методом OST считается: форма тела изменяемая, допускаются складчатые зоны, R -

В качестве необратимого процесса в расчетах OST учитывается переменное трение (тело рассматривается как осциллятор) при обтекании и изменение пограничного слоя, в том числе в складчатых зонах.

Для распределений давлений 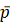 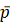текущими значениями формы приводятся статистические распределения вида 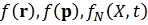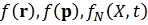, которые позволяют определить распределения:

первого момента случайной плотности ;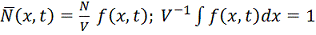

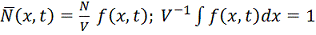- функции 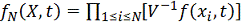 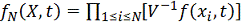в 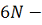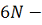мерном фазовом пространстве ;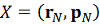

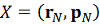значения энтропии Шеннона 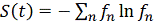 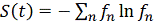для дискретного набора переменных.

Сравнение данных теоретических и экспериментальных показывает, что безмоментная теория (и теория мягких оболочек) не описывают поведение объекта в зоне активного давления потока и зоне теневого контура. Автором показано, что с использованием теории открытых систем можно оценить процесс образования складчатых зон. Складки увеличивают жесткость оболочки в направлении потока и ведут к управляемому пограничному слою, существенно уменьшающему и усилия в материале объекта и перемещения точек объекта.

Автором впервые для пространственных конструкций проведены экспериментальные исследования и теоретические обоснования, позволяющие использовать теорию открытых систем с экспериментальными доработками для расчета пространственных конструкций и сооружений.

По выполненным экспериментальным и теоретическим исследованиям можно придти к выводам:

наибольшая сходимость с экспериментальными исследованиями достигнута с использованием методов теории открытых систем (необратимого кинетического уравнения М.А. Леонтовича).

Уравнение связано с исследованиями открытых систем в неравновесном термодинамическом состоянии. Показано, что для его решения достаточно только одно приближение (гипотеза). Уравнение позволяет оценить диссипативные структуры и становление порядка через флуктуации.

Уравнение учитывает динамические распределения частиц в фазовом пространстве, крупномасштабные флуктуации и два значения интеграла взаимодействия (столкновения) частиц. Интеграл взаимодействия распадается на два значения: индуцированный (отвечающий за взаимоотношение частиц со средой) и внутренний (определяется коррелятором крупномасштабных флуктуаций)

Равновесным решением уравнения в отсутствии внешних сил является распределение Максвелла;

если значение одного (индуцированного) из интегралов столкновения равно нулю и отпадает необходимость оценки части необратимых процессов, осуществляется переход к уравнениям Лиувилля.

При переходе происходит потеря информации, связанные с внешними факторами взаимодействия частиц и учетом средней силы (силы Власова А.А.).

при приближении к мало деформированному телу методами механики сплошной среды вводятся гипотезы, характерные для классической механики (принципы замыкания и суперпозиции, законы сохранения энергии и импульса, сплошности и т.д.).

Гипотезы ведут: к потере информации, к обратимости по времени, к постоянству формы и характеристик материала. Нефизические процессы не учитываются.

при использовании аппарата теории оболочек, дополнительно к приближениям сплошной среды, принимаются приближения срединной поверхности, игнорирования действия погранслоя, нерастяжимость нормального волокна.

Гипотезы ведут к потере информации и пренебрежению рядом процессов.

при использовании аппарата теории мягких оболочек, в дополнении к гипотезам сплошной среды и теории оболочек принимается гипотеза отсутствия сопротивления сжимающим силам без предварительного натяжения. Это практически ликвидирует область применения мягких оболочек как обитаемых защитных сооружений.

Гипотезы (приближения) ведут к весьма ограниченной информации о взаимодействии тела и окружающей среды и к неправильной оценке напряженно-деформированного состояния. Это не означает, что расчеты, методами механики сплошной среды (включая безмоментную теорию оболочек) не должны использоваться при изучении взаимодействий тела с нагрузками и воздействиями.  Виды теоретического исследования методами механики сплошной среды можно считать первыми приближениями к изучению напряженно-деформированного состояния тела. Вид приближения, основанный на теориях мягких оболочек, по потерям информации в результате гипотез  можно считать нулевым приближением.

Описанная иерархическая структура требует аналогичного похода к материаловедению и описанию сред, в частности к описанию необратимых процессов. К наиболее существенным погрешностям методы механики сплошной среды приводят в зоне полного торможения потока (активная зона обтекания).

Для реально разрабатываемых объектов и при определении надежности объекта в течение срока службы использование методов расчета, основанные на гипотезах механики сплошной среды ведут к потере информации по характеристикам процесса и ошибкам в значении функций распределения усилий и перемещений.

Использование методов статистической физики открытых систем предоставляет возможность создавать сооружения с управляемыми параметрами надежности и прочности в течение срока службы и определить предельные состояния сооружений в течение всего срока службы.

Особенно важно то, что методы физики открытых систем позволяют создавать конструкции и сооружения с регулируемой по срокам службы надежностью систем.

Список литературы.

деформированный воздух поток оболочка

1. М.А. Леонтович. Введение в термодинамику. Статистическая физика. М.,Наука.1983.

. И.Р. Пригожин. Неравновесная статистическая механика. М.,УРСС.2007.

. Л.Д. Ландау. Е.М. Лифшиц. Механика, т. I. М.,Физматлит.2004.

. А.Л. Гольденвейзер. Теория упругих тонких оболочек. М., ГИТЛ. 1953.

. Р.П. Кузьмина. Мягкие оболочки. М., Факториал Пресс. 2005.

. С.А. Алексеев. Основы общей теории мягких оболочек. В сб. РПК XI с. 5-37. М., Стройиздат. 1967.

. СП 20.13330.2011. Нагрузки и воздействия, (П3.1.11. Сфера). М., 2011

. DIN 4134-1983, DIN V ENV 1991-2-4=1996

. Э.Симиу. Р. Сканланд. Воздействия ветра на здания и сооружения. М., Стройиздат, 1984.

. Отчет ЦАГИ №2412. М., 1980г

. В.П.Поляков. Взаимодействие модели мягкой воздухоопорной оболочки с потоком воздуха. В сборнике Теория мягких оболочек. Издательство Ростовского университета. 1976.

. Д.А. Бейлин. В.П. Поляков. О взаимодействии мягких оболочек сферической формы с потоком воздуха. Труды XII конференции по теории оболочек и пластин. Ереван. Издательство Ереванского университета.,1980, с138-143

. В.М. Никиреев, И.А. Даниляк. Расчет мягкой сферической оболочки на ветровую нагрузку. В сборнике Теория мягких оболочек. Издательство Ростовского университета. 1976.

. Ю.Н.Работнеов. Некоторые решения безмоментной теории оболочек. ПММ т.1, вып.5-6. ИПМ. М.,1946.

. Д.А. Бейлин, В.П. Поляков и др. Использование стереофотограмметрического метода для исследования напряженно-деформированного состояния мягкой оболочки сферической формы в потоке воздуха. М.,Ученые записки ЦАГИ том XII, №6. Стр.66-76. 1982.