Основы физики

Задача № 1

 

Условие

Масса снаряда 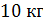 масса орудия  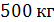при выстреле снаряд получает кинетическую энергию 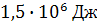. Какую кинетическую энергию получает ствол орудия следствии отдачи?

Решение

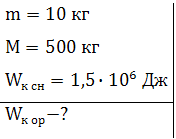
Поскольку до выстрела система орудие - снаряд покоилась в системе отсчёта, связанной с Землёй, то после выстрела суммарный импульс этой системы равен нулю, следовательно, импульсы снаряда и орудия по абсолютной величине равны:

 

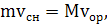
откуда скорость орудия сразу после выстрела равна:

 

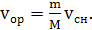
По определению, кинетическая энергия снаряда определяется выражением:

 

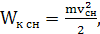
тогда кинетическая энергия орудия равна:

 

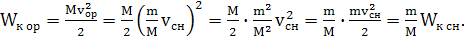
Подставляя числовые параметры, получаем:

 

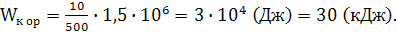
Ответ

 

 

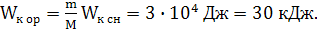
Задача № 2

 

Условие

Найти импульс, полную и кинетическую энергию электрона, движущего со скоростью, равной .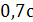

Решение

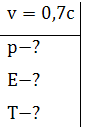
Импульс релятивистского электрона определяется выражением:

 

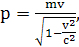
где 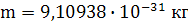 - масса покоя электрона.

Полная энергия электрона определяется выражением:

 

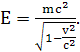
Поскольку энергия покоя электрона равна

 

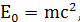
то его кинетическая энергия определяется выражением:

 

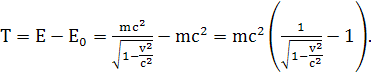
Подставляя числовые параметры и учитывая величину скорости света 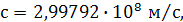 получаем:

 

 

 

 

 

 

 

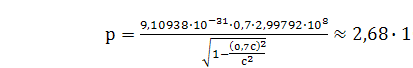
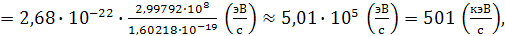
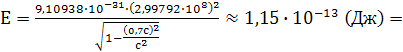
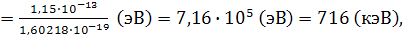
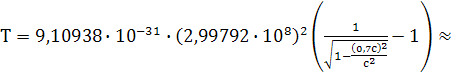
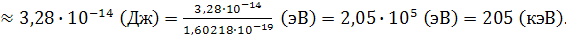
Ответ

 

 

 

 

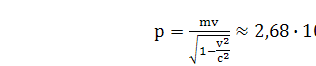
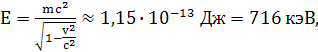
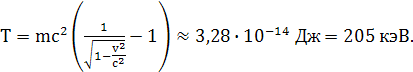
Задача № 3

 

Условие

При температуре 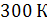 и давлении 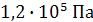. Плотность смеси водорода и азота 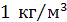. Определить молярную массу смеси.

Решение

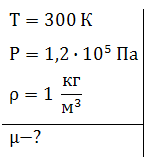
Используем уравнение состояния Менделеева-Клапейрона, описывающее поведение идеального газа:

 

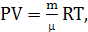
где 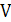 и 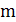 - соответственно объем и масса смеси газов,

 

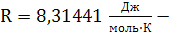
универсальная газовая постоянная.

Выражаем из уравнения Менделеева-Клапейрона молярную массу и, учитывая определение плотности вещества

 

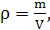
получаем:

 

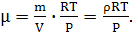
Подставляя числовые параметры, получаем:

 

 

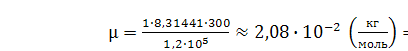
Ответ

 

 

 

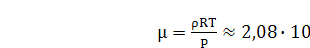
Задача № 4

 

Условие

Определить коэффициент внутреннего трения воздуха при температуре .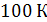

Решение

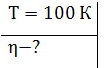
Поскольку температуры кипения основных компонентов воздуха - азота, кислорода и аргона - ниже заданной температуры 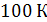 (при атмосферном давлении), то при указанной температуре воздух все ещё будет оставаться газом, близким по составу к атмосферному.

Коэффициент внутреннего трения (или динамическая вязкость) газа определяется выражением:

импульс энергия трение вязкость

 

 

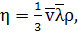
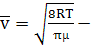
средняя скорость теплового движения молекул воздуха,

 

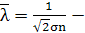
средняя длина свободного пробега, 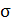 - площадь эффективного сечения молекул, 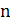 - их концентарция.

Из уравнения состояния идеального газа в форме

 

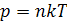
получаем выражение для концентрации молекул

 

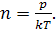
Из уравнения Менделеева-Клапейрона

 

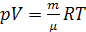
следует выражение для плотности газа:

 

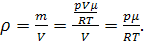
Средний диаметр молекул воздуха 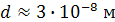, поэтому площадь эффективного сечения молекул равна:

 

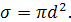
В результате выражение для коэффициента внутреннего трения приобретает вид:

 

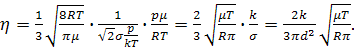
Подставляя числовые параметры, величину среднего диаметра молекул воздуха 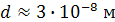, молярную массу воздуха 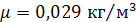, а также значения констант - универсальной газовой постоянной

 

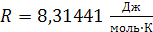
и постоянной Больцмана

 

 

 

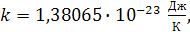
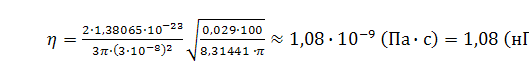
Ответ

 

 

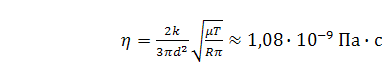
Задача № 5

 

Условие

При каком процессе выгоднее производить расширение воздуха: изобарическом или изотермическом, если объем увеличивается в 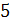 раз. Начальная температура газа в обоих случаях одинакова.

Решение

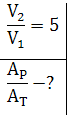
Полная работа, совершаемая газом при изменении объёма от 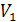 до 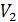, определяется выражением:

 

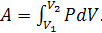
Следовательно, при изобарическом процессе, т.е. при 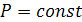 работа, выполняемая газом равна:

 

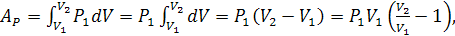
откуда, учитывая уравнения состояния

 

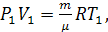
получаем:

 

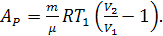
При изотермическом процессе, т.е. при 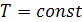, подставляя выражение для давления, полученное из уравнения состояния:

 

 

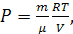
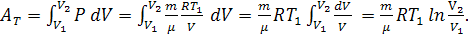
Следовательно, отношение величин работы в обоих процессах равно:

 

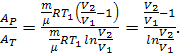
Подставляя числовые параметры, получаем:

 

следовательно, в изобарическом процессе газ совершает в 2,48 раз больше работы, чем в аналогичном (по изменению объёма) изотермическом.

Ответ

 

 

 

следовательно, в изобарическом процессе газ совершает в 2,48 раз больше работы, чем в аналогичном (по изменению объёма) изотермическом

 

Задача № 6

 

Условие

Найти изменение энтропии при нагревании 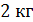 воды от 0 до  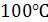и последующем превращении ее в пар при той же температуре.

Решение

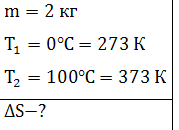
По определению приращение энтропии равно:

 

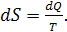
При нагревании воды до температуры превращения в пар на нагревание на 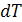 расходуется количество теплоты 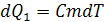, где

 

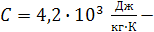
удельная теплоёмкость воды. Следовательно, изменение энтропии определяется выражением:

 

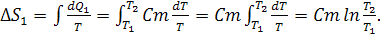
На превращение воды в пар потребуется количество теплоты, равное

 

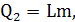
Где

 

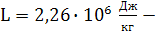
удельная теплота парообразования воды. Тогда изменение энтропии при образовании пара, учитывая постоянство температуры, равно:

 

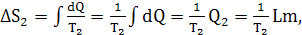
откуда находим суммарное изменение энтропии воды во всём процессе:

 

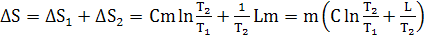
Подставляя числовые параметры, получаем:

 

 

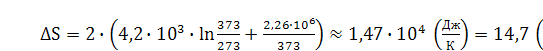
Ответ