Методы многомерной оптимизации: многомерная оптимизация методом Хука и Дживса

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

Отчет по лабораторной работе за курс:

«Теория оптимального планирования и управления»

кафедры 302

Тема

«Методы многомерной оптимизации: многомерная оптимизация методом Хука и Дживса»

Выполнила студентка

группы 03-323:

Ежова О.С.

Преподаватель:

Красовская М.А.

Москва

Постановка задачи

Найти методом Хука и Дживса с непрерывным шагом:

MIN F₁(x)= (Х₁-4)⁴ +(X₁-3 X₂ )²,

с начальной точкой X₀=(1;0)

Предусмотреть ввод точности .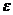

Провести: многомерный оптимизация дживс розенброк

1.      Нахождение экстремума функции F₁(X) при различных значениях начальной точки;

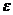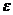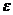2.      Определение экстремума заданной функции при различных значениях точности (=0.01, =0.1, =0.001);

Алгоритм метода

Графики функции

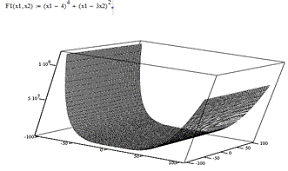
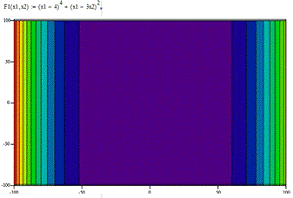
Результаты работы программы

Начальная точка (1;0)

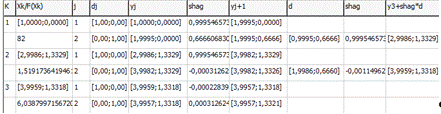
1) Начальная точка X₀ = [1;0]

Точность ε = 0.1

Опт. значение аргумента (3,8826;1,3109)

Опт. значение функции 0,00269660220874356

Кол-во итераций метода 3

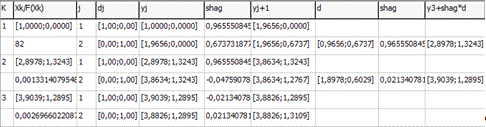
) Точность ε = 0.01

Опт. значение аргумента (4,0037;1,3344)

Опт. значение функции 1,48019246160121E-7

Кол-во итераций метода 3

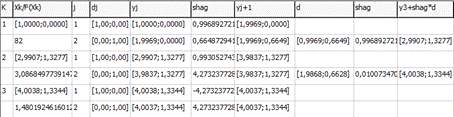
) Точность ε = 0.001

Опт. значение аргумента (3,9957;1,3321)

Опт. значение функции 6,03879971567203E-7

Кол-во итераций метода 3

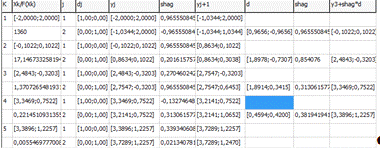
Начальная точка (-2;2)

1) Точность ε = 0.1

Опт. значение аргумента (3,7289;1,2470)

Опт. значение функции 0,00554697770081615

Кол-во итераций метода 5

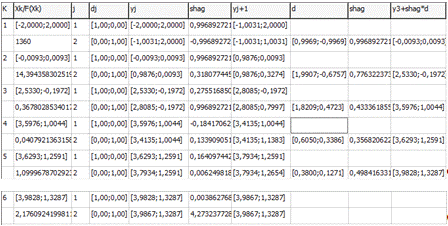
) Точность ε = 0.01

Опт. значение аргумента (3,9867;1,3287)

Опт. значение функции 2,17609241998115E-7

Кол-во итераций метода 6

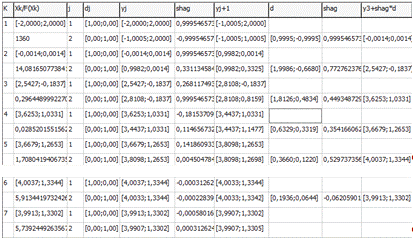
3) Точность ε = 0.001

Опт. значение аргумента (3,9907;1,3305)

Опт. значение функции 5,73924492635677E-7

Кол-во итераций метода 7

Начальная точка (4;2)

1) Точность ε = 0.1

Опт. значение аргумента (4,5855;1,5198)

Опт. значение функции 0,118199132492491

Кол-во итераций метода 2

2) Точность ε = 0.01

Опт. значение аргумента (4,5914;1,5296)

Опт. значение функции 0,122304388908469

Кол-во итераций метода 2

3) Точность ε = 0.001

Опт. значение аргумента (4,0108;1,3372)

Кол-во итераций метода 5

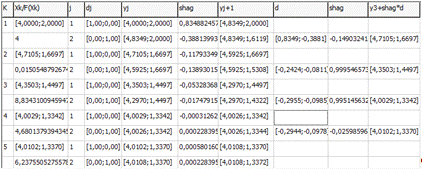
Листинг программы

unit Xuk;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, StdCtrls, Grids;= class(TForm): TEdit;: TEdit;: TLabel;: TLabel;: TLabel;: TComboBox;: TLabel;: TLabel;: TLabel;: TStringGrid;: TEdit;: TEdit;: TEdit;: TButton;: TEdit;: TLabel;: TEdit;: TEdit;FormCreate(Sender: TObject);Button1Click(Sender: TObject);

{ Private declarations }

{ Public declarations };Tper = class(TObject):real;:real;;schityvanie;func (h:real):real;sechenie(var c:real);: TForm1;,t1,t2,x1,x2,e,F:real;,j,v,q:integer;,y,xp,d:Tper;,ystr,dstr:string;

{$R *.dfm}TForm1.FormCreate(Sender: TObject);.Items.Add('(x1-2)^4+(x1-2*x2)^2');.Items.Add('4*x1+8*x2-2*x1^2-2*x2^2');:=Tper.Create;:=Tper.Create;:=Tper.Create;:=Tper.Create;;

//считывание начальных значений

procedure schityvanie;

var,s,i,p:integer;,str1:string;:boolean;:='';.one:=0;.two:=0;:=true;o:=0 to 9 dos:=0 to Form1.StringGrid1.RowCount do.StringGrid1.Cells[o,s]:='';:=0;.StringGrid1.RowCount:=10;:=2;.one:=StrToFloat(Form1.Edit2.Text);.two:=StrToFloat(Form1.Edit3.Text);:=StrToFloat(Form1.Edit4.Text);:=1;.stringgrid1.Cells[0,0]:='K';.stringgrid1.Cells[1,0]:='Xk/F(Xk)';.stringgrid1.Cells[2,0]:='j';.stringgrid1.Cells[3,0]:='dj';.stringgrid1.Cells[4,0]:='yj';.stringgrid1.Cells[5,0]:='shag';.stringgrid1.Cells[6,0]:='yj+1';.stringgrid1.Cells[7,0]:='d';.stringgrid1.Cells[8,0]:='shag';.stringgrid1.Cells[9,0]:='y3+shag*d';;

//вычисление значения функцииfunc(h:real):real;Form1.ComboBox1.Text='(x1-2)^4+(x1-2*x2)^2' then:=((y.one+h*d.one)-2)*((y.one+h*d.one)-2)*((y.one+h*d.one)-2)*((y.one+h*d.one)-2)+

((y.one+h*d.one)-2*(y.two+h*d.two))*((y.one+h*d.one)-2*(y.two+h*d.two))func:=4*(y.one+h*d.one)+8*(y.two+h*d.two)-2*(y.one+h*d.one)*(y.one+h*d.one)-2*(y.two+h*d.two)*(y.two+h*d.two);;

//метод золотого сеченияsechenie(var c:real);,b,Fn,Fm,m,n:real;:=0;:=0;:=StrToFloat(Form1.Edit5.Text);:=StrToFloat(Form1.Edit8.Text);:=0.618;:=a+(1-alfa)*(b-a);:=a+alfa*(b-a);:=func(n);:=func(m);(b-a)>=e doFn > Fm then:=n;:=m;:=Fm;:=a+alfa*(b-a);:=func(m);:=m;:=n;:=Fn;:=a+(1-alfa)*(b-a);:=func(n);;;:=(a+b)/2;

end;

//метод Хука и Дживса

procedure TForm1.Button1Click(Sender: TObject);,w,num:integer;,Zfun,per:real;:boolean;:string;:=0;:=0;:=2;:=0;:=0;;:='['+FloatToStrF(x.one,ffFixed,7,4)+';'

+ FloatToStrF(x.two,ffFixed,7,4)+']';.one:=x.one;.two:=x.two;:=func(0);.stringgrid1.Cells[1,2]:=FloatToStr(Zfun);:='['+FloatToStrF(x.one,ffFixed,7,4)+';'

+ FloatToStrF(x.two,ffFixed,7,4)+']';:=false;not flag doj:= 1 to num do:=j mod 2;(q);j of

:.one:=1;.two:=0;;

:.one:=0;.two:=1;;;:='['+FloatToStrF(d.one,ffFixed,2,2)+';'

+ FloatToStrF(d.two,ffFixed,2,2)+']';(Shag);w <> 0 then(k);.stringgrid1.Cells[0,q]:=IntToStr(k);.stringgrid1.Cells[1,q]:=xstr;;.stringgrid1.Cells[2,q]:=IntToStr(j);.stringgrid1.Cells[3,q]:=dstr;.stringgrid1.Cells[4,q]:=ystr;.stringgrid1.Cells[5,q]:=FloatToStr(Shag);.one:=y.one+shag*d.one;.two:=y.two+shag*d.two;:='['+FloatToStrF(y.one,ffFixed,7,4)+';'

+ FloatToStrF(y.two,ffFixed,7,4)+']';.stringgrid1.Cells[6,q]:=ystr;q>9 then Form1.StringGrid1.RowCount:=Form1.StringGrid1.RowCount+1;;.one:=x.one;.two:=x.two;.one:=y.one;.two:=y.two;:=sqr((x.one-xp.one)*(x.one-xp.one)+(x.two-xp.two)*(x.two-xp.two));(per<e) then flag:=true.one:=x.one-xp.one;.two:=x.two-xp.two;:='['+FloatToStrF(d.one,ffFixed,7,4)+';'

+ FloatToStrF(d.two,ffFixed,7,4)+']';(Shag);.one:=x.one+shag*d.one;.two:=x.two+shag*d.two;:='['+FloatToStrF(y.one,ffFixed,7,4)+';'

+ FloatToStrF(y.two,ffFixed,7,4)+']';:=ystr;w = 0 then.stringgrid1.Cells[7,q]:=dstr;.stringgrid1.Cells[8,q]:=FloatToStr(Shag);.stringgrid1.Cells[9,q]:=ystr;;q>100 then:=true; (‘функция не оптимизируется’);

end;

end;q>2 then:=func(0);.stringgrid1.Cells[1,q]:=FloatToStr(Zfun);;;.Edit1.Text:=FloatToStr(k);.Edit6.Text:='['+FloatToStrF(x.one,ffFixed,7,4)+';'

+ FloatToStrF(x.two,ffFixed,7,4)+']';.Edit7.Text:=FloatToStr(Zfun);;

end.

Сводные таблицы

Хук и Дживс

Розенброк

Выводы

В ходе лабораторной работы был изучен метод многомерной оптимизации Хука и Дживса с непрерывным шагом.

Метод относится к категории методов,в которых используется поиск по направлению. Алгоритмы,в которых используется такой поиск, называют алгоритмами ускоряющего шага. Каждая итерация этих алгоритмов состоит из двух этапов: поиск вдоль координатных осей, или, исследующий поиск; поиск по образцу, или ускоряющий шаг.

Была написана программа и с помощью неё изучена функция

F(X) = (Х₁-4)⁴ +(X₁-3X₂)²

Для наглядности результатов были проварьированы точность (основное значение критерия остановки) и начальная точка.

Были сделаны следующие выводы:

количество итераций увеличивается с увеличением точности

количество итераций увеличивается в зависимости от удаленности начальной точки от оптимального решения..

Экспериментальное сравнение алгоритмов Хука-Дживса и Розенброка по числу вычислений и по числу вызова оптимизируемой функции в процессе оптимизации показывает в пользу алгоритма Розенброка. Но в методе Розенброка вычислительные затраты идут на пересчет системы ортогональных направлений.