Расчет и оптимизация электрической цепи

Расчет и оптимизация электрической цепи

Курсовая работа

«Расчет и оптимизация электрической цепи»

Новокузнецк, 2010

Введение

Целью данной работы является математическое моделирование электрической схемы, расчет этой схемы и оптимизация. Оптимизация заключается в нахождении таких значений заданных элементов оптимизации, чтобы функция изменения напряжения во времени стала близка к идеальной.

Для простоты оптимизации вводится целевая функция, которая по сути является суммой квадратов разностей идеальной и оптимизируемой функций в моменты времени, определяемые частотой дискретизации и временем окончания дискретизации.

Задачи

Для заданной схемы электрической цепи (рис. 1) необходимо:

1)      Рассчитать электрическую цепь:

a)       Найти значение токов во всех ветвях.

b)      Найти напряжение на нагрузке Q элементов, где Q - L₂, C₃.

2)      Оптимизировать схему, варьируя параметрами R₃ и C₂, чтобы напряжение на нагрузке u^*_H(t)=15*sin (w*t+2π/3). Время для произведения задачи оптимизации выбрать 1 мин с начала функционирования электрической схемы, время дискретизации 0,1 с.

Метод многомерной оптимизации: метод покоординатного спуска.

Метод одномерной оптимизации: метод простого перебора.

Исходные данные:

1.  Идеальный источник напряжения:

u(t)=100*sin(wt), f=50Гц;

2.  Элементы с постоянными характеристиками:

а) Резисторы:

R₁=500 Ом, R₂=1000 Ом, R₄=100 Ом;

б) Конденсаторы:

С₁=100 мкФ, С ₃=200 мкФ;

в) Катушки индуктивности:

L₁=1 мГн, L₂=5 мГн;

3.  Элементы с переменными характеристиками:

а) R₃=[100 Омч1000 Ом], R_3ном=500 Ом;

б) С₂=[20 мкФч100 мкФ], С_2ном=50 мкФ;

1. Расчет электрической цепи

1.1 Ручной расчет

Найдем сопротивления элементов и ветвей:

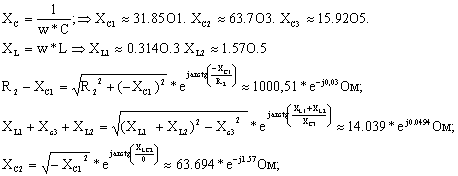
По первому и второму закону Кирхгофа получаем систему:

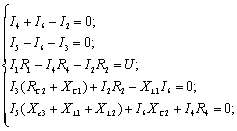
Приведем подобные и подставим известные значения:

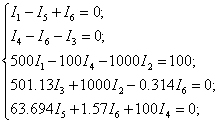
Упростим систему, используя метод контурных токов. Для этого выразим

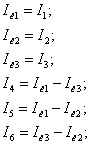
Тогда она примет вид:

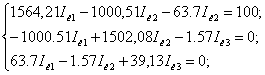
Найдем решение системы по методу Халецкого.

Результат решения методом Халецкого:

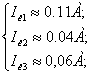
Подставив в замену метода контурных токов, получим:

Проверим правильность найденного решения с помощью уравнения баланса мощностей источника и приемников электрической энергии.

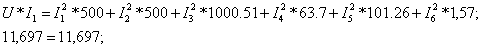
Значит, найденное решение правильно.

Далее, рассчитаем значение напряжения на заданной нагрузке при номинальных параметрах. Для этого рассчитаем сопротивление на участке L₂, C₃.

.

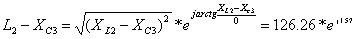Таким образом, изменение напряжения на нагрузке описывается уравнением u_H(t)=23,995*sin (w*t+1.571). Очевидно, что оно не соответствует заданному u^*_H(t)=15*sin (w*t+2π/3).

1.2 Оптимизация схемы

Метод покоординатного спуска.

Пусть нужно найти наименьшее значение целевой функции u=f(M)=f (x1, x2,…, xn). Здесь через М обозначена точка n-мерного пространства с координатами x1, x2,…, xn: M=(x1, x2,…, xn). Выберем какую-нибудь начальную точку М0=(x10, x20,…, xn0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f (x1, x20, x30,…, xn0). Тогда она превратится в функцию одной переменной x1. Изменяя эту переменную, будем двигаться от начальной точки x1=x10 в сторону убывания функции, пока не дойдем до ее минимума при x1=x11, после которого она начинает возрастать. Точку с координатами (x11, x20, x30,…, xn0) обозначим через М1, при этом f(M0) >= f(M1).

Фиксируем теперь переменные: x1=x11, x3= x30,…, xn=xn0 и рассмотрим функцию f как функцию одной переменной x2: f (x11, x22, x30…, xn0). Изменяя x2, будем опять двигаться от начального значения x2=x20 в сторону убывания функции, пока не дойдем до минимума при x2=x21. Точку с координатами {x11, x21, x30… xn0} обозначим через М2, при этом f(M1) >=f(M2).

Проведем такую же минимизацию целевой функции по переменным x3, x4,…, xn. Дойдя до переменной xn, снова вернемся к x1 и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М0, М1, М2,…, которой соответствует монотонная последовательность значений функции f(M0) >= f (M1)>= f(M2) >=… Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области.

Отметим, что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция f (x1, x2,…, xn) задана явной формулой и является дифференцируемой, то мы можем вычисллить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов.

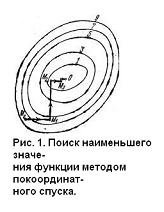
На рис. 1 изображены линии уровня некоторой функции двух переменных u= f (х, у). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода. Когда мы приступаем к решению реальной задачи оптимизации, такого рисунка, содержащего в себе готовый ответ, у нас, конечно, нет.

Пусть требуется решить задачу (2):

(x) ->min, х ОRn.                                                                  (2)

В двумерном пространтсве R2. Решение задачи (2) методом покоординатного спуска, иначе называемого методом Гаусса - Зейделя, производят по следующей общей схеме.

Выбирают произвольно начальную точку х(0) из области определения функции f(х). Приближения х(k) определяются соотношениями (3):

(k+1)=x(k)+t(k) S(k) (k=0,1,2,…),

где вектор направления спуска s(k) - это единичный вектор, совпадающий с каким-либо координатным направлением (например, если S(k) параллелен х1, то S(k)= {1,0,0,…, 0}, если он параллелен x2, то S(k)={0, 1, 0,…, 0} и т.д.); величина t(k) является решением задачи одномерной минимизации:

f (x(k)+ts(k)) -> min, t ОR1, (k=0,1,2,…),

и может определяться, в частности, методом сканирования.

Детальная реализация общей схемы в двумерном случае R2 дает траекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), х~(k), x (k+1) (k=0, 1, 2,) (рис. 2). При k=0, исходя из начальной точки х(0)=(x1 (0), x2 (0)), находят точку х~(0)= (x1~(0), x2 (0)), минимума функции одной переменной f (x1, x2 (0)); при этом f (x~(0))<=f (x(0)).Затем находят точку минимума x(1) функции f (x1~(0), x2) по второй координате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируя вторую координату точки х(1), находят точку минимума х~(1)= (x1~(1), x2 (1)), функции f (x1, x2 (1)) одной переменной x(1); при этом f (x~(1))<=f (x(1))<=f (x(0)). Точку х(2) получают, минимизируя целевую функцию f (x1~(1), x2), вновь по коорданате х2, фиксируя координату x1~(1), точки x(1), и т.д.

Условием прекращения вычислительной процедуры при достижении заданной точности e может служить неравенство

||x (k+1) - x(k) ||<e                                                                  (4)

Блок-схема поиска минимума функции двух переменных методом покоординатного спуска.

Метод простого перебора

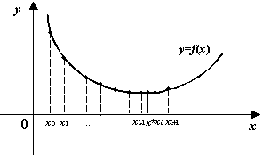
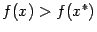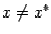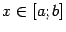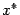Будем предполагать, что искомый минимум является строгим, то есть при всех , и других точек локального минимума на отрезке нет. Предположим также, что точка минимума  - внутренняя точка отрезка. Зададимся точностью 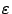, с которой будем приближённо отыскивать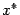. Приближённое значение точки минимума обозначим 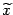, то есть  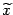- это такое число, что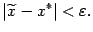

Простейший способ обнаружить точку 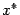 с точностью  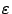- это перебирать точки 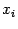 отрезка 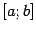 с шагом 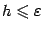, начиная с 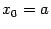, до тех пор, пока не будет выполнено условие 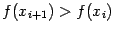, то есть пока функция не начнёт возрастать после точки минимума. При этом точка 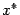 может оказаться либо на отрезке, либо на отрезке (cм. следующий чертёж):

Рис. 9.15. Два случая расположения точки минимума при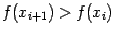

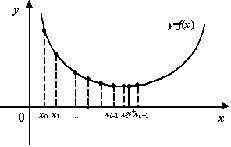
Если теперь положить 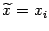, то в любом из двух случаев будет выполнено неравенство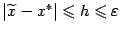, то есть точка минимума будет найдена с нужной нам точностью. За приближённое значение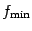 нужно теперь взять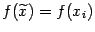. Дополнительного вычисления функции при этом не потребуется, поскольку значение 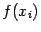 уже было найдено ранее.

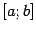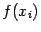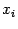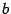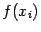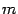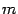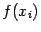Если не предполагать, что локальный минимум на отрезке  только один и что точка минимума - внутренняя точка отрезка, то придётся изменить метод так: вычислять значения  до тех пор, пока точка  не достигнет правого конца отрезка - точки ; на каждом шаге сравнивать текущее значение с минимальным из предыдущих значений , заменяя это минимальное значение  на  при 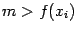. Наконец, вычислить  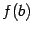(если точка  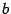не совпадает с последней из точек 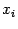) и также сравнить с минимальным из предыдущих значений. 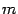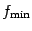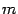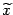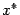После этой процедуры  будет приближённо равно , а та точка, в которой получено значение функции, равное  - приближённым значением  точки  минимума.

Заметим, что метод простого перебора при поиске точки экстремума аналогичен методу простого перебора при поиске корня уравнения .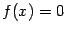

Расчет оптимизации схемы

Многомерная оптимизация производится методом покоординатного спуска, который заключается в пошаговом переходе от начальных значений аргументов функции к значениям, при которых значения функции удовлетворяют заданным условиям. В процессе каждого шага метода покоординатного спуска в задаче выполняется метод одномерной оптимизации - метод простого перебора, заключающийся в переборе всех заданных значений аргумента, при котором значение оптимизируемой функции минимально.

Оптимизируемая функция имеет вид 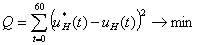, где t-время проведения задачи оптимизации, равное 1 мин.

Для нахождения значения тока на заданной нагрузке преобразуем систему уравнений с учетом фазового сдвига между током и напряжением:

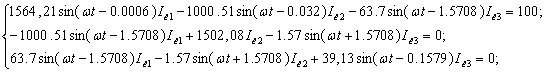
Критерием завершения итерационного процесса является выполнение одного из следующих условий:

,

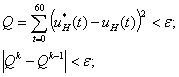где ε - заданная точность поиска, k - номер итерации.

Например, для времени проведения задачи оптимизации 60 с, шага дискретизации 0,1 с и ε=1 получим значение целевой функции равное 2190326 при первой итерации. Такое значение не удовлетворяет заданным условиям, поэтому мы продолжаем поиск оптимального значения целевой функции в рамках значений наших аргументов.

2. Программная реализация

2.1 Информационное обеспечение

В процессе написания программы были созданы следующие классы:

1)      TVetv - класс ветвей схемы. Обладает полями:

а)       FSopr:double - хранит общее сопротивление ветви

б)      XC, XL:double - хранит емкостное и индуктивное сопротивления ветви.

в)      FUgol: double - хранит фазовый сдвиг между током и напряжением.

г)       FSToka: double - хранит значение силы тока ветви.

Содержит процедуру constructor create (Rv, Lv, Cv:double) - процедура создания ветви при начальных значениях сопротивления, индуктивности, емкости.

2)      TUchastok - класс участков оптимизации. Потомок класса TBrunch, обладает теми же полями и полем FTension: Double, которое служит для хранения значения напряжения на участке оптимизации. Содержит процедуры:

а)       constructor create (Ru, Cu, t:double) создает участок оптимизации при задании начальных индуктивности, емкости и момента времени оптимизации.

б)      procedure Raschet вычисляет разницу dU между Uopt и Uisk за время проведения задачи оптимизации.

Переменные созданных классов:

1)      Vetv: array [1..5] of TBrunch - массив ветвей электрической схемы.

2)      Uchastok:TUchastok - участок оптимизации.

Массивы:

1)      R, L, C: array [1..5] of Double - исходные данные ветви (сопротивление, индуктивность, емкость).

2)      FOpt: array [1…50] of Double - массив значений целевой функции, хранящий значение каждой итерации.

Действительные переменные:

1)      Rv, Lv, Cv: Double - эти переменные используются при создании новой ветви.

2)      Lu, Cu: double - эти переменные используются при создании участка оптимизации.

3)      Ik1, Ik2, Ik3: Double - контурные токи схемы.

4)      U, Uopt, Uisk: Double - напряжения (источника, заданное, на участке оптимизации, разница между Uopt и Uisk) схемы.

5)      t:double - время проведения задачи оптимизации.

6)      minR, minC, minRv, minCv, min: double - используются в процессе оптимизации; minR - запоминает оптимальное значение R₃ во время итерационного процесса, minC - запоминает оптимальное значение С₂ во время итерационного процесса.

7)      z - золотое сечение, определяется по формуле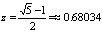

8)      S:array [1..6] of double; - массив для расчёта сопротивлений ветвей; используется для решения системы уравнений методом Гаусса.

Целые переменные:

1)      Time. Value: integer - максимальное время проведения задачи оптимизации; не более 60 с.

2)      StepAngle. Value: integer - шаг дискретизации; не более 0,01 с.

3)      Pogr. Value: integer - погрешность ε.

Логические переменные:

1)      Nominal: Boolean - логическая переменная; при истинном значение производится расчет при номинальных значениях C2 и R3, при ложном - с учетом фазового сдвига между током и напряжением.

2.2 Математический аппарат

моделирование электрический сопротивление халецкий

Одним из прямых (точных) методов решения систем линейных уравнений является метод основанный на схеме Халецкого.

Пусть система линейных уравнений дана в матричном виде.

=b                                          (1)

где А - квадратная матрица порядка n, а x, b - векторы столбцы.

Представим матрицу А в виде произведения нижней треугольной матрицы С и верхней треугольной матрицы В с единичной диагональю, т.е.

А=СВ,

где

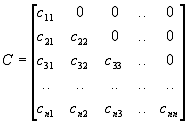
Причем элементы с_ij и b_ij определяются по формулам:

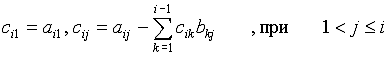
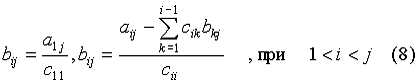           (2)

Уравнение (1) можно записать в следующем виде:

CBx=b.                                                               (3)

Произведение Bx матрицы B на вектор-столбец x является вектором-столбцом, который обозначим через y:

=y.                                                            (4)

Тогда уравнение (2) перепишем в виде:

=b.                                                            (5)

Здесь элементы c_ij известны, так как матрица А системы (1) считается уже разложенной на произведение двух треугольных матриц С и В.

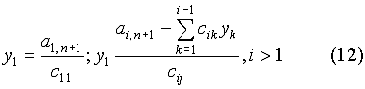(6)

неизвестные y_i удобно вычислять вместе с элементами b_ij.

После того как все y_i определены по формулам (6), подставляем их в уравнение (4).

Так как коэффициенты b_ij определены (2), то значения неизвестных, начиная с последнего, вычисляем по следующим формулам:

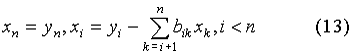
2.3 Алгоритмическое обеспечение

Алгоритм оптимизации:

2.4 Программное обеспечение

Написанная программа представляет собой несколько файлов. Среди них самыми важными являются Project1.dpr, Unit1.dfm и Unit1.pas.

Файл Project1.dpr, проект программ, связывает между собой все файлы, входящие в состав программы.

Файл Unit1.dfm - внешний вид, интерфейс программы. Подробнее о нем рассказано в п. 3.2.

Файл Unit1.pas содержит весь программный код и представляет собой используемые функции, процедуры, переменные и компоненты. Подробнее его можно рассмотреть в приложении.

Файл Shema.jpg необходим для отображения электрической схемы, для которой производились расчёты и оптимизация

3. Скриншот

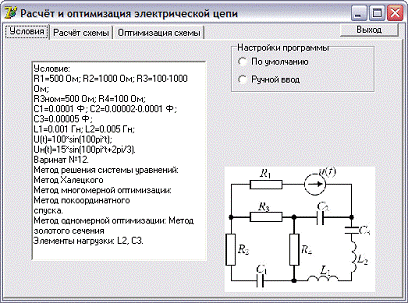
Рис. 5 - Скриншот «Ввод данных»

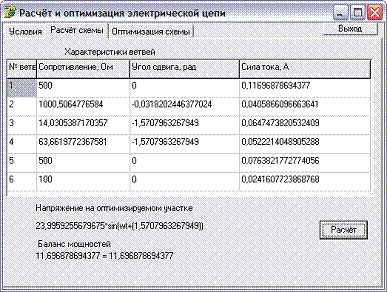
Рис. 6 - Скриншот «Расчёт схемы»

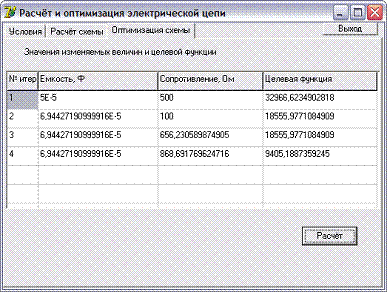
Рис. 7- Скриншот «Оптимизация схемы»

Заключение

В процессе разработки программы было выяснено, что решение системы уравнений методом Халецкого легко программируется. Выяснено, что матричным методом можно решать системы из любого количества уравнений.

Также был рассмотрен метод многомерной оптимизации - метод покоординатного спуска. Этот метод легок в программировании, так как не требует знания функции в явном виде. Но у этого метода есть недостаток: в случае, если функция быстрее всего убывает в сторону какого-то одного предела, то достигнув этого предела, оптимизация завершается, хотя, возможно, что это только точка локального минимума.

Приложения

Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, StdCtrls, Grids, ComCtrls, Spin, ExtCtrls, jpeg;= class: double;, XL:double;: double;: double;create (Rv, Lv, Cv:double);;= class(TVetv): Double;create (Lu, Cu, t: Double);Raschet;;= class(TForm): TPageControl;: TTabSheet;: TTabSheet;: TMemo;: TStringGrid;: TButton;: TLabel;: TLabel;: TSpinEdit;: TSpinEdit;: TSpinEdit;: TLabel;: TLabel;: TLabel;: TLabel;: TLabel;: TLabel;: TButton;: TTabSheet;: TLabel;: TStringGrid;: TButton;: TImage;: TRadioGroup;Vvod (Sender: TObject);Button1Click (Sender: TObject);Haletsky (t:double);Button2Click (Sender: TObject);Face (Sender: TObject);Button3Click (Sender: TObject);RadioGroup1Click (Sender: TObject);

{Private declarations}

{Public declarations};: TForm1;:array [1..6] of TVetv;:TUchastok;, c, l, s:array [1..6] of double;, Lv, Cv: Double;: Boolean;:array [1..20000] of double;, Cu: double;, U, Uopt, Uisk, dU, C2, Q, Q1, Q2:double;:array [1..50] of double;:integer;

{$R *.dfm}TVetv.create (Rv, Lv, Cv:double);create;Cv=0 then else XC:=1/(100*Pi*Cv);Lv=0 then else XL:=100*Pi*Lv;:=sqrt (sqr(Rv)+sqr (XL-XC));(Rv=0) and ((XL-XC)<0) then FUgol:=-Pi/2 else(Rv=0) and((XL-XC)>0) then FUgol:=Pi/2 else:=arctan((XL-XC)/Rv);;TUchastok.create (Lu, Cu, t: Double);create (1,1,1);:=sqrt (sqr(XL-XC));((XL-XC)<0) then FUgol:=-Pi/2 else((XL-XC)>0) then FUgol:=Pi/2;:=Vetv[5].FSToka;Nominal then FNapr:=FSopr*FSTokaFNapr:=FSopr*FSToka*sin (100*Pi*t+FUgol);;TUchastok. Raschet;:=0; Uisk:=0; Uopt:=0; Q:=0;t<=Form1. Time. Value do. Haletsky(t);:=L[3] - 0.001; Cu:=C[3];:=TUchastok.create (Lu, Cu, t);:=15*sin((100*Pi*t)*Pi/180+2*Pi/3);:=Uchastok.FNapr*sin((100*Pi*t)*Pi/180+Uchastok.FUgol);:=Q+sqr (Uopt-Uisk);:=t+Form1. StepAngle. Value/10;;;TForm1. Vvod (Sender: TObject);i:integer;[1]:=500; R[2]:=1000; R[3]:=0; R[4]:=0; R[6]:=100;[1]:=0; L[2]:=0; L[3]:=0.001+0.005; L[4]:=0; L[5]:=0; L[6]:=0;[1]:=0; C[2]:=0.0001; C[3]:=0.0002; C[5]:=0; C[6]:=0;nominal then begin[5]:=500;[4]:=0.00005;;i:=1 to 6 do:=R[i]; Lv:=L[i]; Cv:=C[i];[i]:=TVetv.create (Rv, Lv, Cv);;;TForm1. Button1Click (Sender: TObject);i:integer;:=True;

// Ввод данных. Cells [0,0]:='№ ветви';. Cells [1,0]:='Сопротивление, Ом';. Cells [2,0]:='Угол сдвига, рад';. Cells [3,0]:='Сила тока, А';(sender);i:=1 to 6 do.cells [0, i]:=inttostr(i);.cells [1, i]:=floattostr (Vetv[i].FSopr);.cells [2, i]:=floattostr (Vetv[i].FUgol);;(t);i:=1 to 6 do StringGrid1.cells [3, i]:=floattostr (Vetv[i].FSToka);:=L[3] - 0.001; Cu:=C[3];:=TUchastok.create (Lu, Cu, t);. Caption:=floattostr (abs(Vetv[1].FSToka*U))+' = '+floattostr (sqr(Vetv[1].FSToka)*S[1]+sqr (Vetv[2].FSToka)*S[2]+sqr (Vetv[3].FSToka)*S[3]+sqr (Vetv[4].FSToka)*S[4]+sqr (Vetv[5].FSToka)*S[5]+sqr (Vetv[6].FSToka)*S[6]);. Caption:=floattostr (Uchastok.FNapr)+'*sin (wt+('+floattostr (Uchastok.FUgol)+'))';;TForm1. Haletsky (t:double);a, d, c:array [1.. 3,1..3] of double;, x, y:array [1..3] of double;, i, n: Integer;, Ik2, Ik3: Double;:=3;Nominal theni:=1 to 6 do[i]:=Vetv[i].FSopr;:=100;i:=1 to 6 do[i]:=abs (Vetv[i].FSopr*sin((100*Pi*t)*Pi/180+Vetv[i].FUgol));:=abs (100*sin((100*Pi*t)*Pi/180));;[1,1]:=S[1]+S[4]+S[5]; a [1,2]:=-S[5]; a [1,3]:=-S[4];[2,1]:=-S[5]; a [2,2]:=S[2]+S[5]+S[6]; a [2,3]:=-S[6];[3,1]:=-S[4]; a [3,2]:=-S[6]; a [3,3]:=S[3]+S[6]+S[4];[1]:=U; b[2]:=0; b[3]:=0;i:=1 to 3 do:=1;[i, j]:=a [i, j];;j:=1 to 3 do[1, j]:=a [1, j]/d [1,1];[2,2]:=a [2,2] - d [2,1]*c [1,2];[2,3]:=1/d [2,2]*(a [2,3] - d [2,1]*c [1,3]);[3,2]:=a [3,2] - d [3,1]*c [1,2];[3,3]:=a [3,3] - d [3,1]*c [1,3] - d [3,2]*c [2,3];[1]:=b[1]/d [1,1];[2]:=1/d [2,2]*(b[2] - d [2,1]*y[1]);[3]:=1/d [3,3]*(b[3] - d [3,1]*y[1] - d [3,2]*y[2]);[3]:=y[3];[2]:=y[2] - c [2,3]*x[3];[1]:=y[1] - c [1,2]*x[2] - c [1,3]*x[3];:=x[1];:=x[2];:=x[3];[1].FSToka:=Ik1;[2].FSToka:=Ik2;[3].FSToka:=Ik3;[4].FSToka:=Ik1-Ik3;[5].FSToka:=Ik1-Ik2;[6].FSToka:=Ik3-ik2;;TForm1. Button2Click (Sender: TObject);minR, minC, MaxR, MaxC, C1, C2, R1, R2, z, min:double;1;g:=1 to 100 do. Cells [0, g]:='';. Cells [1, g]:='';. Cells [2, g]:='';. Cells [3, g]:='';;:=False;. Cells [0,0]:='№ итер.';. Cells [1,0]:='Емкость, Ф';. Cells [2,0]:='Сопротивление, Ом';. Cells [3,0]:='Целевая функция';:=1;[4]:=0.00005; R[5]:=500;(Sender);. Raschet;:=Q;. Cells [0, g]:=inttostr(g);. Cells [1, g]:=floattostr (C[4]);. Cells [2, g]:=floattostr (R[5]);. Cells [3, g]:=floattostr(min);min<pogr. Value then goto 1;:=(sqrt(5) - 1)/2; C1:=0; C2:=0; R1:=0; R2:=0;:=False;:=0.00002; MinR:=100;:=0.0001; MaxR:=1000;not Nominal do:=g+1;[4]:=minC; R[5]:=minR+100;(Sender);. Raschet;:=Q;[4]:=maxC; R[5]:=maxR+100;(Sender);. Raschet;:=Q;Q1=Q2 then:=minC+z*(MaxC-MinC);:=maxC-z*(MaxC-MinC);[g]:=Q1;;Q1<Q2 then:=minC;:=maxC-z*(MaxC-MinC);[g]:=Q1;;Q1>Q2 then:=minC+z*(MaxC-MinC);:=maxC;[g]:=Q2;;:=C1;:=C2;((abs (QOpt[g])<1) or ((g>1) and (abs (Qopt[g] - Qopt [g-1])<1))) then Nominal:=True;. Cells [0, g]:=inttostr(g);. Cells [1, g]:=floattostr(minc);. Cells [2, g]:=floattostr(minr);. Cells [3, g]:=floattostr (Qopt[g]);;C2-C1<0.001;:=g+1;[4]:=minC; R[5]:=minR+100;(Sender);. Raschet;:=Q;[4]:=maxC; R[5]:=maxR+100;(Sender);. Raschet;:=Q;Q1=Q2 then:=minR+z*(MaxR-MinR);:=maxR-z*(MaxR-MinR);[g]:=Q1;;Q1<Q2 then:=minR;:=maxR-z*(MaxR-MinR);[g]:=Q1;;Q1>Q2 then:=minR+z*(MaxR-MinR);:=maxR;[g]:=Q2;;:=R1;:=R2;((abs (QOpt[g])<1) or ((g>1) and (abs (Qopt[g] - Qopt [g-1])<1))) then Nominal:=True;. Cells [0, g]:=inttostr(g);. Cells [1, g]:=floattostr(minc);. Cells [2, g]:=floattostr(minr);. Cells [3, g]:=floattostr (Qopt[g]);;R2-R1<0.001;

// Вывод данных;

:end;TForm1. Face (Sender: TObject);

Form1. Caption:='Расчёт и оптимизация электрической цепи';

label2. Caption:='Время проведения задачи'+#13#10+'оптимизации, с';

label5. Caption:='Время' +#13#10+'дискретизации, с/100';

label8. Caption:='Погрешность';

label9. Caption:='Характеристики ветвей';

Label6. Caption:='Баланс мощностей';

Label4. Caption:='Напряжение на оптимизируемом участке';

Label7. Caption:='Значения изменяемых величин и целевой функции';

Shema. Picture. LoadFromFile ('Shema.jpg');. Proportional:=True;. Visible:=true;. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;;TForm1. Button3Click (Sender: TObject);;;TForm1. RadioGroup1Click (Sender: TObject);RadioGroup1. ItemIndex=0 then. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;. Visible:=false;. Value:=1;. Value:=1;. Value:=1;;RadioGroup1. ItemIndex=1 then. Visible:=true;. Visible:=true;. Visible:=true;. Visible:=true;. Visible:=true;. Visible:=true; end; end; end.