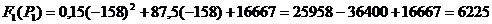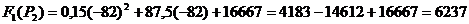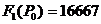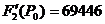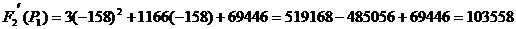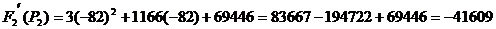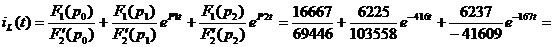Анализ трехфазных электрических цепей и переходных процессов в линейных электрических цепях с сосредоточенными параметрами
АНАЛИЗ
ТРЁХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ
ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
АНАЛИЗ ТРЁХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
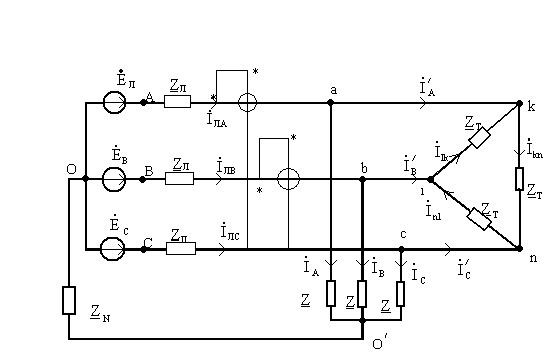
Схема данной электрической цепи:
Исходные данные:
|
Первая
гармоника фазы Λ
|
Третья
гармоника фазы Λ
|
Пятая
гармоника фазы Λ
|
|
ЕА(1)
|
ZΛ(1)
|
ZT(1)
|
Z
|
ZN(1)
|
ЕА(3)
|
ЕА(5)
|
|
В
|
Ом
|
Ом
|
Ом
|
Ом
|
В
|
В
|
|
127
|
j5
|
j20
|
50
|
j1
|
50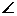 10040 10040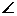 -100 -100
|
|
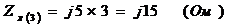
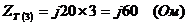
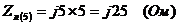
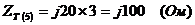
Преобразуем треугольник в
эквивалентную звезду с сопротивлением плеча 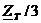 :
:
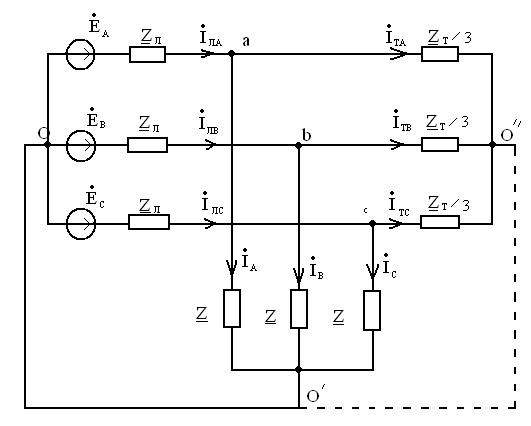
В полученной схеме вследствие её
симметрии нейтральные точки генератора и нагрузки могут быть объединены и
расчет целесообразно вести для одной фазы независимо от других, например, для
фазы А.
Рассчитаем первую гармонику всех
токов
Схема для расчета первой гармоники
фазы А будет иметь вид:
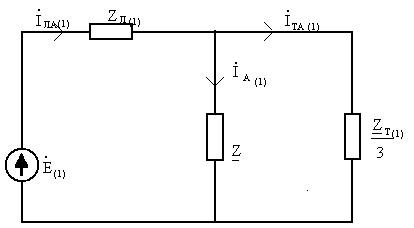
Определим токи фаз, А:
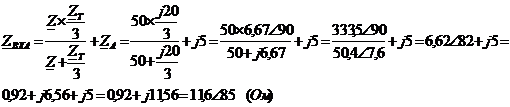
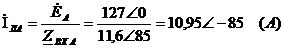
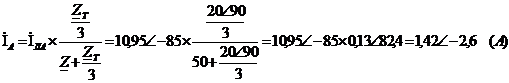
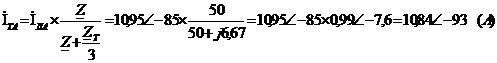
Найдём токи для фаз В и С:
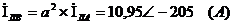
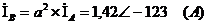
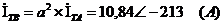
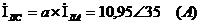
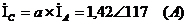
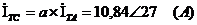
Определим токи в фазах треугольника,
учитывая, что при указанных на схеме условных положительных направлениях токов,
нагрузка симметричная:
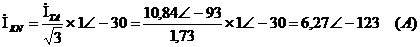
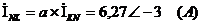
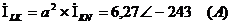
Рассчитаем третью гармонику всех
токов
Третья гармоника имеет нулевую
последовательность фаз, так что токи с одинаковыми индексами из разных фаз
будут равны между собой. Также появится ток в нулевом проводе.
Схема для расчета третьей гармоники
фазы А имеет вид:
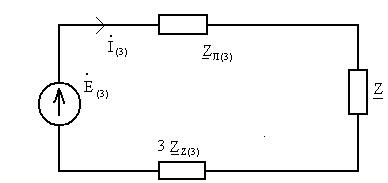
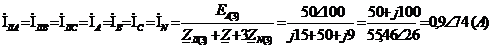
Рассчитаем
пятую гармонику всех токов
Схема для расчета пятой гармоники
фазы А имеет вид:
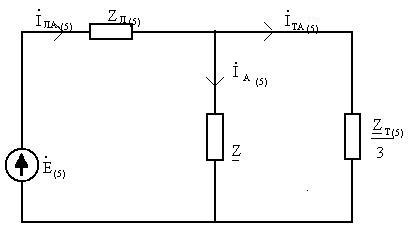
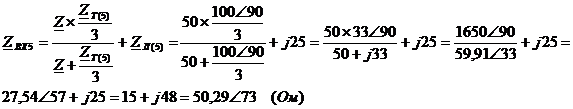
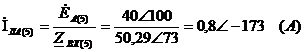
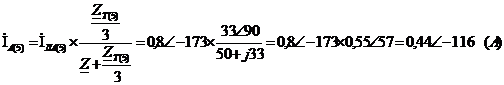
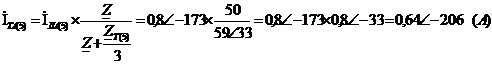
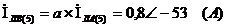
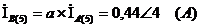
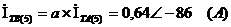
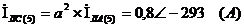
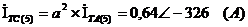
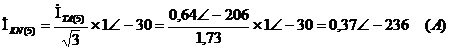
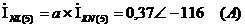
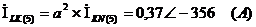
Мгновенные значения ЭДС и токов фазы
А и тока в нулевом проводе:
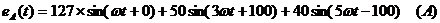
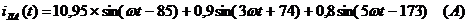
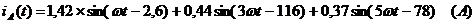
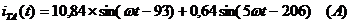
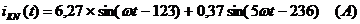
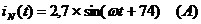
Построим векторно-топографическую
диаграмму
Для построения необходимо найти
потенциалы всех точек (А, В, С, а, в,
с, О, О/), примем потенциал точки О
равным нулю, следовательно, потенциал точки О/ тоже равен нулю. Потенциалы
остальных точек равны:
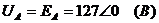 ,
,
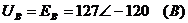 ,
,
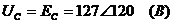 ,
,
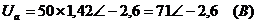 ,
,
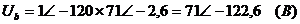 ,
,
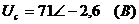 .
.
Определим показания ваттметров
Активную мощность Р, потребляемую в нагрузке
трёхфазной цепи , можно как сумму показаний ваттметров, включённых в данном
случае в фазы А и В по схеме двух ваттметров, т. е. Р = РА +РВ . Показания
каждого из ваттметров могут быть определены по формулам:
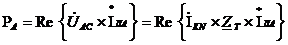 ;
;
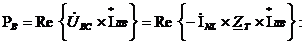
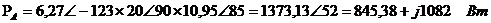
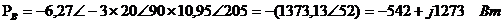
Баланс мощностей
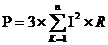
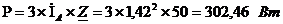
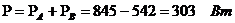
Рассчитаем погрешность:
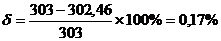
Напряжение между точками А и n
(UAn):
Для первой гармоники.
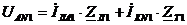 :
:
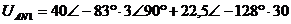 :
:
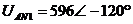 В
В
Для третей гармоники.
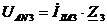 :
:
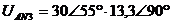 :
:
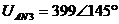 В
В
Для пятой гармоники.
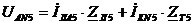 :
:
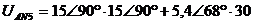 :
:
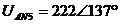 В
В
Мгновенное значение
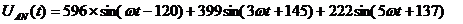
График заданной несинусоидальной ЭДС
фазы А.
Мгновенные выражения э.д.с. в фазах.
Фазы А.
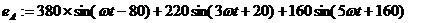 В
В
Фазы В.
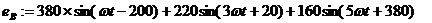 В
В
Фазы С.
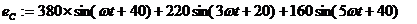 В
В
Амплитудно-частотные и фазо-частотные
спектры ЭДС фазы А
Мгновенное выражение э.д.с. в фазы А
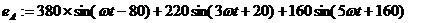
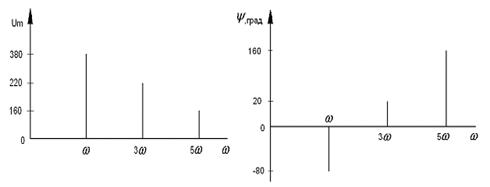
Амплитудно-частотные и
фазо-частотные спектры напряжения Uan.
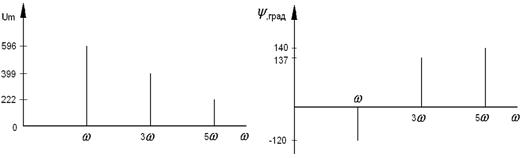
Мгновенное значение
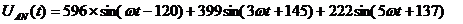 В
В
АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
ток напряжение электрический
линейный
Классический метод:
Исходные данные:
R1 = 200 Oм
R2 = 300 Ом
U = 120 В
С = 50 мкФ
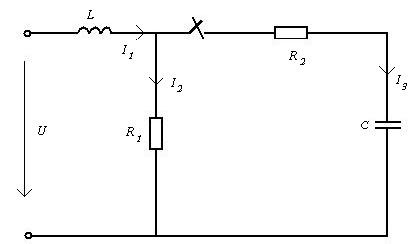
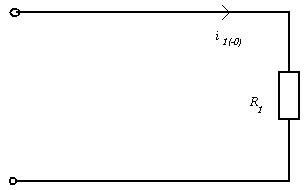
Схема до коммутации:
1) t = -0
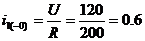
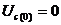
2) t = ∞ 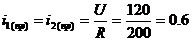
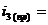 0
0
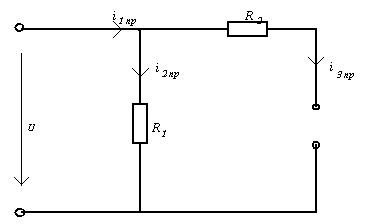
Определение корней
характеристического уравнения (t = 0):
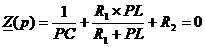
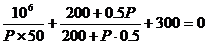
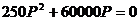
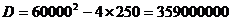

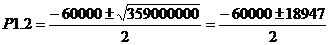
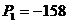 ;
; 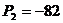
Определение зависимых начальных
условий (t = 0):
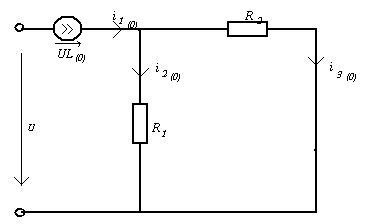
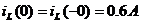
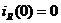
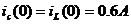
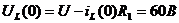
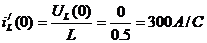
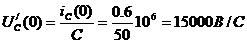
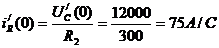
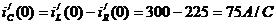
Определения постоянных
интегрирования
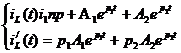
Подставим в них t
= 0
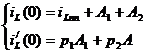
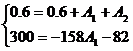
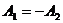
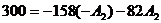
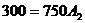
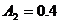
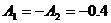
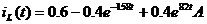
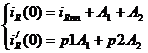
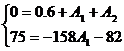
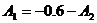
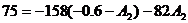
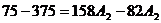
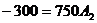
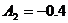
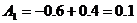
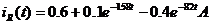
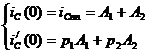
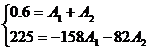
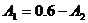
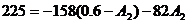
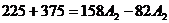
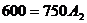
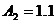
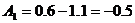
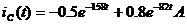
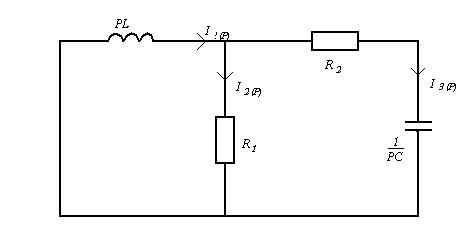
Операторный метод
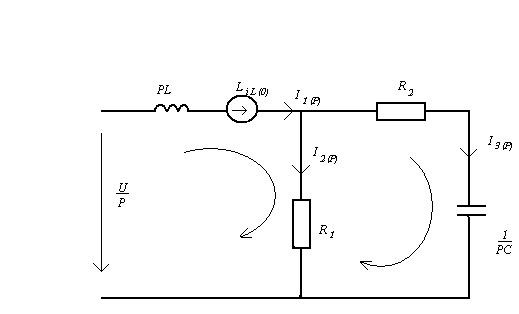
Операторные изображения токов найдены методом
контурных токов
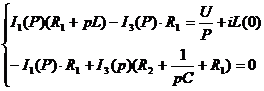
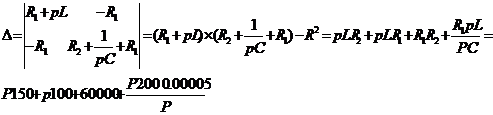
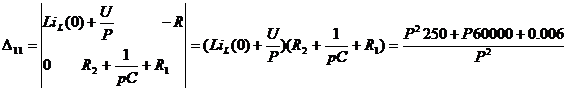
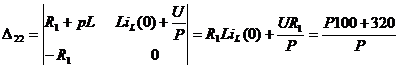
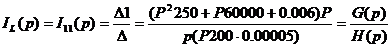
По теореме разложения:
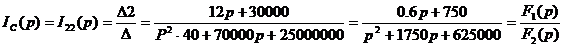
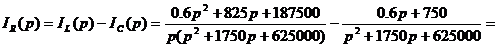
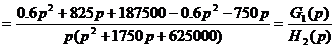
Находим корни 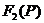
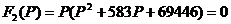
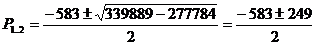
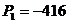
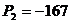
Найдем производную. 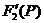
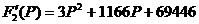
Находим ток i1(t)
Подставляем найденные корни в 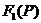 :
: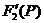
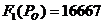
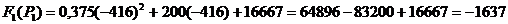
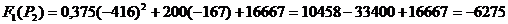
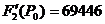
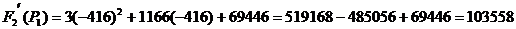
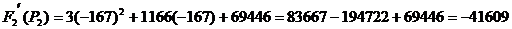
Искомый ток
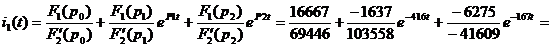
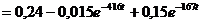 А
А
Находим ток iС(t)
Корни: 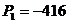
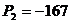
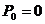 ,
, 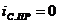
Найдем производную. 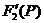
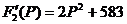
Подставляем найденные корни в 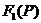 :
: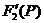
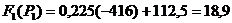
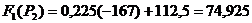
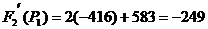
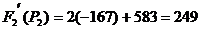
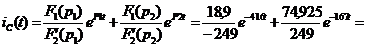
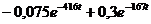 А
А
Находим ток iL(t)
Корни: 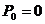
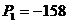
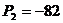
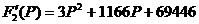
Подставляем найденные корни в 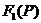 :
: