Линейные алгебры малых размерностей
Министерство
образования Республики Беларусь
Учреждение
образования
«Гомельский
государственный университет
имени
Франциска Скорины»
Факультет
математический
Кафедра
алгебры и теории чисел
Курсовая
работа
Линейные
алгебры малых размерностей
Гомель
2010
Содержание
Введение
.Основные
определения
.Алгебры.
Ассоциативные алгебры
.Алгебры
Ли
.Нильпотентные
алгебры Ли
.1
Эквивалентность различных определений нильпотентности
.Разрешимые
алгебры Ли
.Описание
алгебр Ли малых размерностей
.Заключение
Список
использованных источников
Введение
Алгебры Ли прочно вошли в математику в конце
прошлого века. Их теория благодаря вниманию многих выдающихся математиков
обогатилась целым рядом тонких и красивых результатов, влияние которых
простирается далеко за пределы алгебры. Поэтому отсутствие книги учебного
характера по теории алгебр Ли давно воспринималось как досадный пробел в
математической литературе. Отчасти это объяснялось тем фактом - благоприятным
во всех других отношениях, - что теории групп Ли и алгебр Ли продолжительное
время развивались параллельно, а преобладание методов анализа и топологии лишь
способствовало укоренившейся привычке смотреть на аппарат алгебр Ли прежде
всего как на полезное и мощное средство линеаризации теоретико-групповых задач.
Алгебраические же основания теории оставались до некоторых пор в тени, созревая
на страницах журнальных статей, особенно многочисленных за последние два
десятилетия.
Алгебры Ли представляют собой один из
классических объектов современной математики. Их теория находится в особом
положении как по полноте структурной информации, по крайней мере, в классе
конечномерных алгебр Ли, так и по многочисленным связям с другими разделами
математики, среди которых следует упомянуть теорию групп Ли.
Теория представления алгебр Ли до сих пор не
имеет, по существу, самостоятельного статуса. Это связано, например, с
необозримостью задачи классификации простых модулей над алгебрами Ли. Развитие
теории представлений алгебр Ли традиционно связано с теорией представления групп
Ли.
Теория алгебр Ли выросла из теории Ли
непрерывных групп. Основным результатом последней является сведение «локальных»
задач, относящихся к группам Ли, к соответствующим задачам теории алгебр Ли, т.
е. к задачам линейной алгебры. Каждой группе Ли сопоставляется алгебра Ли над
полем вещественных или комплексных чисел, и устанавливается соответствие между
аналитическими подгруппами группы Ли и подалгебрами ее алгебры Ли, при котором
инвариантным подгруппам соответствуют идеалы, абелевым подгруппам - абелевы
подалгебры и т. д. Изоморфизм алгебр Ли эквивалентен локальному изоморфизму
соответствующих групп Ли.
В последнее время введение соответствующих
алгебр Ли оказалось полезным при изучении двух других разделов теории групп.
Первым из этих разделов является теория свободных групп, которую можно изучать
при помощи свободных алгебр Ли, пользуясь методом, впервые предложенным
Магнусом. Хотя эта связь не такая тесная, как в теории Ли, применение алгебр Ли
привело к важным результатам относительно свободных групп и других классов
абстрактных групп. В частности, необходимо отметить результаты по так
называемой ослабленной проблеме Бернсайда: ограничены ли порядки конечных
групп, имеющих фиксированное число r
образующих и удовлетворяющих соотношению хm=1,
где m - фиксированное
положительное целое число? Стоит указать, что важную роль в этих приложениях к
теории абстрактных групп играют алгебры Ли простой характеристики.
Наряду с группами важную роль в теории симметрий
играют такие алгебраические объекты, как ассоциативные алгебры и алгебры Ли.
1.Основные определения
Кольцо R
- это непустое множество с операциями сложения и умножения, причем относительно
сложения R - абелева группа, и обе операции связаны законами дистрибутивности
x(y+z)=xy+xz,
(x+y)z=xz+yz,
где x,y,z
- произвольные элементы из R.
Алгеброй называют линейное пространство, в
котором кроме сложения и умножения на числа определена операция умножения
элементов пространства, причем умножение и сложение удовлетворяют законам
дистрибутивности
a(αb+βc)=αaβ+βac,
(αb+βc)a=αba+βca,
где α, β - числа,
а a,b,c
- элементы алгебры.
Если линейное пространство алгебры
рассматривается над полем вещественных (комплексных) чисел, то алгебру называют
вещественной (комплексной ).
Допустим, что в некотором кольце К для любых
трех элементов x,y,z
справедливо соотношение
x(yz)+y(xz)+
z (xy)
=0.
В этом случае мы скажем, что в К выполняется
тождество Якоби.
Алгеброй Ли называется векторное
пространство L с
умножением (билинейным отображением (ξ1, ξ2) →[ ξ1, ξ2] произведения
L 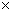 L в L), которое
антисимметрично
L в L), которое
антисимметрично
[ ξ1, ξ2]+ [ ξ2, ξ1]=0
и удовлетворяет тождеству Якоби
[ ξ1, [ξ2, ξ3]] + [ ξ2, [ξ3, ξ1]] +[ ξ3, [ξ1, ξ2]] =0
для всех ξ1, ξ2, ξ3  L.
L.
Пусть L есть К -
алгебра Ли V - некоторый
К - модуль. Мы говорим, что V является К - модулем, если
существует К - билинейное отображение L 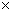 V → V,
удовлетворяющее следующей аксиоме ( в записи которой x,y
V → V,
удовлетворяющее следующей аксиоме ( в записи которой x,y  L, v
L, v  V, yv - образ
пары (y,v) при данном
билинейном отображении):
V, yv - образ
пары (y,v) при данном
билинейном отображении):
(xy)v=x(yv)-y(xv).
Подпространство К пространства L называется
подалгеброй алгебры Ли L, если [ К,К] 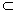 К, и идеалом
этой алгебры, если [ К, L]
К, и идеалом
этой алгебры, если [ К, L] 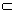 К.
К.
Если К, N-идеалы
алгебры L, то
пересечение К  N,
произведение [К, N] и сумма K + N
подпространств К, N векторного пространства L также
являются идеалами алгебры L, причем [К, N]
N,
произведение [К, N] и сумма K + N
подпространств К, N векторного пространства L также
являются идеалами алгебры L, причем [К, N] 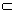 =K
=K  N. Если K
N. Если K  N = 0, то [К N]=0; при
этом идеал K + N называется
прямой суммой идеалов К, N алгебры L и
обозначается символом К
N = 0, то [К N]=0; при
этом идеал K + N называется
прямой суммой идеалов К, N алгебры L и
обозначается символом К 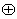 N. Если в
алгебре L существуют
такие идеалы К, N, что L= К
N. Если в
алгебре L существуют
такие идеалы К, N, что L= К 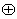 N, то алгебра
L называется
разложимой в прямую сумму своих подалгебр К и N.
N, то алгебра
L называется
разложимой в прямую сумму своих подалгебр К и N.
Алгебра L называется
разрешимой, если L(n) = 0 для
некоторого n > 0.
Алгебра Ли называется нильпотентной,
если для некоторого положительного целого n L(n)=0.
Пусть K,
N-разрешимые идеалы алгебры Lr.
Факторалгебра (K+N)/N изоморфна
разрешимой алгебре К/(К 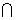 N) и, значит,
разрешима. Поэтому идеал K + N разрешим
как расширение разрешимой алгебры (K+N)/N с помощью
разрешимой алгебры N. Отсюда следует, что разрешимый идеал R
максимальной размерности в конечной алгебре Ли Lr является
единственным и содержит все разрешимые идеалы алгебры Lr. Этот
максимальный разрешимый идеал R называется радикалом алгебры Lr.
N) и, значит,
разрешима. Поэтому идеал K + N разрешим
как расширение разрешимой алгебры (K+N)/N с помощью
разрешимой алгебры N. Отсюда следует, что разрешимый идеал R
максимальной размерности в конечной алгебре Ли Lr является
единственным и содержит все разрешимые идеалы алгебры Lr. Этот
максимальный разрешимый идеал R называется радикалом алгебры Lr.
Алгебра Ли Lr называется
полупростой, если ее радикал равен нулю.
2.Алгебры. Ассоциативные алгебры
В линейных (векторных) пространствах
заданы две алгебраические операции - сложение и умножение на числа. Алгеброй
называют линейное пространство, в котором кроме сложения и умножения на числа
определена операция умножения элементов пространства, причем умножение и сложение
удовлетворяют законам дистрибутивности
a(αb+βc)=αaβ+βac,
(αb+βc)a=αba+βca,
где α, β - числа, а a,b,c - элементы
алгебры.
Если линейное пространство алгебры
рассматривается над полем вещественных ( комплексных ) чисел, то алгебру
называют вещественной (комплексной ). Алгебры бывают конечномерными и
бесконечномерными. Если умножение в алгебре коммутативно, то есть ab=ba для любых
элементов a и b алгебры, то
алгебру называют коммутативной. Если в алгебре А существует элемент е, такой
что ае=еа=а для любых элементов а А, то е называют единицей алгебры
А, а алгебру А - алгеброй с единицей. Если для любых трех элементов a,b,c алгебры А
выполняется условие ассоциативности (ab)c=a(bc), то А
называют ассоциативной алгеброй.
А, то е называют единицей алгебры
А, а алгебру А - алгеброй с единицей. Если для любых трех элементов a,b,c алгебры А
выполняется условие ассоциативности (ab)c=a(bc), то А
называют ассоциативной алгеброй.
Пример 1. Множество
всех комплексных чисел - вещественная ассоциативная алгебра с единицей.
Пример 2. Множество Mat(n,C) всех
комплексных квадратных матриц размерности n -
ассоциативная алгебра относительно обычных сложения и умножения матриц. Эта
алгебра некоммутативна.
Пример 3. Множество
С∞(Rn) всех комплексных бесконечно
дифференцируемых функций на Rn образуют
комплексную коммутативную ассоциативную алгебру относительно обычных сложения и
умножения функций.
Линейное подпространство В алгебры А
называют подалгеброй в А, если В является алгеброй относительно заданного в А
умножения, то есть произведение элементов из В принадлежит В.
Если В - подалгебра алгебры А и для
всех а А, b
А, b B элемент ab (элемент ba) лежит в В,
то В называют левым (правым) идеалом. Если же для всех а
B элемент ab (элемент ba) лежит в В,
то В называют левым (правым) идеалом. Если же для всех а А, b
А, b B как ab, так и ba принадлежит
В, то В - двусторонний идеал (или просто идеал) алгебры А. Алгебру, не имеющую
нетривиальных идеалов, называют простой.
B как ab, так и ba принадлежит
В, то В - двусторонний идеал (или просто идеал) алгебры А. Алгебру, не имеющую
нетривиальных идеалов, называют простой.
Пример 4. Алгебра Mat(n,C) простая.
Пусть А1 и А2
- алгебры . Отображение φ
из
А1 в А2 называют гомоморфизмом, если φ сохраняет
линейные операции и умножение, то есть если для всех a,b  А1
и для всех чисел α,β
имеем
А1
и для всех чисел α,β
имеем
φ (
αa+βb)= αφ(a)+βφ(b),
φ(ab)=φ(b)φ(a).
Если гомоморфизм φ алгебры А1
на алгебру А2 взаимно однозначен, то он называется изоморфизмом.
Изоморфизм алгебры А на себя называют автоморфизмом А. Множество всех
автоморфизмов алгебры А образует группу, обозначаемую через Aut А. Взаимно
однозначное отображение φ
алгебры
в себя называют антиавтоморфизмом, если
φ (
αa+βb)= αφ(a)+βφ(b),
φ(ab)=φ(b)φ(a).
3.Алгебры Ли
Алгеброй Ли называется векторное
пространство L с
умножением (билинейным отображением (ξ1, ξ2) →[
ξ1, ξ2]
произведения L 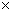 L в L), которое
антисимметрично
L в L), которое
антисимметрично
[ ξ1, ξ2]+ [ ξ2, ξ1]=0
и удовлетворяет тождеству Якоби
для всех ξ1, ξ2, ξ3  L.
Произведение [ ξ1, ξ2] называется
коммутатором векторов ξ1 и ξ2. Любое
векторное пространство можно превратить в алгебру Ли. Если, например,
определить умножение, пологая [ ξ1, ξ2]=0 для всех
векторов ξ1, ξ2
рассматриваемого пространства, то получается алгебра Ли, называемая
коммутативной, или абелевой. Размерностью алгебры Ли L называется
размерность векторного пространства L. Алгебра L размерности
r будет
обозначаться также символом Lr.
L.
Произведение [ ξ1, ξ2] называется
коммутатором векторов ξ1 и ξ2. Любое
векторное пространство можно превратить в алгебру Ли. Если, например,
определить умножение, пологая [ ξ1, ξ2]=0 для всех
векторов ξ1, ξ2
рассматриваемого пространства, то получается алгебра Ли, называемая
коммутативной, или абелевой. Размерностью алгебры Ли L называется
размерность векторного пространства L. Алгебра L размерности
r будет
обозначаться также символом Lr.
Пусть Lr - алгебра
Ли, ξ1,…, ξr - базис
соответствующего векторного пространства Lr. Разложение
коммутатора любой пары базисных векторов по этому базису имеет вид
[ ξi, ξj]=ckij ξk,
где ckij (I,j,k=1,…,r) -
вещественные числа. Числа ckij называются структурными
константами ( в данном базисе ) алгебры Lr и образуют
аффинный тензор над векторным пространством Lr.
Антисимметричность коммутатора и тождества Якоби накладывают следующие условия
на структурные константы:
ckij+ ckji=0, ckim cmin+ ckjm cmni+ cknm cmij=0.
Линейное отображение f: L→K называется
гомоморфизмом алгебры L в алгебру К, если для всех векторов
ξ,
ξ’ из L выполняется
равенство
f([ξ, ξ’])=[ f(ξ), f(ξ’)].
Множество f-1(0) всех
векторов из L, которые
при гомоморфизме f переходят в нулевой вектор
пространства К, называется ядром гомоморфизма f. Если f отображает L на К и f-1(0)=0, то
гомоморфизм f называется
изоморфизмом, а алгебры L и К - изоморфными. Изоморфизм
алгебры L на себя
называется автоморфизмом.
Пусть L - алгебра
Ли, К и N - подпространство
векторного пространства L, а К 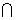 N обозначает
их пересечение. Суммой подпространств К, N называется
подпространство К+ N, состоящее из всех векторов вида η+ ξ
(η
N обозначает
их пересечение. Суммой подпространств К, N называется
подпространство К+ N, состоящее из всех векторов вида η+ ξ
(η  К, ξ
К, ξ  N), а их
произведением [К,
ξ]
- линейная оболочка всех коммутаторов [ η, ξ] (η
N), а их
произведением [К,
ξ]
- линейная оболочка всех коммутаторов [ η, ξ] (η  К, ξ
К, ξ  N). Если К
N). Если К N=0, то К+ N называется
прямой суммой подпространствах К, N.
N=0, то К+ N называется
прямой суммой подпространствах К, N.
Подпространство К пространства L называется
подалгеброй алгебры Ли L, если [ К,К] 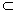 К, и идеалом
этой алгебры, если [ К, L]
К, и идеалом
этой алгебры, если [ К, L] 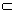 К.
К.
Если К, N-идеалы
алгебры L, то
пересечение К  N,
произведение [К, N] и сумма K + N
подпространств К, N векторного пространства L также
являются идеалами алгебры L, причем [К, N]
N,
произведение [К, N] и сумма K + N
подпространств К, N векторного пространства L также
являются идеалами алгебры L, причем [К, N] 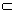 =K
=K  N. Если K
N. Если K  N = 0, то [К N]=0; при
этом идеал K + N называется
прямой суммой идеалов К, N алгебры L и
обозначается символом К
N = 0, то [К N]=0; при
этом идеал K + N называется
прямой суммой идеалов К, N алгебры L и
обозначается символом К 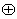 N. Если в
алгебре L существуют
такие идеалы К, N, что L= К
N. Если в
алгебре L существуют
такие идеалы К, N, что L= К 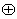 N, то алгебра
L называется
разложимой в прямую сумму своих подалгебр К и N. Пусть теперь К - идеал, a
N-подалгебра алгебры L, причем K
N, то алгебра
L называется
разложимой в прямую сумму своих подалгебр К и N. Пусть теперь К - идеал, a
N-подалгебра алгебры L, причем K  N=0; тогда
прямая сумма K + N
подпространств К, N пространства L является подалгеброй алгебры L и
называется полупрямой суммой подалгебр К и N алгебры L. Если при
этом L = К+ N, то
говорят, что алгебра L является полупрямой суммой своих
подалгебр К и N.
N=0; тогда
прямая сумма K + N
подпространств К, N пространства L является подалгеброй алгебры L и
называется полупрямой суммой подалгебр К и N алгебры L. Если при
этом L = К+ N, то
говорят, что алгебра L является полупрямой суммой своих
подалгебр К и N.
Пусть К-идеал алгебры L. Семейство L/К попарно
непересекающихся смежных классов ξ + K естественно
снабжается структурой алгебры Ли. Полученная алгебра L/К
называется факторалгеброй алгебры L по идеалу
К, а гомоморфизм ξ→
ξ+К
алгебры L на алгебру L/К -
естественным, или каноническим, гомоморфизмом; ядром этого гомоморфизма
являетсяидеал К. Сама алгебра L называется при этом расширением
алгебры L/К с помощью
К.
Алгебра Ли L(1) = [L, L] называется
производной алгеброй алгебры Ли L. По построению, L(1) является
идеалом в L.
Производные алгебры более высокого порядка определяются рекуррентно: L(n+1) = (L(n))(1),
n=1, 2, ...
Алгебра L называется
разрешимой, если L(n) = 0 для
некоторого n > 0.
Простейшим примером разрешимой алгебры является коммутативная алгебра Ли.
Разрешимы также все одномерные и двумерные алгебры Ли. Подалгебра и гомоморфный
образ любой разрешимой алгебры, очевидно, разрешимы; в частности, разрешима
факторалгебра разрешимой алгебры по любому ее идеалу. Кроме того, если идеал K алгебры L и
факторалгебра L/K разрешимы,
то сама алгебра L также разрешима. Действительно,
если K(n) = 0, (L/K)(m) = 0 для
некоторых положительных n, т, a f: L→ L/K - естественный
гомоморфизм, то f(L(m))=(f(L))(m)= (L/K)(m)=0, откуда
следует, что L(m) 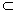 К и
К и
L(n+m)=0.
Алгебра Ли называется нильпотентной,
если для некоторого положительного целого n L(n)=0.
При помощи индукции легко проверить,
что L(n) 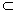 L(n). В самом
деле, L(0)=L(0), и если L(n)
L(n). В самом
деле, L(0)=L(0), и если L(n) 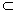 L(n), то
L(n), то
L(n+1)=[
L(n) , L(n)] 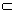 [L(n), L]
[L(n), L] 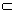 L(n+1).
L(n+1).
Таким образом, нильпотентная алгебра
является разрешимой. Обратное не верно: например, двумерная некоммутативная
алгебра Ли , определяемая коммутативным соотношением
[X,Y]=X,
разрешима, но не нильпотентна.
Пусть K,
N-разрешимые идеалы алгебры Lr.
Факторалгебра (K+N)/N изоморфна
разрешимой алгебре К/(К 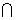 N) и, значит,
разрешима. Поэтому идеал K + N разрешим
как расширение разрешимой алгебры (K+N)/N с помощью
разрешимой алгебры N. Отсюда следует, что разрешимый идеал R
максимальной размерности в конечной алгебре Ли Lr является
единственным и содержит все разрешимые идеалы алгебры Lr. Этот
максимальный разрешимый идеал R называется радикалом алгебры Lr.
N) и, значит,
разрешима. Поэтому идеал K + N разрешим
как расширение разрешимой алгебры (K+N)/N с помощью
разрешимой алгебры N. Отсюда следует, что разрешимый идеал R
максимальной размерности в конечной алгебре Ли Lr является
единственным и содержит все разрешимые идеалы алгебры Lr. Этот
максимальный разрешимый идеал R называется радикалом алгебры Lr.
Алгебра Ли Lr называется
полупростой, если ее радикал равен нулю. Заметим, что всякий коммутативный
идеал разрешим. С другой стороны, алгебра L, содержащая
ненулевой разрешимый идеал К, содержит также ненулевой коммутативный идеал - им
является предпоследний элемент последовательности производных: К, К(1),..,К(n-1),К(n)=0. Поэтому
алгебра Ли полупроста в том и только том случае, если она не имеет отличных от
нуля коммутативных идеалов.
Полупростой будет любая
конечномерная алгебра L, распадающаяся в прямую сумму
L=К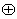 …
…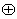 N
N
своих идеалов K,…,N,
являющимися простыми алгебрами.
4.Нильпотентные алгебры Ли
.1 Эквивалентность различных
определений нильпотентности
Теорема. Следующие условия на
алгебру Ли L над кольцом
К эквивалентны (с - некоторое натуральное число):
. Lс 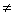 {0}, Lс+1={0};
{0}, Lс+1={0};
. Zc-1(L) 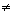 L, Zc(L)=L;
L, Zc(L)=L;
. L обладает
конечным центральным рядом длины с и не обладает таким рядом длины с -1;
. для любой расстановки скобок
произведение с+1 элемента алгебры L равно нулю,
и при некоторой расстановки скобок произведение некоторых элементов не равно
нулю;
. в L выполняются
тождество
х1х2…хс+1
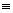 0
0
и не выполняется тождество
х1х2…хс
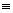 0.
0.
Доказательство. Заметим вначале, что
для любых натуральных s и r справедливо
включение LsLt 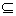 Ls+t.
Действительно, заметим, что LsL1=Ls+1 по
определению нижнего центрального ряда. Проводя индукцию по r, получаем
Ls+t.
Действительно, заметим, что LsL1=Ls+1 по
определению нижнего центрального ряда. Проводя индукцию по r, получаем
LsLr+1=
Ls(LrL1) 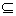 ( LsLr )L1+
Lr (LsL1)=Ls+rL1+LrLs+1=Ls+r+1.
( LsLr )L1+
Lr (LsL1)=Ls+rL1+LrLs+1=Ls+r+1.
Здесь мы воспользовались тождеством
Якоби, предположением индукции и определением членов нижнего центрального ряда.
Для доказательства эквивалентности
утверждений 1-3 достаточно заметить, что если L обладает
центральным рядом длины с
L=L0 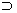 L1
L1 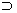 …
… 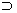 Lc={0}, (1)
Lc={0}, (1)
то, согласно свойствам верхнего и
нижнего рядов, получаем, что для любого неотрицательного l имеем
Ll+1 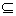 L1 и Zl(L)
L1 и Zl(L) 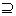 Lc-1.
Lc-1.
Поэтому в этом случае Lс+1={0} и Zс(L)= L. Выбирая в
качестве ряда (1) соответственно нижний и верхний центральные ряды, мы получаем
все нужные нам импликации (1) 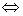 (2)
(2) 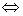 (3).
(3).
Докажем теперь, что из (1) следует
(4). Действительно, докажем по индукции, что для любой расстановки скобок σ и любых х1х2…хl+1  L выполняется
a= (х1х2…хl+1 )σ
L выполняется
a= (х1х2…хl+1 )σ  Ll+1 . Основание
индукции при l=0 очевидно.
Предполагая утверждение доказанным при меньших значениях l, заметим,
что для некоторого s<l имеем a= (х1х2…хs )τ(хs+1…хl+1 )π, где π и τ - некоторые
расстановки скобок. По предположению индукции (х1х2…хs )τ
Ll+1 . Основание
индукции при l=0 очевидно.
Предполагая утверждение доказанным при меньших значениях l, заметим,
что для некоторого s<l имеем a= (х1х2…хs )τ(хs+1…хl+1 )π, где π и τ - некоторые
расстановки скобок. По предположению индукции (х1х2…хs )τ  Ls , а (хs+1…хl+1 )π
Ls , а (хs+1…хl+1 )π Ll-s+1. Согласно
замечанию в начале доказательства а
Ll-s+1. Согласно
замечанию в начале доказательства а  Ls Ll-s+1
Ls Ll-s+1 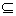 Ll+1. Значит,
предполагая (1) выполненным, получим, что для любых х1х2…хc+1 и любой
расстановки σ
имеем
в L
Ll+1. Значит,
предполагая (1) выполненным, получим, что для любых х1х2…хc+1 и любой
расстановки σ
имеем
в L
a= (х1х2…хс+1)σ=0.
Заметим теперь, что из определения с
очевидностью следует, что для любого l идеал Ll является К
- подмодулем, порожденным всевозможными правонормированными произведениями
х1х2 …хl , xi  L , i=1,2,…,l.
L , i=1,2,…,l.
Поэтому, если хотя бы одно из
произведений х1…хс отлично от нуля, то . Lс 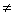 {0}.
Понятно, далее, что (4)
{0}.
Понятно, далее, что (4) 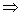 (5)
(5) 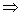 (1). Теорема
доказана.
(1). Теорема
доказана.
Алгебра Ли, удовлетворяющая
эквивалентным условиям данной теоремы, называется нильпотентной ступени с.
5.Разрешимые алгебры Ли
Определим неассоциативный одночлен σl ( x1,…,x2l) индукцией
по l, полагая σ0 (х)=х и
σl+1(x1,…,x2l+1)=σl(x1,…,x2l) σl(x1,…,x2l+1).
Теорема. Следующие
условия на алгебру Ли и L над кольцом К эквивалентны.
. Для некоторого целого l 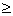 1 L(l-1)
1 L(l-1) 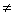 {0},a L(l)={0}.
{0},a L(l)={0}.
. В L имеется
конечный разрешимый ряд идеалов
L=L0 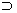 L1
L1 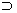 …
… 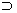 Ll={0}
Ll={0}
(т.е. такой, что Li/Li+1 - абелева
алгебра), и число l - наименьшая длина таких рядов.
. В L имеется ряд
подалгебр
L=М0
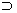 М1
М1
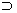 …
… 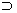 Мc={0}, где М2i
Мc={0}, где М2i 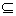 Mi+1 и число l -
наименьшая длина таких рядов.
Mi+1 и число l -
наименьшая длина таких рядов.
. В L
тождественно выполняется соотношение σl ( x1,…,x2l)=0,
А σl-1 ( x1,…,x2l-1)=0 не
является тождеством L.
Доказательство. Ряд коммутантов
обладает тем свойством, что для разрешимого ряда и любого n 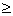 0
выполняется Ln
0
выполняется Ln 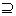 Ln. Значит,
(1) и (2) эквивалентны. Далее, если справедливо (3), то, в силу свойства М2i
Ln. Значит,
(1) и (2) эквивалентны. Далее, если справедливо (3), то, в силу свойства М2i 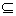 Mi+1, по
индукции L(n)
Mi+1, по
индукции L(n) 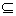 Mi, откуда L(l)={0}.
Значит, выполнено (1); если L(l-1)={0}, то ряд
коммутантов будет иметь меньшую длину, чем ряд в (3), что невозможно. Таким
образом, (1) и (3) эквивалентны. Утверждение (4) вытекает из (1), так как индуктивное
определение элементов σl(x1,…,x2l)
показывает, что для любых v1,…,v2l
Mi, откуда L(l)={0}.
Значит, выполнено (1); если L(l-1)={0}, то ряд
коммутантов будет иметь меньшую длину, чем ряд в (3), что невозможно. Таким
образом, (1) и (3) эквивалентны. Утверждение (4) вытекает из (1), так как индуктивное
определение элементов σl(x1,…,x2l)
показывает, что для любых v1,…,v2l  L элемент σl(v1,…,v2l) лежит в L(l). Для
доказательства обратного заметим, что L(l) как К -
модуль порождается элементами σl(v1,…,v2l), vi
L элемент σl(v1,…,v2l) лежит в L(l). Для
доказательства обратного заметим, что L(l) как К -
модуль порождается элементами σl(v1,…,v2l), vi  L. Это
утверждение справедливо при l=0. Предполагая его справедливым для
L(l-1) есть К -
оболочка элементов σl-1(v1,…,v2l-1), v1,…,v2l-1
L. Это
утверждение справедливо при l=0. Предполагая его справедливым для
L(l-1) есть К -
оболочка элементов σl-1(v1,…,v2l-1), v1,…,v2l-1  L. По
определению тогда L(l) является К
- оболочкой произведений таких элементов, равных элементам вида
L. По
определению тогда L(l) является К
- оболочкой произведений таких элементов, равных элементам вида
σl-1(v1,…,v2l-1) σl-1(v2l-1+1,…,v2)= σl(v1,…,v2l).
Таким образом, если выполнено (4),
то и выполнено (1). Теорема доказана.
Алгебра L,
удовлетворяющая условиям (1) - (4), называется разрешимой ступени l.
6.Описание алгебр Ли малых
размерностей
Опишем теперь все алгебры Ли,
размерность которых меньше четырех. Пусть (e1,e2,…,en) - базис
алгебры Ли L; тогда [eiei]=0, [eiej]=-[ejei], и поэтому
для задания таблицы умножения в этом базисе достаточно определить произведения
[eiei] для i<j. Будем
использовать в наших рассуждениях эти сокращенные таблицы умножения:
I. Dim
L=1. Тогда L=Фе,
[ee]=0.
(a) L’=0, L - абелева.
(b) L’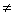 0. Поскольку
L=Фе+Фf, L’= Ф[ef] имеет
размерность единицу.
0. Поскольку
L=Фе+Фf, L’= Ф[ef] имеет
размерность единицу.
Мы можем выбрать элемент е так, что L’=
Фe. Следовательно, L
совпадает с ассоциативной алгеброй. Эта алгебра - единственная неабелева
алгебра Ли размерности 2.
III. Dim
L=3.
(a) L’=0, L - абелева.
(b) Dim L’=1, L’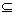 N, где
N - центр.
Если
L’=Фе,
то мы запишем
N, где
N - центр.
Если
L’=Фе,
то мы запишем
L=Фе+Фf+Фg.
Тогда L’=
Ф[fg]. Поэтому можно
положить [fg]=e.
Таким образом, алгебра L
имеет базис (e,f,g)
с таблицей умножения
[fg]=e,
[ef]=0, [eg]=0.
(1)
(с) L’=1, L’ 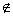 N,
N,
где N - центр.
Если L’=Фе, то
существует элемент f, такой, что [ef] 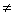 0. Тогда [ef]=βe
0. Тогда [ef]=βe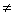 0 и можно
положить [ef]=е. Поэтому
Фе+Фf - неабелева
алгебра L размерности
2. Так как R
0 и можно
положить [ef]=е. Поэтому
Фе+Фf - неабелева
алгебра L размерности
2. Так как R 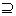 L’, где R - идеал, а
так как R -
совершенная алгебра, то L=R
L’, где R - идеал, а
так как R -
совершенная алгебра, то L=R 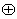 ξ , где ξ=Фg. Поэтому ξ имеет базис
(e,f,g) с таблицей
умножения
ξ , где ξ=Фg. Поэтому ξ имеет базис
(e,f,g) с таблицей
умножения
[ef]=e, [eg]=0, [fg]=0. (2)
(d) Dim L’=2. Алгебра
L’ не может
быть неабелевой двумерной алгеброй Ли L, так как
тогда имели бы место равенства L=R 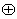 ξ и L’=R’=R. Но R’
ξ и L’=R’=R. Но R’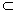 R . Поэтому L’ абелева.
Пусть L’= Фе+Фf и L=Фе+Фf+Фg. Тогда L’= Ф [eg]+ Ф [fg] и,
следовательно, ad g индуцирует
взаимно однозначное линейное отображение в L’. Поэтому
алгебра L имеет базис
(e,f,g) с таблицей
умножения
R . Поэтому L’ абелева.
Пусть L’= Фе+Фf и L=Фе+Фf+Фg. Тогда L’= Ф [eg]+ Ф [fg] и,
следовательно, ad g индуцирует
взаимно однозначное линейное отображение в L’. Поэтому
алгебра L имеет базис
(e,f,g) с таблицей
умножения
[ef]=0, [eg]=αe+βf, [fg]=γe+δf, (3)
где А= 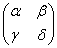 -
невырожденная матрица. Обратно, в каждом пространстве L с базисом (e,f,g) мы можем
определить произведение [ab] так, что выполнены условия
(3) и условие [aа]=0. Тогда [ [ef] g ]+[ [fg] e ]+ +[ [ge] f ]=0, и
поэтому L является
алгеброй Ли. Какие изменения можно внести в таблицу умножения (3)? Наш выбор
базиса равносилен следующему: мы выбираем базис (e,f) алгебры L’ и
дополняем его элементом g так, чтобы получить базис алгебры L. При
изменении базиса L’ матрица А переходит в подобную
матрицу М-1АМ. Допустимым изменением элемента g является
замена этого элемента на элемент ρg+х, ρ
-
невырожденная матрица. Обратно, в каждом пространстве L с базисом (e,f,g) мы можем
определить произведение [ab] так, что выполнены условия
(3) и условие [aа]=0. Тогда [ [ef] g ]+[ [fg] e ]+ +[ [ge] f ]=0, и
поэтому L является
алгеброй Ли. Какие изменения можно внести в таблицу умножения (3)? Наш выбор
базиса равносилен следующему: мы выбираем базис (e,f) алгебры L’ и
дополняем его элементом g так, чтобы получить базис алгебры L. При
изменении базиса L’ матрица А переходит в подобную
матрицу М-1АМ. Допустимым изменением элемента g является
замена этого элемента на элемент ρg+х, ρ  Ф, х
Ф, х  L’.
L’.
Тогда [e, ρg +х ]=ρ[eg], [f, ρg+х]=ρ[fg],
вследствие чего матрица А переходит в матрицу ρА. Поэтому
матрица А в таблице умножения (3) мы можем заменить любой матрицей вида ρВ, где В -
матрица, подобная А. Это означает, что мы имеем взаимно однозначное
соответствие между алгебрами L, удовлетворяющими условиями Dim L=3, Dim L’=2, и
классами сопряженных элементов в двумерной группе коллинеаций.
Если основное поле алгебраически замкнуто,
мы можем выбрать матрицу А в одной из следующих форм:
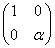 , α
, α 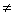 0;
0; 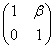 , β
, β 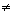 0.
0.
Это приводит к таким таблицам
умножения:
[ef]=0, [eg]=е, [fg]=αf,
[ef]=0, [eg]=е+ βf, [fg]=f.
Различным элементам α соответствуют
различные алгебры 1, поэтому мы получаем бесконечно много
неизоморфных алгебр.
(e) Dim L’=3. Пусть (e1,e2,e3) - базис, и
положим [e2e3]=f1,
[e3e1]=f2,
[e1e2]=f3.
Тогда (f1, f2, f3) - тоже базис. Запишем fi= 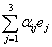 , где А=(αij) -
невырожденная матрица. Единственное условие Якоби, которое нужно наложить,
следующее: [f1e1]+[f2e2]+[f3e3]=0. Отсюда
получаем соотношение
, где А=(αij) -
невырожденная матрица. Единственное условие Якоби, которое нужно наложить,
следующее: [f1e1]+[f2e2]+[f3e3]=0. Отсюда
получаем соотношение
0= α12[e2e1]+ α13[e3e1]+ α21[e1e2]+ α23[e3e2]+ α31[e1e3]+ α32[e2e3]= -α12f3 + α31f2+ +α21f3- α23f1- α31f2+ α32f1.
Поэтому αij= αji, так что А
- симметрическая матрица. Пусть (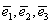 ) - другой базис, где
) - другой базис, где 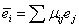 , М=(μij) -
невырожденная матрица. Положим
, М=(μij) -
невырожденная матрица. Положим
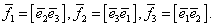
Для тройки (i,j,k),
полученной циклической перестановкой индексов (1, 2, 3), имеем формулы
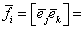 [∑μjrer, ∑μkses]=
[∑μjrer, ∑μkses]= 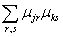 [ eres]=(μj2 μk3- μj3 μk2)f1+(
μj3 μk1- μj1 μk3)f2+
+( μj1 μk2- μj2 μk1)f3=∑νirfr.
[ eres]=(μj2 μk3- μj3 μk2)f1+(
μj3 μk1- μj1 μk3)f2+
+( μj1 μk2- μj2 μk1)f3=∑νirfr.
1 Следует
исключить случай, когда элементы α 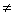 0, α’
0, α’ 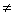 0 связаны
соотношением α
α’=1. Тогда
они определяют одну и туже алгебру, так как
0 связаны
соотношением α
α’=1. Тогда
они определяют одну и туже алгебру, так как
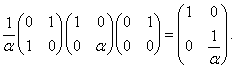
Матрица N=( νij)=adj
M’=(M’)-1det M’1. Матрица А
связывает элементы f с элементами е, а матрица M-1
связывает элементы е с элементами 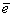 . Поэтому, если
. Поэтому, если 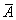 - матрица (
- матрица (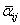 ), такая,
что
), такая,
что 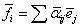 , то
, то
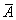 =(det M’)(M’)-1AM-1.
(4)
=(det M’)(M’)-1AM-1.
(4)
Матрицы А и В называются
мультипликативно коградиентными, если В=ρN’AN, где N -
невырожденная матрица и ρ
- отличный
от нуля элемент поля Ф. В этом случае можно записать В=ρσ2(σ-1N)’A (σ-1N),σ=ρ det N,и если
матрицы имеют три столбца и три
строки, то мы положим M=σN-1
и В=μ(M-1)’AM-1,μ=ρσ2=det M.
Таким образом, мы получам соотношение (4).
Вследствие этого матрицы А и 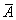 (симметрические)
должно быть мультипликативно коградиентны.
(симметрические)
должно быть мультипликативно коградиентны.
Поэтому каждой алгебре L,
удовлетворяющей нашим условиям, однозначно сопоставляется единственный класс
невырожденных мультипликативно коградиентных симметрических матриц. Имеется
столько алгебр, сколько существует классов таких матриц. Далее мы будем
предполагать, что характеристика основного поля отлична от 2.
Тогда каждый коградиентный класс
содержит диагональную матрицу вида diag{α,β,1},αβ
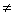 0. Отсюда
следует, что базис может быть выбран так, что выполняются равенства
0. Отсюда
следует, что базис может быть выбран так, что выполняются равенства
[e1e2]=e3, [e2e3]=αe1, [e3e1]=βe2. (5)
Если основное поле - поле
вещественных чисел, имеются две различные алгебры, соответствующие выбору α=β=1 и α=-1,
β=1. Если
поле алгебраически замкнуто, то можно положить α=β=1. Мы опишем
сейчас некоторую частную алгебру в семействе алгебр, удовлетворяющих условию Dim L=3= Dim L’. Наложим на
алгебру L следующие
условие: существует элемент h  L, такой, что
ad h имеет
характеристический корень α
L, такой, что
ad h имеет
характеристический корень α 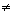 0, α
0, α 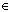 Ф. Тогда
найдется вектор е
Ф. Тогда
найдется вектор е 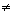 0, такой,
что [eh]=e ad h αe
0, такой,
что [eh]=e ad h αe 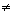 0, и так как
[hh]=0, то е и h - линейно
независимы и являются частью базиса (e1,e2,e3)
0, и так как
[hh]=0, то е и h - линейно
независимы и являются частью базиса (e1,e2,e3) 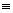 (e, h,f). Если (f1,
f2, f3) определены как раньше, то симметрическая матрица
(αij) имеет вид
(e, h,f). Если (f1,
f2, f3) определены как раньше, то симметрическая матрица
(αij) имеет вид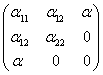 . (6)
. (6)
Из формул [eh]=αe, [h,h]=0, [fh]=-αf-α11e-α12h, следует,
что характеристические корни эндоморфизма ad h равны 0, α, -α.
Мы можем заменить f
характеристическим вектором, соответствующим корню -α, так как этот
вектор линейно независим относительно пары (e, h).
Здесь М’ - матрица,
получающаяся из М транспонированием, adj М’-
присоединенная матрица матрицы М’, det М’
- определитель матрицы М’.
Мы видим, таким образом, что
существует единственная алгебра, удовлетворяющая нашим условиям.
Поэтому мы можем предположить, что [eh]=αe, [fh]=-αf. Если
заменить h на 2α-1h, то
получится [eh]=2e, [fh]=-2f. Из формулы
(6) следует, что [ef]=βh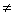 0.
0.
Заменив f на β-1f, мы
получим базис (e, f,h) с законом
умножения
[eh]=2e, [fh]=-2f, [ef]=h. (7)
7.Заключение
Алгебры Ли представляют собой один
из классических объектов современной математики. Их теория находится в особом
положении как по полноте структурной информации, по крайней мере, в классе
конечномерных алгебр Ли, так и по многочисленным связям с другими разделами
математики, среди которых следует упомянуть теорию групп Ли.
Теория представления алгебр Ли до
сих пор не имеет, по существу, самостоятельного статуса. Это связано, например,
с необозримостью задачи классификации простых модулей над алгебрами Ли.
Развитие теории представлений алгебр Ли традиционно связано с теорией
представления групп Ли.
Алгеброй Ли называется векторное
пространство L с
умножением (билинейным отображением (ξ1, ξ2) →[
ξ1, ξ2]
произведения L 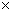 L в L), которое
антисимметрично
L в L), которое
антисимметрично
[ ξ1, ξ2]+ [ ξ2, ξ1]=0
и удовлетворяет тождеству Якоби
[ ξ1, [ξ2, ξ3]] + [ ξ2, [ξ3, ξ1]] +[ ξ3, [ξ1, ξ2]] =0
для всех ξ1, ξ2, ξ3  L.
Произведение [ ξ1, ξ2] называется
коммутатором векторов ξ1 и ξ2. Любое
векторное пространство можно превратить в алгебру Ли. Если, например,
определить умножение, пологая [ ξ1, ξ2]=0 для всех
векторов ξ1, ξ2 рассматриваемого
пространства, то получается алгебра Ли, называемая коммутативной, или абелевой.
Размерностью алгебры Ли L называется размерность векторного
пространства L.
L.
Произведение [ ξ1, ξ2] называется
коммутатором векторов ξ1 и ξ2. Любое
векторное пространство можно превратить в алгебру Ли. Если, например,
определить умножение, пологая [ ξ1, ξ2]=0 для всех
векторов ξ1, ξ2 рассматриваемого
пространства, то получается алгебра Ли, называемая коммутативной, или абелевой.
Размерностью алгебры Ли L называется размерность векторного
пространства L.
8. Список использованных источников
алгебра ли математика
нильпотентная
1.
Бахтурин А.Ю. «Тождество в алгебрах Ли» Москва - Минск 1985г.
.
Джекобсон Н. «Алгебры Ли»М: Мир 1966г.
.
Голод П.И. «Математические основы теории симметрии»