Теория множеств
Содержание
Введение
. Понятие
множества. Обозначения множества и его элементов. Конечные и бесконечные
множества
. Подмножество
. Пустое
и универсальное множества
. Способы
задания множеств
. Операции
над множествами
. Отношения
на множествах
Заключение
Список
используемой литературы
Введение
Тема моего реферата - теория множеств. Мое
знакомство с множествами началось еще в начальной школе на уроках математики.
Тогда мы изучали множества птиц, учеников в классе, четных и нечетных чисел.
Уже в средней школе были изучены свойства, действия над множествами,
бесконечные множества, область определения функции как один из примеров
множеств и т.д. Тема эта была мною исследована достаточно подробно, поэтому я
бы хотела обобщить весь изученный материал в данной работе.
На каждом шагу нам приходится сталкиваться с тем
трудно определимым понятием, которое выражается словом «совокупность».
Например, можно говорить о совокупности людей, присутствующих в данной комнате,
о совокупности гусей, плавающих в пруду, о совокупности чисел-делителей числа
30 и т.д. В каждом из этих случаев можно было бы вместо слова «совокупность»
употребить слово «множество».
В математике постоянно приходится иметь дело с
различными множествами: множество вершин или диагоналей какого-либо многоугольника,
точек на прямой и т.д. Роль, которую понятие множества играет в современной
математике, определяется не только тем, что сама теория множеств стала в
настоящее время весьма обширной и содержательной дисциплиной, но главным
образом тем влиянием, которое теория множеств, возникшая в 70-х годах XIX
века, оказывала и оказывает на всю математику в целом.
Теория множеств или учение о
множествах было создано в 1870 году немецким математиком Георгом Кантор
<#"517267.files/image001.gif">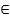 А если же данный элемент a не
принадлежит
множеству А, то пишут а ÏА.
А если же данный элемент a не
принадлежит
множеству А, то пишут а ÏА.
В различных приложениях дискретной математики
чаще всего встречаются конечные множества. Интуитивный смысл этого
термина ясен: такие множества содержат конечное число элементов. Число
элементов конечного множества A называют мощностью этого множества и
обозначают символом Card A или |A|. Наряду с конечными множествами в математике
рассматривают и бесконечные множества, то есть такие, которые содержат
бесконечно много элементов. Так, например, бесконечно множество натуральных
чисел N, множество рациональных чисел Q , множество
действительных чисел R.
. Подмножество
Если любой элемент множества A является
элементом другого множества B , то говорят, что A есть подмножество
множества B , и пишут: A Ì B. Например, множество всех
натуральных чисел N является подмножеством всех действительных чисел R:
N Ì
R. Из определения непосредственно следует, что A Ì
A , то есть всякое множество является подмножеством самого себя.
Если A Ì B , а B Ì
A , то пишут A = B и говорят, что множества A и B равны.
Во многих случаях, чтобы выделить в данном
множестве некоторое подмножество, добавляют к его характеристическому признаку
(см. гл. 4) то или иное дополнительное условие. Например, подмножество
натуральных чисел выделяется в множестве целых чисел добавлением условия n>0,
а подмножество равносторонних треугольников в множестве всех треугольников -
добавлением условия a=b=c
(где a,b,c
- длины сторон треугольника).
В математике часто встречаются теоремы, в
которых речь идет о том, что одно множество является частью другого. К примеру,
в теореме « Диагонали четырехугольника с равными сторонами взаимно
перпендикулярны» речь идет о двух множествах: А - множество всех ромбов, В -
множество всех четырехугольников с взаимно перпендикулярными диагоналями. И
теорема состоит в том, что АÌ В.
множество математика бесконечный
3. Пустое и универсальное множества
В теории множеств отдельно вводится множество,
которое не содержит ни одного элемента. Такое множество называется пустым
и обозначается символом Æ. Если A есть пустое множество,
то пишут: A = Æ. Зачем же его вообще вводят? Стоит
отметить, что когда множество задано своим характеристическим свойством, то не
всегда заранее известно, существует ли хоть один элемент с таким свойством.
Например, пусть множество А состоит из всех четырехугольников таких, что) все
их углы прямые,) диагонали имеют различную длину.
Для человека, не знающего геометрии,
ничего противоречивого в этих требованиях нет. Однако из теоремы о равенстве
диагоналей прямоугольника следует, что множество таких четырехугольников пусто.
Пустыми являются также множества треугольников, сумма углов которых отлична от
180 , множество
квадратных трехчленов, имеющих больше двух корней и т.д.
, множество
квадратных трехчленов, имеющих больше двух корней и т.д.
В любой конкретной задаче приходится
иметь дело только с подмножествами некоторого, фиксированного для данной
задачи, множества. Его принято называть универсальным. Оно обычно
обозначается U (от англ.
<#"517267.files/image003.gif">
- В частности, само универсальное
множество содержит себя в качестве одного из многих элементов
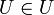
- Любое множество является
подмножеством
<#"517267.files/image005.gif">
- В частности, само универсальное
множество является своим подмножеством
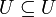
- Объединение
<#"517267.files/image007.gif">
- В частности, объединение
универсального множества с самим собой равно универсальному множеству
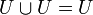
- Пересечение
<#"517267.files/image009.gif">
- В частности, пересечение
универсального множества с самим собой равно универсальному множеству
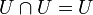
- Исключение
<#"517267.files/image011.gif">
- В частности, исключение
универсального множества из себя равно пустому множеству
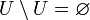
- Исключение любого множества из
универсального множества равно дополнению
<#"517267.files/image013.gif">
- Дополнение универсального множества
есть пустое множество.

4. Способы задания множеств
Возможны различные способы задания множеств:
· перечисление
всех его элементов или список
В этом случае элементы множества записывают
внутри фигурных скобок, например: А = {1, 2, a, x} или B = {река Нил, город
Москва, планета Уран}. Но этот способ применим только к конечным множеством, да
и то далеко не ко всем
· указание характеристического
свойства его элементов
Характеристическое свойство - свойство,
которым обладают все, принадлежащие данному множеству элементы, а не
принадлежащие - не обладают. Чаще всего при этом используют запись A = { x|P( x
) }, которую читают следующим образом: "A есть множество элементов x
таких, что для них выполняется свойство P( x )".
В геометрии часто приходится иметь дело с
множествами точек, заданными теми или иными характеристическими свойствами.
Такие множества точек называют геометрическими местами точек. Например,
говорят так: «Окружностью называется геометрическое место точек плоскости,
равноудаленных от этой плоскости». Это означает, что множество точек плоскости,
равноудаленных от данной точки этой плоскости совпадает с множеством точек
некоторой окружности.
Задание множеств их характеристическими
свойствами иногда приводит к осложнениям. Может случиться, что два различных
характеристических свойства задают одно и то же множество, т.е. всякий элемент,
обладающий одним свойством, обладает и другим, и обратно. Например, в
арифметике свойство «целое число делится на 2» задает то же множество, что и
свойство «последняя цифра числа делится на 2».
· с помощью порождающей процедуры например:
E = { x| x = 3k, k - любое
натуральное число.}
Наряду с порождающей процедурой существует распознающая
или разрешающая процедура, которая позволяет определить, принадлежит
данный объект множеству или нет. Для множества E распознающая процедура
заключается в разложении числа на простые множители.
. Операции над множествами
· Из двух множеств А и В можно
образовать новое множество, объединяя все элементы множества А и все элементы
множества. Объединением множеств А и В называется новое множество,
состоящее из тех и только тех элементов, которые входят хотя бы в одно из
множеств А или в множество В.
Объединение множеств А и В
обозначают A
 B:
B:
A
 B=
B=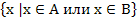
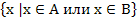 .
.
*Для иллюстрации соотношения между
множествами пользуются схемами, называемыми диаграммами Эйлера - Венна,
на которых множества изображаются овалами, в частности кругами:
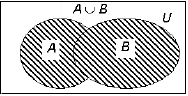
· Если даны два множества, то можно
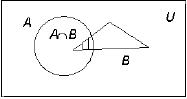
образовать новое множество, составленное из общих элементов этих множеств. Пересечением
множеств А и В называется новое множество, содержащее те и только те
элементы, которые входят одновременно и в множество А, и в множество В.
Пересечение множеств А и В
обозначают A
 B:
B:
A
 B={x |x
B={x |x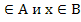
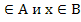 }.
}.
· Разностью
множеств A и B называется множество всех тех элементов множества A, которые не
принадлежат множеству B.
Разность множеств A
и B обозначают A\B:
A\B = {x |x
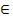
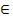 A и x
B}.
A и x
B}.

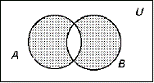
· Симметрической разностью
множеств A и B называется множество, состоящее из элементов исходных множеств,
за исключением общих элементов.
Симметрическую разность множеств A и B обозначают A
 B:
B:
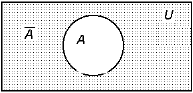
· Абсолютным дополнением
множества A называется множество всех элементов, не принадлежащих A, т.е.
множество `
A = U\A,
где U - универсальное множество.
Свойства операций
Для любых множеств A,B,C выполняются следующие
тождества:
1. A 
 B = B
B = B 
 A, A
A, A 
 B = B
B = B 
 A
A
(коммутативность объединения и пересечения);
2. A
 ( B
( B 
 C ) = ( A
C ) = ( A 
 B )
B ) 
 C, A
C, A 
 ( B
( B 
 C ) = ( A
C ) = ( A 
 B )
B )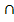
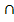 C
C
(ассоциативность объединения и пересечения);
3. A 
 ( B
( B 
 C ) = ( A
C ) = ( A 
 B )
B )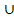
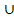 ( A
( A
 C ),
C ),
A 
 ( B
( B 
 C ) = ( A
C ) = ( A 
 B )
B ) 
 ( A
( A
 C )
C )
(дистрибутивность);
. A 
 A = A, A
A = A, A 
 A = A
A = A
(идемпотентность);
5. A 
 U = U, A
U = U, A 
 U = A, A
U = A, A 
 Æ= A, A
Æ= A, A
 Æ= Æ,
Æ= Æ,
5. A 
 `A = U, A
`A = U, A 
 `A=Æ
`A=Æ
(свойства универсального и пустого множеств);
. `A
= A
(закон двойного дополнения);
7. ____ ____
A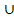
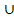 B = `A
B = `A 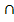
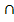 `B, A
`B, A 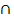
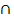 B = `A
B = `A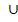
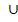 `B
`B
(законы де Моргана).
. Отношения на множествах
Прежде чем приступить к раскрытию темы отношений
на множествах, введем понятие прямого произведения множеств.
Упорядоченной парой
называют пару элементов (x,y)
такую, что равенство двух пар (x,y)=(a,b)
возможно тогда и только тогда, когда x
= a и y
= b.
Прямым (декартовым) произведением 2-х
множеств A и B
называется множество
A
 B= {(x, y) |x ÎA, y ÎB}
B= {(x, y) |x ÎA, y ÎB}
Например, если A= {a,b,c,d,e,f,g,h}, B=
{1,2,3,4,5,6,7,8}, то A
 B= {(a,1),(a,2),…(h,7),(h,8)}-
множество, содержащее обозначения всех 64-х клеток шахматной доски.
B= {(a,1),(a,2),…(h,7),(h,8)}-
множество, содержащее обозначения всех 64-х клеток шахматной доски.
Свойства прямого произведения:
1) По определению полагают, что
A
 Æ= Æ
Æ= Æ
A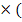
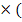 B ÈC)= (A
B ÈC)= (A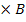
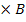 )È(A
)È(A
 C)
C)
A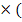
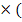 B ÇC)= (A
B ÇC)= (A
 B)Ç(A
B)Ç(A
 C)
C)
*Прямое произведение множеств не
является коммутативным, т.е A
 B ≠B
B ≠B
 A.
A.
Наконец, отметим, что число
элементов прямого произведения 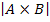
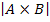 =
= 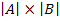
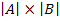 .
.
Отношения служат одним из способов задания
взаимосвязи между элементами множеств. Наиболее изученными и чаще всего
используемыми являются так называемые унарные и бинарные отношения. Для
обозначения отношений будем использовать малые буквы греческого алфавита ρ,
τ,
σ
и т.д.
Унарное (одноместное) отношение соответствует
наличию какого-то определенного признака (свойства) у элементов множества Х
(например, признак «быть отрицательным» на множестве Z целых чисел). Все
элементы, обладающие выделенным признаком, образуют некоторое подмножество ρ
Ì
Х. Это подмножество ρ и называют унарным
отношением на множестве Х.
Бинарные (двуместные) отношения
используют как характеристику некоторой взаимосвязи между элементами множества X. Элементами
бинарного отношения являются упорядоченные пары прямого произведения X
 X, и, следовательно, само бинарное
отношение может быть задано как некоторое подмножество прямого произведения ρ ÌX
X, и, следовательно, само бинарное
отношение может быть задано как некоторое подмножество прямого произведения ρ ÌX
 X.
X.
Так, например, на множестве M всех
студентов университета можно ввести следующее отношение «принадлежности к
одному факультету»: σ ÌM 
 M и упорядоченная пара (a,b)
M и упорядоченная пара (a,b)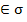
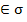 тогда и только тогда, когда студенты
a и b обучаются
на одном факультете.
тогда и только тогда, когда студенты
a и b обучаются
на одном факультете.
В общем случае можно рассматривать n-местное
отношение как любое фиксированное подмножество ω прямого
произведения ω Xn. При этом
говорят, что элементы x1, x2,… xn множества X находятся в
отношении ω, если
упорядоченный набор (x1, x2,… xn )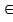
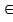 ω.
ω.
Тождественным (единичным) отношением
на множестве X называется
отношение ex (иногда
просто символ e), которое
содержит только пары вида (x,x) для любого
элемента x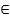
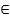 X.
X.
Полным (универсальным) отношением
на множестве является отношение U=X
 X.
X.
Пусть на множестве задано отношение ρ ÌX
 X, тогда обратным к данному
отношению называют отношение ρ-1 такое, что
пара (x,y)
принадлежит ρ-1 тогда и
только тогда, когда пара (y,x)
принадлежит ρ.
X, тогда обратным к данному
отношению называют отношение ρ-1 такое, что
пара (x,y)
принадлежит ρ-1 тогда и
только тогда, когда пара (y,x)
принадлежит ρ.
Поскольку каждое отношение на X является
подмножеством полного отношения, для отношений определены все операции над
множествами. Так, например, мы можем рассматривать объединение, пересечение,
разность двух отношений ρ, σÎ X
 X. Определено и дополнение `ρ = U\ ρ отношения ρ до полного
отношения.
X. Определено и дополнение `ρ = U\ ρ отношения ρ до полного
отношения.
Теперь приведем пример описания практической
задачи с использованием элементов теории множеств.
Пример 1. Пусть на предприятии существует 2 вида
затрат на производство: постоянные и переменные. К постоянным затратам
относятся:
) затраты на аренду помещения (r)
) затраты на электроэнергию (e)
) затраты на оплату повременного труда (h)
К переменным затратам относятся:
) затраты на оплату сдельного труда (s)
) затраты на сырье и материалы (m)
Обозначим множество постоянных затрат A,
а переменных - B. Таким
образом, A={r,
e, h}
B ={s, m}.Множества r, e, h являются
подмножествами множества A, а множества s, m -
подмножествами множества B. Множество общих затрат P в таком
случае можно представить как объединение множеств A и B: P = A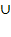
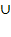
P
Заключение
В процессе работы мы узнали о самых основных
положениях теории множеств таких как определение множества, конечные и
бесконечные множества, обозначения множеств, способы их задания, подмножество.
Наглядные примеры помогли нам лучше усвоить эти понятия. В настоящее время
теория множеств является одной из основ таких областей математики как
функциональный анализ, топология, общая алгебра и т.д. Ведутся глубокие
исследования и в самой теории множеств. Эти исследования связаны с самыми
основами математики.
Элементами теории множеств могут быть самые
разнообразные предметы: буквы, атомы, числа, функции, точки, углы и т.д. Отсюда
с самого начала ясна чрезвычайная широта теории множеств и ее приложимость к
очень многим областям знания (математике, механике, физике). Сегодня мы знаем,
что, логически говоря, возможно вывести почти всю современную математику из
единого источника-теории множеств.
Список используемой литературы
Виленкин Н.Я. Рассказы о множествах. - М.:
Наука, 1969.
Корн Г., Корн Т. Справочник по математике. - М.:
Наука, 1974.
Математическая энциклопедия (в 5 томах) /Под
ред. И.М. Виноградова. - М.: Сов. энциклопедия, 1977.
Яглом И.М. Булева структура и ее модели. - М.:
Советское радио, 1980.