Методы анализа электрических цепей переменного тока
Мордовский
государственный университет им. Н.П. Огарева
Светотехнический
факультет
Кафедра
теоретической и общей электротехники
Курсовая
работа по ТОЭ
МЕТОДЫ
АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Автор курсовой работы
Калинин М.В.
Руководитель работы
Н. Р. Некрасова
Саранск
2006
Содержание
Введение
. Трехфазная
электрическая цепь с лампами накаливания
.1 Определение
токов и напряжений цепи
.2 Показание
амперметра
.3 Векторная
диаграмма токов и топографическая диаграмма напряжений
.4 Волновые
диаграммы
.5 Мощность,
измеряемая ваттметрами
.6
Моделирование цепи и расчет пускового режима ее работы
.7
Определение ударных коэффициентов тока в пусковом режиме
Введение
Все методы расчета разделяются на две группы:
. расчет по мгновенным значениям
. расчет по действующим значениям токов и напряжений
При расчете по мгновенным значениям составляются уравнения по законам
Кирхгофа для мгновенных значений. При этом получается система дифференциальных
уравнений. Рассчитываем мгновенные значения токов и напряжений для отдельных
моментов времени, отстающих друг от друга на временной интервал Dt. Получаем зависимости i (t) и u
(t). Такой расчет будет называться - расчет во временной области.
При расчете по действующим значениям сводят форму напряжений и токов к
синусоидальной. Выражают синусоидальную величину в комплексном виде и
составляют систему уравнений в комплексном виде. Получается алгебраическая
система уравнений, которая решается в общем виде через определители.
Наиболее часто применяется расчет по действующим значениям токов и
напряжений методом комплексных амплитуд (символическим методом).
В настоящее время существует ряд программ для ЭВМ, с помощью которых
легко выполняется расчет во временной области. Например, MicroCap V.
1. Трехфазная электрическая цепь с лампами накаливания
Питание нагрузки осуществляется от симметричного трехфазного источника с
частотой 50 Гц. Заданы схема цепи и ее параметры. Нелинейный элемент Rл
представляет собой сопротивление лампы накаливания, значение которого задано
для установившегося режима. Линейное напряжение источника Uл=380 В (Xс = 900
Ом, Rл = 250 Ом, R2 = 900Ом, XL2 = 900 Ом).
Требуется:
Для установившегося режима:
Определить мгновенные значения всех токов и напряжений цепи;
Найти показание амперметра;
Построить векторную диаграмму токов и топографическую диаграмму
напряжений;
Построить график изменения тока, измеряемого амперметром, в зависимости
от времени за один период;
Определить мощность, измеряемую ваттметрами.
Для переходного процесса, возникающего при включении цепи:
Создать компьютерную модель данной цепи и с ее помощью построить кривые
зависимости токов ламп от времени, приняв, что в момент включения сопротивление
Rл в десять раз меньше, чем при установившемся процессе, а затем увеличивается,
достигая заданного значения через два периода. Сравнить результаты машинного
расчета с п.1.1;
Найти ударные коэффициенты токов ламп

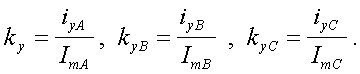
Указания:
а)
Расчет переходного процесса выполнить с помощью пакета программ MicroCap V.
б)
Диаграмма токов должна быть наложена на топографическую диаграмму напряжений и
изображена другим цветом.
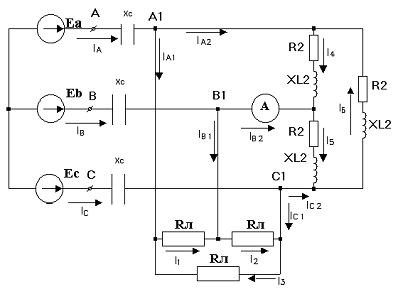
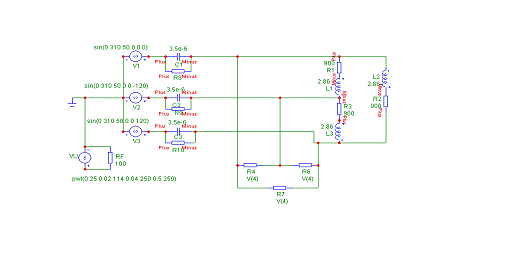
Рисунок 1 - Схема электрической цепи.
1.1 Определение мгновенных значений токов и напряжений цепи
Определяем фазное напряжение генератора:

Преобразуем
треугольники в схеме рисунка 1 в эквивалентные звезды (рисунок2):
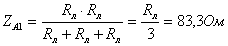
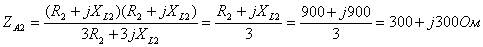 .
.
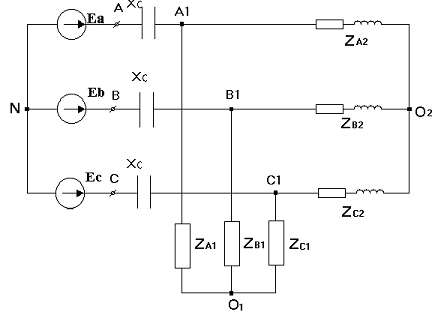
Рисунок
2
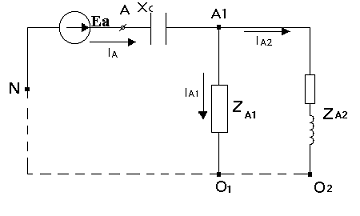
Рисунок
3
Поскольку
цепь симметрична, то напряжение смещения нейтрали отсутствует, токи и
напряжения в фазах по модулю равны между собой. Поэтому рассчитаем лишь одну
фазу А (рисунок 3). Поскольку 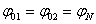 , можем
их закоротить. Рассчитаем эту цепь с помощью закона Ома. Найдем сопротивление
параллельного участка цепи.=83.3; b=300+300i; c= (a*b)/ (a+b)
, можем
их закоротить. Рассчитаем эту цепь с помощью закона Ома. Найдем сопротивление
параллельного участка цепи.=83.3; b=300+300i; c= (a*b)/ (a+b)
c
= 72.0739 + 8.7864i
abs(c)
ans = 72.6075
angle(c)*180/3.14
ans = 6.9541
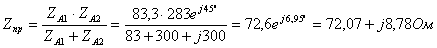
=-900i;
b=72.07+8.78i; c=a+b= 7.2070e+001 -8.9122e+002ii
abs(c)
ans
= 894.1293
angle(c)*180/3.14
ans
= -85.4200
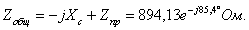
Применяем
закон Ома:=220; b =7.2070e+001 -8.9122e+002i; c=a/b
c = 0.0198 + 0.2452i
ans = 0.2460
angle(c)*180/3.14
ans = 85.4200
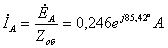
Найдем
напряжение на разветвленном участке.=0.0198 + 0.2452i; b=72.0739 + 8.7864i;
c=a*b= -0.7274 +17.8465i
abs(c)
ans = 17.8613
angle(c)*180/3.14
ans = 92.3807
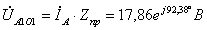 .
.
=-0.7274
+17.8465i; b=83.3; c=a/b= -0.0087 + 0.2142i
abs(c)
ans
= 0.2144
angle(c)*180/3.14
ans
= 92.3808
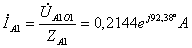 ;
;
=-0.7274
+17.8465i; b=300+300i; c=a/b
c = 0.0285 + 0.0310i
abs(c)
ans = 0.0421
angle(c)*180/3.14
ans = 47.3580
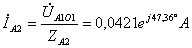 .
.
Известно,
что ток треугольника при симметричной нагрузке в 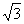 раз
меньше линейного тока и опережает его на 30°.
раз
меньше линейного тока и опережает его на 30°.
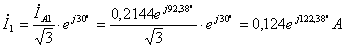 ;
;
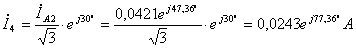 .
.
Токи
остальных фаз отличаются от найденных сдвигом по фазе на 120°.
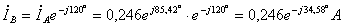 ;
;
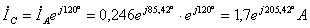 ;
;
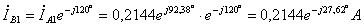 ;
;
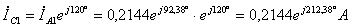 ;
;
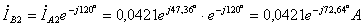 ;
;
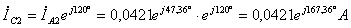 ;
;
 ;
;
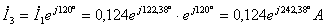 ;
;
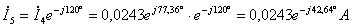 ;
;
 .
.
Найдем
линейное напряжение на потребителях.
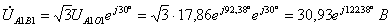 ;
;
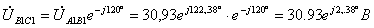 ;
;
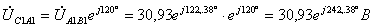 .
.
Находим
мгновенные значения токов и напряжений.A = 0.246× sin (wt + 85.42°) = 0.348 sin (wt + 85.42°) A;B =
0.246×
sin (wt + 85.42°) = 0.348 sin (wt + 85.42°) A;B =
0.246× sin (wt - 34.58°) = 0.348 sin (wt - 34.58°) A;C =
0.246×
sin (wt - 34.58°) = 0.348 sin (wt - 34.58°) A;C =
0.246× sin (wt + 205.42°) = 0.348 sin (wt + 205.42°) A;A1 =
0.214×
sin (wt + 205.42°) = 0.348 sin (wt + 205.42°) A;A1 =
0.214× sin (wt +92.38°) = 0.303 sin (wt +92.38°) A;B1 =
0.214×
sin (wt +92.38°) = 0.303 sin (wt +92.38°) A;B1 =
0.214× sin (wt - 27.62°) = 0.303 sin (wt - 27.62°) A;C1 =
0.214×
sin (wt - 27.62°) = 0.303 sin (wt - 27.62°) A;C1 =
0.214× sin (wt + 212.38°) = 0.303 sin (wt + 212.38°) A;A2 =
0,042×
sin (wt + 212.38°) = 0.303 sin (wt + 212.38°) A;A2 =
0,042× sin (wt - 47.36°) = 0,059 sin (wt - 47.36°) A;B2 =
0,042×
sin (wt - 47.36°) = 0,059 sin (wt - 47.36°) A;B2 =
0,042× sin (wt - 72.64°) = 0,059 sin (wt - 72.64°) A;C2 =
0,042×
sin (wt - 72.64°) = 0,059 sin (wt - 72.64°) A;C2 =
0,042× sin (wt + 167.36°) = 0,059 sin (wt + 167.36°) A;1 =
0.124×
sin (wt + 167.36°) = 0,059 sin (wt + 167.36°) A;1 =
0.124× sin (wt +122.38°) = 0.175 sin (wt +122.38°) A;2 =
0.124×
sin (wt +122.38°) = 0.175 sin (wt +122.38°) A;2 =
0.124× sin (wt +2.38°) = 0.175 sin (wt +2.38°) A;3 =
0.124×
sin (wt +2.38°) = 0.175 sin (wt +2.38°) A;3 =
0.124× sin (wt + 242.38°) = 0.175 sin (wt + 242.38°) A;4 =
0, 0243×
sin (wt + 242.38°) = 0.175 sin (wt + 242.38°) A;4 =
0, 0243× sin (wt + 77.36°) = 0.034 sin (wt +77.36°) A;5 =
0, 0243×
sin (wt + 77.36°) = 0.034 sin (wt +77.36°) A;5 =
0, 0243× sin (wt - 42.64°) = 0.034 sin (wt - 42.64°) A;6 =
0, 0243×
sin (wt - 42.64°) = 0.034 sin (wt - 42.64°) A;6 =
0, 0243× sin (wt + 197.36°) = 0.034 sin (wt + 197.36°) A;AB=380×
sin (wt + 197.36°) = 0.034 sin (wt + 197.36°) A;AB=380× sin (wt + 30°) = 537 sin (wt + 30°) B;BC=380×
sin (wt + 30°) = 537 sin (wt + 30°) B;BC=380× sin (wt + 30° - 120°) = 537 sin (wt - 90°) B;CA=380×
sin (wt + 30° - 120°) = 537 sin (wt - 90°) B;CA=380× sin (wt + 30° + 120°) = 537 sin (wt + 150°) B;A1O1=17.86×
sin (wt + 30° + 120°) = 537 sin (wt + 150°) B;A1O1=17.86× sin (wt +92.38°) = 25.25 sin (wt - 49°) B;B1O1=17.86×
sin (wt +92.38°) = 25.25 sin (wt - 49°) B;B1O1=17.86× sin (wt + 92.38° - 120°) = 25.25 sin (wt - 27.62°) B;C1O1=17.86×
sin (wt + 92.38° - 120°) = 25.25 sin (wt - 27.62°) B;C1O1=17.86× sin (wt - 92.38° + 120°) = 25.25 sin (wt + 212.38°) B;A1B1=30.93×
sin (wt - 92.38° + 120°) = 25.25 sin (wt + 212.38°) B;A1B1=30.93× sin (wt + 122.38°) = 43.74 sin (wt - 122.38°) B;B1C1=30.93×
sin (wt + 122.38°) = 43.74 sin (wt - 122.38°) B;B1C1=30.93× sin (wt + 2.38°) = 43.74 sin (wt + 2.38°) B;C1A1=30.93×
sin (wt + 2.38°) = 43.74 sin (wt + 2.38°) B;C1A1=30.93× sin (wt + 242.38°) = 43.74 sin (wt + 242.38°) B;
sin (wt + 242.38°) = 43.74 sin (wt + 242.38°) B;
1.2
Показание амперметра
электрический амперметр ваттметр ток
Определим показание амперметра, включенного в цепь. Он показывает
действующее значение тока IB2.
A = IB2 = 0,042 A.
1.3 Векторная диаграмма токов и топографическая диаграмма
напряжений
По найденным значениям построим векторную диаграмму токов и
топографическую диаграмму напряжений (Рисунок 4).
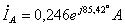 ;
; 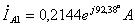 ;
; 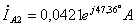 ;
;
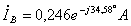 ;
; 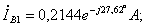 ;
; 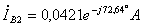 ;
;
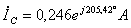 ;
; 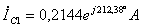 ;
; 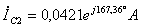 ;
;
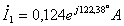 ;
; 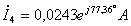 ;
;
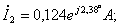 ;
; 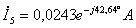 ;
;
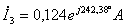 ;
; 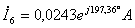 .
.
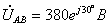 ;
; 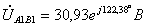 ;
;
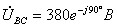 ;
; 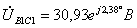 ;
;
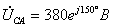 ;
; 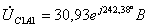 .
.
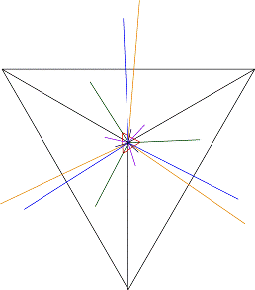
Рисунок
4 - Векторная диаграмма токов и топографическая диаграмма напряжений
1.4
Волновые диаграммы
График
изменения тока в зависимости от времени за один период
Ток
амперметра равен iB2 = 0,059 sin (wt - 72.64°) A.
Построим
кривую этого тока за период (рисунок 5).
t=[0:0.0000005:0.00005];
w=[125600];=[0.059*sin(w*t-72.64*pi/180)];
plot(t,i1)
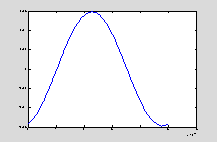
Рисунок 5 - График изменения тока в зависимости от времени за
один период
1.5 Мощность, измеряемая ваттметрами
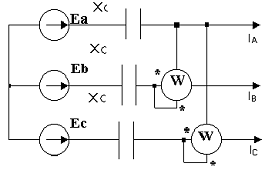
Рисунок
6 - Схема включения ваттметров
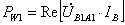 ;
;
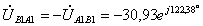 ;
;
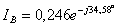 ;=16.56-26.12i;b=0.2025-0.14i;c=a*b
;=16.56-26.12i;b=0.2025-0.14i;c=a*b
c = -0.3034 - 7.6077i
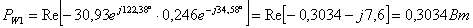 ;
;
=-14.34-27.4i;b=-0.222-0.105i;c=a*b
c = 0.3065 + 7.5885i
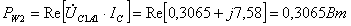 .
.
1.6 Моделирование цепи и расчет пускового режима ее работы
Сопротивление ламп накаливания в момент включения схемы в десять раз
меньше, чем в установившемся режиме. Задано, что это сопротивление возрастает и
через два периода станет равным 250 Ом.л уст .=250 Ом;л(0) =25
Ом.
Чтобы учесть изменение сопротивления лампы в переходном процессе,
построим компьютерную модель в MicroCap V. В этой системе есть возможность
задать любое сопротивление, изменяющееся так же, как потенциал некоторого
управляющего источника напряжения VU (см. рисунок 7).
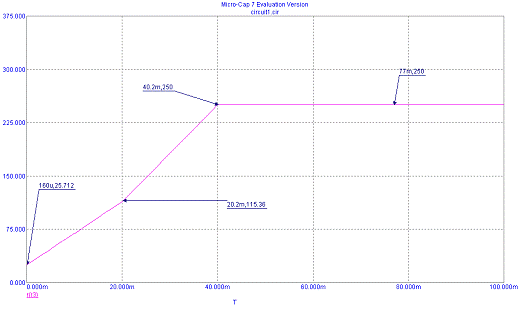
Кривые зависимости токов ламп от времени были построены с помощью этой
модели (рисунок 7a)
.7 Определение ударных коэффициентов тока в пусковом режиме
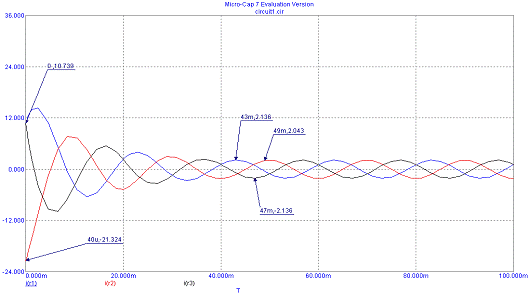
Из кривых зависимости токов ламп от времени, построенных с помощью
системы Micro-Cap V (рисунок 7a), находим наибольшие (ударные) значения токов в
пусковом режиме, а также максимальные значения токов в установившемся режиме:y1
= 10,739 A; ImA = 2.136 A;y2 = 21,324A; ImB
= 2.043 A;y3 = 10,739A. ImC = 2.136 A.
Рассчитаем ударные коэффициенты токов ламп
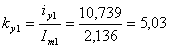 ;
;
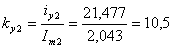 ;
;
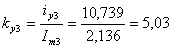 .
.
Отсюда
видим, что в процессе пуска токи ламп превышают амплитудные значения
установившегося режима в 5 и 10 раз, что можно объяснить малым сопротивлением
ламп накаливания в холодном состоянии.