Применение криволинейных интегралов в различных областях наук

Применение криволинейных интегралов в различных областях наук

Введение

Математика является точной абстрактной наукой, изучающей количественные соотношения и пространственные формы.

Точность математики означает, что основным методом в математических исследованиях являются логические рассуждения, а результаты исследований формулируются в строгой логической форме. Абстрактность же математики означает, что объектами ее изучения являются модели (математические). В этих моделях математика изучает соотношения между их элементами, количественные и качественные связи между ними, их форму. Одна и та же математическая модель может описывать с определенным приближением свойства очень далеких друг от друга по своему конкретному содержанию реальных явлений.

Математика неустанно продолжает развиваться, в ней создаются новые методы, появляются новые разделы. Развитие математики в целом определяет уровень ее использования и оказывает существенное влияние на развитие других наук и техники. В свою очередь, задачи практики, прогресс других фундаментальных и прикладных наук приводят к созданию новых направлений математики, стимулируют ту или иную направленность математических исследований, расширяют возможность применения математических методов.

В данной работе будет рассмотрено применение криволинейных интегралов в различных областях наук, в частности физики, механики и т.д.

Криволинейный интеграл первого рода

Для того чтобы естественным путем прийти к определению криволинейного интеграла, рассмотрим одну механическую задачу, которая к нему приводит.

Пусть на плоскости дана непрерывная простая спрямляемая кривая (К), вдоль которой расположены массы, причем известна их линейная плотность 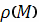 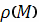во всех точках M кривой. Требуется определить массу 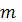 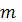всей кривой (К).

криволинейный интеграл магнитный поле

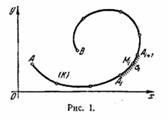
Рис. 1

С этой целью между концами 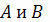 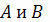кривой вставим произвольно ряд точек 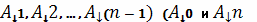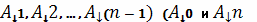для симметрии обозначений отождествляются с 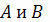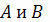). Эти точки пронумерованы в направлении от 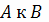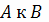, хотя ничто не мешает перенумеровать их и в обратном направлении.

Взяв какую-нибудь точку 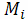 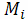на дуге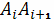 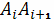 кривой, вычислим плотность 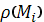 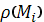в этой точке. Приближенно считая, что такова же плотность во всех точках этого участка, и обозначая длину дуги 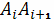 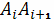через 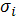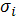, для массы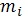 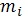 этой дуги будем иметь приближенное выражение

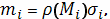
а для всей искомой массы - выражение

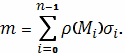
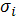
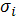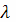
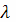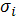
Погрешность этого последнего, связанная с сделанным выше приближенным допущением, будет стремиться к нулю, если длины  всех участков стремятся к нулю. Таким образом, обозначая через  наибольшую из длин  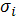для получения точной формулы остается лишь перейти к пределу:

.

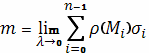
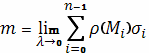Станем же изучать вообще пределы этого рода и, отвлекаясь от рассмотренной задачи, возьмем произвольную «функцию точки» 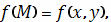 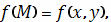заданную вдоль непрерывной простой спрямляемой кривой 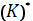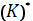, и повторим указанный процесс: разбив кривую 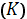 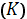) на элементарные дуги 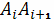 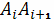и выбрав на них произвольно по точке 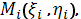 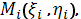вычислим значения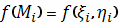 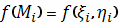 в них и составим сумму

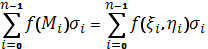
она представляет собой также своего рода «интегральную сумму».

Аналогичный процесс может быть применен и в случае замкнутой кривой, если за точку 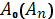 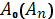выбрать любую ее точку, а остальные точки 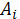 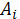расположить в соответствии с тем или другим направлением на кривой.

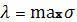
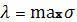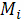
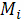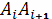
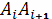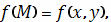
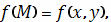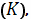
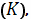Если при стремлении  к нулю интегральная сумма имеет определенный конечный предел I, не зависящий ни от способа дробления кривой (K), ни от выбора точек  на участках , то он называется криволинейным интегралом (первого типа) от функции  взятым по кривой или по пути и обозначается символом

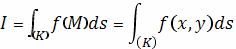
(где 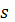 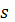есть длина дуги кривой и 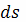 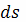напоминает об элементарных длинах .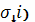

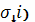Таким образом, полученное выше выражение для массы материальной кривой может быть переписано так:

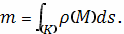
Отметим особо, что в приведенном определении не играет никакой роли направление, которое может быть придано пути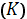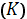. Если, например, эта кривая не замкнута и под 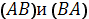 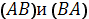разуметь разно направленные кривые, то

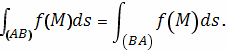
Криволинейный интеграл второго рода

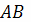
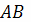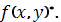
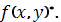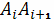
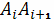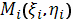
Пусть дана непрерывная кривая  (которую мы для простоты предположим незамкнутой) и пусть вдоль нее снова задана некоторая функция  Разложив кривую точками  на части, выберем на отрезке кривой  по произволу точку  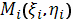и вычислим в ней значение функции 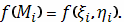 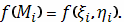Но это значение умножим на этот раз не на длину дуги 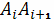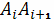, а на величину проекции этой дуги, скажем, на ось 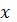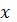, т.е. на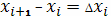 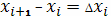; затем составим сумму

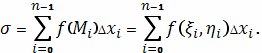
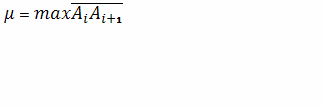
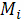
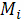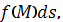
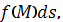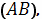
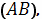Если при стремлении  нулю эта сумма имеет конечный предел I, не зависящий ни от способа дробления кривой, ни от выбора точек , то этот предел называется криволинейным интегралом (второго типа) от  взятым по кривой или по пути  и обозначается символом

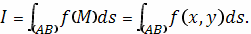
Аналогично, умножая значение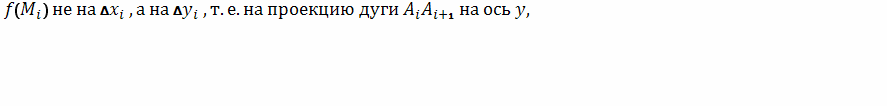и составляя сумму

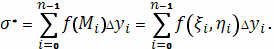
как предел ее получим криволинейный интеграл (второго типа) от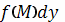

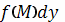
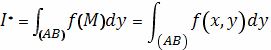
Если вдоль кривой 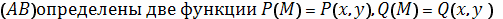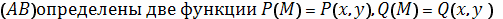и существуют интегралы

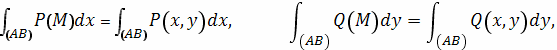
то и их сумму называют криволинейным интегралом («общего вида») и полагают

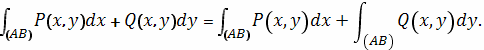
Сопоставим теперь определение криволинейного интеграла второго типа с определением криволинейного интеграла первого типа. При очевидном сходстве оба определения имеют существенное различие: в случае интеграла первого типа при составлении интегральной суммы значение функции 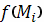 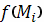умножается на длину 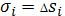 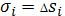участка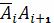 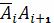 кривой, а в случае интеграла второго типа это значение 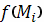 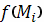умножается на проекцию 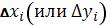 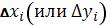упомянутого участка на ось .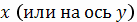

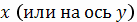Направление пути 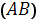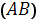, вдоль которого производится интегрирование, не играет роли в случае первого типа, ибо длина 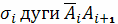 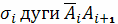от этого направления не зависит. Иначе обстоит дело с интегралом второго типа: проекция упомянутой дуги на ту или другую из осей существенно зависит от направления дуги и меняет знак с изменением этого направления на обратное. Таким образом, для интегралов второго типа будет

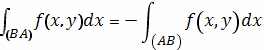
и, аналогично,

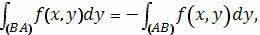
Причем из существования интегралов справа уже вытекает существование интегралов слева, и обратно.

Подобным же образом можно ввести понятие криволинейного интеграла второго типа, распространенного на пространственную кривую 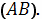 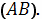Именно, если функция 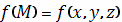 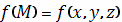задана в точках этой кривой, то строим сумму

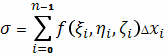
и рассматриваем ее предел при условии стремления к нулю 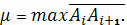 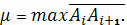этот предел называется криволинейным интегралом (второго типа) от 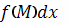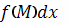и обозначается символом

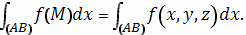
Аналогично определяются интегралы вида

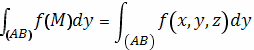
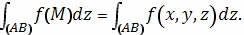
Наконец, рассматривается и интеграл («общего вида»)

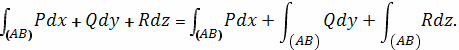
Здесь также направление интегрирования меняет знак интеграла.

Приложения криволинейных интегралов

Теперь можно перейти непосредственно к приложениям криволинейных интегралов. Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, рассмотрим геометрические и физические.

Геометрические.

С помощью криволинейных интегралов вычисляются:

Длина кривой

Пусть 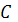 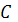является гладкой, кусочно-непрерывной кривой, которая описывается вектором 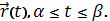 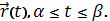Длина данной кривой выражается следующим криволинейным интегралом

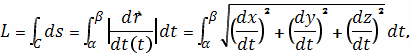
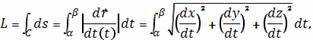
где 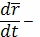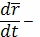производная, а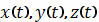 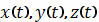-компоненты векторной функции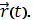

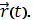
Если кривая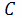 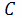задана в плоскости, то ее длина выражается формулой

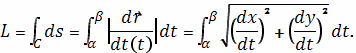
Если кривая 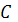 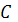представляет собой график заданной явно, непрерывной и дифференцируемой функции 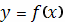 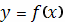в плоскости O xy,то длина такой кривой вычисляется по формуле

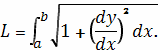
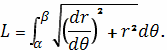
Пример 1

Найти длину кривой 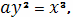 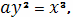при условии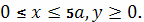

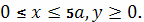
Решение.

Запишем функцию в виде 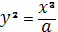 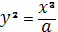или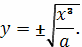

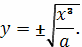
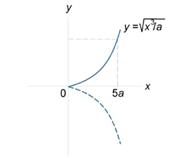
Рис. 2

Поскольку y ≥ 0, то мы возьмем только положительный корень в уравнении кривой. Длина кривой равна

Пример 2

Вычислить длину параболы 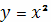 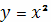в интервале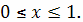

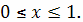
Решение.

Применяя формулу 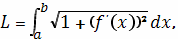 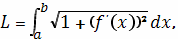находим, что

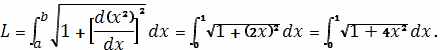
Для вычисления полученного интеграла сделаем замену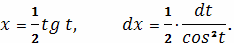

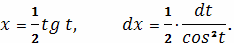
Следовательно, При 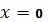 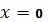получаем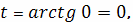 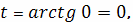 а при 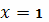 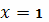- соответственно,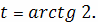 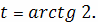 Тогда длина участка параболы равна

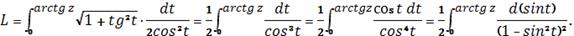
Сделаем еще одну замену. Положим

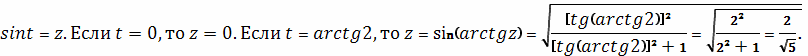
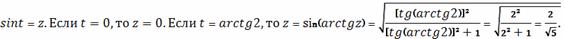
В приведенном выше выражении мы использовали тригонометрическое соотношение

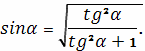
В результате длина кривой равна

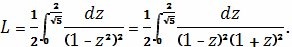
Разложим подынтегральное выражение на сумму элементарных рациональных дробей.

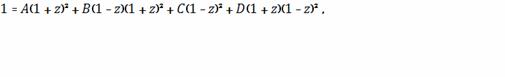
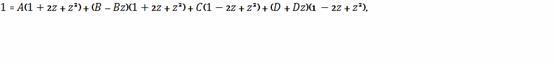
Следовательно,

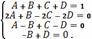
Решая данную систему уравнений, находим коэффициенты

.

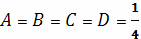
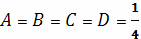Площадь области, ограниченной замкнутой кривой

Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости 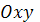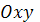. Тогда площадь области R, ограниченной данной кривой, определяется формулами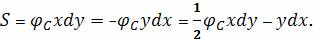

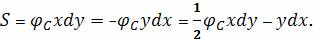
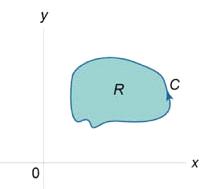
Рис. 3

Здесь предполагается, что обход кривой C производится против часовой стрелки.

Если замкнутая кривая C задана в параметрическом виде 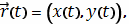 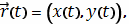то площадь соответствующей области равна

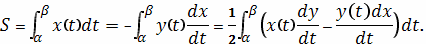
Пример 3

Найти площадь области, ограниченной гиперболой 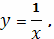 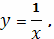осью 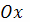 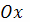и вертикальными прямыми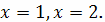

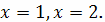
Решение.

Вычислим площадь с помощью криволинейного интеграла.

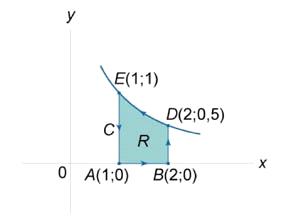
Рис. 4

Решение.

Вычислим площадь с помощью криволинейного интеграла.

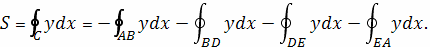
Найдем отдельно каждый из интегралов.

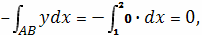
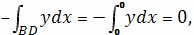
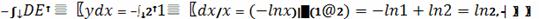
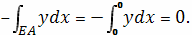
Следовательно, площадь заданной области равна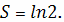

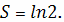
Пример 4

Найти площадь области, ограниченной эллипсом, заданным параметрически в виде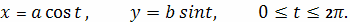

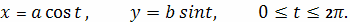
Решение.

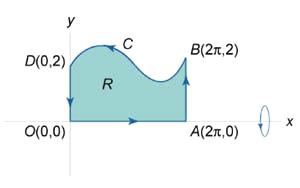
Рис. 5

Применим сначала формулу

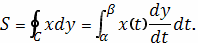
Получаем

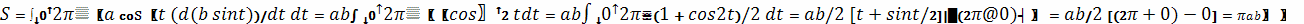
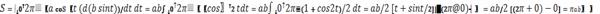
Площадь данной фигуры можно вычислить, используя также и две другие формулы:

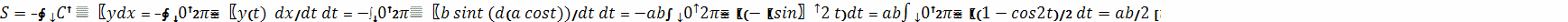
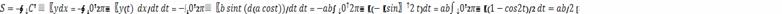
Объем тела, образованного вращением замкнутой кривой относительно оси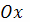

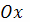
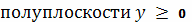
Предположим, что область R расположена в верхней  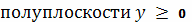и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки.

В результате вращения области R вокруг оси 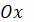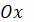образуется тело Ω. Объем данного тела определяется формулами

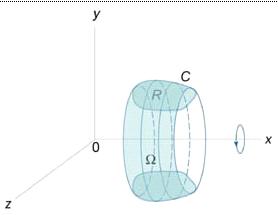
Рис. 6

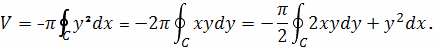
Пример 5

Решение.

Рис. 7

Объем этого тела найдем по формуле:

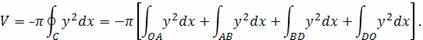
Вычислим криволинейные интегралы

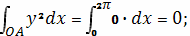
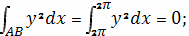
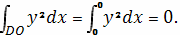
Следовательно, объем тела равен

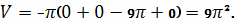
Пример 6

Найти объем эллипсоида, образованного вращением эллипса с полуосями .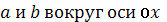

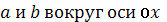Решение.

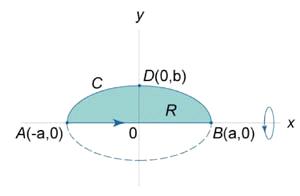
Рис. 8

Воспользуемся параметрическими уравнениями эллипса  Мы можем ограничиться рассмотрением половины эллипса, лежащей в верхней полуплоскости 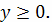 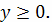Тогда объем эллипсоида с полуосями 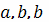 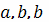будет равен

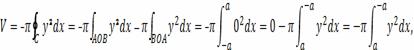
где под функцией 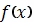 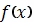подразумевается верхняя половина эллипса. Переходя к параметрической форме записи, находим объем

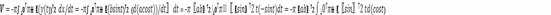
Отсюда, в частности, следует, что объем шара (при этом 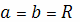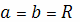) равен

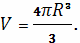
Физические

С помощью криволинейных интегралов вычисляются:

Масса кривой

Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью 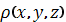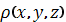. Тогда общая масса кривой выражается через криволинейный интеграл первого рода

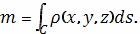
Если кривая C задана в параметрическом виде с помощью векторной функции

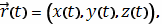
то ее масса описывается формулой

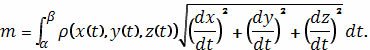
В случае плоской кривой, заданной в 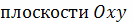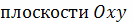, масса определяется как

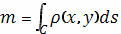
или в параметрической форме

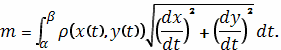
Пример 7

Определить массу проволоки, имеющей форму отрезка от точки 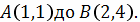 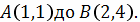Масса распределена вдоль отрезка с плотностью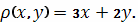

Решение.

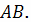
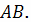
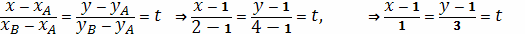
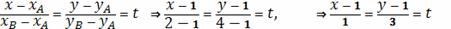Составим сначала параметрическое уравнение прямой

 или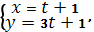

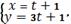
где параметр 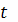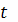изменяется в интервале 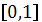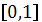. Тогда масса проволоки равна

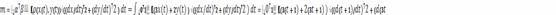
Пример 8

Найти центр масс проволоки, имеющей форму кардиоиды 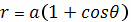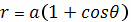, где с плотностью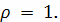

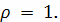
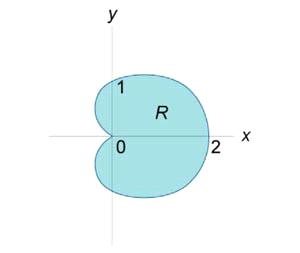
Рис. 9

Решение.

Очевидно, в силу симметрии, 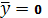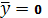. Чтобы найти координату центра масс 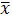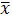, достаточно рассмотреть верхнюю половину кардиоиды.

Предварительно найдем полную массу кардиоиды. В полярных координатах получаем

Вычислим момент первого порядка 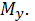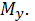Используя формулу

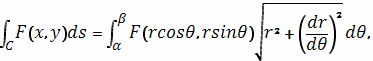
Полагая 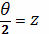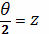(нижний и верхний пределы интегрирования становятся равными, соответственно, 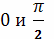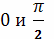), можно записать

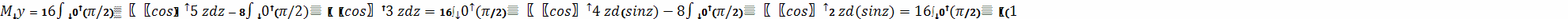
Тогда

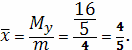
Следовательно, координаты центра масс кардиоиды равны .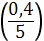

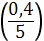Центр масс и моменты инерции кривой

Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности 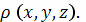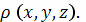Тогда координаты центра масс кривой определяются формулами

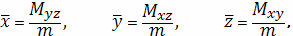
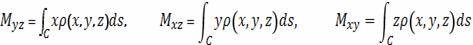
− так называемые моменты первого порядка.

Моменты инерции относительно осей 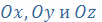 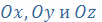определяются формулами

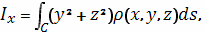
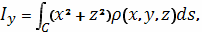
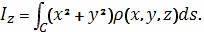
Пример 9

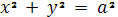
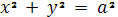Вычислить момент  в форме окружности  с плотностью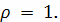

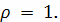
Решение.

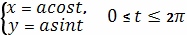
Момент инерции 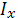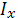относительно оси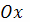 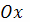 вычисляется по формуле

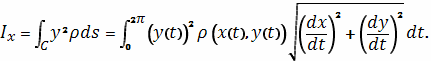
Проводя вычисления, получаем

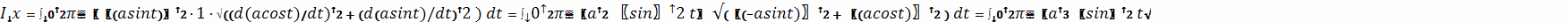
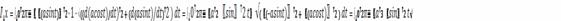
Работа поля

Работа при перемещении тела в силовом поле 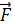 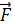вдоль кривой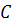 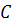выражается через криволинейный интеграл второго рода

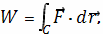
где 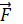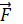− сила, действующая на тело, 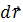 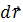− единичный касательный вектор. Обозначение 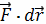 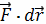означает скалярное произведение векторов 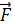 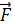и .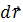

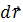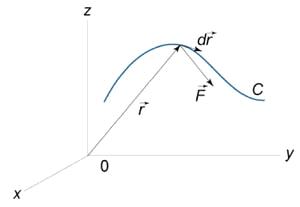
Рис. 10

Заметим, что силовое поле 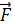 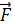не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы 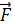 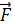иногда может оказаться отрицательной.

Если векторное поля задано в координатной форме в виде

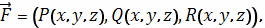
то работа поля вычисляется по формуле

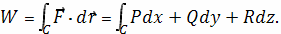
В частном случае, когда тело двигается вдоль плоской кривой 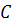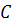в плоскости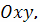 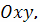 справедлива формула

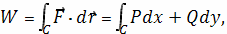
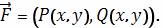
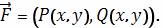
Если траектория движения 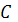 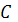определена через параметр 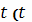 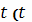часто означает время), то формула для вычисления работы принимает вид

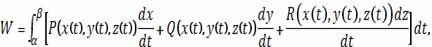
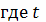
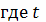 изменяется в интервале от .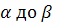

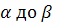Если векторное поле 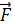 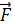потенциально, то работа по перемещению тела из точки 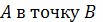 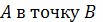выражается формулой

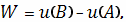
где − 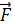 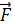потенциал поля.

Пример 10

Найти работу, совершаемую полем 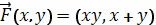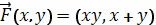при перемещении тела от начала координат 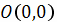 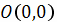до точки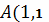 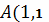) по траектории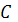 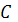, где

) С − отрезок прямой 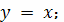 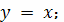2) С - кривая .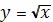

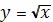Решение.

Вычислим работу при перемещении вдоль прямой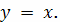

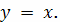
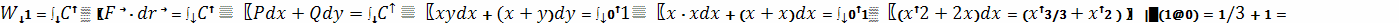
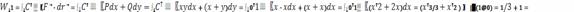
Определим теперь работу при перемещении вдоль кривой .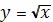

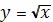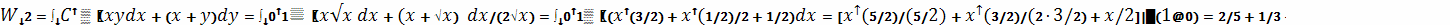
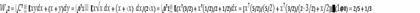
Пример 11

Тело массой 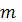 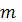брошено под углом к горизонту 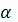 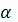с начальной скоростью 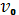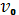. Вычислить работу силы притяжения 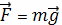 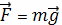за время движения тела до момента соударения с землей.

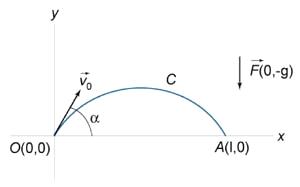
Рис. 11

Решение.

Запишем закон движения тела в параметрической форме.

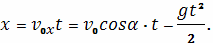
При соударении с землей 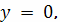 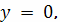так что время полета тела равно

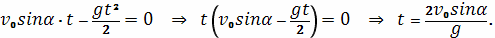
Силу притяжения запишем в виде 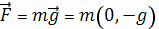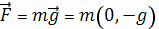. Тогда работа за время перемещения тела равна

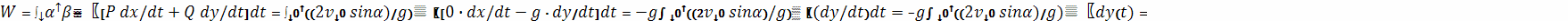
Полученный результат объясняется тем, что гравитационное поле Земли является потенциальным, поскольку выполняется равенство

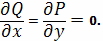
Найдем потенциал этого поля. В общем виде он записывается как

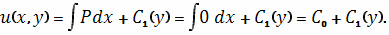
Полагая 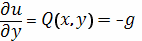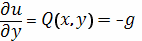, находим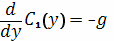 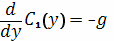 или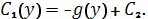

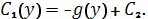
Таким образом, потенциал гравитационного поля равен

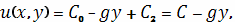
где C − константа, которую можно положить равной 0. В результате получаем потенциал в виде

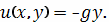
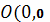
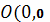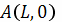
Отсюда видно, что при перемещении тела из начальной точки ) до конечной точки 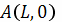работа равна

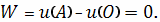
Магнитное поле вокруг проводника с током (Закон Ампера)

Криволинейный интеграл от магнитного поля с индукцией 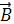 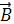вдоль замкнутого контура 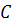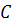пропорционален полному току, протекающему через область, ограниченную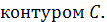

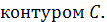
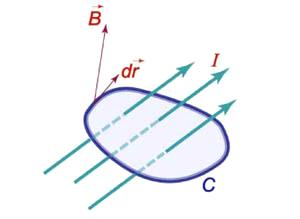
Рис. 12

Это выражается формулой ,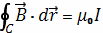

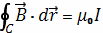где 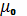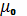- магнитная проницаемость вакуума, равная 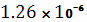 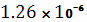Н/м.

Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея)

Электродвижущая сила 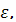 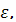наведенная в замкнутом контуре 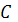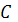, равна скорости изменения магнитного потока 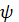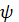, проходящего через данный контур

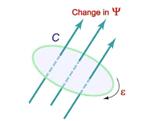
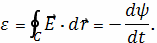
Рис. 13

Пример 12

Оценить значение электродвижущей силы 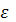 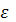и электрического поля 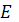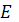, возникающих в кольце радиусом 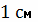 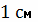у пассажира самолета, при полете самолета в магнитном поле Земли со скоростью

Решение.

Согласно закону Фарадея

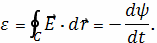
Предположим, что магнитное поле 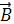 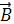перпендикулярно плоскости кольца. Тогда за время 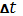 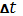изменение потока равно

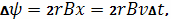
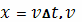
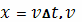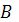
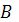где, − скорость самолета,  − индукция магнитного поля Земли. Из последнего выражения получаем

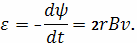
Подставляя заданные величины

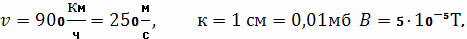
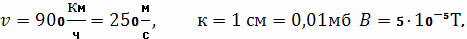
находим значение э.д.с.:

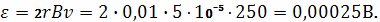
Как видно, это вполне безопасно для авиапассажиров. Напряженность возникающего электрического поля найдем по формуле. В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл.

Следовательно, напряженность электрического поля равна

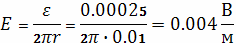
Заключение

Современный научный работник или инженер должен в достаточной степени хорошо владеть как классическими, так и современными математическими методами исследования, которые могут применяться в его области. Для того чтобы иметь возможность с успехом применять математические методы при изучении того или иного вопроса, нужно, конечно, прежде всего, иметь необходимые знания, уметь правильно обращаться с математическим аппаратом, знать границы допустимого использования рассматриваемой математической модели.

В данной работе я попыталась наиболее обширно раскрыть применение криволинейного интеграла в различных областях наук. Благодаря криволинейным интегралам можно вычислить многие физические величины, что, конечно же, облегчает работу научных работников. Я считаю, что математика - универсальная наука, и более чем уверена, что без нее не существовала ни одна современная наука. Применение математики обширно, начиная с физики и заканчивая, казалось бы далекой от математики наукой - медициной.

Список использованной литературы

1.       Л.Д. Кудрявцев «Курс математического анализа», 2 том, Москва «Высшая школа» 1988 г.

2.       Г.М. Фихтенгольц «Курс дифференциального и интегрального исчисления», 3 том, «Наука» 1969 г.

.        Г.М. Фихтенгольц «Основы математического анализа», 2 том.

.        К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко «Сборник задач по высшей математике», 2 часть, «Айрис-пресс» 2007 г.

.        Д. Письменный «Конспект лекций по высшей математике», «Айрис-пресс» 2007 г.

.        www.math24.ru <http://www.math24.ru>

.        А.П. Аксёнов «Математический анализ» Санкт - Петербург 2000 г.

.        В.Р. Гаврилов, Е.Е. Иванова, В.Д. Морозова «Кратные и криволинейные интегралы. Элементы теории поля», 7 часть Москва 2003 г.