Аналоги теореми порівняння Колмогорова та їх застосування
Міністерство
освіти і науки України
Дніпропетровський
національний університет імені Олеся Гончара
Механіко-математичний
факультет
Кафедра
математичного аналізу і теорії функцій
ДИПЛОМНА
РОБОТА
ПЕРШОГО
(БАКАЛАВРСЬКОГО) РІВНЯ ВИЩОЇ ОСВІТИ
Аналоги
теореми порівняння Колмогорова та їх застосування
РЕФЕРАТ
Дипломна робота освітньо- кваліфікаційного рівня
бакалавр :30 с., 13 рис., 10 джерел.
Об’єктом дослідження є ідеальні сплайни Ейлера
та їх аналоги.
Мета: отримання аналогів теореми порівняння Колмогорова.
Методи дослідження: класичні методи
математичного та функціонального аналізу.
Одержані теореми порівняння для 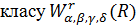 є
новими.
є
новими.
Результати дослідження можуть бути застосовані
при дослідженні екстремальних задачфункціонального аналізу та теорії
наближення.
Ключові слова: ТЕОРЕМА ПОРІВНЯННЯ КОЛМОГОРОВА,
СПЛАЙНИ ЕЙЛЕРА, НЕСИМЕТРИЧНІ СПЛАЙНИ.
SUMMARY
The graduation paper consists of 30
pages, 13 pictures, and 10 references.object of research isideal Euler splines
and their analogues.objective of research is proofof Kolmogorov’s comparison
theorem analogues.methods are classic methods of math and functional
analysis.theorems for the classof functions 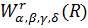 are
new.results can be used for research of extremal problems of Functional
Analysis and Approximation Theory.words: Kolmogorov`s comparison theorem, Euler
splines, nonsymmetrical splines.
are
new.results can be used for research of extremal problems of Functional
Analysis and Approximation Theory.words: Kolmogorov`s comparison theorem, Euler
splines, nonsymmetrical splines.
ВСТУП
Теоремами порівняння називають твердження, які
дають оцінку тій чи іншій характеристиці функції із деякого класу через
відповідну характеристику деякої фіксованої функції. Останню функцію можна
вважати еталонною або стандартною для даного класу; її також називають функцією
порівняння для даного класу.
Першу теорему такого типу довів А. М. Колмогоров.
Він показав, що ідеальні ейлеровісплайни є функціями порівняння для функцій з
класу  .
.
Як сам результат, так і метод його доведення
зіграли велику роль. Завдяки теоремі порівняння були виведені точні нерівності
для норм похідних типу відомої нерівності Колмогорова. Згодом використання
ідей, пов’язаних із теоремами порівняння, дало можливість отримати ряд нових
точних результатів, які з’ясовують екстремальні властивості функцій.
З огляду на вищевказане, тема роботи актуальна.
ОСНОВНІ ПОЗНАЧЕННЯ
множина усіх дійсних чисел.множина усіх
натуральних чисел.
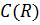 - множина
неперервних на усій осі функцій.
- множина
неперервних на усій осі функцій.
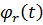 - ідеальний сплайн
Ейлера, порядку r.
- ідеальний сплайн
Ейлера, порядку r.
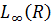 - простір вимірних
і суттєво обмежених функцій f: R
- простір вимірних
і суттєво обмежених функцій f: R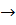 Rз нормою
Rз нормою  .
.
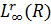 ,
, 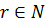 -
простір функцій f:R
-
простір функцій f:R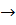 R таких, що похідна
R таких, що похідна
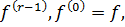 локальноабсолютнонеперервнаі
локальноабсолютнонеперервнаі
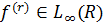 .
.
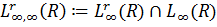 .
.
 ,
, 
 ,
, 
Для  та
X=C(R) або
та
X=C(R) або  ,
, =
= .
.
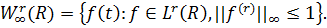
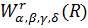 - клас усіх функцій
f, які мають r-1 похідну,
- клас усіх функцій
f, які мають r-1 похідну,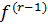 - локально
абсолютно неперервнаі
- локально
абсолютно неперервнаі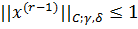 ,
, 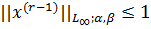 .
.
РОЗДІЛ 1. ВІДОМІ РЕЗУЛЬТАТИ
Введемо поняття функції порівняння.
Скажемо, що  є
функцією порівняння для функції f
є
функцією порівняння для функції f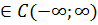 ,
якщо
,
якщо 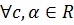 різниця
різниця
 -[f(t+
-[f(t+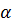 )+c]
на кожному проміжку монотонності
)+c]
на кожному проміжку монотонності  або
не змінює знак, або змінює один раз, до того ж з «+» на «-» там, де
або
не змінює знак, або змінює один раз, до того ж з «+» на «-» там, де  спадає,
і з «-» на «+» там, де
спадає,
і з «-» на «+» там, де  зростає.
Зрозуміло, що якщо функція
зростає.
Зрозуміло, що якщо функція  є функцією
порівняння для функції f(t), то функція
є функцією
порівняння для функції f(t), то функція 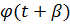 є
функцією порівняння для функції f(t) .
є
функцією порівняння для функції f(t) .
Функції порівняння відомі для багатьох класів
(див. наприкл.[1], [3], [6], [7], [9], [10] та інші). В наступних підрозділах
ми наводимо деякі з відомих результатів стосовно цієї тематики.
.1 Теорема порівняння, симетричний випадок
Нехай 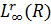 (r=1,2,….)-
множина заданих і r-1 раз неперервно диференційованих на усій осі функцій f(t)
таких, що
(r=1,2,….)-
множина заданих і r-1 раз неперервно диференційованих на усій осі функцій f(t)
таких, що  і
і 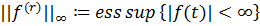 .
.
Покладемо 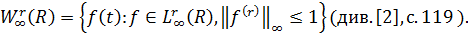
У якості функцій порівняння будуть виступати
ідеальні сплайни Ейлера (див. [1], c. 64).
Для 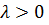 покладемо
покладемо
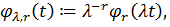 де
де
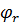 -
ідеальний сплайн Ейлера, тобто
-
ідеальний сплайн Ейлера, тобто 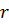 - та періодична
первісна функції sign (sin (t)) (див. рис.1,2).
- та періодична
первісна функції sign (sin (t)) (див. рис.1,2).
Тоді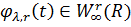 .
.

рис.1

рис. 2
Теорема порівняння у цьому випадку має вигляд
(див. [2], с. 119) :
Теорема А.Нехай  .
Якщо функція
.
Якщо функція 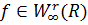 і числоλ
вибрано так, що
і числоλ
вибрано так, що  , то функція
, то функція 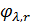 є
функцією порівняння для функції
є
функцією порівняння для функції 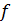 .
.
Існує аналогічне формулювання цієї теореми.
Теорема B.Нехай і при деякому
і при деякому  . Якщо
. Якщо 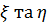 такі,
що f(ξ)=
такі,
що f(ξ)= ,
тоді
,
тоді 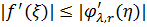 .
.
.2 Несиметричний випадок
Існує певне коло задач аналізу, в якому замість
«симетричного» класу  доводиться
розглядати його «несиметричний» аналог. Далі буде наведений «несиметричний»
аналог теореми порівняння (див. [2], с. 127).
доводиться
розглядати його «несиметричний» аналог. Далі буде наведений «несиметричний»
аналог теореми порівняння (див. [2], с. 127).
Для чисел 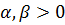 позначимо
позначимо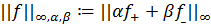 ,
,
де 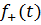 та
та
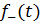 -
відповідно додатна та від’ємна частини функції f(t), а через
-
відповідно додатна та від’ємна частини функції f(t), а через  позначимо
клас функцій
позначимо
клас функцій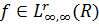 , таких, що
, таких, що
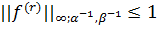 .
.
Екстремальною функцією у цьому класі буде
несиметричний ідеальний сплайн Ейлера 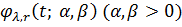 ,
який визначається наступним чином:
,
який визначається наступним чином:
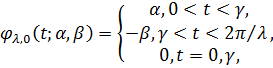
де число γ=γ(α,β)
обрали
так, щоб виконувалось рівняння
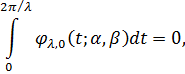
звідси γ=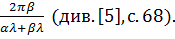
Продовжимо її періодично на усю вісь.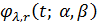 -
первісна із нульовим середнім на періоді від функції
-
первісна із нульовим середнім на періоді від функції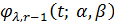 ,
тоді
,
тоді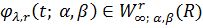 (див. рис. 3,4).
(див. рис. 3,4).

рис. 3
рис. 4
У несиметричному випадку справедлива наступна
теорема порівняння (див.  :
:
ТеоремаC.Нехай 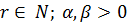 ;
;
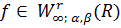 і
число λ
обрали
так, що для всіх
і
число λ
обрали
так, що для всіх 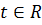
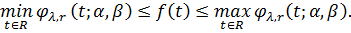
Тоді функція 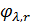 є
функцією порівняння для функції
є
функцією порівняння для функції 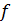 .
.
Введемо класи
 .
.
 .
.
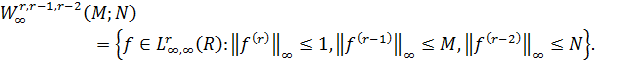
Нехай  Визначимо
T:=
Визначимо
T:=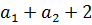 .Визначимо
функцію
.Визначимо
функцію 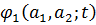 наступним
чином (див. [4], с. 2). На відрізку [0;T] покладемо
наступним
чином (див. [4], с. 2). На відрізку [0;T] покладемо
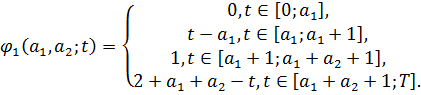
(див. рис.5)
Продовжимо функцію 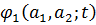 на
відрізок [T;2T]рівнянням
на
відрізок [T;2T]рівнянням
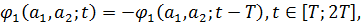 а потім періодично
із періодом
а потім періодично
із періодом 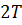 на усю вісь.
на усю вісь.
Через  ,де
,де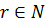 будемо позначати сплайн Ейлера порядку r (тобто
будемо позначати сплайн Ейлера порядку r (тобто 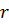 -
ту періодичну первісну функції sgn(sin(t))із середнім значенням нуль на
періоді) (функції
-
ту періодичну первісну функції sgn(sin(t))із середнім значенням нуль на
періоді) (функції 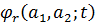 вперше розглядав
Родов[8]).
вперше розглядав
Родов[8]).

рис.5
Для 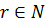 ,
,
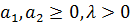 і
і
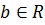 покладемо
покладемо
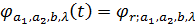 (t):=
(t):=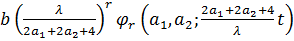 .
.
Відзначимо,
що
функція
 є
є
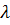 -
періодичною
(див.
[4], с. 3)
-
періодичною
(див.
[4], с. 3)
ТеоремаD.Нехай  і
і
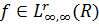 .
Нехай виконується одна із умов.
.
Нехай виконується одна із умов.
Числа  ,
,
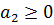 ,
λ
,
λ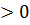 і
і 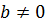 такі,
що
такі,
що
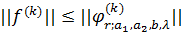 ,
, 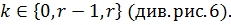

рис. 6
Числа 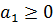 ,
,
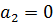 ,
λ
,
λ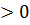 і
і 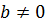 такі,
що
такі,
що
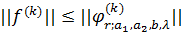 ,
, 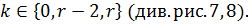

рис. 7

рис. 8
Числа 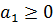 ,
,
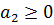 ,
λ
,
λ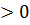 і
і 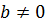 такі,
що
такі,
що
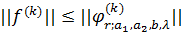 ,
, 
Тоді функція 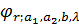 є
функцією порівняння для функції
є
функцією порівняння для функції 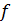 .
.

рис. 9

рис. 10
Зауваження. Попередня теорема демонструє, що при
відповідному підборі параметрів  ,
, 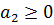 ;
;
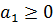 ,
,
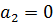 ;
;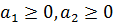 функція
функція 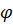 буде
функцією порівняння для функції f для класів
буде
функцією порівняння для функції f для класів  відповідно.
відповідно.
РОЗДІЛ 2. ФУНКЦІя 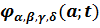 ТА
ЇЇ ВЛАСТИВОСТІ
ТА
ЇЇ ВЛАСТИВОСТІ
.1 Означення екстремальної функції
У даній роботі розглядається клас 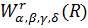 ,
на якому ми задамо несиметричний сплайн
,
на якому ми задамо несиметричний сплайн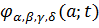 .
.
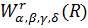 - клас усіх функцій
f, які мають r-1 похідну,
- клас усіх функцій
f, які мають r-1 похідну,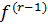 - локально
абсолютно неперервнаі
- локально
абсолютно неперервнаі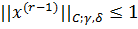 ,
, 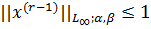 .
.
Нехай 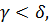 побудуємо
функцію
побудуємо
функцію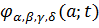 .
.
Нехай  ,
,
 -
довільне,
-
довільне, 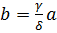 ,
, 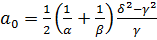 .
.
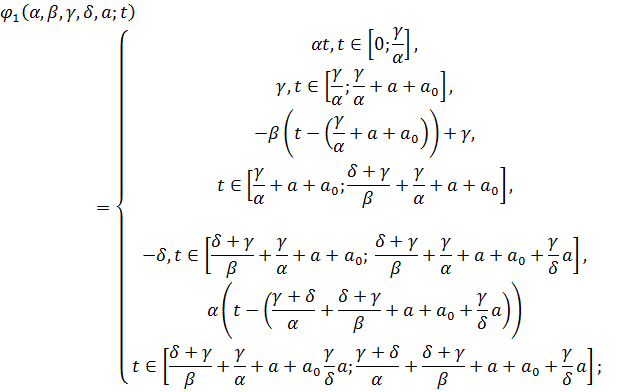
(див. рис. 11)

рис. 11
Продовжимо функцію 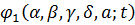 періодично
на всю вісь з періодом T=
періодично
на всю вісь з періодом T=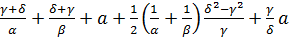 .
.
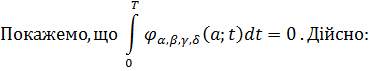
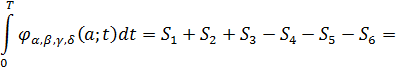
 (2.3.1)
(2.3.1)
Розглянемо 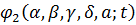 ,
що є первісною
,
що є первісною 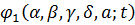 з нульовим
середнім на періоді. Тоді в силу (2.3.1)
з нульовим
середнім на періоді. Тоді в силу (2.3.1) 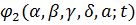 ,
є також періодичною. Аналогічно для будь- якого r
,
є також періодичною. Аналогічно для будь- якого r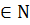 ,
,
 -
це первісна функції
-
це первісна функції 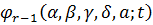 з нульовим середнім
на періоді.
з нульовим середнім
на періоді.
.2 Деякі властивості екстремального сплайна
Відзначимо основні властивості .
.
З означення 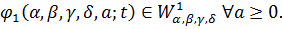 Оскільки
Оскільки
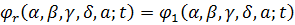 ,звідси випливає,
що
,звідси випливає,
що

 має два нулі на
періоді і при r
має два нулі на
періоді і при r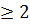 строго монотонна
між точками локального екстремуму.
строго монотонна
між точками локального екстремуму.
Лема. Нехай f належить простору 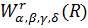 .
.
Тоді 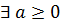 :
: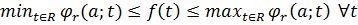 .
.
Доведення. В силу означення 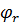 ,
,
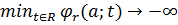 ,
,
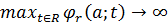 ,при
,при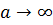 .
Тоді
.
Тоді 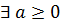 ,
таке, що
,
таке, що
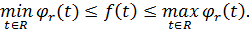
РОЗДІЛ 3.ОСНОВНІ РЕЗУЛЬТАТИ
Теорема. Якщо f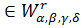 (R),
(R),
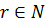 і
і
 таке,
що
таке,
що
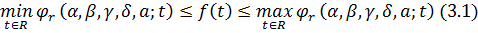
для будь- якого 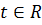 ,
то функція
,
то функція є функцією
порівняння для функції f(t).
є функцією
порівняння для функції f(t).
Доведення.Скористаємось методом математичної
індукції.
Далі для скорочення записів будемо писати 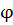 замість
замість
 .
.
Базис: Нехай r=1.
Доведемо, що якщо f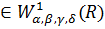 і
і
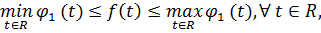
то функція 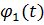 є
функцією порівняння для функції f(t).
є
функцією порівняння для функції f(t).
Позначимо 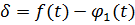 .
.
 ,
, 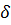 (
(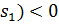 і
і 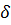 (
(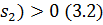
Нехай  функції
функції
 ,
на якому функція
,
на якому функція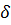 змінює знак з «-»
на «+».
змінює знак з «-»
на «+».
Нехай (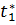 ,
,
 -проміжок
строгої монотонності
-проміжок
строгої монотонності  .
.
Оскільки 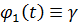 на
(
на
(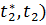 ,
і
,
і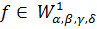 (R),
тоотримаємо
(R),
тоотримаємо 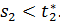
Оскільки 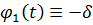 на
(
на
(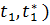 ,
і
,
і 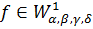 (R),
тоотримаємо
(R),
тоотримаємо 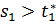 .
.
Тоді ( ),
отже
),
отже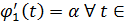 (
(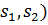 .
.
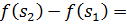
 .
.
Отримали протиріччяз (3.2), отже 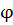 є
функцією порівняння для f у випадку r=1.
є
функцією порівняння для f у випадку r=1.
Індуктивне припущення. Нехай твердження
справедливе при r=k-1, тобто, якщо  і
виконується
і
виконується

то функція є функцією порівняння для функції f(t).
є функцією порівняння для функції f(t).
Доведемо твердження при r=k. Нехай 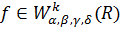 і
і
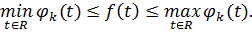
Доведемо, що функція  є
функцією порівняння для функції f(t).
є
функцією порівняння для функції f(t).
Для цього спочатку доведемо, що

Припустимо супротивне. Нехай (3.3) не
виконується. Це можливо у наступних 3 випадках:
випадок: 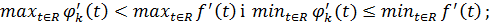
випадок: 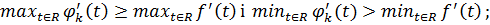
випадок: 0
Розглянемо 3 випадок, інші випадки розглядаються
аналогічно.
Без зменшення загальності можемо вважати, що
 (3.4)
(3.4)
Оскільки замість 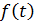 ми
можемо розглянути функцію
ми
можемо розглянути функцію 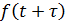 , де
, де 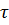 -
-
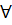 число,
будемо вважати, що
число,
будемо вважати, що
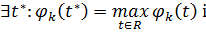
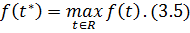
Нехай 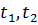 -
найближчі ліворуч та праворуч від
-
найближчі ліворуч та праворуч від  нулі
функції
нулі
функції 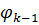 ,
функція
,
функція  зростає
на (
зростає
на ( і спадає на (
і спадає на ( .
.
В силу (3.1)
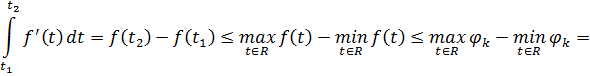

⇒ (
( :0
:0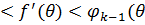 ).
Будемо вважати, що
).
Будемо вважати, що 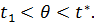
Розглянемо функцію
 , тоді g
, тоді g ,
,

 .
.
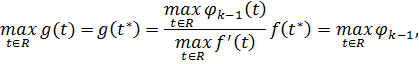
і в силу (3.4)

Тобто, для g усі умови індуктивного припущення
виконуються.
 розглянемо функцію
h(t)
розглянемо функцію
h(t) h(t)=g(t+
h(t)=g(t+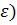 .В
силу означення h для неї також виконуються умови з індуктивного припущення.
Дійсно,h
.В
силу означення h для неї також виконуються умови з індуктивного припущення.
Дійсно,h
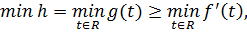

крім того, h(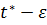 )=g(
)=g(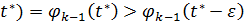 ,
враховуючи (3.6) можемо обрати
,
враховуючи (3.6) можемо обрати  настільки малим,
щоб виконувалось h(
настільки малим,
щоб виконувалось h( тоді різниця
тоді різниця 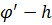 змінює
знак з «-» на «+»,отже
змінює
знак з «-» на «+»,отже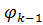 не є функцією
порівняння для функції h, що суперечить індуктивному припущенню.Таким чином ми
довели (3.3).
не є функцією
порівняння для функції h, що суперечить індуктивному припущенню.Таким чином ми
довели (3.3).
Повернемось до доведення індуктивного
припущення.
Нехай r=k і f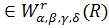 ,
така, що виконується (3.1). Тоді справедливі нерівності (3.3).
,
така, що виконується (3.1). Тоді справедливі нерівності (3.3).
Розглянемо різницю 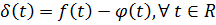 .
.
Припустимо супротивне, що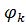 не є функцією порівняння для функції f,
не є функцією порівняння для функції f,
Можемо вважати, що на проміжку зростання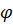 ,є
зміни знаку функції
,є
зміни знаку функції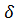 з «-» на «+».
з «-» на «+».
Нехай 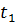 ,
,
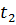 -
проміжок зростання
-
проміжок зростання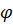 і
і
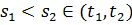

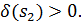
Розглянемо  (t)=(1-
(t)=(1-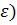 f(t)-
f(t)-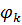 (t),
де
(t),
де 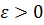 вибрано
так, щоб
вибрано
так, щоб
 (
(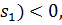

В силу (3.1)
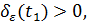
 (див. рис. 12).
(див. рис. 12).

рис. 12
Тоді існують точки А, В, С:
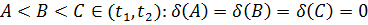 і
і 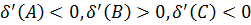
(див. рис. 13).
рис. 13
можемо вважати, що дві з 3 точок 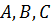 лежать
на (
лежать
на (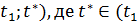 ,
,
 така,
що
така,
що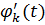 зростає на (
зростає на (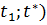 і спадає на (
і спадає на ( .
Але тоді функція
.
Але тоді функція 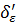 змінює знак з «-»
на «+» на проміжку зростання (
змінює знак з «-»
на «+» на проміжку зростання (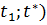 функції
функції 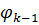 ,
отже
,
отже 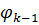 не
є функцією порівняння для функції (1-
не
є функцією порівняння для функції (1-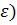 f,
що суперечить індуктивному припущенню. Теорема доведена.
f,
що суперечить індуктивному припущенню. Теорема доведена.
ВИСНОВКИ
теорема колмогоров функція
екстремальний
Дипломна робота присвячена отриманню аналогів
теореми порівняння Колмогорова для класу функцій, що задаються обмеженнями на
несиметричні норми старших похідних.
У першому розділі буларозглянута теорема
порівняння Колмогорова для різних класів.
У третьому розділі була доведена теорема
порівняння для класу
 (-
(-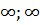 ).
).
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ
[1]
Корнейчук Н. П. Сплайны в теории приближений- М.: Наука. Главная редакция
физико- математической литературы, 1984, 352 с., с. 64.
[2]
Корнейчук Н. П Точные константы в теории приближения- М.: Наука . Гл. ред.
физ.- мат. лит., 1987.-424 с., с. 94, с. 104, с. 119.
[3]
Корнейчук Н. П. Экстремальные задачи теории приближения. Главная редакция
физико- математической литературы изд- ва «Наука», М., 1976, с. 113.
[4]
В. Ф. Бабенко, О. В. Коваленко Теоремы сравнения производных и некоторые их
приложения. Вісник ДНУ, 2012,Том 1, №1, 1-9ISSN 9128- 0912.
[5]В.
Ф. Бабенко, Н. П. Корнейчук, В. А. Кофанов, С. А. Пичугов Неравенства для
производных и их приложения, Киев, Наукова думка, 2003, с. 66, с. 69.
[6]Колмогоров
А. Н. о неравенствах между верхними гранями последовательных производных
произвольной функции на бесконечном интервале .// В кн. А. Н. Колмогоров,
избранные труды, Математика и механика, М. Наука, 1985, с. 252- 263.
[7]
Корнейчук Н. П., Бабенко В. Ф., Лигун А. А. Экстремальные свойства полиномов и
сплайнов.- Киев. Наук.думка 1992, -304 с.
[8]
Родов А. М. Зависимость между верхними гранями производных функций
действительного переменного // Изв. АН СССР. Сер. Мат.- 1946. 10. с.- 257-270.
[9]
Корнейчук Н. П., Лигун А. А., Доронин В. Г. Аппроксимация с ограничениями -
Киев: Наукова думка, 1982,- 250 с.
[10]
Babenko V. F., Kofanov V. A., Pichugov S. A. Inequalities for norms of
intermediate derivatives of periodic functions and their applications// Ibid.- N
3.- P. 251- 376.