Анализ стохастических колебаний прямоугольной пластины
Введение
Поведение конструкций,
подверженных воздействию статистических и динамических
нагрузок, зависит от ряда факторов случайной природы. Эти факторы по своему
происхождению могут быть разбиты на две группы.
К одной группе относятся геометрические и физические
параметры самой конструкции: случайные отклонения от идеальной геометрической
формы, разброс способов осуществления краевых условий, разброс упругих и
прочностных характеристик материала и т.д.
Ко второй группе принадлежат случайные факторы,
характеризующие нагрузку и другие внешние условия эксплуатации.
Перечисленные факторы в той или иной мере
присущи любой конструкции. Но вопросы исследования методов теории случайных
колебаний интенсивнее всего разрабатываются в теории пластин и оболочек [1,6].
Этому можно дать два объяснения. Во-первых,
тонкостенные конструкции особенно чувствительны к малым изменениям начальной
формы, малым вариациям краевых условий и т.д. Во-вторых, тонкостенные
конструкции являются наиболее интересными в современной технике объектами для
приложения методов теории случайных процессов. В качестве примера достаточно
указать на элементы обшивки летательных аппаратов, испытывающих случайную
нагрузку под действием атмосферной турбулентности, пульсаций в турбулентном
пограничном слое, акустического излучения от работающих авиадвигателей,
метеоритной пыли и т.д.
Хорошо известно, что пластинки обладают более
густым спектром частот собственных колебаний, чем стержни и стержневые системы.
Поэтому, если частоты возбуждения достаточно велики, то так называемая
отстройка от резонанса становятся практически неосуществимой. Положение
усугубляется, когда возбуждение имеет сплошной спектр, как, например, в случае
нагрузок, порождаемых атмосферной турбулентностью или акустическим излучением
работающих двигателей. Одновременно может возбуждаться группа форм колебаний,
которым соответствуют различные волновые числа. В связи с этим задача
определения напряжений и об оценке усталостной прочности пластинок,
колеблющихся с различными частотами спектра, представляет значительный
практический интерес.
Если волновые числа достаточно велики, то для
форм колебаний могут быть построены асимптотические выражения. Эти выражения
пригодны всюду, кроме областей, непосредственно примыкающих к границе контура
или к другим линиям, на которых задаются граничные условия; граничным условиям
асимптотические выражения, вообще говоря, не удовлетворяют. Между тем опыт
показывает, что колеблющиеся пластинки обычно разрушаются от усталости у
заделанных кромок, у подкрепляющих элементов и в других аналогичных местах.
Поэтом у возникает мысль об отыскании таких решений, которые удовлетворяли бы
всем граничным условиям на контуре, и стремились бы к асимптотическим
выражениям для форм колебаний, при удалении во внутреннюю области. Найденные
таким образом решения для пограничной области во многом напоминают решения,
описывающие простой краевой эффект в оболочках. При статическом расчете
оболочек ищут такие решения для пограничной зоны, которые удовлетворяют всем
граничным условиям на примыкающем контуре и асимптотически стремятся к
безмоментному решению по мере удаления от границы контура. Здесь требуется
неограниченное приближение к асимптотическим выражениям для форм собственных
колебаний. По аналогии с краевым эффектом в оболочках, отклонение от
асимптотических представлений для форм колебаний, наблюдающееся в пограничной
области, будем называть динамическим краевым эффектом [4].
Расчленяя решение уравнения колебаний пластинки
на асимптотическое решение во внутренней области, и на решение, описывающее
динамический краевой эффект, получаем метод динамического расчета пластинок,
особенно эффективный в случае пластинок прямоугольных в контуре и, произвольно
закрепленных по контуру. При рассмотрении вынужденных колебаний, которым соответствуют
достаточно большие волновые числа, предлагается использовать разложения в ряды
по асимптотическим выражениям для форм собственных колебаний.
Найдя коэффициенты этого ряда и используя связь
между решением во внутренней области и динамическим краевым эффектом, легко
вычислить напряжения в пограничной зоне. Хотя метод является обоснованным лишь
для достаточно больших волновых чисел, в ряде случаев он дает вполне
удовлетворительное решение и для низших форм колебаний. Так, он оказался весьма
эффективным средством для вычисления всего спектра частот собственных колебаний
прямоугольной пластинки, жестко или упруго защемленной по контуру.
В курсовой работе предполагается подход к
анализу стохастических колебаний прямоугольной пластины, жестко защемленной со всех
сторон и находящейся под действием поперечной нагрузки типа «белый шум».
1. Постановка задачи для прямоугольной пластины
1.1 Математическая постановка задачи
Объектом исследования является тонкая,
изотропная однослойная прямоугольная пластина со сторонами a,
b и постоянной
толщиной
h, находящаяся под
действием случайной нагрузки.
Уравнение вынужденных поперечных колебаний имеет
вид:
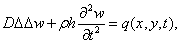 (1.1)
(1.1)
Граничные условия пластины, жестко
заделаной по внешнему контуру:
 при х = 0, а
при х = 0, а
 при у = 0, b (1.2)
при у = 0, b (1.2)
Начальные условия:
w=0 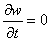 при t=0 (1.3)
при t=0 (1.3)
Внешняя нагрузка представляет собой
пространственно-временной ”белый шум” с
характеристиками:
математическое ожидание
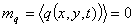
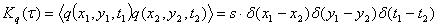 (1.4)
(1.4)
Спектральная плотность:
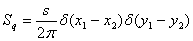 (1.5)
(1.5)
где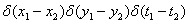 - дельта функции; s -
интенсивность белого шума.
- дельта функции; s -
интенсивность белого шума.
Ставится задача вычисления корреляционной
функции обобщенных координат с последующим определением корреляционной функции
прогиба пластины.
.2 Случайная нагрузка и методы ее описания
Имеется широкий круг проблем строительной
механики, применение статистических методов к которым вполне оправдано и, более
того, для которых статистические методы являются наиболее адекватным средством
исследования. Поэтому целесообразно ввести такие понятия как случайная величина
нагрузки и случайный процесс нагружения.
Под нагрузками понимаются не только внешние
силы, но и внешние кинематические воздействия - заданные перемещения системы
или ее отдельных точек, а также тепловые воздействия, излучения и т.п.
Будем различать два основных класса случайных
нагрузок - нагрузки, задаваемые в виде случайных функций времени, и нагрузки,
задаваемые в виде случайных функций времени и координат.
Описание первого класса нагрузок осуществляется
методами теории случайных процессов, для описания второго класса требуется
привлечение теории случайных полей [1,11,14].
Функции, значения которых при фиксированных
значениях аргументов являются случайными величинами, называется случайными
функциями. В прикладных задачах аргументом случайных функций часто является
время; случайные функции времени называют обычно случайными процессами.
Пульсации скорости и давления в турбулентном потоке, шум реактивного двигателя,
толчки, испытываемые транспортным средством при движении по неровному пути,
представляют собой случайные процессы.
Пусть внешнее воздействие характеризуется
элементами q из пространства Q,
а поведение системы u из
пространства U. Математическая
природа элементов обоих пространств, вообще говоря, произвольна. Это могут быть
числа, векторы, тензоры, функции одной или нескольких переменных и т.п.
Вместо полного вероятностного описания путем
задания меры в функциональных пространствах нередко используется частичное
описание. При этом широко применяются интегралы по вероятностной мере:
математические описания, дисперсии и другие моменты от случайных величин,
моментные и корреляционные функции от случайных процессов. Вероятность
случайного события интерпретируется как объективная мера, эквивалентная
эмпирической частоте.
Для получения вероятностных характеристик
системы необходимо иметь соответствующую статистическую информацию. Но в
распоряжении экспериментатора очень редко находится количество экземпляров,
достаточное для того, чтобы делать надежные статистические выводы, К счастью
многие вероятностные свойства систем обладают эргодичностью. Эти свойства
проявляются не только в ансамбле реализаций, но и во времени и в пространстве.
Такие вероятностные свойства можно изучать, наблюдая за поведением одного
экземпляра во времени или изучая, как эти свойства меняются при переходе от
одной точки к другой.
Корреляционные методы основаны на изучении
связей между некоторыми характеристиками входных и выходных процессов - между
корреляционными или между соответствующими родственными им функциями. Функции,
описывающие статистическую связь (кореляцию) между значениями в разные моменты
времени называются корреляционными функциями.
Пусть q1(t),
q2(t)
… qn(t)
- некоторые случайные функции времени. Будем обозначать < > осреднение по
ансамблю реализаций.
Рассмотрим характеристики процесса, образуемые
по следующим правилам:
Kjk=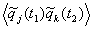 , jkm=
, jkm=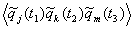 ,
,
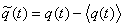 ,
,
(j, k, m=
1,2,…n) (1.6)
Характеристики Kjk, Kjkm и т.д.
называются корреляционными функциями второго, третьего и т.д. порядков. для
исчерпывающего описания процесса необходимо знать полную систему корреляционных
функций.
Значительная часть информации о
случайном процессе все же заключена в средних < q(t) > и
корреляционных функциях второго порядка
В ряде задач (например, в тех
задачах, где заранее известно, что обобщенные координаты подчиняются
нормальному распределению) указанных характеристик достаточно для построения
совместных плотностей вероятностей и последующего решения вопросов надежности.
Описание случайного процесса
упрощается, если он является стационарным, т.е. если все его статистические
характеристики остаются неизменными во времени.
Средние значения для стационарного
случайного процесса постоянны, а корреляционные функции зависят лишь от
разностей t1-t2, t1- t3 и т.д. В
частности, корреляционные функции второго порядка выражаются по формулам:
Kjk(τ)=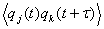 (1.7)
(1.7)
Почти все представляющие интерес
стационарные случайные нагрузки обладают также свойством эргодичности. Для
эргодических случайных процессов осреднение по ансамблю реализаций может быть
заменено осреднением по времени.
В частности,
Kjk(τ)=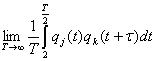 (1.8)
(1.8)
Введем также представление Фурье для
корреляционной функции
Kjk(τ)=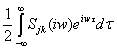 (1.9)
(1.9)
Функции Sjk(τw)
- будем называть совместными спектральными плотностями. Если процесс содержит
дискретные составляющие, то спектральные плоскости будут иметь особенности типа
дельта функций. Пусть одномерный процесс состоит из стационарной
последовательности некоррелированных импульсов, продолжительность которых
стремится к нулю, а величина остается конечной. Корреляционная функция такого
процесса выражается через дельта функцию δ(t),
а спектральная плотность постоянна на всей частоте оси:
K(τ)=s.δ(τ), S(ω)=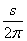 (1.10)
(1.10)
Такой процесс называется
дельта-коррелированным, а постоянная s в формулах
(1.10) интенсивностью белого шума. Корреляционная функция белого шума принимает
в нуле бесконечное значение, т.е. дисперсии процесса не существует. «Белый» шум
представляет собой все же чрезмерную абстракцию, поскольку его полная мощность,
пропорциональная интегралу
 (1.11)
(1.11)
оказывается бесконечно большой.
Чтобы мощность процесса оставалась конечной, вводится ограничивающая частота ω.
Более реальной моделью будет
усеченный «белый» шум спектральная плотность которого постоянна на отрезке и
равна нулю вне этого отрезка.
2. Асимптотический метод
исследования задач о колебаниях упругих прямоугольных пластин
.1 Динамический краевой эффект при
упругих колебаниях пластинок
Рассмотрим собственные колебания
прямоугольной в плане упругой пластинки со сторонами а и b и
постоянной толщиной h (Рисунок 2.1).
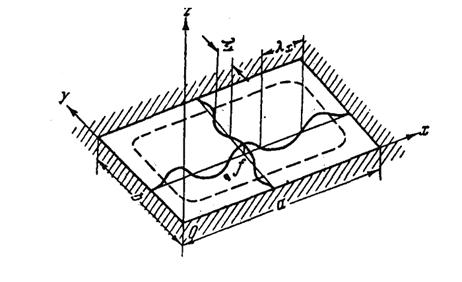
Рисунок 2.1 - Схема колебаний
прямоугольной пластины с жестким защемлением.
Условия на контуре пластины будем
пока считать произвольными. Уравнение колебаний пластинки имеет вид [4,9,10]
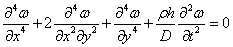 (2.1)
(2.1)
где ω(х, у, t) -
нормальный прогиб, D - цилиндрическая жесткость ρ - плотность
материала пластинки.
Подстановкой
где ω - частота
собственных колебаний, уравнение (2.1) приводится к виду:
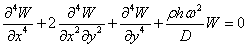 (2.2)
(2.2)
Рассмотрим выражение
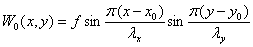 (2.3)
(2.3)
где f, х0,
у0, λx, λy - некоторые
константы. Это выражение удовлетворяет уравнению (2.2) и соответствует частоте
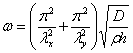 (2.4)
(2.4)
но не удовлетворяет граничным
условиям. Для подчинения этим условиям мы располагаем лишь чётырьмя
константами: f, х0,
у0, λx, λy, так как f
определяется из начальных условий. Как мы увидим ниже, при определенном выборе
этих констант выражение (2.3) можно рассматривать как асимптотическое решение
краевой задачи, соответствующее заданным условиям на контуре и справедливым при
λx‹‹а, λy‹‹b в области,
достаточно удаленной от контура пластинки.
Решение вблизи границы х = 0 будем
искать в виде:
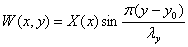 (2.5)
(2.5)
Подстановка в уравнение (2.3) дает
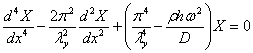
Соответствующее характеристическое
уравнение
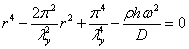
имёет два чисто мнимых и два
действительных корня
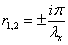 ,
,
 (2.6)
(2.6)
Общий интеграл уравнения (2.5) имеет
вид
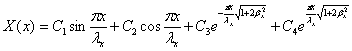
В этом интеграле последний член,
неограниченно возрастающий с увеличением х, должен быть отброшен. Первые два
оставшихся члена полностью соответствуют асимптотическому представлению (2.3)
для внутрённей области пластинки; первые три члена, взятые вместе, описывают
динамический краевой эффект в пограничной зоне:

Пользуясь выражением (2.6) нетрудно
оцёнить ширину области динамического краевого эффекта.
Учитывая, что С32~С12
+ С22 можно считать, что, вклад последнего члена в
выражение (2.1) оценивается множителем
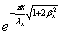
Пусть х = λх. Тогда при βх=1 имеем  . Даже в
самом неблагоприятном случае (βх= 0) получается
. Даже в
самом неблагоприятном случае (βх= 0) получается 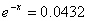 . Таким
образом, ширина области динамического краевого эффекта не превышает длины
полуволны.
. Таким
образом, ширина области динамического краевого эффекта не превышает длины
полуволны.
Рассмотрим некоторые частные случаи граничных
условий, положив в основу решение (2.6) для полностью защемленной
стороны Х(0)=Х′(0)=0;
Отсюда
С2+С3=0, 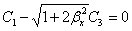
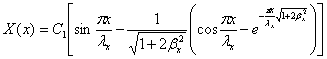
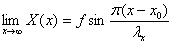 (2.7)
(2.7)
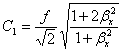 ,
,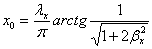
Окончательно получаем

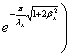 (2.8)
(2.8)
Имея выражение (2.8), нетрудно найти
изгибающие моменты в пластинке в зоне краевого эффекта. Поскольку изгибающий
момент
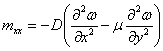 (2.9)
(2.9)
то для линий, вдоль которых
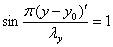
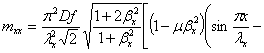
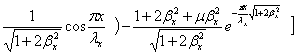 (2.10)
(2.10)
Поведение прогиба и изгибающего
момента в зоне краевого эффекта показано на рисунке 2.2 и 2.3. При вычислениях
было принято, что βх=1, μ=0,25.
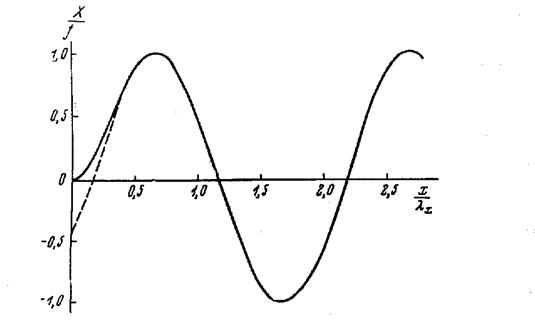
Рисунок 2.2 - Схема поведения
прогиба в зоне краевого эффекта
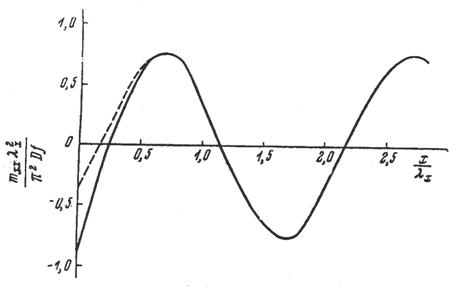
Рисунок 2.3 - Схема поведения
изгибающего момента в зоне краевого эффекта. Штриховыми линиями показаны
решения для внутренней области.
Рассмотрим более общий случай
упругого защемления с коэффициентом жесткости с. Тогда:
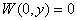 ,
,
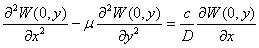
функция Х (х) должна удовлетворять
условиям;
X(0) = 0, 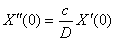
C2+C3=0
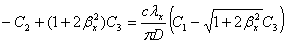
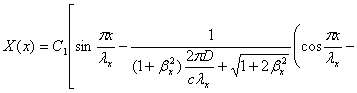
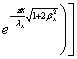 (2.11)
(2.11)
Из условия (2.7) найдем, что
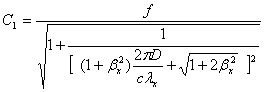 (2.12)
(2.12)
При с→0 выражение (2.11) с
коэффициентом (2.12) превращается в обычное решение для свободно опертой
пластинки; при с→+∞ мы приходим к выражению (2.7).
Не будем останавливаться здесь на
других случаях граничных условий, рассмотрение которых элементарно. В
частности, можно построить решение, описывающее динамический краевой эффект
вблизи подкрепляющего стержневого элемента, который сопротивляется изгибу и
кручению.
Из изложенного следует, что для
типичных краевых условий легко установить связь между максимальным напряжением σ в зоне
краевого эффекта и амплитудой f колебаний во внутренней, области.
Например, для заделанного края
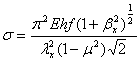 (2.13)
(2.13)
Это соотношение соответствует
некоторой паре длин полуволн λх, λу,: или
некоторой паре волновых чисел m, n. В общем
случае
 (2.14)
(2.14)
где fmn- обобщенные
координаты, характеризующие вклад каждой формы колебаний в движение пластинки, smn -
коэффициенты динамического краевого эффекта.
До сих пор мы рассматривали задачу
об исследовании динамического краевого эффекта при собственных колебаниях,
полагая длины полуволн λх, λу известными.
Покажем, как могут быть найдены эти величины и попутно частоты собственных
колебаний пластинки.
Рассмотрим, например, прямоугольную
в плане пластинку, защемленную. по всему контуру. Наряду с функцией Х(х),
рассмотрим функцию
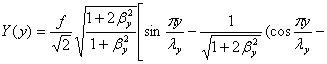
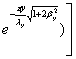
где β= λх/λу.
Выражение
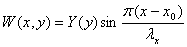
удовлетворяет всем краевым условиям
на границе у = 0 и при больших у приближается к,,внутреннему” решению
(2.3).
Формы собственных колебаний
прямоугольной защемленной по всему контуру пластинки распадаются на четыре
группы по типам симметрии. Для первого типа (симметричные в обоих направлениях
формы) должно быть
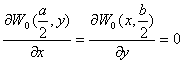
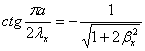 ,
, 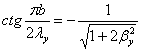 (2.15)
(2.15)
для второго типа (антисимметричные в
обоих направлениях формы)
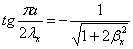 ,
, 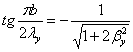 (2.16)
(2.16)
два смешанных типа получим,
комбинируя одно из условий из (2.15) с другим из (2.16).
Для каждого типа мы имеем систему
двух уравнений с двумя неизвестными длинами полуволн λх, λу. Найдя эти
величины, легко вычислить соответствующую собственную частоту (2.4).
Этот метод применим, строго говоря,
лишь при условии, что λх<<а, λу<<b.
Вычисления показывают, однако, что
он дает удовлетворительные решения даже для общей формы колебаний защемленной
пластинки.
Рассмотрим вначале цилиндрический.
изгиб (λу→∞,
βх→0).
Легко найдем, что
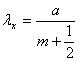 (m=1,2,…)
(2.17)
(m=1,2,…)
(2.17)
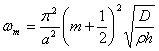 (m=1,2,…)
(2.18)
(m=1,2,…)
(2.18)
совпадающую с хорошо известной
асимптотической формулой. При m= 1 точное решение дает в формуле
для частоты числовой коэффициент 4,7302=22,373, в то время как
асимптотическая формула (2.18) содержит коэффициент 3,1422. 1,5002
= 22,207 Разница составляет менее 1 %.
Применим тот же метод к квадратной
пластинке а =b. При этом
особенно простое решение получается для тех форм колебаний, у которых λх=λу
Тогда уравнения (2.15) и (2.16)
принимают вид
 ,
, 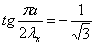
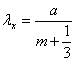 (m=1,2,…)
(m=1,2,…)
причем нечетные волновые числа m
соответствуют симметричным формам колебаний, четные - антисимметричным формам.
Собственные частоты определяются по
формуле
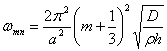 (m=1,2,…)
(2.19)
(m=1,2,…)
(2.19)
Рассмотрим теперь общий случай.
Уравнения типа (2.15) и (2.16) легко могут быть сведены к одному уравнению,
содержащему отношение βх= λх/λу
Это уравнение получается общим для
всех четырех типов форм колебаний.
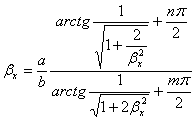 (m=1,2,…)
(2.20)
(m=1,2,…)
(2.20)
где обратные тригонометрические
функции понимаются в смысле главного значения. При больших m и n имеет место
асимптотическая формула
 (2.21)
(2.21)
для квадратной защемленной пластинки
вычисления были сделаны Игути, который искал решение уравнение в виде ряда,
удовлетворяющего условиям на контуре, и использовал прием, близкий к
вариационному. Значения коэффициентов частоты α в формуле
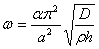
найденные Игути, и значения,
полученные асимптотическим методом, приведены в таблице. Расхождение по этим
значениями невелико.
Таблица 2.1 - Сравнение значений
коэффициентов частоты по Игути и найденных асимптотическим методом
|
m
|
n
|
βx
|
a/λx
|
a/λy
|
α
|
Расхождение
%
|
|
|
|
|
|
Данный
метод
|
По
Игути
|
|
|
1
|
1
|
1,0000
|
4/3
|
4/3
|
3,556
|
3,646
|
2,53
|
|
2
|
1
|
2,0265
|
2,4372
|
1,2027
|
7,386
|
7,437
|
0,69
|
|
2
|
2
|
1,0000
|
7/3
|
7/3
|
10,889
|
10,965
|
0,70
|
|
3
|
1
|
3,0375
|
3,4688
|
1,1420
|
13,337
|
13,396
|
0,42
|
|
3
|
2
|
1,5079
|
3,4012
|
16,656
|
16,717
|
0,37
|
|
3
|
3
|
1,0000
|
10/3
|
10/3
|
22,222
|
-
|
-
|
|
4
|
1
|
4,0432
|
4,4816
|
1,1084
|
21,313
|
-
|
-
|
|
4
|
2
|
2,0132
|
4,4366
|
2,2038
|
24,540
|
24,631
|
0,36
|
|
4
|
3
|
1,3370
|
4,3822
|
3,2784
|
29,960
|
-
|
-
|
|
4
|
4
|
1,0000
|
13/3
|
13/3
|
37,556
|
-
|
-
|
2.2 Стохастические колебания пластин
Решение (1.1) - (1.4) представляют в виде
разложения по формам собственных колебаний Wmn(x,y):
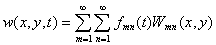 (2.22)
(2.22)
Функции Wmn(x,y)
удовлетворяют однородное уравнение:
 (2.23)
(2.23)
а также краевые условия на контуре
пластин. Здесь ωmn - частоты
собственных незатухающих колебаний.
Подстановка в (2.22) приводит к
уравненниям:
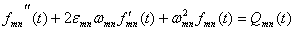 (2.24)
(2.24)
В уравнениях (2.24) введено члены,
которые имеют производные f /mn(t) и
учитывают угасание [7,8]; коэффициенты угасания εmn в общем
случае считаются разными [5].
Через 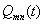 обозначены обобщенные силы:
обозначены обобщенные силы:
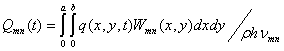 (2.25)
(2.25)
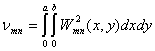 - норма собственной функции Wmn(x,y). (2.26)
- норма собственной функции Wmn(x,y). (2.26)
Соответственно [1] при εmn<<1
побочные элементы матрицы малые в сравнении с главными, а для остальных
справедлива приближенная формула:
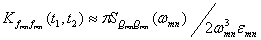 (2.27)
(2.27)
Для вычисления собственных частот
при краевых условиях жесткого защемления используется асимптотический метод.
Метод основан на представлении
решений в виде сумы некоторого решения и решений, которые удовлетворяют краевым
условиям. Асимптотические выражения для собственных функций находят путем
склеивания решений, которые найдены для каждого края области. Погрешность
такого склеивания быстро падает с ростом номера функции (волнового числа).
Придерживаясь асимптотического
метода, ищут внутреннее решение в виде:
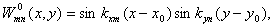 (2.28)
(2.28)
где kxm и kyn -
неизвестные волновые числа, x0 и y0 - фазы
породного решения. Это выражение соответствует частоте:
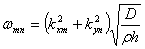 (2.29)
(2.29)
Частное решение (2.28) краевым
условиям не удовлетворяет. Приближенное решение задачи ищут, рассматривая
выражение (2.28) как некоторое порождающее решение, которое справедливо во
внутренней области, то есть, достаточно удаленной от краев. Задача будет решена,
если окажется возможным построение частных решений, каждое из которых будет
удовлетворять два краевых условия на одном из краев пластины и будет
приближаться к порожденному решению в меру отдаления от краев.
Решение, которое удовлетворяет
краевым условиям при x=0 ищут в виде:
 (2.30)
(2.30)
Подстановка выражения (2.30)
приводит к уравнению:
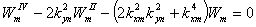 (2.31)
(2.31)

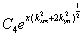 (2.32)
(2.32)
Мнимые корни уравнения (2.31)
соответствуют порождающему решению (2.28), действительные корни - решениям,
которые удовлетворяют краевым условиям. Таким образом, в пластинах всегда имеет
место динамичный краевой эффект.
Это условие будет удовлетворено,
если отбросить в интеграле (2.32) член, который возрастает при увеличении x:
 (2.33)
(2.33)
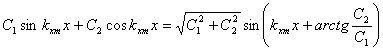
Среди членов, которые остались в
(2.33), два первых полностью соответствуют порожденному решению (2.28), а
первые три члена рассмотренные вместе
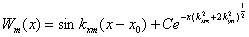 (2.34)
(2.34)
описывают динамический эффект у
приграничной зоне.
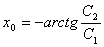
Удовлетворяя краевые условия при х =
0, имеют:
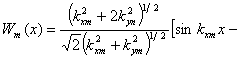
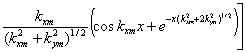 (2.35)
(2.35)
Решение, которое удовлетворяет
краевым условиям про х = а, ищут в виде:
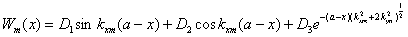 (2.36)
(2.36)
Определив константы в формуле
(2.36), окончательно получают:

 (2.37)
(2.37)
Решения, которые удовлетворяют
краевым условиям при у = 0 и у =b и приближаются к решению во
внутренней области пластинки, записываются аналогично. Таким образом, выражение
для защемленной пластины имеет вид:
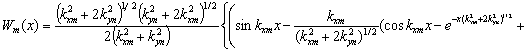
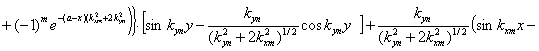
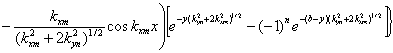 (2.38)
(2.38)
Волновые числа kxm и kym находятся
путем склеивания решений, которые удовлетворяют краевые условия на
противоположных сторонах контура пластины. Решения (2.31) з учетом (2.36) и
(2.37), которые удовлетворяют краевым условиям при х = 0 и х = а, приближаются
к внутренней области к одному и тому породному решению.
Будем требовать в соответствии с
этим выполнение условия:
kxm(x-x0)sin
kyn(y-y0)=±sin kxm(a-x-x0)sin kyn(y-y0)
(2.39)
Положительный знак соответствует
симметричным относительно точки х=а/2 решениям. Система уравнений для
определения волновых чисел имеет вид:
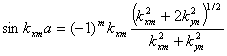 ;
;
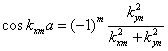
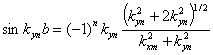
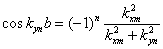 (2.40)
(2.40)
Отклонение функции Wmn(x,y) от
действительных колебаний, а также и погрешность определения обобщенных сил 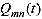 асимптотично
уменьшаются с ростом m и n.
асимптотично
уменьшаются с ростом m и n.
3. Определение корреляционной
функции прогиба пластины
Корреляционная функция прогиба
пластины имеет вид:
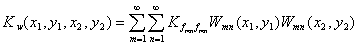 (3.1)
(3.1)
где 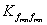 вычисляется по формуле (2.27).
вычисляется по формуле (2.27).
В соответствии с [1] имеем:
 (3.2)
(3.2)
Норма собственных функций имеет вид:
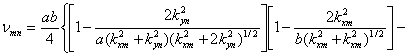
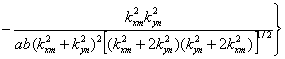 (3.3)
(3.3)
С ростом чисел m и n норма νmn
приближается к ab/4.
Если подставить в (3.2) значения Wmn(x,y)
соответственно с (2.38) и выполнить интегрирование, получают:
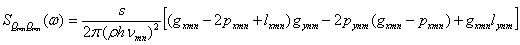 (3.4)
(3.4)
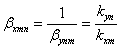 (3.5)
(3.5)
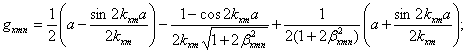 (3.6)
(3.6)
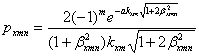 ( 3.7)
( 3.7)
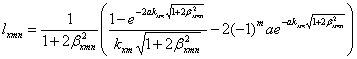 (3.8)
(3.8)
Соотношения для gynm, pynm, lynm получают
путем круговой замены индексов m и n, х и у, а
также параметров a и b.
Некоторые вычисления по формуле
(3.1) для пластин с параметрами [3] иллюстрируются графиками. Как видно,
усиление краевых условий ведет к увеличению корреляции прогибов.
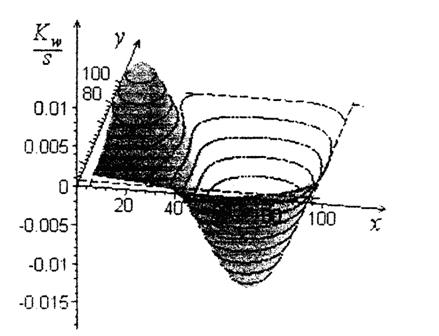
Рисунок 3.1 - Корреляционная функция
прогиба пластины Кw(x,y,a/45,/b/2) в случае
краевых условий жесткого защемления.
Предложенный подход позволяет
получить в закрытом виде асимптотическое решение задачи та исследовать влияние
условия внешней нагрузки, типа демпфирования.
Выводы
В работе решена задача исследования
всего спектра частот при сложных граничных условиях с помощью асимптотического
метода. Одно из достоинств этого метода в том, что при увеличении частот
возрастает также и точность вычислений.
При этом решение выражается в виде
сумы внутреннего решения и поправочных решений, которые называются
динамическими краевыми эффектами. Для каждой границы необходимо строить
решение, удовлетворяющее дифференциальному уравнению и условиям на
соответствующей границе.
Полученные решения склеивают.
Благодаря этому можно получить систему трансцендентных уравнений для
параметров, определяющих как внутреннее решение и краевые эффекты.
Асимптотическое решение может быть
построено для всей окрестности углов и ребер.
Получены аналитические выражения
корреляционной функции прогиба пластины, стохастических колебаний пластины.
математический
прямоугольный пластина асимптотический
Литература
1. Болотин В.В. Случайные колебания
упругих систем. - М.: Наука, 1979. - 46 с.
. Прочность. Устойчивость.
Колебания. Справочник. /под общей редакцией И.А. Биргера и Я.Г. Пановко/, Т.З.
- М.: «Машинострой», 1968. - 310 с.
. Диментбер М.Ф. Вынужденные
колебания пластин при нагрузке, представляющей случайный процесс. //Инженерный
журнал. - 1961 г. Т.1 вып.2
. Болотин В.В. Динамический краевой
эффект. /Инженерный сборник/, - М.: Стройиздат. 1980 г.
. Болотин
В.В. Применение методов теории вероятностей и теории надежности в расчетах
сооружений. - М.: Стройиздат. 1971. - 256 с.
. Болотин В.В. Методы теории
вероятностей и теории надежности в расчетах сооружений. - М.: Стройиздат. 1982.
- 352 с.
. Пановко Я.Г. Внутреннее трение при
колебаниях упругих систем. - М.: Физматлит. 1960. - 193 с.
. Сорокин Е.С. К теории внутреннего
трения при колебаниях механических систем. - М.: Гостстройиздат. 1960. - 129 с.
. Тимошенко С.П. и Войновский -
Кригер С. Пластины и оболочки. - М.: Наука. 1966. - 635 с.
. Физический энциклопедический
словарь/под ред. А.М. Прохорова. - М.: Советская энциклопедия, 1983. - 724 с.
. Пугачев В.С., Синицын И.Н.
Стохастические дифференциальные системы. - М.: Наука, 1985. - 69 с.
. Бендат Дж. Пирсон А. Изменение и
анализ случайных данных. - М.: Мир, 1971. - 408 с.
. Бендат Дж. Пирсон А. Прикладной
анализ случайных данных. - М.: Мир, 1989. - 137 с.
. Пугачев В.С. Теория случайных
функций и ее применение к задачам автоматического управления. - М.: Физматлит.
1960. - 883 с