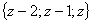Операции с матрицами

Операции с матрицами

1. В декартовой прямоугольной системе координат даны координаты вершин пирамиды ABCD. Постройте чертеж и решите следующие задачи:

а) докажите, что система векторов  линейно независима;

б) постройте вектор , где M и N - середины ребер AD и BC соответственно, найдите его координаты и его разложение по базису ;

в) найдите длину ребра AB;

г) вычислите величину угла между ребрами AB и AC;

д) напишите уравнение прямой АВ;

е) составьте уравнение плоскости АВС;

ж) напишите уравнение высоты, опущенной из вершины D на плоскость АВС.

A (1,-1,0), B (2,3,1),C (-1,1,1),D (4,-3,5).

Решение

а) Найдем координаты векторов:

Найдем смешанное произведение

Значит, векторы линейно независимы и образуют базис.

б) Координаты точек

Пусть имеет в базисе  координаты . Тогда:

Подставим координаты:

.

Составим и решим систему уравнений

Решаем систему методом Крамера. Основной определитель системы:

∆ = 1 (2 10-2 (-2)) - 4 ( (-2) 10-2 3) +2 ( (-2) (-2) - 2 3) = 124

Заменим 1-ый столбец матрицы А на вектор результата В.

-2	-2	3
4	2	-2
-3	2	10

Найдем определитель полученной матрицы.

∆₁ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ =

= (-2) (2 10-2 (-2)) - 4 ( (-2) 10-2 3) + (-3) ( (-2) (-2) - 2 3) = 62

 

Заменим 2-ый столбец матрицы А на вектор результата В.

1-23
4	4	-2
2	-3	10

Найдем определитель полученной матрицы.

∆₂ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ = 1 (4 10- (-3) (-2)) - 4 ( (-2) 10- (-3) 3) +2 ( (-2) (-2) - 4 3) = 62 ,

Заменим 3-ый столбец матрицы А на вектор результата В.

1	-2	-2
4	2	4
2	2	-3

Найдем определитель полученной матрицы.

∆₃ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ =

= 1 (2 (-3) - 2 4) - 4 ( (-2) (-3) - 2 (-2)) +2 ( (-2) 4-2 (-2)) = - 62

 

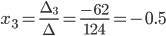
Выпишем отдельно найденные переменные Х - новые координаты  

  

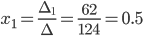
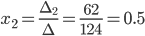
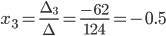
в) длина ребра AB;

г) величина угла между ребрами AB и AC

Координаты векторов:

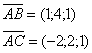
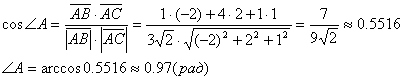
д) напишите уравнение прямой АВ

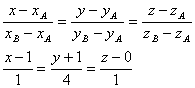
 - прямая АВ

е) составьте уравнение плоскости АВС;

Составим определитель

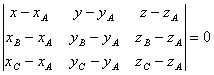
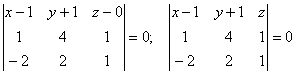
Раскрываем определитель по первой строке.

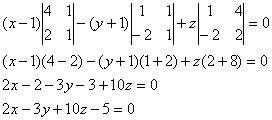
Уравнение плоскости АВС:

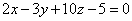
ж) уравнение высоты, опущенной из вершины D на плоскость АВС

Нормальный вектор плоскости АВС 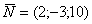 является направляющим вектором прямой

Уравнение прямой

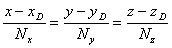
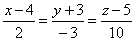 - высота DH

. Для матриц А и В выполните следующие операции

А) .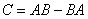

Б) .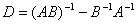

В) .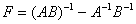

Г) .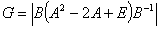

Д) ,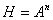

где n - любое натуральное число.

.

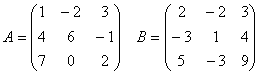
Решение

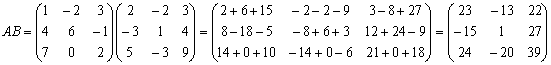
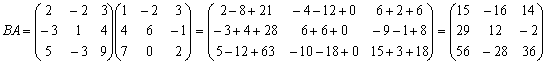
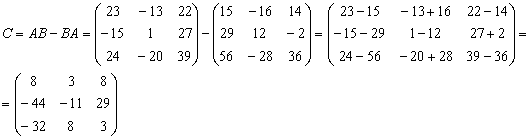
Б) .

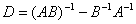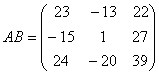
Главный определитель

∆=23 (139- (-2027)) - (-15 (-1339- (-2022))) +24 (-1327-122) =3360

Определитель отличен от нуля, следовательно матрица является невырожденной и для нее можно найти обратную матрицу.

Обратная матрица будет иметь следующий вид:

где A_ij - алгебраические дополнения.

Транспонированная матрица

Найдем алгебраические дополнения матрицы A^T.

 ∆_1,1= (139-27 (-20)) =579

∆_1,2=- (-1339-22 (-20)) =67

 ∆_1,3= (-1327-221) =-373

∆_2,1=- (-1539-2724) =1233

 ∆_2,2= (2339-2224) =369

∆_2,3=- (2327-22 (-15)) =-951

∆_3,1= (-15 (-20) - 124) =276

∆_3,2=- (23 (-20) - (-1324)) =148

∆_3,3= (231- (-13 (-15))) =-172

Обратная матрица.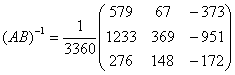

Для матриц А и В найдем обратные

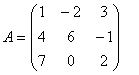
Главный определитель ∆=1 (62-0 (-1)) - 4 (-22-03) +7 (-2 (-1) - 63) =-84

Определитель отличен от нуля, следовательно матрица является невырожденной и для нее можно найти обратную матрицу A^-1.

Транспонированная матрица.

Найдем алгебраические дополнения матрицы A^T.

∆_1,1= (62- (-10)) =12 ∆_1,2=- (-22-30) =4

∆_1,3= (-2 (-1) - 36) =-16

∆_2,1=- (42- (-17)) =-15 ∆_2,2= (12-37) =-19

∆_2,3=- (1 (-1) - 34) =13

∆_3,1= (40-67) =-42 ∆_3,2=- (10- (-27)) =-14

операция матрица пирамида ребро

∆_3,3= (16- (-24)) =14

Обратная матрица.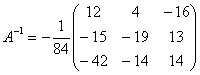

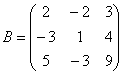
Главный определитель

∆=2 (19- (-34)) - (-3 (-29- (-33))) +5 (-24-13) =-40

Обратная матрица будет иметь следующий вид:

где A_ij - алгебраические дополнения.

Транспонированная матрица.

∆_1,1= (19-4 (-3)) =21 ∆_1,2=- (-29-3 (-3)) =9

∆_1,3= (-24-31) =-11

∆_2,1=- (-39-45) =47 ∆_2,2= (29-35) =3

∆_2,3=- (24-3 (-3)) =-17

∆_3,1= (-3 (-3) - 15) =4 ∆_3,2=- (2 (-3) - (-25)) =-4

∆_3,3= (21- (-2 (-3))) =-4

Обратная матрица.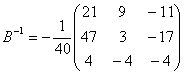

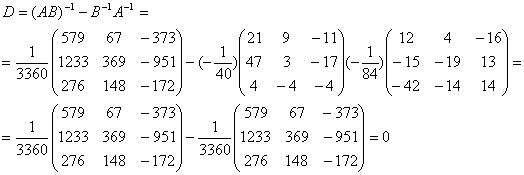
В) .

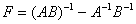Г) .

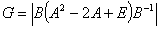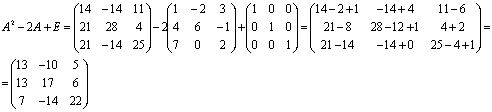
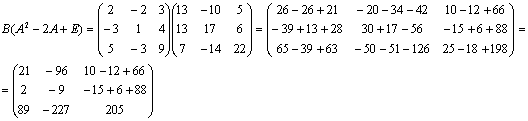
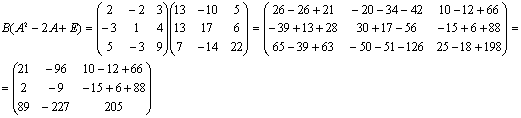
Д) ,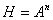

где n - любое натуральное число.

Пусть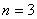

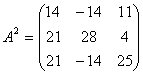
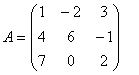
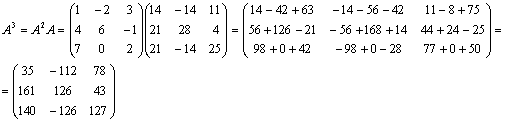
. Решить матричное уравнение .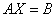

.

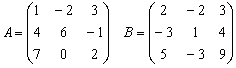
Решение

Домножим слева на обратную матрицу к А

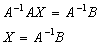
Главный определитель матрицы А ∆=1 (62-0 (-1)) - 4 (-22-03) +7 (-2 (-1) - 63) =-84

Обратная матрица будет иметь следующий вид:

где A_ij - алгебраические дополнения.

Транспонированная матрица.

Найдем алгебраические дополнения матрицы A^T.

∆_1,1= (62- (-10)) =12 ∆_1,2=- (-22-30) =4

∆_1,3= (-2 (-1) - 36) =-16

∆_2,1=- (42- (-17)) =-15 ∆_2,2= (12-37) =-19

∆_2,3=- (1 (-1) - 34) =13

∆_3,1= (40-67) =-42 ∆_3,2=- (10- (-27)) =-14

∆_3,3= (16- (-24)) =14

Обратная матрица.

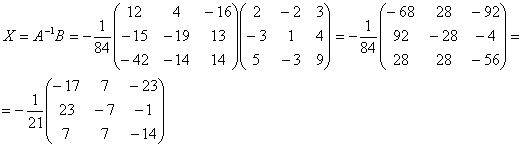
. Решить систему линейных уравнений матричным методом и методом Крамера:

.

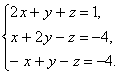
Решение

Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.

Определитель: ∆ = 2 (2 (-1) - 1 (-1)) - 1 (1 (-1) - 1 1) + (-1) (1 (-1) - 2 1) = 3

Заменим 1-ый столбец матрицы на вектор результата.

111
-4	2	-1
-4	1	-1

Найдем определитель полученной матрицы.

∆₁ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ =

= 1 (2 (-1) - 1 (-1)) - (-4) (1 (-1) - 1 1) + (-4) (1 (-1) - 2 1) = 3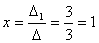

Заменим 2-ый столбец матрицы на вектор результата В.

211
1	-4	-1
-1	-4	-1

Найдем определитель полученной матрицы.

∆₂ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ =

=2 ( (-4) (-1) - (-4) (-1)) - 1 (1 (-1) - (-4) 1) + (-1) (1 (-1) - (-4) 1) = - 6

 

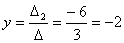
Заменим 3-ый столбец матрицы А на вектор результата В.

2	1	1	2	-4
-1	1	-4

Найдем определитель полученной матрицы.

∆₃ = (-1) ^{1 + 1}a₁₁∆₁₁ + (-1) ^{2 + 1}a₂₁∆₂₁ + (-1) ^{3 + 1}a₃₁∆₃₁ =

=2 (2 (-4) - 1 (-4)) - 1 (1 (-4) - 1 1) + (-1) (1 (-4) - 2 1) = 3

 

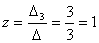
Решение системы: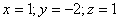  

Проверка:

+1 (-2) +11 = 1 11+2 (-2) - 11 = - 4 -11+1 (-2) - 11 = - 4

. Исследовать и решить системы линейных уравнений методом Гаусса:

.

 

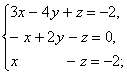
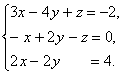
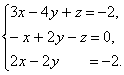
Решение

)

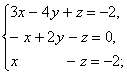
Работаем со столбцом №1 Добавим 3-ю строку к 2-й:

3	-4	1	-2
-1	2	-1	0
0	2	-2	-2

Умножим 1-ю строку на (k = 1/3 = ¹/₃) и добавим к 2-й:

3	-4	1	-2
0	2/3	-2/3	-2/3
0	2	-2	-2

Работаем со столбцом №2 Умножим 2-ю строку на (k = - 2/²/₃ = - 3) и добавим к 3-й:

3	-4	1	-2
0	2/3	-2/3	-2/3
0	0	0	0

Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:

1	-4/3	1/3	-2/3
0	1	-1	-1
0	0	0

Теперь исходную систему можно записать как:

x= - ²/₃ - ( - ⁴/₃y + ¹/₃z) = ^{- 2}/₃ +⁴/₃y - ¹/₃z y = - 1 - ( - z) = - 1+z

-ая строка является линейной комбинацией других строк.

Необходимо переменную z принять в качестве свободной переменной и через нее выразить остальные переменные.

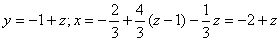
Общее решение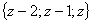

)

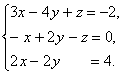
Запишем систему в виде расширенной матрицы:

3	-4	1	-2
-1	2	-1	0
2	-2	0	-4

Для удобства вычислений поменяем строки местами:

3-41-2
2	-2	0	-4
-1	2	-1	0

Работаем со столбцом №1 Умножим 2-ю строку на (k = 1/2 = ¹/₂) и добавим к 3-й:

3	-4	1	-2
2	-2		-4
0	1	-1	-2

Умножим 1-ю строку на (k = - 2/3 = - ²/₃) и добавим к 2-й:

3	-4	1	-2
0	2/3	-2/3	-8/3
0	1	-1	-2

Работаем со столбцом №2 Умножим 2-ю строку на (k = - 1/²/₃ = - ³/₂) и добавим к 3-й:

3	-4	1	-2
0	2/3	-2/3	-8/3
0	0	0	2

Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:

1	1/3	-2/3
0	1	-1	-4
0	0	0	2

Ранг основной матрицы системы равен r (A) =2.

Ранг расширенной матрицы равен r=3 (в основной матрице системы имеется нулевая строка). Таким образом, система не имеет решения.

3)

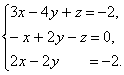
Запишем систему в виде расширенной матрицы:

3	-4	1	-2
-1	2	-1	0
2	-2	0	-2

Для удобства вычислений поменяем строки местами:

3-41-2
2	-2	0	-2
-1	2	-1	0

Работаем со столбцом №1 Умножим 2-ю строку на (k = 1/2 = ¹/₂) и добавим к 3-й:

3	-4	1	-2
2	-2		-2
0	1	-1	-1

Умножим 1-ю строку на (k = - 2/3 = - ²/₃) и добавим к 2-й:

3	-4	1	-2
0	2/3	-2/3	-2/3
0	1	-1	-1

Работаем со столбцом №2 Умножим 2-ю строку на (k = - 1/²/₃ = - ³/₂) и добавим к 3-й:

3	-4	1	-2
0	2/3	-2/3	-2/3	0	0	0

Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:

1	-4/3	1/3	-2/3
0	1	-1	-1
0	0	0	0

Теперь исходную систему можно записать как:

x= - ²/₃ - ( - ⁴/₃y + ¹/₃z) y = - 1 - ( - z)

Необходимо переменную z принять в качестве свободной переменной и через нее выразить остальные переменные.

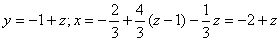
Общее решение