Оптимизация портфеля ценных бумаг
Оглавление
Введение
Глава 1. Теоретические основы оптимизации портфеля ценных бумаг
1.1 Формирование оптимального портфеля ценных бумаг
1.2 Паевые инвестиционные фонды на российском рынке
1.3 Теоретические основы Копула-функций
Глава 2. Использование копула-функций для оптимизации портфеля
ценных бумаг на основе CVaR по российским ПИФ
2.1 Анализ данных по выбранным паевым инвестиционным фондам
2.2 Оптимизация портфелей ценных бумаг на основе CVaR
2.3 Тестирование оптимальных портфелей на контрольных данных и
анализ полученных результатов
Заключение
Список литературы
Приложения
Введение
За последние несколько десятков лет мировой финансовый рынок
продемонстрировал очень высокие темпы роста, как по объемам торговли, так и по
количеству торгуемых инструментов. Сейчас очень сложно представить инвестора,
владеющего только лишь одним активом. Как правило, вложение средств
производится в набор таких инструментов, называемым портфелем ценных бумаг. В
него могут входить как инструменты одного вида, например, только акции или
только облигации, так и различные активы: ценные бумаги, производные финансовые
инструменты, недвижимость и т.д. Главной целью формирования портфеля ценных
бумаг является стремление инвестора получить наиболее высокую доходность при
заданном уровне риска или же иметь наиболее низкий риск для заданного уровня
доходности. Это достигается, прежде всего, за счет эффекта диверсификации, т.е.
распределения средств инвестора между различными активами, а также за счет
тщательного подбора финансовых инструментов.
Моделирование портфелей ценных бумаг является специфической
задачей составления такого сочетания ценных бумаг, которое бы удовлетворяло
выбранной инвестиционной стратегии. Выбор ценных бумаг для инвестирования при
этом основывается на двух основных процессах: анализе поведения ценных бумаг на
основе их исторических котировок и прогнозировании динамики их котировок в
будущем. Прогнозирование, при этом, является процессом с неопределенной
степенью вероятности, так как на котировки ценных бумаг влияет множество
факторов, от локальных до глобальных, поэтому подготовка адекватной модели
является чрезвычайно трудной задачей. Процесс анализа является определенным по
своей сути, так как берется уже известная информация о ценных бумагах, которая
анализируется по метрикам, оценивающим соотношение доходности и риска.
Разнообразие вариантов сочетаний ценных бумаг приводит к тому, что существует
значительное количество привлекательных для инвестирования элементов. Это
приводит к решению задачи моделирования множества портфелей ценных бумаг из
определенной совокупности рыночных элементов по заданному количеству элементов
в портфеле.
Повышение эффективности рынка, рост статистической базы,
прогресс в области вычислительной техники и развитие научных знаний привели к
возникновению современной теории управления портфелем ценных бумаг. Она
основана на использовании статистических и математических методов подбора
инструментов в портфель, а также на ряде новых концептуальных подходов. Основу
современной портфельной теории составляют сформулированные Гарри Марковицем в
1950-х годах идеи по управлению портфелем ценных бумаг. Его подход предполагает
анализ ожидаемых средних значений и вариаций финансовых активов и выбор на их
основе оптимальных весов, с которыми инвестор должен включить каждую
рассматриваемую бумагу в свой портфель [32]. В 90-е годы прошлого века
портфельная теория обогатилась концепцией VAR (Value-at-Risk). Изобретение
банком J.P. Morgan в 1992 г. данной методики объясняется тем, что во многих
случаях дисперсия не может рассматриваться как подходящий показатель измерения
риска портфеля. Например, дисперсия не учитывает возможную скошенность в
распределении доходности портфеля, если оно не является симметричным [59,
c.28]. Таким образом, новая методология благодаря своему преимуществу по
сравнению с "Классической теорией" привлекла как научных
исследователей, так и практиков и по настоящий момент времени широко
используется в различных направлениях, связанных с оценкой рисков.
В мировой научной литературе существует множество работ,
посвященных оптимизации портфеля ценных бумаг и управления риском на основе
показателя VaR, например, Basak and Shapiro [4], Chen [7] и Goh et al. [19].
Однако, существует ряд недостатков VaR как меры риска. Во-первых, VaR сложно оптимизировать
для дискретных распределений (когда его расчет производится при помощи
сценариев), поскольку в данном случае он не будет выпуклой и гладкой функцией и
будет иметь множество локальных экстремумов. Во-вторых, он не является
когерентной мерой риска, в частности может возникнуть ситуация, когда
диверсификация портфеля может увеличить величину VaR (будет нарушаться свойство
субаддитивности). Для преодоления данного недостатка RockfellerandUryasev
предложили альтернативную меру риска - ConditionalValue-at-Risk (CVaR). Pflug
[40] показал, что CVaR является когерентной и выпуклой мерой риска
(удовлетворяет всем трем вышеперечисленным свойствам). Это послужило причиной
тому, что множество исследователей используют именно CVaR в качестве меры риска
для управления портфелем ценных бумаг и других экономических и финансовых
проблем (например: JohnandHafize [25], Huangetal. [23], Zhu and Fukushima
[55], Yau et al. [53], Sawik [44], Claro and Pinho de Sousa [9]).
Для процедуры оптимизации портфеля ценных бумаг на основе
CVaR ключевую роль играет задача выбора и оценки совместного распределения
доходностей ценных бумаг - "претендентов" на включение в портфель.
Исследования показывают, что для финансовых данных наблюдается отклонение их
совместного распределения от многомерного нормального закона. Примером может
служить асимметрия доходностей рыночных активов, которая больше в периоды спада
на рынке, чем в периоды подъема на рынке (Erbetal., 1994 [11]; Longin, Solnik,
2001 [30]; Ang, Chen, 2002 [1]; Patton, 2004, 2006 [37,38]). Таким образом,
многомерное нормальное распределение не является хорошей моделью для описания
совместного распределения многих экономических и финансовых проблем, что
приводит к проблеме поиска более адекватных многомерных моделей. Теория копула-функций
- один из лучших способов ее решения. Теория копула-функций берет свое начало с
работ Hoeffding в 1940г. [22] и Sklar в 1959 г. [47,48], однако свое развитие и
широкое использование она получила лишь к концу 1990‑х гг. Количество
исследований с применением копула-функций увеличивается достаточно быстро, см.
(Wang, 1998 [49]; Frees, Valdez, 1998 [16]; Embrechtsetal., 1999 [10]).
Несмотря на то, что теория копула-моделей исследована относительно полно,
проблема оценивания и статистические выводы для копула-моделей, в определенном
контексте, все еще требуют дальнейших исследований, см. Genest, Favre, 2007
[17]. За последние годы предложены различные методы оценивания параметров
копула-функций, начиная с параметрических (Jondeau, Rockinger, 2003 [26]; Patton,
2004, 2006а, б [37,38]; Fantazzini, 2009б [12]), полупараметрических (Genest et
al., 1995 [17,18]; Breymann et al., 2003 [5]; Fantazzini, 2010 [13,14), и
заканчивая непараметрическими методами (Fermanian, Scaillet, 2003 [15]).
Новым направлением развития является использование копул к
моделированию многомерных распределений в задачах оптимизации структуры
портфеля. Здесь стоит отметить такие работы, как (Hennessy, Lapan, 2002 [21];
Алексеев и др., 2006 [56]). Кроме того, большинство исследователей в данном
направлении используют в качестве меры риска именно CVaR из-за его преимуществ
описанных выше. Lauprete, Samarov, Welsch, 2002 [28]; Autchariyapanitkul,
Chanaim, Sriboonchitta, 2015 [3] на основе исторических данных оценивали
портфели минимального риска с использованием распределения Стьюдента для
копулы. ManyingBaiandLujieSun [31] в своей работе применяли 3-х мерные
Архимедовы копулы для анализа данных, а (PuHuang, DharmashankarSubramanian,
JieXu, 2010 [41]) - Нормальные копулы. Помимо данных работ существует много
исследований по оптимизации портфеля ценных бумаг на основе несимметричных мер
риска, см. (Xubiao He, Pu Gong, 2009 [51]; Iakovos Kakouris, Berç Rustem, 2014 [24]) идругие.
Таким образом, данная тема является очень популярной и
привлекает внимание исследователей по всему миру. Кроме того отсутствуют работы
по оптимизации портфеля ценных бумаг, состоящего из паев российских ПИФ на
основе копула функций. Все это говорит об актуальности выбранной тематики
исследования.
Целью настоящей работы является получение оптимального
портфеля ценных бумаг на основе CVaR с использованием копула-функций для оценки
многомерного распределения на примере российского рынка открытых ПИФов.
Для достижения данной цели были поставлены следующие задачи,
определившие состав и логику настоящей работы:
Проверить используемые данные на "нормальность" с
помощью теста Колмогорова-Смирнова и на "тяжелые хвосты" при помощи
ядерных оценок функции плотности
Построить копула-функции и выбрать лучшие из них на основе
критерия Акаике
Смоделировать множество портфелей ценных бумаг на основе
метода Случайных портфелей
Построить прогноз распределения доходности ценных бумаг на
трех временных горизонтах инвестирования: месяц, квартал и полугодие
Оценить ожидаемую доходность и CVaR для каждого
сгенерированного портфеля и построить достижимые множества для всех
рассматриваемых временных горизонтов
Выбрать оптимальные портфели и сравнить их с результатами
"Классической теории" Марковица на контрольных данных
Объектом исследования являются открытые Паевые Инвестиционные
фонды российского рынка, входящие в десятку фондов с наибольшей стоимостью
чистых активов.
Предметом исследования выступают оптимальные портфели,
составленные из паев объектов исследования.
Методология исследования основана на применении
копула-функций, метода Случайных портфелей, метода непараметрической оценки
CVaR, метода Маровица, метода Монте-Карло
Структура работы состоит из введения, двух глав, заключения и
списка использованных источников.
Во введении определены актуальность, цель и задачи, объект и
предмет исследования, характеристика степени разработанности темы, методическая
и информационная база.
В первой главе рассматриваются теоретико-методологические
основы процесса построения оптимальных портфелей для ПИФ. В ней изложена
Классическая теория управления портфелем ценных бумаг, а также новые
направления в данной области - использование CVaR и VaR в качестве мер риска,
описаны основы функционирования ПИФ на российском рынке, рассказано об
теоретических основах построения и использования копула-функций для
моделирования многомерного распределения.
Во второй главе подробно изучены и проанализированы исходные
данные на предмет подчинения нормальному распределению и толщины хвостов
распределения, приведена методология и построены оптимальные портфели разных
типов на трех временных горизонтах, протестированы результаты данных портфелей
на контрольной выборке и проанализированы полученные результаты.
В заключении подведены итоги исследования, содержатся выводы
и практические рекомендации.
портфель оптимизация ценная бумага
Глава
1. Теоретические основы оптимизации портфеля ценных бумаг
1.1
Формирование оптимального портфеля ценных бумаг
Основу современной портфельной теории составляют
сформулированные Гарри Марковицем в 1950-х годах идеи по управлению портфелем
ценных бумаг. Его подход предполагает анализ ожидаемых средних значений и
вариаций доходности финансовых активов и выбор на их основе оптимальных весов,
с которыми инвестор должен включить каждую рассматриваемую бумагу в свой
портфель. В классической теории в качестве ожидаемого значения доходности может
выступать среднее арифметическое, среднее геометрическое, медиана или модельное
значение, например, на основе модели CAPM, а также некоторые другие [32]. Для
определения доходности портфеля используется следующая формула:
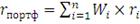
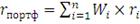 (1)
(1)
где
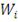
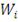 - доля
- доля 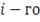
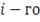 актива в портфеле,
актива в портфеле, 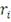
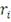 - доходность
- доходность 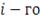
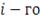 актива.
актива.
В качестве меры риска или изменчивости (вариации) актива Марковец
предложил использовать дисперсию, которая характеризует разброс доходности
относительно ее средней величины.
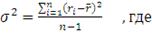
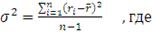 (2)
(2)
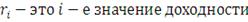
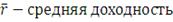
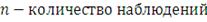
Для определения общего риска портфеля (его дисперсии) формула
расчета такова:
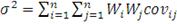
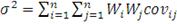 (3)
(3)
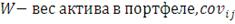
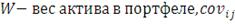 - ковариация (мера линейной зависимости) доходности
- ковариация (мера линейной зависимости) доходности 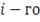
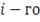 актива с доходностью
актива с доходностью 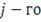
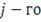 актива, где:
актива, где:
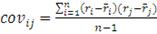
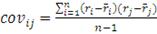 (4)
(4)
Если объединить в портфель некоторое число активов (рассмотрим
случай с четырьмя активами), то можно построить портфельное множество с
различными сочетаниями параметров риска и доходности, варьируя удельные веса 
 инструментов в портфеле. Таким образом, мы получим фигуру ABCDE,
изображенную на рисунке 1, которая представляет собой все достижимое множество
портфелей.
инструментов в портфеле. Таким образом, мы получим фигуру ABCDE,
изображенную на рисунке 1, которая представляет собой все достижимое множество
портфелей.
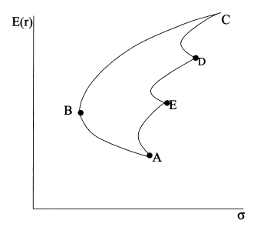
Рисунок 1: Достижимое множество
Рациональный инвестор будет стремиться минимизировать риск и
увеличить доходность, поэтому всем возможным портфелям, представленным на рис.
1, вкладчик предпочтет только те, которые расположены на отрезке ВС, поскольку
они являются доминирующими. Доминирующий портфель - это портфель, который имеет
наибольшую доходность для заданного уровня риска или минимальный риск для
заданного значения доходности. Набор портфелей на отрезке ВС называют эффективным
набором. Эффективный набор портфелей - это набор, состоящий из доминирующих
портфелей. Набор портфелей на участке ВС называют еще эффективной границей или
эффективной границей Марковца. Она была открыта Г. Марковцем в 50-х годах.
Чтобы определить данную границу, необходимо на основе уравнения (3) рассчитать
удельные веса активов в портфеле, при которых минимизируется значение его
дисперсии для каждого данного уровня доходности при условии, что 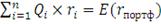
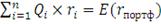 и
и 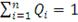
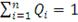 . Данный метод называется методом Марковца [58, c.6-60].
. Данный метод называется методом Марковца [58, c.6-60].
Для выбора оптимального портфеля из эффективной границы
используется функция полезности инвестора или его склонность к риску. Это
означает, что более склонный к риску инвестор будет выбирать портфель с более
высоким риском и с более высокой доходностью и наоборот. Оптимальным портфелем
будет тот, который задан точкой касания кривой безразличия инвестора и
эффективной границы.
В 90-е годы прошлого века портфельная теория обогатилась
концепцией VAR (Value-at-Risk). VaR - это показатель риска, который показывает,
какую максимальную сумму денег может потерять портфель инвестора в течение
определенного периода времени с заданной доверительной вероятностью
(показатель, говорящий о том, какое количество раз из каждых 100 раз потери в
стоимости портфеля не превысят данного уровня). Появление методики VaR (она
была представлена публике банком J. P. Morgan в 1992 г.) объясняется тем, что
во многих случаях дисперсия не может рассматриваться как подходящий показатель
измерения риска портфеля. Например, дисперсия не учитывает возможную
скошенность в распределении доходности портфеля, если оно не является
симметричным [58, c.6-60]. Однако, существует ряд недостатков VaR как меры
риска. Во-первых, VaR сложно оптимизировать для дискретных распределений (когда
его расчет производится при помощи сценариев), поскольку в данном случае он не
будет выпуклой и гладкой функцией и будет иметь множество локальных
экстремумов. Во-вторых, он не является когерентной мерой риска [42,43]. Мера
риска 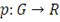
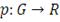 называется когерентной, если она удовлетворяет следующим
свойствам:
называется когерентной, если она удовлетворяет следующим
свойствам:
Монотонность: если 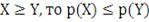
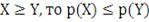
Субаддитивность: 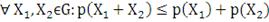
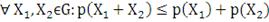
Отражает свойство диверсификации портфелей, т.е. добавление
активов в портфель не должно увеличивать его риск.
Положительная однородность: 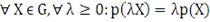
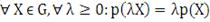
Является предельным случаем свойства субаддитивности, когда
выполняется строгое равенство. В реальности свойство 3 может не выполняться,
так как риск может зависеть от величины позиции, например, из-за ограничений
ликвидности [2, c. 206-218].
В случае, когда доходности инструментов, входящих в портфель не
являются нормально распределенными, диверсификация портфеля может увеличить
величину VaR, т.е. будет нарушаться свойство субаддитивности. Для преодоления
данного недостатка RockfellerandUryasev предложили альтернативную меру риска -
ConditionalValue-at-Risk (CVaR). CVaR как мера риска очень тесно связан с
показателем VaR поскольку показывает величину средних потерь для данного уровня
доверительной вероятности в случае, если убытки превысят значение VaR. Таким
образом, показатель средних ожидаемых потерь представляет собой условное
математическое ожидание потерь при условии, что их величина оказалась больше
значения VaR [42,43].
При вложении капитала в портфель ценных бумаг прибыль или убыток
инвестора зависят от размера капитала, вложенного в каждый финансовый
инструмент и от их будущих цен. Тогда 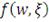
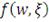 будет обозначать функцию потерь, где веса в портфеле заданы вектором
будет обозначать функцию потерь, где веса в портфеле заданы вектором
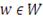
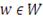 (
(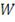
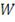 - это портфельное множество), а неопределенности, например,
рыночные цены, - вектором
- это портфельное множество), а неопределенности, например,
рыночные цены, - вектором 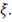
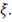 Таким образом, вышеприведенная функция является обратной по
отношению к функции прибыли и ее отрицательное значение будет означать
получение инвестором дохода. Для каждого вектора весов
Таким образом, вышеприведенная функция является обратной по
отношению к функции прибыли и ее отрицательное значение будет означать
получение инвестором дохода. Для каждого вектора весов 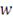
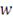 функция потерь имеет распределение задаваемое вектором
функция потерь имеет распределение задаваемое вектором 
 . Для удобства мы будем предполагать, что распределение данной
функции, в свою очередь, имеет плотность, обозначаемую в дальнейшем как
. Для удобства мы будем предполагать, что распределение данной
функции, в свою очередь, имеет плотность, обозначаемую в дальнейшем как 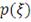
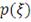 . Тогда вероятность, что потери не превысят заданной величины
. Тогда вероятность, что потери не превысят заданной величины 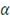
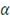 , может быть представлена следующим образом:
, может быть представлена следующим образом:
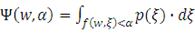
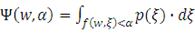 (5)
(5)
Как функция от 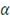
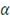 для фиксированного
для фиксированного 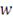
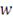 ,
, 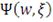
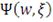 представляет кумулятивную функцию распределения потерь, связанных
с выбором
представляет кумулятивную функцию распределения потерь, связанных
с выбором 
 . Так с ростом
. Так с ростом 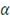
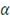 функция
функция 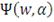
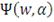 не убывает и предположим также для простоты, что она является
непрерывной.
не убывает и предположим также для простоты, что она является
непрерывной.
Значения 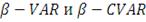
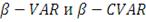 для функции потерь, связанной с вектором
для функции потерь, связанной с вектором 
 и с любым уровнем значимости
и с любым уровнем значимости 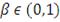
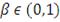 обозначим как
обозначим как 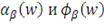
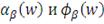 соответственно, тогда:
соответственно, тогда:
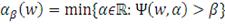
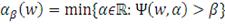 (6)
(6)
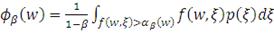
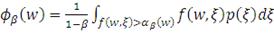 (7)
(7)
В первой формуле 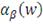
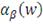 - это крайняя левая точка непустого интервала, состоящего из
значений
- это крайняя левая точка непустого интервала, состоящего из
значений 
 , для которых вероятность того, что потери не превысят заданной
величины
, для которых вероятность того, что потери не превысят заданной
величины 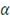
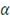 равна
равна 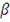
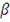 . Во второй формуле вероятность, что убытки превысят значение
. Во второй формуле вероятность, что убытки превысят значение 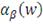
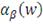 равна
равна 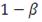
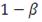 (это следует из определения вероятности). Таким образом,
(это следует из определения вероятности). Таким образом, 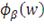
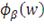 - это условное ожидание потерь больших
- это условное ожидание потерь больших 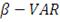
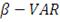 при заданном векторе весов
при заданном векторе весов 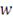
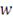 . Уровень доверительной вероятности
. Уровень доверительной вероятности 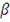
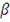 зависит от субъективного подхода управляющего портфелем к этому
вопросу (обычно он равен 95% или 99%).
зависит от субъективного подхода управляющего портфелем к этому
вопросу (обычно он равен 95% или 99%).
Ключом к оптимизации портфеля ценных бумаг на основе 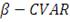
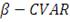 выступает представление
выступает представление 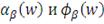
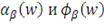 в терминах функции
в терминах функции 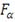
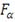 на
на 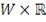
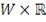 :
:
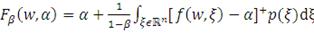
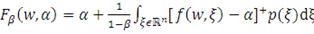 (8)
(8)
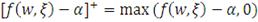
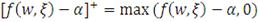 (9)
(9)
Как функция от 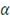
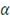 ,
, 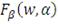
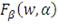 - это выпуклая и непрерывно дифференцируемая функция, а
- это выпуклая и непрерывно дифференцируемая функция, а 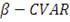
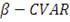 , связанный с убытками при заданном
, связанный с убытками при заданном 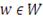
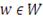 может быть определен как:
может быть определен как:
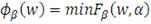
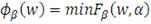 (10)
(10)
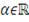
В этой формуле набор значений 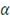
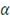 , при которых функция достигает своего минимума, обозначим как:
, при которых функция достигает своего минимума, обозначим как:
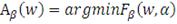
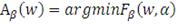 при
при 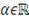
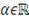 . (11)
. (11)
Данный набор является непустым, закрытым и ограниченным интервалом
(может содержать всего лишь одну точку). Тогда 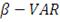
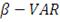 может быть представлен в виде:
может быть представлен в виде:
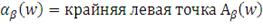
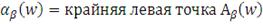 (12)
(12)
Кроме того, всегда выполняется следующее тождество:
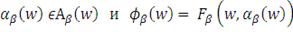
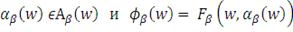 (13)
(13)
Таким образом, значение 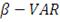
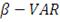 всегда принадлежит решению уравнения (11), а
всегда принадлежит решению уравнения (11), а 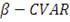
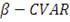 равен значению функции
равен значению функции 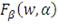
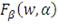 , если
, если 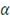
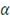 заменить на
заменить на 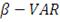
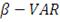 .
.
Минимизация значения 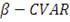
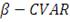 функции потерь по
функции потерь по 
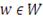 эквивалентна минимизации функции
эквивалентна минимизации функции 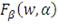
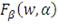 по всем
по всем 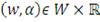
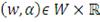 :
:
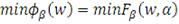
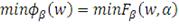 (14)
(14)
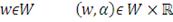
Рассматриваемая функция в точке 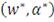
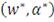 достигает своего второго минимума тогда и только тогда, когда
достигает своего второго минимума тогда и только тогда, когда 
 достигает своего первого минимума и
достигает своего первого минимума и 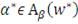
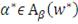 . В частности, когда
. В частности, когда 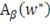
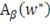 - это одноточечное множество (на практике как правило так и
бывает), то минимизация функции
- это одноточечное множество (на практике как правило так и
бывает), то минимизация функции 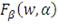
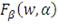 по
по 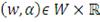
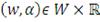 приводит к получению (не обязательно одной) пары
приводит к получению (не обязательно одной) пары 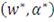
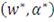 , где набор
, где набор 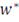
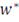 минимизирует
минимизирует 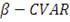
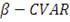 , а
, а 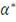
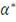 - это значение соответствующего
- это значение соответствующего 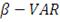
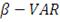 [42].
[42].
Таким образом, оставшаяся задача для вычисления оптимального
портфеля ценных бумаг, используя подход, основанный на показателе CVaR - оценка
вероятностного распределения функции потерь. Так можно оценить 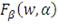
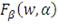 при помощи набора
при помощи набора 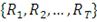
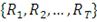 реализации случайной величины ξ, где
реализации случайной величины ξ, где 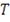
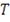 - это размер выборки. Rockafellar and Uryasev для аппроксимации
- это размер выборки. Rockafellar and Uryasev для аппроксимации 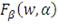
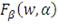 в уравнении (8) предложили следующую формулу [20, c.216-218]:
в уравнении (8) предложили следующую формулу [20, c.216-218]:
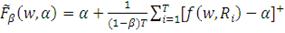
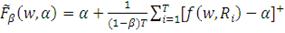 (15)
(15)
Используя рассмотренные выше меры риска, можно построить
"новое" портфельное множество и найти его эффективную границу,
использую в качестве меры риска не дисперсию как у Марковица, а величину CVaR.
Тогда график будет выглядеть следующим образом:
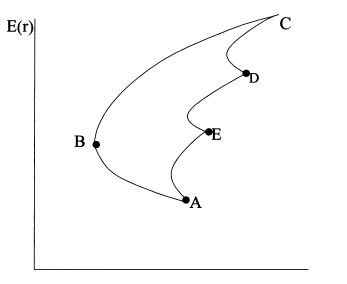
Рисунок 2: Достижимое множество CVaR
Рациональный инвестор будет стремиться минимизировать риск и
увеличить доходность, поэтому всем возможным портфелям, представленным на
рис.2, вкладчик предпочтет только те, которые расположены на отрезке ВС,
поскольку они являются доминирующими. Чтобы определить эффективную границу,
необходимо рассчитать удельные веса активов в портфеле, при которых
минимизируется значение его CVaR для каждого данного уровня доходности.
Как было отмечено выше, каждый инвестор стремиться получить как
можно большую доходность при заданном уровне риска и как можно меньший риск при
заданном уровне доходности (в классической портфельной теории это предпосылки,
называемые "ненасыщаемость" и "избегание риска"). Таким
образом, рассчитав риск и доходность для двух портфелей ПИФ мы однозначно
сможем сделать вывод, что один из них более эффективен чем другой, если
доходность у первого по сравнению со вторым будет выше а риск меньше. На
практике такие ситуации случаются очень редко, и, зачастую, риск и доходность у
одного портфеля высокие, а у другого низкие, что делает невозможным их
сравнение на основе только этих двух показателей. Для разрешения такой ситуации
было разработано несколько коэффициентов, позволяющих в определенной степени
соотнести риск и доходность. Давайте рассмотрим основные из них более подробно.
Коэффициент Шарпа (коэффициент "доходность-разброс" или RVAR)
Данный коэффициент был придуман нобелевским лауреатом У. Шарпом и
опубликован в его статье в 1966г. Он учитывает избыточную доходность (т.е.
доходность, полученную сверх безрисковой ставки) и весь риск портфеля (как
рыночный, так и нерыночный или несистематический), выражаемый дисперсией.
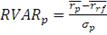
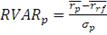 (16)
(16)
Где 
 -средняя доходность портфеля за период,
-средняя доходность портфеля за период, 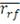
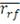 - средняя безрисковая ставка за период,
- средняя безрисковая ставка за период, 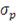
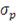 - СКО портфеля.
- СКО портфеля.
Графически коэффициент Шарпа может быть представлен следующим
образом:
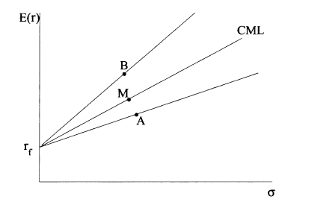
Рисунок 3: Графическая иллюстрация коэффициента Шарпа
На этом графике портфель B - более эффективен, чем рыночный
портфеля М, лежащий на СМL, а портфель А - менее эффективен. [58, c.355-391; 67
c.886-902]
С течением времени Шарп немного изменил свой взгляд на расчет
избыточной доходности: он предложил использовать не безрисковую доходность в
числителе его формулы, а доходность бенчмарка. Таким образом, его формула
принимает следующий вид:
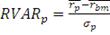
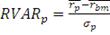 , где (17)
, где (17)
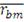
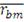 - средняя доходность бенчмарка.
- средняя доходность бенчмарка.
Выбор бенчмарка зависит от анализируемых активов, целей анализа и
суждения аналитика (на практике обычно в качестве такого выбирается какой-либо
индекс с широкой базой).
Недостатками коэффициента Шарпа являются предположение о
нормальном распределении доходности портфеля, поскольку на самом деле это не
всегда так (может наблюдаться некоторая скошенность распределения), высокая
чувствительность к параметрам и учет нерационального риска.
Коэффициент Модильяни
Коэффициент Модильяни был предложен американским экономистом Ф.
Модильяни в статье "Risk-adjustedperformance: howtomeasure it and
why", опубликованной в издании Journal of Portfolio Management в 1997г.
Данный коэффициент рассчитывается следующим образом:
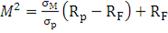
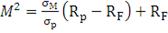 (18)
(18)
Коэффициент Модильяни, как и коэффициент Шарпа, основывается на
суммарном (общем) риске финансового актива. Однако его отличием является то,
что он оценивает, какая доходность была бы получена, если бы суммарный риск
актива был равен рыночному риску. Кроме того, коэффициент Модильяни дает не
безразмерную величину, а представляет собой доходность в процентах, тем самым
являясь более понятным показателем для инвестора [33]
Коэффициент Трейнора (коэффициент "доходность-изменчивость" или RVOL)
Годом раньше Шарпа была опубликована Статья Трейнора, в которой он
предлагал в качестве меры риска брать бету β акции, характеризующей степень влияния
рынка на доходность фонда. Таким образом, данный коэффициент учитывает
избыточную доходность (т.е. доходность полученную сверх безрисковой ставки) и
рыночный риск портфеля.
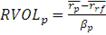
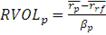 (19)
(19)
Графически коэффициент Трейнора может быть изображен:
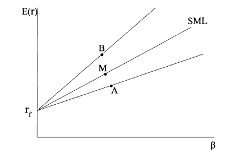
Рисунок 4: Графическая иллюстрация коэффициента Трейнора
По сравнению с рыночным портфелем портфель "В"
управляется более эффективно, а портфель "А" - менее.
Стоит отметить, что коэффициенты Шарпа и Трейнора могут давать
различную оценку эффективности портфеля в случае наличия у него большого
собственного (несистематического риска).
Альфа Йенсена
В статье "ThePerformanceofMutualFundsinthePeriod",
опубликованной в издании JournalofFinance в 1968г., Йенсен предложил использовать
коэффициент Альфа (известный как Альфа Йенсена), который представляет собой
превышение доходности портфеля над его ожидаемой доходностью:
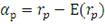
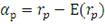 (20)
(20)
Величина ожидаемой доходности может быть найдена из модели CAPM,
откуда она равна:
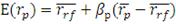
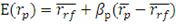 (21)
(21)
Следовательно, коэффициент Йенсена можно представить как:
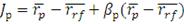
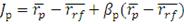 (22)
(22)
Если обе части выражения поделить на 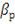
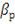 то мы получим модифицированный коэффициент Трейнора (его так
называли К. Смит и Д. Тито) [57; 58, c.355-391; 67 c.886-902].
то мы получим модифицированный коэффициент Трейнора (его так
называли К. Смит и Д. Тито) [57; 58, c.355-391; 67 c.886-902].
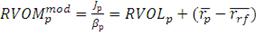
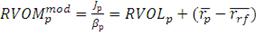 (23)
(23)
Коэффициент Сортино. В качестве меры риска там используется корень из так называемой
полудисперсии, т.е. дисперсии посчитанной только для отрицательных отклонений
от средней доходности и вычисляемой следующим образом:
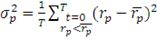
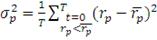 (24)
(24)
Отсюда коэффициент Сортино может быть представлен:
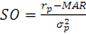
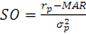 (25)
(25)
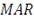
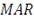 (minimum acceptable return) - минимальный уровень доходности на
который согласен инвестор.
(minimum acceptable return) - минимальный уровень доходности на
который согласен инвестор.
Коэффициент Омега
Данный коэффициент был предложен в 2002 г. C. Keating и W. F.
Shadwick. Функция Омега является более комплексным индикатором по сравнению со
всеми вышеперечисленными коэффициентами и дает полную характеристику
распределения результатов портфеля с точки зрения его риска и доходности. Она
учитывает не только первые два момента функции распределения, но еще и более
высокие моменты. Формула для расчета следующая:
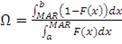
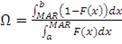 (26)
(26)
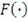
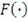 - кумулятивная функция распределения, интервал
- кумулятивная функция распределения, интервал 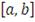
 - значения доходностей,
- значения доходностей, 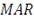
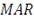 - минимальный уровень доходности на который согласен инвестор
[27].
- минимальный уровень доходности на который согласен инвестор
[27].
1.2 Паевые
инвестиционные фонды на российском рынке
В России появление коллективного института инвестиций связано
с началом процесса приватизации государственного имущества в 90-х годах
прошлого столетия. Насчитывалось порядка 500 инвестиционных фондов, большинство
из которых были чековыми (их акции обменивались на приватизационные чеки).
Однако из-за неразвитости, как всей экономической системы страны, так и
финансового рынка в частности, такие фонды не имели успеха. [59, c.25-27]
Современный период функционирования данных финансовых институтов связан с
появлением 29 ноября 2001 года Федерального закона №156-ФЗ "Об
Инвестиционных фондах", что создало правовые основы их функционирования.
Под Паевым инвестиционным фондом принято понимать
обособленный имущественный комплекс без образования юридического лица,
привлекающий финансовые ресурсы инвесторов и вкладывающий их в различные активы
на финансовом рынке. В зависимости от таких активов, выделяют следующие виды
ПИФ: фонды акций, облигаций, фондов, товарного рынка, недвижимости, денежного
рынка, прямых инвестиций, художественных ценностей, долгосрочных прямых
инвестиций, а также кредитные, смешанные, индексные, ипотечные, венчурные,
рентные фонды и хедж-фонды.
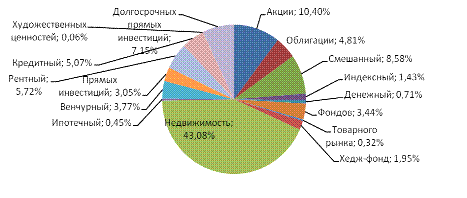
Рисунок 5: Структура рынка ПИФ России по состоянию на март
2016 г.
Также паевые инвестиционные фонды могут быть открытыми
(эмитируют паи с обязательством их последующего выкупа по требованию держателя
таких ценных бумаг), закрытыми (эмитируют паи без обязательства их последующего
выкупа, т.е. инвестор может получить обратно вложенные деньги, только продав
ценные бумаги на вторичном рынке) и интервальными (эмитируют паи с
обязательством их последующего выкупа по требованию держателя таких ценных
бумаг в заданные интервалы времени) [66].
В настоящее время в России преобладают закрытые паевые фонды
(1136 шт., что составляет около 74% от общего количества данных финансовых
институтов). На втором месте по распространенности идут открытые паевые фонды
(их 354 шт. или 23% от общего числа), количество же интервальных составляет 49
шт., а доля рынка - 3%. Кроме того некоторые ПИФ предназначены только для
квалифицированных инвесторов (их список закреплен законодательно), что означает
недоступность вложения средств в их ценные бумаги рядовыми инвесторами [66].
Доступность (минимальный размер инвестиций обычно составляет
1000 рублей) и высокие результаты деятельности (за счет экономии на
транзакционных издержках и налогах) привели к тому, что за последнее
десятилетие паевые фонды неуклонно набирали популярность, как в России, так и
во всем мире, о чем свидетельствует как рост их числа, так и величины стоимости
их чистых активов.
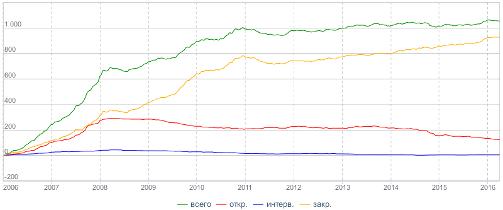
Рисунок 6: Динамика числа ПИФ в России
Рисунок 7: Динамика СЧА ПИФ в России
Доходность для инвестора при вложении денежных средств в ПИФ
представляет собой прирост стоимости инвестиционного пая (все получаемые
периодические платежи по ценным бумагам, входящим в портфель выбранного фонда,
например, дивиденды по акциям, купоны по облигациям не выплачиваются владельцем
паев). Поэтому формула расчета следующая:
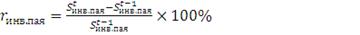
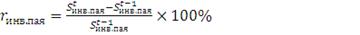 (27)
(27)
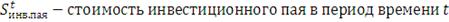
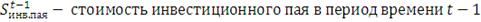
Стоимость одного инвестиционного пая рассчитывается как отношение
стоимости чистых активов фонда, эмитировавшего данный пай к количеству
выпущенных им паев.
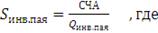
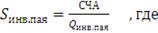 (28)
(28)
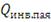
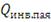 - количество выпущенных паев,
- количество выпущенных паев, 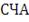
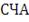 - стоимость чистых активов фонда
- стоимость чистых активов фонда
Стоимость чистых активов (СЧА) - это денежная оценка рыночной цены
активов инвестиционного фонда за минусом его обязательств (вознаграждение
управляющей компании, депозитарию, по маржинальным операциям, если он имеет
право на их осуществление и д. р.) [66].
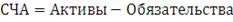
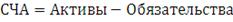 (29)
(29)
Несмотря на то, что любой ПИФ диверсифицирует свои активы,
вкладывая капитал в различные финансовые инструменты, у инвестора сохраняется
определенная группа рисков, связанная с качеством управления данным фондом.
Данное обстоятельство приводит к необходимости распределения финансовых
ресурсов между несколькими ПИФами и, таким образом, возникает задача грамотного
формирования и управления портфелем, состоящего из множества паев. Для данных
целей наиболее привлекательным объектом инвестиций выступают открытые ПИФ что
связано с их относительно высокой ликвидностью, что является очень важным
фактором.
1.3
Теоретические основы Копула-функций
Копула-функция является функцией, агрегирующей всю информацию
относительно структуры зависимости между компонентами случайного вектора. Когда
в качестве компонент копула-функции берутся частные функции распределения,
которые необязательно принадлежат одному и тому же семейству распределений, получаем
многомерную функцию распределения. Как следствие, эта теория позволяет
достаточно гибко моделировать структуру зависимости между различными
переменными, которые могут иметь разные частные распределения. С помощью
копула-функций описываются законы многомерного распределения вероятностей. Они
определяются частными одномерными распределениями анализируемого многомерного
закона и характером зависимостей, существующих между компонентами
рассматриваемой многомерной случайной величины [36 c.7-48; 51, c.99-137].
Функция 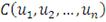
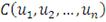 от
от 
 переменных, определенная на единичном гиперкубе
переменных, определенная на единичном гиперкубе 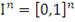
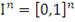 , (т.е.
, (т.е. 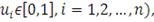
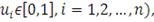 называется копула-функцией, если она обладает следующими
свойствами:
называется копула-функцией, если она обладает следующими
свойствами:
Область значения функции - единичный интервал 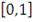
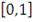
Если 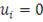
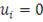 по крайней мере для одного
по крайней мере для одного 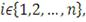
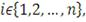 то
то 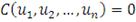
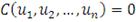
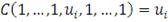
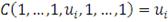 для любых
для любых 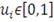
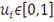
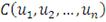
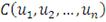 является n-возрастающей функцией в том смысле, что для всех
является n-возрастающей функцией в том смысле, что для всех 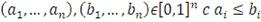
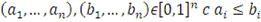 справедливо равенство:
справедливо равенство:
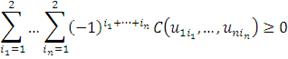
Где 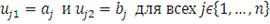
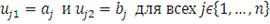
Теперь сформулируем теорему Склара, которая показывает роль
копула-функций в описании многомерных распределений вероятностей. Пусть 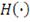
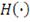 - n-мерная функция распределения с частными распределениями
- n-мерная функция распределения с частными распределениями 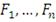
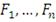 . Тогда существует n-мерная копула-функция
. Тогда существует n-мерная копула-функция 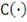
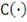 такая, что для всех действительных
такая, что для всех действительных 
 :
:
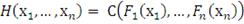
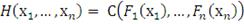 (30)
(30)
Если все частные функции распределения непрерывны, то копула
функция определена единственным образом; в противном случае 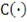
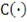 определена единственным образом только лишь на области
определения
определена единственным образом только лишь на области
определения
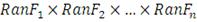
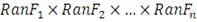 ,
,
где
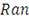
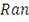 - область значений частных функций распределения.
- область значений частных функций распределения.
Если 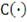
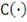 - копула-функция, а
- копула-функция, а 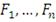
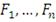 - функции распределения, то функция
- функции распределения, то функция 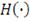
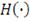 , определяемая выражением (30), является совместной функцией
распределения с частными распределениями
, определяемая выражением (30), является совместной функцией
распределения с частными распределениями 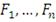
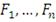 . Последнее утверждение теоремы представляет большой интерес в
задаче моделирования многомерных функций распределения, поскольку из него
следует, что можно связывать вместе любые
. Последнее утверждение теоремы представляет большой интерес в
задаче моделирования многомерных функций распределения, поскольку из него
следует, что можно связывать вместе любые 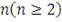
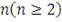 одномерных функций распределения разного типа (не обязательно из
одного семейства), используя любую копула-функцию, для того чтобы получить
двумерные или многомерные функции распределения.
одномерных функций распределения разного типа (не обязательно из
одного семейства), используя любую копула-функцию, для того чтобы получить
двумерные или многомерные функции распределения.
Пусть 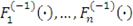
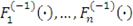 - обратные (в обобщенном смысле) функции частных распределений.
Тогда для каждого
- обратные (в обобщенном смысле) функции частных распределений.
Тогда для каждого 
 из единичного n-мерного куба существует единственная
копула-функция
из единичного n-мерного куба существует единственная
копула-функция 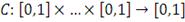
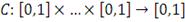 такая, что:
такая, что:
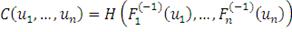
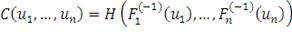 (31)
(31)
Таким образом, копула-функция - это такая функция, которая, с
использованием знания об одномерных частных распределениях, позволяет получить
многомерную функцию распределения, поскольку функция распределения случайного
вектора полностью описывает его вероятностную структуру, куда, в частности,
входит структура зависимости его компонент. Копула-функции дают возможность
разделить описание распределения случайного вектора на две части: частные
распределения компонент и структура их зависимостей.
Для копула-функций, аналогично функциям распределения, можно
определить понятие плотности. В частности, плотность 
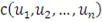 , ассоциированная с копула-функцией
, ассоциированная с копула-функцией 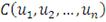
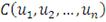 , определяется соотношением:
, определяется соотношением:
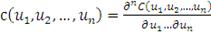
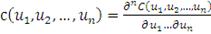 (32)
(32)
Более того, применяя следствие теоремы Склара и рассматривая
непрерывные случайные величины, можно видеть, что плотность копула-функции c
 ассоциирована с плотностью совместной функции распределения
ассоциирована с плотностью совместной функции распределения 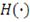
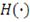 , обозначенной как
, обозначенной как 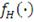
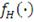 , следующим образом (каноническое представление) [64, c.100-115]:
, следующим образом (каноническое представление) [64, c.100-115]:
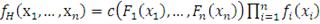
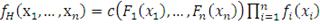 (33)
(33)
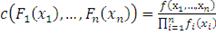
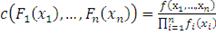 (34)
(34)
Существует несколько альтернативных методов для решения задачи
моделирования совместного распределения с учетом теоремы Шкляра. Фактически
множество комбинаций определяется возможностью параметрической и
непараметрической оценки копулы и частных распределений. Все варианты можно
обобщить в три метода: параметрический, полупараметрический и
непараметрический.
Параметрический метод
Данный класс методов предполагает параметризацию как частных
распределений, так и копулы. Если базовый подход MLE (Maximum Likelihood
Estimation) максимизирует функцию правдоподобия одновременно по частным
распределениям и по копуле, то метод "от частных распределений"
(Inference for Margin - IFM) разбивает оценку на два этапа: вначале -
параметризацию частных распределений, затем - копулы.
Полупараметрический метод
Полупараметрический метод также предполагают двухэтапную оценку
копулы. Но на первом этапе вместо параметрической оценки частных распределений
берутся эмпирические распределения, а на втором - происходит параметрическая
оценка копулы.
Непараметрический метод
Среди непараметрических методов оценки копул можно выделить два
подхода: на основе оценки эмпирической копулы и ядерных оценок. Первый подход
предполагает оценку функции распределения эмпирической копулы, которая отражает
число случаев, когда исходы случайных величин одновременно попали в выбранную
ячейку сетки разбиения всего множества вероятностного пространства [62].
Для оценки многомерного распределения необходимо выбрать вид
копула-функции, который наилучшим образом описывает зависимость между исходными
данными. Существует несколько семейств копула-функций, каждое из которых
содержит в себе различные виды.
Эллиптические копула-функции
Класс эллиптических распределений включает, главным образом, класс
симметричных распределений, которые являются довольно популярными в современных
финансах. Они позволяют моделировать многомерные экстремальные события,
формируя зависимость, не совпадающую с зависимостью многомерного нормального
распределения, и использовать распределение с большим эксцессом, чем эксцесс нормального
распределения. Таким образом, эллиптические копула-функции - это попросту
копула-функции многомерных распределений эллиптического типа. Эллиптические
распределения определяются следующим образом:
Пусть 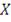
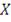 -
- 
 -мерный случайный вектор и
-мерный случайный вектор и 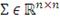
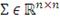 - симметричная и неотрицательно определенная матрица. Если
существует
- симметричная и неотрицательно определенная матрица. Если
существует 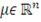
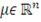 и функция
и функция 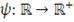
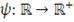 такие, что характеристическая функция
такие, что характеристическая функция 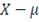
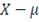 имеет вид:
имеет вид:
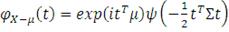
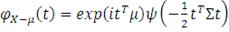 (35)
(35)
Для любого 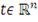
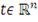 , то
, то 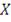
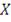 называют случайным вектором, имеющим распределение эллиптического
типа с параметрами
называют случайным вектором, имеющим распределение эллиптического
типа с параметрами 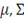
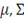 . Копула-функция
. Копула-функция 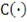
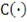 называется эллиптической, если она отвечает распределению
эллиптического типа. Функция плотности распределения эллиптического типа в
случае ее существования имеет вид:
называется эллиптической, если она отвечает распределению
эллиптического типа. Функция плотности распределения эллиптического типа в
случае ее существования имеет вид:
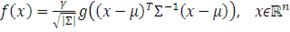
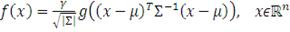 (36)
(36)
Для некоторой функции 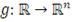
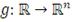 , которая удовлетворяет условию:
, которая удовлетворяет условию: 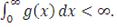
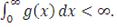 Функцию
Функцию 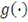
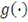 называют оператором плотности распределения эллиптического типа
или генерирующей функцией. Нормирующая константа
называют оператором плотности распределения эллиптического типа
или генерирующей функцией. Нормирующая константа 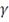
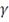 может быть определена явным образом с использованием перехода к
полярным координатам. В результате получим:
может быть определена явным образом с использованием перехода к
полярным координатам. В результате получим:
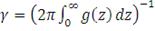
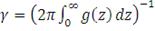 (37)
(37)
Таблица 1: Копула-функции эллиптического типа
|
Распределение
|
Генератор
|
Константа
|
|
Нормальное
|
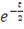
|
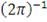
|
|
Коши
|
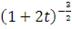
|
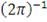
|
|
Стьюдента
|
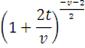
|
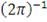
|
|
Логистическое
|
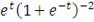
|
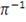
|
|
Лапласа
|
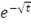
|
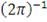
|
|
Котца
|
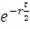
|
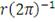
|
|
Экспоненциальное
|
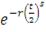
|
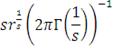
|
Наиболее часто встречающими из вышеперечисленных
копула-функций являются нормальная копула и копула Стьюдента, которые также
были использованы и в настоящей работе. Их популярность при анализе финансовых
данных обусловлена тем, что они позволяют моделировать портфели высокой
размерности, являясь при этом относительно легко оцениваемыми. Кроме того,
данные функции позволяют генерировать наблюдения при помощи относительно
простых алгоритмов.
Нормальная копула функция определяется следующим образом:
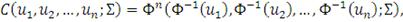
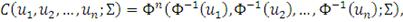 (38)
(38)
где 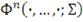
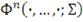 - это
- это 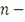
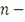 мерная нормальная функция распределения с нулевыми средними
значениями и ковариационной матрицей
мерная нормальная функция распределения с нулевыми средними
значениями и ковариационной матрицей 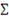
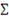 .
. 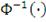
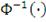 - обратная функция для одномерного стандартного нормального
распределения.
- обратная функция для одномерного стандартного нормального
распределения.
Плотность нормальной копула-функции может быть получена из
уравнения (32) с использованием канонического представления:
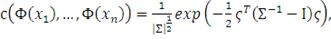
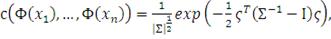 (39)
(39)
где 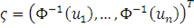
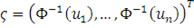 - вектор, компонентами которого являются значения обратной
функции для стандартного одномерного гауссовского распределения в точках
- вектор, компонентами которого являются значения обратной
функции для стандартного одномерного гауссовского распределения в точках 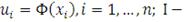
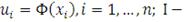 единичная матрицакопула-функция (копула Стьюдента)
единичная матрицакопула-функция (копула Стьюдента)
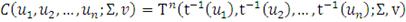
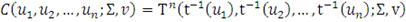 (40)
(40)
где 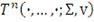
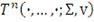 - это
- это 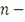
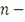 мерная функция распределения Стьюдента с ковариационной матрицей
мерная функция распределения Стьюдента с ковариационной матрицей 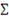
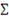 и
и 
 степенями свободы.
степенями свободы. 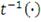
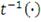 - обратная функция для одномерного распределения Стьюдента. При
- обратная функция для одномерного распределения Стьюдента. При 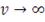
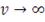 копула функция Стьюдента сходится к нормальной копула-функции.
копула функция Стьюдента сходится к нормальной копула-функции.
Плотность T копула-функции может быть получена из уравнения (32) и
канонического представления:
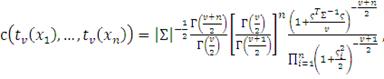
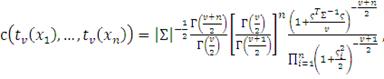 (41)
(41)
где 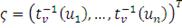
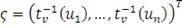 - вектор, компонентами которого являются значения обратной
функции для распределения Стьюдента в точках
- вектор, компонентами которого являются значения обратной
функции для распределения Стьюдента в точках 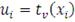
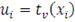 .
.
Архимедовы копулы
Архимедовы копула-функции обеспечивают аналитическую гибкость и
широкий спектр различных мер зависимости. По следующим причинам эти
копула-функции могут быть использованы в широком диапазоне приложений:
Архимедовы копула-функции могут быть представлены в явном
аналитическом виде, в отличие от семейства эллиптических копула-функций,
которые определяются в неявной форме.
Архимедовы копула-функции допускают относительно простое
построение, включая вычислительную реализацию.
Многие параметрические семейства копула-функций принадлежат этому
классу.
Рассмотрим непрерывную, строго убывающую и выпуклую функцию 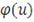
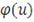 с неотрицательными значениями, определенную при
с неотрицательными значениями, определенную при 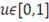
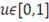 и удовлетворяющую условию
и удовлетворяющую условию 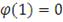
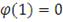 . Определим псевдообратную функцию
. Определим псевдообратную функцию 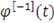
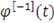 соотношением:
соотношением:
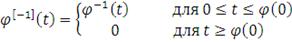
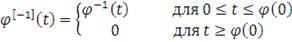 (42)
(42)
где 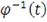
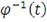 - обычная обратная функция к функции
- обычная обратная функция к функции 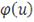
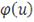 .
.
Тогда функцию 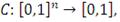
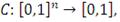 определенную как
определенную как
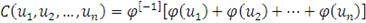
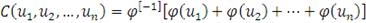 , (43)
, (43)
Называют архимедовой копула-функцией с генератором 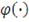
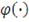 и соответствующими диапазонами параметра
и соответствующими диапазонами параметра 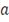
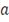 .
.
Таблица 2: Архимедовы Копула-функции
|
Название
|
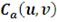
|
Генератор 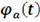 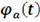 Диапазон параметра Диапазон параметра  
|
|
|
Клейтона
|
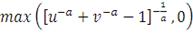
|
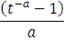
|
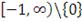
|
|
Гумбеля
|
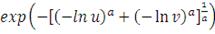
|
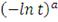
|
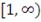
|
|
Франка
|
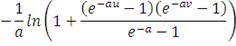
|
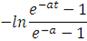
|
|
Плотность архимедовых копула функций может быть вычислена по
формуле:
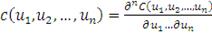
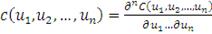 (44)
(44)
или если генератор 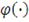
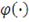 дважды непрерывно дифференцируем,
дважды непрерывно дифференцируем,
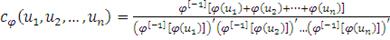
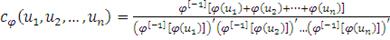 (45)
(45)
Это означает, что, зная генератор 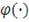
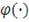 и его обратную функцию
и его обратную функцию 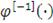
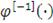 , ее первую и вторую производные, можно получить архимедову
копула-функцию и ее плотность [36 c.7-48; 52, c.99-137; 64, c.100-120].
, ее первую и вторую производные, можно получить архимедову
копула-функцию и ее плотность [36 c.7-48; 52, c.99-137; 64, c.100-120].
Таким образом, мы рассмотрели наиболее часто встречающиеся
копула-функции и теоретические основы для моделирования многомерных
распределений с помощью данного инструмента, который будет использован в
следующей главе.
Глава 2.
Использование копула-функций для оптимизации портфеля ценных бумаг на основе
CVaR по российским ПИФ
2.1 Анализ
данных по выбранным паевым инвестиционным фондам
В данной работе объектом исследования выступают открытые
Паевые инвестиционные фонды на российском рынке. Для проведения исследования
были выбраны десять ПИФов с наибольшей стоимостью чистых активов (СЧА) по
состоянию на 29.02.2016г. В число таких фондов вошли два фонда акций, два
смешанных фонда, один фонд фондов и пять фондов облигаций. В выборку не попали
ПИФ, которые не торговались все 3 года либо имеющие плохую ликвидность:
"Резервный. Валютные инвестиции" - СЧА равно 4 397 699 202,03;
"Сбербанк - Биотехнологии" - СЧА равно 3 576 398 683,71 и
"Резервный" - СЧА равно 3 195 211 569,2.
Таблица 3: Исследуемые ПИФ
|
№ п. п.
|
ПИФ
|
Категория
|
Управляющая компания
|
СЧА (руб.)
|
|
1
|
Райффайзен - Облигации
|
Облигации
|
Райффайзен Капитал
|
6 297 163 156, 20
|
|
2
|
Газпромбанк - Облигации плюс
|
Облигации
|
Газпромбанк - Управление активами
|
4 658 050 337,88
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
Облигации
|
Сбербанк Управление Активами
|
4 486 700 056,66
|
|
4
|
Империя
|
Смешанный
|
БК-Сбережения
|
4 386 257 029,07
|
|
5
|
Райффайзен - США
|
Фондов
|
Райффайзен Капитал
|
3 403 343 019,23
|
|
6
|
Сбербанк - Еврооблигации
|
Облигации
|
Сбербанк Управление Активами
|
3 395 640 086,87
|
|
7
|
Альфа-Капитал Стратегические инвестиции
|
Смешанный
|
Альфа-Капитал
|
3 177 348 590,10
|
|
8
|
Альфа-Капитал Резерв
|
Облигации
|
Альфа-Капитал
|
2 867 605 912,62
|
|
9
|
Сбербанк - Потребительский сектор
|
Акции
|
Сбербанк Управление Активами
|
2 770 617 117,16
|
|
10
|
УРАЛСИБ Первый
|
Акции
|
УРАЛСИБ
|
2 726 979 319,00
|
Были получены стоимости паев по каждому ПИФ за период 3 года
(с 01.03.2013 по 01.03.2016 г.) - всего 753 значения. На их основе была
рассчитана доходность по торговым дням по формуле (10) - всего 752 значения.
Если у фонда были дни, когда стоимость пая отсутствовала, то пропущенные
значения заменялись на средне-арифметические между двумя соседними датами. Вся
данная выборка была поделена на обучающую (572 значения доходности) и контрольную
(180 значений доходности) для оптимизации портфеля ценных бумаг и проверки
результатов оптимизации.
Анализ исследуемых ценных бумаг включает в себя проведение
двух последовательных этапов: тестирование данных на подчинение нормальному
закону распределения с помощью теста Колмогорова-Смирнова и получение
представления о "толщине хвостов" эмпирических распределений ценных
бумаг на основе построения ядерных оценок функций плотности.
Тестирование данных на "нормальность"
Проведение тестов на "нормальность" означает
проверку статистической значимости того, что истинное распределение
рассматриваемых данных можно описать при помощи нормального закона:
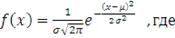
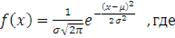 (46)
(46)
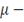
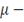 математическое ожидание (мода, медиана)
математическое ожидание (мода, медиана) 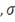
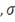 - среднеквадратическое отклонение (СКО).
- среднеквадратическое отклонение (СКО).
Для данных целей используют, как правило, либо критерий
Колмогорова-Смирнова, либо критерий Шапиро-Вилка. В настоящей работе из-за
относительной простоты был использован критерий Колмогорова-Смирнова с уровнем
значимости 95%.
Пусть 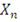
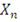 - выборка независимых, одинаково распределенных величин,
- выборка независимых, одинаково распределенных величин, 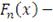
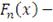 эмпирическая функция распределения,
эмпирическая функция распределения, 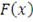
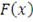 - истинная функция распределения. Тогда статистика Колмогорова
может быть найдена как:
- истинная функция распределения. Тогда статистика Колмогорова
может быть найдена как:
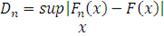
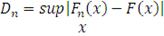 (47)
(47)
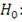 выборка подчиняется распределению
выборка подчиняется распределению 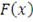
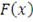
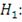
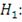 выборка не подчиняется распределению
выборка не подчиняется распределению 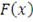
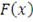
Если статистика 
 , то
, то 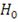
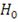 отвергается и принимается
отвергается и принимается 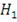
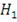 . Иначе гипотеза
. Иначе гипотеза 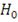
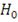 принимается на уровне значимости
принимается на уровне значимости 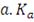
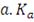 - процентная точка распределения Колмогорова [35, c.295-314]. По
результатам проведенного теста были получены следующие значения статистик и
соответствующих им значений p-value:
- процентная точка распределения Колмогорова [35, c.295-314]. По
результатам проведенного теста были получены следующие значения статистик и
соответствующих им значений p-value:
Таблица 4: Результаты тестов на Нормальность данных
|
№ п. п.
|
ПИФ
|
Значение статистики 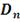 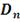 p-valueВывод p-valueВывод
|
|
|
|
1
|
Альфа-Капитал Резерв
|
0.241
|
0
|
Распределение не "нормальное"
|
|
2
|
УРАЛСИБ Первый
|
0.065
|
0.0037
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
0.211
|
0
|
Распределение не "нормальное"
|
|
4
|
Райффайзен - Облигации
|
0.199
|
0
|
Распределение не "нормальное"
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
0.114
|
0
|
Распределение не "нормальное"
|
|
6
|
Сбербанк - Потребительский сектор
|
0.078
|
0.0002
|
Распределение не "нормальное"
|
|
7
|
Райффайзен - США
|
0.106
|
0
|
Распределение не "нормальное"
|
|
8
|
Империя
|
0.183
|
0
|
Распределение не "нормальное"
|
|
9
|
Сбербанк - Еврооблигации
|
0.155
|
0
|
Распределение не "нормальное"
|
|
10
|
Газпромбанк - Облигации плюс
|
0.232
|
0
|
Распределение не "нормальное"
|
Таким образом, мы можем увидеть, что ни одна бумага с
доверительной вероятностью 95% не может считаться распределенной по нормальному
закону. Из этого следует, что применение классической теории Марковица с
предположением о нормальности распределения доходностей ценных бумаг может дать
плохие результаты и привести к выбору далеко не оптимального портфеля ценных
бумаг.
Проверка "толщины хвостов"
Непараметрическая оценка функции плотности распределения 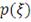
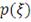 для одномерного случайного вектора
для одномерного случайного вектора 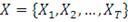
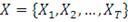 или по-другому оценка Розенблатта-Парзена может быть представлена
в виде:
или по-другому оценка Розенблатта-Парзена может быть представлена
в виде:
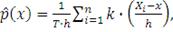
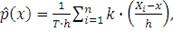 (48)
(48)
где 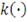
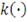 - ядро (симметричная взвешивающая функция), а
- ядро (симметричная взвешивающая функция), а 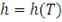
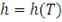 - ширина окна (параметр сглаживания, зависящий от Т). Таким
образом, представленная оценка очень схожа с гистограммой (в ней индикаторная
функция заменена на ядро), однако она, в свою очередь, позволяет устранить два
существенных недостатка, присущих последней: разрывность и как следствие
недифференцируемость и отсутствие центрирования вокруг точки, в которой
требуется оценить плотность.
- ширина окна (параметр сглаживания, зависящий от Т). Таким
образом, представленная оценка очень схожа с гистограммой (в ней индикаторная
функция заменена на ядро), однако она, в свою очередь, позволяет устранить два
существенных недостатка, присущих последней: разрывность и как следствие
недифференцируемость и отсутствие центрирования вокруг точки, в которой
требуется оценить плотность.
Для целей настоящей работы ядерная функция 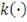
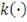 и ширина окна
и ширина окна 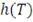
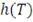 должны удовлетворять следующим ограничениям:
должны удовлетворять следующим ограничениям:
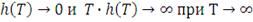
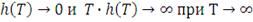 (условие состоятельности, т.е. с ростом выборки смещение
исчезает)
(условие состоятельности, т.е. с ростом выборки смещение
исчезает)
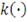
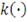 - положительно
определена
- положительно
определена
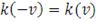
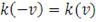 (симметричность)
(симметричность)
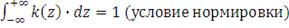
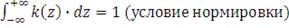
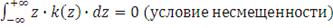
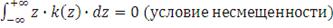
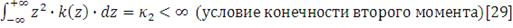
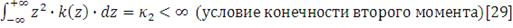
Как для теоретических, так и для практических целей ядерная оценка
не чувствительна к выбору ядерной функции. Главная задача ядра, как было
упомянуто выше - обеспечить гладкость и дифференцируемость результирующей
оценки при минимальной ошибке. Существует целый ряд ядерных функций с
одинаковой относительной эффективностью, так что можно выбирать ядро на основе
вычислительной сложности. В качестве ядерных функций обычно используются симметричные
одномодальные функции плотности:
Таблица 5: Ядерные функции
|
Ядро
|
Формула
|
|
Гауссовское ядро
|
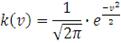
|
|
Ядро Епанечникова
|
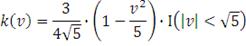
|
|
Треугольное ядро
|
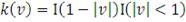
|
|
Прямоугольное (равномерное) ядро
|
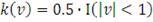
|
Вид этих функций представлен на следующем рисунке:
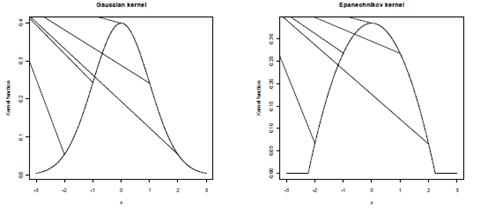
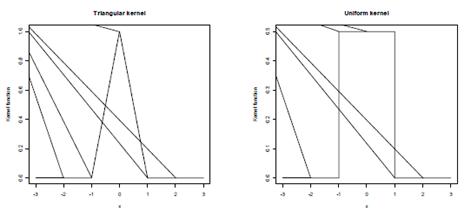
Рисунок 8: Ядерные функции
В отличие от выбора ядерной функции, выбор подходящей ширины окна 
 является ключевым аспектом корректного непараметрического
анализа, поскольку именно ширина окна определяет поведение оценки в конечных
выборках. Выбирать величину h следует так, чтобы оценка была как можно ближе к
истинной плотности распределения, т.е. минимизировать разницу между
является ключевым аспектом корректного непараметрического
анализа, поскольку именно ширина окна определяет поведение оценки в конечных
выборках. Выбирать величину h следует так, чтобы оценка была как можно ближе к
истинной плотности распределения, т.е. минимизировать разницу между 
 и
и 
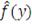 .
.
Существует два основных подхода к определению величины
сглаживающего множителя (ширины интервала):
Фиксированная ширина интервала на всей выборке. В рамках этого
подхода выделяют:
правило подстановки (ruleofthumb)
метод перекрёстной проверки (cross-validation)
Ширина интервала меняется в зависимости от локальной концентрации
наблюдений. В рамках этого подхода выделяют:
Обобщенныйметодближайшихсоседей (generalized nearest neighbors)
Адаптивный методближайших соседей (adaptive nearest neighbors)
[45,46]
В данной работе было использовано ядро Гаусса с фиксированной
шириной интервала 
 из-за его вычислительной простоты и легкой аналитической
интерпретации. В результате были получены следующие оценки для функции
плотности по каждой ценной бумаге:
из-за его вычислительной простоты и легкой аналитической
интерпретации. В результате были получены следующие оценки для функции
плотности по каждой ценной бумаге:
Рисунок 9: Ядерные оценки функции плотности по рассматриваемым ПИФ
Как мы можем увидеть из данного рисунка, по всем ПИФ наблюдаются
толстые хвосты в левой части, поскольку плотность эмпирического распределения
(непрерывная линия) в данных областях выше плотности Нормального распределения
(пунктирная красная линия). Мы можем сделать вывод, что вероятность
экстремальных негативных событий выше чем у позитивных и использование
симметричных меры риска - СКО и дисперсии может привести к неправильной оценки
истинного риска и как следствие будет сформирован портфель ценных бумаг не
отвечающий критериям оптимальности. Выходом из данной ситуации является
использование нессиметричных мер риска, например, VaR или CVaR.
Таким образом, после проведенного предварительного анализа
используемых данных мы можем заключить, что рассмотрение и использование в
качестве меры риска показателя CVaR значительно может улучшить наши результаты.
Это связано, во-первых, с "ненормальностью" распределения, а,
во-вторых, с толщиной левых "хвостов", используемых в данной работе
доходностей ПИФ.
2.2
Оптимизация портфелей ценных бумаг на основе CVaR
Процедура оптимизации портфеля ценных бумаг представляет
собой выбор из портфельного множества того портфеля, который соответствует
критериям оптимальности для инвестора. В данной работе предполагается
построение двух видов оптимальных портфелей ценных бумаг: портфель минимального
риска и портфель максимального модифицированного коэффициента Шарпа. Под
модифицированным коэффициентом Шарпа в дальнейшем мы будим понимать:
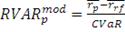
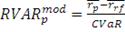 (49)
(49)
Таким образом, данный коэффициент аналогичен стандартному
коэффициенту Шарпа за тем исключением, что здесь в качестве меры риска
используется не стандартное отклонение 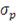
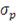 , а CVaR. Предполагается получение оптимальных портфелей с
использованием CVaR в качестве меры риска на трех различных временных
интервалах: месяц, квартал и полугодие. Это позволит получить более полное
представление об эффективности инвестирования на тот или иной срок, а также
выявить различия оптимальных портфелей на разных горизонтах инвестирования. В
качестве безрисковой ставки
, а CVaR. Предполагается получение оптимальных портфелей с
использованием CVaR в качестве меры риска на трех различных временных
интервалах: месяц, квартал и полугодие. Это позволит получить более полное
представление об эффективности инвестирования на тот или иной срок, а также
выявить различия оптимальных портфелей на разных горизонтах инвестирования. В
качестве безрисковой ставки 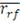
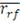 в данной работе была использована ставка по российским ГКО по
состоянию на 1 марта 2016г., которая равна 9,6% годовых.
в данной работе была использована ставка по российским ГКО по
состоянию на 1 марта 2016г., которая равна 9,6% годовых.
У используемого в настоящей работе подхода к оценке оптимальных
портфелей существуют следующие основные предпосылки:
Отсутствуют короткие продажи, т.е. веса ценных бумаг в портфелях
положительные
Отсутствие транзакционных издержек, налогов и комиссионных сборов
Бесконечная делимость активов
Сгенерированное портфельное множество является полным, т.е.
полностью описывает все возможные комбинации ценных бумаг в портфеле
Инвестор основывает свой выбор оптимального портфеля только на
основе показателя его доходности и риска, а прочие факторы, например, фактор
ликвидности в расчет не берутся.
Постоянство функции плотности вероятности, т.е. оценка функции
плотности на основе исторических данных будет состоятельной и неизменной во
времени
Предлагаемый метод получения оптимальных портфелей был применен к
обучающей выборке и включает в себя три основных этапа: моделирование множества
портфелей, создание параметрических копула функций и выбор оптимальных из них,
расчет оптимальных портфелей на основе CVaR. Рассмотрим каждый из них более
детально.
) Моделирование множества портфелей
Для целей построения достижимого портфельного множества и
определения эффективной границы необходимо рассмотреть всевозможные портфели,
т.е. перебрать все комбинации весов активов. Главной задачей на данном этапе
является формирование как можно более полного и всеобъемлющего набора весов для
чего на практике активно используется метод Монте-Карло. Пусть нам необходимо
смоделировать для портфеля, состоящего и 
 активов их веса. Ограничением здесь будет выступать условие
активов их веса. Ограничением здесь будет выступать условие 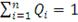
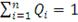 . Тогда, используя алгоритм метода Случайных портфелей, выполняем
следующие операции:
. Тогда, используя алгоритм метода Случайных портфелей, выполняем
следующие операции:
Моделируем 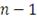
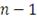 равномерно распределенных случайных величин на отрезке
равномерно распределенных случайных величин на отрезке 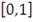
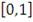 получая набор
получая набор 
 . Под равномерным распределением понимают - распределение
случайной вещественной величины, принимающей значения, принадлежащие интервалу
[a,b], характеризующееся тем, что плотность вероятности на этом интервале
постоянна и равна:
. Под равномерным распределением понимают - распределение
случайной вещественной величины, принимающей значения, принадлежащие интервалу
[a,b], характеризующееся тем, что плотность вероятности на этом интервале
постоянна и равна:
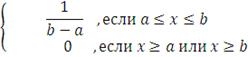
Упорядочиваем их по возрастанию, получаем 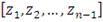
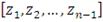 , такие что
, такие что
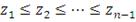
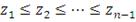 и добавляем концы интервала
и добавляем концы интервала 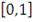
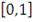 в качестве
в качестве 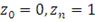
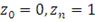
Получаем вектор весов портфеля 
 :
:
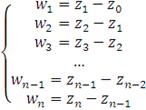
Таким образом, в результате мы получаем один случайный портфель с
весами 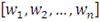
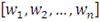 . Выполнив данный алгоритм большое число раз подряд (в данной
работе
. Выполнив данный алгоритм большое число раз подряд (в данной
работе 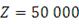
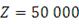 ), мы получим необходимое нам портфельное множество. В итоге мы
получим матрицу
), мы получим необходимое нам портфельное множество. В итоге мы
получим матрицу 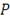
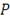 размерности
размерности 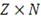
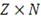 , где
, где 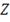
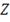 - количество генерируемых портфелей, а
- количество генерируемых портфелей, а 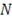
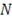 - количество ценных бумаг.
- количество ценных бумаг.
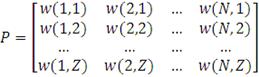
Результат генерации 2000 случайных портфелей для трех активов
представлен на Рисунке 10.
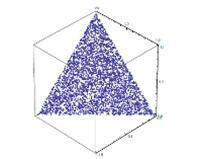
Рисунок 10: Множество сгенерированных портфелей для трех активов
Как мы можем увидеть вся треугольная область равномерно заполнена
и отсутствуют какие либо "непокрытые" участки, что говорит о хороших
результатах моделирования портфельного множества [50, c.6].
) Создание параметрических копула функций и выбор оптимальных из
них.
В данной работе предполагается использование четырех наиболее
популярных и часто используемых на практике копула-функций, рассмотренных
ранее: Нормальная копула, копула Стьюдента, копула Гумбеля и копула Клейтона.
Для создания многомерной полупараметрической копулы необходимо в качестве
исходных данных использовать эмпирические кумулятивные функции распределения по
каждому ПИФ. Пусть 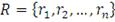
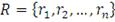 - набор доходностей по каждой рассматриваемой ценной бумаге,
тогда соответствующий ему вектор
- набор доходностей по каждой рассматриваемой ценной бумаге,
тогда соответствующий ему вектор 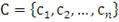
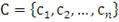 из значений кумулятивной функции распределения может быть найден:
из значений кумулятивной функции распределения может быть найден:
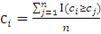
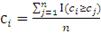 (50)
(50)
Отсюда, значение 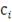
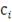 соответствует вероятности того, что доходность по данной ценной
бумаге окажется меньше или равна значению
соответствует вероятности того, что доходность по данной ценной
бумаге окажется меньше или равна значению 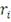
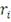 .
.
После получения значений векторов 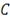
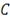 по каждой ценной бумаге мы генерируем копула-функции и выбираем
лучшую из них на основе критерия Акаике (AIC). Этот метод позволяет выбрать
копула-функцию, которая отвечает наименьшему значению из следующих:
по каждой ценной бумаге мы генерируем копула-функции и выбираем
лучшую из них на основе критерия Акаике (AIC). Этот метод позволяет выбрать
копула-функцию, которая отвечает наименьшему значению из следующих:
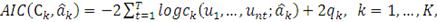
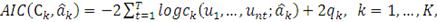 (51)
(51)
где 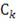
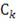 -
- 
 модель копула-функции,
модель копула-функции, 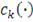
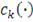 - плотность для
- плотность для 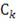
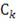 ;
; 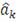
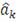 - вектор параметров копула-функции
- вектор параметров копула-функции 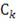
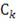 ,
, 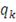
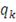 - число параметров, от которых зависит функция
- число параметров, от которых зависит функция 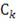
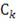 . Функция
. Функция 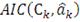
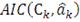 в определенном смысле штрафует модели с большим числом
параметров. AIC предполагает, что наиболее адекватная модель находится среди
рассматриваемых моделей [63, c.100-101]. Были получены следующие значения
данного критерия для используемых копула-функций:
в определенном смысле штрафует модели с большим числом
параметров. AIC предполагает, что наиболее адекватная модель находится среди
рассматриваемых моделей [63, c.100-101]. Были получены следующие значения
данного критерия для используемых копула-функций:
Таблица 6: Результаты критерия Акаике
|
Копула
|
Нормальная
|
Стьюдента
|
Гумбеля
|
Клейтона
|
|
Значение AIC
|
544,4253
|
888,8338
|
408,3167
|
486,6486
|
Исходя из полученных результатов, мы можем выбрать наилучшую
копула-функцию для дальнейшего моделирования многомерного распределения
доходностей ПИФ. Такой копулой является копула Стьюдента из семейства
Эллиптических копул.
) Расчет оптимальных портфелей на основе CVaR
Используя созданные копулы на предыдущем шаге, генерируем 180, 90
и 30 значений доходности (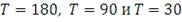
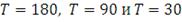 ) по каждой ценной бумаге из многомерного распределения для
полугодового, трехмесячного и месячного горизонтов инвестирования
соответственно. В итоге получаем три матрицы
) по каждой ценной бумаге из многомерного распределения для
полугодового, трехмесячного и месячного горизонтов инвестирования
соответственно. В итоге получаем три матрицы 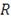
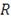 , имеющие следующий вид:
, имеющие следующий вид:
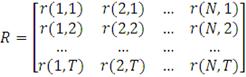
На основе полученных значений доходности мы рассчитываем кумулятивную
(месячную, квартальную и полугодовую) доходность для каждой ценной бумаги по
следующей формуле:
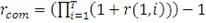
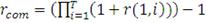 (52)
(52)
В итоге мы получаем вектор кумулятивных доходностей за
рассматриваемый период времени. Повторяя данную итерацию достаточно большое
число раз (Q=1000) мы получаем следующую матрицу кумулятивных доходностей по
рассматриваемым ПИФам:
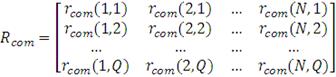
На заключительном шаге нам необходимо перейти к матрице
кумулятивных доходностей по каждому портфелю ПИФов. Для этого необходимо
выполнить следующие вычисления:
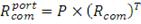
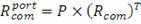 (53)
(53)
Отсюда мы можем найти ожидаемое значение доходности и CVaR по
каждому портфелю ценных бумаг. Ожидаемая доходность рассчитывается как
среднее-арифметическое значений доходностей портфеля (элементов каждого столбца
матрицы 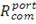
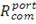 ). Непараметрическая оценка CVaR может быть получена следующим
образом:
). Непараметрическая оценка CVaR может быть получена следующим
образом:
Ранжируем значения полученных доходностей по убыванию
Находим элемент с порядковым номером 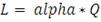
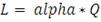 , где
, где 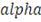
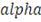 - уровень значимости. Как правило, используют уровни значимости
равные 90%, 95% или 99%. Данный элемент соответствует значению VaR с выбранным
уровнем значимости (в данной работе
- уровень значимости. Как правило, используют уровни значимости
равные 90%, 95% или 99%. Данный элемент соответствует значению VaR с выбранным
уровнем значимости (в данной работе 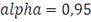
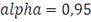 )
)
Рассчитываем CVaR как средне-арифметическое значение всех
элементов, порядковый номер которых превышает 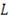
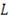
Таким образом, получив значения ожидаемой доходности и CVaR по
каждому сгенерированному портфелю ценных бумаг, мы можем построить Достижимое
множество для каждого периода инвестирования, где по оси ординат в качестве
меры риска будет использоваться CVaR, а не Дисперсия как в Классической теории.
Все три представленных множества имеют стандартную форму и являются выпуклыми.
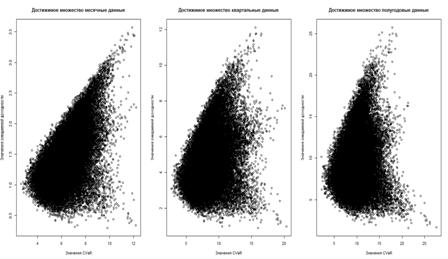
Рисунок 11: Достижимые множества для трех горизонтов
инвестирования
На основе построенных множеств мы можем найти по каждому из них
портфели с минимальным значением риска (CVaR) и с максимальным значением
модифицированного коэффициента Шарпа. Для расчета коэффициента Шарпа
воспользуемся эффективными безрисковыми ставками для месяца, квартала и
полугодия и формулой (16):
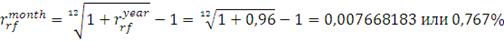
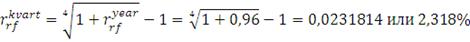
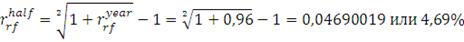
Оптимальные портфели для месячного горизонта инвестирования
выглядят следующим образом:
Таблица 7: Оптимальные портфели по CVaR для месяца
|
№ п. п.
|
ПИФ
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
|
1
|
Альфа-Капитал Резерв
|
10,495%
|
17,301%
|
|
2
|
УРАЛСИБ Первый
|
0,716%
|
0,793%
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
0,182%
|
7,576%
|
|
4
|
Райффайзен - Облигации
|
2,512%
|
18,087%
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
2,743%
|
3,383%
|
|
6
|
Сбербанк - Потребительский сектор
|
6,288%
|
1,574%
|
|
7
|
Райффайзен - США
|
26,963%
|
0,062%
|
|
8
|
Империя
|
9,070%
|
9,331%
|
|
9
|
Сбербанк - Еврооблигации
|
1,439%
|
0,357%
|
|
10
|
Газпромбанк - Облигации плюс
|
39,593%
|
41,537%
|
Как мы можем видеть, портфель минимального риска является
более диверсифицированным по сравнению с портфелем максимального коэффициента
Шарпа. Наибольший удельный вес в портфеле минимального риска занимает
"Газпромбанк - Облигации плюс" - 42%, а в портфеле максимального
коэффициента Шарпа - "Райффайзен - США" с весом 27% и также Газпромбанк
- Облигации плюс" - 40%. Полученные портфели обладают следующими
характеристиками на обучающей выборке данных:
Таблица 8: Характеристики оптимальных портфелей по CVaR для
месяца
|
Портфель
|
Доходность
|
CVaR
|
VaR
|
Коэффициент Шарпа
|
|
Минимального риска
|
0,9293%
|
2,4406%
|
2, 2005%
|
0,06659344
|
|
Максимального значения коэффициента Шарпа
|
2,1745%
|
5,3333%
|
4,6233%
|
0,263947
|
Оптимальный портфель по коэффициенту Шарпа обладает как более
высокой доходностью, так и более высоким риском (значения CVaR и VaR) по
сравнению с портфелем минимального риска, однако премия за единицу риска у него
значительно меньше.
Оптимальные портфели для трехмесячного горизонта
инвестирования выглядят следующим образом:
Таблица 9: Оптимальные портфели по CVaR для квартала
|
№ п. п.
|
ПИФ
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
|
1
|
Альфа-Капитал Резерв
|
4,885%
|
0,013%
|
|
2
|
УРАЛСИБ Первый
|
1,157%
|
5,657%
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
1,621%
|
1,046%
|
|
4
|
Райффайзен - Облигации
|
10,535%
|
0,359%
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
1,259%
|
8,400%
|
|
6
|
Сбербанк - Потребительский сектор
|
2,810%
|
5,398%
|
|
7
|
Райффайзен - США
|
10,589%
|
1,221%
|
|
8
|
Империя
|
6,532%
|
6,893%
|
|
9
|
Сбербанк - Еврооблигации
|
1,832%
|
0,551%
|
|
10
|
Газпромбанк - Облигации плюс
|
58,779%
|
70,462%
|
Наибольшие удельные веса в обоих портфелях занимает
"Газпромбанк - Облигации плюс" по 59% и 70% соответственно.
Данные веса, особенно в портфеле минимального риска, могут
быть объяснены низкими значениями корреляции ПИФа, что дает высокий эффект
диверсификации портфеля.
Вышеприведенные портфели обладают следующими показателями на
обучающей выборке данных:
Таблица 10: Характеристики оптимальных портфелей по CVaR для
квартала
|
Портфель
|
Доходность
|
CVaR
|
VaR
|
Модифицированный Коэффициент Шарпа
|
|
Минимального риска
|
3,3349%
|
2,2433%
|
1,810%
|
0,4532712
|
|
Максимального значения коэффициента Шарпа
|
4,6471%
|
2,8284%
|
2,0959%
|
0,8234127
|
Оптимальный портфель по коэффициенту Шарпа обладает как более
высокой доходностью (4,65% против 3,33%), так и более высоким риском (значения
CVaR и VaR равны 2,83% и 2,1% против 2,24% и 1,8% соответственно) по сравнению
с портфелем минимального риска.
Оптимальные портфели для полугодового горизонта
инвестирования выглядят следующим образом:
Таблица 11: Оптимальные портфели по CVaR для полугодия
|
№ п. п.
|
ПИФ
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
|
1
|
Альфа-Капитал Резерв
|
4,885%
|
4,885%
|
|
2
|
УРАЛСИБ Первый
|
1,157%
|
1,157%
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
1,621%
|
1,621%
|
|
4
|
Райффайзен - Облигации
|
10,535%
|
10,535%
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
1,259%
|
1,259%
|
|
6
|
Сбербанк - Потребительский сектор
|
2,810%
|
2,810%
|
|
7
|
Райффайзен - США
|
10,589%
|
10,589%
|
|
8
|
Империя
|
6,532%
|
6,532%
|
|
9
|
Сбербанк - Еврооблигации
|
1,832%
|
1,832%
|
|
10
|
Газпромбанк - Облигации плюс
|
58,779%
|
58,779%
|
Как мы можем наблюдать, мы получили одинаковые портфели, как
для целей минимизации риска, так и для целей максимизации модифицированного
коэффициента Шарпа. Кроме того, данные портфели совпадают с оптимальным
портфелем коэффициента Шарпа для квартальных данных. Это говорит нам о том, что
данный портфель обладает привлекательными характеристиками для инвестора, как
на разных горизонтах инвестирования, так и для разных целевых функций,
описывающих его предпочтения. Полученные результаты, на мой взгляд, связаны с
низкими рисками на данном временном промежутке, что служит также причиной
максимизации коэффициента. Вышеприведенные портфели обладают следующими
характеристиками на обучающей выборке данных:
Таблица 12: Характеристики оптимальных портфелей по CVaR для
полугодия
|
Портфель
|
Доходность
|
CVaR
|
VaR
|
Коэффициент Шарпа
|
|
Минимального риска
|
9,3767%
|
0,8519%
|
-0,0123%
|
5,50151767
|
|
Максимального значения коэффициента Шарпа
|
9,3767%
|
0,8519%
|
-0,0123%
|
5,50151767
|
Здесь стоит отметить, что у портфелей наблюдается очень
высокий показатель доходности, равный 9,37% при достаточно низком уровне риска
(значение VaR отрицательное, что означает положительную доходность).
На основе полученных выше результатов можно сделать следующие
основные выводы по составленным оптимальным портфелям ценных бумаг:
Полученные для каждого периода инвестирования два оптимальных
портфеля - всего 6 портфелей показали достаточно хорошие результаты на
обучающей выборке данных, как с позиции их доходности, так и с позиции цены за
единицу риска.
Наиболее привлекательным объектом инвестиций является ПИФ
"Газпром - Облигации плюс" - его удельный все почти во всех портфелях
превышает 50%, что является очень высоким показателем. Кроме данного ПИФ также
имеют значительные веса в портфелях: "Райффайзен - Облигации",
"Райффайзен - США", "Империя" и "Сбербанк -
Потребительский сектор".
Рассматривая привлекательность инвестиций с позиции категории
фондов можно отметить, что в данном показателе лидируют Фонды облигаций (в
среднем их доля составляет 74,1%). На втором месте идут смешанные фонды акций -
их доля 10,53%, на третьем фонды фондов - 10%, а на четвертом месте - фонды
акций с долей, раной 5,39%.
2.3
Тестирование оптимальных портфелей на контрольных данных и анализ полученных
результатов
Для анализа результатов используемого в настоящей работе
метода поиска оптимального портфеля ценных бумаг важным моментом является
сопоставление его с результатами Классической теории, которая является в своем
роде определенным бенчмарком в данной области. Для получения оптимальных
портфелей по Марковицу необходимо оценить ожидаемые доходности и ковариационную
матрицу по историческим данным рассматриваемых ПИФов на основе формул (1), (2),
(3) и (4). Были получены следующие результаты:
Таблица 13: Ожидаемые доходности ПИФов
|
№ п. п.
|
ПИФ
|
Ожидаемая дневная доходность
|
СКО
|
|
1
|
0,02802%
|
0,486924%
|
|
2
|
УРАЛСИБ Первый
|
-0,00839%
|
1,139826%
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
0,00421%
|
0,528004%
|
|
4
|
Райффайзен - Облигации
|
0.02293%
|
0,412216%
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
0.01217%
|
0,502013%
|
|
6
|
Сбербанк - Потребительский сектор
|
0.08588%
|
1,302492%
|
|
7
|
Райффайзен - США
|
0.16401%
|
1,662932%
|
|
8
|
Империя
|
0.05622%
|
0,79708%
|
|
9
|
Сбербанк - Еврооблигации
|
0.10699%
|
1,58453%
|
|
10
|
Газпромбанк - Облигации плюс
|
0.03421%
|
0,18886%
|
Все рассматриваемые ПИФы имеют положительную ожидаемую
доходность за исключением "УРАЛСИБ Первый". Наибольшее значение
наблюдается у "Райффайзен - США" и составляет 0,16% или 79,24% в
годовом выражении. Наименьшим риском обладает "Газпромбанк - Облигации
плюс", который равен 0,18886%.
Корреляционная матрица выглядит следующим образом:
Таблица 14: Корреляционная матрица
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
1,00
|
0,44
|
0,26
|
0,45
|
0,38
|
0,53
|
0,54
|
0,68
|
0,65
|
0,26
|
|
2
|
0,44
|
1,00
|
0,23
|
0,21
|
0,43
|
0,59
|
0,33
|
0,41
|
0,38
|
0,14
|
|
3
|
0,26
|
0,23
|
1,00
|
0,26
|
0,18
|
0,15
|
-0,02
|
0,07
|
0,03
|
0,39
|
|
4
|
0,45
|
0,21
|
0,26
|
1,00
|
0,30
|
0,28
|
0,27
|
0,34
|
0,32
|
0,50
|
|
5
|
0,38
|
0,43
|
0,18
|
0,30
|
1,00
|
0,32
|
0,27
|
0,34
|
0,36
|
0,25
|
|
6
|
0,53
|
0,59
|
0,15
|
0,28
|
0,32
|
1,00
|
0,57
|
0,64
|
0,63
|
0,04
|
|
7
|
0,54
|
0,33
|
-0,02
|
0,27
|
0,27
|
0,57
|
1,00
|
0,84
|
0,88
|
-0,02
|
|
8
|
0,68
|
0,41
|
0,07
|
0,34
|
0,34
|
0,64
|
0,84
|
1,00
|
0,90
|
0,05
|
|
9
|
0,65
|
0,38
|
0,03
|
0,32
|
0,36
|
0,63
|
0,88
|
0,90
|
1,00
|
0,03
|
|
10
|
0,26
|
0,14
|
0,39
|
0,50
|
0,25
|
0,04
|
-0,02
|
0,05
|
0,03
|
1,00
|
Как мы можем увидеть, значение коэффициентов корреляции в
целом достаточно низкие, что открывает возможности для диверсификации портфеля
ценных бумаг и снижения его общего риска. Наибольшее значение коэффициента у
ПИФов "Империя" и "Сбербанк - Еврооблигации", которое равно
0,9. Наименьшее - у "Сбербанк - Фонд облигаций Илья Муромец" и
"Райффайзен - США", а также у "Газпромбанк - Облигации
плюс" и "Райффайзен - США" (оно равно - 0,2).
Используя смоделированное множество портфелей, мы можем
построить достижимое множество по Марковицу по аналогии с пунктом 2.2, однако в
качестве меры риска будет выступать Дисперсия, а не CVaR. Полученное множество
является выпуклым и имеет стандартную классическую форму.
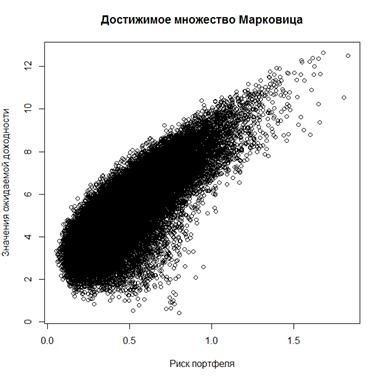
Рисунок 12: Достижимое множество по Марковицу
На основе построенного достижимого множества мы можем найти
два оптимальных портфеля: портфель с максимальным значением коэффициента Шарпа
и портфель минимального риска, которому соответствует крайняя левая точка
представленного множества. Из-за малого объема выборки мы не будем находить
оптимальные портфели по Марковицу на основе месячных, квартальных и полугодовых
данных, а предположим, что оптимизация для всех рассматриваемых периодов
производится по дневным данным. Для расчета коэффициента Шарпа воспользуемся
эффективной дневной безрисковой ставкой по аналогии с предыдущим пунктом:
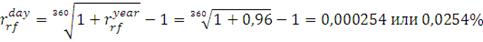
Эффективные портфели выглядят следующим образом:
Таблица 15: Оптимальные портфели по Марковицу
|
№ п. п.
|
ПИФ
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
|
1
|
Альфа-Капитал Резерв
|
6,424%
|
13,804%
|
|
2
|
УРАЛСИБ Первый
|
0,588%
|
6,435%
|
|
3
|
Сбербанк - Фонд облигаций Илья Муромец
|
4,658%
|
7,170%
|
|
4
|
Райффайзен - Облигации
|
0,755%
|
5,718%
|
|
5
|
Альфа-Капитал Стратегические инвестиции
|
0,950%
|
1,602%
|
|
6
|
Сбербанк - Потребительский сектор
|
0, 199%
|
0,972%
|
|
7
|
Райффайзен - США
|
54,038%
|
1,359%
|
|
8
|
Империя
|
2,571%
|
0,702%
|
|
9
|
Сбербанк - Еврооблигации
|
2,374%
|
1,648%
|
|
10
|
Газпромбанк - Облигации плюс
|
27,443%
|
60,590%
|
Портфель минимального риска является более
диверсифицированным по сравнению с портфелем максимального коэффициента Шарпа -
число ПИФ с долей менее 1% у него два против четырех у последнего. Наибольший
удельный веса портфеле минимального риска занимает "Газпромбанк -
Облигации плюс" - 61%, в то время как у второго портфеля это
"Райффайзен - США" с долей 54% соответственно. Данные портфели
обладают следующими характеристиками на обучающей выборке данных:
Таблица 16: Характеристики оптимальных портфелей по Марковицу
|
Портфель
|
Доходность
|
Риск
|
Коэффициент Шарпа
|
|
Минимального риска
|
0,0311%
|
0,2519%
|
0,0223018
|
|
Максимального значения коэффициента Шарпа
|
0,1044%
|
0,9750%
|
0,08096282
|
После того как мы получили набор весов каждого ПИФ для
каждого оптимального портфеля, необходимо проверить результаты (доходность и
риск) на контрольных данных. Для этого необходимо посчитать фактически
реализованную доходность и риск каждого сформированного портфеля по формулам
(1) и (3). После чего мы сможем рассчитать коэффициент Шарпа по каждому такому
портфелю, используя безрисковую ставку доходности по аналогии с пунктом 2.2
Основывая свои предпочтения на данном коэффициенте, мы сможем выявить какой
подход дает более хорошие результаты на различных временных интервалах и есть
ли смысл использовать подход отличный от классического. Поскольку в
предложенном в настоящей работе подходе в качестве меры риска используется не
СКО, а CVaR становится невозможным сравнение сформированных оптимальных
портфелей. Для устранения этого недостатка в качестве меры риска для сравнения
будем использовать стандартный показатель среднеквадратического отклонения и на
его основе рассчитывать коэффициенты Шарпа. Для данных расчетов необходимо
привести полученное СКО к месячному, квартальному и полугодовому значению на
основе следующих формул:
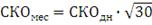
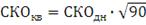
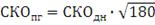
Таким образом, нам необходимо будет сравнить по два
оптимальных портфеля (портфель минимального риска и портфель максимального
коэффициента Шарпа) на трех горизонтах инвестирования (месяц, квартал и
полугодие).
Таблица 17: Сравнение портфелей на месячных данных
|
Портфели по Марковицу
|
Портфели по CVaR
|
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
|
Доходность
|
2,3231%
|
4,7676%
|
2,7004%
|
3,5299%
|
|
Риск (СКО)
|
0,7581%
|
4,6466%
|
0,8749%
|
2,9989%
|
|
Коэффициент Шарпа
|
2,052712
|
0,861008
|
2,210138
|
0,921371
|
Как мы можем увидеть из вышеприведенной таблицы, портфель
минимального риска по CVaR показал лучший результат (Коэффициент Шарпа равен
2,21 против 2,05 у подхода Марковица). Это обусловлено его высокой доходностью,
в то время как по риску он оказался несколько хуже. Портфель, основанный на
максимизации коэффициента Шарпа по CVaR, также, опередил аналогичный портфель
по Марковицу (Коэффициент Шарпа равен 0,86 против 0,92). Это в свою очередь
связано с достаточно высоким риском последнего (почти в полтора раза больше), в
то время как по показателю доходности он был значительно лучше (на 1,2%). Кроме
того стоит отметить, что портфели минимального риска значительно обошли по
своим показателям портфели максимального коэффициента для обоих сравниваемых
подходов. Исходя из полученных результатов, если инвестор предполагает
производить инвестиции на небольшой срок (до одного месяца), то предлагаемый в
настоящей работе подход даст результаты, лучше классического подхода.
Таблица 18: Сравнение портфелей на квартальных данных
|
Портфели по Марковицу
|
Портфели по CVaR
|
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
|
Доходность
|
9,5448%
|
-4,9249%
|
8,4167%
|
6,3705%
|
|
Риск (СКО)
|
2,1284%
|
11,4164%
|
2,5117%
|
3,6424%
|
|
Коэффициент Шарпа
|
3,395409
|
-0,63444
|
2,428053
|
1,112543
|
Как мы можем увидеть из вышеприведенной таблицы, портфель
минимального риска по CVaR показал результат немного хуже классического подхода
(Коэффициент Шарпа равен 3,4 против 2,43), что обусловлено в первую очередь его
более высокой доходностью и в меньшей степени более низким риском. Портфель,
основанный на максимизации коэффициента Шарпа по методу Марковица, значительно
уступил аналогичному портфелю на основе CVaR (Коэффициент Шарпа равен 1,11
против - 0,63). Это в свою очередь связано с его отрицательной доходностью и
более высоким показателем риска. Кроме того стоит отметить, что, как и для
месячных данных, портфели минимального риска значительно обошли по своим
показателям портфели максимального коэффициента для обоих сравниваемых
подходов. Исходя из полученных результатов, инвестору необходимо использовать
предложенный подход, если свои предпочтения он основывает на коэффициенте Шарпа
и его горизонт инвестирования равен кварталу.
Таблица 19: Сравнение портфелей на полугодовых данных
|
Портфели по Марковицу
|
Портфели по CVaR
|
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
Портфель минимального риска
|
Портфель максимального коэффициента Шарпа
|
|
Доходность
|
19,1071%
|
79,0667%
|
33,1504%
|
33,1504%
|
|
Риск (СКО)
|
3,3762%
|
13,0822%
|
4,6267%
|
4,6267%
|
|
Коэффициент Шарпа
|
4,27017
|
5,685317
|
6,15132
|
6,15132
|
Как портфель минимального риска, так и портфель максимального
коэффициента Шарпа по CVaR показал результаты лучше, чем у классического
подхода (Их коэффициенты Шарпа равны 6,15 против 4,27 и 6,15 против 5,68
соответственно). Это обстоятельство обусловлено для портфелей минимального
риска более высокой доходностью, хотя риск также немного больше. Для портфелей,
основанных на максимизации коэффициента Шарпа, это связано с их сильным
различием в риске (более чем в 3 раза). В отличие от результатов, полученных на
месячных и квартальных данных, портфели минимального риска не были лучше
портфелей максимального коэффициента для обоих сравниваемых подходов (для
предложенного подхода на основе CVaR их результаты совпали). Исходя из
полученных результатов, инвестору необходимо использовать предложенный подход,
если свои предпочтения он основывает или на коэффициенте Шарпа или на условии
минимизации риска и его горизонт инвестирования равен полугодию.
Таким образом, на основе полученных результатов можно сделать
следующие основные выводы:
Метод, основанный на применении в качестве меры риска CVaR,
необходимо использовать в следующих случаях:
если инвестор предполагает производить инвестиции на
небольшой срок (до одного месяца)
если свои предпочтения инвестор основывает на коэффициенте
Шарпа и его горизонт инвестирования равен кварталу
если горизонт вложения финансовых ресурсов для инвестора
равен полугодию
Предлагаемый в настоящей работе метод оптимизации портфеля
ценных бумаг продемонстрировал достаточно хорошие результаты, как в абсолютном,
так и в относительном выражении. Во-первых, он показал на всех трех
рассматриваемых горизонтах инвестирования положительную высокую доходность (в
среднем около 45% в годовом выражении). Во-вторых, сравнивая результаты с
классическим методом Марковица, можно сказать, что последний уступил - он был
лучше только в одном случае из шести, причем различия в результатах были не
существенные. На мой взгляд, это связано в первую очередь с тем фактом, что
доходности рассматриваемых ценных бумаг не распределены по нормальному закону и
из-за этого метод Марковица показывает результаты хуже.
Наиболее привлекательным горизонтом инвестирования для
инвестора является полугодие, поскольку для всех видов оптимальных портфелей и
подходов к оптимизации коэффициенты Шарпа для этого периода значительно выше.
Это обусловлено наличием положительного долгосрочного тренда в динамике цен
паев, а также снижением показателя волатильности.
Сравнивая два вида оптимальных портфелей, рассмотренных в
работе, можно сказать, что портфель минимального риска на выбранных данных
оказался гораздо привлекательнее как объект инвестиций, чем портфель
максимального коэффициента Шарпа. Это связано, на мой взгляд, с тем, что хоть и
доходность не входит в целевую функцию данных портфелей, однако минимизация
риска более важна из-за наличия положительного возрастающего тренда в ценах
паев.
Заключение
Целью настоящей работы являлось получение оптимального
портфеля ценных бумаг на основе CVaR с использованием копула-функций для оценки
многомерного распределения на примере российского рынка открытых ПИФов. Для
данной цели были проделаны два последовательных этапа: изучение теоретических
аспектов данного направления исследований и практическое построение оптимальных
портфелей ценных бумаг на их основе.
Классическая теория управления портфелем ценных бумаг,
предложенная Гарри Марковицем в 1950-х годах, хотя и является основой данного
направления в финансовой науке, но имеет много недостатков, главный из которых
- Нормальность распределения доходностей ценных бумаг. В связи с этим в 90-е
годы прошлого века появилась концепция VAR (Value-at-Risk). VaR - это
показатель риска, который показывает, какую максимальную сумму денег может
потерять портфель инвестора в течение определенного периода времени с заданной
доверительной вероятностью. Однако, у VaR существует, в свою очередь, тоже ряд
недостатков как меры риска, главный из которых - отсутствие когерентности. Для
преодоления данного недостатка RockfellerandUryasev предложили альтернативную
меру риска - ConditionalValue-at-Risk (CVaR). CVaR как мера риска очень тесно
связан с показателем VaR, поскольку представляет собой условное математическое
ожидание потерь при условии, что их величина оказалась больше значения VaR.
Каждый инвестор стремиться получить как можно большую
доходность при заданном уровне риска и как можно меньший риск при заданном
уровне доходности. Как следствие возникает задача поиска оптимального портфеля
ценных бумаг при заданной целевой функции полезности инвестора. В качестве
такой функции может выступать условие минимизации риска, максимизации
доходности или, например, один из коэффициентов эффективности: Коэффициент
Шарпа, Коэффициент Модильяни, Коэффициент Трейнора, Альфа Йенсена, Коэффициент
Сортино, Коэффициент Омега.
Поскольку портфель ценных бумаг включает в свой состав достаточно
большое число инструментов, то их совместное распределение описывается
многомерным законом. Таким образом, перед нами встает задача смоделировать
структуру зависимости между различными переменными, которые могут иметь разные
частные распределения. Одним из лучших инструментов для решения данной задачи
являются копула-функции. Основу данной теории составляет теорема Склара,
сформулированная в 1959 году. Ее основным следствием является то, что можно
связывать вместе любые 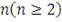
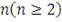 одномерных функций распределения разного типа (не обязательно из
одного семейства), используя любую копула-функцию, для того чтобы получить
двумерные или многомерные функции распределения. Таким образом, Копула-функции
дают возможность разделить описание распределения случайного вектора на две
части: частные распределения компонент и структура их зависимостей и могут быть
использованы в портфельной теории.
одномерных функций распределения разного типа (не обязательно из
одного семейства), используя любую копула-функцию, для того чтобы получить
двумерные или многомерные функции распределения. Таким образом, Копула-функции
дают возможность разделить описание распределения случайного вектора на две
части: частные распределения компонент и структура их зависимостей и могут быть
использованы в портфельной теории.
Для проведения исследования были выбраны десять ПИФов с наибольшей
стоимостью чистых активов (СЧА) по состоянию на 29.02.2016г. В число таких
фондов вошли два фонда акций, два смешанных фонда, один фонд фондов и пять
фондов облигаций. Анализ исследуемых ценных бумаг включает в себя проведение
двух последовательных этапов:
Тестирование данных на "нормальность"
По результатам проведенного теста можно сделать вывод, что ни одна
бумага с доверительной вероятностью 95% не может считаться распределенной по
нормальному закону. Из этого следует, что применение классической теории
Марковица с предположением о нормальности распределения доходностей ценных
бумаг может дать плохие результаты и привести к выбору далеко не оптимального
портфеля ценных бумаг.
Проверка "толщины хвостов"
В данной работе было использовано ядро Гаусса с фиксированной
шириной интервала 
 для построения ядерной функции плотности по каждой ценной бумаге.
На основе полученных оценок можно сделать вывод, что по всем ПИФ наблюдаются
толстые хвосты в левой части, следовательно, вероятность экстремальных
негативных событий выше чем у позитивных и использование симметричных меры
риска - СКО и дисперсии может привести к неправильной оценке истинного риска.
для построения ядерной функции плотности по каждой ценной бумаге.
На основе полученных оценок можно сделать вывод, что по всем ПИФ наблюдаются
толстые хвосты в левой части, следовательно, вероятность экстремальных
негативных событий выше чем у позитивных и использование симметричных меры
риска - СКО и дисперсии может привести к неправильной оценке истинного риска.
В данной работе было построено два вида оптимальных портфелей
ценных бумаг: портфель минимального риска и портфель максимального
модифицированного коэффициента Шарпа на трех различных временных интервалах:
месяц, квартал и полугодие. Предлагаемый метод получения оптимальных портфелей
был применен к обучающей выборке и включает в себя три основных этапа:
) Моделирование множества портфелей
Для целей построения достижимого портфельного множества и
определения эффективной границы необходимо рассмотреть всевозможные портфели,
т.е. перебрать все комбинации весов активов. Главной задачей на данном этапе
является формирование как можно более полного и всеобъемлющего набора весов для
чего в данной работе был использован метод Случайных портфелей, который показал
очень хорошие результаты.
) Создание параметрических копула функций и выбор оптимальных из
них.
Было использовано четыре наиболее популярных и часто используемых
на практике копула-функции: Нормальная копула, копула Стьюдента, копула Гумбеля
и копула Клейтона. На основе критерия Акаике (AIC) лучшей копулой является
копула Стьюдента.
) Расчет оптимальных портфелей на основе CVaR
Используя созданные копулы на предыдущем шаге мы получили
многомерное распределение доходности рассматриваемых ПИФ и на его основе была
рассчитана кумулятивная (месячная, квартальная и полугодовая) доходность
сначала для каждой ценной бумаги, а потом по каждому сгенерированному портфелю.
Отсюда мы нашли ожидаемое значение доходности и CVaR по каждому портфелю ценных
бумаг и построили Достижимое множество для каждого периода инвестирования, на
основе которых и были найдены необходимые оптимальные портфели. Полученные для
каждого из трех периодов инвестирования два оптимальных портфеля (всего 6
портфелей) показали достаточно хорошие результаты на обучающей выборке данных,
как с позиции их доходности, так и с позиции цены за единицу риска. Наиболее
привлекательным объектом инвестиций является ПИФ "Газпром - Облигации
плюс" - его удельный все почти во всех портфелях превышает 50%. Кроме данного
ПИФ также имеют значительные веса в портфелях: "Райффайзен -
Облигации", "Райффайзен - США", "Империя" и
"Сбербанк - Потребительский сектор". На первом месте по
распространенности Фонды облигаций со средней долей 74,1%, на втором месте идут
смешанные фонды - их доля 10,53%, на третьем фонды фондов - 10%, а на четвертом
месте - фонды акций с долей, раной 5,39%.
Для анализа результатов используемого в настоящей работе метода
поиска оптимального портфеля ценных бумаг важным моментом является сопоставление
его с результатами Классической теории, которая выступает в своем роде
определенным бенчмарком в данной области. После того как мы получили набор
весов каждого ПИФ для каждого оптимального портфеля, были проверены результаты
(доходность и риск) на контрольных данных. Для этого необходимо было посчитать
фактически реализованную доходность и риск каждого сформированного портфеля по
формулам (1) и (3). После чего необходимо рассчитать коэффициент Шарпа по
каждому такому портфелю, используя безрисковую ставку доходности. Основывая
свои предпочтения на данном коэффициенте, мы смогли выявить какой подход дает
более хорошие результаты на различных временных интервалах и есть ли вообще
смысл использовать подход отличный от классического.
На месячных данных портфель минимального риска по CVaRопередил
портфель Марковица, что обусловлено его высокой доходностью, в то время как по
риску он оказался несколько хуже. Портфель, основанный на максимизации
коэффициента Шарпа по CVaR, также, опередил аналогичный портфель по Марковицу,
что в свою очередь связано с достаточно высоким риском последнего, в то время
как по показателю доходности он был значительно лучше.
На квартальных данных портфель минимального риска по CVaR показал
результат немного хуже классического подхода из-за его более высокой доходности
и немного в меньшей степени более низким риском. Портфель, основанный на
максимизации коэффициента Шарпа по методу Марковица, значительно уступил
аналогичному портфелю на основе CVaR, что связано с его отрицательной доходностью
и более высоким показателем риска.
На полугодовых данных, как портфель минимального риска, так и
портфель максимального коэффициента Шарпа по CVaR показал результаты лучше, чем
у классического подхода. Это обстоятельство обусловлено для портфелей минимального
риска более высокой доходностью, хотя риск также немного больше. Для портфелей,
основанных на максимизации коэффициента Шарпа, это связано с их сильным
различием в риске.
Предложенный метод оптимизации портфеля ценных бумаг необходимо
использовать, если инвестор предполагает производить инвестиции на небольшой
срок (до одного месяца), если свои предпочтения инвестор основывает на
коэффициенте Шарпа и его горизонт инвестирования равен кварталу, а также, если
горизонт вложения финансовых ресурсов для инвестора равен полугодию. Он
продемонстрировал достаточно хорошие результаты, как в абсолютном, так и в
относительном выражении. Во-первых, на всех трех рассматриваемых горизонтах
инвестирования наблюдалась положительная высокая доходность (в среднем около
45% в годовом выражении). Во-вторых, сравнивая результаты с классическим
методом Марковица, можно сказать, что последний уступил - он был лучше только в
одном случае из шести, причем различия в результатах были не существенные. На
мой взгляд, это связано в первую очередь с тем фактом, что доходности
рассматриваемых ценных бумаг не распределены по нормальному закону и из-за
этого метод Марковица показывает результаты хуже. Из-за наличия положительного
долгосрочного тренда в динамике цен рассматриваемых паев и снижения
волатильности, наиболее привлекательным горизонтом инвестирования для инвестора
является полугодие, поскольку для всех видов оптимальных портфелей и подходов к
оптимизации коэффициенты Шарпа для этого периода значительно выше.
Сравнивая два вида оптимальных портфелей, рассмотренных в работе,
можно сказать, что портфель минимального риска на выбранных данных оказался
гораздо привлекательнее как объект инвестиций, чем портфель максимального
коэффициента Шарпа. Это связано, на мой взгляд, с тем, что хоть и доходность не
входит в целевую функцию данных портфелей, однако минимизация риска более важна
из-за наличия положительного возрастающего тренда в ценах паев. Поэтому
инвестору в качестве целевой функции необходимо выбирать именно минимум риска.
Таким образом, поставленная цель и соответствующие ей задачи были
достигнуты в полной мере, а предложенный в настоящей работе метод оптимизации
портфеля ценных бумаг показал очень хорошие результаты на использованной
выборке данным и может быть использован инвесторами для принятия решений о
вложении своих финансовых ресурсов в портфель ценных бумаг.
Список
литературы
1. Ang
A., Chen J. (2002). Asymmetric correlations of equity portfolios. Journal of Financial Economics, 63
(3), 443 - 494.
2. Artzner
P., Delbaen F., Eber J. - M., Heath D. Coherent Measures of Risk. //
Mathematical Finance. 1999.
Vol.9. No.3. P. 203-228.
3. Autchariyapanitkul
K., Chanaim S., Sriboonchitta S. Portfolio optimization of stock returns in
high-dimensions: A copula-based approach. Proceedings of the Proceedings of the
18th International Academic Conference, Sep 2015, pages 698-709
. Basak
S, Shapiro A. Value-at-risk based risk management: optimal policies and asset
prices. Review of
Financial Studies 2001; 14: 371-405.
5. Breymann
W., Dias A., Embrechts P. (2003). Dependence structures for multivariate high-frequency
data in finance. Quantitative
Finance, 3, 1 - 14.
6. Cai
ZW, Wang X. Nonparametric estimation of conditional VaR and expected shortfall.
Journal of Econometrics
2008; 147: 120-30.
7. Chen
F.Y. Analytical VaR for international portfolios with common jumps.computers
and Mathematics with Applications 2011; 62: 3066-76.
. Chen
SX. Nonparametric estimation of expected shortfall. Journal of Financial Econometrics 2008;
6 (1): 87-107.
9. Claro
J, Pinho de Sousa J. A multiobjective metaheuristic for a mean-risk multistage
capacity investment problem with process flexibility.computers and Operations
Research 2012; 39: 838-49.
10. Embrechts
P., McNeil A.J., Straumann D. (1999). Correlation and dependency in risk management:
Properties and pitfalls. Working paper, Department of Mathematik, ETHZ, Zurich.
(Now in M. A. H. Dempster (ed.) (2002), Risk Management: Value at Risk and
Beyond, 176 - 223. Cambridge: Cambridge University Press).
. Erb
C., Harvey C., Viskanta T. (1994). Forecasting international equity
correlations. Financial Analysts Journal, 50, 32 - 45.
. Fantazzini
D. (2009а). A dynamic grouped T
copula approach for market risk management. In: G. Gregoriou (ed.), A VaR
Implementation Handbook, 253 - 282, McGraw-Hill: New York.
. Fantazzini
D. (2009б). The effects of
misspecified marginals and copulas on computing the value at risk: A Monte
Carlo study.computational Statistics and Data Analysis, 53 (6), 2168 - 2188.
. Fantazzini
D. (2010). Three-stage semi-parametric estimation of T-copulas: Asymptotics,
finite-sample properties and computational aspects.computational Statistics and
Data Analysis, forthcoming.
. Fermanian
J., Scaillet O. (2003). Nonparametric estimation of copulas for time series. Journal of Risk, 5, 25 - 54.
16. Frees
E.W., Valdez E. (1998). Understanding relationship using copulas. North
American Actuarial Journal, 2, 1 - 25.
. Genest
C., Favre A.C. (2007). Everything you always wanted to know about copula
modeling but were afraid to ask. Journal of Hydrologic Engineering, 12 (4), 347 - 368.
18. Genest
C., Ghoudi K., Rivest L.P. (1995). A semiparametric estimation procedure of
dependence parameters in multivariate families of distribution. Biometrika, 82 (3), 543 - 552.
20. Haixiang,
ZhongfeiLi, YongzengLai Mean-CVaR portfolio selection: A nonparametric
estimation framework.computers & Operations Research 2012; 40: 1014-1022.
. Hennessy
D., Lapan H. (2002): The Use of Archimedean Copulas to Model Portfolio
Allocations // Mathematical Finance. № 12. P.143-154.
22. Hoeffding
D. (1940). Masstabinvariante Korrelationstheorie. Schriften des Mathematischen
Seminars und des Instituts fur Angewandte Mathematik der Universität, 5, 181 - 233.
23. Huang
D.S., Zhu S.S., Fabozzi F.J., Fukushima M. Portfolio selection with uncertain
exit time: a robust CVaR approach. Journal of Economic Dynamics and Control 2008; 32: 594-623.
24. Iakovos
Kakouris, Berç Rustem. Robust portfolio
optimization with copulas European Journal of Operational Research 235 (1):
28-37 2014
. John
M.M., Hafize G.E. Applying CVaR for decentralized risk management of financial
companies. Journal of
Banking and Finance 2006; 30: 627-44.
26. Jondeau
E., Rockinger M. (2003). Conditional volatility, skewness, and kurtosis:
existence, persistence, and comovements. Journal of Economic Dynamics and Control, 27, 1699 - 1737.
27. Keating
C. and Shadwick W.F., "A Universal Performance Measure”, Journal of
Performance Measurement, vol.6, 2002.
. Lauprete
G.J., Samarov A.M., Welsch R.E. Robust portfolio optimization. Metrica 2002.55: 139-149.
29. Li
Q, Racine JS. Nonparametric Econometrics: Theory and Practice. Princeton University Press; 2007.
30. Longin
F., Solnik B. (2001). Extreme correlation of international equity markets. Journal of Finance, 56 (2), 649 -
676.
31. Manying
Bai and Lujie Sun. Application of copula and copula-CVaR in the Multivariate
Portfolio Optimization. 2007
P.108-116
32. Markowitz
H. Portfolio selection. Journal of Finance 1952; 7 (1): 77-91.
. Modigliani
F. and Modigliani L., "Risk-Adjusted Performance”, Journal of Portfolio
Management, winter 1997, pp.45-54.
. Morgan
J.P. Risk Metrics T.M.: Technical Document, 4th ed. New York: Morgan Guaranty
Trust Company; 1996.
35. Myles
Hollander, Douglas A. Wolfe. Nonparametric Statistical Methods. - New York: John Wiley
& Sons, 1973. - 503 с.
. Nelson,
R.B., An Introduction to Copulas, New York: Springer, 1999.
. Patton
A. (2004). On the out-of-sample importance of skewness and asymmetric
dependence for asset allocation. Journal of Financial Econometrics, 2 (1), 130 - 168.
38. Patton
A. (2006а). Estimation of copula
models for time series of possibly different lengths. Journal of Applied Econometrics, 21,
147 - 173.
39. Peracchi
F, Tanase AV. On estimating the conditional expected shortfall. Applied Stochastic Models in Business
and Industry 2008; 24 (5): 471-93.
40. Pflug
G. Some remarks on the value-at-risk and the conditional value-at-risk. In:
Uryasev S, editor. Probabilistic Constrained Optimization: Methodology and
Applications. Dordrecht:
Kluwer Academic Publishers; 2000.
41. Pu
Huang, Dharmashankar Subramanian, Jie Xu. An importance sampling method for
portfolio cvar estimation with Gaussian copula models. Proceedings of the 2010 Winter
Simulation Conference P.2790-2800
42. Rockfeller
T, Uryasev S. Conditional value-at-risk for general loss distribution. Journal of Banking and Finance 2002;
26 (7): 1443-71.
43. Rockfeller
T, Uryasev S. Optimization of conditional value-at-risk. Journal of Risk 2000; 2 (3): 21-4.
44. Sawik
T. Selection of a dynamic supply portfolio in make-to-order environ - ment with
risks.computers and Operations Research 2011; 38: 782-96.
. Scaillet
O. Nonparametric estimation and sensitivity analysis of expected shortfall. Mathematical Finance 2004; 14 (1):
115-29.
46. Scaillet
O. Nonparametric estimation of conditional expected shortfall. Insurance and Risk Management Journal
2005; 74: 639-60.
. Sklar
A. (1959). Fonctions de répartition á n dimensions et leurs marges. Publ.
Inst. Statis. Univ. Paris,8, 229 - 231.
48. Sklar
A. (1996). Random variables, distribution functions, and copulas: Personal look
backward and forward. Lecture
notes. Monograph series, 28, 1 - 14.
49. Wang
S. (1998). Aggregation of correlated risk portfolios: Model and algorithms. Proceedings of the Casualty Actuarial
Society, LXV, 848 - 893.
50. William
T.S. Portfolio optimization for VaR, CVaR, Omega and utility with general
return distributions: a Monte-Carlo approach for long-only and bounded short
portfolios with optional robustness and a simplified approach to covariance
matching, University College London 2011
. Xubiao
He, Pu Gong. Measuring the coupled risks: A copula-based CVaR model. Journal of Computational and Applied
Mathematics 2009 P.97-113
52. Yannick
Malevergne, Didier Sornette - Extreme Financial Risks: From Dependence to Risk
Management, 2005 - P.328
. Yau
S, Kwon R.H., Rogers J.S., Wu. D. Financial and operational decisions in the electricity
sector: contract portfolio optimization with the conditional value - at-risk
criterion. International
Journal of Production Economics 2011; 134: 67-77.
54. Yu
K, Allay A, Yang S, Hand DJ. Kernel quantile based estimation of expected
shortfall. The Journal
of Risk 2010; 12 (4): 15-32.
55. Zhu
SS, Fukushima M. Worst-case conditional value-at-risk with application to
robust portfolio management. Operations Research 2009; 57 (5): 1155-68.
. Алексеев
В.В., Шоколов В.В., Соложенцев Е.Д. (2006): Логико-вероятностное моделирование
портфеля ценных бумаг с использованием копул // Управление финансовыми рисками.
№ 3. C.272-283.
. Берзон
Н.И., Дорошин Д.И. Особенности применения показателей эффективности финансовых
инвестиций // Финансы и кредит. 2012 № 4 (494)
. Буренин
А.Н. Управление портфелем ценных бумаг М., Научно-техническое общество имени
академика СИ. Вавилова, 2008, - 440 с.
. Буренин
А.Н. Рынок ценных бумаг и производных финансовых инструментов: Учебное пособие
- М.: 1 Федеративная Книготорговая Компания, 1998. - 352 с.
. Информационный
ресурс Investfunds. Cbonds Group [Электронный ресурс]. - Режим доступа:
http://pif. investfunds.ru/quotes/
. Информационный
ресурс Сайт Банка России [Электронный ресурс]. - Режим доступа:
http://cbr.ru/hd_base/default. aspx?
prtid=gkoofz_mr&pid=finr&sid=GKO_stavki
. Пеникас
Г.И. Модели "копула" в приложении к задачам финансов // Журнал Новой
Экономической Ассоциации. - 2010. - № 7. - с.24 - 44
. Фантаццини
Д. (2011c). Моделирование многомерных распределений с использованием копула -
функций. III. Прикладная эконометрика, 25 (4), 100 - 130.
. Фантаццини
Д. (2011a). Моделирование многомерных распределений с использованием
копула-функций. I. Прикладная эконометрика, 22 (2), 98 - 134.
. Фантаццини
Д. (2011b). Моделирование многомерных распределений с использованием копула -
функций. II. Прикладная эконометрика, 23 (3), 98 - 132.
. Федеральный
закон от 29 ноября 2001 г. N 156-ФЗ "Об инвестиционных фондах" [Глава
III]
. Шарп
У., Александер Г., Бейли Дж. ИНВЕСТИЦИИ: Пер. с англ. - М.: ИНФРА-М, 2001. -
XII, 1028 с.
Приложения
Приложение 1:
Программный код в среде "Rstudio"
#Загрузкаданных(xlsx)<-read. xlsx ("C:
/Users/Саша/Desktop/пропро. xlsx",sheetIndex=1,header=FALSE)
#исходныеданныеподоходностямПИФ<-Dannie*100#переход к %<-ncol (Dannie)
#количество рассматриваемых бумаг<-Dannie [1: (nrow (Dannie) - 180),] #
Обучающаявыборка<-Dannie [nrow (Dannie) - 179: nrow (Dannie),] #
Контрольнаявыборка<-Obuch<-Kontrol. pif<-c
("Альфа-КапиталРезерв", "УРАЛСИБПервый", "Сбербанк -
ИльяМуромец", "Райффайзен - Облигации",
"Альфа-КапиталСтратег. Инв-ии", "Сбербанк - Потреб.
сектор", "Райффайзен - США", "Империя", "Сбербанк
- Еврооблигации", "Газпромбанк - Облигации плюс")
#Проверка данных на "нормальность". zn<-0.05
#уровень значимости для теста Колмогорова-Смирнова
norm. test. matrix<-matrix (nrow=1,ncol=Q)(i
in 1: Q) {<-ks. test (Dannie [, i], "pnorm", mean = mean (Dannie
[, i]), sd = sd (Dannie [, i])). p. value<-AA$p. value #значения p-value теста. test. matrix
[i] < - znach. p. value
}. norm. raspr<-sum (norm. test. matrix>lvl. zn)
#количество нормально распределенных ценных бумаг
#Построение ядерных оценок функции плотности для
ПИФ(np)<-seq (-7,7,length=10000) #точки для расчета плотности
gr. plotn<-matrix (ncol=Q,nrow=10000)().
par<-par (mfrow = c (2,5))(i in 1: Q) {. dat<-Dannie [, i]. plot < -
npudens (tdat=y. dat,
edat=x,ckertype="gaussian",bwtype="fixed") #плотностьпокаждойценнойбумаге: ядроГаусса, интервалфиксированный. plotn [, i]
<-yad. plot$dens(x, gr. plotn [, i], type="l", main=names. pif
[i],xlab="доходность",ylab="плотность") #графикплотности(x,dnorm
(x,mean=mean (Dannie [, i]),sd=sd (Dannie [, i])),lty="dashed",
col="red") #графикнормальногораспределения
}
#Переход к кумулятивной функции
распределения(copula)<-pobs (A) #эмпирическая кумулятивная функция
распределения по каждой бумаге
#Создание копул. cop< - normalCopula
(dim=Q,dispstr="ex") #нормальная копула. cop< - tCopula (dim=
Q,dispstr="ex") #копула Стьюдента. cop< - gumbelCopula (dim=
Q,param=2) #копула Гумбеля
clay. cop< - claytonCopula (dim= Q,param=2) #копула Клейтона
#Подгонкакопул. fit < - fitCopula (cdf,copula=norm. cop).
fit < - fitCopula (cdf,copula=stud. cop). fit < - fitCopula
(cdf,copula=gumb. cop). fit < - fitCopula (cdf,copula=clay. cop)
#Выбор оптимальной копулы
norm. fit@loglik <mailto:norm.fit@loglik>
stud. fit@loglik
<mailto:stud.fit@loglik>. fit@loglik <mailto:gumb.fit@loglik>
clay. fit@loglik <mailto:clay.fit@loglik>
#Генерируем множество портфелей<-50000 #количество создаваемых
портфелей<-matrix (ncol=Q,nrow=Z) #создаем Z портфелей для Q активов(jin 1:
Z) {<-c (0,1,runif (n=Q-1, min=0, max=1)) #генерируем равномерные величины
из (0,1)<-t (matrix (sort (p))) #упорядочиваем значения по
возрастанию<-ncol (q) #находим число элементов в q<-c (rep (0,times=n-1))
#создаем пустой вектор весов(iin 1: n-1) { #заполняем вектор весов[i] <-q
[i+1] - q [i]
}[j,] <-w # заполняем матрицу портфелей получаем в строчке веса
для всех активов
}
#Моделирование доходностей с многомерным распределением на основе
лучшей копулы<-1000 #количество симуляций. month<-matrix (nrow=NN,ncol=Z)
#матрица для симуляций месячной доходности. kvart<-matrix (nrow=NN,ncol=Z)
#матрица для симуляций квартальной доходности. half<-matrix (nrow=NN,ncol=Z)
#матрица для симуляций полугодовой доходности. month< - matrix
(nrow=NN,ncol=Q) #матрица месячных кумулятивных доходностей по ПИФ. kvart< -
matrix (nrow=NN,ncol=Q) #матрица квартальных кумулятивных доходностей по ПИФ.
half< - matrix (nrow=NN,ncol=Q) #матрица полугодовых кумулятивных доходностей
по ПИФ(ain 1: NN) {<-180 #Количество генерируемых дней. doh. sim< -
rCopula (n=N,copula=stud. fit@copula) #сгенерированные квантили многомерного
распределения<-matrix (nrow=N,ncol=Q) #матрица доходностей
yui.com. month< - matrix
(nrow=1,ncol=Q).com. kvart< - matrix (nrow=1,ncol=Q).com. half< - matrix
(nrow=1,ncol=Q)
for (jin 1: Q) {<-ecdf (A [,j]) #фактическая функция
распределения[,j] <-quantile (hhh,t (cdf. doh. sim [,j])) #заполнение
матрицы доходностей ПИФ.com. month [j] <- (prod (1+yui [1: 30,j] /100) - 1)
*100 #кумулятивная месячная доходность.com. kvart [j] < - (prod (1+yui [1:
90,j] /100) - 1) *100 #кумулятивная квартальная доходность.com. half [j] < -
(prod (1+yui [1: 180,j] /100) - 1) *100 #кумулятивная полугодовая доходность
}
#Считаем CVAR и ожидаемую доходность<-matrix (ncol=Z,nrow=N)
#матрица доходностей портфелей
for (j in 1: Z) {<-0(iin 1: Q) {
ZZ<-ZZ+yui [, i] *Y [j, i] #доходность по каждому портфелю
pir [,j] <-ZZ
}
}. cum. month <-matrix (ncol=Z,nrow=1).
cum. kvart <-matrix (ncol=Z,nrow=1). cum. half <-matrix (ncol=Z,nrow=1)
for (iin 1: Z) {. cum. month [, i] <- (prod ( (pir [1: 30, i]
/100) +1) - 1) *100# Значения кумулятивных доходностей за месяц по каждому
портфелю. cum. kvart [, i] <- (prod ( (pir [1: 90, i] /100) +1) - 1) *100 #
Значения кумулятивных доходностей за 3 месяца по каждому портфелю. cum. half [,
i] <- (prod ( (pir [1: 180, i] /100) +1) - 1) *100 # Значения кумулятивных
доходностей за полугодие по каждому портфелю
}. month [a,] <-doh. cum. month #матрица кумулятивных
доходностей по каждому портфелю для NN симуляций за месяц. kvart [a,] <-doh.
cum. kvart #матрица кумулятивных доходностей по каждому портфелю для NN
симуляций за квартал. half [a,] <-doh. cum. half #матрица кумулятивных
доходностей по каждому портфелю для NN симуляций за полугодие. month [a,] <
- yui.com. month #матрица кумулятивных доходностей по каждому ПИФ для NN
симуляций за месяц. kvart [a,] < - yui.com. kvart #матрица кумулятивных
доходностей по каждому ПИФ для NN симуляций за квартал. half [a,] < - yui.com.
half #матрица кумулятивных доходностей по каждому ПИФ для NN симуляций за
полугодие
}. month <-matrix (ncol=Z,nrow=1).
kvart <-matrix (ncol=Z,nrow=1). half <-matrix (ncol=Z,nrow=1). month
<-matrix (ncol=Z,nrow=1). kvart <-matrix (ncol=Z,nrow=1). half
<-matrix (ncol=Z,nrow=1). month <-matrix (ncol=Z,nrow=1). kvart
<-matrix (ncol=Z,nrow=1). half <-matrix (ncol=Z,nrow=1)
alpha=0.95 #уровень значимости для расчета CVaR и VaR
zn<- (1-alpha) *N(i in 1: Z) {. month
[, i] <-mean (Kol. month [, i]) #значениямесячнойДоходности. kvart [, i] <-mean (Kol. kvart [, i])
#значенияквартальнойДоходности
dohodnost. half [, i] <-mean (Kol. half [, i]) #значения
полугодовой Доходности
olo. month<-sort (Kol. month [, i] *
(-1), decreasing=TRUE). kvart<-sort (Kol. kvart [, i] * (-1),
decreasing=TRUE). half<-sort (Kol. half [, i] * (-1), decreasing=TRUE).
month [i] < - olo. month [zn] # значениямесячного VaR. kvart [i] < - olo. kvart [zn] # значенияквартального VaR
VaR. half [i] < - olo. half [zn] # значения полугодового VaR
CVaR. month [i] <-mean (olo. month [1:
zn]) #значения месячного CVAR. kvart [i] <-mean (olo. kvart [1: zn]) #значения квартального CVAR. half [i] <-mean (olo.
half [1: zn]) #значения полугодового CVAR
}(). par<-par (mfrow = c (1,3))
plot (CVaR. month, dohodnost. month, xlab="Значения
CVaR",ylab="Значения ожидаемой доходности",
main="Достижимое множество месячные данные")(CVaR. kvart, dohodnost.
kvart, xlab="Значения CVaR",ylab="Значения ожидаемой
доходности", main="Достижимое множество квартальные
данные")(CVaR. half, dohodnost. half, xlab="Значения
CVaR",ylab="Значения ожидаемой доходности",
main="Достижимое множество полугодовые данные")
#Поиск оптимального портфеля ценных бумаг modSharpRatio. rate.
day<- ( ( (1+0.096) ^ (1/360)) - 1) *100 #дневная безрисковая ставка
riskfree. rate. month<- ( ( (riskfree.
rate. day/100+1) ^30) - 1) *100#месячная безрисковая ставка. rate. kvart<- ( (
(riskfree. rate. day/100+1) ^90) - 1) *100#квартальная безрисковая ставка. rate. half<- ( ( (riskfree.
rate. day/100+1) ^180) - 1) *100 #полугодовая безрисковая ставка. koef. month<- (dohodnost.
month - riskfree. rate. month) / (CVaR. month) #коэффициент
Шарпа для
CVaR по функции потерь месячные данные.
koef. month<-order (znach. koef. month, decreasing = TRUE)
portf. max. koef. month< - Y [max. koef. month [1],] #веса
ценных бумаг в оптимальном портфеле месячные данные. max. koef. month<-c
(dohodnost. month [max. koef. month [1]], CVaR. month [max. koef. month [1]],
VaR. month [max. koef. month [1]], znach. koef. month [max. koef. month [1]])
#характеристики оптимального портфеля месячные данные(char. max. koef. month)
< - c ("Доходность", "CVaR ","VaR
","Коэффициент"). koef. kvart<- (dohodnost. kvart - riskfree.
rate. kvart) / (CVaR. kvart) #коэффициент Шарпа для CVaR по функции потерь
квартальные данные
max. koef. kvart<-order (znach. koef.
kvart, decreasing = TRUE)
portf. max. koef. kvart< - Y [max. koef. kvart [1],] #веса
ценных бумаг в оптимальном портфеле квартальные данные. max. koef. kvart<-c
(dohodnost. kvart [max. koef. kvart [1]], CVaR. kvart [max. koef. kvart [1]],
VaR. kvart [max. koef. kvart [1]], znach. koef. kvart [max. koef. kvart [1]])
#характеристики оптимального портфеля квартальные данные(char. max. koef. kvart)
< - c ("Доходность", "CVaR ","VaR
","Коэффициент"). koef. half<- (dohodnost. half - riskfree.
rate. half) / (CVaR. half) #коэффициент Шарпа для CVaR по функции потерь
полугодовые данные
max. koef. half<-order (znach. koef.
half, decreasing = TRUE)
portf. max. koef. half< - Y [max. koef. half [1],] #веса ценных
бумаг в оптимальном портфеле полугодовые данные. max. koef. half<-c
(dohodnost. half [max. koef. half [1]], CVaR. half [max. koef. half [1]], VaR.
half [max. koef. half [1]], znach. koef. half [max. koef. half [1]])
#характеристики оптимального портфеля полугодовые данные(char. max. koef. half)
< - c ("Доходность", "CVaR ","VaR
","Коэффициент")
# Портфельминимальногорискапо CVaR. CVaR. month<-order (CVaR. month,
decreasing = FALSE). min. CVaR. month< - Y [min. CVaR. month [1],] #веса ценных бумаг в
портфеле минимального риска месячные данные
char. min. CVaR. month<-c (dohodnost.
month [min. CVaR. month [1]], CVaR. month [min. CVaR. month [1]], VaR. month
[min. CVaR. month [1]], znach. koef. month [min. CVaR. month [1]]) #характеристики портфеля минимального
риска месячные данные(char. min. CVaR. month) < - c ("Доходность",
"CVaR ","VaR ","Коэффициент")
min. CVaR. kvart<-order (CVaR. kvart,
decreasing = FALSE)
portf. min. CVaR. kvart< - Y [min. CVaR. kvart [1],] #веса
ценных бумаг в портфеле минимального риска квартальные данные
char. min. CVaR. kvart<-c (dohodnost. kvart [min. CVaR.
kvart [1]], CVaR. kvart [min. CVaR. kvart [1]], VaR. kvart [min. CVaR. kvart
[1]], znach. koef. kvart [min. CVaR.
kvart [1]]) #характеристики портфеля минимального риска квартальные
данные(char. min. CVaR. kvart) < - c ("Доходность", "CVaR
","VaR ","Коэффициент")
min. CVaR. half<-order (CVaR. half,
decreasing = FALSE). min. CVaR. half< - Y [min. CVaR. half [1],] #веса ценных бумаг в
портфеле минимального риска полугодовые данные
char. min. CVaR. half<-c (dohodnost.
half [min. CVaR. half [1]], CVaR. half [min. CVaR. half [1]], VaR. half [min.
CVaR. half [1]], znach. koef. half [min. CVaR. half [1]]) #характеристики портфеля минимального риска
полугодовые данные(char. min. CVaR. half) < - c ("Доходность",
"CVaR ","VaR ","Коэффициент")
#Достижимое множество портфелей по Марковицу. doh. mark<-matrix
(nrow=1, ncol=Q) #Ожидаемые доходности каждого ПИФ
for (i in 1: Q) {. doh. mark [i] <-mean
(A [, i])
}. mark<-matrix (nrow=1,ncol=Z) #рисккаждогопортфеля. mark<-matrix
(nrow=1,ncol=Z) # доходностькаждогопортфеля
cov. matrix<-cov (A) #Ковариационная матрица ПИФ
for (a in 1: Z) {. mark [a] < - sum
(ogid. doh. mark*Y [a,])<-0(j in 1: Q) {(v in 1: Q) {<-ris+Y [a,j] *Y
[a,v] *cov. matrix [j,v]
}
}. mark [a] <-sqrt (ris)
}()(risk. mark^2, dohodnost. mark*100,
xlab="Рискпортфеля",ylab="Значенияожидаемойдоходности", main="ДостижимоемножествоМарковица")
#Оптимизация портфеля Markovitz на основе SharpRatio. koef.
mark<- (dohodnost. mark - riskfree. rate. day) /risk. mark #коэффициент
Шарпа Марковиц. koef. mark<-order (znach. koef. mark, decreasing = TRUE).
max. koef. mark< - Y [max. koef. mark [1],] #веса ценных бумаг в оптимальном
портфеле месячные данные. max. koef. mark<-c (dohodnost. mark [max. koef.
mark [1]], risk. mark [max. koef. mark [1]], znach. koef. mark [max. koef. mark
[1]]) #характеристики оптимального портфеля месячные данные(char. max. koef.
mark) < - c ("Доходность", "Риск ","Коэффициент")
#Портфель минимального риска по Марковицу. sigma. mark<-order
(risk. mark, decreasing = FALSE). min. sigma. mark< - Y [min. sigma. mark
[1],] #веса ценных бумаг в портфеле минимального риска по Марковицу. min.
sigma. mark<-c (dohodnost. mark [min. sigma. mark [1]], risk. mark [min.
sigma. mark [1]], znach. koef. mark [min. sigma. mark [1]]) #характеристики
портфеля минимального риска по Марковицу(char. min. sigma. mark) < - c
("Доходность", "Риск ","Коэффициент")
#Контрольная выборка, кумулятивные доходности и ковариационные
матрицы
kom. doh. kontr. month<-matrix
(nrow=1,ncol=Q)
kom. doh. kontr. kvart<-matrix (nrow=1,ncol=Q)
kom. doh. kontr. half<-matrix
(nrow=1,ncol=Q)
for (iin 1: Q) {. doh. kontr. month [i] <- (prod (1+B [1: 30,
i] /100) - 1) *100 # месячная кумулятивная доходность по контрольным данным.
doh. kontr. kvart [i] <- (prod (1+B [1: 90, i] /100) - 1) *100 # квартальная
кумулятивная доходность по контрольным данным. doh. kontr. half [i] <- (prod
(1+B [, i] /100) - 1) *100 # полугодовая кумулятивная доходность по контрольным
данным
}. ms. month<-cov (B [1: 30,]) #ковариационная матрица для
месяца по контрольным данным. ms. kvart< - cov (B [1: 90,]) #ковариационная
матрица для квартала по контрольным данным. ms. half< - cov (B)
#ковариационная матрица для полугодия по контрольным данным
#Сравнение оптимальных портфелей. mark. opt. month<-sum (portf.
max. koef. mark*kom. doh. kontr. month) #месячная доходность по портфелю
Марковица. mark. opt. kvart<-sum (portf. max. koef. mark*kom. doh. kontr.
kvart) #месячная доходность по портфелю CVaR. mark. opt. half<-sum (portf.
max. koef. mark*kom. doh. kontr. half) #квартальная доходность по портфелю
Марковица. CVaR. opt. month<-sum (portf. max. koef. month*kom. doh. kontr.
month) #квартальная доходность по портфелю CVaR. CVaR. opt. kvart< - sum
(portf. max. koef. kvart*kom. doh. kontr. kvart) #полугодовая доходность по
портфелю Марковица. CVaR. opt. half< - sum (portf. max. koef. half*kom. doh.
kontr. half) #полугодовая доходность по портфелю CVaR. mark. opt. month<-0. CVaR. opt.
month<-0. mark. opt. kvart<-0. CVaR. opt. kvart<-0. mark. opt.
half<-0. CVaR. opt. half<-0(j in 1: Q) {(v in 1: Q) {. mark. opt.
month< - ris. mark. opt. month + portf. max. koef. mark [j] * portf. max.
koef. mark [v] * cov. ms. month [j,v]. CVaR. opt. month<-ris. CVaR. opt.
month+ portf. max. koef. month [j] * portf. max. koef. month [v] * cov. ms.
month [j,v]. mark. opt. kvart< - ris. mark. opt. kvart+ portf. max. koef.
mark [j] * portf. max. koef. mark [v] * cov. ms. kvart [j,v]. CVaR. opt.
kvart< - ris. CVaR. opt. kvart+ portf. max. koef. kvart [j] * portf. max.
koef. kvart [v] * cov. ms. kvart [j,v]. mark. opt. half< - ris. mark. opt.
half+ portf. max. koef. mark [j] * portf. max. koef. mark [v] * cov. ms. half
[j,v]. CVaR. opt. half< - ris. CVaR. opt. half+ portf. max. koef. half [j] *
portf. max. koef. half [v] * cov. ms. half [j,v]
}
}. mark. opt. month<-sqrt (ris. mark.
opt. month) *sqrt (30) #месячныйрискпопортфелюМарковица. CVaR. opt. month<-sqrt
(ris. CVaR. opt. month) *sqrt (30) #месячныйрискпопортфелю CVaR. mark. opt. kvart<-sqrt (ris. mark. opt. kvart)
*sqrt (90) #квартальныйрискпопортфелюМарковица. CVaR. opt. kvart< - sqrt
(ris. CVaR. opt. kvart) *sqrt (90) #квартальныйрискпопортфелю CVaR. mark. opt. half< - sqrt (ris. mark. opt. half)
*sqrt (180) #полугодовойпопортфелюМарковица. CVaR. opt. half< - sqrt
(ris. CVaR. opt. half) *sqrt (180) #полугодовойрискпопортфелю CVaR
#Сравнениепортфелейсминимальнымриском. mark. min. month<-sum (portf. min.
sigma. mark*kom. doh. kontr. month) #месячнаядоходностьпопортфелюМарковица. mark. min. kvart<-sum (portf. min.
sigma. mark*kom. doh. kontr. kvart) #месячнаядоходностьпопортфелю CVaR. mark. min. half<-sum (portf.
min. sigma. mark*kom. doh. kontr. half) #квартальнаядоходностьпопортфелюМарковица. CVaR. min. month<-sum (portf. min.
CVaR. month*kom. doh. kontr. month) #квартальнаядоходностьпопортфелю CVaR. CVaR. min. kvart< - sum (portf.
min. CVaR. kvart*kom. doh. kontr. kvart) #полугодоваядоходностьпопортфелюМарковица. CVaR. min. half< - sum (portf. min.
CVaR. half*kom. doh. kontr. half) #полугодоваядоходностьпопортфелю CVaR. mark. min. month<-0. CVaR. min.
month<-0. mark. min. kvart<-0. CVaR. min. kvart<-0. mark. min.
half<-0. CVaR. min. half<-0(j in 1: Q) {(v in 1: Q) {. mark. min.
month< - ris. mark. min. month + portf. min. sigma. mark [j] * portf. min.
sigma. mark [v] * cov. ms. month [j,v]. CVaR. min. month<-ris. CVaR. min.
month+ portf. min. CVaR. month [j] * portf. min. CVaR. month [v] * cov. ms.
month [j,v]. mark. min. kvart< - ris. mark. min. kvart + portf. min. sigma.
mark [j] * portf. min. sigma. mark [v] * cov. ms. kvart [j,v]. CVaR. min.
kvart< - ris. CVaR.
min. kvart+ portf. min. CVaR. kvart [j] * portf. min. CVaR. kvart [v] * cov.
ms. kvart [j,v]. mark. min. half< - ris. mark. min. half+ portf. min. sigma.
mark [j] * portf. min. sigma. mark [v] * cov. ms. half [j,v]
ris. CVaR. min. half< - ris. CVaR. min.
half+ portf. min. CVaR. half [j] * portf. min. CVaR. half [v] * cov. ms. half
[j,v]
}
}. mark. min. month<-sqrt (ris. mark.
min. month) *sqrt (30) #месячныйрискпопортфелюМарковица. CVaR. min. month<-sqrt
(ris. CVaR. min. month) *sqrt (30) #месячныйрискпопортфелю CVaR. mark. min. kvart<-sqrt (ris. mark. min. kvart)
*sqrt (90) #квартальныйрискпопортфелюМарковица. CVaR. min. kvart< - sqrt
(ris. CVaR. min. kvart) *sqrt (90) #квартальныйрискпопортфелю CVaR. mark. min. half< - sqrt (ris. mark. min. half)
*sqrt (180) #полугодовойпопортфелюМарковица. CVaR. min. half< - sqrt
(ris. CVaR. min. half) *sqrt (180) #полугодовойрискпопортфелю CVaR
#Результаты. month<-matrix (nrow=3,ncol=4) #итоговая таблица с
месячными данными. kvart<-matrix (nrow=3,ncol=4) #итоговая таблица с
квартальными данными. half<-matrix (nrow=3,ncol=4) #итоговая таблица с полугодовыми
данными
tabl. month [1,] <-c (doh. mark. opt.
month, doh. CVaR. opt. month, doh. mark. min. month, doh. CVaR. min. month).
month [2,] <-c (ris. mark. opt. month, ris. CVaR. opt. month, ris. mark.
min. month, ris. CVaR. min. month). month [3,] < - (tabl. month [1,] -
riskfree. rate. month) / tabl. month [2,]
tabl. kvart [1,] <-c (doh. mark. opt. kvart, doh. CVaR.
opt. kvart, doh. mark. min. kvart, doh. CVaR. min. kvart). kvart [2,] <-c
(ris. mark. opt. kvart, ris. CVaR. opt. kvart, ris. mark. min. kvart, ris.
CVaR. min. kvart)
tabl. kvart [3,] < - (tabl. kvart [1,]
- riskfree. rate. kvart) / tabl. kvart [2,]. half [1,] <-c (doh. mark. opt.
half, doh. CVaR. opt. half, doh. mark. min. half, doh. CVaR. min. half). half
[2,] <-c (ris. mark. opt. half, ris. CVaR. opt. half, ris. mark. min. half,
ris. CVaR. min. half). half [3,] < - (tabl. half [1,] - riskfree. rate.
half) / tabl. half [2,]