Прогнозирование характеристик рынка базового актива
Оглавление
Введение
Глава 1. Теоретические аспекты ценообразования опционов и
извлечения риск-нейтральных вероятностей
1.1 Модели ценообразования опционов
.2 Извлечение риск-нейтральным вероятностей из цен опционов
Глава 2. Recovery theorem Стивена Росса
.1 Рассмотрение общей сути теоремы
.2 Модель с репрезентативным инвестором и вывод формулы
истинных вероятностей
Глава 3. Эмпирические результаты прогнозирования
характеристик рынка базового актива на примере индекса S&P500
.1 Рассмотрение проблем с эмпирическими данными
.2 Интерполяция с условием отсутствия арбитражных
возможностей
.3 Оптимизация
Заключение
Список использованных источников
Введение
Взаимосвязь риска и доходности является основой современных финансов. Так
как риск обычно измеряется в терминах волатильности, хорошо известно, что цены
опционов содержат информацию об этом риске. Одной из наиболее важных идей в
последние двадцать лет являлась идея того, что условную волатильность цены
актива можно извлечь из рыночных цен опционов, выписанных на данный актив.
Учитывая марковские ограничения, было показано, что риск-нейтральные переходные
вероятности также могут быть определены с помощью цен опционов. Относительно
недавно, в 2011 году вышла рабочая статья Стивена Росса, в которой он показал, что
можно также восстановить так называемые «натуральные» или «реальные» переходные
вероятности, используя для этого риск-нейтральные переходные вероятности с
некоторыми ограничениями на предпочтения. Данная работа посвящена получению
этих натуральных вероятностей перехода цены актива из одного состояния в
другое, учитывая проблему неполной информации по котировкам опционов.
Обобщенный подход к оценке распределения доходностей на финансовых рынках
является чисто статистическим. Обычно предполагается, что распределение
доходностей подчиняется какому-то параметрическому классу и используются
исторические наблюдения для оценки неизвестных параметров. Например,
предполагается, что доходности акции следуют нормальному распределению, и мы
оцениваем историческую премию за риск и исторические стандартные отклонения. В
дальнейшем, применяя полученные результаты для размещения своих активов,
предполагается, что будущие доходности зависят от исторически оцененных
распределений.
Однако, выплаты по финансовым инструментам ожидаются только в будущем, и
определенно их текущие рыночные цены содержат информацию о субъективном
распределении этих выплат. Перейдем к рассмотрению известной формулы
ценообразования опционов Блэка-Шоулза-Мертона:
 (1)
(1)
 (2)
(2)
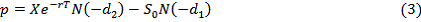 (3)
(3)
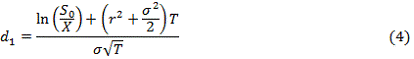 (4)
(4)
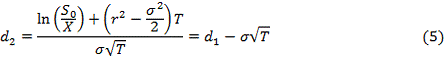 (5)
(5)
Заметим, что в формулах цены опциона call и опциона put не содержится показатель 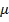 , который обозначает доходность акции. Хотя цена опциона
непосредственно связана с ценой базового актива, и любые колебания цены акции
сразу меняют рыночную цену опциона, из формулы Блэка-Шоулза-Мертона следует,
что доходность акции никак не связана с ценой опциона, и, соответственно,
используя цены опционов, невозможно получить никакую информацию о доходности
базового актива.
, который обозначает доходность акции. Хотя цена опциона
непосредственно связана с ценой базового актива, и любые колебания цены акции
сразу меняют рыночную цену опциона, из формулы Блэка-Шоулза-Мертона следует,
что доходность акции никак не связана с ценой опциона, и, соответственно,
используя цены опционов, невозможно получить никакую информацию о доходности
базового актива.
Данное замечание является несколько противоречивым. Возможно, можно
создать несколько другой класс моделей, в котором всё-таки можно будет связать
доходность по базовому активу и цену опциона.
В мировой научной литературе существует множество работ, посвященных
попытке извлечения из цен опционов какой-либо информации, способной предсказать
движение цены базового актива. Теория извлечения риск-нейтральных вероятностей
из цен опционов датируется работами конца 1970-ых (Ross [19], Breeden and Litzenberger [8]), однако практические
исследования по данной тематике начали проводиться на протяжении 1990-ых (Rubinstein [22], Jackwerth [16], Jackwerth and Rubinstein [17], Ait-Sahalia and Lo [1], Bahra [4] и Malz
[18] ). В особенности стоит выделить работу Jackwerth [16], в которой автор попытался
извлечь из цен опционов информацию о степени неприятия к риску, чтобы
впоследствии добавить ее к риск-нейтральным вероятностям для получения
истинного распределения вероятностей.
Дальнейшее развитие теории об извлечении информации о характеристиках
базового актива из цен опционов принадлежит Steve Ross. В его работе 2011 года (Ross [21]) была изложена совершенно новая теория,
позволяющая без использования исторических данных получить информацию об
истинном распределении вероятностей базового актива в будущем. Так, например, с
помощью его теории можно будет сказать, что вероятность роста стоимости
базового актива через месяц на 5% составляет 15%. В качестве основы работы была
использована модель с репрезентативным инвестором, который решает проблему
оптимизации полезности в двухпериодной модели. Ключевым предположением модели
является гомогенность предпочтений инвестора, то есть предпочтения не меняются
во времени. Ross решил проблему извлечения истинных
вероятностей в дискретном пространстве состояний рынка и сформулировал в
теореме «Recovery Theorem» набор условий, при которых данная проблема имеет
решение. Данная работа вызвала большой резонанс, и впоследствии данной проблеме
уделили внимание Carr and Yu [10] и Backwell [3]. Стоит отметить, что Carr and Yu попытались решить данную проблему в
непрерывном пространстве состояний.
Одной из основных трудностей в извлечении истинных вероятностей из цен
опционов является проблема нехватки данных. Для применения Recovery Theorem необходимо иметь полный набор опционов по страйкам и
периодам к погашению, причем требуемый набор опционов должен отличаться друг от
друга фиксированными приращениями как по страйкам, так и по периодам к
погашению. Учитывая, что на рынке не существует такой полной информации,
применение Recovery Theorem становится практически невозможным.
Таким образом, данная тема является весь актуальной. Была выдвинута абсолютно
новая теория, позволяющая прогнозировать движение базового актива, не используя
исторические данные. Кроме того, учитывая обозначенные проблемы, данная теория
открывает большой простор для новых научных работ по данной тематике.
Целью данной работы является получение истинных вероятностей перехода
стоимости базового актива с помощью использования методов интерполяции и
оптимизации.
Для достижения данной цели были поставлены следующие задачи, определяющие
состав и логику настоящей работы:
· Построить модели поверхности волатильности опционов;
· С помощью построенных моделей интерполировать подразумеваемые
волатильности на нужных страйках и периодах к погашению;
· Перейти от подразумеваемых волатильностей к ценам опционов call;
· Проверить полученные цены опционов call на условие отсутствия арбитражных возможностей и
выбрать наилучшую интерполяционную модель для дальнейшего использования;
· Получить матрицу цен Эрроу-Дебре из цен опционов call, полученных с помощью наилучшей
интерполяционной модели;
· С помощью оптимизации по методу наименьших квадратов с
набором ограничений перейти от матрицы Эрроу-Дебре к матрице переходных цен
Эрроу-Дебре;
· Применить к полученной матрице переходных цен Эрроу-Дебре Recovery Theorem и, таким образом, получить матрицу истинных
вероятностей перехода значений базового актива из одного состояния рынка в
другое.
Объектом исследования является биржевое значение индекса S&P500.
Предметом исследования выступают цены опционов call, выписанных на индекс S&P500.
Методология исследования основана на интерполяционных методах и
оптимизации с ограничениями.
Структура данной работы состоит из введения, трех глав, заключения и
списка использованных источников.
Во введении были сформулированы цели и задачи данной работы, объект и
предмет исследования, была обоснована ее актуальность. Также рассматривалась
степень разработанности данной темы и были выявлены основные проблемы.
Первая глава посвящена теоретическим аспектам ценообразования опционов и
риск-нейтральным вероятностям. В ней рассматривается классическая теория
ценообразования опционов по Блэку-Шоулзу-Мертону и вывод риск-нейтральных
вероятностей из цен опционов.
Вторая глава посвящена теории восстановления истинных вероятностей из цен
опционов, предложенной Steve Ross.
Рассматриваются основные предпосылки модели и объясняется концепция переходных
цен Эрроу-Дебре и их дальнейшее использование для получения истинных
вероятностей с помощью теоремы Перрона-Фробениуса.
Третья глава посвящена практическому решению проблемы с нехваткой данных.
Предлагаются четыре интерполяционных метода для получения цен опционов call с требуемыми страйками и периодами к
погашению. Каждая интерполяционная модель исследуется на соответствие условию
отсутствия арбитражных возможностей и затем выбирается наилучшая модель. Затем
решается проблема оптимизации для перехода к матрице переходных цен
Эрроу-Дебре, из которой потом с помощью Recovery Theorem осуществляется получение истинных вероятностей
перехода значений базового актива из одного состояния рынка в другое.
В заключении подводятся итоги исследования, рассматриваются слабые места
работы, и предлагаются направления для дальнейшего исследования.
Глава 1. Теоретические аспекты ценообразования опционов и извлечения
риск-нейтральных вероятностей
.1 Модели ценообразования опционов
Опцион - это производный финансовый инструмент, стоимость которого
зависит от стоимости другого, как его еще называют, базового актива. Примерами
базового актива могут служить акции, фьючерсы, процентные ставки и прочие
переменные.
Можно выделить два вида опционов: на покупку, или call опционы, и на продажу, или put опционы. Call опцион дает своему владельцу право в определенный
момент времени в будущем купить базовый актив по оговоренной в контракте цене.
Соответственно, put опцион дает
его владельцу право в определенный момент в будущем продать базовый актив по
оговоренной в контракте цене. Зафиксированная в контракте цена, по которой
владелец опциона может его исполнить, называется страйком, или ценой исполнения
опциона. Зафиксированная в контракте дата называется периодом экспирации или
датой истечения контракта. В зависимости от времени, когда можно исполнить
опционный контракт, можно выделить «европейские» и «американские» опционы.
Опцион называется «американским», если его можно исполнить в любой день до
периода экспирации, и «европейским», если его можно исполнить только в день
экспирации. В данной работе мы будем работать только с европейскими опционами.
Как можно заметить, на фондовом и срочном рынке цены активов подчиняются
стохастическому процессу, то есть изменяются во времени непредсказуемо. Если
цена актива может изменяться в любой момент времени, то мы имеем дело со
стохастическим процессом с непрерывным временем. Напротив, стохастический
процесс с дискретным временем характеризует поведение цены актива, который
может изменяться только в фиксированные моменты времени. Если же рассматривать
сами изменения цены актива, то он может принимать как фиксированные значения,
когда сам процесс является дискретным, так любые значения в определенном
интервале, когда процесс является непрерывным. Для того, чтобы перейти к
ценообразованию европейских опционов, необходимо рассмотреть именно
стохастический процесс с непрерывным временем и непрерывной переменной.
Рассмотрим некоторую переменную 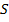 , которая изменяется с течением времени. Считается, что
переменная
, которая изменяется с течением времени. Считается, что
переменная 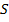 следует марковскому процессу, если выполняются следующие
условия:
следует марковскому процессу, если выполняются следующие
условия:
· Будущее значение переменной 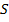 зависит от ее текущего значения;
зависит от ее текущего значения;
· Будущее значение переменной 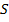 не зависит от ее прошлых значений.
не зависит от ее прошлых значений.
В академической среде принято считать, что поведение цены акции
подчиняется марковскому процессу, то есть цена акции в будущем зависит только
от ее текущего значения, и не зависит от ее прошлых значений.
В рамках марковского процесса поведение цены акции соответствует слабой
форме рыночной эффективности [12]. Это значит, что цена акции содержит всю
информацию о своих предыдущих значениях.
Рассмотрим некоторую переменную, которая следует стохастическому марковскому
процессу. Пусть ее начальное значение равно 10, а изменение переменной в
течение года описывается следующий функцией 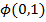 , где
, где 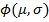 - нормальное вероятностное
распределение с математических ожидание
- нормальное вероятностное
распределение с математических ожидание 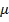 и стандартным отклонением
и стандартным отклонением 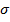 . Рассмотрим распределение
вероятностей за 2 года. В этом случае изменение переменной уже будет
описываться суммой двух нормальных распределений. Учитывая то, что переменная
следует марковскому процессу, то данные два распределение не зависят друг от
друга. Поэтому складывая два нормальные распределения получим, что изменение
переменной за 2 года будет описываться нормальным распределением, математическое
ожидание которого является суммой математических ожиданий частных
распределений, а дисперсия - суммой дисперсий частных распределений. В итоге,
изменение переменной за 2 года описывается случайной величиной с распределением
вероятностей
. Рассмотрим распределение
вероятностей за 2 года. В этом случае изменение переменной уже будет
описываться суммой двух нормальных распределений. Учитывая то, что переменная
следует марковскому процессу, то данные два распределение не зависят друг от
друга. Поэтому складывая два нормальные распределения получим, что изменение
переменной за 2 года будет описываться нормальным распределением, математическое
ожидание которого является суммой математических ожиданий частных
распределений, а дисперсия - суммой дисперсий частных распределений. В итоге,
изменение переменной за 2 года описывается случайной величиной с распределением
вероятностей 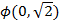 . В общем случае, изменение переменной за период времени
. В общем случае, изменение переменной за период времени 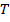 описывается функцией
описывается функцией 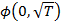 [15, с.260].
[15, с.260].
Частным случаем стохастического марковского процесса является винеровский
процесс, который характеризуется нулевым математическим ожиданием изменения
переменной, и единичной дисперсией. Считается, что переменная 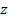 следует винеровскому процессу, если
выполняются следующие условия:
следует винеровскому процессу, если
выполняются следующие условия:
· На протяжении периода времени 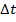 изменение переменной
изменение переменной 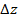 удовлетворяет равенству:
удовлетворяет равенству: 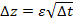 , где
, где 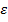 - случайная величина, которая
подчиняется стандартному нормальному распределению
- случайная величина, которая
подчиняется стандартному нормальному распределению 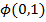 ;
;
· Величины 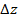 на двух малых промежутках времени
на двух малых промежутках времени 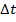 удовлетворяют условию независимости.
удовлетворяют условию независимости.
Первое условие говорит о том, что переменная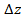 имеет математическое ожидание,
равное нулю, и стандартное отклонение, равное
имеет математическое ожидание,
равное нулю, и стандартное отклонение, равное 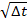 . Второе свойство означает, что
переменная
. Второе свойство означает, что
переменная 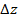 обладает марковским свойством [15, с.261].
обладает марковским свойством [15, с.261].
Как можно заметить, винеровский процесс не совсем подходит для описания
движения цены финансовых активов, так как он полностью состоит из случайной
компоненты. Рассмотрим обобщенный случай винеровского процесса, который также
включает компонент, отвечающий за фиксированные изменения переменной за
промежуток времени. В дальнейшем перейдем к пределу по переменной времени, и
при 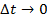 изменение переменной
изменение переменной 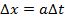 будем представлять в виде
будем представлять в виде 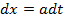 .
.
Обобщенный винеровский процесс для переменной 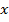 определяется как:
определяется как:
 (6)
(6)
где 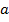 и
и 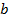 - константы. Коэффициент сноса, или скорость дрейфа
стохастического процесса характеризует среднее изменение переменной за единицу
времени. Коэффициент сноса обобщенного винеровского процесса равен
- константы. Коэффициент сноса, или скорость дрейфа
стохастического процесса характеризует среднее изменение переменной за единицу
времени. Коэффициент сноса обобщенного винеровского процесса равен 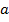 . Коэффициентом диффузии, или
дисперсией стохастического процесса называется величина колебаний за единицу
времени.
. Коэффициентом диффузии, или
дисперсией стохастического процесса называется величина колебаний за единицу
времени.
Рассмотрим данные компоненты по отдельности. Отбросим стохастическую
составляющую и заново перепишем уравнение:
 (7)
(7)
 (8)
(8)
Интегрируя данное уравнение по переменной времени, получим:
 (9)
(9)
где 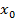 - начальное значение в нулевой момент времени. То есть за
период времени
- начальное значение в нулевой момент времени. То есть за
период времени 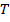 переменная
переменная 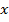 увеличивается на величину
увеличивается на величину 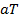 .
.
Второй член обобщенного винеровского процесса представляет собой шум
вокруг линии тренда. Заметим, что величина этого шума в 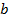 раз больше винеровского процесса.
Пример переменой
раз больше винеровского процесса.
Пример переменой 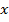 , следующей обобщенному винеровскому процессу изображен на
следующем рисунке 1.
, следующей обобщенному винеровскому процессу изображен на
следующем рисунке 1.
На малых интервалах времени изменение переменной 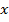 описывается уравнением:
описывается уравнением:
 (10)
(10)
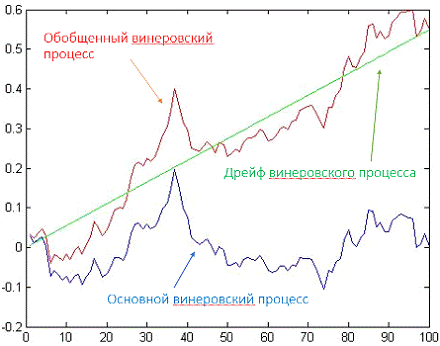
Рисунок 1: Обобщенный винеровский процесс
Аналогично вышепредставленным рассуждением, изменение переменной 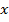 за период времени
за период времени 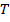 описывается нормальным Гауссовским
распределением с математическим ожиданием, равным
описывается нормальным Гауссовским
распределением с математическим ожиданием, равным 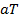 , и среднеквадратическим отклонением,
равным
, и среднеквадратическим отклонением,
равным 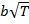 [15, с.264].
[15, с.264].
Для вывода формулы ценообразования опционов по Блэку-Шоулзу необходимо
рассмотреть еще один случайный процесс, отличающийся тем, что его коэффициенты
сноса и диффузии также являются зависимыми переменными от переменной 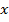 и времени
и времени 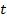 . Данный стохастический процесс
называется процесс Ито. Его можно выразить следующим уравнением:
. Данный стохастический процесс
называется процесс Ито. Его можно выразить следующим уравнением:
 (11)
(11)
где показатели 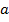 и
и 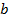 зависят от переменной
зависят от переменной 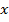 и времени
и времени 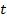 . Переходя к небольшим промежутком времени, данное уравнение
можно переписать как:
. Переходя к небольшим промежутком времени, данное уравнение
можно переписать как:
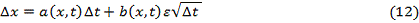 (12)
(12)
C
небольшой натяжкой, математическое ожидание и дисперсия данного процесса на
промежутке времени от 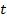 до
до 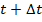 являются постоянными величинами. Они равны
являются постоянными величинами. Они равны 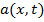 и
и 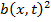 соответственно.
соответственно.
Цена опциона зависит от времени и значения цены базовой акции. Как и все
производны финансовые инструменты, цена опциона является функцией от
стохастических переменных и времени. Таким образом, для дальнейшего вывода
формулы цены опциона необходимо обратить внимание на в целом на свойства тех
функций, которые зависят от случайных факторов [15, с.265].
В 1951 году японский математик Киёси Ито получил важный результат,
который известен как лемма Ито:
Важный результат в связи с этим получен японским математиком Киёси Ито в
1951 году. Он известен как лемма Ито. Вернемся снова к процессу Ито. Лемма Ито,
утверждает, что существует некая функция 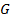 , которая зависит от переменных
, которая зависит от переменных 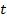 и
и 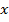 и подчиняется следующему
стохастическому процессу:
и подчиняется следующему
стохастическому процессу:
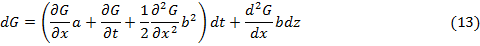 (13)
(13)
Коэффициент сноса функции 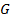 равен
равен
 (14)
(14)
А дисперсия
 (15)
(15)
Данную лемму в дальнейшем мы будем использовать для вывода цены опциона
[15, с.269]. Пока же применим рассмотренные выше теоретические посылки к
ценовому процессу акции. Может показаться разумным использовать обобщенный
винеровский процесс для описания движения цены акции, когда коэффициент сноса
считается постоянной величиной. В данном случае получается, что ожидаемая
доходность зависит от цены акции, однако инвестор планирует получить одну и ту
же ожидаемую доходность независимо от того, сколько на данный момент стоит
акция: 10$, 20$ или 50$.
Заменим предположение о постоянном коэффициенте снова на предположение о
постоянной ожидаемой доходности. В данном случае имеется ввиду ожидаемый
коэффициент сноса, деленный на цену акции. Ожидаемая скорость дрейфа равняется 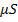 ,
, 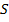 - цена акции в момент времени
- цена акции в момент времени 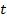 ,
, 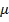 - константа. Предполагая, что дисперсия равна нулю, через
период времени
- константа. Предполагая, что дисперсия равна нулю, через
период времени 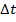 цена акции возрастет на
цена акции возрастет на 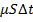 , иначае говоря:
, иначае говоря:
 (16)
(16)
При стремлении 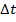 к нулю, получим:
к нулю, получим:
 (17)
(17)
 (18)
(18)
Интегрируя данное выражение по переменной времени от 0 до 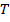 , получим:
, получим:
 (19)
(19)
Смысл данного равенства в том, что при отсутствии дисперсии стоимость
акции за период времени 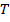 увеличивается на величину процентной ставки
увеличивается на величину процентной ставки 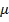 .
.
Однако в реальном мире цены финансовых активов подвержены колебаниям.
Волатильность дохода за период времени 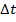 должна быть постоянной в не
зависимости от цены актива. Следовательно, дисперсия акции должна быть прямо
пропорциональна ее цене [15, с.267]. Отсюда, получим:
должна быть постоянной в не
зависимости от цены актива. Следовательно, дисперсия акции должна быть прямо
пропорциональна ее цене [15, с.267]. Отсюда, получим:
 (20)
(20)
 (21)
(21)
Данную формулу обычно используют для моделирования цены акции с помощью
метода Монте-Карло. Применим к данной формуле лемму Ито:
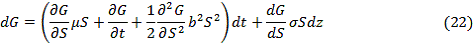 (22)
(22)
Заметим, что значения 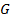 и
и 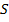 имеют зависимость от одного источника неопределенности
имеют зависимость от одного источника неопределенности 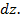 Данное замечание будет важным для
получения результатов Блэка-Шоулза-Мертона.
Данное замечание будет важным для
получения результатов Блэка-Шоулза-Мертона.
Прежде чем начать непосредственный вывод формулы ценообразования
опционов, рассмотрим основные предпосылки модели:
· Цена базового актива следует стохастическому процессу, где 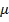 и
и 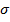 - константы;
- константы;
· Сделки по ценным бумагам совершаются бесплатно, нет учета
налогов;
· Дивиденды не выплачиваются;
· Нет возможности арбитража;
· Разрешено продавать ценные бумаги без покрытия;
· r - безрисковая процентная ставка, которая является постоянной
для всех сроков погашения.
В модели Блэка-Шоулза предполагается, что цена базового актива
описывается следующим стохастическим процессом:

Обозначая цену опциона call
через 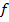 и, применяя лемму Ито, получим:
и, применяя лемму Ито, получим:

Учитывая, что цена опциона, 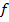 , и цена акции,
, и цена акции, 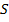 , зависят от одного стохастического источника
, зависят от одного стохастического источника 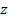 , можно составить линейную комбинацию
из данных активов таким образом, чтобы исключить винеровский процесс. Таким
образом, мы получим портфель, свободный от риска.
, можно составить линейную комбинацию
из данных активов таким образом, чтобы исключить винеровский процесс. Таким
образом, мы получим портфель, свободный от риска.
Для того, чтобы исключить винеровский процесс следует купить акции в
пропорции 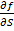 при продаже одного опциона
при продаже одного опциона 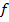 . Обозначая стоимость созданного
портфеля как
. Обозначая стоимость созданного
портфеля как 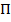 , получим:
, получим:

Изменение стоимости портфеля за период времени 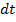 имеет вид:
имеет вид:

Заменяя приращения цены опциона и акции в (26) соответствующими
выражениями из (23) и (24), получим:
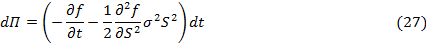
В данном уравнение отсутствует случайный компонент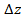 , следовательно на временном
интервале
, следовательно на временном
интервале 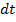 созданный портфель является безрисковым. Такой портфель
должен приносить инвестору доходность, равную безрисковой процентной ставке
созданный портфель является безрисковым. Такой портфель
должен приносить инвестору доходность, равную безрисковой процентной ставке 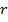 . Поэтому:
. Поэтому:

Подставляя в данное равенство значение стоимости портфеля (25) и
выражение для приращения стоимости портфеля (27), получим:
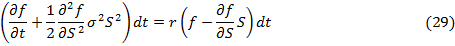
или
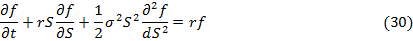
Таким образом, мы вывели дифференциальное уравнение Блэка-Шоулза-Мертона.
Данное уравнение имеет множество решений в зависимости от типа производного
финансового инструмента. Для того, чтобы получить конкретное решение для
определеного дериватива используются краевые условия по переменным 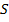 и
и 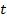 . Рассмотрим краевые условия для
европейского call
опциона:
. Рассмотрим краевые условия для
европейского call
опциона:
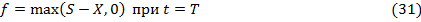
Для европейского put
опциона краевое условие таково:

Учитывая данные ограничения, получим формулы для определения цен
европейских опционов call и
put:

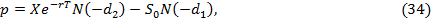
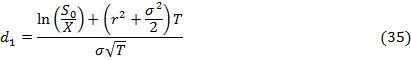
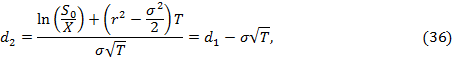
А 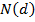 - функция распределения стандартного
нормального распределения
- функция распределения стандартного
нормального распределения
Переменные 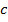 и
и 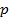 - это цены европейских опционов на покупку и продажу акций
соответственно,
- это цены европейских опционов на покупку и продажу акций
соответственно, 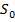 - первоначальная цена акции,
- первоначальная цена акции, 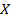 - цена исполнения,
- цена исполнения, 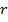 - непрерывно начисляемая безрисковая
процентная ставка,
- непрерывно начисляемая безрисковая
процентная ставка, 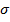 - волатильность цены акции,
- волатильность цены акции, 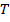 - время, оставшееся до завершения
срока действия опциона;
- время, оставшееся до завершения
срока действия опциона; 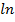 - функция натурального логарифма [5].
- функция натурального логарифма [5].
.2 Извлечение риск-нейтральным вероятностей из цен опционов
Рассмотрим основополагающие работы по риск-нейтральным вероятностям,
чтобы после перейти к теореме Стивена Росса. Огромный вклад был сделан
Douglas T. Breeden и Robert H. Litzenberger в их работе «Prices of State-Contingent Claims Implicit in Option
Prices», которая была опубликована в 1978 году в «The Journal of Business» [7].
В этой работе вводится понятие «элементарного требования» к ценной бумаге
или портфелю ценных бумаг. Под ним подразумевается такая ценная бумага, который
приносит $1.00 в назначенную дату, через период времени 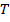 , если стоимость портфеля составит
, если стоимость портфеля составит 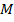 в это время. Если же стоимость
портфеля отличается от
в это время. Если же стоимость
портфеля отличается от 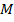 в период времени
в период времени 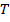 , то данное «элементарное требование»
не приносит ничего. По сути, данный финансовый инструмент представляет из себя
бинарный опцион, по которому тебе выплачивают один доллар при условии, что через
период времени
, то данное «элементарное требование»
не приносит ничего. По сути, данный финансовый инструмент представляет из себя
бинарный опцион, по которому тебе выплачивают один доллар при условии, что через
период времени 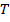 стоимость ценной бумаги или портфеля ценных бумаг будет
стоимость ценной бумаги или портфеля ценных бумаг будет 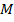 , и ничего в другом случае. Также
такие элементарные требования называют ценами Эрроу-Дебре.
, и ничего в другом случае. Также
такие элементарные требования называют ценами Эрроу-Дебре.
Данная глава посвящена выводу цены 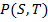 такого элементарного требования из
цен европейских опционов call
на базовый актив. Элементарное требование может быть создано с помощью длинных
и коротких позиций на опционы call с
различными ценами исполнения. Таким образом, ценой элементарного требования
является стоимость реплицирующего портфеля, состоящего из опционов, который
дает требуемые выплаты.
такого элементарного требования из
цен европейских опционов call
на базовый актив. Элементарное требование может быть создано с помощью длинных
и коротких позиций на опционы call с
различными ценами исполнения. Таким образом, ценой элементарного требования
является стоимость реплицирующего портфеля, состоящего из опционов, который
дает требуемые выплаты.
Предположим, что данные элементарные требования выписываются на
агрегированное потребление, которое представляет из себя рыночный портфель.
Также предположим, что стоимость рыночного портфеля через период времени 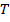 имеет дискретное вероятностное
распределение со следующими состояниями рынка:
имеет дискретное вероятностное
распределение со следующими состояниями рынка:

Обозначим вектор выплат по европейскому опциону call на рыночный портфель с периодом погашения, равным 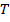 , и ценой исполнения
, и ценой исполнения 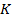 как
как 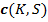 . А цену опциона обозначим как
. А цену опциона обозначим как 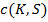 . Для опционов call с ценами исполнения, равными $0,
$1.00 и $2.00, соответствующие платежи, зависящие от состояния рынка,
представлены в следующей таблице:
. Для опционов call с ценами исполнения, равными $0,
$1.00 и $2.00, соответствующие платежи, зависящие от состояния рынка,
представлены в следующей таблице:
Таблица 1: Выплаты по опционов call

Заметим, что как только цены исполнения опциона call возрастают от 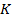 до
до 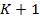 , два изменения происходят в векторе
платежей:
, два изменения происходят в векторе
платежей:
· Во первых, платеж, начиная с 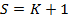 становится равен нулю;
становится равен нулю;
· Во-вторых, платежи во всех состояниях, начиная с 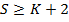 уменьшаются на изменение в цене
исполнения.
уменьшаются на изменение в цене
исполнения.
Таким образом, в этом примере 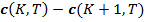 дает платеж в размере $1.00 в каждом
состоянии с
дает платеж в размере $1.00 в каждом
состоянии с  , и
, и 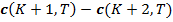 дает платеж в размере $1.00 в каждом состоянии для которых
дает платеж в размере $1.00 в каждом состоянии для которых 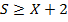 .
.
Ценная бумага, по которой платеж будет в размере $1.00 будет
выплачиваться только если 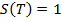 , может быть создана как
, может быть создана как 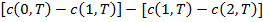 , так как эта комбинация опционов call будет иметь следующий вектор платежей:
, так как эта комбинация опционов call будет иметь следующий вектор платежей:
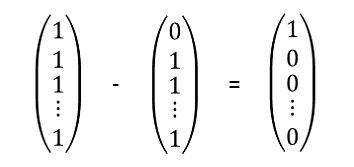
Рисунок 2: Вектор выплат по элементарному требованию
Элементарное требование для любого уровня рынка через период времени 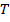 может быть создано в подобной
манере. Если даны цены коллов,
может быть создано в подобной
манере. Если даны цены коллов, 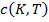 , цены элементарных требований на агрегированный спрос,
, цены элементарных требований на агрегированный спрос, 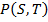 , могут быть рассчитаны с помощью
реплицированного портфеля, составленного из опционов call. Портфель, который приносит $1.00 только если рынок
равен
, могут быть рассчитаны с помощью
реплицированного портфеля, составленного из опционов call. Портфель, который приносит $1.00 только если рынок
равен 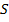 через период времени
через период времени 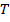 , состоит из длинной позиции по
опциону call с
, состоит из длинной позиции по
опциону call с 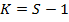 , длинной позиции по опциону call с
, длинной позиции по опциону call с 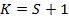 , и двумя короткими позициями по
опционам call с
, и двумя короткими позициями по
опционам call с 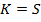 . Так, например, если
. Так, например, если 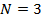 и цены опционов call равны
и цены опционов call равны 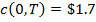 ,
, 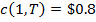 ,
, 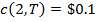 , тогда соответствующие цена
элементарных требований равны:
, тогда соответствующие цена
элементарных требований равны: 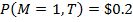 ,
, 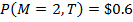 , и
, и 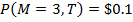 . Также, цена безрисковой дисконтной облигации с периодом
погашения
. Также, цена безрисковой дисконтной облигации с периодом
погашения 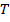 , которая приносит в конце $1.00 будет равна $0.2+$0.6+$0.1=$0.9.
, которая приносит в конце $1.00 будет равна $0.2+$0.6+$0.1=$0.9.
В общем, если размер шага между потенциальными значениями агрегированного
богатства равен 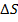 , тогда
, тогда 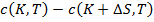 имеет платежный вектор с нулями для агрегированного
богатства
имеет платежный вектор с нулями для агрегированного
богатства 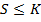 , и с
, и с 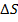 для всех уровней агрегированного богатства, большем или
равном
для всех уровней агрегированного богатства, большем или
равном 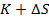
Таким образом, портфель из опционов колл, который приносит $1.00 если
рынок равен 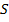 , и 0 в другом случае, равен:
, и 0 в другом случае, равен: 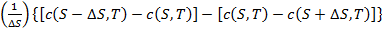 .
.
Так как портфель опционов call,
который дает выплату размером в $1.00 если агрегированное потребление будет
равно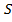 через период времени
через период времени 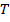 , то стоимость портфеля опционов call равна
, то стоимость портфеля опционов call равна 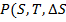 ). Так что, с размером шага в
). Так что, с размером шага в 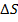 и ценами опционов
и ценами опционов 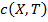 , стоимость портфеля опционов call
, стоимость портфеля опционов call 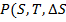 ), деленную на размер шага можно
будет записать как:
), деленную на размер шага можно
будет записать как:
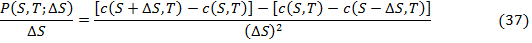
При размере шага, стремящемся к нулю, данная формула примет следующий
вид:
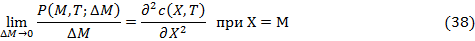
То есть, по сути, риск-нейтральные вероятности определяются второй
производной от функции цены опциона call, взятой по страйку [8. с.625-627].
ценообразование опцион интерполяция актив
Глава 2. Recovery theorem Стивена Росса
.1 Рассмотрение общей сути теоремы
С помощью исторических данных можно только оценить распределение
доходностей акций, однако с помощью цен опционов мы можем также обозревать
распределение цен Эрроу-Дебре. Цены Эрроу-Дебре являются продуктом неприятия к
риску, ценового ядра, и истинного вероятностного распределения. Recovery Theorem позволяет разделить все эти переменные для
определения прогноза доходности и неприятия к риску, используя только цены
Эрроу-Дебре. В общем, это позволяет восстановить ценовое ядро, рыночную премию
за риск.
Финансовый рынок устанавливает цены на ценные бумаги, платежи по которым
зависят от времени. Идея использования этих цен для прогноза будущих значений
волновала умы многих теоретиков и практиков.
Хотя существует богатый рынок опционов на акции и хорошо развитая теория о
том, как, используя их цены, получить риск-нейтральные вероятности, однако
существуют теоретические трудности в использовании этих вероятностей для
прогнозирования вероятностного распределения будущих доходностей, или как их
еще называют, реальных или истинных вероятностей.
Риск-нейтральные доходности являются истинными доходностями, которые были
скорректированы на риск. Под риск-нейтральной мерой, ожидаемые доходности по
всем активам равны риск-нейтральной ставке, так как доходность под
риск-нейтральной мерой равна доходности под истинной мерой за вычетом премии за
риск.
Премия за риск является функцией от частного риска и от рыночной
неприязни риску, и, таким образом, чтобы использовать риск-нейтральные цены для
оценивания истинных вероятностей мы должны знать корректировку на риск, чтобы
мы смогли добавить ее обратно. В моделях с репрезентативным агентом это
означает, что необходимо знать, как неприязнь к риску агента, так и
субъективное вероятностное распределение агента, и обе эти переменные нельзя наблюдать
напрямую. Однако, с помощью «калибровки» рыночных моделей, мы могли бы получить
их.
Невозможность определить текущий рыночный прогноз будущей доходности по
акциям является большой проблемой для научного сообщества. Так как нельзя
непосредственно получить эти прогнозы из цен, остается только использовать
исторические доходности и мнения экспертов и инвестором, пытаясь получить от
них информацию об их оцениваемых рыночных премиях.
Кажется очевидным, что данные премии за риск невозможно получить из цен
опционов, так как неуловимая премия за риск не появляется в результирующей
формуле цены опциона.
Но не всё так прискорбно. Используя модель с репрезентативным инвестором,
и набор предположений, всё-таки можно использовать цены опционов для извлечения
данной премии за риск, и получения истинного вероятностного пространства.
2.2 Модель с репрезентативным инвестором и вывод формулы
истинных вероятностей
В своей работе Steve Ross [19]
рассматривает именно дискретное вероятностное пространство состояния. Хотя были
попытки получить истинные вероятности с помощью непрерывного пространства
состояний [9], даже работа с дискретными данными вызывает множество вопросов.
Поэтому в данной работе будем использовать дискретное вероятностное просранство
состояний.
Рассмотрим дискретное вероятностное пространство с функцией выплат 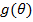 в период времени Т, зависящее от
реализации состояния природы,
в период времени Т, зависящее от
реализации состояния природы, 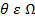 . Из фундаментальной теоремы ценообразования активов [20],
отсутствие арбитража подразумевает существование позитивных цен Эрроу-Дебре,
. Из фундаментальной теоремы ценообразования активов [20],
отсутствие арбитража подразумевает существование позитивных цен Эрроу-Дебре, 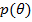 (или в генеральных пространствах,
ценовой функции распределения,
(или в генеральных пространствах,
ценовой функции распределения, 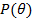 , по которой выплачивают $1.00 в состоянии
, по которой выплачивают $1.00 в состоянии 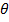 и ничего в любых других состояниях).
Если рынок является полным, тогда эти цены Эрроу-Дебре являются уникальными.
Текущее значение,
и ничего в любых других состояниях).
Если рынок является полным, тогда эти цены Эрроу-Дебре являются уникальными.
Текущее значение, 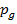 , актива, по которому выплачивается
, актива, по которому выплачивается 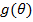 через один период времени можно
задать следующей формулой:
через один период времени можно
задать следующей формулой:

Так как сумма цен Эрроу-Дебре является дисконтированной стоимостью
будущего доллара, пусть 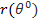 обозначает безрисковую ставку, как функцию от текущего
состояния,
обозначает безрисковую ставку, как функцию от текущего
состояния, 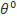 тогда мы можем переписать данное равенство в привычной для
нас форме:
тогда мы можем переписать данное равенство в привычной для
нас форме:
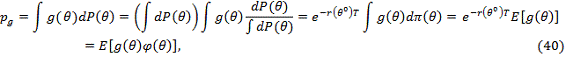
где 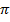 обозначает математическое ожидание мартингальной меры, а
обозначает математическое ожидание мартингальной меры, а 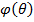 обозначает ценовое ядро, которое
представляет из себя отношение цены Эрроу-Дебре к вероятности, иначе говоря,
производную Радона-Никодима функции
обозначает ценовое ядро, которое
представляет из себя отношение цены Эрроу-Дебре к вероятности, иначе говоря,
производную Радона-Никодима функции 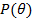 по истинной мере, которую в
дальнейшем будем обозначать как
по истинной мере, которую в
дальнейшем будем обозначать как 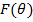 . Если рассматривать непрерывные распределения, то
. Если рассматривать непрерывные распределения, то 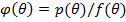 , где
, где 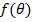 является истинной вероятностью, то
есть тем истинным субъективным вероятностным распределением, а риск-нейтральные
вероятности представляют собой [21, с.6]:
является истинной вероятностью, то
есть тем истинным субъективным вероятностным распределением, а риск-нейтральные
вероятности представляют собой [21, с.6]:
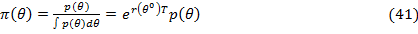
Чтобы перейти к самой сути теоремы Стивена Росса, сначала необходимо
ознакомиться с новым понятием, которое ввёл в своей работе профессор Росс - это
переходные цены Эрроу-Дебре. Отличительной особенность этих переходных цен
является то, что они описывают риск-нейтральные переходные вероятности из
любого состояния рынка и не только текущего состояния.
Предположим, что сейчас рынок находится в некотором состоянии 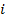 и мы хотим узнать цену бинарного
опциона, по которому мы имеем возможность получить $1, если рынок будет в
состоянии
и мы хотим узнать цену бинарного
опциона, по которому мы имеем возможность получить $1, если рынок будет в
состоянии 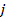 через год.
через год.
Пусть текущее состояние 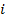 индекса S&P500 составляет 1600, а состояние
индекса S&P500 составляет 1600, а состояние 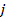 составляет 1450. Разобьем временной
интервал длительностью в один год на четыре части, и рассмотрим возможные
значения индекса в конце третьего квартала. Эти значения схематично
представлены на следующем рисунке.
составляет 1450. Разобьем временной
интервал длительностью в один год на четыре части, и рассмотрим возможные
значения индекса в конце третьего квартала. Эти значения схематично
представлены на следующем рисунке.
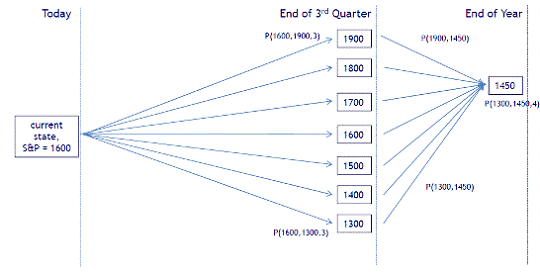
Рисунок 3: Возможные траектории достижения значения индекса 1450 через
год
На это рисунке представлены возможные траектории движения значений
индекса, при которых в конце года индекс будет принимать требуемое нам значение
в 1450 пунктов. Теперь представим, что мы имеем возможность купить бинарный
опцион, по которому нам выплачивают 1$, если значение индекса после третьего
квартала будет 1900 пунктов, а затем упадает до 1450 пунктов к концу года. То
есть в текущий момент времени мы можем зафиксировать стоимость актива, который
принесет нам 1$ при переходе из состояния рынка в 1900 пунктом в состояние
рынка в 1450 пунктов, при условии, что, достигая значение в 1450 пунктом в
конце года, траектория цена актива пройдет через значение в 1900 пунктов в
конце третьего квартала.
Пусть 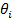 обозначает текущее состояние и
обозначает текущее состояние и 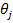 обозначает состояние на один
временной шаг вперед. Предполагая наличие всей возможной рыночной информации,
релевантной для определения будущей эволюции цены акции, обозначим зависимость
цены акции от состояния рынка как
обозначает состояние на один
временной шаг вперед. Предполагая наличие всей возможной рыночной информации,
релевантной для определения будущей эволюции цены акции, обозначим зависимость
цены акции от состояния рынка как 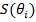 .
.
Из форвардного уравнения для мартингальных вероятностей, получим:
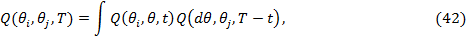
где 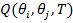 обозначает функцию форвардной мартингальной вероятности
перехода из состояния
обозначает функцию форвардной мартингальной вероятности
перехода из состояния 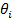 в состояние
в состояние 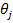 через период времени
через период времени 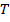 и где интеграл берется по
промежуточному состоянию
и где интеграл берется по
промежуточному состоянию 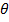 во время
во время 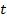 . Заметим, что функция перехода зависит от интервала времени
и не зависит от календарного времени.
. Заметим, что функция перехода зависит от интервала времени
и не зависит от календарного времени.
Это очень сильное предположение, говорящее о гомогенности предпочтений в
модели с репрезентативным инвестором. Оно позволяет сказать, что не только
форвардная мартингальная вероятность перехода из промежуточного состояния рынка
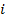 в состояние
в состояние 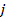 составляет, например, 10%. Но и если
бы мы в текущий момент времени находились в состоянии рынка
составляет, например, 10%. Но и если
бы мы в текущий момент времени находились в состоянии рынка 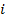 , то риск-нейтральная вероятность
перехода из текущего состояния в состояние
, то риск-нейтральная вероятность
перехода из текущего состояния в состояние 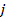 также составляла бы 10% [21, с.7].
также составляла бы 10% [21, с.7].
Это очень общая структура, которую можно по-разному интерпретировать.
Например, состояние может зависеть от различных факторов, описывающих движение
процесса цены базового актива, например, волатильности доходностей, 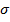 , и текущего значения цены акции,
, и текущего значения цены акции, 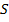 , так что,
, так что, 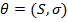 . Если распределение мартингальных
доходностей определяется только волатильностью, тогда переход можно будет
записать как движение из
. Если распределение мартингальных
доходностей определяется только волатильностью, тогда переход можно будет
записать как движение из 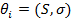 в
в 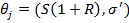 где
где 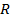 обозначает ставку доходности и
обозначает ставку доходности и
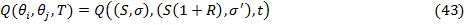
Чтобы упростить обозначения в дальнейшем будем использовать цены
Эрроу-Дебре вместо мартингальных вероятностей, чтобы избежать постоянной
корректировки на ставку процента. Определяя цены Эрроу-Дебре как
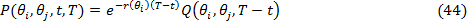
и предполагая процесс, гомогенный по времени, так чтобы он не зависил от
календарного времени, переход из любого периода времени 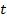 в период времени
в период времени 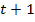 будет представлен как:
будет представлен как:

Учитывая, что значения элементарных требований 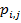 могут быть получены с рынка,
используя цены опционов call,
и учитывая предпосылку гомогенности предпочтений по времени, решая систему
линейных уравнений в которых фигурируют цены Эрроу-Дебре с различными периодами
погашения, мы можем получить риск-нейтральные вероятности перехода рынка из
одного состояния в другое.
могут быть получены с рынка,
используя цены опционов call,
и учитывая предпосылку гомогенности предпочтений по времени, решая систему
линейных уравнений в которых фигурируют цены Эрроу-Дебре с различными периодами
погашения, мы можем получить риск-нейтральные вероятности перехода рынка из
одного состояния в другое.
Полагая, что 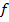 обозначает истинную (гомогенную по времени) вероятность
перехода из одного состояния рынка в другое, ядро в этой структуре определяется
как отношение цены к вероятности в непрерывных пространствах состояний:
обозначает истинную (гомогенную по времени) вероятность
перехода из одного состояния рынка в другое, ядро в этой структуре определяется
как отношение цены к вероятности в непрерывных пространствах состояний:

И эквивалентное утверждение об отсутствии арбитража гласит, что
существует позитивное ядро [21, с.8].
Каноническим примером данной модели может служить модель с
репрезентативным инвестором который принимает решение в двухпериодной модели
потребления и дисконтирующим фактором 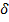 . Пусть
. Пусть 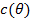 обозначает потребление в период времени
обозначает потребление в период времени 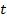 как функцию от состояния, тогда в
двухпериодной модели агент решает проблему максимизации полезности с
ограничениями:
как функцию от состояния, тогда в
двухпериодной модели агент решает проблему максимизации полезности с
ограничениями:
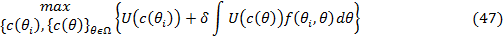
Ограничения:
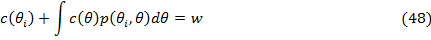
Условие первого порядка для оптимума дает нам интерпретировать ядро как:
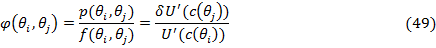
Вышепредставленное уравнение для ядра является равновесным решением для
экономики с полными рынками в которых, например, потребление является
экзогенным и цены определяются условием первого порядка для оптимума [21,
с.8-9].
Согласно Dybvig [13], ядро
является агентской предельной нормой субституции как функции от агрегированного
потребления.
Заметим, в этом примере ядро зависит только от предельной нормы замещения
между будущим и текущим потреблением. Данная независимость от «пути» (
марковское свойство) является ключевым элементов для анализа в работе Росса, и
предполагается, что ядро будет в форме (49). Оно является функцией от конечного
состояния, и зависит от начального состояния только путём деления для
нормализации.
Определение 1: ядро является независимым от перехода, если существует
позитивная функция от состояний, 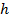 , и позитивная константа,
, и позитивная константа, 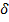 такие, что для любого перехода из
такие, что для любого перехода из 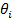 в
в 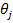 , ядро имеет форму
, ядро имеет форму

Межвременная аддитивная функция полезности является тем примером, который
генерирует ядро, независимое от перехода.
Используя независимость перехода, можно переписать данное выражение как:
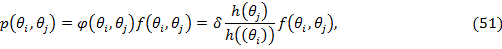
где 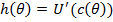 в модели с репрезентативным инвестором. Предполагая, что мы
наблюдаем функцию перехода цен Эрроу-Дебре,
в модели с репрезентативным инвестором. Предполагая, что мы
наблюдаем функцию перехода цен Эрроу-Дебре, 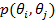 , нашей целью является решение данное
уравнения для восстановления трёх неизвестных: функции натуральной вероятности
перехода,
, нашей целью является решение данное
уравнения для восстановления трёх неизвестных: функции натуральной вероятности
перехода, 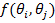 , ядра,
, ядра, 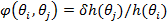 , и дисконтирующего фактора,
, и дисконтирующего фактора, 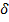 . Незавимость перехода является тем
ключевым фактором, который позволяет разделить ядро и натуральное вероятностное
распределение из (46). Без ограничений на ядро или натуральное распределение,
невозможно разделить их, зная только матрицу перехода цен Эрроу-Дебре.
. Незавимость перехода является тем
ключевым фактором, который позволяет разделить ядро и натуральное вероятностное
распределение из (46). Без ограничений на ядро или натуральное распределение,
невозможно разделить их, зная только матрицу перехода цен Эрроу-Дебре.
Перейдем к дискретным вероятностным пространствам, и в дальнейшем будем
работать именно в них для решения выше обозначенной проблемы. В дискретном
случае уравнение будет выглядеть следующим образом:

где мы можем интерпретировать

В целом, 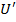 является любой позитивной функцией состояния. Записывая это
в терминах ядра и обозначая текущее состояние как
является любой позитивной функцией состояния. Записывая это
в терминах ядра и обозначая текущее состояние как 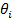 при
при 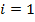 , получим
, получим

Состояния в дискретном случае определяются фильтрацией значений акции,
так что теперь ядро является проекцией более широкого пространства состояний на
более ограниченное пространство, определяемое фильтрацией цены актива. Заметим,
что хотя предельная полезность монотонно убывает в потреблении, она не должна
монотонно убывать в цене актива, 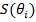 [21, с.9-10].
[21, с.9-10].
Переписывая уравнения состояний из (52) в матричной форме, получим:

где 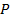 обозначает матрицу mxm перехода цен Эрроу-Дебре,
обозначает матрицу mxm перехода цен Эрроу-Дебре, 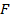 обозначает матрицу mxm натуральных вероятностей, а
обозначает матрицу mxm натуральных вероятностей, а 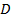 это диагональная матрица следующего
вида:
это диагональная матрица следующего
вида:
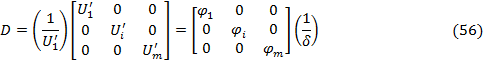
Используя дискретные пространства для цен Эрроу-Дебре, необходимо
убедиться, что отсутствует арбитраж. В модели с экзогенным потреблением
отсутствие арбитража является простым условием равновесия с позитивными ценами
Эрроу-Дебре,
Продолжая анализ, вспомним, что, обозревая переходные цены Эрроу-Дебре, 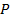 , наша цель найти хоть что-то, что
поможет нам узнать что-нибудь о натуральной мере,
, наша цель найти хоть что-то, что
поможет нам узнать что-нибудь о натуральной мере, 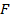 , и ценовом ядре, то есть предельной
норме замещения. Решая уравнение (55) для
, и ценовом ядре, то есть предельной
норме замещения. Решая уравнение (55) для 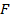 , получим:
, получим:

Понятно, что если мы узнаем D, то сразу же узнаем F.
Однако мы имеем 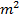 уравнений с
уравнений с 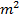 неизвестными вероятностями,
неизвестными вероятностями, 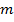 неизвестными предельными
вероятностями, и неизвестным дисконтирующим фактором,
неизвестными предельными
вероятностями, и неизвестным дисконтирующим фактором, 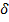 . Мы знаем риск-нейтральную меру,
однако без знания предельных норм замещения в каждом из состояний, не будет
никакой возможности решить систему уравнений и получить натуральную меру
. Мы знаем риск-нейтральную меру,
однако без знания предельных норм замещения в каждом из состояний, не будет
никакой возможности решить систему уравнений и получить натуральную меру 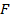 [21, с.12-13].
[21, с.12-13].
Однако, так как 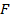 является матрицей, ряды которой являются вероятностями
перехода, и это стохастическая матрица, то есть, позитивная матрица, сумма
рядов которой равна единице, то появляется дополнительное число ограничений:
является матрицей, ряды которой являются вероятностями
перехода, и это стохастическая матрица, то есть, позитивная матрица, сумма
рядов которой равна единице, то появляется дополнительное число ограничений:

где 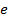 обозначает вектор с единицами во всех измерениях.
обозначает вектор с единицами во всех измерениях.
Используя это условия, получим:



Мы столкнулись с проблемой характеристического корня, и будем надеяться,
что решение данной проблемы будет дискретное. Однако с одним дальнейшим
ограничением, теорема внизу подтверждает, что это так. Из условия
безарбитражности, матрица 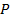 является неотрицательной. Также будем предполагать, что она
является несократимой, то есть все состояния являются достижимыми из всех
других состояний в
является неотрицательной. Также будем предполагать, что она
является несократимой, то есть все состояния являются достижимыми из всех
других состояний в 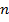 шагов. Например, если
шагов. Например, если 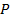 является позитивной, то она
несократима. Матрица
является позитивной, то она
несократима. Матрица 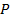 является несократимой, если всегда есть такой путь, что
любое состояния
является несократимой, если всегда есть такой путь, что
любое состояния 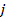 может быть достигнуто из любого состояния
может быть достигнуто из любого состояния 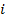 .
.
Разобрав предпосылки модели перейдем к формулировке The Recovery Theorem:
Если отсутствует арбитраж, если ценовая матрица является несократимой, и
если она создана ядром, независящим от перехода, тогда существует единственное
решение проблемы нахождения матрицы истинных вероятностей 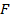 , дисконтирующего фактора
, дисконтирующего фактора 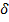 , и ценового ядра,
, и ценового ядра, 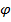 . Другими словами, для любого
заданного набора цен Эрроу-Дебре существует уникальная корреспондирующая
натуральная мера и уникальное ценовое ядро.
. Другими словами, для любого
заданного набора цен Эрроу-Дебре существует уникальная корреспондирующая
натуральная мера и уникальное ценовое ядро.
Доказательство: существование можно также доказать прямым способом, но
это непосредственно вытекает из того факта, что предполагается, что 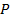 создана из
создана из 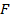 и
и 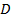 , как было показано чуть ранее.
Проблема нахождения
, как было показано чуть ранее.
Проблема нахождения 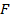 эквивалентна нахождению характеристических корней,
собственных значений, и характеристических векторов, собственных векторов,
матрицы
эквивалентна нахождению характеристических корней,
собственных значений, и характеристических векторов, собственных векторов,
матрицы 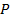 , так как если мы будем знать
, так как если мы будем знать 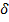 и
и 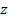 из
из

то ядро может быть найдено из 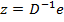 [21, с.14].
[21, с.14].
Из теоремы Перрона-Фробениуса [6] все неотрицательные несократимые
матрицы имеют уникальный позитивный характеристический вектор, 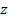 , и соотвествующий ему позитивный
характеристический корень,
, и соотвествующий ему позитивный
характеристический корень, 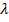 . Характеристический корень
. Характеристический корень 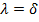 является субъективной ставкой
дисконтирования. Обозначая через
является субъективной ставкой
дисконтирования. Обозначая через 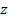 уникальный позитивный характеристический вектор с корнем
уникальный позитивный характеристический вектор с корнем 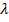 , мы можем найти ядро, так как
, мы можем найти ядро, так как
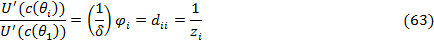
Чтобы получить натуральное вероятностное распределение, воспользуемся
нашем предыдущим анализом из (57), получим [21, с.16]:
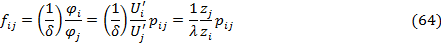
Глава 3. Эмпирические результаты прогнозирования характеристик рынка
базового актива на примере индекса S&P500
.1 Рассмотрение проблем с эмпирическими данными
Предположим, что рынок может описываться только тремя состояниями. Тогда
искомая матрица переходных вероятностей 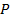 будет иметь размерность 3 на 3 и
представлять из себя:
будет иметь размерность 3 на 3 и
представлять из себя:

где каждый элемент матрицы представляет стоимость переходных цен
Эрроу-Дебре за один промежуток времени. Допустим данный промежуток равен одному
году.
Для того, чтобы найти данную матрицу необходимо найти с рынка матрицу цен
Эрроу-Дебре. Она будет представлять из себя:

Строки матрицы 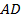 характеризуют возможные состояния рынка, а столбцы
характеризуют период времени, к которому данное состояние должно быть
достигнуто. Пусть в настоящее время рынок находится во втором состоянии. Тогда,
если мы купим бумагу Эрроу-Дебре
характеризуют возможные состояния рынка, а столбцы
характеризуют период времени, к которому данное состояние должно быть
достигнуто. Пусть в настоящее время рынок находится во втором состоянии. Тогда,
если мы купим бумагу Эрроу-Дебре 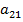 , это будет означать, что если в
течение одного года рынок останется во втором состоянии, то мы получим 1$. Если
же мы купим бумагу
, это будет означать, что если в
течение одного года рынок останется во втором состоянии, то мы получим 1$. Если
же мы купим бумагу 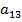 , то нам выплатят 1$ в случае, если рынок достигнет первого
состояния через три года.
, то нам выплатят 1$ в случае, если рынок достигнет первого
состояния через три года.
Учитывая то, что вторая строка матрицы 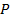 описывает вероятности перехода из
текущего состояния в другие через один год, то элементы данной строки должны
равняться элементам первого столбца матрицы
описывает вероятности перехода из
текущего состояния в другие через один год, то элементы данной строки должны
равняться элементам первого столбца матрицы 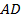 , иначе говоря:
, иначе говоря:

Для того, чтобы получить недостающие элементы матрицы 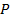 , необходимо решить следующую систему
уравнений:
, необходимо решить следующую систему
уравнений:
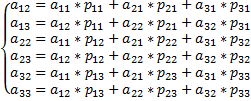
Учитывая то, что некоторые элементы матрицы 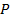 нам уже известны, перепишем систему
уравнений в виде:
нам уже известны, перепишем систему
уравнений в виде:
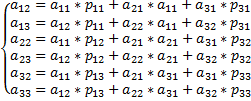
Первой задачей является получение матрицы цен Эрроу-Дебре 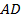 . Сложностью ее получения является
тот факт, что если мы хотим приблизить модель к реальности, то мы должны
рассматривать достаточное большое количество состояний рынка, а это значит, что
мы должны получить множество цен Эрроу-Дебре, которые будут отличаться друг от
друга по страйкам и периодом к погашению. Есть досточное количество опционов по
страйкам, чтобы сформировать цены Эрроу-Дебре на одном периоде к погашению.
Однако для того, чтобы создать цены Эрроу-Дебре отличающихся друг от друга
периодами к погашению с фиксированным изменением по переменной времени, данных
явно недостаточно.
. Сложностью ее получения является
тот факт, что если мы хотим приблизить модель к реальности, то мы должны
рассматривать достаточное большое количество состояний рынка, а это значит, что
мы должны получить множество цен Эрроу-Дебре, которые будут отличаться друг от
друга по страйкам и периодом к погашению. Есть досточное количество опционов по
страйкам, чтобы сформировать цены Эрроу-Дебре на одном периоде к погашению.
Однако для того, чтобы создать цены Эрроу-Дебре отличающихся друг от друга
периодами к погашению с фиксированным изменением по переменной времени, данных
явно недостаточно.
Так, если рассмотреть наиболее ликвидные опционные контракты на индекс S&P500, то мы увидим следующую картину. На 16 февраля 2016 года
котировались опционные контракты со следующими периодами к погашению:
Таблица 2: Периоды к погашению по опционам call на индекс S&P500 на 16.02.16
|
Exp Date
|
Exp Date
|
|
19.02.2016
|
17.06.2016
|
|
26.02.2016
|
30.06.2016
|
|
29.02.2016
|
29.07.2016
|
|
04.03.2016
|
16.09.2016
|
|
11.03.2016
|
30.09.2016
|
|
18.03.2016
|
20.01.2017
|
|
25.03.2016
|
16.06.2017
|
|
31.03.2016
|
15.12.2017
|
|
01.04.2016
|
21.12.2018
|
|
08.04.2016
|
31.12.2019
|
|
15.04.2016
|
31.12.2020
|
|
22.04.2016
|
31.12.2021
|
|
29.04.2016
|
30.12.2022
|
|
06.05.2016
|
29.12.2023
|
|
20.05.2016
|
31.12.2024
|
|
31.05.2016
|
31.12.2025
|
Как можно заметить, по переменной времени опционные контракты сильно
отличаются друг от друга, что не дает создать множество цен Эрроу-Дебре,
отличающихся друг от друга по переменой времени на фиксированную величину.
Беря за исходные данные поверхность волатильностей опционов на
фиксированную дату и построив модель опционной волатильности по двум
измерениям: по страйку и по периоду к погашению, мы можем применить
интерполяционные методы для нахождения теоретических подразумеваемых
волатильностей, из которых затем могут быть получены нужные нам цены
Эрроу-Дебре. Заметим, что интерполяция должна осуществляться, учитывая условие
безарбитражности.
Второй проблемой является возможное отсутствие прямого решения для
системы из линейных уравнений. Рассмотрим ее на конкретном примере.
Пусть матрица цен Эрроу-Дебре имеет вид:
|
State \ Tenor
|
1
|
2
|
|
1
|
0,8
|
0,6
|
|
2
|
0,15
|
0,25
|
Пусть в текущий момент времени рынок находится в 1 состоянии, тогда
матрица переходные вероятностей будет выглядить следующим образом:
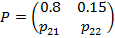
Отсюда, найдем искомые значения 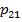 и
и 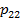 .
.
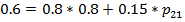
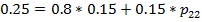
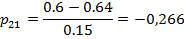
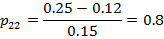
Учитывая условие неотрицательности матрицы, делаем вывод, что решение
системы линейных уравнений прямым способом может привести к результатам,
которые невозможно интерпретировать.
Для решения данной проблемы будем находить элементы матрицы 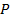 c помощью процедуры оптимизации, подбирая такие значения
элементов матрицы
c помощью процедуры оптимизации, подбирая такие значения
элементов матрицы 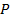 , при которых минимизировалась бы функция ошибок.
, при которых минимизировалась бы функция ошибок.
.2 Интерполяция с условием отсутствия арбитражных
возможностей
Перейдем к непосредственному изучению исходных данных и рассмотрению и
использованию методов интерполяции для получения необходимых теоретических цен
Эрроу-Дебре.
Peter Carr и Dilip B. Madan в своей
работе “A note on sufficient conditions for no arbitrage” сформулировали условия отсутствия
арбитража в ценах опционов. Отсутствие арбитражей по вертикальному спреду,
спреду батерфляй и календарному спреду является достаточным набором условий,
что исключить все статические арбитражи из набора цен опционов, котирующихся
как по страйкам, так и по периодам к погашению [11].
Отсутствие арбитражных возможностей является фундаментальным принципом,
лежащим в основе современной финансовой теории ценообразования. В особенности,
это концепция свойственна утверждению фундаментальной теоремы ценообразования
активов.
Предполагаем, что в зафиксированный момент времени у нас есть информация
о некоторых рыночных котировках европейских call опционов. В данном случае говорится о наборе
котировок, которые имеются по обоим направлениям: как по страйкам, так и по
периодам к погашению.
Пусть 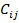 обозначает выбранную котировку опциона call для страйка
обозначает выбранную котировку опциона call для страйка 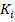 ,
, 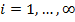 , и периода к погашению
, и периода к погашению 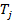 ,
, 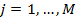 . Будем предполагать, что страйки
. Будем предполагать, что страйки 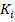 представляют собой возрастающую
положительную последовательность, также как и периоды к погашению
представляют собой возрастающую
положительную последовательность, также как и периоды к погашению 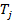 . Также будем предполагать, что
страйки
. Также будем предполагать, что
страйки 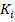 стремятся к бесконечности при
стремлении
стремятся к бесконечности при
стремлении 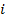 к бесконечности. Более того, расширим полученные котировки
опционов call котировками для опционов call со страйком
к бесконечности. Более того, расширим полученные котировки
опционов call котировками для опционов call со страйком 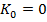 . Для каждого периода к погашению,
эти дополнительные котировки считаются равными
. Для каждого периода к погашению,
эти дополнительные котировки считаются равными 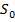 , текущей спот цене. Также
принимаются во внимание цены при периоде погашения
, текущей спот цене. Также
принимаются во внимание цены при периоде погашения 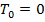 , равные
, равные 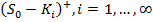 . В результате получаем расширенную
матрицу с ценами
. В результате получаем расширенную
матрицу с ценами 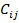 , где
, где 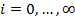 и
и 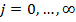 .
.
Для каждого 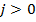 , запишем следующее равенство:
, запишем следующее равенство:
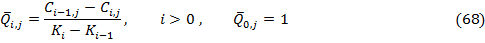
Для каждого 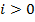 ,
, 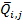 представляет собой стоимость вертикального спреда, который
по опредедению является длинной позицией по
представляет собой стоимость вертикального спреда, который
по опредедению является длинной позицией по 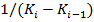 опционам call на страйке
опционам call на страйке 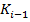 и короткой позиции по
и короткой позиции по 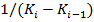 опционам call на страйке
опционам call на страйке 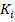 . График выплат по данной позиции по
отношению к граничным ценам акции говорит о том, что выплаты должны быть
ограничены снизу нулем и сверху единицей. Таким образом, первый тест
заключается в проверке для всех значений
. График выплат по данной позиции по
отношению к граничным ценам акции говорит о том, что выплаты должны быть
ограничены снизу нулем и сверху единицей. Таким образом, первый тест
заключается в проверке для всех значений 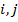 , что
, что 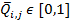
Далее, для всех значений 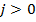 , запишем следующее выражение:
, запишем следующее выражение:
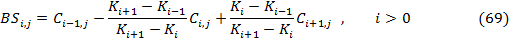
Для всех 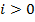 ,
, 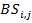 представляет собой стоимость спреда батерфляй, который
определяется как длинная позиция по опциону call на страйке
представляет собой стоимость спреда батерфляй, который
определяется как длинная позиция по опциону call на страйке 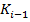 , короткая позиция по
, короткая позиция по 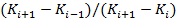 опционам call на страйке
опционам call на страйке 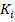 , и длинная позиция по
, и длинная позиция по 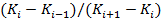 опционам call на страйке
опционам call на страйке 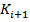 . Учитывая, что выплата по спреду
батерфляй является неотрицательной, сформулируем второй текс как:
. Учитывая, что выплата по спреду
батерфляй является неотрицательной, сформулируем второй текс как:
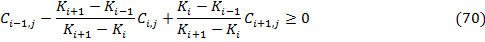
Иначе говоря, необходимо чтобы выполнялось следующее неравенство:
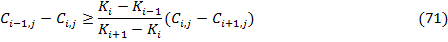
Третий, и финальный тест требует, чтобы для любого дискретного страйка 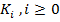 , и для любого дискретного периода к
погашению
, и для любого дискретного периода к
погашению 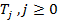 выполнялось следующее условие:
выполнялось следующее условие:
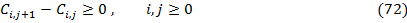
Левостороння часть неравенства представляет собой стоимость календарного
спреда, состоящего из длинной позиции по опциону call с периодом погашения 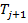 и короткой позиции по опциону call с периодом погашения
и короткой позиции по опциону call с периодом погашения 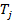 . Оба опциона имеют одинаковые
страйки, равные
. Оба опциона имеют одинаковые
страйки, равные 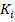 . Таким образом, третий тест предполагает, что календарные
спреды состоящие из соседних периодов к погашению не должны иметь отрицательную
стоимость на каждом периоде к погашению [11].
. Таким образом, третий тест предполагает, что календарные
спреды состоящие из соседних периодов к погашению не должны иметь отрицательную
стоимость на каждом периоде к погашению [11].
Теперь когда мы определились с условиями отсутствия арбитражных
возможностей, рассмотрим интерполяционные методы, которые в дальнейшем будут
использоваться в данной работе. Для интерполяции поверхности волатильностей
опционов будут использоваться следующие методы:
· Cubic splines
· Thin-plate splines
· Biharmonic splines
· Polynomial
Выбор данных методов не случаен. Так в работе Dumas and Fleming 1998 года «Implied Volatility Function: Empirical Test» были осуществлены попытки интерполировать
поверхность волатильности опционов с помощью полиномов [12]. В работе Zhou [24] рассмотрены возможные методы
интерполяции с помощью полиномиального метода, сплайнов, а также ядерных
регрессий. В работе Bliss and Panigirtzoglou [6] рассматривалась модель
натуральных сплайнов.
Рассмотрим каждый из этих методов в отдельности.
По определению, если даны 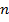 точек,
точек, 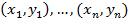 , то кубический сплайн представляет собой кусочно-заданную
функцию следующего вида:
, то кубический сплайн представляет собой кусочно-заданную
функцию следующего вида:
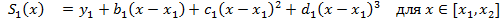

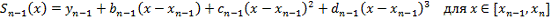
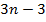 неизвестных выбираются таким образом, чтобы удовлетворять
интерполяционным ограничениям и также некоторым ограничениям гладкости:
неизвестных выбираются таким образом, чтобы удовлетворять
интерполяционным ограничениям и также некоторым ограничениям гладкости:
· Имея данные по функции 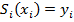 для параметра
для параметра 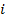 от
от 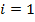 до
до 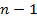 . В дополнении, искомая функция должна удовлетворять условию
непрерывности. Внутренние точки для
. В дополнении, искомая функция должна удовлетворять условию
непрерывности. Внутренние точки для 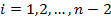 должны следовать этому равенству:
должны следовать этому равенству: 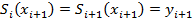 . Таким образом, здесь
. Таким образом, здесь 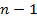 ограничений.
ограничений.
· Во внутренних точках должно выполняться: 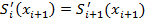 . Данное условие гладкости содержит
. Данное условие гладкости содержит 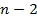 ограничений.
ограничений.
· Во внутренних точках должно выполняться: 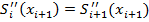 . Данное условие гладкости содержит
также
. Данное условие гладкости содержит
также 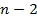 ограничений.
ограничений.
Таким образом, всего имеется 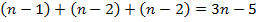 ограничений, однако неизвестных
переменных
ограничений, однако неизвестных
переменных 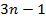 . Для нахождения искомых переменных нужно ввести еще два
ограничения. Стандартная процедура интерполяция кубическими сплайнами в среде Matlab вводит следующие два ограничения
[9]:
. Для нахождения искомых переменных нужно ввести еще два
ограничения. Стандартная процедура интерполяция кубическими сплайнами в среде Matlab вводит следующие два ограничения
[9]:
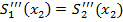
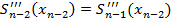
Хотя кубические сплайны широко используются для нахождения гладких кривых
[2] и поверхностей, которые проходят через набор неравномерно расположенных
точек, следует обратить внимание на интерполяционный метод с помощью бигармонических
сплайнов. С точки зрения физики, данный метод похож на попытку с помощью
оказания силового давления на эластичную поверхность заставить ее проходить
через заданные точки. Интерполяционная кривая или поверхность в данном случае
будут удовлетворять бигармоническому уравнению, и, таким образом, удовлетворять
условию минимальной кривизны.
Рассмотрим простой алгоритм нахождения поверхности минимальной кривизны,
которая проходит через набор неравномерно расположенных точек. Алгоритм основан
на функции Грина бигармонического оператора. Интерполяционная кривая или
поверхность в данном случае является линейной комбинацией функций Грина,
центрированных около каждой точки. Их амплитуды подбираются таким образом,
чтобы интерполированная поверхность проходила через все точки.
Хотя этот метод может быть относительно неэффективным и нестабильным, он
очень гибкий. Например, количество функций Грина может быть меньше чем
количество точек. Таким образом, интерполированная кривая или поверхность не
будет проходить через проблемные точки. Преимуществом является то, что данные
метод легко применяется к задачам интерполяции в трех и более измерениях.
Рассмотрим как работает данный метод в одном измерении. Проблема
заключается в нахождении бигармонической функции, которая проходит через 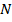 точек. Draftsmen в 19 веке решил данную проблему,
выбирая на эластичной пластине точки, и оказывая на них давление таким образом,
чтобы пластина проходила через нужные точки. Сила, приложенная на пластину
должна была заставить ее оставаться согнутой.
точек. Draftsmen в 19 веке решил данную проблему,
выбирая на эластичной пластине точки, и оказывая на них давление таким образом,
чтобы пластина проходила через нужные точки. Сила, приложенная на пластину
должна была заставить ее оставаться согнутой.
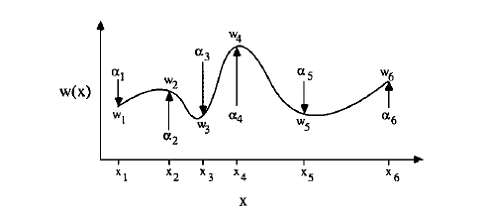
Рисунок 4. Пример бигармонической интерполяции
Функция Грина в точках давления должна удовлетворять бигармоническому
уравнению:

Частное решение данное уравнение представлено в виде:

Когда функция Грина используется для интерполяции 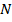 точек,
точек, 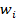 , расположенных на
, расположенных на 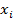 , проблема заключается в:
, проблема заключается в:


Частное решение для вышепредставленных уравнений представляет собой
линейную комбинацию функции Грина в точках приложения силы, центрированных
около каждой точки:

Согласно Sandwell [23],
сила в каждой точке, 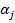 , находится из решения линейной системы (77):
, находится из решения линейной системы (77):

Перейдем к рассмотрению следующего интерполяционного метода, когда
используются Thin-plate splines. Название данного метода относится к физической
аналогии с участием тонкого гибкого листа металла. Подобно тому, как металл
имеет жесткость, и сопротивляется изгибам, также и подгонка методом thin-plate splines назначает штрафы за подобные изгибы, создавая гладкую
подогнанную поверхность.
Thin-plate spline представляет из себя следующую функцию:
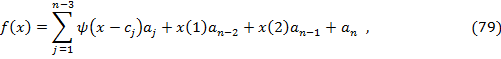
где 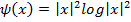 представляет собой базовую функцию thin-plate spline,
представляет собой базовую функцию thin-plate spline, 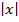 обозначает евклидовую длину вектора
обозначает евклидовую длину вектора 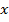 . Здесь независимая переменная
представлена с помощью
. Здесь независимая переменная
представлена с помощью 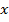 , причем в данном случае
, причем в данном случае 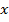 это вектор двух компонентов,
это вектор двух компонентов, 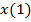 и
и 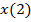 . Соответственно, узлы
. Соответственно, узлы 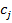 являются точками в
являются точками в 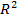 .
.
Оптимизация достигается, минимизируя следующее выражение:
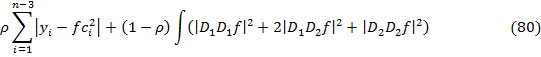
Минимизация идет по всем достаточно гладким функциям 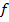 . Здесь
. Здесь 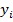 представляет собой значения данных
на узлах
представляет собой значения данных
на узлах 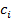 , а
, а 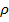 является сглаживающим параметром, и
является сглаживающим параметром, и 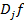 обозначает частную производную
функции
обозначает частную производную
функции 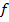 по переменной
по переменной 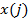 . Интеграл берется по всему
пространству
. Интеграл берется по всему
пространству 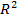 . Верхний предел оператора суммы,
. Верхний предел оператора суммы, 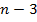 , отображает тот факт, что 3 степень
свободы thin-plate spline ассоциируется с его полиномиальной частью [9].
, отображает тот факт, что 3 степень
свободы thin-plate spline ассоциируется с его полиномиальной частью [9].
Последний использованный интерполяционный метод предполагает
использование полиномов для построение поверхности волатильности. Была
использована пятая степень полинома. Задача предполагает нахождение
коэффициентов в следующей функции, максимально приближающих модель к истинным данных
по методу наименьших квадратов:
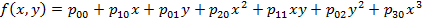
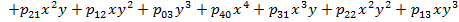
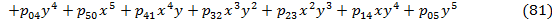
Исходными данными являются поверхность волатильности опционов на индекс S&P500, зафиксированная на 16.02.16. Данная поверхность
волатильности была получена из базы данных Bloomberg. Данная поверхность представляет
собой матрицу размером  , столбцы которой являются страйками, начиная от 563,721 и
заканчивая 5637,2. Столбцы матрицы являются периодами к погашению, начиная от
19.02.2016 и заканчивая 31.12.2018.
, столбцы которой являются страйками, начиная от 563,721 и
заканчивая 5637,2. Столбцы матрицы являются периодами к погашению, начиная от
19.02.2016 и заканчивая 31.12.2018.
Осуществляя построение поверхности волатильности с помощью рассмотренных
выше методов, были получены следующие модели:
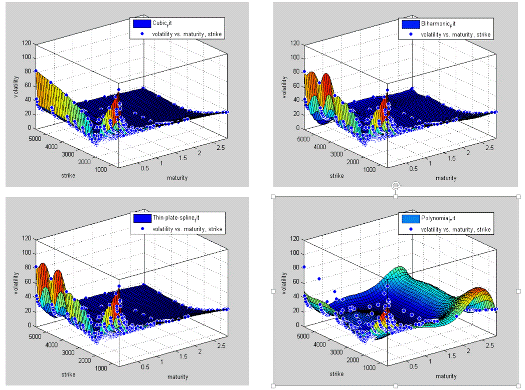
Рисунок 5. Построенные модели поверхности волатильности опционов
Прежде чем приступить к интерполяции волатильностей с помощью полученных
моделей, необходимо определиться с определением периодов к погашению, и
страйков, с помощью которых в дальнейшем будет получено натуральное
вероятностное просранство. Рассмотрим график индекса S&P500
за последнее время [25].
Среднеквадратическое отклонение значения индекса, рассчитанное по
месячным данным с 01.02.2013 по 01.02.2016, составило 114,46 пунктов. Текущее
значение индекса на 16.02.2016 составило 1879,07.
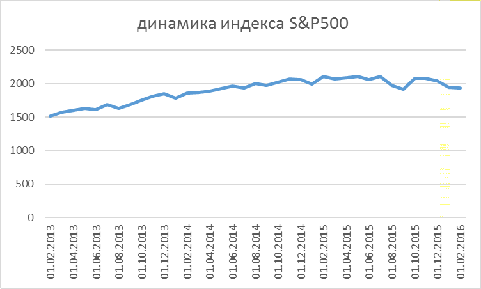
Рисунок 6. Динамика индекса S&P500 по месячным данным
Учитывая, что необходимо, чтобы созданные нами состояния рынка полностью
учитывали все возможные движения индекса, нахождение значении индекса в
интервале от 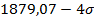 до
до 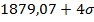 будет вполне приемлемым. Будем использовать шаг в 100
пунктов от текущего значения индекса на 16.02.2016 для моделирования страйков.
Прогноз движения индекса будет сделан на один месяц вперед, поэтому для
моделирования периодов к погашению будем использовать шаг в 1/12 года.
будет вполне приемлемым. Будем использовать шаг в 100
пунктов от текущего значения индекса на 16.02.2016 для моделирования страйков.
Прогноз движения индекса будет сделан на один месяц вперед, поэтому для
моделирования периодов к погашению будем использовать шаг в 1/12 года.
При использовании интерполяции по методу кубических сплайнов была
получена следующая поверхность волатильности опционов:
Таблица 3. Интерполированные подразумеваемые волатильности по методу
кубических сплайнов
|
K\T
|
0,0833
|
0,1667
|
0,25
|
0,3333
|
0,4167
|
0,5
|
0,5833
|
0,6667
|
0,75
|
0,8333
|
1
|
|
1279,07
|
44,12
|
40,98
|
38,30
|
38,39
|
37,79
|
36,64
|
35,66
|
34,96
|
34,24
|
33,68
|
32,23
|
|
1379,07
|
42,04
|
38,37
|
35,97
|
35,72
|
35,17
|
34,14
|
33,33
|
32,68
|
32,14
|
31,66
|
30,43
|
|
1479,07
|
39,53
|
35,68
|
33,50
|
32,97
|
32,50
|
31,68
|
30,98
|
30,51
|
30,05
|
29,61
|
28,65
|
|
1579,07
|
35,70
|
32,61
|
30,95
|
30,35
|
29,91
|
29,23
|
28,64
|
28,32
|
27,91
|
27,53
|
26,88
|
|
1679,07
|
30,83
|
28,99
|
28,07
|
27,67
|
27,29
|
26,77
|
26,29
|
26,12
|
25,77
|
25,47
|
25,09
|
|
1779,07
|
26,65
|
25,43
|
25,14
|
24,87
|
24,77
|
24,39
|
24,05
|
24,00
|
23,74
|
23,53
|
23,39
|
|
1879,07
|
22,49
|
22,02
|
22,17
|
22,11
|
22,24
|
22,07
|
21,90
|
21,93
|
21,80
|
21,70
|
21,66
|
|
1979,07
|
18,21
|
18,39
|
19,05
|
19,33
|
19,49
|
19,57
|
19,65
|
19,72
|
19,77
|
19,84
|
19,87
|
|
2079,07
|
16,34
|
15,65
|
16,72
|
16,81
|
17,23
|
17,18
|
17,28
|
17,68
|
17,90
|
17,94
|
18,05
|
|
2179,07
|
16,10
|
15,17
|
16,25
|
15,48
|
16,75
|
16,20
|
15,35
|
16,57
|
16,55
|
15,99
|
16,39
|
|
2279,07
|
16,57
|
15,05
|
16,03
|
14,84
|
16,29
|
15,15
|
14,19
|
15,71
|
15,32
|
14,68
|
15,08
|
|
2379,07
|
17,69
|
14,97
|
16,07
|
14,73
|
16,38
|
15,13
|
14,02
|
16,04
|
15,10
|
13,78
|
14,23
|
|
2479,07
|
18,88
|
15,43
|
16,10
|
15,03
|
16,50
|
15,11
|
14,06
|
16,13
|
14,85
|
13,53
|
13,81
|
Как можно заметить, теперь мы имеем подразумеваемые волатильности,
отличающиеся друг от друга фиксированными приращениями по периодам к погашению
и фиксированными приращениями по страйкам.
Из данных подразумеваемых волатильностей, используя формулу Блэка-Шоулза,
перейдем к ценам опционов call.
Для использования данной формулы, определимся с входящими в нее параметрами:
ценой спот, безрисковой ставкой, ставкой доходности, страйком, периодом к
погашению. Данные по этим показателям представлены в следующей таблице:
Таблица 4. Параметры модели Блэка-Шоулза для расчета цен опционов call
|
Параметр
|
Значение
|
|
Спот цена, S
|
1879,07
|
|
Страйк, К
|
От 1279,07 до 2479,07 с
шагом 100
|
|
Безрисковая ставка, r
|
0,051
|
|
Ставка доходности, q
|
0,02687
|
|
Периоды погашения, T
|
От 1/12 до 1 с шагом в 1/12
|
|
Подразумеваемые
волатильности
|
Интерполированные значения
|
Значение безрисковой ставки было взято с официального сайта казначейства
США [26]. А ставка доходности была взята из системы Bloomberg. Применяя формулу Блэка-Шоулза,
перейдем от подразумеваемых волатильностей к ценам опционов call.
Перейдя к ценам опционов call,
необходимо убедиться в отсутствии арбитражных возможностей с помощью тестов,
рассмотренных выше [11]. Первый тест по вертикальному спреду дал следующие
результаты.
Таблица 5. Интерполированные значения цен опционов call по методу кубических сплайнов
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,83
|
1,00
|
|
1279,07
|
601,29
|
603,31
|
605,86
|
609,98
|
614,22
|
617,81
|
621,31
|
624,97
|
628,31
|
631,74
|
636,97
|
|
1379,07
|
501,96
|
505,39
|
509,47
|
515,23
|
521,00
|
525,78
|
530,51
|
535,15
|
539,72
|
544,12
|
551,08
|
|
1479,07
|
403,24
|
408,85
|
414,91
|
422,41
|
429,86
|
436,09
|
442,00
|
448,02
|
453,64
|
458,92
|
467,93
|
|
1579,07
|
305,67
|
314,55
|
323,37
|
332,85
|
341,99
|
349,64
|
356,73
|
364,15
|
370,64
|
376,76
|
388,12
|
|
1679,07
|
210,29
|
223,71
|
236,06
|
247,93
|
258,59
|
267,61
|
275,80
|
284,50
|
291,80
|
298,72
|
312,39
|
|
1779,07
|
122,15
|
140,26
|
156,12
|
169,65
|
182,18
|
192,25
|
201,34
|
211,13
|
219,09
|
226,73
|
242,31
|
|
1879,07
|
50,40
|
70,74
|
88,00
|
102,03
|
115,33
|
126,09
|
135,79
|
145,88
|
154,39
|
162,55
|
178,68
|
|
1979,07
|
9,28
|
22,84
|
37,02
|
49,48
|
60,72
|
71,00
|
80,70
|
89,96
|
98,63
|
107,12
|
122,51
|
|
2079,07
|
0,60
|
3,51
|
10,41
|
17,02
|
25,13
|
38,95
|
47,65
|
55,58
|
62,35
|
75,81
|
|
2179,07
|
0,02
|
0,42
|
2,64
|
4,47
|
10,28
|
13,07
|
14,58
|
23,23
|
27,89
|
29,89
|
41,31
|
|
2279,07
|
0,00
|
0,04
|
0,55
|
0,96
|
3,55
|
4,08
|
4,52
|
9,92
|
11,67
|
12,45
|
19,75
|
|
2379,07
|
0,00
|
0,00
|
0,10
|
0,20
|
1,29
|
1,46
|
1,55
|
5,18
|
5,33
|
4,52
|
8,68
|
|
2479,07
|
0,00
|
0,00
|
0,02
|
0,05
|
0,44
|
0,48
|
0,53
|
2,47
|
2,20
|
1,76
|
3,77
|
Таблица 6. Результаты проверки безарбитражности по вертикальному спреду
|
1,000
|
0,999
|
0,997
|
0,995
|
0,992
|
0,989
|
0,986
|
0,983
|
0,980
|
0,978
|
0,975
|
0,971
|
|
1,000
|
0,993
|
0,979
|
0,964
|
0,948
|
0,932
|
0,920
|
0,908
|
0,898
|
0,886
|
0,876
|
0,859
|
|
1,000
|
0,987
|
0,965
|
0,946
|
0,928
|
0,911
|
0,897
|
0,885
|
0,871
|
0,861
|
0,852
|
0,831
|
|
1,000
|
0,976
|
0,943
|
0,915
|
0,896
|
0,879
|
0,864
|
0,853
|
0,839
|
0,830
|
0,822
|
0,798
|
|
1,000
|
0,954
|
0,908
|
0,873
|
0,849
|
0,834
|
0,820
|
0,809
|
0,796
|
0,788
|
0,780
|
0,757
|
|
1,000
|
0,881
|
0,834
|
0,799
|
0,783
|
0,764
|
0,754
|
0,745
|
0,734
|
0,727
|
0,720
|
0,701
|
|
1,000
|
0,717
|
0,695
|
0,681
|
0,676
|
0,668
|
0,662
|
0,655
|
0,653
|
0,647
|
0,642
|
0,636
|
|
0,000
|
0,411
|
0,479
|
0,510
|
0,526
|
0,546
|
0,551
|
0,551
|
0,559
|
0,558
|
0,554
|
0,562
|
|
0,000
|
0,087
|
0,193
|
0,266
|
0,325
|
0,356
|
0,392
|
0,418
|
0,423
|
0,430
|
0,448
|
0,467
|
|
0,000
|
0,006
|
0,031
|
0,078
|
0,125
|
0,148
|
0,187
|
0,244
|
0,244
|
0,277
|
0,325
|
0,345
|
|
0,000
|
0,000
|
0,004
|
0,021
|
0,035
|
0,067
|
0,090
|
0,101
|
0,133
|
0,162
|
0,174
|
0,216
|
|
0,000
|
0,000
|
0,000
|
0,004
|
0,008
|
0,023
|
0,026
|
0,030
|
0,047
|
0,063
|
0,079
|
0,111
|
|
0,000
|
0,000
|
0,000
|
0,001
|
0,002
|
0,008
|
0,010
|
0,010
|
0,027
|
0,031
|
0,028
|
0,049
|
Как видно из таблицы, все значения вертикальных спредов удовлетворяют
условию нахождения в интервале от 0 до 1. Второй тест по спреду батерфляй дал
следующие результаты:
Таблица 7. Результаты проверки безарбитражности по спреду батерфляй
|
7,3488
|
23,346
|
40,352
|
57,151
|
72,572
|
84,039
|
96,337
|
105,33
|
117,67
|
126,58
|
134,66
|
143,47
|
|
0,6066
|
1,3686
|
1,8256
|
1,9267
|
2,0701
|
2,3513
|
2,2988
|
2,6829
|
2,4991
|
2,4211
|
2,7218
|
2,748
|
|
1,1424
|
2,2492
|
3,0202
|
3,2696
|
3,279
|
3,2395
|
3,2285
|
3,2589
|
3,0932
|
3,0437
|
3,3978
|
3,3269
|
|
2,1957
|
3,4568
|
4,2293
|
4,6337
|
4,4663
|
4,4154
|
4,3402
|
4,2234
|
4,1518
|
4,1173
|
4,059
|
4,095
|
|
7,2381
|
7,3976
|
7,3785
|
6,639
|
6,9825
|
6,6625
|
6,481
|
6,276
|
6,1365
|
6,0478
|
5,8544
|
5,6408
|
|
16,394
|
13,923
|
11,812
|
10,667
|
9,5732
|
9,2128
|
8,9053
|
8,1222
|
7,9988
|
7,8188
|
6,7855
|
6,4537
|
|
30,627
|
21,614
|
17,144
|
15,063
|
12,234
|
11,068
|
10,459
|
9,3269
|
8,9534
|
8,7343
|
7,8196
|
7,4609
|
|
32,441
|
28,581
|
24,369
|
20,087
|
19,015
|
15,838
|
13,336
|
13,612
|
12,705
|
10,674
|
10,272
|
9,4667
|
|
8,1025
|
16,236
|
18,835
|
19,919
|
20,746
|
20,563
|
17,385
|
17,895
|
15,354
|
12,306
|
13,453
|
12,199
|
|
0,5568
|
2,7038
|
5,681
|
9,0364
|
8,114
|
9,7014
|
14,3
|
11,108
|
11,476
|
15,019
|
12,831
|
12,941
|
|
0,02
|
0,3502
|
1,6517
|
2,7486
|
4,4704
|
6,3674
|
7,0965
|
8,5691
|
9,8772
|
9,5136
|
10,563
|
10,493
|
|
0,0006
|
0,0327
|
0,3545
|
0,609
|
1,4191
|
1,6379
|
2,0213
|
3,2162
|
5,1661
|
4,9585
|
6,1511
|
Все значения спреда батерфляй удовлетворяют условию нахождения в
интервале от нуля до плюс бесконечности. Последний тест на календарные спреды
дал следующие результаты:
Таблица 8. Результаты проверки безарбитражности по спреду батерфляй
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1,29
|
2,02
|
2,55
|
4,12
|
4,24
|
3,60
|
3,50
|
3,66
|
3,34
|
3,43
|
1,98
|
3,25
|
|
1,96
|
3,43
|
4,08
|
5,76
|
5,77
|
4,77
|
4,73
|
4,65
|
4,57
|
4,40
|
2,76
|
4,19
|
|
3,24
|
5,60
|
6,06
|
7,50
|
7,45
|
6,23
|
5,91
|
6,02
|
5,61
|
5,28
|
3,85
|
5,16
|
|
5,67
|
8,88
|
8,82
|
9,48
|
9,14
|
7,65
|
7,09
|
7,42
|
6,49
|
6,12
|
5,29
|
6,06
|
|
10,29
|
13,42
|
12,35
|
11,87
|
10,66
|
9,02
|
8,18
|
8,71
|
7,30
|
6,92
|
6,68
|
6,99
|
|
22,15
|
18,12
|
15,86
|
13,53
|
12,53
|
10,07
|
9,10
|
9,79
|
7,96
|
7,63
|
7,87
|
7,71
|
|
50,40
|
20,34
|
17,26
|
14,03
|
13,30
|
10,76
|
9,70
|
10,09
|
8,50
|
8,17
|
8,02
|
8,10
|
|
9,28
|
13,56
|
14,19
|
12,46
|
11,24
|
10,28
|
9,70
|
9,25
|
8,67
|
8,48
|
7,27
|
8,13
|
|
0,60
|
2,91
|
6,90
|
6,60
|
8,11
|
6,62
|
7,20
|
8,70
|
7,94
|
6,77
|
6,11
|
7,36
|
|
0,02
|
0,40
|
2,22
|
1,83
|
5,81
|
2,78
|
1,52
|
8,65
|
4,66
|
2,00
|
6,09
|
5,33
|
|
0,00
|
0,04
|
0,51
|
0,42
|
2,59
|
0,53
|
0,44
|
5,41
|
1,75
|
0,78
|
3,89
|
3,41
|
|
0,00
|
0,00
|
0,10
|
0,10
|
1,09
|
0,18
|
0,08
|
3,64
|
0,14
|
-0,80
|
2,74
|
1,42
|
|
0,00
|
0,00
|
0,02
|
0,03
|
0,39
|
0,04
|
0,05
|
1,94
|
-0,27
|
-0,44
|
1,39
|
0,62
|
Как видно из таблицы, три значения являются отрицательными, что создаёт
возможности арбитража. Тем не менее, метод интерполяции с помощью кубических
сплайнов дал весь хороший результат.
При использовании интерполяции по методу бигармонических сплайнов была
получена следующая поверхность волатильности опционов:
Таблица 9. Интерполированные значения подразумеваемых волатильностей по
методу бигармонических сплайнов
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,83
|
0,92
|
1,00
|
|
1279,07
|
46,72
|
39,36
|
37,78
|
38,21
|
37,97
|
36,71
|
35,65
|
34,85
|
34,23
|
33,59
|
32,68
|
31,92
|
|
1379,07
|
44,33
|
37,32
|
35,83
|
35,65
|
35,25
|
34,24
|
33,36
|
32,72
|
32,14
|
31,59
|
30,83
|
30,13
|
|
1479,07
|
39,86
|
35,62
|
33,54
|
33,02
|
32,59
|
31,67
|
30,99
|
30,54
|
30,03
|
29,60
|
28,98
|
28,34
|
|
1579,07
|
34,82
|
32,60
|
31,17
|
30,44
|
29,93
|
29,15
|
28,63
|
28,34
|
27,89
|
27,56
|
27,12
|
26,58
|
|
1679,07
|
30,73
|
29,01
|
28,13
|
27,68
|
27,33
|
26,71
|
26,29
|
26,19
|
25,76
|
25,47
|
25,26
|
24,84
|
|
1779,07
|
26,61
|
25,44
|
25,15
|
24,87
|
24,81
|
24,34
|
24,04
|
24,08
|
23,72
|
23,52
|
23,48
|
23,13
|
|
1879,07
|
22,48
|
22,02
|
22,18
|
22,11
|
22,26
|
21,99
|
21,90
|
21,95
|
21,76
|
21,70
|
21,68
|
21,41
|
|
1979,07
|
18,11
|
18,38
|
19,04
|
19,32
|
19,48
|
19,46
|
19,65
|
19,75
|
19,81
|
19,84
|
19,79
|
19,64
|
|
2079,07
|
16,22
|
15,56
|
16,59
|
16,73
|
17,21
|
16,98
|
17,21
|
17,80
|
17,96
|
17,89
|
17,87
|
17,85
|
|
2179,07
|
15,33
|
14,85
|
15,96
|
15,60
|
16,55
|
15,33
|
15,33
|
16,67
|
16,43
|
16,05
|
16,21
|
16,18
|
|
2279,07
|
16,28
|
15,11
|
16,27
|
15,15
|
16,72
|
14,55
|
14,26
|
16,30
|
15,40
|
14,67
|
15,03
|
14,83
|
|
2379,07
|
16,59
|
15,23
|
16,66
|
15,62
|
16,79
|
14,37
|
14,21
|
16,40
|
14,86
|
13,97
|
14,45
|
13,86
|
|
2479,07
|
19,15
|
15,21
|
15,48
|
16,79
|
14,49
|
14,34
|
16,53
|
14,74
|
13,69
|
14,15
|
13,29
|
Применяя формулу Блэка-Шоулза, перейдем от подразумеваемых волатильностей
к ценам опционов call:
Таблица 10. Интерполированные значения цен опционов call по методу бигармонических сплайнов
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,83
|
1,00
|
|
1279,07
|
601,35
|
603,06
|
605,66
|
609,85
|
614,40
|
617,90
|
621,29
|
624,76
|
628,29
|
631,54
|
636,16
|
|
1379,07
|
502,15
|
505,04
|
509,38
|
515,16
|
521,13
|
525,97
|
530,57
|
535,24
|
539,72
|
543,90
|
550,08
|
|
1479,07
|
403,31
|
408,81
|
414,96
|
422,48
|
430,04
|
436,08
|
442,04
|
448,14
|
453,58
|
458,89
|
466,65
|
|
1579,07
|
305,28
|
314,53
|
323,74
|
333,06
|
342,04
|
349,40
|
356,71
|
364,22
|
370,56
|
376,88
|
386,63
|
|
1679,07
|
210,20
|
223,74
|
236,21
|
247,96
|
258,71
|
267,38
|
275,78
|
284,83
|
291,77
|
298,73
|
310,92
|
|
1779,07
|
122,08
|
140,29
|
156,16
|
169,65
|
182,35
|
192,00
|
201,33
|
211,56
|
219,01
|
226,72
|
240,66
|
|
1879,07
|
50,38
|
70,74
|
88,01
|
102,03
|
115,45
|
125,69
|
135,79
|
146,00
|
154,13
|
162,56
|
176,89
|
|
1979,07
|
9,14
|
22,81
|
36,99
|
49,44
|
60,70
|
70,44
|
80,72
|
90,12
|
98,90
|
107,17
|
120,82
|
|
2079,07
|
0,57
|
3,42
|
10,15
|
16,80
|
25,04
|
30,91
|
38,59
|
48,26
|
55,91
|
62,09
|
74,40
|
|
2179,07
|
0,01
|
0,36
|
2,40
|
4,64
|
9,83
|
10,76
|
14,50
|
23,63
|
27,34
|
30,19
|
40,10
|
|
2279,07
|
0,00
|
0,04
|
0,61
|
1,11
|
4,06
|
3,30
|
4,62
|
11,45
|
11,90
|
12,42
|
18,71
|
|
2379,07
|
0,00
|
0,00
|
0,15
|
0,35
|
1,52
|
1,02
|
1,69
|
5,80
|
4,91
|
4,85
|
7,72
|
|
2479,07
|
0,00
|
0,00
|
0,02
|
0,07
|
0,51
|
0,33
|
0,63
|
2,87
|
2,10
|
1,90
|
3,02
|
Перейдя к ценам опционов call,
необходимо убедиться в отсутствии арбитражных возможностей с помощью тестов,
рассмотренных выше. Первый тест по вертикальному спреду дал следующие
результаты:
Таблица 11. Результаты проверки безарбитражности по вертикальному спреду
|
1
|
1,00
|
1,00
|
1,00
|
0,99
|
0,99
|
0,99
|
0,98
|
0,98
|
0,98
|
0,98
|
0,97
|
0,97
|
|
1
|
0,99
|
0,98
|
0,96
|
0,95
|
0,93
|
0,92
|
0,91
|
0,90
|
0,89
|
0,88
|
0,87
|
0,86
|
|
1
|
0,99
|
0,96
|
0,94
|
0,93
|
0,91
|
0,90
|
0,89
|
0,87
|
0,86
|
0,85
|
0,84
|
0,83
|
|
1
|
0,98
|
0,94
|
0,91
|
0,89
|
0,88
|
0,87
|
0,85
|
0,84
|
0,83
|
0,82
|
0,81
|
0,80
|
|
1
|
0,95
|
0,91
|
0,88
|
0,85
|
0,83
|
0,82
|
0,81
|
0,79
|
0,79
|
0,78
|
0,77
|
0,76
|
|
1
|
0,88
|
0,83
|
0,80
|
0,78
|
0,76
|
0,75
|
0,74
|
0,73
|
0,73
|
0,72
|
0,71
|
0,70
|
|
1
|
0,72
|
0,70
|
0,68
|
0,68
|
0,67
|
0,66
|
0,66
|
0,66
|
0,65
|
0,64
|
0,64
|
0,64
|
|
0
|
0,41
|
0,48
|
0,51
|
0,53
|
0,55
|
0,55
|
0,55
|
0,56
|
0,55
|
0,55
|
0,56
|
0,56
|
|
0
|
0,09
|
0,19
|
0,27
|
0,33
|
0,36
|
0,40
|
0,42
|
0,42
|
0,43
|
0,45
|
0,46
|
0,46
|
|
0
|
0,01
|
0,03
|
0,08
|
0,12
|
0,15
|
0,20
|
0,24
|
0,25
|
0,29
|
0,32
|
0,33
|
0,34
|
|
0
|
0,00
|
0,00
|
0,02
|
0,04
|
0,06
|
0,07
|
0,10
|
0,12
|
0,15
|
0,18
|
0,19
|
0,21
|
|
0
|
0,00
|
0,00
|
0,00
|
0,01
|
0,03
|
0,02
|
0,03
|
0,06
|
0,07
|
0,08
|
0,09
|
0,11
|
|
0
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,01
|
0,01
|
0,03
|
0,03
|
0,03
|
0,04
|
0,05
Все значения спреда батерфляй удовлетворяют условию нахождения в
интервале от нуля до плюс бесконечности. Последний тест на календарные спреды
дал следующие результаты.
Таблица 12. Результаты проверки безарбитражности по спреду батерфляй
|
0
|
8,91
|
22,27
|
41,86
|
58,09
|
71,61
|
85,42
|
97,34
|
109,24
|
117,98
|
126,65
|
135,94
|
141,97
|
|
0
|
0,36
|
1,78
|
1,86
|
2,01
|
2,19
|
2,03
|
2,20
|
2,42
|
2,42
|
2,62
|
2,65
|
2,64
|
|
0
|
0,81
|
1,95
|
3,20
|
3,27
|
3,08
|
3,21
|
3,21
|
3,18
|
3,12
|
3,01
|
3,28
|
3,41
|
|
0
|
2,95
|
3,50
|
3,70
|
4,32
|
4,67
|
4,67
|
4,39
|
4,53
|
4,24
|
3,85
|
4,21
|
4,31
|
|
0
|
6,97
|
7,33
|
7,48
|
6,79
|
6,98
|
6,64
|
6,48
|
6,11
|
6,03
|
6,14
|
5,76
|
5,44
|
|
0
|
16,42
|
13,90
|
11,90
|
10,69
|
9,45
|
9,07
|
8,92
|
7,72
|
7,88
|
7,85
|
6,74
|
6,50
|
|
100
|
30,46
|
21,62
|
17,14
|
15,03
|
12,16
|
11,06
|
10,47
|
9,67
|
9,66
|
8,77
|
7,81
|
7,68
|
|
0
|
32,67
|
28,54
|
24,17
|
19,96
|
19,09
|
15,73
|
12,94
|
14,02
|
12,23
|
10,32
|
10,14
|
9,66
|
|
0
|
8,02
|
16,33
|
19,09
|
20,47
|
20,45
|
19,37
|
18,04
|
17,22
|
14,42
|
13,17
|
13,40
|
12,11
|
|
0
|
0,55
|
2,74
|
5,97
|
8,63
|
9,44
|
12,70
|
14,20
|
12,46
|
13,14
|
14,13
|
13,62
|
12,93
|
|
0
|
0,01
|
0,28
|
1,32
|
2,77
|
3,23
|
5,18
|
6,96
|
6,53
|
8,45
|
10,20
|
10,03
|
10,39
|
|
0
|
0,00
|
0,03
|
0,33
|
0,49
|
1,53
|
1,59
|
1,87
|
2,71
|
4,18
|
4,62
|
4,91
|
6,29
|
Таблица 13. Результаты проверки безарбитражности по календарному спреду
|
1,35
|
1,72
|
2,61
|
4,19
|
4,56
|
3,49
|
3,40
|
3,46
|
3,52
|
3,25
|
2,30
|
2,35
|
|
2,16
|
1,72
|
2,61
|
4,19
|
4,56
|
3,49
|
3,40
|
3,46
|
3,52
|
3,25
|
2,30
|
2,35
|
|
3,32
|
2,90
|
4,34
|
5,78
|
5,97
|
4,85
|
4,59
|
4,67
|
4,48
|
4,17
|
3,21
|
3,00
|
|
5,28
|
5,50
|
6,15
|
7,52
|
7,57
|
6,04
|
5,96
|
6,10
|
5,45
|
5,30
|
4,15
|
3,65
|
|
10,20
|
9,23
|
9,21
|
9,32
|
8,98
|
7,36
|
7,32
|
7,51
|
6,34
|
6,32
|
5,37
|
4,42
|
|
22,08
|
13,54
|
12,47
|
11,75
|
10,74
|
8,67
|
8,40
|
9,05
|
6,94
|
6,96
|
6,94
|
5,29
|
|
50,38
|
18,21
|
15,87
|
13,49
|
12,70
|
9,65
|
9,33
|
10,23
|
7,46
|
7,71
|
8,12
|
5,84
|
|
9,14
|
20,35
|
17,27
|
14,02
|
13,42
|
10,24
|
10,10
|
10,21
|
8,13
|
8,43
|
8,20
|
6,16
|
|
0,57
|
13,66
|
14,19
|
12,45
|
11,26
|
9,74
|
10,29
|
9,40
|
8,78
|
8,26
|
7,32
|
6,35
|
|
0,01
|
2,85
|
6,73
|
6,65
|
8,23
|
5,87
|
7,68
|
9,67
|
7,65
|
6,18
|
6,26
|
6,07
|
|
0,00
|
0,35
|
2,04
|
2,25
|
5,19
|
0,93
|
3,75
|
9,12
|
3,71
|
2,86
|
5,44
|
4,48
|
|
0,00
|
0,04
|
0,57
|
0,49
|
2,95
|
-0,76
|
1,32
|
6,83
|
0,45
|
0,52
|
4,10
|
2,20
|
|
0,00
|
0,00
|
0,15
|
0,19
|
1,18
|
-0,50
|
0,66
|
4,12
|
-0,89
|
-0,06
|
2,58
|
0,29
|
|
0,00
|
0,00
|
0,02
|
0,05
|
0,44
|
-0,18
|
0,29
|
2,24
|
-0,77
|
-0,19
|
1,35
|
-0,24
|
Как видно из таблицы, восемь значений являются отрицательными, что
создаёт возможности арбитража. Таким образом, данный метод является показал
меньшую эффективность чем интерполяция с помощью кубических сплайнов.
При использовании интерполяции по методу Thin-plate splines была
получена следующая поверхность волатильности опционов:
Таблица 14. Интерполированные подразумеваемые волатильности по методу Thin-plate splines
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,83
|
1,00
|
|
1279,07
|
46,89
|
39,45
|
37,83
|
38,24
|
37,99
|
36,73
|
35,67
|
34,24
|
33,60
|
31,94
|
|
1379,07
|
44,47
|
37,39
|
35,87
|
35,67
|
35,27
|
34,26
|
33,37
|
32,72
|
32,15
|
31,59
|
30,14
|
|
1479,07
|
39,88
|
35,63
|
33,55
|
33,02
|
32,59
|
31,67
|
30,99
|
30,54
|
30,03
|
29,60
|
28,35
|
|
1579,07
|
34,82
|
32,59
|
31,16
|
30,43
|
29,93
|
29,15
|
28,63
|
28,34
|
27,89
|
27,56
|
26,58
|
|
1679,07
|
30,73
|
29,01
|
28,13
|
27,68
|
27,33
|
26,71
|
26,29
|
26,19
|
25,76
|
25,47
|
24,85
|
|
1779,07
|
26,61
|
25,44
|
25,15
|
24,87
|
24,81
|
24,34
|
24,04
|
24,08
|
23,72
|
23,52
|
23,14
|
|
1879,07
|
22,48
|
22,02
|
22,18
|
22,11
|
22,26
|
21,99
|
21,90
|
21,95
|
21,76
|
21,70
|
21,42
|
|
1979,07
|
18,11
|
18,38
|
19,04
|
19,32
|
19,48
|
19,46
|
19,65
|
19,75
|
19,81
|
19,84
|
19,64
|
|
2079,07
|
16,22
|
15,56
|
16,59
|
16,73
|
17,21
|
16,98
|
17,21
|
17,80
|
17,96
|
17,89
|
17,85
|
|
2179,07
|
15,34
|
14,86
|
15,96
|
15,60
|
16,55
|
15,33
|
15,33
|
16,67
|
16,43
|
16,05
|
16,19
|
|
2279,07
|
16,28
|
15,10
|
16,27
|
15,15
|
16,72
|
14,55
|
14,26
|
16,30
|
15,40
|
14,67
|
14,83
|
|
2379,07
|
16,59
|
15,23
|
16,66
|
15,62
|
16,79
|
14,37
|
14,21
|
16,40
|
14,86
|
13,97
|
13,86
|
|
2479,07
|
19,17
|
15,22
|
16,40
|
15,48
|
16,79
|
14,49
|
14,34
|
16,53
|
14,74
|
13,70
|
13,30
|
Применяя формулу Блэка-Шоулза, перейдем от подразумеваемых волатильностей
к ценам опционов call:
Таблица 15. Интерполированные цены опционов call по методу Thin-plate splines
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,92
|
1,00
|
|
1279,07
|
601,35
|
603,08
|
605,68
|
609,87
|
614,43
|
617,92
|
621,32
|
624,78
|
628,31
|
633,85
|
636,21
|
|
1379,07
|
502,16
|
505,07
|
509,40
|
515,18
|
521,15
|
526,00
|
530,59
|
535,26
|
539,74
|
547,12
|
550,13
|
|
1479,07
|
403,32
|
408,82
|
414,96
|
422,48
|
430,05
|
436,09
|
442,04
|
448,14
|
453,59
|
463,04
|
466,69
|
|
1579,07
|
305,28
|
314,51
|
323,73
|
333,05
|
342,04
|
349,39
|
356,71
|
364,22
|
370,56
|
382,24
|
386,67
|
|
1679,07
|
210,20
|
223,74
|
236,21
|
247,96
|
258,71
|
267,38
|
275,78
|
284,83
|
291,77
|
305,66
|
310,95
|
|
1779,07
|
122,08
|
140,29
|
156,16
|
169,65
|
182,35
|
192,00
|
201,33
|
211,56
|
219,01
|
234,84
|
240,69
|
|
1879,07
|
50,38
|
70,74
|
88,01
|
102,03
|
115,45
|
125,69
|
135,79
|
146,00
|
154,13
|
170,76
|
176,92
|
|
1979,07
|
9,14
|
22,81
|
36,99
|
49,44
|
60,70
|
70,44
|
80,72
|
90,12
|
98,90
|
114,49
|
120,84
|
|
2079,07
|
0,57
|
3,42
|
10,15
|
16,80
|
25,04
|
30,91
|
38,59
|
48,26
|
55,91
|
68,36
|
74,42
|
|
2179,07
|
0,01
|
0,36
|
2,40
|
4,64
|
9,83
|
10,76
|
14,50
|
23,63
|
27,33
|
35,63
|
40,11
|
|
2279,07
|
0,00
|
0,04
|
0,61
|
1,11
|
4,06
|
3,30
|
4,62
|
11,45
|
11,90
|
16,52
|
18,72
|
|
2379,07
|
0,00
|
0,00
|
0,15
|
0,35
|
1,52
|
1,02
|
1,69
|
5,80
|
4,91
|
7,43
|
7,73
|
|
2479,07
|
0,00
|
0,00
|
0,02
|
0,07
|
0,51
|
0,33
|
0,63
|
2,87
|
2,10
|
3,26
|
3,02
|
Перейдя к ценам опционов call,
необходимо убедиться в отсутствии арбитражных возможностей с помощью тестов,
рассмотренных выше. Первый тест по вертикальному спреду дал следующие
результаты:
Таблица 16. Результаты проверки безарбитражности по вертикальному спреду
|
1
|
1,00
|
1,00
|
1,00
|
0,99
|
0,99
|
0,99
|
0,98
|
0,98
|
0,98
|
0,98
|
0,97
|
0,97
|
|
1
|
0,99
|
0,98
|
0,96
|
0,95
|
0,93
|
0,92
|
0,91
|
0,90
|
0,89
|
0,88
|
0,87
|
0,86
|
|
1
|
0,99
|
0,96
|
0,94
|
0,93
|
0,90
|
0,89
|
0,87
|
0,86
|
0,85
|
0,84
|
0,83
|
|
1
|
0,98
|
0,94
|
0,91
|
0,89
|
0,88
|
0,87
|
0,85
|
0,84
|
0,83
|
0,82
|
0,81
|
0,80
|
|
1
|
0,95
|
0,91
|
0,88
|
0,85
|
0,83
|
0,82
|
0,81
|
0,79
|
0,79
|
0,78
|
0,77
|
0,76
|
|
1
|
0,88
|
0,83
|
0,80
|
0,78
|
0,76
|
0,75
|
0,74
|
0,73
|
0,73
|
0,72
|
0,71
|
0,70
|
|
1
|
0,72
|
0,70
|
0,68
|
0,68
|
0,67
|
0,66
|
0,66
|
0,66
|
0,65
|
0,64
|
0,64
|
0,64
|
|
0
|
0,41
|
0,48
|
0,51
|
0,53
|
0,55
|
0,55
|
0,55
|
0,56
|
0,55
|
0,55
|
0,56
|
0,56
|
|
0
|
0,09
|
0,19
|
0,27
|
0,33
|
0,36
|
0,40
|
0,42
|
0,42
|
0,43
|
0,45
|
0,46
|
0,46
|
|
0
|
0,01
|
0,03
|
0,08
|
0,12
|
0,15
|
0,20
|
0,24
|
0,25
|
0,29
|
0,32
|
0,33
|
0,34
|
|
0
|
0,00
|
0,00
|
0,02
|
0,04
|
0,06
|
0,07
|
0,10
|
0,12
|
0,15
|
0,18
|
0,19
|
0,21
|
|
0
|
0,00
|
0,00
|
0,00
|
0,01
|
0,03
|
0,02
|
0,03
|
0,06
|
0,07
|
0,08
|
0,09
|
0,11
|
|
0
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,01
|
0,01
|
0,03
|
0,03
|
0,03
|
0,04
|
0,05
|
Как видно из таблицы, все значения вертикальных спредов удовлетворяют
условию нахождения в интервале от 0 до 1. Второй тест по спреду батерфляй дал
следующие результаты:
Таблица 17. Результаты проверки безарбитражности по спреду батерфляй
|
0
|
9,02
|
22,40
|
41,91
|
58,07
|
71,55
|
85,35
|
97,27
|
109,20
|
117,97
|
126,58
|
135,89
|
141,88
|
|
0
|
0,34
|
1,76
|
1,84
|
1,99
|
2,18
|
2,01
|
2,18
|
2,41
|
2,41
|
2,61
|
2,64
|
2,64
|
|
0
|
0,81
|
1,95
|
3,20
|
3,27
|
3,09
|
3,22
|
3,21
|
3,19
|
3,12
|
3,02
|
3,29
|
3,42
|
|
0
|
2,95
|
3,53
|
3,72
|
4,34
|
4,68
|
4,68
|
4,41
|
4,54
|
4,25
|
3,86
|
4,22
|
4,31
|
|
0
|
6,97
|
7,32
|
7,47
|
6,78
|
6,98
|
6,64
|
6,47
|
6,11
|
6,03
|
6,14
|
5,76
|
5,44
|
|
0
|
16,42
|
13,90
|
11,89
|
10,69
|
9,45
|
9,07
|
8,92
|
7,72
|
7,88
|
7,85
|
6,74
|
6,50
|
|
100
|
30,46
|
21,62
|
17,14
|
15,03
|
12,16
|
11,06
|
10,47
|
9,67
|
9,66
|
8,77
|
7,81
|
7,68
|
|
0
|
32,67
|
28,54
|
24,17
|
19,96
|
19,09
|
15,73
|
12,94
|
14,02
|
12,23
|
10,32
|
10,14
|
9,66
|
|
0
|
8,01
|
16,33
|
19,09
|
20,47
|
20,45
|
19,37
|
18,04
|
17,22
|
14,42
|
13,17
|
13,40
|
12,10
|
|
0
|
0,55
|
2,74
|
5,97
|
8,62
|
9,44
|
12,70
|
14,20
|
12,46
|
13,14
|
14,13
|
13,62
|
12,93
|
|
0
|
0,01
|
0,28
|
1,32
|
2,77
|
3,23
|
5,18
|
6,96
|
6,53
|
8,45
|
10,20
|
10,03
|
10,39
|
|
0
|
0,00
|
0,03
|
0,33
|
0,49
|
1,53
|
1,59
|
1,87
|
2,72
|
4,18
|
4,62
|
4,91
|
6,29
|
Все значения спреда батерфляй удовлетворяют условию нахождения в
интервале от нуля до плюс бесконечности. Последний тест на календарные спреды
дал следующие результаты:
Таблица 18. Результаты проверки безарбитражности по календарному спреду
|
1,35
|
1,72
|
2,61
|
4,19
|
4,56
|
3,49
|
3,40
|
3,46
|
3,52
|
3,25
|
2,30
|
2,35
|
|
2,16
|
1,72
|
2,61
|
4,19
|
4,56
|
3,49
|
3,40
|
3,46
|
3,52
|
3,25
|
2,30
|
2,35
|
|
3,32
|
2,90
|
4,34
|
5,78
|
5,97
|
4,85
|
4,59
|
4,67
|
4,48
|
4,17
|
3,21
|
3,00
|
|
5,28
|
5,50
|
6,15
|
7,52
|
7,57
|
6,04
|
5,96
|
6,10
|
5,45
|
5,30
|
4,15
|
3,65
|
|
10,20
|
9,23
|
9,21
|
9,32
|
8,98
|
7,32
|
7,51
|
6,34
|
6,32
|
5,37
|
4,42
|
|
22,08
|
13,54
|
12,47
|
11,75
|
10,74
|
8,67
|
8,40
|
9,05
|
6,94
|
6,96
|
6,94
|
5,29
|
|
50,38
|
18,21
|
15,87
|
13,49
|
12,70
|
9,65
|
9,33
|
10,23
|
7,46
|
7,71
|
8,12
|
5,84
|
|
9,14
|
20,35
|
17,27
|
14,02
|
13,42
|
10,24
|
10,10
|
10,21
|
8,13
|
8,43
|
8,20
|
6,16
|
|
0,57
|
13,66
|
14,19
|
12,45
|
11,26
|
9,74
|
10,29
|
9,40
|
8,78
|
8,26
|
7,32
|
6,35
|
|
0,01
|
2,85
|
6,73
|
6,65
|
8,23
|
5,87
|
7,68
|
9,67
|
7,65
|
6,18
|
6,26
|
6,07
|
|
0,00
|
0,35
|
2,04
|
2,25
|
5,19
|
0,93
|
3,75
|
9,12
|
3,71
|
2,86
|
5,44
|
4,48
|
|
0,00
|
0,04
|
0,57
|
0,49
|
2,95
|
-0,76
|
1,32
|
6,83
|
0,45
|
0,52
|
4,10
|
2,20
|
|
0,00
|
0,00
|
0,15
|
0,19
|
1,18
|
-0,50
|
0,66
|
4,12
|
-0,89
|
-0,06
|
2,58
|
0,29
|
|
0,00
|
0,00
|
0,02
|
0,05
|
0,44
|
-0,18
|
0,29
|
2,24
|
-0,77
|
-0,19
|
1,35
|
-0,24
|
Как видно из таблицы, восемь значений являются отрицательными, что
создаёт возможности арбитража. Таким образом, данный метод является показал
меньшую эффективность чем интерполяция с помощью кубических сплайнов.
При использовании интерполяции по полиномиальному методу была получена
следующая поверхность волатильности опционов:
Таблица 19. Интерполированные значения подразумеваемых волатильностей по
полиномиальному методу
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,92
|
1,00
|
|
1279,07
|
44,51
|
38,47
|
34,95
|
33,25
|
32,77
|
33,03
|
33,66
|
34,37
|
34,97
|
35,37
|
35,12
|
|
1379,07
|
40,68
|
34,95
|
31,72
|
30,27
|
30,01
|
30,47
|
31,27
|
32,12
|
32,83
|
33,38
|
33,17
|
|
1479,07
|
37,08
|
31,63
|
28,65
|
27,42
|
27,35
|
27,98
|
28,92
|
29,88
|
30,69
|
31,36
|
31,18
|
|
1579,07
|
33,77
|
28,55
|
25,78
|
24,74
|
24,84
|
25,61
|
26,67
|
27,73
|
28,61
|
29,37
|
29,20
|
|
1679,07
|
30,77
|
25,76
|
23,17
|
22,29
|
22,53
|
23,41
|
24,56
|
25,70
|
26,64
|
27,46
|
27,30
|
|
1779,07
|
28,12
|
23,28
|
20,84
|
20,09
|
20,44
|
21,42
|
22,64
|
23,84
|
24,82
|
25,68
|
25,51
|
|
1879,07
|
25,84
|
21,14
|
18,81
|
18,17
|
18,61
|
19,65
|
20,94
|
22,18
|
23,18
|
24,05
|
23,86
|
|
1979,07
|
23,94
|
19,34
|
17,11
|
16,54
|
17,04
|
18,14
|
19,46
|
20,73
|
21,74
|
22,60
|
22,39
|
|
2079,07
|
22,42
|
17,89
|
15,73
|
15,21
|
15,76
|
16,89
|
18,23
|
19,51
|
20,53
|
21,35
|
21,12
|
|
2179,07
|
21,27
|
16,79
|
14,67
|
14,19
|
14,76
|
15,91
|
17,26
|
18,53
|
19,53
|
20,31
|
20,04
|
|
2279,07
|
20,50
|
16,04
|
13,93
|
13,46
|
14,04
|
15,18
|
16,53
|
17,79
|
18,77
|
19,49
|
19,17
|
|
2379,07
|
20,07
|
15,61
|
13,50
|
13,02
|
13,58
|
14,71
|
16,04
|
17,27
|
18,22
|
18,87
|
18,51
|
|
2479,07
|
19,98
|
15,49
|
13,35
|
12,85
|
13,38
|
14,49
|
15,78
|
16,98
|
17,89
|
18,45
|
18,04
|
Применяя формулу Блэка-Шоулза, перейдем от подразумеваемых волатильностей
к ценам опционов call:
Таблица 20. Интерполированные значения цен опционов call по полиномиальному методу
|
K/T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,92
|
1,00
|
|
1279,1
|
601,3
|
603,0
|
604,8
|
607,0
|
609,8
|
613,6
|
618,4
|
623,9
|
629,8
|
640,8
|
645,1
|
|
1379,1
|
501,9
|
504,4
|
507,1
|
510,3
|
514,4
|
519,8
|
526,3
|
533,8
|
541,6
|
555,5
|
560,7
|
|
1479,1
|
402,8
|
406,6
|
410,3
|
414,8
|
420,5
|
427,8
|
436,5
|
446,1
|
455,8
|
472,7
|
478,8
|
|
1579,1
|
304,9
|
310,5
|
315,5
|
321,5
|
329,2
|
338,8
|
350,0
|
361,9
|
373,6
|
393,1
|
400,0
|
|
1679,1
|
210,2
|
218,3
|
232,7
|
242,6
|
254,8
|
268,4
|
282,6
|
296,2
|
318,0
|
325,4
|
|
1779,1
|
124,5
|
134,9
|
142,7
|
152,0
|
164,1
|
178,5
|
194,3
|
210,3
|
225,3
|
248,8
|
256,3
|
|
1879,1
|
57,6
|
68,1
|
75,6
|
85,3
|
98,1
|
113,6
|
130,4
|
147,3
|
163,0
|
187,0
|
194,3
|
|
1979,1
|
18,3
|
25,3
|
30,5
|
38,3
|
49,5
|
63,7
|
79,7
|
96,0
|
111,1
|
134,2
|
140,9
|
|
2079,1
|
3,5
|
6,1
|
8,5
|
12,7
|
20,0
|
30,6
|
43,5
|
57,4
|
70,9
|
91,5
|
97,2
|
|
2179,1
|
0,4
|
0,9
|
1,5
|
2,9
|
6,2
|
12,3
|
21,0
|
31,4
|
42,1
|
59,1
|
63,6
|
|
2279,1
|
0,0
|
0,1
|
0,2
|
0,5
|
1,5
|
4,1
|
9,0
|
15,8
|
23,4
|
36,2
|
39,6
|
|
2379,1
|
0,0
|
0,0
|
0,0
|
0,1
|
0,3
|
1,2
|
3,5
|
7,4
|
12,4
|
21,3
|
23,6
|
|
2479,1
|
0,0
|
0,0
|
0,0
|
0,0
|
0,1
|
0,3
|
1,3
|
3,4
|
6,3
|
12,2
|
13,6
|
Перейдя к ценам опционов call,
необходимо убедиться в отсутствии арбитражных возможностей с помощью тестов,
рассмотренных выше. Первый тест по вертикальному спреду дал следующие
результаты:
Таблица 21. Результаты проверки безарбитражности по вертикальному спреду
|
1
|
1,00
|
1,00
|
1,00
|
0,99
|
0,99
|
0,99
|
0,99
|
0,98
|
0,98
|
0,97
|
0,97
|
0,96
|
|
1
|
0,99
|
0,99
|
0,98
|
0,97
|
0,95
|
0,94
|
0,92
|
0,90
|
0,88
|
0,87
|
0,85
|
0,84
|
|
1
|
0,99
|
0,98
|
0,97
|
0,96
|
0,94
|
0,92
|
0,90
|
0,88
|
0,86
|
0,84
|
0,83
|
0,82
|
|
1
|
0,98
|
0,96
|
0,95
|
0,93
|
0,91
|
0,89
|
0,87
|
0,84
|
0,82
|
0,81
|
0,80
|
0,79
|
|
1
|
0,95
|
0,92
|
0,91
|
0,89
|
0,87
|
0,84
|
0,82
|
0,79
|
0,77
|
0,76
|
0,75
|
0,75
|
|
1
|
0,86
|
0,83
|
0,82
|
0,81
|
0,79
|
0,76
|
0,74
|
0,72
|
0,71
|
0,70
|
0,69
|
0,69
|
|
1
|
0,67
|
0,67
|
0,67
|
0,67
|
0,66
|
0,65
|
0,64
|
0,63
|
0,62
|
0,62
|
0,62
|
0,62
|
|
0
|
0,39
|
0,43
|
0,45
|
0,47
|
0,49
|
0,50
|
0,51
|
0,51
|
0,52
|
0,52
|
0,53
|
0,53
|
|
0
|
0,15
|
0,19
|
0,22
|
0,26
|
0,30
|
0,33
|
0,36
|
0,39
|
0,40
|
0,42
|
0,43
|
0,44
|
|
0
|
0,03
|
0,05
|
0,07
|
0,10
|
0,14
|
0,18
|
0,23
|
0,26
|
0,29
|
0,31
|
0,32
|
0,34
|
|
0
|
0,00
|
0,01
|
0,01
|
0,02
|
0,05
|
0,08
|
0,12
|
0,16
|
0,19
|
0,21
|
0,23
|
0,24
|
|
0
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,03
|
0,05
|
0,08
|
0,11
|
0,13
|
0,15
|
0,16
|
|
0
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,02
|
0,04
|
0,06
|
0,08
|
0,09
|
0,10
|
Как видно из таблицы, все значения вертикальных спредов удовлетворяют
условию нахождения в интервале от 0 до 1. Второй тест по спреду батерфляй дал
следующие результаты:
Таблица 22. Результаты проверки безарбитражности по спреду батерфляй
|
0
|
6,18
|
15,58
|
24,53
|
34,98
|
48,41
|
65,00
|
83,73
|
102,80
|
120,45
|
135,41
|
147,04
|
155,24
|
|
0
|
0,35
|
0,73
|
0,94
|
1,20
|
1,52
|
1,87
|
2,18
|
2,39
|
2,51
|
2,53
|
2,49
|
2,38
|
|
0
|
1,11
|
1,71
|
1,97
|
2,28
|
2,66
|
3,03
|
3,30
|
3,45
|
3,48
|
3,43
|
3,31
|
3,15
|
|
0
|
3,34
|
3,98
|
4,15
|
4,39
|
4,69
|
4,91
|
5,01
|
4,97
|
4,84
|
4,65
|
4,43
|
4,21
|
|
0
|
8,91
|
8,74
|
8,39
|
8,19
|
8,00
|
7,75
|
7,39
|
6,99
|
6,57
|
6,19
|
5,85
|
5,55
|
|
0
|
18,81
|
16,53
|
15,15
|
13,90
|
12,64
|
11,42
|
10,30
|
8,56
|
7,93
|
7,44
|
7,07
|
|
100
|
27,57
|
24,06
|
22,06
|
19,79
|
17,32
|
15,02
|
13,09
|
11,57
|
10,42
|
9,58
|
8,98
|
8,57
|
|
0
|
24,50
|
23,67
|
22,96
|
21,38
|
19,11
|
16,70
|
14,57
|
12,87
|
11,60
|
10,69
|
10,08
|
9,71
|
|
0
|
11,72
|
13,90
|
15,09
|
15,80
|
15,72
|
14,87
|
13,68
|
12,50
|
11,53
|
10,81
|
10,35
|
10,11
|
|
0
|
2,78
|
4,43
|
5,67
|
7,33
|
9,05
|
10,16
|
10,51
|
10,37
|
10,06
|
9,76
|
9,57
|
9,53
|
|
0
|
0,32
|
0,74
|
1,17
|
2,05
|
3,54
|
5,22
|
6,51
|
7,26
|
7,62
|
7,79
|
7,90
|
8,04
|
|
0
|
0,02
|
0,07
|
0,14
|
0,36
|
0,96
|
2,04
|
3,28
|
4,32
|
5,03
|
5,50
|
5,81
|
6,07
|
Все значения спреда батерфляй удовлетворяют условию нахождения в
интервале от нуля до плюс бесконечности. Последний тест на календарные спреды
дал следующие результаты:
Таблица 23. Результаты проверки безарбитражности по календарному спреду
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1,30
|
1,66
|
1,85
|
2,20
|
2,85
|
3,76
|
4,75
|
5,55
|
5,92
|
5,78
|
5,18
|
4,27
|
|
1,88
|
2,52
|
2,70
|
3,19
|
4,12
|
5,35
|
6,59
|
7,47
|
7,77
|
7,41
|
6,49
|
5,24
|
|
2,81
|
3,77
|
3,76
|
4,43
|
5,71
|
7,29
|
8,73
|
9,62
|
9,73
|
9,05
|
7,76
|
6,11
|
|
4,85
|
5,61
|
5,08
|
5,98
|
7,69
|
9,60
|
11,15
|
11,91
|
11,72
|
10,64
|
8,91
|
6,83
|
|
10,23
|
8,10
|
6,58
|
7,78
|
9,95
|
12,13
|
13,66
|
14,16
|
13,57
|
12,04
|
9,85
|
7,32
|
|
24,53
|
10,41
|
7,72
|
9,36
|
12,04
|
14,41
|
15,81
|
16,01
|
15,02
|
13,06
|
10,44
|
7,51
|
|
57,63
|
10,44
|
7,50
|
9,70
|
12,87
|
15,46
|
16,85
|
16,90
|
15,68
|
13,45
|
10,54
|
7,33
|
|
18,30
|
6,96
|
5,28
|
7,76
|
11,22
|
14,20
|
15,97
|
16,27
|
15,19
|
13,00
|
10,05
|
6,74
|
|
3,47
|
2,65
|
2,34
|
4,25
|
7,31
|
10,54
|
12,95
|
13,94
|
13,43
|
11,64
|
8,94
|
5,78
|
|
0,36
|
0,53
|
0,59
|
1,44
|
3,31
|
6,03
|
8,73
|
10,44
|
10,70
|
9,56
|
7,37
|
4,59
|
|
0,02
|
0,06
|
0,08
|
0,30
|
1,03
|
2,64
|
4,87
|
6,80
|
7,65
|
7,18
|
5,61
|
3,35
|
|
0,00
|
0,00
|
0,01
|
0,04
|
0,23
|
0,92
|
2,30
|
3,91
|
4,96
|
4,97
|
3,96
|
2,26
|
|
0,00
|
0,00
|
0,00
|
0,00
|
0,05
|
0,28
|
0,97
|
2,06
|
2,99
|
3,23
|
2,63
|
1,42
|
В отличие от всех других интерполяционным методов, последний тест по
календарным спредам дал положительный результат. Все элементы
вышепредставленной таблицы удовлетворяют условию неотрицательности. Таким
образом, полиномиальная интерполяция показала наилучшие результаты, и данные,
полученные этим методом, будут в дальнейшем использоваться для нахождения
истинного вероятностного пространства.
Используя цены опционов call,
смоделированные с помощью полиномиальной интерполяции, перейдем от ним к ценам
Эрроу-Дебре с помощью формулы из работы Breeden-Litzenberg [8]. Матрица цен Эрроу-Дебре представлена в следующей таблице:
Таблица 24. Матрица цен Эрроу-Дебре
|
K\T
|
0,08
|
0,17
|
0,25
|
0,33
|
0,42
|
0,50
|
0,58
|
0,67
|
0,75
|
0,92
|
1,00
|
|
1379,07
|
0,003
|
0,007
|
0,009
|
0,012
|
0,015
|
0,019
|
0,022
|
0,024
|
0,025
|
0,025
|
0,024
|
|
1479,07
|
0,011
|
0,017
|
0,020
|
0,023
|
0,027
|
0,030
|
0,033
|
0,034
|
0,035
|
0,033
|
0,032
|
|
1579,07
|
0,033
|
0,040
|
0,042
|
0,044
|
0,047
|
0,049
|
0,050
|
0,050
|
0,048
|
0,044
|
0,042
|
|
1679,07
|
0,089
|
0,087
|
0,084
|
0,082
|
0,080
|
0,077
|
0,074
|
0,070
|
0,066
|
0,058
|
0,055
|
|
1779,07
|
0,188
|
0,165
|
0,151
|
0,139
|
0,126
|
0,114
|
0,103
|
0,093
|
0,086
|
0,074
|
0,071
|
|
1879,07
|
0,276
|
0,241
|
0,221
|
0,198
|
0,173
|
0,150
|
0,131
|
0,116
|
0,104
|
0,090
|
0,086
|
|
1979,07
|
0,245
|
0,237
|
0,230
|
0,214
|
0,191
|
0,167
|
0,146
|
0,129
|
0,116
|
0,101
|
|
2079,07
|
0,117
|
0,139
|
0,151
|
0,158
|
0,157
|
0,149
|
0,137
|
0,125
|
0,115
|
0,103
|
0,101
|
|
2179,07
|
0,028
|
0,044
|
0,057
|
0,073
|
0,090
|
0,102
|
0,105
|
0,104
|
0,101
|
0,096
|
0,095
|
|
2279,07
|
0,003
|
0,007
|
0,012
|
0,021
|
0,035
|
0,052
|
0,065
|
0,073
|
0,076
|
0,079
|
0,080
|
|
2379,07
|
0,000
|
0,001
|
0,001
|
0,004
|
0,010
|
0,020
|
0,033
|
0,043
|
0,050
|
0,058
|
0,061
|
3.3 Оптимизация
Таким образом, мы убедились, что использованный нами интерполяционный
метод помог получить необходимые теоретические цены Эрроу-Дебре. В пункте 3.1
главы 3 была затронута проблема решения системы линейных уравнений,
удовлетворяющая условию неотрицательности матрицы переходных цен Эрроу-Дебре.
Чтобы решить данную проблему придется решить оптимизационную задачу,
максимально близко подбирая искомые значения матрицы переходных цен
Эрроу-Дебре.
Для того, чтобы отыскать элементы искомой матрицы, необходимо
сформулировать функцию ошибок, которая будет представлять из себя ошибки
подбора элементов массива.
Искомая матрица переходных цен Эрроу-Дебре имеет размерность 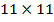 . Обозначим ее через . Обозначим ее через 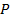 и каждый элемент матрицы обозначим
как и каждый элемент матрицы обозначим
как 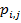 , где , где 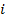 - номер строки, а - номер строки, а 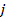 - номер столбца этой матрицы.
Элементы - номер столбца этой матрицы.
Элементы 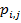 должны подбираться таким образом,
чтобы получить расчетные значения элементов матрицы должны подбираться таким образом,
чтобы получить расчетные значения элементов матрицы 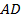 цен Эрроу-Дебре, минимально
отличающиеся от истинных значений. Оптимизация будет происходить по методу
наименьших квадратов с ограничениями. цен Эрроу-Дебре, минимально
отличающиеся от истинных значений. Оптимизация будет происходить по методу
наименьших квадратов с ограничениями.
Расчетное значение элемента 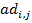 матрицы матрицы 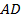 будем обозначать как будем обозначать как 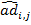 . Учитывая что 6 строка матрицы . Учитывая что 6 строка матрицы 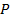 представляет собой значения первого
столбца матрицы представляет собой значения первого
столбца матрицы 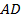 , осталось найти значения матрицы , осталось найти значения матрицы 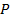 с 1 по 5 строку, и с 7 по 11 строку.
Значения с 1 по 5 строку, и с 7 по 11 строку.
Значения 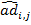 при при 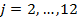 представлены в виде: представлены в виде:

Таким образом функция ошибок имеет вид:
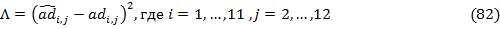
Минимизируя данную функцию 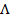 , мы получим искомые значения матрицы
переходных цен Эрроу-Дебре. Оптимизация должна быть произведена с некоторыми
ограничениями: , мы получим искомые значения матрицы
переходных цен Эрроу-Дебре. Оптимизация должна быть произведена с некоторыми
ограничениями:
Так, определимся с краевыми условиями. Нижняя граница для элемента 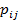 равна нулю, а верхняя граница равна
единице. равна нулю, а верхняя граница равна
единице.
Начальные приближения для элементов матрицы Р зададим равными 0,5.
Предположим, что вероятность остаться в текущем состоянии рынка максимальна
и составляет 35%, вероятность что рынок упадет на одно состояние вниз
составляет 15%, а вероятность что рынок упадет на два состояния вниз составляет
20%. Данная ситуация кажется весьма нереалистичной, так как с точки зрения
здравого смысла вероятность перехода во всё более дальние состояния должна
убывать. Поэтому необходимо сформулировать последнее ограничение, связанное с
унимодальностью строк матрицы Р.
В данной работе будет предполагаться, что вероятность остаться в текущем
состоянии рынка будет максимальной, а вероятности попадания во всё более
дальние состояния рынка должны убывать. Более формально данное ограничение
можно записать как:
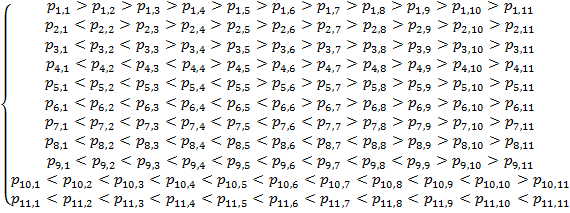
Проведя оптимизацию в среде Matlab с помощью функцию fmincon
была получена следующая матрица перехода цен Эрроу-Дебре:
Таблица 25. Матрица переходных цен Эрроу-Дебре
|
-27%
|
-21%
|
-16%
|
-11%
|
-5%
|
0%
|
5%
|
11%
|
16%
|
21%
|
27%
|
|
-27%
|
0,268
|
0,168
|
0,129
|
0,103
|
0,083
|
0,068
|
0,057
|
0,047
|
0,038
|
0,027
|
0,012
|
|
-21%
|
0,071
|
0,255
|
0,166
|
0,125
|
0,098
|
0,078
|
0,065
|
0,054
|
0,044
|
0,031
|
0,014
|
|
-16%
|
0,042
|
0,093
|
0,252
|
0,162
|
0,118
|
0,092
|
0,076
|
0,064
|
0,051
|
0,035
|
0,015
|
|
-11%
|
0,023
|
0,047
|
0,087
|
0,262
|
0,166
|
0,124
|
0,102
|
0,082
|
0,060
|
0,035
|
0,014
|
|
-5%
|
0,010
|
0,022
|
0,039
|
0,077
|
0,281
|
0,205
|
0,172
|
0,114
|
0,050
|
0,022
|
0,008
|
|
0%
|
0,003
|
0,011
|
0,033
|
0,089
|
0,188
|
0,276
|
0,245
|
0,117
|
0,028
|
0,003
|
0,000
|
|
5%
|
0,007
|
0,015
|
0,026
|
0,046
|
0,088
|
0,310
|
0,271
|
0,173
|
0,044
|
0,016
|
0,006
|
|
11%
|
0,011
|
0,022
|
0,034
|
0,047
|
0,062
|
0,082
|
0,285
|
0,231
|
0,168
|
0,043
|
0,015
|
|
16%
|
0,009
|
0,018
|
0,025
|
0,032
|
0,039
|
0,047
|
0,063
|
0,321
|
0,277
|
0,124
|
0,047
|
|
21%
|
0,007
|
0,015
|
0,021
|
0,026
|
0,031
|
0,037
|
0,047
|
0,072
|
0,231
|
0,377
|
0,137
|
|
27%
|
0,008
|
0,017
|
0,024
|
0,030
|
0,037
|
0,044
|
0,054
|
0,075
|
0,134
|
0,210
|
0,367
|
Строки данной матрицы представляют собой начальные состояния рынка, а
столбцы конечные состояния рынка. Так, например, значение 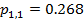 означает, что столько инструмент
Эрроу-Дебре по которому нам выплатят 1$ при условии перехода из состояния означает, что столько инструмент
Эрроу-Дебре по которому нам выплатят 1$ при условии перехода из состояния 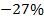 в состояние в состояние 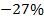 . .
Применяю к матрице переходных цен Эрроу-Дебре теорему Росса, получим
матрицу истинных вероятностей перехода:
Таблица 26. Матрица истинных вероятностей перехода из одного состояния в
другое
|
-27%
|
-21%
|
-16%
|
-11%
|
-5%
|
0%
|
5%
|
11%
|
16%
|
21%
|
27%
|
|
-27%
|
0,268
|
0,169
|
0,129
|
0,103
|
0,083
|
0,068
|
0,056
|
0,047
|
0,038
|
0,027
|
0,012
|
|
-21%
|
0,071
|
0,255
|
0,166
|
0,125
|
0,098
|
0,077
|
0,065
|
0,054
|
0,044
|
0,031
|
0,014
|
|
-16%
|
0,042
|
0,093
|
0,252
|
0,162
|
0,118
|
0,091
|
0,076
|
0,064
|
0,051
|
0,035
|
0,015
|
|
-11%
|
0,023
|
0,047
|
0,087
|
0,262
|
0,166
|
0,123
|
0,102
|
0,082
|
0,06
|
0,035
|
0,014
|
|
-5%
|
0,01
|
0,022
|
0,039
|
0,077
|
0,281
|
0,204
|
0,172
|
0,114
|
0,05
|
0,022
|
0,008
|
|
0%
|
0,004
|
0,011
|
0,034
|
0,09
|
0,189
|
0,276
|
0,247
|
0,118
|
0,028
|
0,003
|
2E-04
|
|
5%
|
0,007
|
0,015
|
0,026
|
0,046
|
0,088
|
0,308
|
0,271
|
0,173
|
0,044
|
0,016
|
0,006
|
|
11%
|
0,011
|
0,022
|
0,034
|
0,048
|
0,062
|
0,081
|
0,284
|
0,232
|
0,169
|
0,043
|
0,015
|
|
16%
|
0,009
|
0,018
|
0,025
|
0,032
|
0,039
|
0,046
|
0,063
|
0,321
|
0,277
|
0,124
|
0,047
|
|
21%
|
0,007
|
0,015
|
0,021
|
0,026
|
0,031
|
0,037
|
0,047
|
0,072
|
0,231
|
0,377
|
0,137
|
|
27%
|
0,008
|
0,017
|
0,024
|
0,03
|
0,037
|
0,044
|
0,054
|
0,075
|
0,134
|
0,367
|
Также, как и в матрице переходных цен Эрроу-Дебре, по строкам
располагаются начальные состояния, а по столбцам конечные состояния. Так
элемент данной матрицы 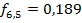 означает, что истинная вероятность перехода из состояния 0%,
т.е. текущего состояния рынка, в состояние -5% равна 18,9%. означает, что истинная вероятность перехода из состояния 0%,
т.е. текущего состояния рынка, в состояние -5% равна 18,9%.
Нас прежде всего интересует центральная строка данной матрицы, которая
представляет собой натуральные вероятности перехода из текущего состояния рынка
во все другие состояния. Данные вероятности представлены на следующей
диаграмме:
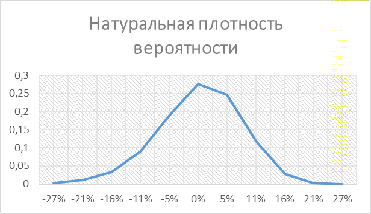
Рисунок 7. Натуральная плотность вероятности
Из матрицы истинных вероятностей следует, что вероятность роста индекса S&P500 через месяц составляет 39,6% против вероятности падения в
32,8%. Математическое ожидание изменения индекса S&P500
составляет 0,26%, что соответствует его значению в 1883,9 пункта на 17.03.2016.
Истинное же значение индекса S&P500 через месяц на 17.03.2016
составило 2040,59 пунктов, то есть был осуществлен рост на 8,6%, что по
построенной модели составляет около 12%.
Заключение
Данная работа была посвящена получению истинных вероятностей перехода
значения стоимости базового актива из одного состояния рынка в другое с помощью
новой концепции, которую Steve Ross назвал Recovery Theorem. Для данной цели были проделы следующие этапы работы:
· Были изучены теоретические аспекты ценообразования опционов и их
взаимосвязи с риск-нейтральными вероятностями;
· Были рассмотрены необходимые условия, при выполнении которых
можно применить к матрице переходных цен Эрроу-Дебре Recovery Theorem для извлечения из цен опционов истинного
вероятностного пространства;
· С помощью методов интерполяции и оптимизации была решена
проблема с нехваткой данных и проблема нахождения матрицы переходных цен
Эрроу-Дебре;
· Из матрицы переходных цен Эрроу-Дебре было получено истинное
вероятностное распределение будущих движений цены базового актива.
Концепция извлечения натуральных вероятностей из цен опционов с помощью Recovery Theorem вызывает некоторые вопросы. Так, предположение о
гомогенности предпочтений инвестора является весьма сильным. Если предпочтения
и вправду являются гомогенными, то может просто стоит оценить эти предпочтения
по историческим данным, ведь они не подвержены изменению во времени. Очевидно,
что спустя 5 лет предпочтения инвестора все же как-то поменяются. Поэтому,
возможно, следует попытаться получить результаты Steve Ross, минуя данную предпосылку.
Задача получения цен Эрроу-Дебре была связана с интерполяционными
методами применяемыми к поверхности волатильности опционов. В данной работе
были использованы следующие методы интерполяци:
· Cubic splines;
· Thin-plate splines;
· Biharmonic splines;
· Polynomial.
Интерполированные цены опционов call проверялись на отсутствие арбитражных возможностей. Все интерполяционные
методы показали хорошие результаты, однако только метод Polynomial показал отсутствие арбитража по всем
спредам: вертикальному спреду, спреду батерфляй и календарному спреду. Именно
данный метод использовался в данной работе для получения цен Эрроу-Дебре.
Для получения матрицы переходных цен Эрроу-Дебре было необходимо решить
оптимизационную задачу с ограничениями. Оптимизация проводилась по методу
наименьших квадратов. А набор ограничений включал в себя:
· Нахождение всех элементов матрицы переходных цен Эрроу-Дебре
в интервале [0,1];
· Унимодальность строк.
Применяя Recovery
Theorem к матрице переходных цен Эрроу-Дебре
была получена матрица истинных вероятностей перехода значения индекса S&P500 из одного состояния рынка в другое. Эта матрица показывает
вероятности перехода из всех возможных состояний рынка в другие состояния, и не
только из текущего состояния. В первую очередь нас интересует центральная
строка данной матрицы, которая представляет истинные вероятности перехода из
текущего состояния рынка в другие состояния. Данная строка может быть
использована для прогноза движения базового актива. Так, например, одной из
стратегий может быть сравнение медианы данного распределения с текущим
состоянием рынка.
Recovery Theorem
предполагает нетривиальные способы получения матрицы цен Эрроу-Дебре с помощью
процедур интерполяции и оптимизации. Если неточно провести данные процедуры, то
на выходе результат может весьма исказится. Поэтому в дальнейшем также следует
работать в этом направлении в попытке получить наиболее оптимальные методы
получения цен Эрроу-Дебре.
Полученные результаты могут вызвать множество вопросов. Один из которых
затрагивает проблему проверки полученных вероятностей и сопоставления их с
историческими данными. Одним из решений данной проблемы является проведение
процедуры получения истинных вероятностей перехода на большом количестве
исторических данных. Прогноз о росте или падении стоимости базового актива
может делаться на основании медианы. Сопоставление прогнозных результатов с истинными
историческими данными может осуществляться на основании статистических тестов с
нулевой гипотезой об отсутствии прогнозных способностей у полученного истинного
распределения вероятностей.
Список использованных источников
1. Ait-Sahalia, Yacine and Andrew Lo (1998).
Nonparametric Estimation of State-Price Densities Implicit in Financial Asset
Prices. Journal of Finance, 499-547.
2. Ahlberg, Harold J., Nilson, Edwin and Walsh
Joseph, 1967. The Theory of Splines and Their Applications. Academic Press,
1967.
. Backwell, Alex,2015,State Prices and
Implementation of the Recovery Theorem, Journal of Risk and Financial
Management 8, 2-16
. Bahra, Bhupinder (1997). Implied Risk-Neutral
Probability Density Function from Option Prices: Theory and Application. Workng
Paper, Bank of England.
. Black, Fischer, and Myron Scholes, 1973, The
pricing of options and corporate liabilities, Journal of Political Economy 81,
637-654.
. Bliss, Robert R. and Panigirtzoglou Nikolaos,
2004, Option-Implied Risk Aversion Estimates, The Journal of Finance
. Boyle, Mike, 2000. Notes on The
Perron-Frobenius Theory of Nonnegative Matrices.
. Breeden, Douglas T., and Robert Litzenberger,
1978, Prices of state contingent claims implicit in option prices, Journal of
Business 51, 621-651.
. Carl de Boor. Spline Toolbox For Use with
Matlab
. Carr, Peter, and Jiming Yu, 2012, Risk,
Return, and Ross Recovery, Journal of Derivatives 20, 38-59.
. Carr, Peter, and Madan, Dilip B, 2005, A note
on sufficient conditions for no arbitrage, Finance Research Letters 2, 125-130
. Dumas, Bernard, Fleming,Jeff and Whaley
Robert E., 1998, Implied Volatility Functions: Empirical Tests, The Journal of
Finance, Vol. 53, No.6. (Dec,.1998),pp.2059-2106
. Dybvig, Philip H., and Christopher G. Rogers,
1997, Recovery of preferences from observed wealth in a single realization,
Review of Financial Studies 10, 151-174.
. Fama, Eugene F., 1970, Efficient capital
markets: A review of theory and empirical work, Journal of Finance 25, 383-417.
. Hull,John (2006). Options, Futures, and Other
Derivatives. New Jersey: Prentice Hall.
. Jackwerth Jens (1996). Recovering Risk
Aversion from Option Prices and Realized Returns. The Review of Financial
Studies. Vol. 13, No. 2, pp. 433-451.
. Jackwerth, Jens and Mark Rubinstein (1996).
Recovering Probability Distributions from Option Prices. Journal of Finance,
1611-1631.
. Malz, Allan (1997). Estimating the
Probability Distribution of the Future Exchange Rate from Options Prices.
Journal of Derivatives, 18-36.
. Ross, Steve (1976). Options and Efficiency.
Quarterly Journal of Economics, 75-89.
. Ross, Steve A., 1976, The arbitrage theory of
capital asset pricing, Journal of Economic Theory 13, 341-360.
. Ross, Steve. “The Recovery Theorem.” Working
paper Sept. 10, 2011 forthcoming in Journal of Finance
. Rubinstein, Mark (1994). Implied Binomial
Tree. Journal of Finance, 771-818.
. Sandwell D.T. (1987), Biharmonic spline
interpolation of GEOS-3 and SEASAT altimeter data, Geophysical Research
Letters, Vol. 2, p. 139 - 142.
. Zhou, Hong Cheng. (2012). Option Implied Risk
Aversion. Master thesis within the major profile of Energy, Natural Resouces
and the Environment. Norwegian school of economics.
25. Информационный финансовый ресурс поисковой системы yahoo.com
. Официальный сайт Казначейства США
Похожие работы на - Прогнозирование характеристик рынка базового актива
|