Аберрационный анализ оптической системы
Министерство
образования и науки РФ
Московский
Государственный Университет Геодезии и Картографии (МИИГАиК)
Факультет
оптико-информационных систем и технологий
Курсовая
работа по дисциплине:
«Основы
оптики»
Тема:
«Аберрационный
анализ оптической системы»
Содержание
. Исходные данные для выполнения
курсовой работы
. Расчет параксиальных лучей и
определение кардинальных элементов оптической системы
. Вычисление положения и диаметра
входного, выходного зрачка и полевой диафрагмы
. Вычисление монохроматических сумм
Зейделя
5.
Вычисление значений 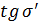
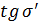 и
и 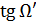
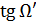 лучей полевого пучка
лучей полевого пучка
.
Вычисление меридиональных и сагиттальных составляющих отдельных
монохроматических аберраций 3-го порядка
.
Вычисление монохроматических аберраций 3-го порядка меридиональных лучей и
элементарных плоских пучков
.
Вычисление хроматических сумм, хроматизма положения и хроматизма увеличения
1-го порядка
.
Сводка результатов вычисления монохроматических аберраций 3-го порядка меридионального
луча и хроматических аберраций 1-го порядка
Список
использованных источников
1. Исходные данные для выполнения курсовой
работы
Объектив.
)Марки стекла К8 Ф1
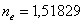
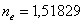
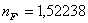
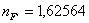
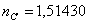
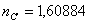
) 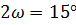
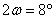 ;
;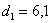 ;
;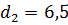
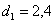
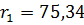
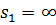
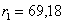
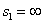
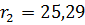
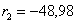
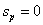
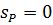
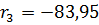
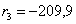
3) Относительное отверстие - 1:4
. Расчет параксиальных лучей и
определение кардинальных элементов оптической системы
.1 Расчет первого параксиального
луча, заднего фокусного расстояния системы и кардинальных отрезков в прямом
ходе.
|
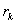 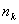 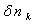 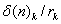 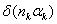 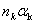 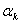 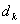 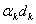 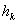
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
0
|
0
|
|
|
|
|
1
|
69,18
|
1,51829
|
0,51829
|
0,00749
|
0,749
|
0,749
|
0,49332
|
6,1
|
3,00924
|
100,00000
|
|
2
|
-48,98
|
1,61687
|
0,09858
|
-0,00201
|
-0,19495
|
0,55405
|
0,34267
|
2,4
|
0,82241
|
96,99076
|
|
3
|
-209,9
|
1
|
-0,61687
|
0,00294
|
0,28273
|
0,83678
|
0,83678
|
|
|
96,16835
|
Расчет задних кардинальных элементов
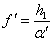 ;
; 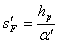 ;
;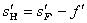
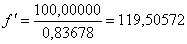
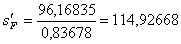
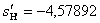
2.2 Расчет первого параксиального
луча для 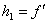 и
и 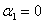 .
.
|
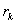 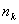 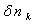 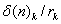 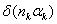 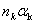 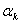 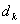 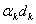 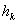
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
0
|
0
|
|
|
|
|
|
1
|
69,18
|
1,51829
|
0,51829
|
0,00749
|
0,89510
|
0,89510
|
0,58954
|
2,4
|
3,59619
|
119,50572
|
|
2
|
-48,98
|
1,61687
|
0,09858
|
-0,00201
|
-0,23298
|
0,66212
|
0,40951
|
6,1
|
0,98282
|
115,90953
|
|
3
|
-209,9
|
1
|
-0,61687
|
0,00294
|
0,33788
|
1,00000
|
1,00000
|
|
|
114,92671
|
2.3 Расчет второго параксиального
луча для 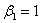 и
и 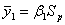 .
.
|
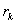 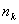 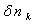 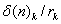 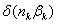 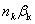 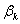 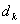 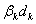 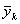
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
1
|
1
|
|
|
|
|
|
1
|
69,18
|
1,51829
|
0,51829
|
0,00749
|
0
|
1
|
0,65864
|
6,1
|
4,01770
|
0
|
|
2
|
-48.98
|
1,61687
|
0,09858
|
-0,00201
|
0,00808
|
1,00808
|
0,62348
|
2,4
|
1,49635
|
-4,01770
|
|
3
|
-209.9
|
1
|
-0,61687
|
0,00294
|
-0,01621
|
0,99187
|
0,99187
|
|
|
-5,51405
|
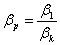
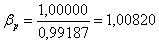
Проверка:
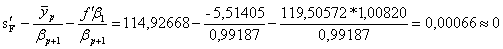
2.4 Расчет первого параксиального
луча в обратном ходе и определение передних кардинальных элементов.
|
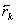 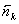 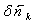 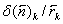 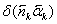 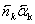 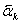 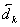 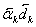 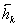
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
1
|
209.9
|
1,61687
|
0,61687
|
0,00294
|
0,29400
|
0,29400
|
0,18183
|
6,1
|
0,43639
|
100
|
|
2
|
48,98
|
1,51829
|
-0,09858
|
-0,00201
|
-0,20012
|
0,09388
|
0,06183
|
2,4
|
0,37716
|
99,56361
|
|
3
|
-69,18
|
1
|
-0,51829
|
0,00749
|
0,74291
|
0,83679
|
0,83679
|
|
|
99,18645
|
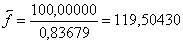
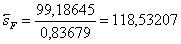
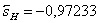
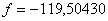
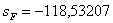
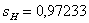
Проверка:
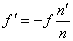
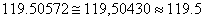
. Вычисление положения и диаметра
входного, выходного зрачка и полевой диафрагмы
.1 Нахождение диаметра апертурной
диафрагмы.
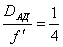
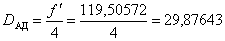
3.2 По условию нам задано положение
входного зрачка, которое совпадает с апертурной диафрагмой (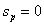 ), поэтому
диаметр входного зрачка равен диаметру апертурной диафрагмы.
), поэтому
диаметр входного зрачка равен диаметру апертурной диафрагмы.
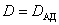
3.3 Расчет положение выходного
зрачка.
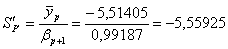
Определим диаметр выходного зрачка:
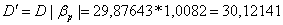
3.4 Расчет положения и диаметра
полевой диафрагмы.
Найдем положение ПД:
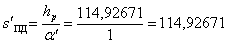
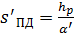
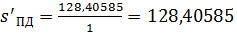
Теперь вычислим диаметр полевой
диафрагмы
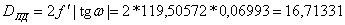
. Вычисление монохроматических сумм
Зейделя
Первая, вторая, третья, четвертая и
пятая суммы Зейделя вычисляются по формулам:
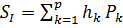
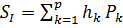 ,
, 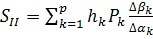
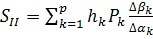 ,
, 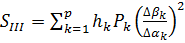
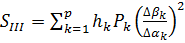 ,
,
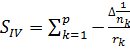
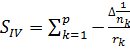 ,
, 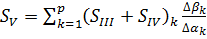
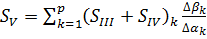
|
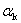 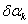 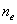 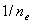 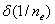 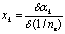 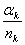 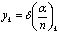 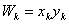
|
|
|
|
|
|
|
|
|
|
0
|
0,58954
|
1
|
1
|
-0,34136
|
-1,72703
|
0
|
0,38829
|
-0,67053
|
|
0,58954
|
-0,18003
|
1,51829
|
0,65864
|
0,04016
|
4,48282
|
0,38829
|
-0,13502
|
-0,60527
|
|
0,40951
|
0,730232
|
1,61687
|
0,61848
|
0,38152
|
1,54773
|
0,25327
|
0,74673
|
1,15574
|
|
1
|
|
1
|
1
|
|
|
1
|
|
|
|
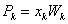 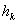 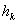 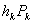 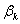 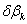 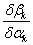 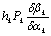 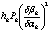
|
|
|
|
|
|
|
|
|
|
1,15813
|
119,50572
|
119,50572
|
138,40319
|
0,65864
|
-0,34136
|
-0,57903
|
-80,13960
|
46,40323
|
|
-2,71332
|
115,90953
|
115,90953
|
-314,44964
|
0,62348
|
-0,03516
|
0,19530
|
-61,42178
|
-11,99567
|
|
1,78877
|
114,92671
|
114,92671
|
205,57775
|
0,99187
|
0,36839
|
0,62387
|
128,25379
|
80,01369
|
|
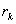 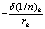 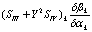
|
|
|
|
69,18
|
0,004934374
|
-67,67359
|
|
-48,98
|
-0,000819926
|
-4,62969
|
|
-209,9
|
0,001817627
|
66,11296
|
Полученные значения сумм Зейделя:
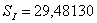
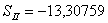
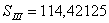
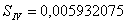
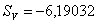
Примечание: Для того, чтобы получить
приведенные суммы Зейделя, которые у нас получились при вычислении на ЭВМ,
нужно полученные нами суммы разделить на фокусное расстояние, кроме 4 суммы,
которую нужно умножить, тогда получим:
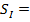
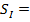 0,24669
0,24669
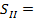
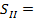 -0,11136
-0,11136
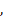
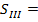
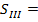 0,95745
0,95745
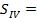
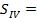 0,70892
0,70892
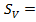
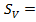 -0,05180
-0,05180
. Вычисление значений 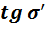
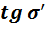 и
и 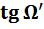
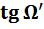 лучей полевого пучка
лучей полевого пучка
Для вычисления в дальнейшем
меридиональной и сагиттальной составляющих поперечной аберрации лучей и
построение фигур рассеяния, которые эти лучи образуют в плоскости изображения,
предварительно необходимо вычислить значения 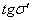
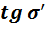 и
и 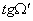
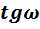 этих лучей. При этом
предполагается, что пучок крайних полевых лучей полностью заполняет входной и
выходной зрачки (отсутствует виньетирование). Из всех лучей названного пучка
используются только 8 лучей, встречающих плоскость выходного зрачка в точках,
лежащих на окружности диаметром
этих лучей. При этом
предполагается, что пучок крайних полевых лучей полностью заполняет входной и
выходной зрачки (отсутствует виньетирование). Из всех лучей названного пучка
используются только 8 лучей, встречающих плоскость выходного зрачка в точках,
лежащих на окружности диаметром 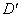 и делят эту окружность на 8 равных
частей.
и делят эту окружность на 8 равных
частей.
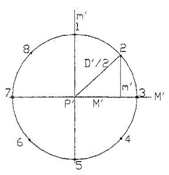
Для начала найдем координаты m’ и M’ указанных
точек в прямоугольной системе координат M’P’m’. После
чего вычислим тангенсы углов 8 лучей с помощью формул:
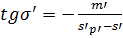
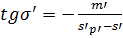 ,
, 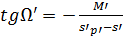
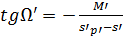
|
№
луча
|
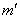 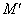 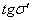 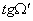
|
|
|
|
|
1
|
15,06071
|
0,00000
|
0.12500
|
0,00000
|
|
2
|
10,64953
|
10,64953
|
0.08839
|
0.08839
|
|
3
|
0,00000
|
15,06071
|
0,00000
|
0.12500
|
|
4
|
-10,64953
|
10,64953
|
-0.08839
|
0.08839
|
|
5
|
-15,06071
|
0,00000
|
-0.12500
|
0,00000
|
|
6
|
-10,64953
|
-10,64953
|
-0.08839
|
-0.08839
|
|
7
|
0,00000
|
-15,06071
|
0,00000
|
-0.12500
|
|
8
|
10,64953
|
-10,64953
|
0.08839
|
-0.08839
|
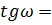
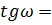 0,06993
0,06993
6. Вычисление меридиональных и
сагиттальных составляющих отдельных монохроматических аберраций 3-го порядка
Прежде, чем приступить к вычислению
меридиональных и сагиттальных составляющих необходимо вычислить инвариант
Лагранджа-Гельгольмца по формуле:
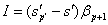
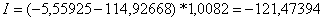
Формулы для вычисления составляющих
сферической аберрации 3-го порядка:

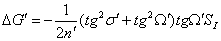
Формулы для вычисления составляющих
комы 3-го порядка:
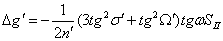
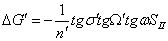
Формулы для вычисления составляющих
астигматизма 3-го порядка:
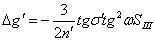
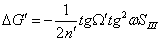
Формула для вычисления составляющих
кривизны изображения 3-го порядка:
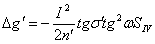
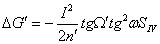
Формула для вычисления составляющих
дисторсии 3-го порядка:
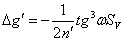
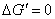
После вычисляем составляющие общей
аберрации по формулам:
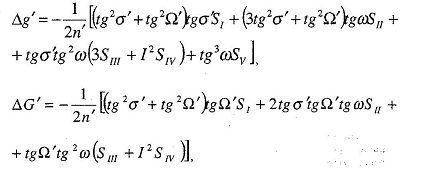
|
№
луча
|
Сферическая
аберрация
|
Кома
|
Астигматизм
|
|
 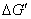 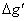 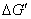 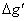 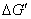
|
|
|
|
|
|
|
1
|
-0.0287900
|
0,0000000
|
0.0218099
|
0,0000000
|
-0.1048968
|
0,0000000
|
|
2
|
-0.0203590
|
-0.0203590
|
0.0145405
|
0,0072703
|
-0.0741803
|
-0.0247268
|
|
3
|
0,0000000
|
-0.0287900
|
0,0072700
|
0,0000000
|
0,0000000
|
-0,0349683
|
|
4
|
0.0203590
|
-0.0203590
|
0.0145405
|
-0,0072703
|
0.0741803
|
-0.0247268
|
|
5
|
0.0287900
|
0,0000000
|
0.0218099
|
0,0000000
|
0.1048968
|
0,0000000
|
|
6
|
0.0203590
|
0.0203590
|
0.0145405
|
0,0072703
|
0.0741803
|
0.0247268
|
|
7
|
0,0000000
|
0.0287900
|
0,0072700
|
0,0000000
|
0,0000000
|
0,0349683
|
|
8
|
-0.0203590
|
0.0203590
|
0.0145405
|
-0,0072703
|
-0.0741803
|
0.0247268
|
|
№
луча
|
Кривизна
изображения
|
Дисторсия
|
Общая
аберрация
|
|
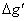 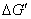 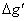 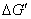 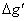 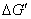
|
|
|
|
|
|
|
1
|
-0.0267510
|
0,0000000
|
0,0010583
|
0,0000000
|
-0,1376786
|
0,0000000
|
|
2
|
-0.0189162
|
-0.0189162
|
0,0010583
|
0,0000000
|
-0,1005567
|
-0,0567317
|
|
3
|
0,0000000
|
-0.0267510
|
0,0010583
|
0,0000000
|
0,0832830
|
-0,0905093
|
|
4
|
0.0189162
|
-0.0189162
|
0,0010583
|
0,0000000
|
0,1290543
|
-0,0712723
|
|
5
|
0.0267510
|
0,0000000
|
0,0010583
|
0,0000000
|
0,1833101
|
0,0000000
|
|
6
|
0.0189162
|
0.0189162
|
0,0010583
|
0,0000000
|
0,1290543
|
0,0712723
|
|
7
|
0,0000000
|
0.0267510
|
0,0010583
|
0,0000000
|
0,0832830
|
0,0905093
|
|
8
|
-0.0189162
|
0.0189162
|
0,0010583
|
0,0000000
|
-0,1005567
|
0,0567317
|
|
№
Луча
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
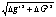 0,13767860,11545620,12299590,14742710,18331010,14742710,12299590,1154562 0,13767860,11545620,12299590,14742710,18331010,14742710,12299590,1154562
|
|
|
|
|
|
|
|
|
После заполнения таблицы, строим фигуру
рассеяния пучка лучей отдельно для сферической аберрации, комы, кривизны
изображения и астигматизма (дисторсия не дает кружки рассеяния). Фигуры
рассеяния представлены на рисунке.
параксиальный луч диафрагма
аберрация
7. Вычисление монохроматических аберраций 3-го
порядка меридиональных лучей и элементарных плоских пучков
Если луч лежит в меридиональной
плоскости, то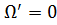
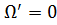 Тогда монохроматические аберрации
вычисляются по следующим формулам.
Тогда монохроматические аберрации
вычисляются по следующим формулам.
Поперечная сф. Аберрация
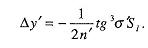
Продольная сф. Аберрация
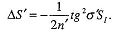
Поперечную и продольную сф.
аберрацию необходимо вычислить для значений 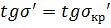
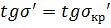 (1-й луч, идущий по краю зрачка) и
значения
(1-й луч, идущий по краю зрачка) и
значения 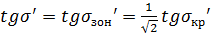
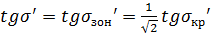 (луч идёт в зоне края зрачка).
(луч идёт в зоне края зрачка).
Продольная и поперечная сф.
аберрация.
При 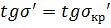
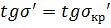 :
: 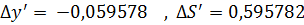
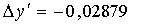
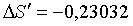
При 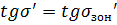
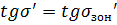 :
: 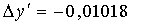
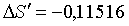
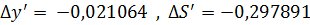
Меридиональная кома
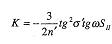
Меридиональную кому необходимо
вычислить для значении значений 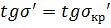
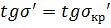 и
и 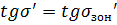
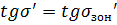 , при
, при 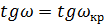
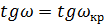 (
(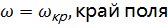
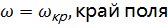 ) и при
) и при 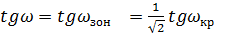
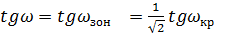 (зона поля).
(зона поля).
Меридиональная кома
При 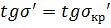
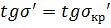 ,
, 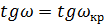
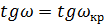 : K= 0,02181
: K= 0,02181
При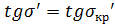
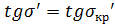 ,
, 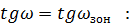
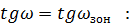 K= 0,01542
K= 0,01542
При 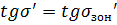
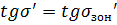 ,
, 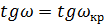
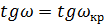 : K= 0,01090
: K= 0,01090
При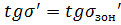
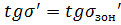 ,
, 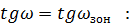
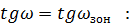 K= 0,00771
K= 0,00771
Меридиональная кривизна изображения:
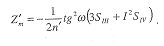
Сагиттальная кривизна изображения:
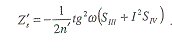
Астигматизм:
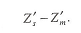
Дисторсия:
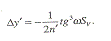
Меридиональную и сагиттальную
кривизну изображения, астигматизм и дисторсию необходимо вычислить при 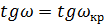
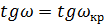 и при
и при 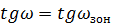
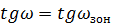 .
.
Меридиональная и сагиттальная
кривизна изображения:
При 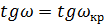
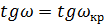 :
: 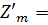
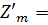 -1,05334
-1,05334 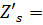
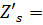 -0,49375
-0,49375
При 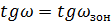
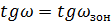 :
: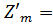
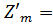 -0,56310
-0,56310 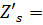
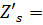 -0,24688
-0,24688
Астигматизм:
При 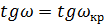
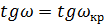 :
: 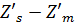
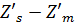 = -0,55959
= -0,55959
При 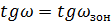
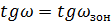 :
: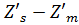
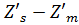 = -0,31622
= -0,31622
Дисторсия:
При 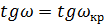
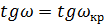 :
: 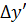
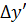 = 0,0010583, При
= 0,0010583, При 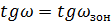
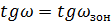 :
: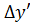
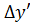 =0,0003742
=0,0003742
. Вычисление хроматических сумм,
хроматизма положения и хроматизма увеличения 1-го порядка
Хроматические суммы 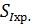
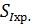 и
и 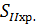
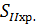 Определяющие соответственно
хроматизм положения и хроматизм увеличения 1-го порядка, вычисляются по
формулам:
Определяющие соответственно
хроматизм положения и хроматизм увеличения 1-го порядка, вычисляются по
формулам:
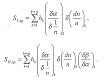
Где 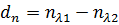
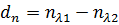 , представляет собою разность
показателей преломления одной и той же среды.
, представляет собою разность
показателей преломления одной и той же среды.
Вычисление сумм, будем вести по
схеме и записывать вычисления в таблицу.
|
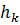
|
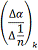
|
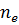
|
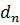 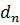 = =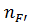 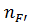 - -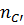 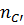 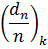
|
|
|
119,50572
|
-1,72703
|
1
|
0
|
0
|
|
115,90953
|
4,48282
|
1,51829
|
0,00808
|
0,00532
|
|
114,92671
|
1,54773
|
1,61687
|
0,01680
|
0,01039
|
|
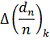
|
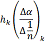
|
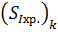
|
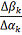
|
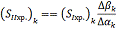
|
|
0,00532
|
-206,38996
|
-1,09799
|
-0,57903
|
0,63577
|
|
0,00507
|
519,60156
|
2,63438
|
-0,19530
|
0,51449
|
|
-0,01039
|
177,87552
|
-1,84813
|
0,62387
|
-1,15299
|
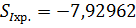
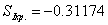 ,
, 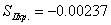
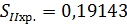
Примечание: Для того, чтобы получить
приведенные хроматические аберрации, которые у нас получились при вычислении на
ЭВМ, нужно полученные нами аберрации разделить на фокусное расстояние, тогда
получим:
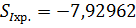
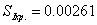 ,
, 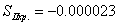
Хроматизм положения 1-го порядка:
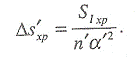
Хроматизм увеличения 1-го порядка:
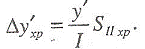
Хроматизм увеличения необходимо
вычислить для 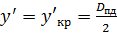
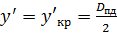 (край поля) и для
(край поля) и для 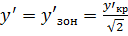
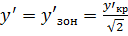 (зона поля).
(зона поля).
Хроматизм положения 1-го порядка:
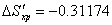
Хроматизм увеличения 1-го порядка:
При 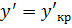
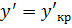 :
: 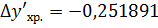
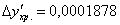
При 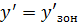
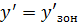 :
: 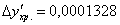
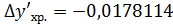
. Сводка результатов вычисления монохроматических
аберраций 3-го порядка меридионального луча и хроматических аберраций 1-го
порядка
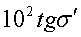 Сферическая аберрацияХром. положения
Сферическая аберрацияХром. положения
|
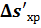 Меридиональная
кома Меридиональная
кома
|
|
|
|
|
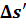
|
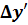
|
|
Край
поля
|
Зона
поля
|
|
|
|
|
|
|
8,839 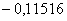
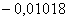
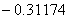
|
0,010900,00771
|
|
|
|
|
|
|
12,500
|
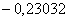 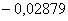 0,021810,01542 0,021810,01542
|
|
|
|
|
|
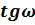
|
Меридиональная
и сагиттальная кривизна и астигматизм
|
Дисторсия
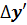
|
Хроматизм
Увеличения 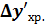
|
|
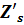
|
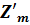
|
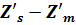
|
|
|
|
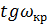
|
-1,05334
|
-0,49375
|
-0,55959
|
0,0010583
|
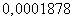
|
|
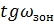
|
-0,56310
|
-0,24688
|
-0,31622
|
0,0003742
|
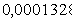
|
Список использованных источников
. Можаров Г.А. «Методические
указания по курсу «Прикладная оптика» для выполнения курсовой работы
«Аберрационный анализ оптической системы»«, Москва, 2002 г.
. Апенко М.И., Дубовик А.С.
«Прикладная оптика», изд. «Наука», Москва, 1982 г.