|
|
|
|
|
|
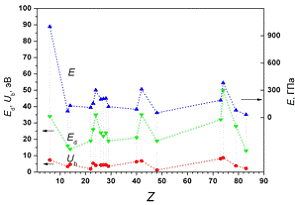
Рисунок 6. Корреляционные кривые пороговой энергии смещения (Ed), энергии связи (Ub)
и модуля Юнга (E) для ряда металлов. Значения Ed
взяты из [1]
|
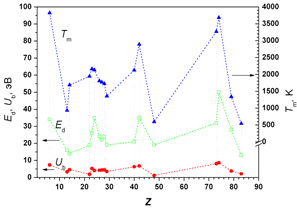
Рисунок 7. Корреляционные кривые пороговой энергии смещения (Ed), энергии связи (Ub)
и температуры плавления (Tm) для ряда металлов
|
|
|
|
|
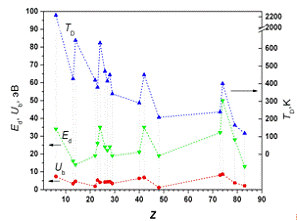
Рисунок 8. Корреляционные кривые пороговой энергии смещения (Ed), энергии связи (Ub)
и температуры Дебая (TD) для ряда металлов
|
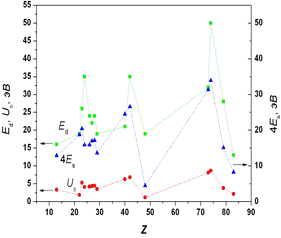
Рисунок 9. Корреляционные кривые пороговой энергии смещения (Ed), энергии связи (Ub)
и 4ES (ES - энергия сублимации) для ряда металлов
|
|
|
|
|
|
|
|
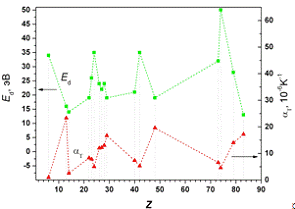
Рисунок 10. Антикорреляционные кривые пороговой энергии
смещения (Ed) и коэффициента температурного расширения (αT)
для ряда металлов
|
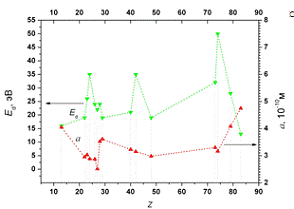
Рисунок 11. Антикорреляционные кривые пороговой энергии
смещения (Ed) и постоянной решетки a для ряда металлов
|
|
|
|
Анализ полученных результатов позволяет сделать следующие выводы:
1. Пороговая энергия смещения Ed коррелирует с
энергией связи Ub, хотя Ub составляет для
металла в среднем 15 % от значения Ed. Это указывает на то,
что и оставшаяся часть Ed каким-то образом определяется
энергией Ub.
2. С энергией смещения Ed также коррелируют
значения E, Tm, ES, TD,
которые очевидно напрямую связаны с энергией Ub.
. Особый интерес вызывают неочевидные антикорреляционные
соотношения Ed и Ub с коэффициентом
температурного расширения αT и постоянной решетки a.
В связи с этим проведем качественные оценки зависимости упругих и
тепловых характеристик некоторых металлов от энергии связи, используя для
простоты вычислений потенциальную энергию парного взаимодействия атомов в
решетке в форме Леннард-Джонса (проблема точности здесь непринципиальна):
|
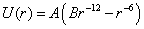 ,(9) ,(9)
|
|
где
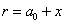 , a0 - равновесное значение
постоянной решетки, x - смещение атома из узла решетки, вызванное
механическим или температурным воздействием.
, a0 - равновесное значение
постоянной решетки, x - смещение атома из узла решетки, вызванное
механическим или температурным воздействием.
Сила
реакции решетки в случае такого воздействия может быть записана следующим образом:
|
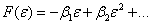 ,(10) ,(10)
|
|
где
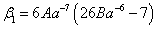 ,
, 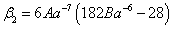 ,
, 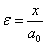 - относительная деформация решетки,
- относительная деформация решетки, 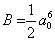 .
.
Для
смещений x формулу (10) можно записать как
|
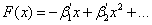 ,(11) ,(11)
|
|
где
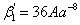 ,
, 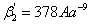 . При
этом величина A определяется следующей формулой:
. При
этом величина A определяется следующей формулой:
|
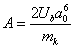 ,(12) ,(12)
|
|
где mk - координационное число, a0
- равновесное значение постоянной решетки.
Из (11) можно получить формулу для модуля упругости Юнга:
|
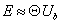 ,(13) ,(13)
|
|
где
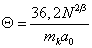 .
.
Коэффициент
температурного линейного расширения αT
оценивается по следующей формуле:
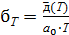 , (14)
, (14)
где
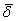 - среднее смещение узла кристаллической решетки при
ее нагревании, T - температура. В свою очередь:
- среднее смещение узла кристаллической решетки при
ее нагревании, T - температура. В свою очередь:
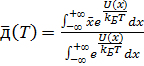 , (15)
, (15)
где
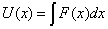 , kB - постоянная Больцмана. С
учетом формул (11), (14) и (15) получим:
, kB - постоянная Больцмана. С
учетом формул (11), (14) и (15) получим:
|
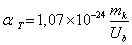 .(16) .(16)
|
|
Обратная пропорциональность αT и Ub удовлетворительно описывает
антикорреляционный характер поведения αT и Ed (так как
значение Ed прямо пропорционально Ub).
Связь температуры Дебая с энергией связи легко получить из известной
формулы:
|
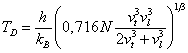 ,(17) ,(17)
|
|
где h - постоянная Планка, kB - постоянная Больцмана, vl и vt - продольная и поперечная скорости
распространения упругих волн в твердом теле. С учетом формулы (13) получим:
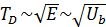 , (18)
, (18)
Из
эмпирической формулы Линдеманна (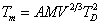 , где A
- постоянная величина, V и M - молярные объем и масса вещества) и
выражения (18) следует
, где A
- постоянная величина, V и M - молярные объем и масса вещества) и
выражения (18) следует 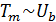 что, в общем-то, очевидно.
что, в общем-то, очевидно.
Температура
плавления, коэффициент всестороннего сжатия, постоянная решетки и постоянная
Грюнайзена γ
связаны между собой соотношением:
|
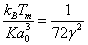 . (19) . (19)
|
|
Отсюда можно получить:
|
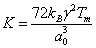 ,(20) ,(20)
|
|
и, как следствие:
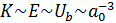 , (21)
, (21)
Такая
же зависимость следует из формулы (13), если положить 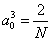 . Обратная пропорциональность между Ub
и
. Обратная пропорциональность между Ub
и 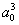 получается также исходя из формулы для энергии
металлического кристалла, полученной в рамках теории псевдопотенциала.
получается также исходя из формулы для энергии
металлического кристалла, полученной в рамках теории псевдопотенциала.
Так
как пороговая энергия смещения коррелирует с Ub, то из
вышеприведенных рассуждений (формулы (13), (16), (18), (20), (21)) следует
удовлетворительная интерпретация представленных на рисунках 5 - 10 графиков.
ГЛАВА 2. РАЗМЕРНЫЕ ЭФФЕКТЫ В НАНОЧАСТИЦАХ
.1 Размерная зависимость упругих свойств наночастиц
Научно-технический прогресс предъявляет все более высокие требования к
материалам, используемым в различных областях человеческой деятельности.
Зачастую этим требованиям традиционные вещества принципиально не удовлетворяют.
В частности, это касается работы устройств и механизмов в экстремальных
условиях (ТВЭЛы и материалы стенок ядерных реакторов, конструкции космических
аппаратов, элементы реактивных двигателей и т.д.). Актуальной проблемой
является также защита различных объектов от разрушающего действия ионизирующих
излучений.
Одним из путей повышения прочностных свойств, температурной и
радиационной стойкости материалов является синтез нанокомпозитных систем,
представляющих собой структурированную наноразмерными частицами матрицу.
Физические свойства матрицы, отдельных наночастиц, их размеры и концентрация в
совокупности определяют характеристики полученного таким образом материала. И
важнейшим фактором здесь является соотношение физико-механических и
теплофизических свойств отдельной наночастицы и материала матрицы с учетом
архитектуры дефектности сформированной при этом приграничной области. Очевидно,
что между макроскопическим и наноразмерным состояниями твердого тела должна
существовать определенная переходная зона (размерная «граница»), обусловленная
изменением физических свойств материала.
Предпринимались попытки установить эту границу (l) исходя из квантово-механических
принципов [50-53]. Величина l
определялась путем приравнивания квантовомеханической энергии электрона
(находящегося в прямоугольной потенциальной яме с учетом влияния соседних
ячеек) энергии Дебая kBTD (kB - постоянная Больцмана, TD - температура Дебая). При этом
получалась универсальная формула, описывающая зависимость любых физических
свойств материалов от их размеров. На наш взгляд нет надобности обсуждать
научную правомочность таких рассуждений. Изменение физико-механических,
магнитных, теплофизических и других свойств наночастиц может быть связано с
деформацией материала, обусловленной поверхностным натяжением, уменьшением
координационного числа в приповерхностном слое, изменением его группы
симметрии, перестройкой архитектуры электронных оболочек, изменением энергии
связи. Существенное влияние на физические свойства именно нано объектов могут
оказывать также различные дефекты структуры.
Рассмотрим изменение модуля упругости Юнга Е, связанное с
деформацией объема наночастицы за счет поверхностного натяжения.
Поверхностное натяжение, характеризуемое соответствующим коэффициентом s, приводит к деформации решетки ε(r), значение которой в рамках теории упругости имеет
следующий вид:
|
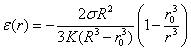 ,(22) ,(22)
|
|
где K - модуль всестороннего сжатия
объемного материала, r0=a0, a0
-постоянная решетки в равновесном состоянии.
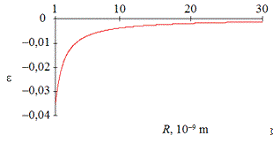
На
рис. 12 приведена зависимость усредненной по объему деформации 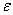 от R.
от R.
|
|
|
Рисунок 12. Зависимость усредненной по объему деформации от
размера частиц
|
Для качественных оценок зависимости Е(R) использовали
формулу, полученную в работе [54]:
|
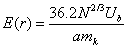 ,(23) ,(23)
|
|
где
N - концентрация атомов решетки, Ub - энергия связи, mk
- координационное число, 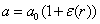 .
.
Энергию
связи для простых металлов определяли из формулы для полной энергии кристалла
|
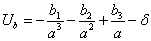 ,(24) ,(24)
|
|
где
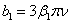 ,
, 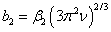 ,
, 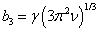 ,
, 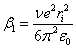 ,
, 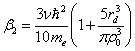 ,
, 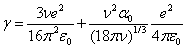 ,
, 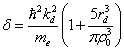 , ri -ионный радиус, rd
- радиус d-состояний, α0 =
1.79, ν - валентность, ε0 -
электрическая постоянная, me - масса электрона, ρ0 -
атомный радиус.
, ri -ионный радиус, rd
- радиус d-состояний, α0 =
1.79, ν - валентность, ε0 -
электрическая постоянная, me - масса электрона, ρ0 -
атомный радиус.
Качественную
зависимость среднего значения координационного числа от радиуса наночастицы
можно представить следующим образом:
|
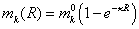 ,(25) ,(25)
|
|
где
κ=108 m-1, 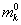 -
координационное число объемного материала.
-
координационное число объемного материала.
Формула
(25) есть результат аппроксимации соответствующих зависимостей, полученных в
компьютерном эксперименте.
Относительно
зависимости плотности поверхностной энергии s от размера
наночастицы R имеются весьма противоречивые мнения. Так в работе
[55] показано, что при уменьшении R величина s существенно возрастает. В исследованиях же авторов
статьи [56] приводится аналитическое выражение для s:
|
 ,(26) ,(26)
|
|
где
σV
- значение s для макрообъектов, 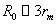 , rm - кратчайшее расстояние между атомами.
, rm - кратчайшее расстояние между атомами.
Формула
(26) свидетельствует о противоположном характере зависимости s(R), т.е с уменьшением R величина s также уменьшается.
В связи с этим в наших расчетах значение s бралось постоянным.
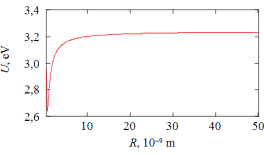
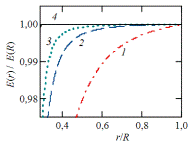
На рис. 13 приведена зависимость энергии связи от размеров алюминиевой
наночастицы, а на рис.14 аналогичная зависимость модуля упругости Юнга для
железа.
|
|
|
Рисунок 13. Зависимость энергии связи от размеров алюминиевой
наночастицы.
|
|
|
|
Рисунок 14. Зависимость модуля упругости Юнга от размера
наночастицы железа (a0<r<R).
|
Касательно зависимости Ub (R)
следует отметить, что в работе [57] методом компьютерного моделирования
установлено возрастание Ub с уменьшением R. Однако такое поведение энергии
связи находится в противоречии с результатами эксперимента и теоретическими
расчетами температуры плавления, которая существенно уменьшается с уменьшением R. И действительно, аппроксимация
экспериментально полученных зависимостей Тm(d) [58-63] описывается следующим выражением:
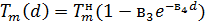 , (27)
, (27)
где d - диаметр наночастицы в нанометрах, 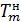 - температура плавления
макроскопического образца,
- температура плавления
макроскопического образца, 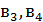 - величины, характерные для данного материала (в частности,
для золота
- величины, характерные для данного материала (в частности,
для золота 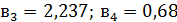 ).
).
Трудно предположить, что температура плавления обратно пропорциональна
энергии связи.
Для качественной оценки размерной зависимости коэффициента температурного
расширения αT использовали соответствующую формулу
(16):
|
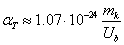 .(28) .(28)
|
|
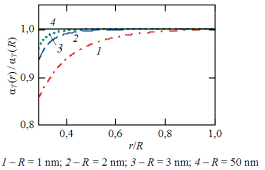
На
рис. 15 приведены размерные зависимости αT(R), полученные с учетом формул Ub (R) и 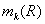 .
.
|
|
|
Рисунок 15. Зависимость коэффициента температурного расширения
от размера наночастицы (a0<r<R).
|
Представляет также интерес оценить поведение такого важного параметра
твердого тела как температура Дебая TD при изменении размеров наночастиц.
Температуру Дебая можно представить формулой (17):
|
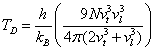 ,(29) ,(29)
|
|
Учитывая
известные выражения для скоростей распространения продольных (vl) и поперечных (vt)
упругих волн в твердых телах и зависимость E(R),
можно показать, что 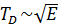 , откуда в свою очередь следует возрастание TD с уменьшением размера наночастицы. Этот же результат
следует из известного соотношения для частот колебаний атомов в деформированной
решетке
, откуда в свою очередь следует возрастание TD с уменьшением размера наночастицы. Этот же результат
следует из известного соотношения для частот колебаний атомов в деформированной
решетке 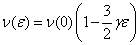 . Следует помнить, что в наночастице
. Следует помнить, что в наночастице 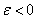 . Кроме того,
. Кроме того, 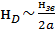 (
(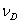 -частота Дебая,
-частота Дебая, 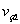 -
скорость звука в твердом теле), что также говорит о возрастающем характере
зависимости TD при уменьшении R.
-
скорость звука в твердом теле), что также говорит о возрастающем характере
зависимости TD при уменьшении R.
Такое
поведение TD противоречит ожидаемому из закона Линдемана (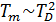 ) возрастанию температуры плавления при уменьшении R.
Как уже указывалось выше, температура плавления наночастиц значительно ниже,
чем у макроскопических объектов. В рамках известных моделей для
макроскопического состояния твердых тел такой ход зависимости Tm(R) не находит
должной интерпретации. Здесь, по-видимому, необходимо брать во внимание
уменьшение энергии связи и координационного числа в наночастицах, увеличение
амплитуды колебаний в узлах решетки (
) возрастанию температуры плавления при уменьшении R.
Как уже указывалось выше, температура плавления наночастиц значительно ниже,
чем у макроскопических объектов. В рамках известных моделей для
макроскопического состояния твердых тел такой ход зависимости Tm(R) не находит
должной интерпретации. Здесь, по-видимому, необходимо брать во внимание
уменьшение энергии связи и координационного числа в наночастицах, увеличение
амплитуды колебаний в узлах решетки (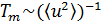 ),
соответствующее изменение плотности поверхностной энергии. Перечисленные
вопросы являются предметом дальнейших исследований.
),
соответствующее изменение плотности поверхностной энергии. Перечисленные
вопросы являются предметом дальнейших исследований.
2.2
Размерная зависимость магнитных свойств наночастицы
Рассмотрим
зависимость магнитных свойств ферромагнитных наночастиц от их размеров.
Эволюция определенного физического параметра x,
характеризующего замкнутую систему (плотность вещества, намагниченность,
поляризованность и т.п.) можно записать в форме Онзагера:
|
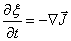 ,(30) ,(30)
|
|
где
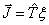 ,
, 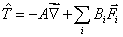 , Ai, Bi - кинетические коэффициенты, характеризующие действие
термодинамических (A) и реальных силовых (Bi)
факторов,
, Ai, Bi - кинетические коэффициенты, характеризующие действие
термодинамических (A) и реальных силовых (Bi)
факторов, 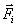 - силы в системе (электрические, упругие и др.). В
случае описания эволюции магнитной структуры в ферромагнетиках уравнение (30)
имеет следующий вид [64]:
- силы в системе (электрические, упругие и др.). В
случае описания эволюции магнитной структуры в ферромагнетиках уравнение (30)
имеет следующий вид [64]:
|
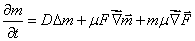 ,(31) ,(31)
|
|
где
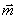 - намагниченность, D -
коэффициент «диффузии» (
- намагниченность, D -
коэффициент «диффузии» (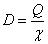 , Q - кинетический коэффициент Онзагера, χ - магнитная восприимчивость), μ - «подвижность», (
, Q - кинетический коэффициент Онзагера, χ - магнитная восприимчивость), μ - «подвижность», (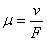 , v
- скорость распространения волны новой фазы,
, v
- скорость распространения волны новой фазы, 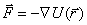 ,
, 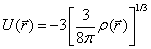 , ρ - электронная плотность [65]). Представляя
, ρ - электронная плотность [65]). Представляя 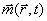 в виде разложения по бегущим волнам можно получить
следующее выражение для величины m:
в виде разложения по бегущим волнам можно получить
следующее выражение для величины m:
|
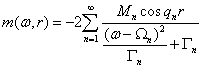 ,(32) ,(32)
|
|
где
ω - частота волны новой фазы, Mn - спектральная амплитуда, Ωn и Γn - резонансная частота и затухание, связанное с диссипацией энергии в системе,
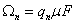 ,
, 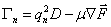 ,
, 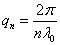 ,
, 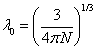 . В
рамках такого подхода переход в упорядоченное состояние представляется как
процесс распространения «волны порядка» при
. В
рамках такого подхода переход в упорядоченное состояние представляется как
процесс распространения «волны порядка» при 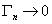 . При
этом ферромагнитная система приходит в «резонанс» при совпадении частоты
воздействующей волны с собственной частотой Ωn. Это происходит при размере наночастицы около 15 нм.
. При
этом ферромагнитная система приходит в «резонанс» при совпадении частоты
воздействующей волны с собственной частотой Ωn. Это происходит при размере наночастицы около 15 нм.
Кроме
того расчет магнитной структуры наночастиц железа был проведен с помощью пакета
микромагнитного моделирования Nmag с гибким методом конечных элементов с
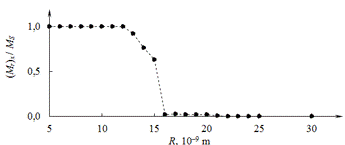
пользовательским интерфейсом на основе языка программирования Python [66]. На рис. 16-18 представлены соответствующие зависимости.
|
|
|
Рисунок 16. Зависимость намагниченности от размера наночастиц.
|
|
|
|
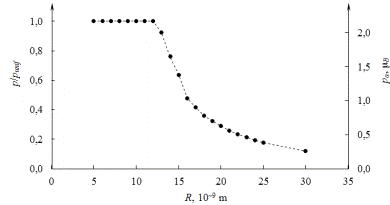
Рисунок 17. Зависимость магнитного момента то размера
наночастицы.
|
|
|
|
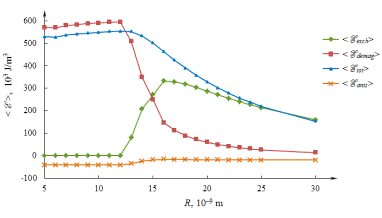
Рисунок 18. Размерные зависимости компонентов полной магнитной
энергии наночастиц.
|
Из полученных закономерностей следует, что магнитная структура наночастиц
ферромагнитных материалов существенно зависит от их размеров.
Размерные
эффекты в наночастицах имеют место также при воздействии различного рода
ионизирующих излучений. Так, например, в работе [67] показано, что упругая и
термоупругая реакции решетки на радиационное воздействие формируют силовые
факторы, приводящие к перемещению точечных дефектов на расстояние l.
Причем если 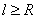 , то возможен их выход на поверхность, что будет
приводить в определенных случаях к уменьшению радиационных нарушений структуры.
, то возможен их выход на поверхность, что будет
приводить в определенных случаях к уменьшению радиационных нарушений структуры.
ГЛАВА
3. АНАЛИЗ ТЕМПЕРАТУРНОГО РАЗОГРЕВА НАНОЧАСТИЦ МАТЕРИАЛА ПРИ РАДИАЦИОННОМ
ВОЗДЕЙСТВИИ И ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
3.1
Температурный разогрев радиационно-поврежденных областей наноструктурированных
материалов
Пусть
при прохождении ускоренного иона с энергией Е0 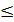 104 эВ через наноструктурированный
материал в наночастице выделятся энергия W0. Тогда соответствующий
температурный разогрев может быть описан следующим выражением [67]:
104 эВ через наноструктурированный
материал в наночастице выделятся энергия W0. Тогда соответствующий
температурный разогрев может быть описан следующим выражением [67]:
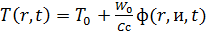 , (33)
, (33)
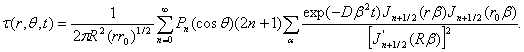
где
T0 - температура окружающей среды, C - удельная
теплоемкость, ρ - плотность материала, r0 -
положение теплового источника, Pn(cosθ) - полином
Лежандра, Jn+1/2(rβ) -
цилиндрическая функция Бесселя полуцелого порядка, β - корни трансцендентного уравнения Jn+1/2(rβ)=0, R
- радиус наночастицы, D - коэффициент диффузии тепла,
Формула
(33) получена путем решения соответствующего уравнения теплопроводности методом
функции Грина для несимметричной задачи параболического типа.
В
предположении, что источник тепловой энергии находится в центре наночастицы (r0=0)
формулу (33) при определенных допущениях можно представить следующим образом:
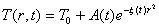 , (34)
, (34)
где
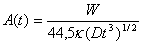 ,
, 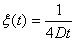 , κ - коэффициент теплопроводности. Формулы (33) и (34)
можно использовать при энергиях ионов, не превышающих 100 кэВ.
, κ - коэффициент теплопроводности. Формулы (33) и (34)
можно использовать при энергиях ионов, не превышающих 100 кэВ.
При
высоких энергиях ионов (105 эВ и выше), когда трек в общих чертах
имеет цилиндрическую форму следует использовать общее уравнение
теплопроводности с источником g(r,t):
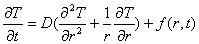 , (35)
, (35)
где
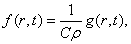 .
.
Функцию
источника g(r ,t) построим в следующем виде:
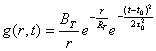 , (36)
, (36)
где
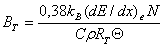 ,
, 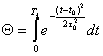 , RT
- радиус трека, t0 - среднее время пролета
высокоэнергетических электронов в треке, τ0 -
полуширина гауссовского распределения плотности энергии в треке (t0~ τ0~5·10-15
c), Tk - время
температурной релаксации процесса. Вид функции g(r,t)
представлен на рис. 19.
, RT
- радиус трека, t0 - среднее время пролета
высокоэнергетических электронов в треке, τ0 -
полуширина гауссовского распределения плотности энергии в треке (t0~ τ0~5·10-15
c), Tk - время
температурной релаксации процесса. Вид функции g(r,t)
представлен на рис. 19.
Для
решения уравнения (35) используем следующие начальные и граничные условия:
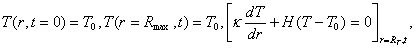 (37)
(37)
где
Rmax - внешняя граница рассматриваемой цилиндрической
области, H - коэффициент теплообмена.
Термоупругие
напряжения в материале определим по формуле:
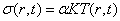 , (38)
, (38)
где
α - коэффициент линейного температурного расширения, K
- модуль всестороннего сжатия.
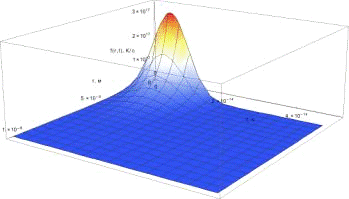
Рисунок
19. Пространственно-временная
конфигурация теплового источника.
При
определенных условиях разогрева будет иметь место генерация дислокаций,
концентрацию которых можно определить из следующего выражения:
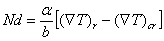 , (39)
, (39)
где
b - вектор Бюргерса, 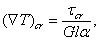
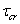 - критическое напряжение, G - модуль сдвига,
l - размер области, где
- критическое напряжение, G - модуль сдвига,
l - размер области, где 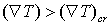
Для
материала TiN на рис. 20 - 23 представлены соответствующие
зависимости температуры T(r ,t), градиента температуры 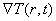 ,
термоупругих напряжений
,
термоупругих напряжений 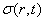 и плотности дислокаций Nd(r ,t).
и плотности дислокаций Nd(r ,t).
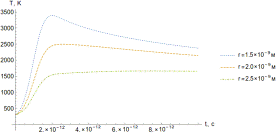
а) б)
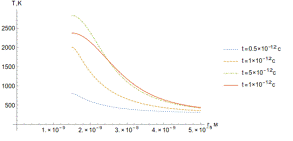
Рисунок 20. Зависимости температуры от времени (а) и пространственной
координаты (б).
а) б)
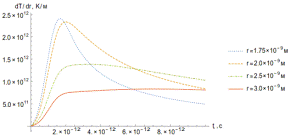
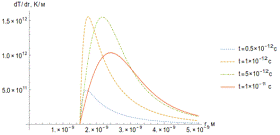
Рисунок 21. Зависимость градиента температуры то времени (а) и
пространственной координаты (б).
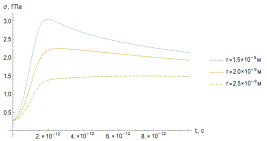
а) б)
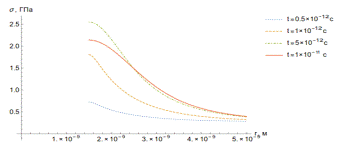
Рисунок 22. Зависимость термоупругих напряжений от времени (а) и
пространственной координаты (б).
а) б)
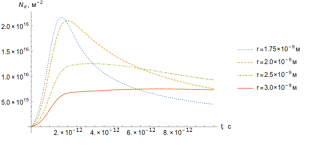
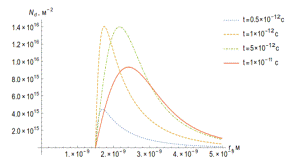
Рисунок 23. Зависимость концентрации дислокаций от времени (а) и
расстояния от трека (б).
Пространственно-временную структуру температурного поля от трека иона
можно определить также с помощью соответствующей функции Грина G(r
,ξ ,t-τ) . Для данной задачи функцию Грина определяем из уравнения
(35) с единичным источником:
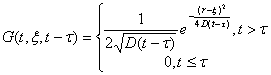 , (40)
, (40)
Тогда
для температуры 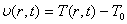 решение (35) может быть записано как
решение (35) может быть записано как
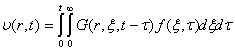 , (41)
, (41)
при
начальном условии 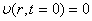 . С учетом (36) формула (41) перепишется окончательно
. С учетом (36) формула (41) перепишется окончательно
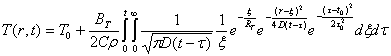 , (42)
, (42)
ГЛАВА 4. ТЕРМОУПРУГОЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
НАНОСТРУКТУРИРОВАННЫХ МАТЕРИАЛОВ, ФОРМИРУЕМОЕ РАДИАЦИОННЫМ ВОЗДЕЙСТВИЕМ.
Рассмотрим термоупругие деформации в отдельной наночастице радиуса R
при сферически симметричном распределении температуры T(r ,t). Уравнение
равновесия в этом случае может быть записано следующим образом:
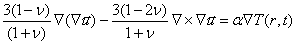 , (43)
, (43)
где
ν - коэффициент Пуассона, 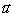 - вектор смещения, α - коэффициент линейного температурного расширения.
- вектор смещения, α - коэффициент линейного температурного расширения.
Для
радиальной деформации это уравнение перепишется следующим образом:
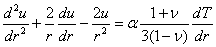 , (44)
, (44)
Так
как для свободной частицы напряжения σrr равны нулю, то
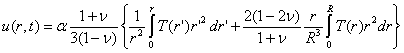 , (45)
, (45)
Для
данного конкретного случая используем формулу (34) для температуры T(r ,t).
Тогда можно получить:
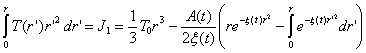 , (46)
, (46)
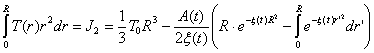 , (47)
, (47)
Очевидно,
что относительная деформация ε(r) в произвольной точке r наночастицы
определяется как du(r)/dr.
Пусть
такая наночастица, характеризуемая модулем сжатия K1, вставлена
в матрицу, модуль сжатия которой K и при этом происходит рассмотренный
выше разогрев включения. Модельно это можно представить как наличие шара,
вставленного в полость меньшего радиуса, вследствие чего имеет место сложный
процесс деформации матрицы шаром, а шара - реакцией матрицы. Важную роль при
анализе напряженно-деформированного состояния системы будет играть максимальное
температурное смещение u(m)
(R) (или
соответствующая деформация ε(n)(R))
свободной наночастицы (см. формулу (44)).
В
результате температурного расширения наночастицы на границе раздела r = R
на матрицу со сторону включения будет действовать определенное равномерное
давление P = - σrr . Из уравнения 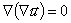 следует явный вид поля смещений u(r,t):
следует явный вид поля смещений u(r,t):
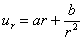 , (48)
, (48)
где
a и b определяются из граничных условий:
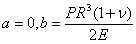 ,
,
Тогда
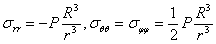 , (49)
, (49)
где
E - модуль упругости Юнга.
Пусть
K1 = K (или E1 = E). Тогда
при разогреве наночастицы, когда смещение ее границы будет равно ur(R), произойдет изменение объема ΔV . При этом
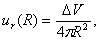 а
а 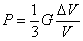 .
Соответствующая деформация ε
равна
.
Соответствующая деформация ε
равна
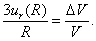 , (50)
, (50)
Величина
ΔV - это та
часть объема, на которое включение отличается от полости уже в сжатом
состоянии. Для того чтобы найти ΔV надо учесть «отдачу», то
есть деформацию самого включения в результате реакции матрицы.
Деформация
матрицы 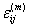 вследствие разогрева наночастицы
вследствие разогрева наночастицы 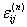 определяется методом Эшелби
определяется методом Эшелби
 , (51)
, (51)
где
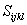 - деформационная матрица.
- деформационная матрица.
Для
сферического включения в однородном изотропном материале эта матрица
превращается в скалярную величину
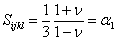 , (52)
, (52)
Тогда
давление со стороны наночастицы на матрицу будет равно:
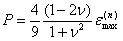 , (53)
, (53)
где
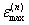 - максимальная дилатация свободной наночастицы в
результате разогрева.
- максимальная дилатация свободной наночастицы в
результате разогрева.
Если
упругие модули наночастицы и матрицы различаются, то из требования сохранения
непрерывности смещений и напряжений на поверхности включения, а также равенства
самих напряжений
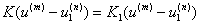 , (54)
, (54)
можно
получить связь между 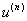 и
и 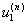 .
.
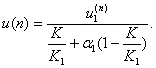 , (55)
, (55)
Тогда
формула для давления в матрице, обусловленного разогревом наночастицы будет
иметь следующий вид
=
Ф(t)F(r,t), (56)
где
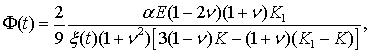 (57)
(57)
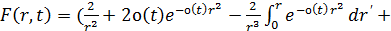
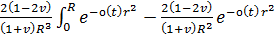 , (58)
, (58)
Следует
отметить, что разогрев матрицы будет приводить к дополнительном возрастанию P.
На рисунках 24, 25 представлены соответствующие зависимости P(r,t).
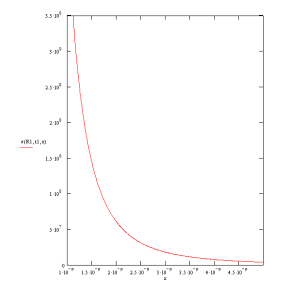
Рисунок
24. Пространственный профиль упругих
напряжений в окрестности наночастицы. размером 1 нм.
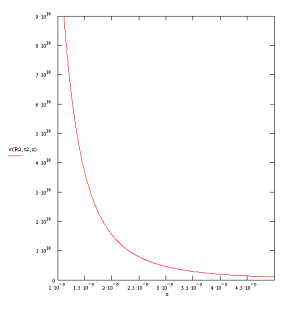
Рисунок
25. Пространственный профиль упругих
напряжений в окрестности наночастицы. размером 5 нм.
ГЛАВА 5. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ФОРМИРОВАНИЯ И ЭВОЛЮЦИИ
ДЕФЕКТНО-ПРИМЕСНОЙ СИСТЕМЫ В НАНОЧАСТИЦАХ ПРИ РАДИАЦИОННОМ ВОЗДЕЙСТВИИ
Экспериментально установлено, что развитие отдельного каскада смещений и
всего трека в целом сопровождается генерацией упругих возмущений среды,
аналогичных слабым ударным волнам. Взаимодействуя с нарушениями структуры
(примеси, точечные дефекты и их комплексы), такие волны при определенных
условиях могут приводить к изменению их пространственного положения и
термодинамического состояния. Сила F, приводящая к таким изменениям,
определяется произведением давления P во фронте волны на сечение
взаимодействия волны S с дефектом. Вычисление S является весьма
сложной задачей, в связи с чем имеющиеся на сегодняшний день соответствующие
аналитические выражения [68] практически не применимы к конкретным расчетам.
Выражение для S получено в работе [69]:
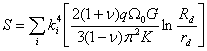 , (59)
, (59)
Физический
механизм передачи энергии волны дефекту весьма сложен и носит опосредованный
характер. В начале процесса энергия волны выделяется в области, искаженной
дефектом. То есть деформированная область является местом трансформации упругой
энергии. Получение же энергии самим дефектом происходит на второй стадии, когда
ударный импульс трансформируется в тепловую форму движения атомов вещества. При
этом в спектре частотных колебаний атомов в деформированной дефектом области
при ее мгновенном разогреве находится составляющая, совпадающая с собственной
частотой ω0
самого дефекта (то есть имеет место резонанс).
Пусть
спектральная функция теплового импульса в области деформации решетки имеет
гауссовский вид с максимумом на частоте ωmax и полушириной δ .
Соответствующие расчеты показывают, что в этом случае дефекту по резонанcному
механизму будет передана энергия:
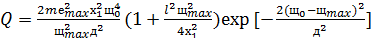 , (60)
, (60)
где
m - масса атома, 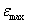 -
максимальная деформация в тепловом импульсе, ld
- величина перемещения дефекта. Значение ld можно таким образом оценить из следующей формулы:
-
максимальная деформация в тепловом импульсе, ld
- величина перемещения дефекта. Значение ld можно таким образом оценить из следующей формулы:
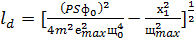 , (61)
, (61)
Резонансный
характер передачи энергии дефекту аналогичен передаче импульса налетающей
атомной частицей в модели индивидуальных столкновений. В связи с этим
энергетическую сторону процесса перемещения дефекта можно выразить следующим
соотношением
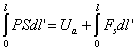 , (62)
, (62)
где
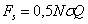 ,
, 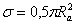 ,
, 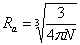 .
.
Как
указывалось выше сила F, действующая на дефект, определяется давлением P
и сечением S (F=P S). Остается оценить величину
давления P, формируемого областью трека при торможении заряженной
частицы в материале.
Касаясь
эволюции пика смещений, следует отметить, что скорость нарастания давления в
нем (1011 ГПа/с) значительно превышает предел динамического
разрушения вещества (~107-108 ГПа/с). Очевидно, что в
этом случае следует ожидать «мгновенного» перехода ансамбля атомов в треке даже
не в «расплавленное», а в «газообразное» состояние.
Рассмотрим
некоторое детали процессов формирования волн деформаций при облучении твердых
тел ионами и взаимодействие этих волн со структурными нарушениями решетки.
Пусть Н - функция Гамильтона (точнее ее плотность) волны деформаций в
кристалле, а ρ - эффективная плотность массы движущегося вещества на
ее фронте. Тогда для массой скорости 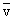 волны
можно записать:
волны
можно записать:
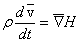 , (63)
, (63)
Где
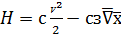 ,
, 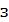 -
коэффициент, характеризующий «взаимодействие» волны с веществом и определяющий
«расход» скорости при её движении по кристаллу,
-
коэффициент, характеризующий «взаимодействие» волны с веществом и определяющий
«расход» скорости при её движении по кристаллу, 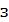 ~ lΔ
~ lΔ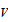 , l - ширина фронта ударного возмущения среды,
Δ
, l - ширина фронта ударного возмущения среды,
Δ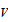 - изменение массовой скорости, обусловленное
нелинейными эффектами.
- изменение массовой скорости, обусловленное
нелинейными эффектами.
Представим
каскад столкновений в виде цилиндра радиуса RТ и высотой Lc и пусть внутри нее в момент времени t = 0 генерируются
прямоугольный импульс скорости 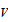 0. Задачу рассмотрим для изотропного случая среды,
используя цилиндрическую систему координат:
0. Задачу рассмотрим для изотропного случая среды,
используя цилиндрическую систему координат:
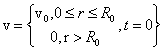 , (64)
, (64)
Давление
P0 на границу каскада определим исходя из соотношений 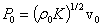 и
и 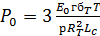 . Тогда:
. Тогда:
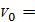
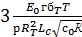 , (65)
, (65)
где
Е0 - энергия налетающего иона. Решая при таких условиях
уравнение (63) получим:
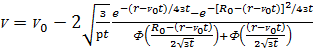 , (66)
, (66)
где
Ф(х) - функция ошибок, r’ -
точка наблюдения.
Формула
(66) учитывает диффузионный характер изменения скорости и в связи с этим
представляет собой более общее выражение для известной в физике волновых
процессов N-волны.
Давление
Р во фронте волны (66) можно оценить из соотношения P
= ρcv (с -
скорость звука в твердом теле).
Распространяясь
по кристаллу, такая волна взаимодействует с дефектами, приводя при определенных
условиях к изменению их пространственного положения и термодинамического
состояния. В зависимости от величины давления механизмы такого взаимодействия
могут быть различными. При высоких значениях Р этот процесс идет через
стадию термализации энергии упругой волны в области, искаженной дефектом. Cила
взаимодействия 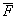 волны с дефектом может быть определена следующим
выражением:
волны с дефектом может быть определена следующим
выражением:
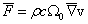 , (67)
, (67)
где Ω0
- объем дилатации дефекта.
Если дефект характеризуется энергией активации Um, то
для его перемещения из одного равновесного положения в ближайшее другое
необходима сила Fm ~ 2Um/a0
(а0 - период решетки).
Динамику движения дефекта можно оценить также в рамках модели фононного
газа. Действительно, силу 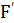 , действующую на дефект при рассеянии фононов, можно
определить из формулы:
, действующую на дефект при рассеянии фононов, можно
определить из формулы:
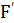 =
= 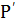 S , (68)
S , (68)
где
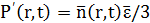 - давление фононного газа;
- давление фононного газа; 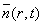 - средняя концентрация фононов;
- средняя концентрация фононов; 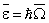 - средняя энергия фонона.
- средняя энергия фонона.
Скорость
распространения фонона может быть оценена из формулы 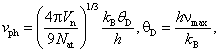 где Vn
- объем наночастицы; Nat
- число атомов в наночастице; kB
- постоянная Больцмана; θD -
температура Дебая; h - постоянная Планка; νmax - максимальная частота колебаний атомов. Величина vph имеет
порядок 103 м/с.
где Vn
- объем наночастицы; Nat
- число атомов в наночастице; kB
- постоянная Больцмана; θD -
температура Дебая; h - постоянная Планка; νmax - максимальная частота колебаний атомов. Величина vph имеет
порядок 103 м/с.
Энергия
колебаний Eк в
кристаллической решетке по модели Дебая определяется из выражения
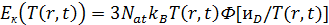 , (69)
, (69)
где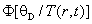 - функция Дебая.
- функция Дебая.
Средняя
концентрация фононного газа может быть определена как
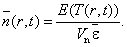 (70)
(70)
С
учетом (69) и (70) формула (68) переписывается следующим образом:
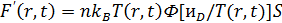 , (71)
, (71)
В
общем случае перемещение дефекта (например, междоузельного атома) может быть
оценено из динамического уравнения:
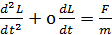 , (72)
, (72)
где
m - масса (в общем случае эффективная) междоузельного атома.
На
рис. 24 (а, б) представлены результаты компьютерного моделирования процесса
перемещения дефекта под действием силы F.
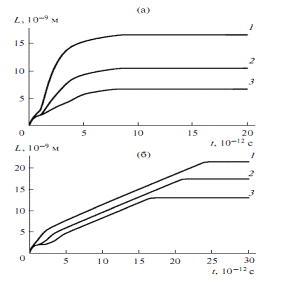
Рисунок
26. Результаты моделирования
перемещения дефекта, расположенного относительно центра пика на расстояниях 8 (1),
16 (2), 24 (3) нм, для двух подходов: a - классической
теории твердого тела; б - модели фононного газа.
ЗАКЛЮЧЕНИЕ
Детально
исследованы динамические процессы, происходящие в наноразмерном металлическом
объекте при внедрении ионов различных энергий. Показано, что упругая и
термоупругая реакции решетки на радиационное воздействие формируют силовые
факторы, существенно влияющие на эволюцию дефектно-примесной системы,
результатом чего является выход дефектов на поверхность. Такая самоорганизация
наночастиц при воздействии ионизирующих излучений является основой для создания
наноструктурированных радиационно-стойких материалов, способных длительное
время выдерживать интенсивные радиационные нагрузки.
Полученные
в данной работе результаты позволяют более глубоко понять физическую природу
такой важнейшей характеристики радиационной стойкости материалов, как пороговая
энергия смещения Ed. Это указывает способы повышения Ed. Следует отметить, что полученные корреляции физических величин и Ed.могут быть использованы для дополнительной
корректировки экспериментально определенных или теоретически рассчитанных
значений Ed, не встроившихся в общую корреляционную картину.
При
уменьшении размеров частиц происходит изменение всех их физических свойств. Как
следует из полученных в работе результатов, это изменение начинается с величины
15-20 нм, которую можно считать «границей», разделяющей макро- и нанообласть.
Естественно лишены оснований утверждения о едином законе изменения всех
физических свойств при уменьшении размеров частиц.
Особый
интерес представляет использование ферромагнитных наночастиц в качестве битовых
ячеек новых устройств магнитной записи и хранения информации со сверхвысокой
плоностью, высокочувствительных сенсоров и датчиков в бионанотехнологиях,
медицине и других областях. Принцип действия указанных устройств и элементов в
большинстве случаев основан на перераспределении намагниченности в нанообъекте
(тонкой перестройке его магнитной структуры) под действием внешнего магнитного
поля. В этой связи представляется актуальным провести дальнейшие исследования
влияния деформаций, изменения координационного числа и симметрии структуры на
магнитные свойства наночастиц и их ансамблей.
Однако,
кроме ряда положительных эффектов в наноструктурированных материалах при
радиационном воздействии возникают явления, приводящие к их разрушению. Это, в
первую очередь, генерация дислокаций на границе наночастица-матрица,
термоупругие поцессы в области трека высокоэнергетического иона, диффузионный
рост наночастиц и др. Кроме того, при уменьшении размера наночастиц,
существенно снижается их температура плавления. Очевидно, что использование такого
наноструктурированного материала при высоких температурах не представляется
возможным. В связи с этим, необходимо рассмотреть другую форму архитектуры
наноструктурированного вещества, позволяющю избежать вышеуказанных негативных
явлений.
СПИСОК ЛИТЕРАТУРЫ
1. Andrievskii
R.A. Effect of Irradiation on the Properties of Nanomaterials / R.A.
Andrievskii // The Physics of Metals and Metallography. - 2010.- Vol. 110. -
No. 3. - pp. 229-240.
. Andrievskii
R.A. Behavior of radiation defects in nanomaterials / R.A. Andrievskii // Rev.
Adv. Mater. Sci. - 2011.- Vol. 29. - pp. 54-67.
. Rose
M. Phase stability of nanostructured materials under heavy ion irradiation / M.
Rose, G. Gorzawski, G. Miehe, A.G. Balogh, H. Hahn // NanoStructured Materials.
- 1995.- Vol. 6. - pp. 731-734.
. Rose
M. Instability of irradiation induced defects in nanostructured materials / M.
Rose, A.G. Balogh, H. Hahn // Nuclear Instruments and Methods in Physics
Research B. - 1997.- Vol. 127/128. - pp. 119-122.
5. Андриевский
Р.А. Термическая стабильность наноматериалов / Р.А. Андриевский // Успехи
химии. - 2002.- T. 70. - C. 967-981.
6. Shen
T.D. Radiation tolerance in a nanostructure: Is smaller better? / T.D. Shen //
Nuclear Instruments and Methods in Physics Research B. - 2008.- Vol. 266. - pp.
921-925.
. Zhu
Y. Nanostructures in Ti processed by severe plastic deformation / Y. Zhu, J.
Huang, J. Gubicza, T. Ungár, Y. Wang, E. Ma, R. Valiev // J. Mater. Res. - 2003.- Vol. 18. -
pp. 1908-1917.
. Samaras
M. Computer simulation of displacement cascades in nanocrystalline Ni / M.
Samaras, P. Derlet, H. Van Swygenhoven, M. Victoria // Phys. Rev. Lett. -
2002.- Vol. 88. - pp. 125505(1-9).
. Shen
T.D. Enhanced radiation tolerance in nanocrystalline MgGa2O4
/ T.D. Shen, Sh. Feng, M. Tang, J.A. Valdez, Y. Wang, K.E. Sickafus // Appl.
Phys. Lett. - 2007.- Vol. 90. - pp. 263115(1-3).
.
Kilmametov A.R. Enhanced ion irradiation resistance of bulk nanocrystalline
TiNi alloy / A.R. Kilmametov, D.V. Gunderov, R.Z. Valiev, A.G. Balogh, H. Hahn
// Scr. Mater. - 2008.- Vol. 59. - pp. 1027-1030.
.
Meldrum A. Nanocrystalline Zirconia can be amorphized by ion irradiation / A.
Meldrum, L.A. Boatner, R.C. Ewing // Phys. Rev. Lett. - 2002.- Vol. 88. - pp.
025503(1-3).
.
Sickafus K.E. Radiation damage effects in zirconia / K.E. Sickafus, Hj. Matzke,
Th. Hartman, K. Yasuda, J.A. Valdez, P. Chodak III, M. Nastasi, R.A. Verrall //
J. Nucl. Mater. - 1999.- Vol. 274. - pp. 66-77.
.
Kurushita H. Development of ultra-fine grained W-(0.25-0.8)wt% TiC and superior
resistance to neutron and 3 MeV He-ion irradiations / H. Kurushita, S.
Kobayashi, K. Nakai, T. Ogawa, A. Hasegawa, K. Abe, H. Arakawa, S. Matsuo, T.
Takida, K. Takebe, M. Kawai, N. Yoshida // J. Nucl. Mater. - 2008.- Vol. 377. -
pp. 34-40.
.
Wan Q. Ion irradiation tolerance of Ti-Si-N nanocomposite coating / Q. Wan, B.
Yang, H.D. Liu, Q.S. Mei, Y.M. Chen // Surface & Coatings Technology. -
2016.- Vol. 305. - pp. 165-169.
.
Leconte Y. Comparizon study of structural damage under irradiation in SiC
nanostructured and conventional ceramics / Y. Leconte, I. Monnet, M. Levalois,
M. Morales, X. Portier, L. Thome, N. Herlin-Boime, C. Reynaud // Mater. Res.
Soc. Symp.Proc. - 2007.- Vol. 981. - pp. JJ07-11.
.
Johannessen B. Amorphization of embedded Cu nanocrystals by ion irradiation /
B. Johannessen, P. Kluth, D.J. Llewellyn, G.J. Foran, D.J. Cookson, M.C.
Ridgway // Appl. Phys. Lett. - 2007.- Vol. 90. - pp. 073119 (1-3).
.
Miao P. Thermal stability of nanostructured ferritic alloy / P. Miao, G.R.
Odette, T. Yamamoto, M. Alinger, D. Klingensmith // J. Nucl. Mater. - 2008.-
Vol. 377. - pp. 59-64.
.
McClintock D.A. Mechanical properties of neutron irradiated nanostructured
ferritic alloy 14YWT / D.A. McClintock, D.T. Hoezlzer, M.A. Sokolov, R.K.
Nanstad // J. Nucl. Mater. - 2009.- Vol. 386-388. - pp. 307-311.
.
Matsuoka H. Microstructure and mechanical properties of neutron-irradiated
ultra-fine-grained SUS316L stainless steels and electrodeposited
nanocrystalline Ni and Ni-W alloys / H. Matsuoka, T. Yamasaki, Y.J. Zheng, T.
Mitamura, M. Teresawa, T. Fukami // Mater. Sci. Eng. A. - 2007.- Vol. 449-451.
- pp. 790-793.
20.
Василенко Р.Л. Влияние облучения ионами азота и гелия на структуру и
электросопротивление нанокристаллических V-N-покрытий / Р.Л.
Василенко, В.Н. Воеводин, А.Г. Гугля, М.Л. Литвиненко, Ю.А. Марченко, И.М.
Неклюдов // ФММ. - 2007.- Т. 103. - №3. - pp. 310-316.
21.
Guglya A. Effect of helium ion irradiation on the structure and electrical
resistivity of nanocrystalline Cr-N and V-N coatings / A. Guglya, I. Nekludov,
R. Vasilenko // Rad. Eff. Def. Sol. - 2007.- Vol. 162. - pp. 643-649.
.
Wang H. Ion irradiation effects in nanocrystalline TiN coatings / H. Wang, R.
Araujo, J.G. Swadener, Y.Q. Wang, X. Zhang, E.G. Fu, T. Cagin // Nucl. Instr.
Meth. Phys. Res. B. - 2007.- Vol. 261. - pp. 1162-1166.
.
Popović M. Structural characterization of
TiN coatings on Si substrates irradiated with Ar ions /
M. Popović, M. Novaković, N. Bibić // Mater. Character. - 2009.- Vol.
60. - pp. 1463-1470.
.
Lee S.-H. Thermal stability and mechanical properties of SiC
particulatereinforced Si-C-N composites after
heating at 2000 ºC / S.-H. Lee // J. Eur. Cer. Soc. - 2009.- Vol. 29. - pp.
3387-3393.
.
Ovid’ko I.A. Irradiation-induced amorphization processes in nanocrystalline
solids / I.A. Ovid’ko, A.G. Sheiderman // Apll. Phys. A. - 2005.- Vol. 81. -
pp. 1083-1088.
.
Lach T.G. Role of Interfaces on the Trapping of He in 2D and 3D Cu-Nb
Nanocomposites / T. G. Lach, E. Ekiz, R. S. Averback, N.A. Mara, P. Bellon //
J. Nucl. Mater. - 2015.- Vol. 466. - pp. 36-42.
.
Li N. He ion irradiation damage in AlNb multilayers / N. Li, M.S. Martin, O.
Anderoglu, A. Misra, L. Shao, H. Wang, X. Zhang // J. Appl. Phys. - 2009.- Vol.
105. - pp. 123522(1-8).
.
Milosavljevi´c M. A comparison of Ar ion
implantation and swift heavy Xe ion irradiation effects on immiscible AlN/TiN
multilayered nanostructures / M.
Milosavljevi´c, A. Grce, D. Peruˇsko, M. Stojanovi´c, J.
Kovaˇc, G. Draˇziˇc, A.Yu. Didyk, V. A. Skuratov // Materials Chemistry
and Physics. - 2012.- Vol. 133. - pp. 884- 892.
.
Perusko D. On the ion irradiation stability of Al/Ti versus AlN/TiN multilayers
/ D. Perusko, M.J. Webb, V. Milinovic´, B.
Timotijevic´, M. Milosavljevic´, C. Jeynes, R.P. Webb // Nucl. Instr. Meth.
Phys. Res. B. - 2008.- Vol. 266. - pp. 1749-1753.
.
Kim I. Size-dependent radiation tolerance in ion irradiated TiN/AlN nanolayer
films / I. Kim, L. Jiao, F. Khatkhatay, M.S. Martin, J. Lee, L. Shao, X. Zhang,
J.G. Swadener, Y.Q. Wang, J. Gan, J.I. Cole, H. Wang // J. Nucl. Mater. -
2013.- Vol. 441. - pp. 47-53.
.
Chen F. Formation of He-rich layers observed by neutron reflectometry in the He
ions irradiated Cr/W multilayers: Effects of Cr/W interfaces on the He trapping
behavior / F. Chen, X. Tang, H. Huang, X. Li, Y. Wang, Ch. Huang, J. Liu, H.
Li, Da Chen // ACS Appl. Mater. Interfaces. - 2016.- Vol. 8. - pp. 24300-24305.
.
Li N. He ion irradiation damage in Fe/W nanolayer films / Nan Li, E.G. Fu, H.
Wang, J.J. Carter, L. Shao, S.A. Maloy, A. Misra, X. Zhang // J. Nucl. Mater. -
2009.- Vol. 389. - pp. 233-238.
.
Wang H. Ion irradiation effects in nanocrystalline TiN coatings / H. Wang, R.
Araujo, J.G. Swadener, Y.Q. Wang, X. Zhang, E.G. Fu, T. Cagin // Nucl. Instr.
Meth. Phys. Res. B. - 2007.- Vol. 261. - pp. 1162-1166.
34. Вас Гэри С. Основы радиационного
материаловедения. Металлы и сплавы. Москва: ТЕХНОСФЕРА, 2014. - 992 с.
.
Зеленский В.Ф. Радиационные дефекты и распухание металлов / В.Ф. Зеленский,
И.М. Неклюдов, Т.П. Черняева // Киев: Наук. Думка - 1988. - 294 с.
36.
ASTM E521-96 Standard Practice for Neutron Radiation Damage Simulation by
Charged-Particle Irradiation. West Conchohocken: ASTM International - 1996. -
p. 21.
.
Nordlund K. Molecular dynamics simulations of threshold displacement energies /
K. Nordlund, J. Wallenius, L. Malerba // Nucl. Instrum. Methods Phys. Res. B. -
2006. - V. 246. - P. 322.
.
Zepeda-Ruiz L.A. Molecular dynamics study of the threshold displacement energy
in vanadium / L.A. Zepeda-Ruiz, S. Han, D.J. Srolovitz, R. Car // Phys. Rev. B.
- 2003. - V. 67. - P. 134114.
.
Wolfer W.G. Fundamental Properties of Defects in Metals / W.G. Wolfer //
Comprehensive Nuclear Materials. - 2012. - V.1. - P.1.
.
Комаров Ф.Ф. Дефекты
структуры в ионоимплантированном кремнии / Ф.Ф. Комаров, А.П. Новиков, В.С.
Соловьев, С.Ю. Ширяев // Минск: Унивеситетское - 1990. - 318 с.
. Lucas G. Ab initio
molecular dynamics calculations of threshold displacement energies in silicon
carbide / G. Lucas, L. Pizzagalli // Phys. Rev. B. - 2005. - V. 72. - P.
161202R.
.
Lucas G. First-Principles Simulations of Frenkel
Pair Formation and Annealing in Irradiated ß-SiC / G. Lucas, L. Pizzagalli // Nucl.
Instrum. Methods Phys. Res. B. - 2005.
- V. 229. - P. 359.
.
Devanathan R. Displacement energy surface in 3C and 6H SiC / R. Devanathan,
W.J. Weber // J. Nuclear Mater. - 2000. - V. 278. - P. 258.
.
Lefevre J. Silicon threshold displacement energy determined by
photoluminescence in electron-irradiated cubic silicon carbide / J. Lefevre,
J.M. Costantini, S. Esnouf, G. Petite // J. Appl. Phys. - 2009. - V. 105. - P.
023520.
.
Zhao S. Status of radioactive ion beams at the HRIBF / S. Zhao, J. Xue, C. Lan,
L. Sun, X. Wang, S. Yan // Nucl. Instrum. Methods Phys. Res. B. - 2012. - V. 286. - P.
119.
.
Devanathan R. Radiation-induced amorphization resistance and radiation / R.
Devanathan, W.J. Weber // J. Appl. Phys. - 2005. - V.98. - P. 086110.
.
Xiao H.Y. Ab initio molecular dynamics simulations of threshold displacement
energies in SrTiO3 / H.Y. Xiao, F. Gao, W.J. Weber // J. Phys.
Condens. Matter. - 2010. - V.22. - P. 415801.
.
Steffen H.J. Spatially Heterogeneous Dynamics in Liquids: Insights From
Simulation / H.J. Steffen, D. Marton, J.W. Rabalais // Phys. Rev. Lett. B. -
1992. - V. 68. - № 11. - P. 1726.
49.
Кошкин В.М. Зоны неустойчивости и короткоживущие дефекты в физике кристаллов /
В.М. Кошкин // Физика низких температур. - 2002. - Т. 28 - № 819. - С. 963-977.
. Liopo V.A. Bloch theorem
and geometrical criterion of nanoscale physics / V.A. Liopo // Proceeding on
Actual problems of Solid State Physics, Minsk - 2013. - Vol. 3 - pp. 52-54.
.
Feruz Y. Towards a universal size-dependent strength of face-centered cubic
nanoparticles / Y. Feruz, D.Mordehai // Acta Mater. - 2016. - V. 103 - P.
433-441.
.
Yao Y. Size effect of surface energy density of nanoparticles / Y. Yao, Y. Wei,
S.Chen // Surf. Sci. - 2015. - V. 636 - P. 19-24.
.
Luo W. Gibbs free energy, surface stress and melting point of nanoparticle / W.
Luo, W. Hu // Physica B - 2013. - V. 495 - P. 90-94.
.
Uglov V.V. On the physical nature of the threshold displacement energy in
radiation physics / V.V. Uglov, N.T. Kvasov, G.E. Remnev, P.V. Polikarpov // J.
Surf. Investigation. X-ray, Synchrotron Neutron Tech. - 2015. - V. 9 - P.
1206-1212.
.
Jiang Q. Size-dependet cohesive energy of nanocrystals / Q. Jiang, J.C. Li,
B.Q. Chi // Chem. Phys. Lett. - 2002. - V. 366 - P. 551-554.
.
Medasani B. Theoretical study of the surface energy, stress and lattice
contraction of silver nanoparticles / B. Medasani, Y. H. Park, I. Vasiliev //
Phys. Rev. B. - 2007. - V. 75 - P. 235436.
.
Jiang Q. Lattice contraction and surface stress of fcc nanocrystals / Q. Jiang,
L.H. Liang, D.S. Zhao // J. Phys. Chem. B - 2001. - V.105 - P. 6275-6277.
.
Ouyang G. Atomistic origin of lattice strain of stiffness of nanoparticles / G.
Ouyang, W.G. Zhu, C.Q. Sun, Z.M. Zhu, S.Z. Liao // Phys. Chem. Chem. Phys. -
2010. - V. 12 - P. 1543-1549.
.
Zhu Y.F. Modeling of the melting point, Debye temperature, thermal expansion
coefficient, and the specific heat of nanostructured materials / Y.F. Zhu, J.S.
Lian, Q. Jiang // J. Phys. Chem. - 2009. - V. 113 - P. 16896-16900.
.
Li H. Size-dependent melting point pf nanoparticles based on bond number
calculation / H. Li, P.D. Han, X.B. Zhang, M. Li // Mater. Chem. Phys. - 2013.
- V. 137 - P. 1007-1011.
.
Omar M. S. Models for mean bonding length, melting point and lattice thermal
expansion of nanoparticle materials / M.S. Omar // Mater. Res. Bull. - 2012. -
V. 47 - P. 3518-3522.
.
Li O.A. Size dependent magnetic and magneto-optical properties of Ni0.2Zn0.8Fe2O4
nanoparticles / O.A. Li, C.R. Lin, H.Y. Chen, H.S. Hsu, K.Y. Shin, I.S. Edel,
K.W. Wu, Y.T. Tseng, S.G. Ovchinnikov, J.S. Lee // J. Magn. Mater. - 2016. - V.
408 - P. 206-212.
.
Upadhyay S. Influence of crystallite size on the magnetic properties of Fe3O4
nanoparticles / S. Upadhyay, K. Parekh, B. Pandey // J.Alloys Compd. -
2016. - V. 678 - P. 478-485.
.
Wite R. Long-range order n solids / R. Wite, T. Jebell // M:Mir - 1982. - P.
448.
.
Slater J.C. A simplification of the Hartree-Fock Method / J.C. Slater // Phys.
Rev. - 1951. - V. 81 - P. 385-390.
.
Fischbacher T. A systematic approach to multiphysics extentions of
finite-element based micromagnetic simulations / T. Fischbacher, M. Franchin,
G. Bordignon, H. Fangohr // IEEE Trans. Mag. - 2007. - V. 43 - P. 2896-2898.
.
Uglov V.V. Dynamic processes in metal nanoparticles under irradiation / V.V.
Uglov, G.E. Remnev, N.T. Kvasov, I.V. Safronof // J. Surf. Invest., X-ray,
Synchrotron Neutron Tech. - 2014. - V. 8 - P. 703-707.
68.
Займан Дж. Принципы теории твердого тела / Дж. Займан // М: Мир - 1966. - C. 478.