Резонансные явления в линейных и нелинейных электрических цепях и их использование в цепях

Курсовая работа

Резонансные явления в линейных и нелинейных электрических цепях и их использование в цепях

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

. ПОНЯТИЕ О ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ И РЕЗОНАНСЕ

.1 Определение электрических цепей

.2 Понятие о резонансе в физике

. РЕЗОНАНС В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

.1 Понятие и характеристика линейной электрической цепи

.2 Явление резонанса в линейной электрической цепи

.2.1 Резонанс напряжений

.2.2 Резонанс токов

.2.3 Резонанс в разветвленной цепи

.3.4 Резонанс взаимной индукции

. РЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

.1 Понятие нелинейных электрических цепей

.2 Понятие нелинейной емкости

.3 Параметрический резонанс в нелинейном контуре

. ПРАКТИЧЕСКАЯ ЧАСТЬ

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Резонанс это значительное увеличение амплитуды колебаний напряжения или тока в элементах электрической цепи. Колебательный процесс в электрических цепях можно сравнить с механическими колебаниями маятника, качелей или стального шарика, подвешенного на длинной пружине.

Колебательный процесс в механике связан с преобразованием потенциальной энергии в кинетическую и наоборот. Колебательный процесс в электрических цепях также связан с преобразованием энергии электрического поля в энергию магнитного поля и наоборот. В связи с этим можно сделать вывод, что колебательный процесс, а, следовательно, и резонанс может возникнуть в электрических цепях, содержащих накопители энергии двух видов: в электрическом поле - емкость C и в магнитном поле - индуктивность L. В реальной электрической цепи часть электромагнитной энергии безвозвратно теряется в связи с потерями. Этот процесс моделируется активным сопротивлением R. Таким образом, электрическая цепь, содержащая элементы R, L и C называется колебательным контуром.

Актуальность темы данной работы заключается в том, что явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей.

Целью данной работы является подробное рассмотрение явления резонанса в линейных и нелинейных электрических цепях.

В рамках поставленной цели прорабатываются следующие задачи:

-       рассмотрение понятия резонанса и электрических цепей;

-       резонанс в линейных электрических цепях;

-       резонанс в нелинейных электрических цепях.

1. ПОНЯТИЕ О ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ И РЕЗОНАНСЕ

.1 Определение электрических цепей

Электрической цепью называется совокупность элементов, образующих пути для прохождения электрического тока. Электрическая цепь состоит из активных и пассивных элементов.

Активными элементами считаются источники электрической энергии (источники напряжения и тока), к пассивным элементам относятся резисторы, катушки индуктивности, электрические конденсаторы.

Количественные характеристики элементов электрической цепи называются ее параметрами. Например, параметрами источника постоянного напряжения являются его ЭДС и внутреннее сопротивление. Параметром резистора служит его сопротивление катушки - ее индуктивность L и конденсатора - емкость С [2].

Напряжение или ток, подводимые к цепи, будем называть воздействующим или входным сигналом. Воздействующие сигналы можно рассматривать как различные функции времени, изменяющиеся по некоторому закону z(t). Например, z(t) может быть постоянной величиной, изменяться во времени по периодическому закону или иметь апериодический характер. Напряжения и токи, возникающие под влиянием внешнего воздействия в интересующей нас части электрической цепи и также являющиеся функциями времени х(t), будем называть реакцией (откликом) цепи или выходным сигналом.

Любой пассивный элемент реальной электрической цепи в той или иной степени обладает активным сопротивлением, индуктивностью и емкостью. Однако, чтобы облегчить изучение процессов в электрической цепи и ее расчет, реальная цепь заменяется идеализированной, состоящей из отдельных пространственно разделенных элементов R, L, С.

При этом считается, что проводники, соединяющие элементы цепи, не обладают активным сопротивлением, индуктивностью и емкостью. Такая идеализированная цепь называется цепью с сосредоточенными параметрами, и основанные на ней расчеты дают во многих случаях хорошо подтверждаемые опытом результаты.

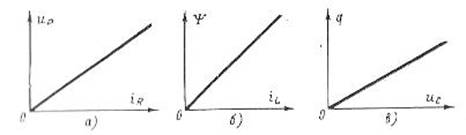
Электрические цепи с постоянными параметрами - это такие такие цепи, в которых сопротивления резисторов R, индуктивность катушек L и емкость конденсаторов С являются постоянными, не зависящими от действующих в цепи токов и напряжений. Такие элементы называются линейными. Если сопротивление резистора R не зависит от тока, то линейная зависимость между падением напряжения и током выражается законом Ома ur = R х i_r, а вольт-амперная характеристика резистора (представляет собой прямую линию (рис. 1, а). Если индуктивность катушки не зависит от величины (протекающего в ней тока, то потокосцепление самоиндукции катушки ψ прямо пропорционально этому току ψ= L х i_l (рис. 1, б). Наконец, если емкость конденсатора С не зависит от приложенного напряжения uc то заряд q, накопленный на пластинах, и напряжение u_c связаны между собой линейной зависимостью графически показанной на рис. 1, в.

 <#"903447.files/image002.gif"> вызывает в каком-либо ее элементе (или участке) появление тока , то изменение величины  в  раз вызывает изменение тока 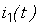 в такое же число раз. То есть выполняются соотношения [5, c.381 - 383]:

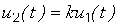; (2.1)

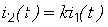, (2.2)

Они выражают основное свойство линейной цепи. Помимо этого такие цепи удовлетворяют принципу суперпозиции, согласно которому реакция линейной цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым воздействием в отдельности.

Иными словами, если приложенное напряжение можно представить в виде суммы 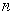 слагаемых

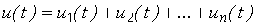, (2.3)

то возникающий в каком-либо элементе (или участке) цепи ток также будет представлять собой сумму 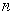 слагаемых

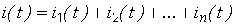. (2.4)

В последнем выражении 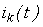 представляет собой ток, появление которого вызвано воздействием напряжения .

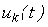Еще одним свойством линейных электрических цепей является свойство дуальности. При этом под дуальностью понимают схожесть по структуре выражений, описывающих зависимость напряжения от тока для одного элемента цепи, и тока от напряжения - для другого. Соответственно сами элементы называются дуальными.

Например, для индуктивности L связь между напряжением и током определяется известным соотношением:

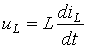. (2.5)

Дуальным к нему будет уравнение, связывающее ток через другой элемент и напряжение на нем, сходное по виду. Этим уравнением является зависимость между током и напряжением для емкости [5, 8]:

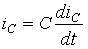. (2.6)

Таким образом, L и С - дуальные элементы.

К числу уравнений такого типа можно отнести также известные выражения:

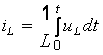, (2.7)

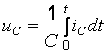, (2.8)

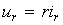(2.9)

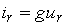(2.10)

Для последней пары уравнени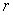й  и 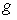 - сопротивление и проводимость соответственно. Для линейных электрических цепей свойство дуальности проявляется в тождественности уравнений для токов и напряжений при замене всех входящих в них величин на дуальные. Например, уравнениям контурных токов одной цепи можно поставить в соответствие дуальные уравнения узловых потенциалов другой (или наоборот). Пример дуальных цепей приведен на рис. 2 [7, c.52 - 54].

Системы уравнений, описывающие данные цепи, также являются дуальными:

для схемы рис. 2, а ,  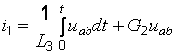(2.11);

для схемы рис. 2, б 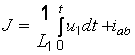, 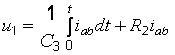(2.12).

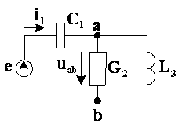
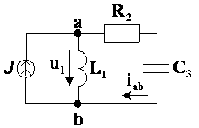
                   А                                           б

Рис. 2. Дуальные цепи

Обобщая сказанное, можно ввести следующее определение: дуальными являются пары физических величин, понятий и законов электрических цепей, соответствующие друг другу в дуальных соотношениях.

2.2 Явление резонанса в линейной электрической цепи

2.2.1 Резонанс напряжений

В электрической цепи, содержащей катушки индуктивности L и конденсаторы C, возможны свободные гармонические колебания энергии между магнитным полем катушки:

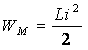(2.13)

и электрическим полем конденсатора:

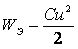.(2.14)

Угловая частота этих колебаний wo, называемых свободными или собственными, определяется структурой цепи и параметрами ее отдельных элементов R, L, C.

Резонансным режимом цепи или просто резонансом называется явление увеличения амплитуды гармонических колебаний энергии в цепи, наблюдаемое при совпадении частоты собственных колебаний wo с частотой вынужденных колебаний w, сообщаемых цепи источником энергии (w_o = w).

На этом основании условие для резонансного режима можно сформулировать через параметры элементов схемы, а именно: входное сопротивление и, соответственно, входная проводимость схемы со стороны выводов источника энергии должна носить чисто активный характер: Zвх=Rвх; Yвх=Gвх; Xвх=0; Bвх=0; или в комплексной форме: Im[Zвх]=0, Im[Yвх]=0.

Резонанс в цепи с последовательным соединением источника энергии и реактивных элементов L и C получил название резонанса напряжений. Простейшая схема такой цепи показана на рис.3.

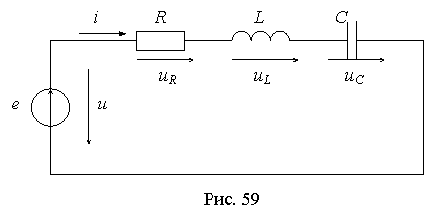
Рис.3. Структура резонансной цепи

Комплексное входное сопротивление схемы:

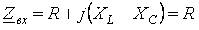.(2.14)

Условие резонанса напряжений:

_э = XL - XC =0 или wL - 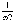=0, (2.15)

откуда w₀ =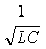 - резонансная или собственная частота.

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источника w. В резонансном режиме полное сопротивление схемы имеет минимальное значение и равно активному сопротивлению:

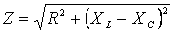= R, (2.16)

ток максимален и совпадает по фазе с напряжением источника: I=E/R; j = 0.

Векторная диаграмма напряжений и тока показана на рис. 4 [7, c.62].

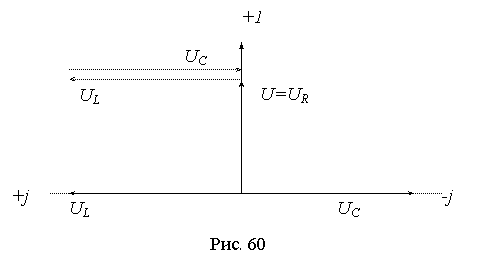
Рис.4. Векторная форма резонанса напряжений

Напряжения на реактивных элементах равны по модулю, противоположны по фазе и взаимно компенсируют друг друга:

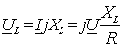; (2.17)

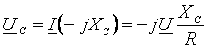, (2.18)

а напряжение на резисторе равно напряжению источника: UR=IR=U=E.

Напряжения на реактивных элементах могут значительно превосходить напряжение источника U = Е при условии, что XL=XC>>R:

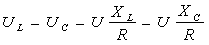(2.19)

Выясним энергетические процессы, протекающие в цепи в резонансном режиме. Пусть в цепи протекает ток i =Imsinwt, тогда напряжение на конденсаторе составит:

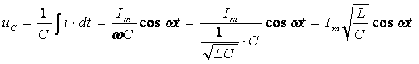(2.20).

Сумма энергий магнитного и электрического полей равна:

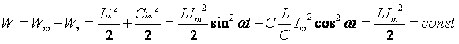(2.21)

Таким образом, сумма энергий магнитного и электрического полей равна постоянному значению. Между магнитным и электрическим полями происходит непрерывный обмен энергией, суммарное значение которой постоянно, а обмен энергией между источником и цепью отсутствует, при этом поступающая от источника энергия преобразуется в другие виды.

Электрическая цепь с последовательным соединением элементов R, L, C в технике получила название последовательного колебательного контура.

Свойства такой цепи как колебательного контура характеризуют следующие параметры, такие, как резонансная частота (2.22), волновое сопротивление (2.23) и добротность контура (2.24) [2, 6].

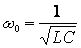(2.22)

r = 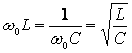 (2.23)

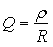(2.24)

Чем больше добротность контура Q, тем выразительнее проявляются в нем резонансные явления, например, напряжения на реактивных элементах больше напряжения источника в Q раз: UL = UC = UQ.

При изменении частоты источника w = var будут изменяться сопротивления реактивных элементов и, как следствие, будут изменяться ток в цепи и напряжения на отдельных участках.

Частотными характеристиками контура называются зависимости сопротивлений отдельных элементов и участков от частоты:

_L =wL, (2.25)_C = 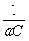(2.26)=XL-XC, (2.27)=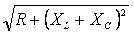(2.28)

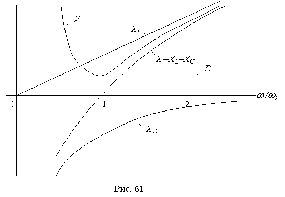
Рис.6. Графическое отображение частотных характеристик

Резонансными характеристиками называются зависимости режимных параметров от частоты: U_L, U_C, I, j = f(w) (рис. 7).

Полосой пропускания резонансного контура называют область частот Dw = w1-w2, на границах которой ток I в 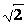 раз меньше своего максимального значения, т.е. I=0, 707Imax. Полоса пропускания контура обратно пропорциональна его добротности: Dw = 1/Q. На рис. 7 в относительных единицах представлено семейство резонансных характеристик с различными значениями добротности [2, c.118].

Рис.7. Частотные характеристики

Практическое применение резонанс напряжений находит в области радиотехники и техники связи. В электроэнергетике явление резонанса напряжений из-за сопутствующих ему перенапряжений может привести к нежелательным последствиям. Например, при подключении к генератору или трансформатору кабельной линии, не замкнутой на приемном конце на нагрузку (в режиме холостого хода), вся цепь может оказаться в резонансом режиме, при этом напряжения на отдельных участках цепи могут появиться высокие напряжения.

2.2.2 Резонанс токов

Резонанс в цепи с параллельным соединением источника энергии и реактивных элементов L и C получил название резонанса токов. Простейшая схема такой цепи показана на рис. 8.

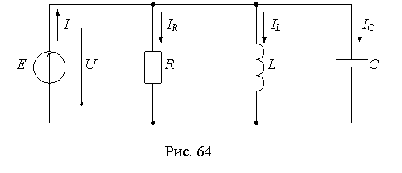
Рис.8. Схема цепи с резонансом токов

Комплексная входная проводимость схемы:

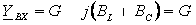(2.29)

Условие резонанса токов:

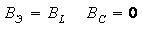или(2.30)

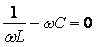, (2.31)

откуда резонансная (собственная) частота:

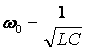(2.32)

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источника w [2, 6].

В резонансном режиме полная проводимость схемы равна активной проводимости и имеет минимальное значение:

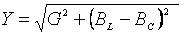= G, (2.33)

а ток источника также минимален и совпадает по фазе с напряжением источника (j = 0): I =UY = UG.

Токи в ветвях с реактивными элементами IL=U(-jBL), IC =U(jBC) равны по модулю, противоположны по фазе и компенсируют друг друга, а ток в резисторе G равен току источника (I=IG=UG). Равные по модулю токи в реактивных элементах IL = IC могут значительно превосходить ток источника I при условии, что BL=BC>>G.

Векторная диаграмма токов и напряжений показана на рис. 9.

Электрическая цепь с параллельным соединением элементов G, L и C в технике получила название параллельного колебательного контура.

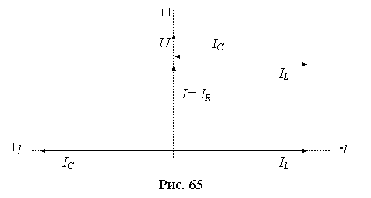
Рис.10. Векторная форма резонанса токов

Свойства такой цепи как колебательного контура характеризуют следующие параметры: резонансная частота (2.34), волновая проводимость (2.35) и добротность контура (2.36).

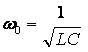(2.34)

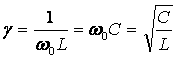(2.35)

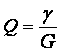(2.37)

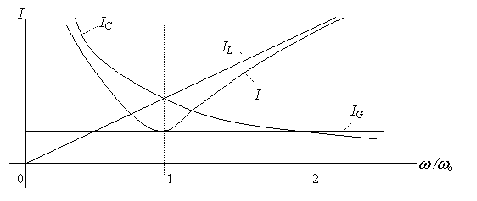
Рис.11. Графическое отображение резонансных характеристик

Резонанс токов находит широкое применение в области радиотехники и техники связи. В электроэнергетике компенсация реактивной мощности на промышленных предприятиях с помощью параллельного подключения конденсаторных батарей, по сути дела, представляет собой мероприятие, при котором также достигается резонанс токов [1, c.247].

2.2.3 Резонанс в разветвленной цепи

Возникновение резонанса токов возможно в разветвленной цепи с параллельным соединением индуктивного, емкостного и резистивного сопротивлений. При известном напряжении питания 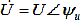, значение общего тока в комплексной форме будет равно:

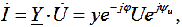где(2.38)

 комплексная проводимость цепи и полная проводимость цепи;

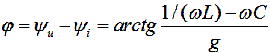(2.40)

- угол сдвига фаз между напряжением питания цепи и общим током.

Тогда действующее значение общего тока будет равно:

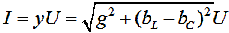(2.41)

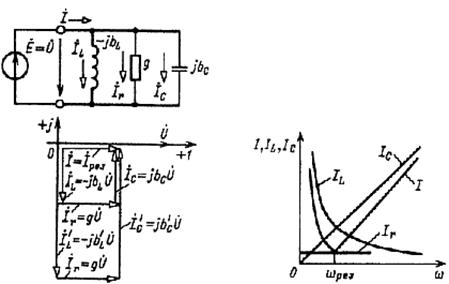
Рис.12. К определению резонанса токов в разветвленной цепи

Когда в параллельной цепи возникает резонансная частота 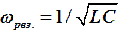, индуктивная b_L и емкостная b_C проводимости равны между собой, поэтому аргумент комплексной проводимости равен нулю. То есть ψ_u=ψ_i и полная проводимость цепи равна активной проводимости y=g, при этом общий токI_рез.=gU имеет минимальное значение.

Режим цепи с параллельными ветвями, при котором общий ток совпадает по фазе с напряжением, называется резонансом токов.

При резонансе токов действующие значение токов, которые протекают в индуктивности L и емкости C, одинаковые, а сдвиг фаз между ними равен 180^о, это связано с тем что ток в индуктивности отстает от общего напряжения на угол 90^о, а ток в емкости опережает напряжение на входе на угол 90^о.

Если мы при резонансе токов будем увеличивать индуктивную и емкостную проводимости в n раз, тогда токи в этих ветвях также возрастут в n раз, а вот общий ток при этом останется тем же I_рез.=gU.

Если активная проводимость g равна нулю, то и полная проводимость yцепи равна нулю. При этом ток источника также будет равен нулю, что в принципе эквивалентно разомкнутой цепи.

В параллельных ветвях помимо индуктивности L и емкости C может быть и активные элементы r_L и r_C, которые могут учитывать потери энергии в проводах. Условием возникновения резонанса тока в этом случае будет равенство проводимостей параллельных цепей:

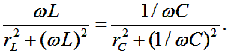(2.42)

2.3.4 Резонанс взаимной индукции

Определим резонансные частоты и частотные характеристики в цепи, изображенной на рис. 3.23.

В радиотехнике и в технике связи часто используют явление резонанса в индуктивно связанных колебательных контурах с большой добротностью. В связи с этим для упрощения расчета пренебрежем активным сопротивлением вторичного контура.

Собственные частоты контуров, при которых в них наступает резонанс, в случае отсутствия взаимной индукции равны:

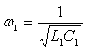и 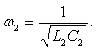(2.43)

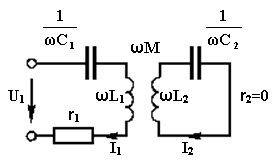
Рис. 13. Индуктивно-связанные контуры

Имеем уравнения рассматриваемой цепи

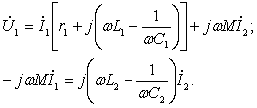(2.44)

Выражая 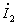 из второго уравнения через  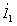и подставляя в первое уравнение, получаем

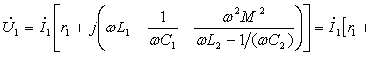
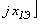.(2.45)

Условием резонанса напряжений будет равенство нулю эквивалентного реактивного сопротивления, т.е. x_1Э = 0, откуда

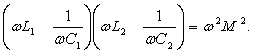(2.46)

Разделив на (ωL₁ωL₂) обе части этого выражения, получим

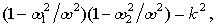(2.47)

где 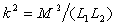 есть квадрат коэффициента связи, причем k²< 1.

Решая это уравнение относительно ω, найдем частоты 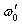 и 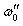, отвечающие резонансу напряжений, из выражения

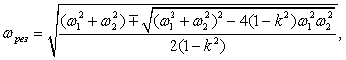(2.48)

где ω_рез равна либо 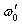, либо .

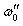Если оба контура предварительно были настроены на одну частоту ω₁ = ω₂ = ω₀, то частоты 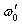 и 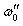 находятся из выражения 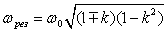, т.е. они оказываются равными

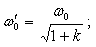(2.49)

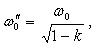(2.50)

причем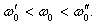

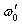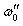При частотах  и  сопротивление цепи оказывается минимальным и равным r₁, а ток I₁достигает максимальных значений: I₁= U₁/r₁.

При ω = ω₀ имеем х_1Э = 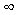 и ток I₁=0. Это можно пояснить следующим образом: при частоте ω₀ имеет место резонанс во вторичном контуре х₂= ωL₂ - 1/( ωC₂)=0, и при условии r₂ = 0 получается z₂ = 0. Как видно из уравнения для второго контура, при конечном значении тока 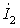 ЭДС взаимной индукции  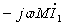должна быть равна нулю, т.е. I₁=0. Ток 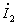 устанавливается таким, чтобы ЭДС взаимной индукции  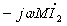со стороны второго контура уравновесила приложенное к первому контуру напряжение, что видно из первого уравнения при I₁ = 0. Этот случай по своему характеру аналогичен резонансу токов в контуре без потерь.

На рис. 14 представлена частотная характеристика I₁(ω) при U₁ = const, а также частотная характеристика x_1Э(ω).

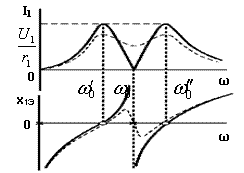
Рис. 14. Частотные характеристики: I₁(ω) при U₁ = const и x_1Э(ω)

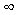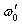Полюсами функции x_1Э(ω) являются частоты ω = 0, ω = ω₀ и ω = . Ее нулями являются частоты ω =и ω =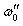. В соответствии со сказанным в предыдущем разделе во всем диапазоне частот соблюдается условие dx_1Э/dω > 0 и полюсы и нули чередуются. Штриховыми линиями показаны частотные характеристики при r₂ ≠ 0. Таким образом, резонансная кривая I₁ = F₁(ω) цепи, состоящей из двух связанных контуров с малым затуханием, имеет два максимума и один минимум.

3. РЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

.1 Понятие нелинейных электрических цепей

В теории линейных цепей предполагалось, что параметры всех элементов цепи являются постоянными величинами, не зависящих от токов и напряжений. Каждому идеальному элементу цепи приписывалось определенное значение его параметра: резистору - сопротивление R, катушке - индуктивность L, конденсатору - емкость C. Физические характеристики таких элементов (u=R×i - для резистора, ψ =L×i - для катушки, q=C×u - для конденсатора) описываются уравнением прямой линии y = a×x, поэтому такие элементы получили общее название линейных, а электрические цепи, состоящие из таких элементов, также называются линейными.

Идеальных линейных элементов в природе не существует. В действительности параметры всех элементов в той или иной мере зависят от их физического состояния, т.е. от тока, напряжения, температуры. Если эта зависимость выражена незначительно, то ею при расчете цепей пренебрегают и элементы считают линейными.

Однако существует обширный класс элементов электрических цепей, параметры которых существенно зависят от тока и напряжения и эту зависимость необходимо учитывать при расчете электрических цепей. Такие элементы получили название нелинейных, так как их физические характеристики не могут быть описаны уравнением прямой линии. Таким элементам нельзя придать определенное значение параметра сопротивления R, индуктивности L и емкости C. С целью отличия нелинейных элементов от линейных на электрических схемах на обозначение элемента наносятся дополнительный знак «клюшка» (рис. 12):

При расчете электрических цепей нелинейные элементы задаются их физическими характеристиками в исследуемом диапазоне значений физических параметров. Эти характеристики получили следующие названия: а)для нелинейного резистора u=f(i) или i=f(u) - вольт-амперная характеристика или сокращенно ВАХ; б)для нелинейной катушки y=f(i) или i=f(ψ) - вебер-амперная характеристика или сокращенно ВАХ; в)для нелинейного конденсатора q=f(u) или u=f(q) - кулон-вольтная характеристика или сокращенно КВХ [1, 4].

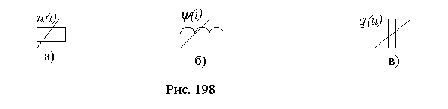
Рис.12. Нелинейная электрическая цепь

Электрическая цепь называется нелинейной, если она содержит хотя бы один нелинейный элемент.

Состояние нелинейной цепи постоянного тока в установившемся режиме можно описать системой нелинейных алгебраических уравнений, составленных для схемы цепи по законам Кирхгофа. В математике не существует стандартных методов решения систем нелинейных алгебраических уравнений, и, как следствие, на практике не существует общих методов расчета нелинейных цепей постоянного тока, таких, как метод контурных токов и метод узловых потенциалов для линейных цепей.

Одна из главных особенностей нелинейных цепей состоит в том, что к ним неприменим принцип наложения. Докажем это положение на примере расчета схемы рис. 13, в которой включены последовательно два источника ЭДС (Е₁, Е₂) и нелинейный резистор с заданной ВАХ I = kU₂.

Действительный ток в исходной схеме рис. 201а определится по заданному уравнению ВАХ:

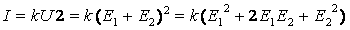Equation Section (Next)Equation Section (Next)(3.1)

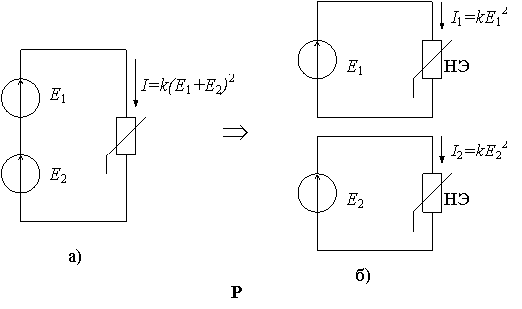
Рис.13. Схемы нелинейных электрических цепей

Ток, рассчитанный по методу наложения (рис. 3б):

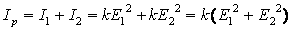(3.2)

Сравнение правых частей равенств показывает, что .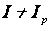

Метод расчета для каждой нелинейной цепи постоянного тока устанавливается индивидуально. Выбор того или другого метода зависит от конкретных условий задачи: структуры схемы цепи, характера нелинейности ВАХ нелинейных элементов, требований к результату расчета и др. Возможно применение не одного, а нескольких методов, каждый из которых позволяет более четко определить одну из сторон процесса в цепи.

В нелинейных цепях могут возникать особые процессы, которые в принципе невозможны в линейных цепях. Многообразием таких процессов объясняется широкое применение устройств на нелинейных элементах в различных областях современной техники. Современные средства связи, радиоэлектроника, компьютерная техника основаны на использовании нелинейных свойств элементов электрических цепей [2, 7].

Перечислим некоторые явления, имеющие место в нелинейных цепях, которые находят практическое применение в электроэнергетике:

-       преобразование переменного тока в постоянный или выпрямление;

-       преобразование постоянного тока в переменный произвольной частоты или инвертирование;

-       преобразование переменного тока одной частоты в переменный ток другой частоты;

-       стабилизация режимных параметров (напряжения или тока) на некоторых участках цепи при изменении этих параметров на других участках;

-       трансформация постоянного тока и напряжения;

-       усиление сигналов по напряжению, по току или по мощности;

-       возможность существования нескольких установившихся режимов цепи при одних и тех же параметрах элементов;

-       скачкообразные изменения режима цепи и т.д.

3.2 Понятие нелинейной емкости

Уравнение вынужденных колебаний нелинейного контура при нечетной характеристике возвращающей силы и не слишком больших амплитудах колебаний имеет вид [3]:

Параметр g характеризует нелинейность контура. Предполагается, что gx² << 1.

Исследование уравнения (3.4) показывает, что частота собственных колебаний системы зависит от амплитуды А колебаний и определяется выражением:

w² = 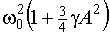. (3.4)

Из этого выражения видно, что при увеличении амплитуды колебаний собственная частота нелинейного контура, равная w₀ при малых амплитудах, увеличивается при g > 0 и уменьшается при g < 0 (рис. 14).

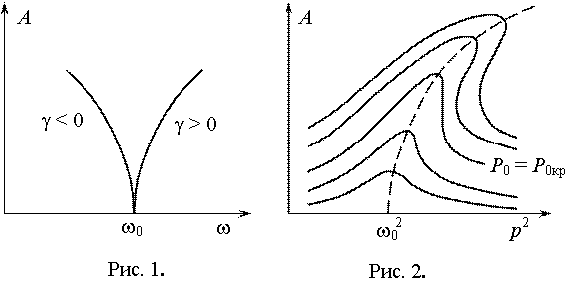
Рис.14. Значения собственной частоты нелинейного контура

Знак g определяется поведением средней величины нелинейного параметра контура при изменении амплитуды. В нашем случае нелинейным параметром является ёмкость. Если с ростом амплитуды колебаний средняя емкость контура увеличивается, то g < 0. Если же средняя емкость падает с ростом амплитуды, то g > 0. Решение уравнения (3.4) может быть найдено, например, методом гармонического приближения или методом медленно меняющихся амплитуд. Семейство резонансных кривых нелинейного контура, полученное указанными методами при g > 0, заданном значении d и при различных значениях амплитуды внешней силы, показано на рис. 15.

Как видно из рис. 2, резонансные кривые могут быть двух видов.

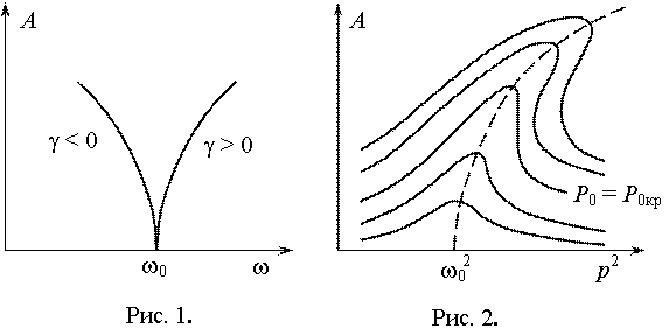
Рис.15. Семейство резонансных кривых нелинейного контура

Кривые одного вида соответствуют значениям амплитуды внешней силы, меньшим некоторой критической величины, и характеризуются однозначной зависимостью амплитуды вынужденных колебаний от частоты внешней силы. Резонансные кривые этого вида представляют собой несколько деформированные резонансные кривые для обычного линейного контура. Максимум у них смещён в сторону больших частот в соответствии с уравнением (3.5) при g > 0 [3, 6].

Другой вид резонансных кривых соответствует амплитудам внешней силы, большим некоторого критического значения P_0кр. У резонансных кривых этого вида имеются участки с неоднозначной зависимостью амплитуды вынужденных колебаний от частоты внешнего воздействия. В области частот, где резонансные кривые являются трехзначными, среднее значение амплитуды неустойчиво, поэтому при экспериментальном исследовании резонансных кривых наблюдаются скачки амплитуды при достижении границ неустойчивой области. При противоположном знаке g резонансные кривые будут иметь наклон в противоположную сторону.

В системах с нелинейными потерями изменение амплитуды колебаний не влияет на собственную частоту колебательного контура. Поэтому резонансные кривые таких систем не имеют наклона. Характерной особенностью резонансной кривой контура с нелинейными потерями является наличие плоской вершины (обычно потери увеличиваются с ростом амплитуды). В реальных системах с нелинейными элементами (например, с полупроводниковыми диодами) могут одновременно меняться активные и реактивные параметры. По форме резонансной кривой, полученной экспериментально, можно судить о том, какой из нелинейных параметров играет в схеме бóльшую роль.

3.3 Параметрический резонанс в нелинейном контуре

Параметрическим резонансом называется явление возбуждения колебаний за счет периодического изменения энергоемкого параметра колебательной системы. Легче всего явление параметрического резонанса наблюдается, когда частота внешней силы p близка к удвоенной собственной частоте 2w₀ резонансной системы, т. е. когда p » 2w₀.

Если в контуре с нелинейным конденсатором происходят вынужденные колебания, то под их влиянием модулируется емкость нелинейного конденсатора. Частота и амплитуда модуляции емкости определяются частотой и амплитудой вынужденных колебаний. Параметрическое возбуждение колебаний возникает, если p » 2w₀ и глубина модуляции емкости имеет достаточно большую величину. Последнее условие выполняется лишь при достаточно большой амплитуде вынужденных колебаний с частотой p. Для теоретического исследования явления параметрического резонанса необходимо проанализировать решения уравнения 3.5, описывающего движения в контуре с нелинейной реактивностью при действии на этот контур внешней силы с частотой p [3].

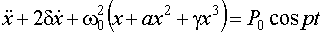, (3.5)

При параметрическом возбуждении колебаний в контуре будут одновременно наблюдаться два процесса: вынужденные колебания с частотой p и параметрически возбужденные колебания с частотой 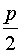 » w₀, поэтому решение уравнения (3.6) целесообразно искать в виде суммы колебаний с частотами p и :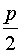

x = Acospt + Bcos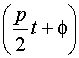(3.6)

Для A и B методом медленно меняющихся амплитуд могут быть получены следующие выражения:

A = 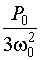, (3.7)

B = . (3.8)

Здесь x = 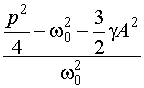 - расстройка с учетом поправки на неизохронность нелинейного контура, m = 4a²A² - коэффициент модуляции реактивного параметра с частотой p; q = .

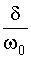Из выражений для x и m следует, что коэффициент a при x² в уравнении (3.6) определяет глубину модуляции реактивного параметра при наличии колебаний в нелинейном контуре, а от коэффициента g при x³ зависит только величина поправки к собственной частоте w₀ на неизохронность нелинейного контура.

На рис. 16 приведен график зависимости амплитуды B параметрически возбужденных колебаний от частоты p внешней силы при g > 0. Выражения для B, x, m и q позволяют найти частоты внешней силы, соответствующие точкам D и C на рис. 16:

p_D = 2w₀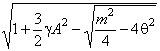, (3.9)

p_C = 2w₀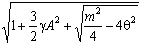(3.10)

Эти точки определяют полосу частот, в пределах которой возможно параметрическое возбуждение колебаний. При уменьшении амплитуды внешнего воздействия точки D и C сближаются, и при m £ 4q, т. е. при амплитуде внешней силы P₀ £ 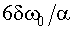, становится невозможным [3, 5].

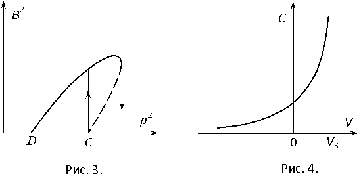
Рис.16. График зависимости амплитуды B параметрически возбужденных колебаний от частоты p внешней силы при g > 0

На практике в качестве нелинейной емкости обычно используется барьерная емкость запертого p-n-перехода полупроводникового диода. Для объяснения физической природы барьерной емкости рассмотрим кристалл полупроводника, в котором имеется область с электронной проводимостью (область n) и область с дырочной проводимостью (область p).

При контакте p- и n- областей часть электронов из n- области переходит в область p, а часть дырок из переходит в n- область; в последней вблизи границы образуется нескомпенсированный положительный заряд неподвижных ионизированных доноров.

Соответственно в p- области из-за ухода дырок образуется отрицательный объемный заряд неподвижных ионизированных акцепторов. Между этими зарядами возникает электрическое поле, которое препятствует дальнейшему переходу электронов в область p и дырок в область n. Разность потенциалов между областями p и n, образующаяся при контакте, равна разности работ выхода электронов. При подаче на запирающего напряжения V высота потенциального барьера между областями p и n возрастает на величину приложенного напряжения, увеличивается и электрическое поле в переходе. Это приводит к расширению p-n-перехода. Электроны и дырки, вытолкнутые полем из перехода, уходят вглубь областей p и n, вследствие чего увеличивается положительный объемный заряд в области n и отрицательный в области p. При подаче на p-n-переход прямого напряжения высота потенциального барьера уменьшается, переход сужается, заряды уменьшаются. Таким образом, изменения напряжения, приложенного к переходу, приводят к изменению объемного заряда в переходе, т. е. переход действует как емкость [1, 3].

Расчет показывает, что величина этой емкости зависит от напряжения на p-n-переходе в соответствии с выражением

C = C₀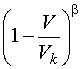(3.11)

гдеC₀ - величина емкости при напряжении равном нулю,

V_k - контактная разность потенциалов,

V - приложенное напряжение.

Величина b зависит от распределения примесей в переходе. Обычно . График зависимости емкости p-n-перехода от приложенного напряжения изображен на рис. 17.

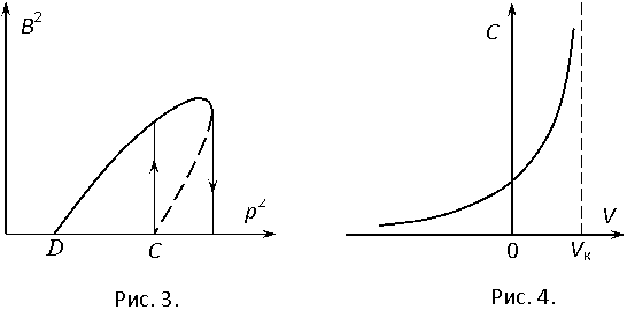
Рис. 17. График зависимости емкости p-n-перехода от приложенного напряжения

Из рисунка видно, что емкость наиболее сильно меняется при напряжении равном нулю или даже при положительных напряжениях. Однако необходимо иметь в виду, что полупроводниковый диод при положительных напряжениях начинает пропускать ток, поэтому емкость p-n-перехода оказывается зашунтированной нелинейным сопротивлением. При достаточно больших отрицательных напряжениях в p-n-переходе происходит пробой и диод начинает пропускать ток в обратном направлении. В области напряжений V_пр < V < 0 ток через диод мал и сам диод является добротным нелинейным конденсатором. При V < 0 и V < V_пр малое сопротивление шунтирует его емкость, вследствие чего добротность нелинейного конденсатора ухудшается. Поэтому при использовании полупроводникового диода в качестве нелинейной емкости необходимо так выбирать рабочую точку, чтобы не заходить в область малого активного сопротивления. Одновременно необходимо добиваться максимального изменения емкости. Возможны два способа создания необходимого смещения на диоде: подача принудительного смещения от внешней батареи и создание автосмещения, использующего ток самого диода [3, c.12].

В последнем случае напряжение смещения получается за счет выпрямления диодом переменного напряжения, возникающего на конденсаторе колебательного контура. Очевидно, что напряжение автосмещения зависит от амплитуды колебаний в контуре и по абсолютной величине растет с увеличением амплитуды.

4. ПРАКТИЧЕСКАЯ ЧАСТЬ

Каждая из программ САПР (EDA) может иметь свою специализацию и лучше выполнять основные задачи, для которых предназначалась, а чем она универсальнее, тем сложнее может быть работа с ней. Так программа PSIM (www.powersimtech.com) предназначена к анализу силовых преобразовательных устройств и систем. В этом ее специфика, это она делает лучше, чем другие программы, но, видимо, есть то, что она не делает или делает не лучшим образом. Начать работу с ней можно почти сразу, а по мере накопления опыта можно решать все более и более сложные задачи.

Завершив все соединения (рис.18), обозначив все элементы схемы и задав их величину, можно начать симуляцию либо с помощью инструментального меню, либо через основное меню (Simulate-Run Simulation).

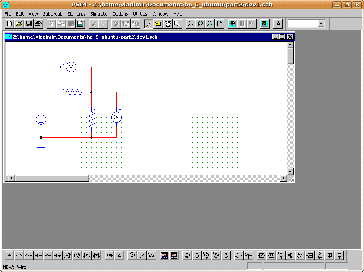
Рис.18. Схема цепи

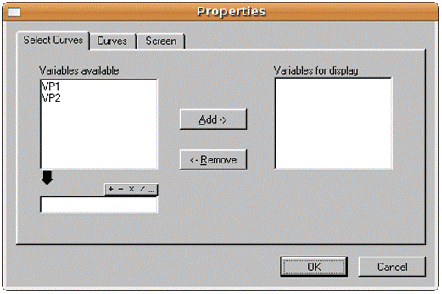
Рис. 19. Диалоговое окно выбора функции, отображающей результаты симуляции

В данном случае есть два измерительных прибора - вольтметры VP1 и VP2. Щелкнув по первому из них, а затем по клавишам Add -> и OK, можно получить результаты измерений первым вольтметром.

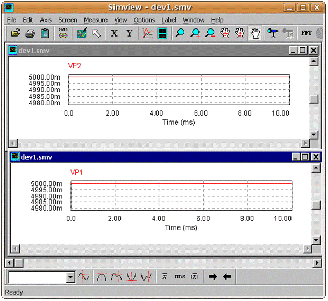
Рис. 20. Результаты измерений в окне обозревателя

А повторив всю процедуру для другого вольтметра, получить результаты измерения вторым вольтметром. Оба графика располагаются в окне обозревателя удобным образом, если перетащить их или воспользоваться средствами раздела Window основного меню, позволяющими расположить окна каскадом или «черепицей», возможность присутствующая, практически, в любом редакторе.

Как и следовало ожидать, а мы уже знаем законы Ома и Кирхгофа, ЭДС источника поровну распределяется в виде падения напряжения на двух резисторах равной величины. То есть, 10 вольт источника питания делятся на два напряжения по 5 вольт.

Есть и другая возможность увидеть эти результаты - не использовать обозреватель, а воспользоваться основным меню программы, где в разделе Simulate есть подраздел Runtime Graphs, открывающий подменю всех полученных функции при симуляции. В этом случае окно программы выглядит так:

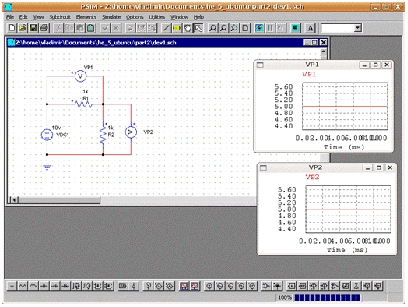
Рис. 2.11. Вывод результатов измерений в основном окне программы

Если резисторы имеют разное сопротивление, то можно, прибегнув к расчетам, определить эти два напряжения. В первую очередь определим общее сопротивление цепи, сложив сопротивление резисторов R1 и R2. Разделим ЭДС на это сопротивление, получив ток, протекающий в цепи, а затем умножим этот ток на величину сопротивления R1, получив напряжение на нем, затем на величину R2 для получения второго напряжения.

ЗАКЛЮЧЕНИЕ

Электрической цепью называется совокупность элементов, образующих пути для прохождения электрического тока. Электрическая цепь состоит из активных и пассивных элементов. Электрические цепи с постоянными параметрами - это такие цепи, в которых сопротивления резисторов R, индуктивность катушек L и емкость конденсаторов С являются постоянными, не зависящими от действующих в цепи токов и напряжений. Такие элементы называются линейными.

Резонанс - резкое возрастание амплитуды результирующих колебаний при совпадении собственных колебаний системы. Так как при резонансе внешняя сила совершает за период максимальную положительную работу над колебательной системой, то условие резонанса можно определить как условие максимальной передачи энергии колебательной системе.

Линейные электрические цепи представляют собой частный случай электрических цепей и характеризуются тем, что вольт-амперные характеристики всех элементов цепи линейны, а состояние самой цепи описывается с помощью линейных алгебраических уравнений с постоянными коэффициентами. В линейной электрической цепи, содержащей катушки индуктивности L и конденсаторы C, возможны свободные гармонические колебания энергии между магнитным полем катушки. В линейной электрической цепи возможен резонанс токов и резонанс напряжений.

Резонанс в цепи с последовательным соединением источника энергии и реактивных элементов L и C получил название резонанса напряжений. Резонанс в цепи с параллельным соединением источника энергии и реактивных элементов L и C получил название резонанса токов. Идеальных линейных элементов в природе не существует. В действительности параметры всех элементов в той или иной мере зависят от их физического состояния, т.е. от тока, напряжения, температуры.

Если эта зависимость выражена незначительно, то ею при расчете цепей пренебрегают и элементы считают линейными. Однако существует обширный класс элементов электрических цепей, параметры которых существенно зависят от тока и напряжения и эту зависимость необходимо учитывать при расчете электрических цепей. Такие элементы получили название нелинейных, так как их физические характеристики не могут быть описаны уравнением прямой линии. Электрическая цепь называется нелинейной, если она содержит хотя бы один нелинейный элемент. Метод расчета для каждой нелинейной цепи постоянного тока устанавливается индивидуально.

Если в контуре с нелинейным конденсатором происходят вынужденные колебания, то под их влиянием модулируется емкость нелинейного конденсатора. Частота и амплитуда модуляции емкости определяются частотой и амплитудой вынужденных колебаний. Параметрическое возбуждение колебаний возникает, если p » 2w₀ и глубина модуляции емкости имеет достаточно большую величину.

Явление электрического резонанса широко используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур. Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот. На явлении резонанса основана вся радиосвязь.

Необходимость учета возможности резонанса в электрической цепи. В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии. Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.       Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для студентов электротехнических, энергетических и приборостроительных специальностей вузов.-7-е изд., перераб. и доп.- М.: Высш. школа, 2008. - 528 с.

.        Бессонов Л.А. Теоретические основы электротехники: Электромагнитное поле: Учебник для студентов вузов.-7-е изд., перераб. и доп.- М.: Высш. школа, 2008. - 231 с.

.        Белов А.А. Нелинейный и параметрический резонанс. Методическое пособие. - М.: Издательство МГУ, 2002 - 16 с.

.        Матханов П.А. Основы анализа электрических цепей. - М.: Высш. шк., 1990. - 400 с.

.        Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. В 2-х т.: Учебник для вузов. Том 1. - 3-е изд., перераб. и доп. - Л.: Энергоиздат, 2007. - 536 с.

.        Теоретические основы электротехники. В 3-х ч. - Ч. I. Атабеков Г.И. Линейные электрические цепи: Учебник для вузов. - 5-е изд., испр. и доп. - М.: Энергия, 2008. - 592 с.

.        Федосов В.П. Радиотехнические цепи и сигналы. Радиотехнические цепи и сигналы: учеб. пособие для самостоятельного изучения / ТРТУ, Каф. ТОР. - Таганрог: Изд-во ТРТУ, 2004. - 207 с.