Наивыгоднейшее распределение нагрузки потребителей в энергосистеме

Наивыгоднейшее распределение нагрузки потребителей в энергосистеме

Курсовая работа

Наивыгоднейшее распределение нагрузки потребителей в энергосистеме

Содержание

1. Постановка задачи

. Определение характеристики относительного прироста расхода топлива конденсационной тепловой электростанции

. Оптимальное распределение нагрузки между агрегатами тепловой электростанции

. Оптимальное распределение активной нагрузки между блоками КЭС с учётом стоимости топлива

. Определение графика электрической нагрузки потребителей ЭЭС

. Оптимальное распределение нагрузки в энергосистеме с ТЭС и ГЭС без учёта потерь активной мощности

. Оптимальное распределение нагрузки в энергосистеме с ТЭС и ГЭС с учётом потерь активной мощности в электрической сети

. Оптимальное распределение реактивной нагрузки потребителей между ГЭС и ТЭС

. Анализ планируемого электрического режима ЭЭС

Заключение

Литература

1. Постановка задачи

Рассмотрим основные положения задачи оптимизации смешанной энергосистемы, состоящей из двух конденсационных электростанций (КЭС-1, 2), одной гидроэлектростанции (ГЭС) и четырех подстанций потребителей электроэнергии, связанных воздушными линиями (ВЛ) 110 кВ (рис. 1). Требуется определить оптимальное распределение электрической нагрузки потребителей по условию минимума затрат на производство электроэнергии на электрических станций.

Для КЭС-1 задан состав работающих блоков, состоящий из разных типов. Для каждого типа известны основные технико-экономические характеристики парогенераторов и турбогенераторов. В составе КЭС-2 работают четыре блока по 25 МВт, которые определяют заданную для электростанции характеристику относительного прироста (ХОП) расхода топлива.

Рис. 1. Электроэнергетическая система.

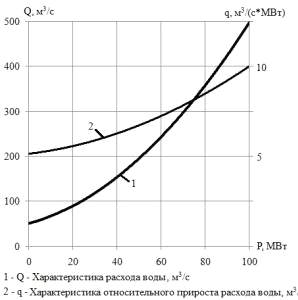Рис. 2 Характеристики расхода воды и относительного прироста расхода воды.

На ГЭС включены в работу два гидроагрегата с рабочей мощностью по 50 МВт. Среднесуточный расход воды для ГЭС составляет Qср=275 м3/с, а минимальный - Qmin=90 м3/с. Характеристики расхода воды и относительного прироста расхода воды для ГЭС приведены на рис. Исходные данные по КЭС-1, 2, электрическим нагрузкам потребителей, суммарной нагрузки энергосистемы и длинам ВЛ 110 кВ приведены в таблицах 1.-5.

Таблица 1. Характеристики блоков КЭС-1.

Блок	N	q1, Гкал/МВт	P0, МВт	q2, Гкал/МВт	Qxx, Гкал	Тип ПГ
К-50	1	2, 2	45	2, 3	11	ТП-70
К-100	2	1, 9	85	2, 4	18	ТП-80

Таблица 2 Характеристики КЭС-

P, МВт	55	82	82	100
ε, тут/МВт·ч	0, 28	0, 34	0, 36	0, 42

Таблица 3. КПД парогенераторов.

ТП-70	Q, Гкал	60	70	80	90	100	110	120
	КПД (N-2)	85, 1	85, 3	85, 6	85, 8	85, 9	86	85, 8
ТП-80	Q, Гкал	100	120	140	160	180	200	220
	КПД (N-2)	85, 4	85, 8	86, 1	86, 3	86, 4	86, 3	86, 1

Таблица 4. График нагрузки от Рм (Pм=380 МВт).

t	α	1	2	3	4	5	6
Pн1, %	0, 5	58	65	90	90	100	70
Pн2, %	0, 15	65	70	92	93	100	75
Pн3, %	0, 15	50	60	100	85	90	85
Pн4, %	0, 2	55	68	100	85	95	85

Таблица 5. Длины ЛЭП.

Длины ЛЭП, км	L1	L2	L3	L4	L5	L6	L7	L8	L9
	30	53	-	28	42	45	38	40	32

Для определения оптимальных режимов работы КЭС-1, 2 и ГЭС необходимо решить следующие задачи:

.        Для КЭС-1 построить характеристики относительных приростов расхода топлива для каждого типа блоков, затем графическим методом построить характеристику относительного прироста электростанции в целом и составить диспетчерскую график нагрузки.

Определить оптимальное распределение активной нагрузки между блоками КЭС-1 при работе первого и второго блока на природном газе и мазуте, имеющих разные цены.

.        Построить суточные графики активной нагрузки отдельных подстанций и суммарный суточный график потребления электроэнергии.

.        Для энергосистемы графическим методом найти оптимальное распределение суточного графика активной нагрузки между электростанциями без учета потерь активной мощности в сети, обеспечив заданный средний расход воды на ГЭС с точностью не менее 5 процентов.

.        Найти оптимальное распределение активной нагрузки между электрическими станциями с учетом потерь активной мощности в электрической сети. Для ГЭС проверить заданный суточный расход воды по результатам оптимального распределения.

.        Для наибольших нагрузок провести расчет электрического режима в программном пакете «Космос» при найденных оптимальных активных мощностях электростанций и выбранной реактивной нагрузке их. Затем найти оптимальное распределение реактивных нагрузок между электростанциями. Результаты представить в виде диспетчерских графиков. При расчетах электрических режимов принять в качестве балансирующего узла шины высокого напряжения ГЭС.

Далее показан ход решения вышеуказанных задач с применением программных пакетов MathCad и КОСМОС.

2. Определение характеристики относительного прироста расхода топлива конденсационной тепловой электростанции

Критерием оптимального распределения активной мощности, которую должна вырабатывать конденсационная тепловая электростанция (КЭС) за час в соответствии с диспетчерским графиком, является минимальный расход топлива. Условием оптимального распределения нагрузки между блоками электростанций является равенство относительных приростов расхода топлива для всех параллельно работающих блоков. При распределении нагрузки в энергосистеме используются аналогичные характеристики электростанций (ЭС).

Расчет характеристики относительного прироста (ХОП) расхода топлива ЭС начинают с определения характеристик всех установленных и включенных в работу блоков. ХОП блока определяется текущим техническим состоянием основного оборудования блока, парогенератора и турбогенератора. Основой для построения являются нормативные характеристики этого оборудования. Для каждого типа блоков задаются характеристики К.П.Д. парогенератора от его тепловой нагрузки и расходные характеристики турбогенератора. ХОП блока брутто строится по точкам в рабочем диапазоне нагрузки блока. Минимальная мощность определяется парогенератором, который не допускает глубокой разгрузки из-за возможного погасания факела, останова и последующей растопки котла. Максимальная мощность ограничивается номинальными параметрами оборудования.

При определении характеристик для парогенератора используется зависимость К.П.Д. от часовой производительности, определяемой в тоннах свежего пара или в Гкал. Для турбогенератора используется типовая характеристика расхода тепла, состоящая из двух отрезков прямых с возрастанием наклона при мощности Р0.

Характеристика описывается формулой (1) с использованием δ-функции, равной нулю при P ≤ P0 и 1 при P > P0,

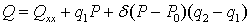, (1)

где: Р - мощность блока в МВт, - расход тепла в Гкал, - расход холостого хода, , q2 - относительные приросты расхода тепла на участках характеристики.

Расчёт ХОП блока начинают с построения характеристики относительного прироста εк(Q) парогенератора методом обратного баланса. В соответствии с методом для каждой произвольно выбираемой точки Qi заданной характеристики котла находят значение 0 и определяют потери тепла в Гкал

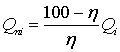.(2)

По найденным точкам строится график в виде плавной кривой и методом конечных приращений в каждой точке определяется производная в относительных единицах

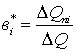.(3)

Относительный прирост для котла в именованных единицах т.у.т./Гкал определяется по формуле

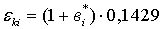.(4)

Все расчётные данные рекомендуется оформить в виде таблицы, столбцы которой соответствуют параметрам Qi, ηi, Qпi, вi*, εкi, а строки разным значениям выработки тепла Q. Полученные расчётом точки εкi для парогенераторов ТП-70 и ТП-80 сведём соответственно в таблицы 6 и 7 и построим зависимости εк(Q) (рис. 3, 4.):

Таблица 6. Относительный прирост расхода топлива для ТП-70.

Qi, Гкал	h, %	Qп, Гкал	ΔQп, Гкал	в*, о.е.	εк, т.у.т/Гкал
60	84, 5	11	-	-	-
70	84, 8	12, 547	1, 547	0, 155	0, 1651
80	85, 1	14	1, 46	0, 146	0, 1638
90	85, 3	15, 51	1, 51	0, 151	0, 1645
100	85, 4	17, 096	1, 586	0, 1586	0, 1656
110	85, 2	19, 12	2, 024	0, 2024	0, 1718
120	85	21, 17	2, 05	0, 205	0, 1722

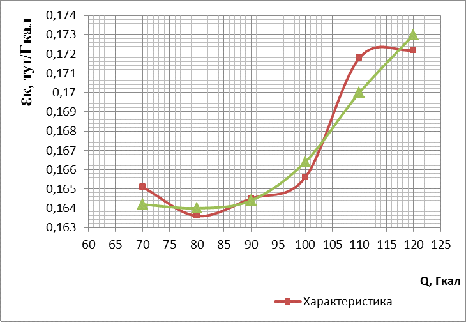
Рис. 3. Характеристика относительного прироста расхода топлива для ТП-70.

Рабочий диапазон мощности блока снизу ограничивается минимальной загрузкой котла Q1 и в соответствии с расходной характеристикой ТГ определяется по формуле

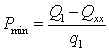.(5)

Таблица 7. Относительный прирост расхода топлива для ТП-80.

Qi, Гкалh, %Qп, ГкалΔQп, Гкалв*, о.е.εк, т.у.т/Гкал
100	85, 4	17, 096	-	-	-
120	85, 8	19, 86	2, 764	0, 1382	0, 16265
140	86, 1	26	2, 74	0, 137	0, 16248
160	86, 3	25, 4	2, 8	0, 14	0, 163
180	86, 4	28, 333	2, 933	0, 147	0, 164
200	86, 3	31, 75	3, 417	0, 171	0, 167
220	86, 1	35, 517	3, 768	0, 1884	0, 17

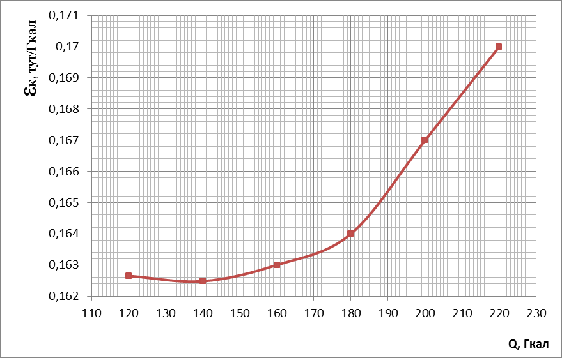
Рис. 4. Характеристика относительного прироста расхода топлива для ТП-80.

В связи с этим рекомендуется следующий алгоритм расчёта характеристики относительного прироста εк(P) блока электростанции.

. Намечаются несколько точек Pi в диапазоне Pmin, …, Pн с обязательным включением точки P0.

Для каждой точки определяется относительный прирост qт турбогенератора, равный q1 или q В точке P0 принимаются оба значения, что и определяет разрыв в характеристике блока при этой мощности.

. Определяется расход тепла на ТГ по формуле (1).

. По характеристике котла εк(P) для найденного расхода тепла определяют прирост εкi.

. Относительный прирост блока т.у.т./(МВт×ч) определяется как произведение соответствующих приростов котла и турбогенератора

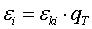(6)

Результаты расчёта сведём в таблицы 8 и 9 для блоков К-50 и К-100 соответственно. Полученную характеристику относительного прироста блока представим в виде графика, дополнив её вертикальными участками на границах рабочего диапазона (рис. 5). В таком виде она будет использована в дальнейшем при графическом распределении нагрузки.

Таблица 8. Относительный прирост блока К-50.

Р, МВт	q, Гкал/МВт	Q, Гкал	εк, тут/Гкал	εбл, тут/МВт×ч
25	2, 2	66	0, 1642	0, 36124
30	2, 2	77	0, 164	0, 361
35	2, 2	88	0, 1643	0, 3615
40	2, 2	99	0, 1667	0, 3652
45	2, 2	110	0, 17	0, 374
45	2, 3	110	0, 17	0, 391
50	2, 3	121, 5	0, 1732	0, 39836

Таблица 9. Относительный прирост блока К-100.

Р,	q,	Q,	εк,	εбл,
МВт	Гкал/МВт	Гкал	т.у.т./Гкал	т.у.т./ МВт*ч
55	1, 9	122, 5	0, 1626	0, 30894
60	1, 9	132	0, 1625	0, 30875
65	1, 9	141, 5	0, 1626	0, 30894
70	1, 9	151	0, 1628	0, 30932	1, 9	160, 5	0, 163	0, 3097
80	1, 9	170	01634	0, 31
85	1, 9	179, 5	0, 164	0, 3116
85	2, 4	179, 5	0, 164	0, 3936
90	2, 4	191, 5	0, 1656	0, 39744
95	2, 4	203, 5	0, 1676	0, 40224
100	2, 4	215, 5	0, 1694	0, 40656

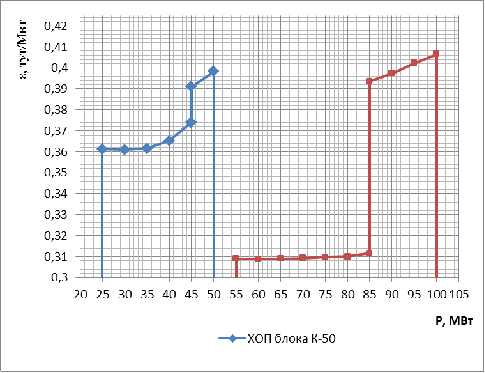
Рис. 5. Характеристики относительного прироста блоков КЭС-1.

3. Оптимальное распределение нагрузки между агрегатами тепловой электростанции

Характеристика относительного прироста КЭС строится при условии оптимального распределения мощности между блоками ЭС. Критерием оптимального распределения является минимум расхода топлива при работе всех блоков на одинаковом топливе или минимум затрат при работе их на топливе с разной стоимостью. Условием оптимального распределения активной мощности между блоками ЭС является равенство их относительных приростов:

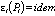(7)

Оптимальную нагрузку блоков можно найти графическим методом. Для этого необходимо построить ХОП блоков в одинаковом масштабе по оси приростов, затем для разных значений одинакового для всех блоков прироста по характеристикам найти нагрузку каждого типа блоков и общую нагрузку КЭС путем суммирования найденных мощностей с учетом числа блоков каждого типа. Для характеристик с линейными участками достаточно провести суммирование только для тех значений приростов, при которых меняется наклон участков. Полученные таким образом точки образуют ХОП электростанции (рис. 6).

Оптимальное распределение общей нагрузки Р0 находят обратным ходом: на оси мощности КЭС откладывается величина Р0, определяется соответствующий ей прирост, и для этого одинакового для всех блоков значения по ХОП блоков находят мощность каждого. Результаты распределения представляются в виде диспетчерской таблицы (таблица 10), которая помогает дежурному инженеру станции обеспечивать выполнение диспетчерского графика при минимальных расходах топлива. Диспетчерские таблицы строятся для разных составов включенных в работу блоков. В них для разных значений общей нагрузки Р0 в рабочем диапазоне для заданного состава указывается оптимальная мощность каждого блока.

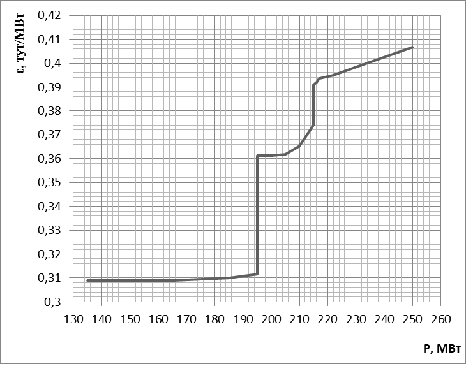
Рис. 6. Характеристика относительного прироста топлива КЭС-1.

Таблица 10. Диспетчерская таблица.

Р0, МВт	Блоки			Прирост, т у.т./МВт.ч
	РК-50, МВт	РК-100, МВт	РК-100, МВт
135	25	55	55	0, 3089
140	25	57, 5	57, 5	0, 30887
150	25	62, 5	62, 5	0, 30889
160	25	67, 5	67, 5	0, 30892
170	25	72, 5	72, 5	0, 30894
180	25	77, 5	77, 5	0, 30966
190	25	82, 5	82, 5	0, 3108
200	30	85	85	0, 3612
210	40	85	85	0, 3652
220	47	86, 5	86, 5	0, 3941
230	50	90	90	0, 39836
240	50	95	95	0, 4031
250	50	100	100	0, 40656

4. Оптимальное распределение активной нагрузки между блоками КЭС с учётом стоимости топлива

При работе блоков на разном топливе, имеющем цены с1 и с2 в руб/т.у.т., критерием оптимального распределения является минимум затрат на топливо при выполнении условия баланса мощности. Условием оптимальности в этом случае также, как и при минимизации расхода топлива, является равенство относительных приростов затрат, измеряемых в руб/МВт×ч,

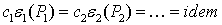.(8)

Рассмотрим случай, когда блок К-50 работает на газе, а блок К-100 на мазуте, с1=1000 руб/м3 и с2=5000 руб/м3. Учитывая, что коэффициенты приведения к условному топливу для газа и мазута соответственно составляют 1, 15 и 1, 37 получим сК-50=869, 57 руб/т.у.т., сК-150=3649, 64 руб/т.у.т. В этом случае оптимальное распределение нагрузки КЭС между блоками и построение диспетчерской таблицы выполняется аналогично, но ХОП расхода топлива должны быть построены в ценовых единицах по оси ординат в одинаковом масштабе. Результаты расчетов для блоков К-50 и К-100 сведём соответственно в таблицы 11 и 1 ХОП затрат блоков К-50, К-100 и КЭС-1 приведены на рис. 7. и 8.

Таблица 11. Относительный прирост для блока К-50.

Р,  МВт	q, Гкал/МВт	Q, Гкал	εк, т.у.т./Гкал	εбл,  т.у.т./ МВт*ч	εбл,  руб/ МВт*ч
25	2, 2	66	0, 1642	0, 36124	314, 12
30	2, 2	77	0, 164	0, 361	313, 9
35	2, 2	88	0, 1643	0, 3615	314, 35
40	2, 2	99	0, 1667	0, 3652	317, 57
45	2, 2	110	0, 17	0, 374	325, 22
45	2, 3	110	0, 17	0, 391	340
50	2, 3	121, 5	0, 1732	0, 39836	346, 4

Таблица 12. Относительный прирост для блока К-100.

Р,  МВт	q, Гкал/МВт	Q, Гкал	εк, т.у.т./Гкал	εбл,  т.у.т./ МВт*ч	εбл,  руб/ МВт*ч
55	1, 9	122, 5	0, 1626	0, 30894	1127, 52
60	1, 9	132	0, 1625	0, 30875	1126, 83
65	1, 9	141, 5	0, 1626	0, 30894	1127, 52
70	1, 9	151	0, 1628	0, 30932	1128, 91
75	1, 9	160, 5	0, 163	0, 3097	1130, 29
80	1, 9	170	01634	0, 31	1131, 39
85	1, 9	179, 5	0, 164	0, 3116	1137, 23
85	2, 4	179, 5	0, 164	0, 3936	1436, 5
90	2, 4	191, 5	0, 1656	0, 39744	1450, 513
95	2, 4	203, 5	0, 1676	0, 40224	1468
100	2, 4	215, 5	0, 1694	0, 40656	1483, 8

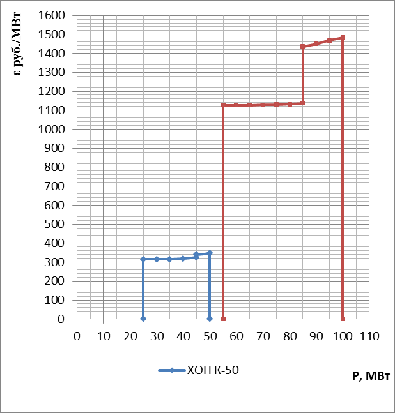
Рис. 7. ХОП затрат блоков с учетом работы на разном виде топлива и различной ценой.

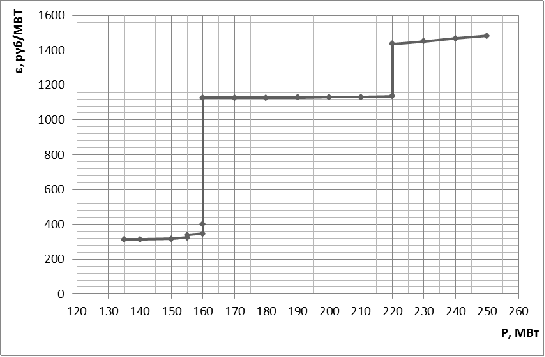
Рис. 8. ХОП затрат КЭС-1 с учетом работы на разном виде топлива.

Диспетчерская таблица 13, построенная по минимуму затрат на топливо, будет отличаться от таб. 10.

Таблица 13. Диспетчерская таблица с учетом стоимости топлива.

Рн, МВт	Блоки			Прирост, руб./МВт.ч
	РК-50, МВт	РК-100, МВт	РК-100, МВт
135	30	55	55	314
140	40	55	55	317, 6
150	50	55	55	346, 4
160	50	60	60	1127
170	50	65	65	1127
180	50	70	70	1129
190	50	75	75	1130
200	50	80	80	1131, 4
210	50	85	85	1137
220	50	90	90	1450, 5
230	50	95	95	1468
240	50	100	100	1483
250	30	55	55	314

Неучёт стоимости топлива при распределении нагрузки между блоками может привести к значительному перерасходу денежных средств и, как следствие, к повышению себестоимости вырабатываемой электроэнергии. Далее необходимо оценить суточный перерасход денежных средств в том случае, когда оптимальные мощности блоков, работающих на разном топливе, определены по условию равенства относительных приростов расхода топлива, т.е. без учета цены топлива. Для определения перерасхода можно использовать тот факт, что относительный прирост является производной расхода или затрат на топливо

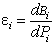, (9)

и поэтому, любое приращение функции при изменении аргумента от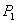 до 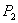 определяется, как определённый интеграл,

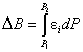.(10)

Интеграл, равный площади фигуры, можно приближённо определить как площадь трапеции (рис. 9).

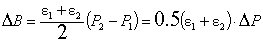.(11)

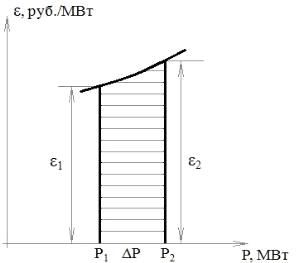
Рис. 9. Графическое пояснение определения перерасхода средств.

Оценим перерасход денежных средств для случая, когда оптимальные мощности блоков, работающих на разном топливе, определены по условию равенства относительных приростов расхода топлива, т.е. без учёта цены топлива. Суточная нагрузка станции рассчитана далее в разделе «Оптимальное распределение нагрузки без учёта потерь». Определим нагрузки блоков по условию равенства относительных приростов расхода топлива без учёта цены и с учётом цены. Полученные значения сведём в таблицу 14.

Таблица 14 Диспетчерская таблица с учетом и без учета стоимости топлива

t, ч	P КЭС-1, МВт	P, МВт (без учета стоимости топлива)			P, МВт (с учетом стоимости топлива)
		К-50	К-50	К-100	К-50	К-50	К-100
0..4	135	25	55	55	25	55	55
4..8	135	25	55	25	55	55
8..12	195	25	85	85	50	72, 5	72, 5
1.16	180	25	77, 5	77, 5	50	65	65
16..20	206	35	85, 5	85, 5	50	78	78
20..24	188	50	69	69	50	69	69

Перерасход средств в каждом 4-х часовом интервале определим как разность перерасхода за счёт перегруза блока К-100 и снижения расхода за счёт недогруза блока К-50 при распределении нагрузки без учёта стоимости. Просуммировав перерасход по всем периодам, получим искомое значение перерасхода денежных средств за сутки, равное 58109 рублей и 40 копеек.

. Определение графика электрической нагрузки потребителей ЭЭС

Суточный график электрической нагрузки потребителей ЭЭС условно делится на три характерные зоны (рис. 10): базисную - 1, лежащую ниже линии минимальной нагрузки; полупиковую - 2, расположенную между линиями минимальной и среднесуточной нагрузок; пиковую - 3, лежащую выше линии средней нагрузки.

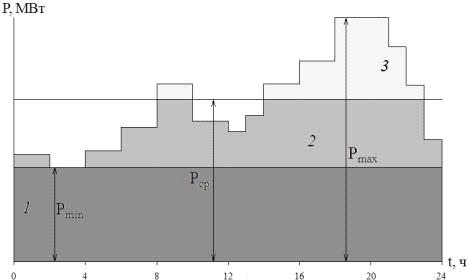
Рис. 10. Пример суточного графика электрической нагрузки потребителей.

Исходной информацией (таб. 15) для построения суточного графика электрической нагрузки потребителей ЭЭС является сумма типовых графиков нагрузок 4-х узлов (подстанций) ЭЭС. В примере максимальная активная нагрузка потребителей составляет Рм=380 МВт. Максимальная электрическая нагрузка каждого потребителя определяется долевым коэффициентом α, который задается преподавателем. По умолчанию эти коэффициенты можно принять равными 0.5, 0.15, 0.15 и 0.

Таблица 15. Суточный график электрической нагрузки потребителей.

t, ч	Нагрузка 1		Нагрузка 2		Нагрузка 3		Нагрузка 4		Общая нагрузка ЭЭС, МВт
	№ гр	Pmax	№ гр	Pmax	№ гр	Pmax	№ гр	Pmax
	2	190	3	57	4	57	5	76
	P1, %	P1, МВт	P2, %	P2, МВт	P3, %	P3, МВт	P4, %	P4, МВт
0..4	58	110, 2	65	37, 05	58	33, 06	65	49, 4	229, 71
4..8	65	123, 5	73	41, 61	65	37, 05	70	53, 2	255, 36
8..12	95	180, 5	100	57	90	51, 3	92	69, 32	358, 12
1.16	75	142, 5	85	48, 45	90	51, 3	93	70, 68	312, 93
16..20	100	190	50	51, 3	100	57	100	76	374, 3
20..24	80	152	85	48, 45	70	39, 9	75	57	297, 35

Суточный график электрической нагрузки характеризуется следующими показателями (рис. 11):

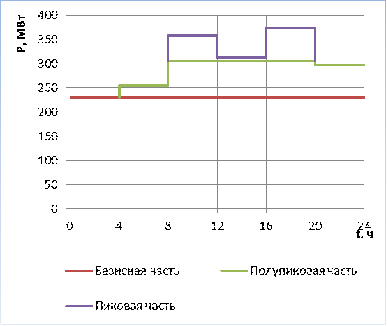
Рис. 11. График электрической нагрузки энергосистемы.

максимальная активная нагрузка ;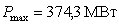

минимальная нагрузка ;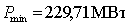

среднесуточная нагрузка ;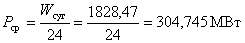

где 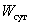 - суточное потребление электроэнергии;

коэффициент неравномерности графика ;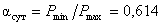

плотность графика нагрузки .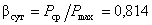

. Оптимальное распределение нагрузки в энергосистеме с ТЭС и ГЭС без учёта потерь активной мощности

В рассматриваемой ЭЭС параллельно с ТЭС работает ГЭС, водохранилище которой позволяет обеспечивать суточный цикл регулирования с заданным среднесуточным расходом воды Q0=275 м3/с и обязательным санитарным пропуском Qmin=90 м3/с.

Критерием оптимизации в смешанной ЭЭС является минимум расхода топлива на ТЭС за цикл регулирования (сутки) при использовании заданного среднесуточного расхода воды на ГЭС Qср. Условием оптимального распределения активной нагрузки в смешанной ЭЭС без учета потерь активной мощности в электрической сети является равенство ХОП энергоносителей, которое должно соблюдаться для каждой ступени t графика нагрузки внутри цикла регулирования,

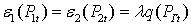, (12)

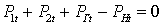, (13)

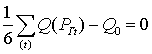. (14)

где:Q(Pг) - расчетный расход воды на ГЭС, q(Pг) - удельный прирост расхода воды, λ - удельная экономия.

Оптимизация проводится методом последовательных приближений путем подбора для ГЭС такой удельной экономии λ, при которой соблюдается условие баланса по воде. В качестве исходного приближения λ0 принимается такое значение, при котором скорректированная ХОП ГЭС qλ0 попадает в диапазон изменения ХОП ε(P) КЭС-1 и КЭС-2 (рис. 12).

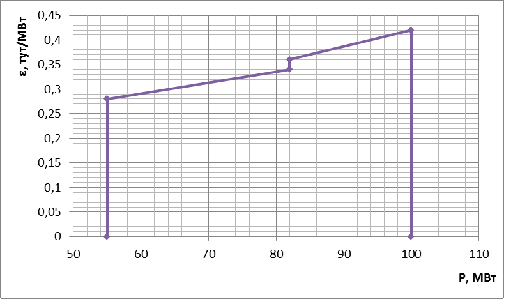
Рис. 1 Характеристика относительного прироста КЭС-

Минимальная нагрузка ГЭС определяется по расходной характеристике (рис. 13) и заданному санитарному пропуску Qmin.

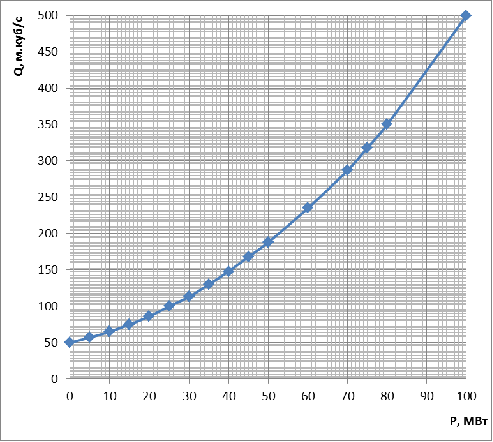
Рис. 13. Характеристика расхода воды на ГЭС.

В качестве исходного приближения принимаем значение 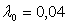т.у.т.*с/м3, при котором скорректированная ХОП 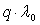 ГЭС (рис. 14) попадает в диапазон изменения ХОП ε(P) КЭС-1 и КЭС-2 (табл. 16).

Таблица 16. Корректировка характеристики ГЭС.

Р, МВт	0	20	40	60	80	100
q, м3/с·МВт	5, 1	5, 75	6, 4	7, 2	8, 3	10
0, 20400, 2240, 2520, 2920, 340, 4000

Оптимальное распределение нагрузки между ЭС найдём графическим методом. Для этого построим характеристики КЭС-1, КЭС-2 и ГЭС в одинаковом масштабе по оси ХОП.

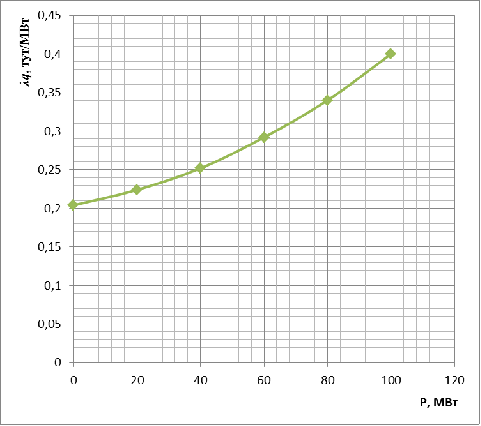
Рис. 14. Скорректированная ХОП ГЭС.

Затем принимая одинаковое значение относительного прироста для каждой ЭС, определяем активную мощность ЭЭС, как сумму активных мощностей ЭС. В результате получим ХОП ЭЭС (рис. 15). По известному графику электрической нагрузки потребителей и полученным ХОП ЭЭС, КЭС-1, КЭС-2, ГЭС определим активную мощность каждой электростанции в течение суток. По мощности ГЭС и расходной характеристике Q(Рг) определяют расход воды Qt и заполним таблицу 17. Затем рассчитывают средний расход воды за сутки Qср=1/6٠Qt, который сравнивают с заданным Q0. Если разность полученного среднего расхода и заданного находится в пределах 5 %, то расчёт можно закончить.

Òàáëèöà 17 Ñóòî÷íàÿ çàãðóçêà ÃÝÑ.

Óäåëüíàÿ ýêîíîìèÿ	Ð, ÌÂò Q, ì3/ñ	Ñòóïåíè ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè						Qñð, ì3/ñ	Qñð - Q0, ì3/ñ
		1	2	3	4	5	6
	Ð	39, 71	60, 46	81, 72	64, 93	85, 3	45, 35
	Q	150	245	370	260	375	200	266, 67	8, 33

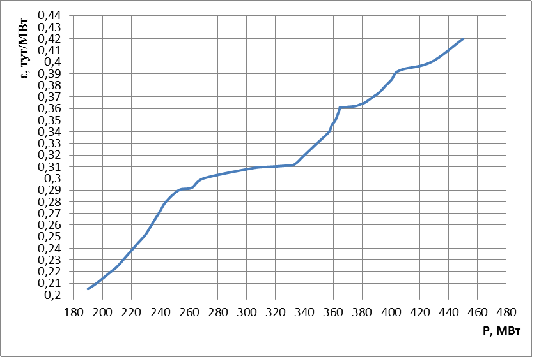
Ðèñ. 15. Õàðàêòåðèñòèêà îòíîñèòåëüíîãî ïðèðîñòà ÝÝÑ.

 ïðîòèâíîì ñëó÷àå ïðèíèìàåòñÿ íîâîå ïðèáëèæåíèå λ0 è ðàñ÷¸ò ïîâòîðÿåòñÿ. Ñóòî÷íûé ïåðåðàñõîä âîäû ñîñòàâëÿåò 17, 372 ì3/ñ, ÷òî ñîñòàâëÿåò 3, 03% îò çàäàííîãî çíà÷åíèÿ â 275 ì3/ñ è óäîâëåòâîðÿåò ïÿòèïðîöåíòíîìó ïîðîãó. Êðîìå òîãî, íà êàæäîì èíòåðâàëå ãðàôèêà çàãðóçêè ÃÝÑ ñîáëþäàåòñÿ óñëîâèå ñàíèòàðíîãî ïðîïóñêà âîäû â ðàçìåðå 90 ì3/ñ. Îêîí÷àòåëüíîå ðàñïðåäåëåíèå ìîùíîñòè ìåæäó ýëåêòðè÷åñêèìè ñòàíöèÿìè áóäåò ñëåäóþùèì (òàáë. 18):

Òàáëèöà 18. Ðàñïðåäåëåíèå íàãðóçêè ìåæäó ýëåêòðè÷åñêèìè ñòàíöèÿìè.

t	Ðí, ÌÂò	ÐÊÝÑ-1, ÌÂò	ÐÊÝÑ-2, ÌÂò	ÐÃÝÑ, ÌÂò	QÃÝÑ, ì3/ñ
1	229, 71	135	55	39, 71	150
2	255, 46	135	60	60, 46	245
3	358, 72	195	82	81, 72	370
4	312, 93	180	68	64, 93	260
5	374, 3	206	88	85, 3	375
6	297, 35	188	64	45, 35	200

. Îïòèìàëüíîå ðàñïðåäåëåíèå íàãðóçêè â ýíåðãîñèñòåìå ñ ÒÝÑ è ÃÝÑ ñ ó÷¸òîì ïîòåðü àêòèâíîé ìîùíîñòè â ýëåêòðè÷åñêîé ñåòè.

Êðèòåðèé îïòèìàëüíîãî ýëåêòðè÷åñêîãî ðåæèìà ñ ó÷åòîì ïîòåðü àêòèâíîé ìîùíîñòè â ýëåìåíòàõ ýëåêòðè÷åñêîé ñåòè èìååò âèä:

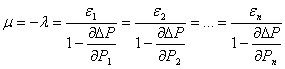.(15)

Êîýôôèöèåíò μ íàçûâàþò óäåëüíûì ïðèðîñòîì çàòðàò ñèñòåìû, ïîñêîëüêó îí ó÷èòûâàåò âëèÿíèå ïîòåðü àêòèâíîé ìîùíîñòè â ýëåêòðè÷åñêîé ñåòè íà ðàñõîä òîïëèâà íà ÊÝÑ-1, ÊÝÑ- Ïðîèçâîäíàÿ 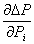 ïðåäñòàâëÿåò ñîáîé îòíîñèòåëüíûé ïðèðîñò ïîòåðü àêòèâíîé ìîùíîñòè. Ðåøàÿ ñèñòåìó óðàâíåíèé (15) ñîâìåñòíî ñ (13) è (14) ÷èñëåííûì ñïîñîáîì îïðåäåëÿþòñÿ îïòèìàëüíûé ýëåêòðè÷åñêèé ðåæèì ÝÝÑ.

Äèôôåðåíöèðóÿ ôîðìóëó ïîòåðü ïî óçëîâûì ìîùíîñòÿì èñòî÷íèêîâ, íàõîäèì îòíîñèòåëüíûé ïðèðîñò ïîòåðü àêòèâíîé ìîùíîñòè. Íàïðèìåð, ïðèðîñò ïîòåðü ïî ìîùíîñòè âòîðîãî óçëà äëÿ ðàññìàòðèâàåìîé ýëåêòðè÷åñêîé ñõåìû ñîñòàâèò

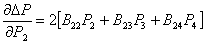.(16)

Ïðè ïîäñòàíîâêå ÷èñëîâûõ çíà÷åíèé óçëîâûõ ìîùíîñòåé ïðèíèìàåì: ìîùíîñòü, âõîäÿùàÿ â óçåë (èñòî÷íèê), - ïîëîæèòåëüíà, ìîùíîñòü, âûõîäÿùàÿ èç óçëà (íàãðóçêè), - îòðèöàòåëüíà. Ïðåäïîëàãàÿ, ÷òî ïîòåðè àêòèâíîé ìîùíîñòè ðàñïàäàþòñÿ íà äâå ñàìîñòîÿòåëüíûå ÷àñòè, îäíà èç êîòîðûõ çàâèñèò òîëüêî îò àêòèâíûõ ìîùíîñòåé óçëîâ, äðóãàÿ - òîëüêî îò ðåàêòèâíûõ ìîùíîñòåé, âû÷èñëÿåì ïåðâóþ ñîñòàâëÿþùóþ ïîòåðü:

=ΔP=B22٠P22+B33٠P32+B44٠P42+B55٠P52+B66٠P62+B77٠P72+ +2(B23٠P2٠P3+B24٠P2٠P4+B25٠P2٠P5+B26٠P2٠P6+B27٠P2٠P7+ +B34٠P4٠P3+B35٠P3٠P5+B36٠P3٠P6+B37٠P3٠P7+B45٠P4٠P5+B46٠P4٠P6+

+ B47٠P4٠P7+B56٠P5٠P6+B57٠P5٠P7+B67٠P6٠P7)(17)

Äàëüíåéøèå ðàñ÷åòû ïðîèçâîäèì ïî ýòîìó àëãîðèòìó â ïðîãðàììíîì êîìïëåêñå MathCAD â ôàéëå «Ïðèðîñò ïîòåðü àêòèâíîé ìîùíîñòè». Ïîòåðè àêòèâíîé ìîùíîñòè ñ÷èòàþòñÿ äëÿ êàæäîãî èç 6 èíòåðâàëîâ âðåìåíè â ñóòêàõ.

Âîñïîëüçîâàâøèñü ìåòîäîì åäèíè÷íûõ òîêîâ, îïðåäåëèì êîýôôèöèåíòû òîêîðàñïðåäåëåíèÿ êàæäîé âåòâè ýëåêòðè÷åñêîé ñõåìû è íàéä¸ì ýëåìåíòû òðåóãîëüíîé ìàòðèöû êîýôôèöèåíòîâ ïîòåðü àêòèâíîé ìîùíîñòè B äëÿ çàäàííîé ÝÝÑ.

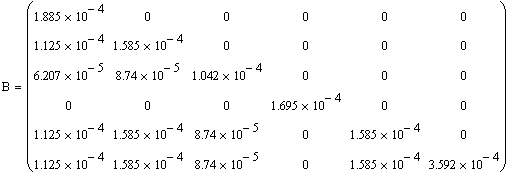
Çíà÷åíèå ïîòåðü àêòèâíîé ìîùíîñòè ΔP â ýëåìåíòàõ ýëåêòðè÷åñêîé ñåòè îïðåäåëÿþòñÿ ôóíêöèåé äâóõ ïåðåìåííûõ f(Pê2, Pê1), àðãóìåíòàìè êîòîðîé ÿâëÿþòñÿ àêòèâíûå ìîùíîñòè Pê2 è Pê1, âûðàáàòûâàåìûå ÊÝÑ-2 è ÊÝÑ-1 ñîîòâåòñòâåííî.

 êà÷åñòâå ïðèìåðà, ïðèâåäåì ðàñ÷¸ò äëÿ ïåðâîãî èíòåðâàëà âðåìåíè ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè, çàäàâøèñü íà÷àëüíûìè ïðèáëèæåíèÿìè, ïðèâåäåííûìè â òàá. 18.

Ââåäåì òåõíè÷åñêèå îãðàíè÷åíèÿ ïî àêòèâíîé ìîùíîñòè äëÿ ÊÝÑ-1 è ÊÝÑ-2:

Îïðåäåëèì ìèíèìóì öåëåâîé ôóíêöèè ñ ó÷åòîì çàäàííûõ îãðàíè÷åíèé äëÿ âñåõ èíòåðâàëîâ ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè ñ èñïîëüçîâàíèåì ïðîãðàììíîãî êîìïëåêñà MathCAD.  ðåçóëüòàòå ðàñ÷åòîâ ïîëó÷èì îïòèìàëüíîå ðàñïðåäåëåíèå íàãðóçîê ìåæäó ÊÝÑ-1, ÊÝÑ-2 è ÃÝÑ ñ ó÷åòîì ïîòåðü àêòèâíîé ìîùíîñòè (òàáë. 19) è ðàñõîäîì âîäû (òàáë. 20).

Òàáëèöà 19 Îïòèìàëüíîå ðàñïðåäåëåíèå íàãðóçêè ìåæäó ýëåêòðîñòàíöèÿìè

t	Pc, ÌÂò	∆P, ÌÂò	PÊÝÑ-1, ÌÂò	PÊÝÑ-2, ÌÂò	PÃÝÑ, ÌÂò	QÃÝÑ, ì3/ñ
0..4	229, 71	3, 0	135	50	47, 72	175
4..8	255, 46	3, 29	135	50	73, 66	310
8..12	358, 72	6, 61	208, 23	60, 34	96, 15	471
1.16	312, 93	4, 88	170, 35	50	97, 46	477
16..20	374, 3	7, 48	210, 37	74, 67	96, 74	474
20..24	297, 35	4, 20	153, 8	50	97, 68	478

Òàáëèöà 20 Ñóòî÷íûé ðàñõîä âîäû íà ÃÝÑ

Óäåëüíàÿ	Ìîùíîñòü Ðàñõîä	Ñòóïåíè ÃÝÍ						Qñð	Qñð-Qo
ýêîíîìèÿ		1	2	3	4	5	6
0, 04	Ð, ÌÂò	47, 72	73, 66	96, 15	97, 46	96, 74	97, 68
	Q, êóá.ì/ñ	175	310	471	477	474	478	397, 5	122, 5

Ñðåäíåñóòî÷íûé ðàñõîä âîäû íà ÃÝÑ ñîñòàâèë 397, 5 ì3/ñ, ÷òî ïðåâûøàåò çàäàííûé ðàñõîä âîäû 275 ì3/ñ íà 44, 5% è, â äàëüíåéøåì, ìîæåò ïðèâåñòè ê áûñòðîìó ñðàáàòûâàíèþ âîäîõðàíèëèùà. Äëÿ ñíèæåíèÿ ðàñõîäà âîäû íà ÃÝÑ äî çàäàííîé âåëè÷èíû íåîáõîäèìî ðàçãðóçèòü ÃÝÑ â òå÷åíèå íåäåëè, íàïðèìåð â âûõîäíûå äíè. Äðóãèì âîçìîæíûì ðåøåíèåì ðàçãðóçêè ÃÝÑ ÿâëÿåòñÿ óâåëè÷åíèå ïðîïóñêíîé ñïîñîáíîñòè ËÝÏ (L1, L5, L8), ÷òî îáåñïå÷èò ÊÝÑ-2 âûäà÷ó áîëüøåé àêòèâíîé ìîùíîñòè.

Öåëüþ îïòèìèçàöèè ðàñïðåäåëåíèÿ ðåàêòèâíûõ íàãðóçîê ïîòðåáèòåëåé ÿâëÿåòñÿ ìèíèìèçàöèÿ ïîòåðü àêòèâíîé ìîùíîñòè â ýëåêòðè÷åñêèõ ñåòÿõ. Îïðåäåëèì îïòèìàëüíîå ðàñïðåäåëåíèå ðåàêòèâíûõ íàãðóçîê ìåæäó ÝÑ ñ èñïîëüçîâàíèåì ïðîãðàììíîãî ïàêåòà MathCAD.

Ïðèíÿâ îáîáù¸ííûé êîýôôèöèåíò àêòèâíîé ìîùíîñòè äëÿ êàæäîãî ïîòðåáèòåëÿ ðàâíûì 0, 85, îïðåäåëèì çíà÷åíèÿ ðåàêòèâíûõ íàãðóçîê íà ñóòî÷íîì èíòåðâàëå (òàáë. 21). Ïðè íàéäåííîé ðàíåå àêòèâíîé çàãðóçêå ãåíåðàòîðû ÝÑ ìîãóò èìåòü ðàñïîëàãàåìóþ ðåàêòèâíóþ ìîùíîñòü, êîòîðàÿ ìåíüøå ïîòðåáíîé, ïîýòîìó íåîáõîäèìî ïðîâåðèòü, äåôèöèòíà ëè ÝÝÑ ïî ðåàêòèâíîé ìîùíîñòè.

Òàáëèöà 21 Ðåàêòèâíàÿ íàãðóçêà ïîòðåáèòåëåé ýíåðãîñèñòåìû

t, ÷	Íàãðóçêà 1		Íàãðóçêà 2		Íàãðóçêà 3		Íàãðóçêà 4		Îáùàÿ íàãðóçêà ñèñòåìû, ÌÂÀð
	¹ ãð	Qmax	¹ ãð	Qmax	¹ ãð	Qmax	¹ ãð	Qmax
	1	117, 75	2	35, 33	4	35, 33	4	47, 1
	Q1, %	Q1, ÌÂÀð	Q2, %	Q2, ÌÂÀð	Q3, %	Q3, ÌÂÀð	Q4, %	Q4, ÌÂÀð
0..4	58	68, 3	65	22, 96	58	20, 49	65	30, 615	142, 365
4..8	65	76, 54	73	25, 79	65	22, 96	70	32, 97	158, 26
8..12	95	111, 86	100	35, 33	90	31, 8	92	43, 332	222, 232
1.16	75	88, 31	85	30, 03	90	31, 8	93	43, 803	193, 943
16..20	100	117, 75	50	31, 79	100	35, 33	100	47, 1	231, 97
20..24	80	94, 2	85	30, 03	70	24, 731	75	35, 325	159, 061

Äëÿ ïåðâîãî èíòåðâàëà ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè:

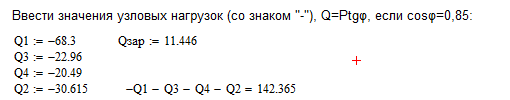
Âû÷èñëèì ìèíèìóì öåëåâîé ôóíêöèè çàòðàò:

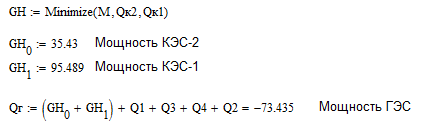
Òàêèì îáðàçîì, ðåàêòèâíàÿ ìîùíîñòü, âûðàáàòûâàåìàÿ íà ÃÝÑ ñîñòàâëÿåò 11, 446 ÌÂàð. Àíàëîãè÷íî âûïîëíÿþòñÿ ðàñ÷åòû äëÿ îñòàëüíûõ èíòåðâàëîâ ãðàôèêà íàãðóçêè. Ðåçóëüòàòû îïòèìèçàöèè ðåàêòèâíûõ ìîùíîñòåé ñâåäåì â òàáëèöó 22:

Òàáëèöà 22 Áàëàíñ ðåàêòèâíîé ìîùíîñòè â ÝÝÑ

Ðåàêòèâíàÿ ìîùíîñòü	Èíòåðâàëû âðåìåíè ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè
	0..4	4..8	8..12	1.16	16..20	20..24
QÊÝÑ-1, ÌÂÀð	95, 489	107, 29	145	129, 67	145	127
QÊÝÑ-2, ÌÂÀð	35, 43	39, 524	65, 79	52, 83	75, 524	45, 81
QÃÝÑ, ÌÂÀð	11, 446	11, 446	11, 446	11, 446	11, 446	11, 446
Qçàð, ÌÂÀð	11, 446
Qí, ÌÂÀð	142, 365	211, 996	222, 322	193, 943	231, 97	196, 061

Çíà÷åíèå ðåàêòèâíîé ìîùíîñòü òóðáîãåíåðàòîðîâ è ãèäðîãåíåðàòîðîâ áóäåì îïðåäåëÿòü ïî ñòàíäàðòíîé äèàãðàììå ðàñïîëàãàåìîé ìîùíîñòè (ðèñ. 16).

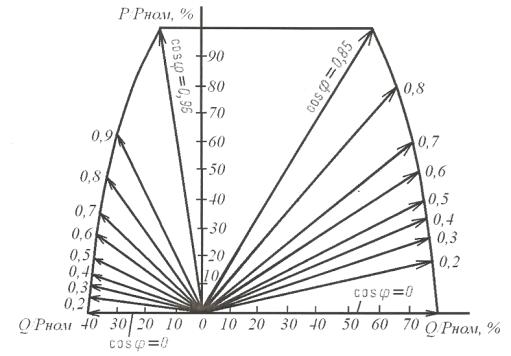
Ðèñ. 16. Äèàãðàììà ðàñïîëàãàåìîé ìîùíîñòè ãåíåðàòîðîâ.

Äîïóñòèì, ÷òî ïðè îïòèìàëüíîé àêòèâíîé íàãðóçêå ãåíåðàòîðû ÝÑ âûäàþò ðàñïîëàãàåìóþ ðåàêòèâíóþ ìîùíîñòü. Ðàññ÷èòàåì îòíîñèòåëüíóþ âåëè÷èíó àêòèâíîé ìîùíîñòè ãåíåðàòîðà äëÿ âå÷åðíåãî ìàêñèìóìà ñóòî÷íîãî ãðàôèêà ýëåêòðè÷åñêîé íàãðóçêè (16-20 ÷):

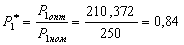
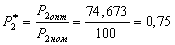
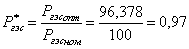
Ïî äèàãðàììå ðàñïîëàãàåìîé ìîùíîñòè ãåíåðàòîðà îïðåäåëÿåì ðàñïîëàãàåìûå ðåàêòèâíûå ìîùíîñòè ÝÑ.

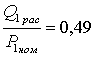
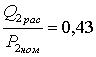
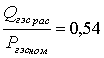
Ðàñïîëàãàåìûå ðåàêòèâíûå ìîùíîñòè ÝÑ:

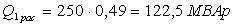
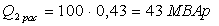
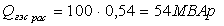
Îïðåäåëèì çàðÿäíóþ ìîùíîñòü âñåõ âîçäóøíûõ ëèíèè:

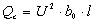
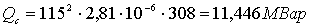
Áàëàíñîâîå óðàâíåíèå ðåàêòèâíîé ìîùíîñòè ïðèìåò âèä:

,

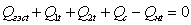ãäå: 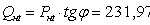ÌÂàð

, 5 +43 + 54 +11, 446 - 231, 97 = -1, 024 ÌÂàð

Îòðèöàòåëüíàÿ âåëè÷èíà ðåàêòèâíîé ìîùíîñòè ñâèäåòåëüñòâóåò î íàëè÷èè íåáîëüøîãî äåôèöèòà ðåàêòèâíîé ìîùíîñòè â ÝÝÑ.  ðàññìàòðèâàåìûé ïåðèîä âðåìåíè äåôèöèò ðåàêòèâíîé ìîùíîñòè ìîæåò áûòü óñòðàíåí ðåãóëèðîâàíèåì òîêà âîçáóæäåíèÿ ãåíåðàòîðîâ ÝÑ. Ïðè áîëüøåì äåôèöèòå ðåàêòèâíîé ìîùíîñòè â ÝÝÑ íåîáõîäèìî ðàññìîòðåòü âîïðîñ î ïðèìåíåíèè äîïîëíèòåëüíûõ èñòî÷íèêîâ ðåàêòèâíîé ìîùíîñòè - áàòàðåé ñòàòè÷åñêèõ êîíäåíñàòîðîâ âûñîêîãî íàïðÿæåíèÿ.  ñëó÷àå çíà÷èòåëüíîãî èçáûòêà ðåàêòèâíîé ìîùíîñòè â ÝÝÑ íåîáõîäèìî ðàññìîòðåòü òåõíè÷åñêèå ìåðîïðèÿòèÿ ïî å¸ êîìïåíñàöèè çà ñ÷åò ïðèìåíåíèÿ ñèíõðîííûõ êîìïåíñàòîðîâ è øóíòèðóþùèõ ðåàêòîðîâ â ìàãèñòðàëüíûõ ýëåêòðè÷åñêèõ ñåòÿõ îáúåäèíåííîé ÝÝÑ.

. Àíàëèç ïëàíèðóåìîãî ýëåêòðè÷åñêîãî ðåæèìà ÝÝÑ

Äëÿ àíàëèçà íàéäåííîãî îïòèìàëüíîãî ðåæèìà â ÷àñû íàèáîëüøèõ è íàèìåíüøèõ íàãðóçîê èñïîëüçóåì ïðîãðàììó ÊÎÑÌÎÑ.  êà÷åñòâå èñõîäíûõ äàííûõ äëÿ ðàñ÷åòà ðåæèìà ïî ïðîãðàììå èñïîëüçóåì ñîïðîòèâëåíèÿ R è X âñåõ âåòâåé, à òàêæå óçëîâûå ìîùíîñòè P è Q. Äëÿ ïîòðåáèòåëåé îíè îïðåäåëÿþòñÿ ïî ñóòî÷íûì ãðàôèêàì àêòèâíîé íàãðóçêè è çàäàííîìó tg φ. Àêòèâíûå è ðåàêòèâíûå ìîùíîñòè ÝÑ îïðåäåëÿþòñÿ ïî ðåçóëüòàòàì, ïðèâåäåííûì â òàá. 19 è 22  êà÷åñòâå áàëàíñèðóþùåãî óçëà ïî íàïðÿæåíèþ ïðè ðàñ÷åòå óñòàíîâèâøåãî ýëåêòðè÷åñêîãî ðåæèìà ýíåðãîñèñòåìû ïðèíèìàåì ÃÝÑ. (ðèñ. 17.)

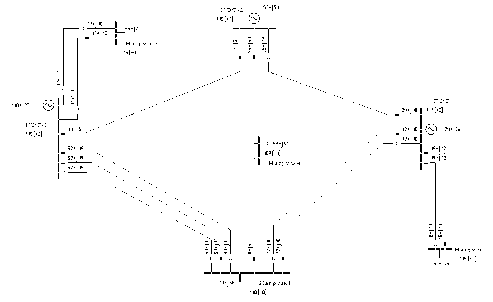
Ðèñ. 17. Ýëåêòðè÷åñêàÿ ñõåìà ýíåðãîñèñòåìû â «ÊÎÑÌÎÑ».

Íàïðÿæåíèå íà øèíàõ âûñîêîãî íàïðÿæåíèÿ ýëåêòðîñòàíöèé ÊÝÑ-1 è ÊÝÑ-2 ïðèìåì ðàâíûì 115 êÂ. Ðåæèìó ìàêñèìàëüíûõ íàãðóçîê â ðàññìàòðèâàåìûé ñóòî÷íûé ãðàôèê ýëåêòðè÷åñêîé íàãðóçêè áóäåò ñîîòâåòñòâîâàòü èíòåðâàë âðåìåíè ñ 16 äî 20 ÷, à ðåæèìó ìèíèìàëüíûõ íàãðóçîê - èíòåðâàë âðåìåíè ñ 0 äî 4 ÷. Ðåçóëüòàòû ðàñ÷åòîâ óñòàíîâèâøèõñÿ ýëåêòðè÷åñêèõ ðåæèìîâ äëÿ ìàêñèìàëüíûõ è ìèíèìàëüíûõ íàãðóçîê ïîòðåáèòåëåé ýíåðãîñèñòåìû ïðèâåäåíû â òàáëè÷íîé ôîðìå ïðîãðàììû «ÊÎÑÌÎÑ».

Ðåçóëüòàòû ðàñ÷åòà óñòàíîâèâøåãî ýëåêòðè÷åñêîãî ðåæèìà äëÿ ìàêñèìàëüíûõ íàãðóçîê ïîòðåáèòåëåé:

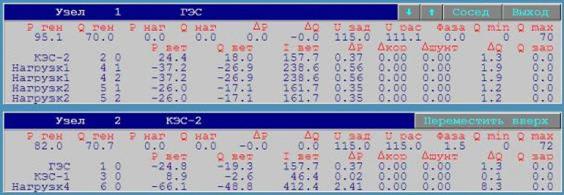
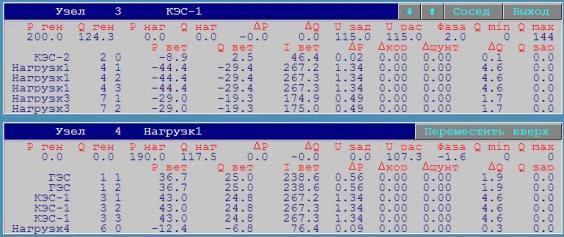
Èíòåãðàëüíûå ïàðàìåòðû ðåæèìà ìàêñèìàëüíûõ íàãðóçîê ïîòðåáèòåëåé:

Âûâîä: Óñòàíîâèâøèåñÿ çíà÷åíèÿ íàïðÿæåíèé â óçëàõ ïîòðåáèòåëåé íå ïðåâûøàþò ïðåäåëüíî äîïóñòèìûõ çíà÷åíèé ïî ÃÎÑÒ 13109-97.

Ðåçóëüòàòû ðàñ÷åòà óñòàíîâèâøåãî ýëåêòðè÷åñêîãî ðåæèìà äëÿ ìèíèìàëüíûõ íàãðóçîê ïîòðåáèòåëåé:

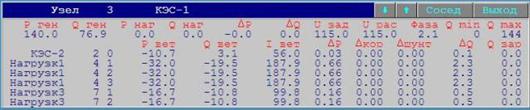
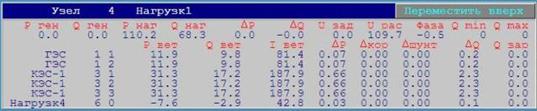
Èíòåãðàëüíûå ïàðàìåòðû ðåæèìà ìèíèìàëüíûõ íàãðóçîê ïîòðåáèòåëåé:

Âûâîä: Óñòàíîâèâøèåñÿ çíà÷åíèÿ íàïðÿæåíèé â óçëàõ ïîòðåáèòåëåé íå ïðåâûøàþò ïðåäåëüíî äîïóñòèìûõ çíà÷åíèé ïî ÃÎÑÒ 13109-97.

Çàêëþ÷åíèå

Îïòèìèçàöèÿ ðåæèìîâ ýëåêòðîñòàíöèé è ýíåðãîñèñòåì íàïðàâëåíà íà óäîâëåòâîðåíèå òðåáîâàíèé ïîòðåáèòåëåé ê ýêîíîìè÷íîñòè ýíåðãîñíàáæåíèÿ. Ïðè îïòèìèçàöèè ïîâûøàåòñÿ ýôôåêòèâíîñòü èñïîëüçîâàíèÿ ýíåðãîðåñóðñîâ è îáîðóäîâàíèÿ ýíåðãîñèñòåìû. Çàäà÷è îïòèìàëüíîãî ðàñïðåäåëåíèÿ ýëåêòðè÷åñêîé íàãðóçêè ìåæäó ýëåêòðè÷åñêèìè ñòàíöèÿìè ðåøàþòñÿ ñ ó÷åòîì ïðîñòðàíñòâåííîé è âðåìåííîé èåðàðõèè, â ñòðîãîé è óïðîùåííîé ïîñòàíîâêå, ïî ðàçëè÷íûì êðèòåðèÿì îïòèìèçàöèè. Äëÿ íèõ ãëóáîêî ðàçðàáîòàíû òåîðåòè÷åñêèé àïïàðàò, àëãîðèòìû è ïðîãðàììû. Îáúÿñíÿåòñÿ ýòî òåì, ÷òî îíè ïîâñåìåñòíî èñïîëüçóþòñÿ ïðè ýêñïëóàòàöèè è ïëàíèðîâàíèè ðàçâèòèÿ ýëåêòðîýíåðãåòè÷åñêèõ ñèñòåì. Êàæäàÿ çàäà÷à îïòèìèçàöèè ïðè ïðîìûøëåííîé ðåàëèçàöèè èìååò ìíîãî òîíêîñòåé, êîòîðûå èçëîæåíû â íîðìàòèâíûõ äîêóìåíòàõ.  êóðñîâîé ðàáîòå ïðèâåäåíû ïðèìåðû ðåøåíèÿ ýòèõ çàäà÷ è ôèçè÷åñêèé ñìûñë óñëîâèé îïòèìàëüíîñòè, ñîñòàâëÿþùèõ òîò ìèíèìóì, êîòîðûé äîñòàòî÷åí äëÿ óãëóáëåííîãî ñàìîñòîÿòåëüíîãî èçó÷åíèÿ âîïðîñà.

êîíäåíñàöèîííûé òåïëîâîé ýëåêòðîñòàíöèÿ ïîòðåáèòåëü

Ëèòåðàòóðà

Îñíîâíàÿ

Îïòèìèçàöèÿ ðåæèìîâ ýíåðãîñèñòåì: Ó÷åáíîå ïîñîáèå / Ï.È. Áàðòîëîìåé, Ò.À. Ïàíèêîâñêàÿ. Åêàòåðèíáóðã: ÓÃÒÓ - ÓÏÈ, 2008. - 164 ñ.

Ìàêîêëþåâ Á.È. Àíàëèç è ïëàíèðîâàíèå ýëåêòðîïîòðåáëåíèÿ. - Ì.: Ýíåðãîàòîìèçäàò, 2008. - 296 ñ.

Ò.À. Ôèëèïïîâà è äð. Îïòèìèçàöèÿ ðåæèìîâ ýëåêòðîñòàíöèé è ýíåðãîñèñòåì: Ó÷åáíèê /Ò.À. Ôèëèïïîâà, Þ.Ì. Ñèäîðêèí, À.Ã. Ðóñèíà; - Íîâîñèá. ãîñ. òåõí. óí-ò. - Íîâîñèáèðñê, 2007. - 356 ñ.

Èåðàðõè÷åñêèå ìîäåëè â àíàëèçå è óïðàâëåíèè ðåæèìàìè ýëåêòðîýíåðãåòè÷åñêèõ ñèñòåì / Î.À. Ñóõàíîâ, Þ.Â. Øàðîâ - Ì.: Èçäàòåëüñêèé äîì ÌÝÈ, 2007. - 312 ñ.

Ëûêèí À.Â. Ýëåêòðè÷åñêèå ñèñòåìû è ñåòè: Ó÷åá. ïîñîáèå. - Ì.: Óíèâåðñèòåòñêàÿ êíèãà; Ëîãîñ, 2006. - 254 ñ.

Ôèëèïïîâà Ò.À. Ýíåðãåòè÷åñêèå ðåæèìû ýëåêòðè÷åñêèõ ñòàíöèé è ýëåêòðîýíåðãåòè÷åñêèõ ñèñòåì: Ó÷åáíèê - Íîâîñèáèðñê: Èçä-âî ÍÃÒÓ, 2005. - 300 ñ.

Äîïîëíèòåëüíàÿ

Áîðîâñêèé Þ.Â.: Ñîâðåìåííûå ïðîáëåìû ìèðîâîé ýíåðãåòèêè. - Ì.: Navona, 2011

Êîòåí¸â Ñ.Â.: Ðàñ÷åò è îïòèìèçàöèÿ òîðîèäàëüíûõ òðàíñôîðìàòîðîâ. - Ì.: Ãîðÿ÷àÿ ëèíèÿ - Òåëåêîì, 2011

Àëõàñîâ À.Á.: Âîçîáíîâëÿåìàÿ ýíåðãåòèêà. - Ì.: ÔÈÇÌÀÒËÈÒ, 2010

Áàøàðèí Ñ.À.: Òåîðåòè÷åñêèå îñíîâû ýëåêòðîòåõíèêè. - Ì.: Àêàäåìèÿ, 2010

Â.Ã. Åðåìèí è äð. ; ðåö.: À.Â. Òîòàé, Ã.Ï. Áàáêèí: Áåçîïàñíîñòü æèçíåäåÿòåëüíîñòè â ýíåðãåòèêå. - Ì.: Àêàäåìèÿ, 2010

Ìèëëõîóí Äæ.: Íåçàäåéñòâîâàííûé ýíåðãåòè÷åñêèé ðåçåðâ Ðîññèè. - Ì.: Öåíòð Êàðíåãè, 2010

Ìóðîìöåâ Þ.Ë.: Òåîðåòè÷åñêèå îñíîâû ýíåðãîñáåðåãàþùåãî óïðàâëåíèÿ. - Ì.: ßÍÓÑ-Ê, 2010

Òðåíèí Ä.: Àðêòèêà: âçãëÿä èç Ìîñêâû. - Ì.: Ìîñêîâñêèé Öåíòð Êàðíåãè, 2010

Ì-âî îáðàçîâàíèÿ è íàóêè ÐÔ, Íèæåãîðîäñêèé ãîñ. òåõíè÷åñêèé óí-ò èì. Ð.Å. Àëåêñååâà ; àâò.-ðàçðàá.: Ã.ß. Âàãèí è äð.: Ìåòîäèêà ïðîâåäåíèÿ ýíåðãåòè÷åñêèõ îáñëåäîâàíèé (ýíåðãîàóäèòà) îáðàçîâàòåëüíûõ ó÷ðåæäåíèé. - Íèæíèé Íîâãîðîä: ÍÃÒÓ, 2009

Îëà Äæ.: Ìåòàíîë è ýíåðãåòèêà áóäóùåãî. Êîãäà çàêîí÷àòñÿ íåôòü è ãàç. - Ì.: ÁÈÍÎÌ, 2009

ïîä ðåä. Ã.Ã. Ðàííåâà ; ðåö.: Â.Í. Ìàëèíîâñêèé, Â.Ë. Øêóðàòíèê: Èíôîðìàöèîííî-èçìåðèòåëüíàÿ òåõíèêà è ýëåêòðîíèêà. - Ì.: Àêàäåìèÿ, 2009

Àëõàñîâ À.Á.: Ãåîòåðìàëüíàÿ ýíåðãåòèêà. - Ì.: ÔÈÇÌÀÒËÈÒ, 2008

ÁåëÃÓ, Êàô. îáùåé, íåîðãàíè÷åñêîé è àíàëèòè÷åñêîé õèìèè ; ñîñò.: À.À. Ñìîëèêîâ è äð. ; ðåö.: Â.È. Ïàâëåíêî, Î.Å. Ëåáåäåâà: Ïðèêëàäíàÿ íàíîõèìèÿ. - Áåëãîðîä: ÁåëÃÓ, 2008

Äåíê Ñ.Î.: Âîçîáíîâëÿåìûå èñòî÷íèêè ýíåðãèè ; íà áåðåãó ýíåðãåòè÷åñêîãî îêåàíà. - Ïåðìü: Ïåðìñêèé ãîñóäàðñòâåííûé òåõíè÷åñêèé óíèâåðñèòåò, 2008

Îòâ. ðåä. Â.À. Ãóñåéíîâ: Þæíûé Êàâêàç: òåíäåíöèè è ïðîáëåìû ðàçâèòèÿ (1992-2008 ãîäû). - Ì.: Êðàñíàÿ çâåçäà, 2008

Äåíê Ñ.Î.: Ýíåðãåòè÷åñêèå èñòî÷íèêè è ðåñóðñû áëèçêîãî áóäóùåãî. - Ïåðìü: Ïðåññòàéì, 2007

Ñîêîëîâ Á.À.: Êîòåëüíûå óñòàíîâêè è èõ ýêñïëóàòàöèÿ. - Ì.: Àêàäåìèÿ, 2007

Òêà÷åíêî Ã.È.: Îñíîâû ýíåðãîñáåðåæåíèÿ. - Áåëãîðîä: ÁåëÃÓ, 2007

Ïðàâèëà òåõíè÷åñêîé ýêñïëóàòàöèè òåïëîâûõ ýíåðãîóñòàíîâîê. - Ì.: Îìåãà-Ë, 2006

Ãèòåëüìàí Ë.Ä.: Ýíåðãåòè÷åñêèé áèçíåñ. - Ì: Äåëî, 2006

Ì-âî òîïëèâà è ýíåðãåòèêè ÐÔ: Ïðàâèëà òåõíèêè áåçîïàñíîñòè ïðè ýêñïëóàòàöèè òåïëîìåõàíè÷åñêîãî îáîðóäîâàíèÿ ýëåêòðîñòàíöèé è òåïëîâûõ ñåòåé. - [Á.Ì.]: [Á.È.], 2006

Ì-âî òðóäà è ñîöèàëüíîãî ðàçâèòèÿ ÐÔ ; Ì-âî ýíåðãåòèêè ÐÔ: Ìåæîòðàñëåâûå ïðàâèëà ïî îõðàíå òðóäà (ïðàâèëà áåçîïàñíîñòè) ïðè ýêñïëóàòàöèè ýëåêòðîóñòàíîâîê ÏÎÒ ÐÌ-016-2001 ÐÄ 153-34.0-03.150-00. - Ì.: Îìåãà-Ë, 2006

Îôîðì. Å. Îñüìèíèíîé: Ïðàâèëà óñòðîéñòâà ýëåêòðîóñòàíîâîê. - Ì.: Îìåãà-Ë, 2006

ÐÀÍ; Ïîä îáù. ðåä. Í.À. Ïëàòý; Ñîñò.: Ò.Â. Ìàâðèíà, Â.À. Ïîïîâ: Íàóêà-íåèñ÷åðïàåìûé ðåñóðñ. - Ì.: Academia, 2006

Ðàçìåùåíî íà Allbest.ru