Исследование статики, кинематики и динамики механической системы
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
высшего
образования
АМУРСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
(ФГБУ ВО
«АмГУ»)
Факультет
дизайна и технологий
Кафедра
Сервисных технологий и общетехнических дисциплин
Специальность
13.03.01 - Теплоэнергетика и теплотехника (профиль:Энергообеспечение
предприятий)
КУРСОВАЯ
РАБОТА
на тему:
Исследование статики, кинематики и динамики механической системы
по дисциплине
«Теоретическая механика»
Благовещенск
2017
Задание
ускорение тело вектор опора
1.Тема курсовой работы «Исследование реакций опор составных конструкций,
кинематики и динамики механической системы»
. Срок сдачи студентом законченного проекта 10.06.2016 г.
. Исходные данные к курсовому проекту приведены в листе исходных данных.
. Содержание курсового проекта:
определение реакций опор плоской составной конструкции (система двух тел)
аналитическим способом и на ЭВМ;
расчет плоских ферм аналитическим способом и на ЭВМ;
определение реакций опор пространственной конструкции аналитическим
способом и на ЭВМ;
определение скоростей и ускорений точек твердого тела при плоском
движении;
исследование движения механической системы различными методами.
. Перечень материалов приложения
Приложение А Определение реакций опор плоской составной конструкции при
помощи программы PSFNM.
Приложение Б Расчет плоской фермы на ПЭВМ при помощи программы PIVOT
Приложение В Определение реакций опор пространственной составной
конструкции при помощи программы SSFNP.
.Дата выдачи задания 21.02.2016 г.
Лист исходных данных
Реферат
Курсовая работа содержит 75с., 29 рисунков, 14 таблиц, 3 приложения, 10
источников.
СКОРОСТЬ, УСКОРЕНИЕ, ПЛОСКОЕ ДВИЖЕНИЕ, РЕАКЦИЯ ОПОР, СОСТАВНАЯ
КОНСТРУКЦИЯ, ФЕРМА, ДИНАМИКА, МЕХАНИЧЕСКАЯ СИСТЕМА.
Цель работы - определение реакций опор и исследовать кинематику и
динамику механической системы.Расчет плоской составной конструкции производится
аналитическим способом. Расчет фермы производится аналитическим способом и на
ЭВМ. Расчет пространственной конструкции производится аналитическим способом и
на ЭВМ. Нахождение скоростей и ускорений точек твердого тела аналитическим
способом. Сравнение различных методов решения: дифференциальные уравнения
движения механической системы; теорема об изменении кинетической энергии; закон
движения центра масс, закон изменения количества движения, общее уравнение
динамики.
В результате проделанной работы было установлено, что при использовании
любого метода, для расчета механической системы, результаты одинаковы.
Содержание
Введение
. Определение реакции опор плоской составной конструкции
.1 Описание составной конструкции
.2 Определение реакции опор балки СB
.3 Определение реакций опор балки АС
.4 Расчет главного вектора и главного момента плоской системы
сил
.5 Расчет на ПЭВМ
.6 Вывод по проведенным расчетам
. Расчет плоских ферм
.1 Определение внешних реакций в опорных узлах
.2 Определение усилий в стержнях методом вырезания узлов
.3 Определение усилий в стержнях фермы методом сечений
.4 Расчет главного вектора и главного момента
.5 Расчет плоской фермы на ПЭВМ при помощи программы PIVOT
Выводы по разделу
. Определение реакций опор пространственной консрукции
.1 Описание составной конструкции
.2 Определение реакций опор пространственной конструкции
.3 Расчет главного вектора и главного момента
.4 Расчет на ПЭВМ
Вывод по проведенным расчетам
. Кинематическое исследование кривошипно - ползунного
механизма
.1 Описание кривошипно-ползунного механизма
.2 Определение скоростей, ускорений точек А, В, С а так же
угловой скорости и ускорения шатуна АВ
.3 Результаты расчетов
. Динамика механической системы
.1 Описание механической системы
.2 Применение дифференциальных уравнений к исследованию
движения механической системы
.3 Применение общего уравнения динамики к исследованию
движения механической системы
.4 Применение теоремы об изменении кинетической энергии к
исследованию движения механической системы
.5 Применение уравнений Лагранжа II рода к исследованию
движения механической системы
.6 Определение скорости и ускорения центра масс механической
системы
.7 Определение количества движения механической системы
.8 Определение главного вектора внешних сил механической
системы
Вывод по проведенным расчетам
Заключение
Библиографический список
Введение
Курс теоретической механики является фундаментальной дисциплиной при
подготовке бакалавров любого профиля, в том числе бакалавров по автоматизации
производственных процессов.
Основные законы и принципы теоретической механики служат базой для многих
инженерных наук, а также широко используются в большинстве специальных
дисциплин.
Проектирование, изготовление, испытания и грамотная эксплуатация
современных машин, механизмов, конструкций и сооружений невозможно без знания
основных законов, теорем и принципов теоретической механики.
Теоретическая механика - наука об общих законах механического движения и
взаимодействия материальных тел. Под этим следует понимать, что теоретическая
механика изучает законы механического движения, справедливые для любых
материальных тел.
Все технические расчеты, которые выполняются при проектировании различных
сооружений, при проектировании машин, при изучении полета снаряда, движения
потока жидкости или газа, движения отдельных звеньев механизмов и машин, при
анализе различных технологических процессов, основаны на применении законов
теоретической механики.
Механику надо знать при расчете технологических процессов в
машиностроении и в металлургии, в текстильной и легкой промышленности, при
добыче полезных ископаемых и в технологических процессах пищевой
промышленности, в сельскохозяйственном производстве - при обработке почвы,
внесении удобрений, поливке, уборке урожая и т.д.
Механика - научная основа всех видов строительства от сооружения платин,
мостов и дорог до возведения высотных зданий и высочайших башен телевидения; а
также всех видов транспорта - от морских судов и железнодорожных поездов до
реактивных самолетов, ракет и лунохода.
Механика составляет значительную часть науки о Земле, науки о движении
воздушных масс, о движении океанских волн, течений рек и ледников, о
геологических преобразованиях земной коры, о землетрясениях (сейсмология), и
вулканической деятельности.
По законам механики происходит передвижение животных по суше, полет птиц
и насекомых в воздухе, плавание рыб и морских животных в воде, процесс
кровообращения и движения лимфы в живом организме, процессы деления клеток и
образования мускульной силы. Медицина использует механику при диагностике
болезней и создании искусственных органов человеческого тела.
Механика сыграла основную роль в развитии теоретических основ
воздухоплавания и теории движения ракет. Полет космических кораблей по заданным
орбитам обеспечивают приборы, основанные на использовании тончайших
особенностей механических явлений.
Механическое движение, основные законы которого изучает теоретическая
механика, встречается повсюду - в природе и технике, дома, на улице и на
производстве. Для того, чтобы хорошо понимать и разбираться в окружающем нас
мире, в происходящих вокруг нас явлениях, необходимо знать основные законы
механического движения.
Целью курсовой работы является доказательство возможности использования
методов общетеоретических дисциплин для решения конкретных инженерных задач,
приобретение навыков самостоятельного решения практических задач.
Задачей курсовой работы является определение реакций связей плоской и
пространственной конструкций, исследование кинематики многозвенного механизма,
и, исследование динамики механической системы различными методами.
1. Определение реакции опор плоской составной конструкции
Произвольной плоской системой сил называется совокупность сил, линии
действия которых, находятся в одной плоскости.
Составная конструкция - это совокупность связанных между собой твердых
тел - элементов конструкции, образующих жесткую статически определяемую
механическую систему. Определение реакций опор (внешних и внутренних
соединений) являются одним из основных этапов расчета таких конструкций.
1.1 Описание составной конструкции
Плоская составная конструкция (рисунок 1), состоит из двух балок АС и ВС,
соединенных внутренним шарниром С. В такой конструкции связи, соединяющие ее
части называются внутренними - шарнир С, а связи, присоединяющие ее к другим
телам - внешними - опоры А и В.
Конструкция нагружена сосредоточенной силой F1 = 10 кН, F2 = 8 кН, моментом М = 25 кН·м и
распределенной нагрузкой, интенсивность которой q = 1,8 кН/м

Рисунок 1- Составная конструкция
Расчет составной конструкции заключается в определении внешних и
внутренних связей.
Составляем расчетную схему левой части составной конструкции (рисунок 2).
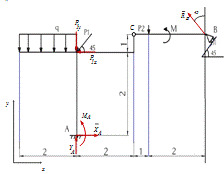
Рисунок 2 - Расчетная схемасоставной конструкции
На сновании принципа освобождаемости от связей - «всякое несвободное тело
можно, мысленно отбросив связи, рассматривать как свободное, если действия
связей заменить реакциями связей», заменяем внешние связи соответствующими
реакциями.
На составную конструкцию наложены связи:А - жесткая заделка, В -
шарнирно-подвижная опора (цилиндрический шарнир).
Шарнирно-подвижная опора В допускает поворот тела в любом направлении в
плоскости. Так как основание опоры подвижное, то тело может свободно
перемещаться в плоскости, параллельной этому основанию, но не может
перемещаться перпендикулярно к основанию т.к. при этом нарушается связь.
Поэтому реакция таких опор направлена перпендикулярно опорной поверхности.
Таким образом, направление реакции RB будет известно, а ее величина
неизвестна.
Балка-консоль А представляет собой внедрение данного тела в другое, при
котором, нет взаимных перемещений этих тел. При действии на балку плоской системы
сил в заделке возникает пара сил с моментом МА - реактивный момент,
препятствующий повороту балки, и произвольно направленная сила реакции RА, препятствующая поступательным перемещениям, которую
заменяем ее составляющими XА и YА.
Механическая система находится в равновесии под действием заданных сил и
реакций связей, которые необходимо определить.
Общее количество неизвестных внешних реакций в задаче - 4 (XА,YА, RB, MA).
Для плоской системы сил можно составить только три уравнения равновесия,
поэтому, для определения четырех неизвестных реакций связей этих уравнений
недостаточно. Задача решается путем расчленения системы на отдельные тела и
составления уравнений равновесия для каждого. Действие отброшенных частей
заменяются внутренними силами, которые по отношению к рассматриваемому телу
играют роль внешних сил, а действие связей заменяется соответствующими
реакциями связей.
Расчленяем конструкцию на две отдельные части и составляем уравнения
равновесия для каждой части. При этом в месте сочленения тел возникают две
реакции внутренних связей в цилиндрическом шарнире С, величина и направление
которых неизвестны. На основании аксиомы равенства действия и противодействия
они будут для каждой части попарно равны по модулю и противоположны по
направлению.
.2 Определение реакции опор балки СB
Рассмотримправая часть конструкции (рисунок 3).
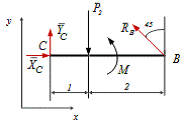
Рисунок 3 -Расчетная схема правая часть конструкции
Для определения реакций связей используем условия и уравнения равновесия
плоской системы сил.
Условия равновесия плоской системы сил: «для равновесия плоской системы
сил необходимо и достаточно, чтобы главный вектор и главный момент системы сил
были равны нулю».
Главный вектор плоской системы сил это векторная сумма всех сил.
Главный вектор для балки СB
будет иметь вид:
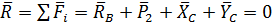 (1)
(1)
Главный момент плоской системы сил это векторная сумма моментов всех сил.
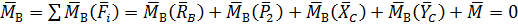 (2)
(2)
Для определения реакций связей записываем основную форму уравнений
равновесия плоской системы сил для каждого из двух элементов конструкции.
«Для равновесия плоской системы сил необходимо и достаточно, чтобы
алгебраическая сумма проекций всех активных сил и реакций связей на каждую из
двух координатных осей была равна нулю, и, одновременно, алгебраическая сумма
моментов этих же сил относительно любого центра в плоскости их действия были
равны нулю».
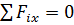
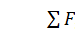
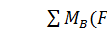
Для балки СB эти уравнения
будут иметь вид:
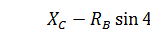 (3)
(3)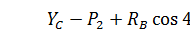 (4)
(4)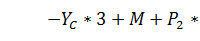 (5)
(5)
Из выражения (5) выразим YC, получим:
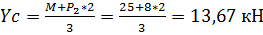 (6)
(6)
Из формулы (4) выразим 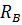 , получим:
, получим:
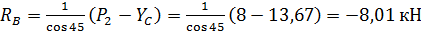 (7)
(7)
Из формулы (3) выразим ХC, получим:
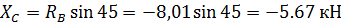 (8)
(8)
1.3
Определение реакций опор балки АС
Составляем расчетную схему балки АС (рисунок 4). Учитываем, что в шарнире
C реакции связи будут направлены
противоположно реакциям, обозначенным на рисунке 3.
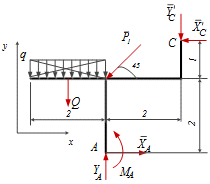
Рисунок 4- Расчетная схема левой часть конструкции
Математическое выражение главного вектора для балки BС будет иметь вид:
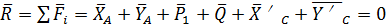 (9)
(9)
где Q=q·2=1.8·2=3.6 кН - сосредоточенная сила, которой
заменяем распределенную нагрузку интенсивность q.
Линия действия сосредоточенной силы проходит через центр тяжести эпюр
распределенной нагрузки.
Главный момент плоской системы сил это векторная сумма моментов всех сил.
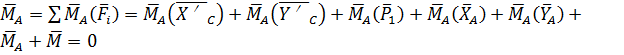 (10)
(10)
Записываем уравнения равновесия балки AС
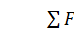
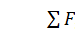
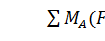
Для балки СB эти уравнения
будут иметь вид:
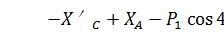 (11)
(11)
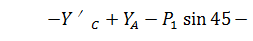 (12)
(12)
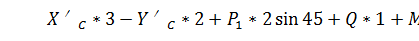 (13)
(13)
Из выражения (11) найдем 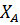 :
:
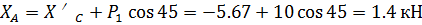 (14)
(14)
Из выражения (12) найдем 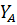 :
:
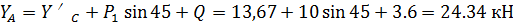
Из выражения (13) найдем 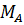 :
:
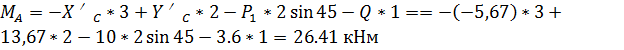
Определяем модуль реакции RАи RС:
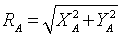 (15)
(15)
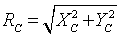 (16)
(16)
Подставив значения, получим:
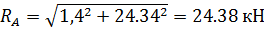
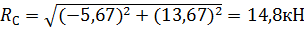
Для проверки правильности расчетов необходимо
убедиться в том, что соблюдаются уравнения равновесия сил, приложенных ко всей
конструкции, представленной на рисунке 2.
Сила P! наклонная, для упрощения расчетов, найдем в
соответствии с теоремой Вариньона её проекции на оси координат:
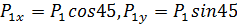 .
.
Для этого записываем уравнения моментов относительно точки C системы сил, приложенных к составной
конструкции:
Проверочное уравнение для всей системы: 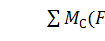
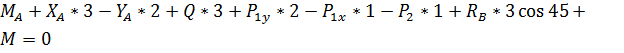
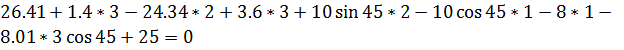

.4 Расчет главного вектора и главного момента плоской системы
сил
Основными характеристиками системы сил, приложенных к механической
системы являются две величины - главный вектор и главный момент.
Определяем модуль главного вектора заданных систем сил для балки BC: 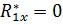
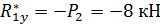
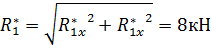
Определяем модуль главного вектора заданных систем сил для балки АС:
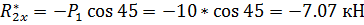
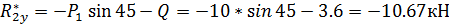
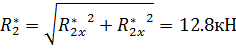
Главный момент плоской системы сил - это алгебраическая сумма всех
моментов.
Определяем модуль главного момента заданных систем сил для балки АC относительно точкиС:
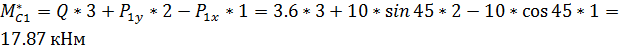
Определяем модуль главного момента заданных систем сил для балки BC относительно точкиС:
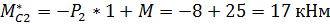
1.5 Расчет на ПЭВМ
Для проверки результатов произведем расчет конструкции на ПЭВМ по
программе PSFNM.
Составляем таблицы для ввода в ПЭВМ
Таблица 1 - Таблица сил
|
№ звена
|
Число сил
|
Проекции сил
|
Точка приложения силы
|
Обозначение на схеме
|
|
|
Fx
|
Fy
|
M
|
XF
|
YF
|
|
|
1
|
2
|
0
|
-3.6
|
0
|
1
|
2
|
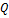
|
|
|
-7.07
|
-7.07
|
0
|
2
|
2
|
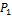
|
|
1
|
3
|
0
|
0
|
25
|
0
|
0
|
М
|
|
|
0
|
-8
|
0
|
5
|
3
|
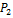
|
Таблица 2 - Таблица опор
|
Код опоры
|
Направляющие векторы
|
Точка приложения
|
Обозначение на схеме
|
|
С1
|
С2
|
С3
|
С4
|
RX
|
RY
|
RZ
|
XF
|
YF
|
|
|
1
|
3
|
2
|
1
|
0
|
0
|
0
|
2.0
|
0
|
A
|
|
1
|
2
|
2
|
0
|
0
|
0
|
0
|
4.0
|
3.0
|
C
|
|
2
|
2
|
1
|
0
|
-0.707
|
0.707
|
0
|
7.0
|
3.0
|
B
|
1.6 Вывод
по проведенным расчетам
Таблица 3 - Сравнение результатов расчетов
|
Значения реакций в опорах
полученные аналитическим методом [kН]
|
|
XA
|
YA
|
XВ
|
YB
|
XС
|
YС
|
|
1.4
|
24.34
|
5.66
|
5.66
|
-5.67
|
13.67
|
|
Значения реакций в опорах,
полученные при расчете на ПЭВМ [kН]
|
|
1.4
|
24.34
|
5.66
|
5.66
|
7,383
|
6,04
|
Можно сделать вывод, что расчеты, сделанные аналитическим методом и на
ЭВМ абсолютно одинаковые.
2. Расчет плоских ферм
Фермы широко используются в современном производстве, в основном для
перекрытия больших пролётов: мосты, стропильные системы промышленных зданий,
спортивные сооружения.
Фермой называется шарнирно-стержневая геометрически неизменяемая
конструкция. Если оси всех стержней фермы лежат в одной плоскости, то ее
называют плоской фермой. Точки, в которых сходятся оси стержней, называются
узлами фермы, а те узлы, которыми ферма опирается на основание, называются
опорными узлами.
Стержни плоской фермы, расположенные по верхнему контуру, образуют
верхний пояс, а расположенные по нижнему контуру - нижний пояс фермы.
Вертикальные стержни называются стойками, а наклонные - раскосами.
Расстояние между осями опор фермы называется ее пролетом. Стойки и
раскосы образуют решетку фермы (рисунок 5).
При расчетах усилий в стержнях фермы используют следующие допущения:
все стержни фермы являются абсолютно твердыми и прямолинейными;
весом стержней пренебрегают, считая их невесомыми;
внешние силы приложены только в узлах фермы;
все узлы фермы - идеальные шарниры, т.е. трением в шарнирах можно
пренебречь.
Перечисленные выше допущения позволяют приближенно считать, что на каждый
из узлов фермы действует только сходящаяся система сил и, следовательно,
стержни фермы либо растянуты, либо сжаты.
В статике доказывается, что между числом стержней S статически определенной фермы и
числом ее узлов n существует
зависимость:
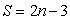 (17)
(17)
Если число стержней меньше, то ферма не будет жесткой. Если больше, то во
всех стержнях усилия определить методами статики не удастся. Задача будет
статически неопределимой.
Усилия в отдельных стержнях загруженной фермы могут оказаться равными
нулю. Такие стержни принято называть нулевыми.
Основными методами (способами) определения усилий в стержнях фермы
являются:
метод вырезания узлов;
метод сечений, названный методом Риттера.
Рассчитать ферму это значит определить внешние реакции в опорных узлах и
усилия в каждом стержне.
.1 Определение внешних реакций в опорных узлах
Определить реакции опор фермы (рисунок 5) под действием вертикальной
нагрузкиР2=7 кН, 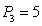 кН и горизонтальной Р1=3
кН, а также усилия в стержнях фермы - методом вырезания узлов, и сделать
проверку методом сечения Риттера в стержнях 8, 9 и 10.
кН и горизонтальной Р1=3
кН, а также усилия в стержнях фермы - методом вырезания узлов, и сделать
проверку методом сечения Риттера в стержнях 8, 9 и 10.
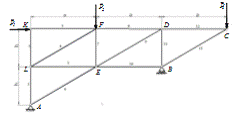
Рисунок 5 - Cхема фермы
Расчет фермы всегда начинается с определения неизвестных сил реакций
связей фермы в ее опорных узлах. Составляются три уравнения равновесия для
системы всех внешних сил, действующих на ферму. Из уравнений равновесия
определяются реакции в опорных узлах. Затем приступают к определению усилий в
стержнях фермы.
Освобождаем ферму от связей, заменяя их реакциями связей:
На ферму наложены следующие связи - шарнирно - неподвижная опора А,
шарнирно -подвижная опора В.
На основании принципа освобождаемости от связей, заменяем внешние связи
их реакциями.
Шарнирно-подвижная опора В допускает поворот тела в любом направлении в
плоскости. Так как основание опоры подвижное, то тело может свободно
перемещаться в плоскости, параллельной этому основанию, но не может
перемещаться перпендикулярно к основанию т.к. при этом нарушается связь.
Поэтому реакция таких опор направлена перпендикулярно опорной поверхности.
Таким образом, направление реакции RB будет известно, а ее величина
неизвестна.
В шарнирно-неподвижной опореAвозникает реактивная сила, проходящая через центр шарнира. Ее
составляющими являются вертикальная сила YА, препятствующая вертикальному смещению (вверх-вниз) и
горизонтальная сила ХA,
препятствующая горизонтальному смещению (вправо-влево).
Механическая система находится в равновесии под действием заданных сил и
реакций связей, которые необходимо определить.
Общее количество неизвестных внешних реакций в задаче - 3 (RB, XА,YА).
Проверяем статическую определимость фермы.
=2·8-3
=13
Рассматриваем ферму в целом как твердое тело, к которому приложена
уравновешенная плоская система сил. Мысленно отбрасываем внешние связи и
заменяем их действие соответствующими реакциями.
Составляем расчетную схему фермы (рисунок 6).
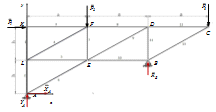
Рисунок 6 - Расчетная схема
Записываем уравнения равновесия фермы.
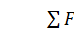
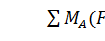
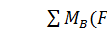
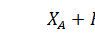 (17)
(17)
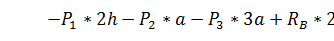 (18)
(18)
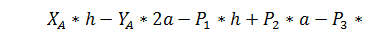 (19)
(19)
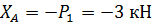
Из (18) находим
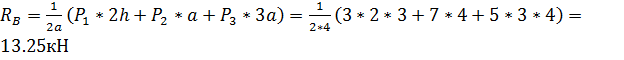
Из (19) находим
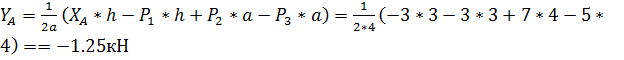
Проверяем правильность решения, составив уравнение равновесия: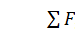
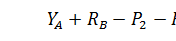
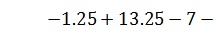

.2 Определение
усилий в стержнях методом вырезания узлов
Определение усилий в стержнях фермы по способу вырезания узлов состоит в
том, что мысленно вырезают узлы фермы, прикладывают к ним соответствующие
внешние силы и реакции стержней и составляют уравнения равновесия сил,
приложенных к каждому узлу. Так как в начале расчета фермы неизвестно, какие
стержни растянуты, а какие сжаты, то изначально предполагают, что все стержни
растянуты - реакции стержней направлены от узлов.
Если в результате вычислений получают ответ со знаком « - », то
соответствующий стержень сжат.
Последовательность вырезания узлов определяется условием, что число
неизвестных сил, приложенных к узлу, не должно превышать числа уравнений
равновесия сил. Тогда эти неизвестные сразу определяются из уравнений
равновесия сил, действующих на этот узел.
Определим усилия в стержнях 1-13 методом вырезания узлов. Для этого
мысленно вырезаем каждый узел поочередно, прикладываем внешние силы и реакции
стержней, составляем по два уравнения равновесия, т.к. узел представляет собой
систему сходящихся сил.
Для равновесия плоской системы сходящихся сил необходимо и достаточно,
чтобы суммы проекций этих сил на каждую из двух координатных осей были равны
нулю.
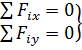 (20)
(20)
Вырезаем узел C:
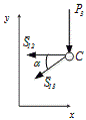
Рисунок 7 - Узел C
Составим уравнения (20)
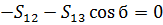 (21)
(21)
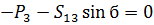 (22)
(22)
Где из прямоугольного треугольника BCD
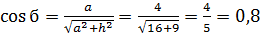

Из (22) находим
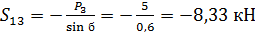
Из (21) находим
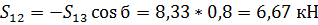
Вырезаем узел В:
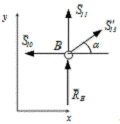
Рисунок 8 - Узел C
Составим уравнения (20)
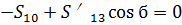 (23)
(23)
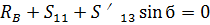 (24)
(24)
Где согласно аксиоме о равенстве действия и противодействия
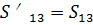
Из (23) находим
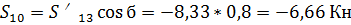
Из (24) находим
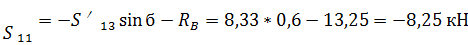
Вырезаем узел D:
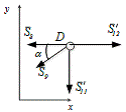
Рисунок 9 - Узел D
Составим уравнения (20)
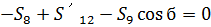 (25)
(25)
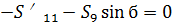 (26)
(26)
Где согласно аксиоме о равенстве действия и противодействия
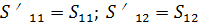
Из (26) находим
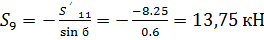
Из (25) находим
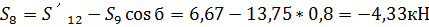
Вырезаем узелК:
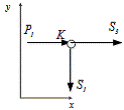
Рисунок 10 - Узел К
Составим уравнения (20)
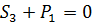 (27)
(27)
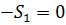 (28)
(28)
Из (28) находим
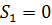
Из (27) находим
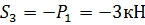
Вырезаем узел А:
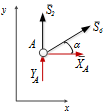
Рисунок 11 - УзелА
Составим уравнения (20)
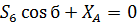 (29)
(29)
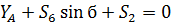 (30)
(30)
Из (29) находим
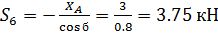
Из (30) находим
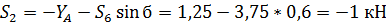
Вырезаем узел L:
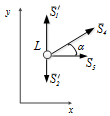
Рисунок 12 - Узел L
Составим уравнения (20)
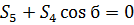 (31)
(31)
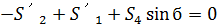 (32)
(32)
Где согласно аксиоме о равенстве действия и противодействия

Из (31) находим
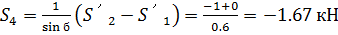
Из (32) находим
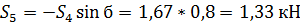
Вырезаем узел F:
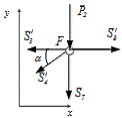
Рисунок 13 - Узел F
Составим уравнения (20)
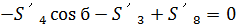 (33)
(33)
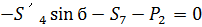 (34)
(34)
Где согласно аксиоме о равенстве действия и противодействия
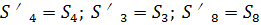
Из (34) находим
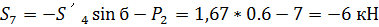
(33) используем для проверки найденных реакций


2.3 Определение усилий в стержнях фермы методом сечений
Определение усилий в стержнях фермы заключается в том, что проводят
сечение через три стержня фермы. Мысленно отбрасывают большую часть фермы,
заменяя ее действие на оставшуюся часть усилиями, приложенными в
соответствующих сечениях стержней и направленными в сторону отброшенной части.
Чтобы определить усилие в стержне фермы, составляют уравнение моментов сил,
действующих на оставшуюся часть фермы, относительно моментной точки - точки, в
которой пересекаются два стержня, кроме искомого. Эта точка называется точкой Риттера.
Знаки полученных ответов покажут, сжат стержень или растянут.
Для нахождения усилий в стержнях 8, 9, 10 проведем сечение I-I и рассмотримправую часть, заменяя ее действие усилиями 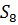 ,
, 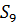 и
и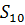 , направленными в сторону отброшенной части.
, направленными в сторону отброшенной части.
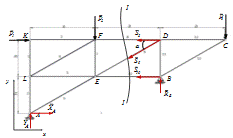
Рисунок 15- Метод Риттера
Определяем усилия в стержне 8. В данном случае точкой Риттера будет точка
Е.
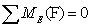
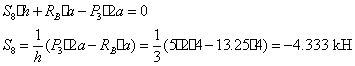
Определяем усилия в стержне 10. В данном случае точкой Риттера будет
точка D.
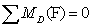
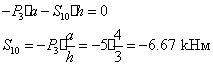
Определяем усилия в стержне 9. Составим уравнение равновесия:
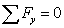
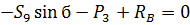
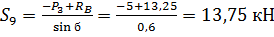
.4 Расчет главного вектора и главного момента
Определим модуль главного вектора заданных систем сил по проекциям на
координатные оси.
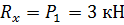
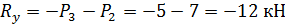
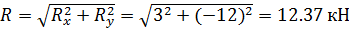
Вычислим главный момент заданных сил относительно точки А.
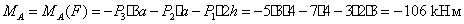

2.5 Расчет плоской фермы на ПЭВМ при помощи программы PIVOT
Составляем таблицы для ввода в ПЭВМ
Таблица 4 - Таблица сил
|
Число сил
|
№ силы
|
Проекции сил
|
Точка приложения силы
|
Обозначение силы
|
|
|
Fx
|
Fy
|
M
|
X
|
Y
|
|
|
3
|
1
|
3
|
0
|
0
|
0
|
9
|
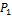
|
|
2
|
0
|
-7
|
0
|
4
|
9
|
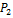
|
|
3
|
0
|
-5
|
0
|
12
|
9
|
|
Таблица 5 - Таблица параметров опор
|
Код реакции
|
Направляющие векторы
|
Точка приложения
|
Обозначение на схеме
|
|
С1
|
С2
|
С3
|
С4
|
Rx
|
Ry
|
XF
|
YF
|
|
|
1
|
2
|
2
|
0
|
0
|
0
|
0
|
0
|
A
|
|
1
|
2
|
1
|
0
|
0
|
1.0
|
8
|
3
|
В
|
Таблица 6
- Таблица узлов
|
№ узла п/п
|
Число стержней в узле
|
Координаты узла
|
Обозначение узла
|
|
|
ХF
|
YF
|
|
|
1
|
2
|
0
|
0
|
А
|
|
2
|
4
|
0
|
3
|
L
|
|
3
|
2
|
0
|
6
|
K
|
|
4
|
4
|
4
|
6
|
F
|
|
5
|
4
|
8
|
6
|
D
|
|
6
|
2
|
12
|
6
|
C
|
|
7
|
3
|
8
|
3
|
В
|
|
8
|
5
|
4
|
3
|
E
|
Таблица 7
- Таблица стержней
|
№ узла п/п
|
|
|
1
|
2; 3
|
|
2
|
1; 2
|
|
3
|
3; 4
|
|
4
|
2; 4
|
|
5
|
2; 8
|
|
6
|
1; 8
|
|
7
|
4; 8
|
|
8
|
4; 5
|
|
9
|
5; 8
|
|
10
|
7; 8
|
|
11
|
5; 7
|
|
12
|
5; 6
|
|
13
|
6; 7
|
Таблица 8 - Сравнение результатов расчетов фермы
|
№стержня п/п
|
Метод вырезания узлов [kH]
|
Методом сечений Риттера
|
Результаты расчета на ПЭВМ
|
|
S1
|
0
|
|
0
|
|
S2
|
-1
|
|
-1
|
|
S3
|
-3
|
|
-3
|
|
S4
|
-1,67
|
|
-1,67
|
|
S5
|
1,33
|
|
1,33
|
|
S6
|
3,75
|
|
3,75
|
|
S7
|
-6
|
|
-6
|
|
S8
|
-4,33
|
-4,333
|
-4,33
|
|
S9
|
13,75
|
13.75
|
13,75
|
|
|
S10
|
-6,67
|
-6,67
|
-6,67
|
|
|
S11
|
-8,25
|
|
-8,25
|
|
|
S12
|
6,67
|
|
6,67
|
|
|
S13
|
-8,33
|
|
-8,33
|
|
|
|
|
|
|
|
Рассчитаем погрешности вычислений по формуле
 (35)
(35)
Выводы по разделу
Произведен расчет усилий в стержнях методом вырезания узлов, усилий в
стержнях 8, 9, 10 методом Риттера и расчет на ПЭВМ по программе PIVOT.
Результаты занесены в таблицу 8. Был произведен расчет главного вектора и
главного момента.
Можно сделать вывод, что расчеты, сделанные аналитическим методом и на
ЭВМ, одинаковые.
Максимальная погрешность измерений равна 0,08%.
3. Определение реакций опор пространственной консрукции
3.1 Описание составной конструкции
Однородная прямоугольная плита весом G закреплена в точке А сферическим шарниром, а в токе В
цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым
стержнем.
Сферический шарнир А. Он позволяет телу поворачиваться, но не разрешает
линейные перемещения. Реакция сферического шарнира R приложена к его центру и может быть направлена по любому
радиусу шарнира.
Если в пределах стержня от шарнира до шарнира никаких сил к нему не
приложено (опорный стержень нельзя нагружать силам в какой-нибудь его средней
части и вес стержня не учитывается), то реакция стержня направлена вдоль
стержня.
На плиту действуют две силы Q иG.
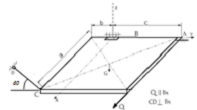
Рисунок 16 - Пространственная конструкция
3.2
Определение реакций опор пространственной конструкции
Записываем условия и уравнения равновесия пространственной системы сил.
Для равновесия пространственной системы сил необходимо и достаточно,
чтобы главный вектор и главный момент системы равнялись нулю.
Реакция опорного стрежня RC направлена по стержню, она наклонная, поэтому заменяем ее проекциями по
координатным осям:

Реакции опор А и В раскладываем по осям координат 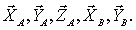
Получили пространственную систему сил (рисунок 17).
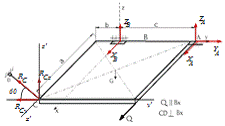
Рисунок 17 - Расчетная схема
Составляем уравнения равновесие пространственной системы сил:
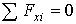
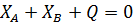 (36)
(36)
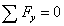
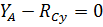 (37)
(37)
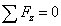
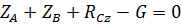 (38)
(38)
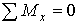
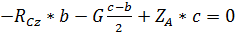 (39)
(39)

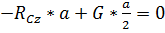 (40)
(40)
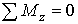
 (41)
(41)
Из выражения (40) найдем RCz:
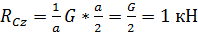
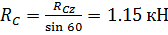
Из выражения (41) найдем XA:
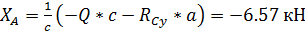
Из выражения (36) находим:
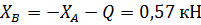
Из выражения (37) найдем:
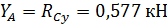
Из выражения (39) найдем:
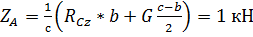
Из выражения (38) найдем:
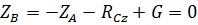
Для проверки расчетов введем новую систему координат и составим уравнения
моментов относительно новых координатных осей
 , сумма моментов сил относительно оси х'
, сумма моментов сил относительно оси х'
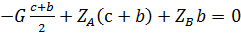
=0
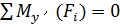 , сумма моментов сил относительно оси у'
, сумма моментов сил относительно оси у'
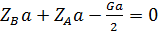
0=0
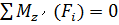 , сумма моментов сил относительно оси z'
, сумма моментов сил относительно оси z'
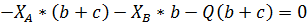
=0
3.3 Расчет
главного вектора и главного момента
Определим модуль главного вектора заданных систем сил по проекциям на
координатные оси:
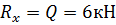
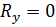
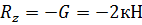
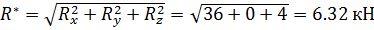
Вычислим главный момент заданных сил:

.4 Расчет на ПЭВМ
Для проверки результатов произведем расчет конструкции на ПЭВМ по
программе SSFNP
Составляем таблицы для ввода в ПЭВМ
Таблица 9 - Таблица сил
|
Число сил
|
№ силы
|
Проекции сил
|
Точка приложения силы
|
Обозначение силы
|
|
|
Fx
|
Fy
|
Fz
|
Mx
|
My
|
Mz
|
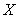
|

|
Z
|
|
|
1
|
1
|
6
|
0
|
0
|
0
|
0
|
0
|
0,6
|
0,6
|
0
|
Q
|
|
2
|
0
|
0
|
-2
|
0
|
0
|
0
|
0,3
|
0,1
|
0
|
G
|
Таблица 10 - Таблица опор
|
Код реакции
|
Направляющие векторы
|
Точка приложения
|
Обозначение на Схеме
|
|
С
|
С
|
С
|
С
|
Rx
|
Ry
|
Rz
|
Mx
|
My
|
Mz
|
XF
|
YF
|
ZF
|
|
|
1
|
2
|
3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0,6
|
0
|
A
|
|
1
|
2
|
2
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
B
|
|
1
|
2
|
1
|
0
|
0
|
-0,5
|
0,866
|
0
|
0
|
0
|
0,6
|
-0,4
|
0
|
C
|
Вывод по проведенным расчетам
Таблица 11 - Сравнение результатов расчетов
|
XA, kH
|
YA, kH
|
ZA,kH
|
ZB,kH
|
ХB,kH
|
RC,kH
|
|
Значения реакций в опорах
полученные аналитическим методом [kН]
|
|
-6,57
|
0,577
|
1
|
0
|
0,57
|
1,15
|
|
Значения реакций в опорах,
полученные при расчете на ПЭВМ [kН]
|
|
-6,57
|
0,5777
|
1
|
0
|
0,57
|
1,15
|
Расчет погрешностей результатов по формуле (35):
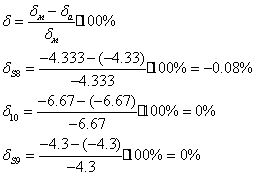
Произведен расчет реакций опор и сил, расчет на ПЭВМ по программе SSFNP.
Результаты занесены в таблицу 11. Был произведен расчет главного вектора
и главного момента.
Можно сделать вывод, что расчеты, сделанные аналитическим методом и на
ЭВМ одинаковые.
Максимальная погрешность измерений составляет 0,12%.
4. Кинематическое исследование кривошипно - ползунного
механизма
.1 Описание кривошипно-ползунного механизма
Кривошип ОА кривошипно-ползунного механизма вращаясь вокруг неподвижной
оси О с угловой скоростью 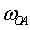 и угловым ускорением
и угловым ускорением 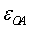 , приводит в движение шатун АВ
соединенный с ним шарнирно в точке А.
, приводит в движение шатун АВ
соединенный с ним шарнирно в точке А.
Ползун В перемещается в направляющих по горизонтальной прямой.
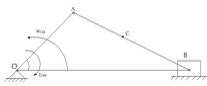
Рисунок 18 - Кривошипно-ползунный механизм.
Механизм состоит из трех подвижных звеньев: кривошип ОА, шатун АВ, ползун
В. Кривошип вращается вокруг неподвижной оси с заданной угловой скоростью 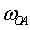 . Точка А во время движения будет
описывать окружность радиус которой ОА с центром в точке О. Скорость точки А -
. Точка А во время движения будет
описывать окружность радиус которой ОА с центром в точке О. Скорость точки А -  направлена по касательной к этой
окружности, то есть перпендикулярно звену ОА в соответствии с заданным
направлением вращения угловой скорости
направлена по касательной к этой
окружности, то есть перпендикулярно звену ОА в соответствии с заданным
направлением вращения угловой скорости 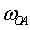 кривошипа ОА.
кривошипа ОА.
4.2 Определение скоростей, ускорений точек А, В, С а так же
угловой скорости и ускорения шатуна АВ
Определяем скорости точек В и С шатуна.
Из условия задачи определяем скорость точкиА:
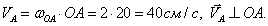 (40)
(40)
Для определения скоростей точек определим положение мгновенного центра
скоростей шатуна АВ, т.е. восстановим перпендикуляры к скоростям 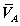 и
и 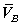 , точка их пересечения и является мгновенным центром
скоростей шатуна АВ- точка Р. В данном положении механизма совпадают с точкой В.
, точка их пересечения и является мгновенным центром
скоростей шатуна АВ- точка Р. В данном положении механизма совпадают с точкой В.
VB=VP=0 (41)
АР=АВ
Определяем угловую скорость шатуна wАВ:
wАВ=VA/AB=40/60=0.67c-1 (42)
Направление 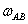 найдем, повернув вектор
найдем, повернув вектор 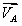 вокруг МЦС (т.В)
вокруг МЦС (т.В)

Рисунок 19 - Построение МЦС
Скорость точки С равна:
VС=ωАВВС=0,67·30=20 см/с
Определяем ускорение точки В.
ТочкаВ принадлежит стержню АВ. Чтобы найти  , надо знать ускорение какой-нибудь
другой точки стержня АВ (точка А), которую принимаем за полюс.
, надо знать ускорение какой-нибудь
другой точки стержня АВ (точка А), которую принимаем за полюс.
Тогда ускорение точкиВ определяется векторным равенством:
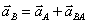 или
или 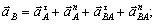 (43)
(43)
где 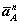 ‒ нормальное ускорение точкиА, выбранной за
полюс;
‒ нормальное ускорение точкиА, выбранной за
полюс;
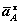 - касательное ускорение точкиА;
- касательное ускорение точкиА;
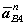 ‒ нормальное (центростремительное) ускорение во
вращательном движении вокруг полюса;
‒ нормальное (центростремительное) ускорение во
вращательном движении вокруг полюса;
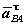 ‒ касательное (вращательное) ускорение точкиВ во
вращательном движении вокруг полюса.
‒ касательное (вращательное) ускорение точкиВ во
вращательном движении вокруг полюса.
Вычисляем нормальное и касательное ускорения точкиА:
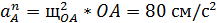 (44)
(44)
 (45)
(45)
аA=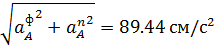
Вектор нормального ускорения 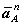 направлен по радиусу к центру
вращенияО, вектор касательного ускорения
направлен по радиусу к центру
вращенияО, вектор касательного ускорения 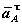 направлен противоположно вектору
скорости точки А.
направлен противоположно вектору
скорости точки А.
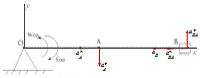
Рисунок 20 - Расчетная схема для определения аВ
Нормальное ускорение точки В относительно точки А
определяется по формуле:
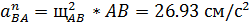 (46)
(46)
Для определения ускорения ползунаВ спроецируем векторное равенство
(45) на ось x:
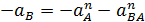
Отсюда:
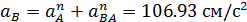
Определяем угловое ускорение шатуна 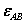 .
.
Для этого сначала определим 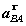 . Cпроецируем векторное равенство (45) на ось y:
. Cпроецируем векторное равенство (45) на ось y:
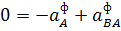
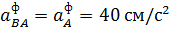
Теперь из равенства 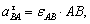 , получим:
, получим:
εАВ=
Определяем ускорение точки С.
Для этого воспользуемся равенством:
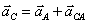 или
или 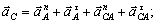 (46)
(46)
Где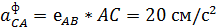
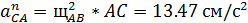
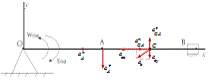
Рисунок 21 - Расчетная схема для определения аС
Спроецируем (47) на оси координат
аСх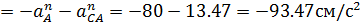
аСy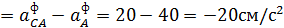
аС=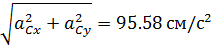
4.3 Результаты расчетов
Таблица12- Таблица результатов:
|
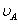 , , 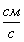
|
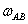 , , 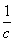
|
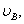 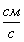
|
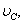 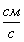
|
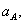 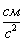
|
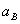 , , 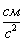
|
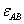 , , 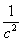
|
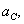 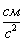
|
|
40
|
0,67
|
0
|
20
|
89,442
|
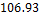
|
0.67
|
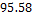
|
5.
Динамика механической системы
5.1 Описание механической системы
Механическая система под действием сил тяжести приходит в движение из
состояния покоя. Необходимо определить законы, скорости, ускорения движения
всех тел, силы натяжения в ветвях нити, силу трения, кинетическую энергию
механической системы, работу сил при заданном перемещении, главный вектор сил
инерции, скорость и ускорение центра масс системы, главный вектор внешних сил,
действующих на систему, количества движения механической системы. Начальное
положение системы показано на (Рисунок 22).
Силы тяжести тел равны: 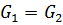 =
= =G;
=G; 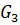 =G; радиусы тел 2, 3 и 4 имеют следующие соотношения: R3= R4=R, r2=r3=0.5R.
=G; радиусы тел 2, 3 и 4 имеют следующие соотношения: R3= R4=R, r2=r3=0.5R.

Рисунок 22 - Общая схема механической системы.
Тело 1 - груз; тело 2 - блок, сплошной однородный цилиндр; 3 -блок; тело
4 -блок, сплошной однородный цилиндр.
5.2
Применение дифференциальных уравнений к исследованию движения механической
системы
Для заданной механической системы определить ускорения для каждого тела,
входящего в систему. Определить натяжение в ветвях нити. Массой нити
пренебречь.
Для составления дифференциального уравнения движения системы, рассмотрим
каждое тело системы отдельно.
Выберем движение системы таким образом, чтобы груз 1 опускался.
Схема данной механической системы изображены на (Рисунок 22).
Тело 1.
На тело действуют сила тяжести 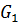 ; сила натяжении нити
; сила натяжении нити 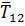 , которая характеризует действие
отброшенной части конструкции на тело 1 (рис.23).
, которая характеризует действие
отброшенной части конструкции на тело 1 (рис.23).
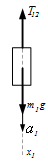
Рисунок 23 - Система сил, действующая на тело 1
В данной механической системе груз 1 совершает поступательное движение.
Дифференциальное уравнение движения тела 1 имеет вид:
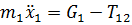 или
или 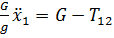 (47)
(47)
Тело 2
На тело действуют сила тяжести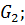 реакция опоры
реакция опоры 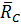 , которую мы разложим на составляющие
, которую мы разложим на составляющие
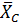 и
и  сила натяжения нити
сила натяжения нити  , которая характеризует действие
отброшенной нити с телом 1 на тело 2; сила натяжения нити
, которая характеризует действие
отброшенной нити с телом 1 на тело 2; сила натяжения нити 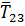 , которая характеризует действие
отброшенной нити с телами 3 и 4 на тело 2 (рис.24).
, которая характеризует действие
отброшенной нити с телами 3 и 4 на тело 2 (рис.24).
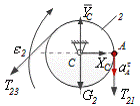
Рисунок 24 - Система сил, действующая на тело 2
Дифференциальное уравнение вращательного движения тела 2 примет вид:
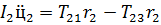 (49)
(49)
Где момент инерции для второго тела относительно оси вращения определим
по выражению
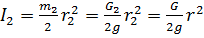
Т.к. нить не растягивается и отсутствует проскальзывание, то угловое
ускорение равно:
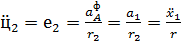 (50)
(50)
Тогда (50) примет вид:
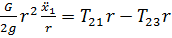
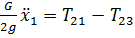 (51)
(51)
Тело 3
На тело действуют сила тяжести тела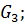 сила натяжения участка нити
сила натяжения участка нити 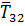 , которая характеризует действие отброшенной
нити с телами 2 и 1 на тело 3; силы натяжения участков нити
, которая характеризует действие отброшенной
нити с телами 2 и 1 на тело 3; силы натяжения участков нити 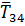 и
и 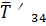 , которые характеризуют действие
отброшенной нити с телом 4 на тело 3; реакция опоры
, которые характеризуют действие
отброшенной нити с телом 4 на тело 3; реакция опоры 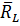 , которую мы разложим на составляющие
, которую мы разложим на составляющие
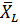 и
и 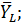 (рис.25).
(рис.25).
Блок 3 - вращение вокруг неподвижной оси:

Рисунок 25 - Система сил, действующая на тело 3
Дифференциальное уравнение вращательного движения тела 3 примет вид:
 (52)
(52)
Где момент инерции для тела 3 относительно оси вращения определим по
выражению
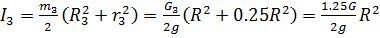
Т.к. нить не растягивается и отсутствует проскальзывание, то угловое
ускорение равно:
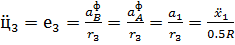
Тогда (52) примет вид
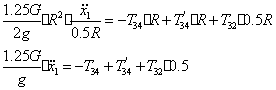 (53)
(53)
Тело 4
На тело действуют сила тяжести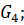 реакция опоры
реакция опоры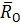 , которую мы разложим на составляющие
, которую мы разложим на составляющие
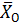 и
и 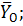 силы натяжения нитей
силы натяжения нитей 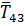 и
и 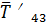 , которые характеризует действие
отброшенной нити с остальной частью на тело 4 (рис.26).
, которые характеризует действие
отброшенной нити с остальной частью на тело 4 (рис.26).
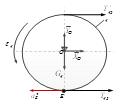
Рисунок 26 - Система сил, действующая на тело 4
Дифференциальное уравнение вращательного движения тела 2 примет вид:
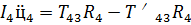 (54)
(54)
Где момент инерции для второго тела относительно оси вращения определим
по выражению
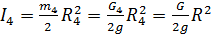
Т.к. нить не растягивается и отсутствует проскальзывание, то угловое
ускорение равно:
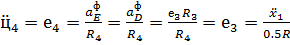 (55)
(55)
Тогда (54) примет вид
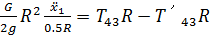
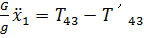 (56)
(56)
Из (56) выразим
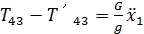 (57)
(57)
Согласно закону равенства действия и противодействия
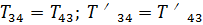
Подставим в (53)
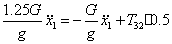
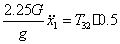
Выразим 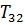
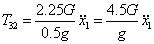 (58)
(58)
Согласно закону равенства действия и противодействия
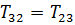
Подставим в (51)
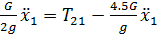
Выразим
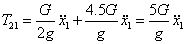
Согласно закону равенства действия и противодействия
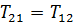
Подставим в выражение (48):

тогда
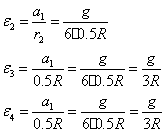
Сила натяжения:
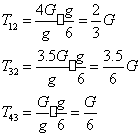
.3 Применение общего уравнения динамики к исследованию
движения механической системы
Формулировка: если механическая система, на которую наложены голономные,
стационарные, идеальные связи, движется с ускорением, то добавляя к действующим
на нее активным силам и их моментам фиктивные силы и моменты сил инерции,
получим формально уравновешенную систему сил, для которой можно применить
принцип возможных перемещений.
Механическая система под действием силы тяжести приходит в движение из
состояния покоя, необходимо определить ускорения всех тел, входящих в систему.
Массами нитей и силами трения пренебречь. Схема механической системы показана
на (рисунке 22)
Покажем на механической системе веса тел 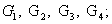 ускорения груза
ускорения груза 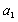 ; возможные перемещения груза
; возможные перемещения груза 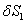 ; возможные углы поворота блоков
; возможные углы поворота блоков 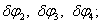 силы инерции тел механической
системы -
силы инерции тел механической
системы - 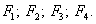 (рисунок 26).
(рисунок 26).
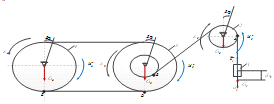
Рисунок 26 - Схема к исследованию механической системы с помощью общего
уравнения динамики
В данном методе решения задачи применим общее уравнение динамики:
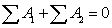 (59)
(59)
Где
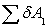 - сумма работ активных сил на возможном перемещении системы;
- сумма работ активных сил на возможном перемещении системы;
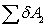 сумма работ сил инерции на возможном перемещении системы.
сумма работ сил инерции на возможном перемещении системы.
«Если механическая система, на которую наложены голономные, стационарные,
идеальные связи, движется с ускорением, то, добавляя к действующей на неё
активным силам и моментам этих сил фиктивные силы инерции и моменты сил
инерции, получим формально уравновешенную систему сил, к которой можно применить
принцип возможных перемещений».
Так как система приходит в движение из состояния покоя, то направления
ускорений тел соответствуют направлениям их движения.
Будем считать, что движение системы таково, что тело 1 опускается.
На систему действуют следующие активные силы
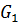 ,
, 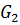 ,
, 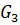 ,
,  - силы тяжести соответствующих тел;
- силы тяжести соответствующих тел;
Приложим к системе силы инерции
Тело1
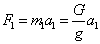 (направлена против
(направлена против 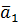 )
)
Тело 2
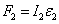 (направлена против
(направлена против 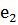 )
)
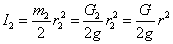
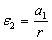
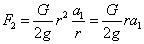
Тело 4
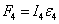 (направлена против
(направлена против 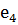 )
)
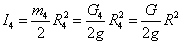
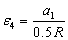
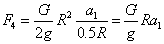
Тело 3
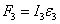 (направлена против
(направлена против 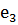 )
)
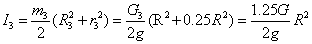
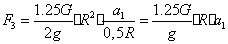
Зададим возможное перемещение системе и найдем работу активных сил на
этом виртуальном перемещении
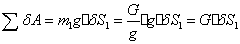 (60)
(60)
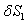 - виртуальное перемещение тела 1
- виртуальное перемещение тела 1
Определим работу сил инерции на заданном виртуальном перемещении
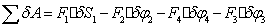 (61)
(61)
Согласно кинематическим связям тел механизма
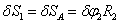
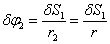 (62)
(62)
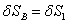
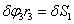
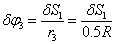
 (63)
(63)
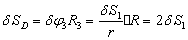
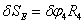

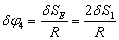 (64)
(64)
С учетом значений сил инерции, (60)-(64) (59) примет вид

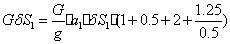
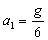
тогда
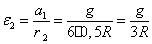
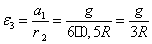
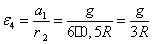
5.4 Применение теоремы об изменении кинетической энергии к
исследованию движения механической системы
Формулировка: изменение кинетической энергии при перемещении механической
системы из одного положения в другое равно алгебраической сумме работ всех
внешних и внутренних сил, действующих на систему на этом перемещении.
Кинетической энергией материальной точки называется половина произведения
массы этой точки на квадрат её скорости:
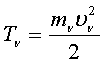 (65)
(65)
Кинетическая энергия является скалярной положительной величиной.
В системе СИ, единицей измерения энергии является джоуль: 1 Дж = 1 Н∙м.
Кинетическая энергия системы материальных точек - это сумма кинетических
энергий всех точек системы:
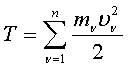 (66)
(66)
Механическая система под действием сил тяжести приходит в движение из
состояния покоя. Учитывая трение скольжения груза 1 , пренебрегая другими
силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить
скорости движения всех тел, входящих в механическую систему в тот момент
времени, когда пройденный грузом путь станет равным S. Начальное положение системы показано на рисунке 6.
Покажем на механической системе внешние силы, скорость груза v1; перемещение груза S; углы поворота блоков φ2, φ3, φ4 (рисунок 27).
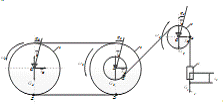
Рисунок 27 - Расчетная схема к исследованию механической системы с
помощью теоремы об изменении кинетической энергии
Применим теорему об изменении кинетической энергии системы:
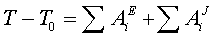 , (67)
, (67)
Где
 и
и 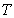 - кинетическая энергия системы в
начальном и конечном положении;
- кинетическая энергия системы в
начальном и конечном положении; 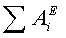 - сумма работ внешних сил, приложенных к системе, на
перемещении системы из начального положения в конечное;
- сумма работ внешних сил, приложенных к системе, на
перемещении системы из начального положения в конечное;
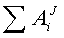 - сумма работ внутренних сил системы
на том же перемещении.
- сумма работ внутренних сил системы
на том же перемещении.
Для рассматриваемой системы, состоящей из абсолютно твёрдых тел,
соединённых нерастяжимыми нитями и стержнями,
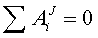 . (68)
. (68)
Так как в начальном положении система находится в покое, то Т0=0.
Следовательно, уравнение (66) принимает вид:
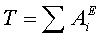 (69)
(69)
Вычислим кинетическую энергию системы в конечном положении как сумму
кинетических энергий тел 1, 2, 3 и 4:
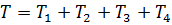 (70)
(70)
Первое тело совершает поступательное движение, тогда
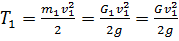 (71)
(71)
Тело 2 совершает вращательное движение, тогда
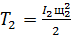 (72)
(72)
Где
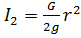 - момент инерции тела 2 относительно оси вращения.
- момент инерции тела 2 относительно оси вращения.
Тело 3 совершает вращательное движение, тогда:
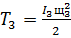 (73)
(73)
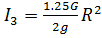 - момент инерции тела 3 относительно оси вращения.
- момент инерции тела 3 относительно оси вращения.
Тело 4 совершает вращательное движение, тогда:
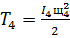 (74)
(74)
Где
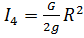 - момент инерции тела 4 относительно оси вращения.
- момент инерции тела 4 относительно оси вращения.
Выражение (70)примет вид:
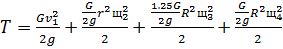 (75)
(75)
Выразим все скорости через скорость тела 1
Согласно кинематическим связям тел механизма
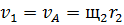
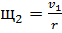 (76)
(76)
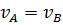
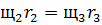
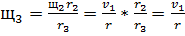 (77)
(77)
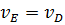
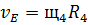
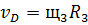
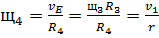 (78)
(78)
С учетом (76)-(78) (75) примет вид
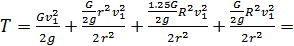
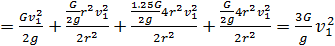 (79)
(79)
Найдём сумму работ всех внешних сил, приложенных к системе, на заданном
её перемещении:
На систему действуют следующие силы
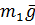 ,
, 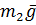 ,
, 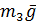 ,
, 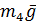 - силы тяжести соответствующих тел;
- силы тяжести соответствующих тел;
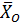 ,
, 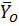 ,
, 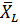 ,
, 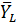 ,
,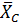 ,
,  - реакции опор тел 3,4 и 2.
- реакции опор тел 3,4 и 2.
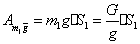
 - т.к. тело 2 вертикально не перемещается
- т.к. тело 2 вертикально не перемещается
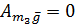 - т.к. тело 3 вертикально не перемещается
- т.к. тело 3 вертикально не перемещается
 - т.к. тело 4 вертикально не перемещается
- т.к. тело 4 вертикально не перемещается
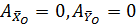 ,
,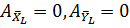 ,
,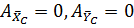 - т.к. точки приложения
- т.к. точки приложения 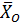 ,
, 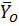 ,
, 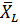 ,
, 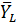 ,
,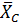 ,
,  не перемещаются
не перемещаются
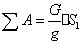 (80)
(80)
Согласно теореме, об изменении кинетической энергии системы, приравниваем
значения (79) и (80):
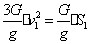
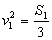
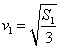
5.5 Применение уравнений Лагранжа II рода к исследованию движения
механической системы
Уравнения Лагранжа второго рода представляют собой систему обыкновенных
дифференциальных уравнений второго порядка относительно неизвестных обобщенных
координат q1, q2, …, qk , описывающих движение
механической системы, подчиненной идеальным связям. Уравнениями Лагранжа можно
пользоваться при изучении движения любой механической системы с геометрическими
связями независимо от того, сколько точек или тел входят в систему, как
движутся эти тела и какое движение (абсолютное или относительное)
рассматривается.
Силы, действующие на систему, представлены в виде обобщенных сил, куда
входят только внешние силы, а все реакции идеальных связей автоматически
исключаются и их можно не показывать на чертеже. Также, если на систему
действуют силы трения, то их включают в число внешних сил.
Механическая система под действием силы тяжести приходит в движение из
состояния покоя, необходимо определить ускорения всех тел, входящих в систему.
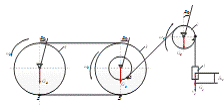
Рисунок 28 - Схема к исследованию механической системы с помощью
уравнений Лагранжа II рода
Т.к. система с одной степенью свободы, то достаточно одного уравнения для
описания движения системы.
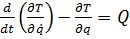 (81)
(81)
где:
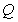 - обобщенные силы;
- обобщенные силы;
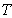 - кинетическая энергия механической
системы;
- кинетическая энергия механической
системы;
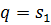 - обобщенная координата;
- обобщенная координата;
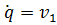 - обобщенная скорость.
- обобщенная скорость.
Согласно (79):

Тогда
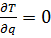 (82)
(82)
 (83)
(83)
Вычислим обобщенную силу Q по формуле:
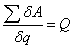 (84)
(84)
Где согласно (80)
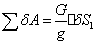
Тогда обобщенная сила:
 (85)
(85)
Подставляем (82), (83) и (85) в (81)
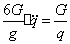
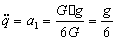
тогда
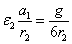
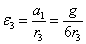
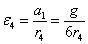
5.6
Определение скорости и ускорения центра масс механической системы
Воспользуемся теоремой о движении центра масс механической системы: Центр
масс механической системы движется как материальная точка массой, равной массе
всей системы, к которой приложены все внешние силы, действующие на систему, то
есть произведение массы системы на ускорение её центра масс равно
геометрической сумме всех действующих на систему внешних сил или главному
вектору этих сил (внутренние силы не могу изменять центр масс механической
системы).
Пусть точка К - центр масс системы, тогда
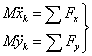 (86)
(86)
Выразим проекцию ускорения центра масс системы на ось x через соответствующие проекции
ускорений центров масс тел системы:
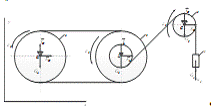
Рисунок 29 - Механическая система
 (87)
(87)
Аналогично выразим проекцию ускорения центра масс системы на ось y через соответствующие проекции
ускорений центров масс тел системы:
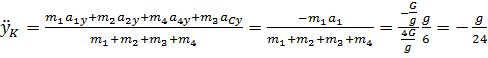 (88)
(88)
Тогда ускорение центра масс системы равно
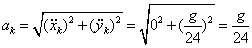
 - проекция скорости на ось х
- проекция скорости на ось х
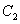 - константа интегрирования
- константа интегрирования
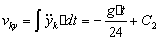 - проекция скорости на ось y
- проекция скорости на ось y
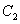 - константа интегрирования
- константа интегрирования
Т.к. система в начальный момент времени находилась в покое, то
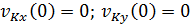
Тогда
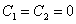
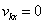 (89)
(89)
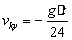 (90)
(90)
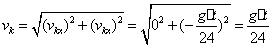
.7 Определение количества движения механической системы
Теорема об изменении количества движения системы - одна из общих теорем
динамики, является следствием законов Ньютона. Связывает количество движения с
импульсом внешних сил, действующих на тела, составляющие систему. В качестве
системы, о которой идёт речь в теореме, может выступать любая механическая
система, состоящая из любых тел.
Количеством движения (импульсом) механической системы называют величину,
равную сумме количеств движения (импульсов) всех тел, входящих в систему.
Импульс внешних сил, действующих на тела системы, - это сумма импульсов всех
вешних сил, действующих на тела системы.
Теорема об изменении количества движения системы утверждает: изменение количества
движения системы за некоторый промежуток времени равно импульсу внешних сил,
действующих на системы, за тот же промежуток времени.
По определению центра масс:
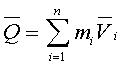 (91)
(91)
Согласно теореме об изменении количества движения:
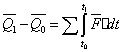
Т.к. силы постоянны и системы в начальный момент находилась в покое, то:
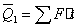
В проекциях на оси координат:
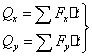 (92)
(92)
Согласно (86):
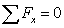
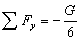
Тогда
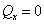 - проекция
количества движения системы на ось х.
- проекция
количества движения системы на ось х.
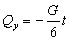 - проекция
количества движения системы на ось у.
- проекция
количества движения системы на ось у.
Тогда модуль количества движения системы равен:
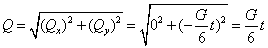
5.8
Определение главного вектора внешних сил механической системы
Главный вектор механической системы равен геометрической сумме всех
действующих на систему внешних сил, а также по теореме о движении центра масс
главный вектор равен массе всей системе, к которой приложены все внешние силы,
действующие на систему, то есть произведение массы системы на ускорение её
центра масс.
Согласно теореме о движении центра масс (86):
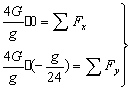
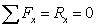 - проекция главного вектора внешних сил на ось х
- проекция главного вектора внешних сил на ось х
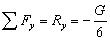 - проекция главного вектора внешних сил на ось y
- проекция главного вектора внешних сил на ось y
Тогда модуль главного вектора внешних сил равен
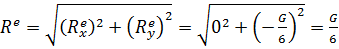
Вывод по
проведенным расчетам
В ходе исследования данной механической системы были применены
дифференциальные уравнения движения тел системы, общее уравнение динамики
(принцип Даламбера-Лагранжа), теорема об изменении кинетической энергии
механической системы, уравнение Лагранжа II рода, теорема о движении центра
масс и теорема о количестве движения. Мы убедились в справедливости общих
теорем динамики путем нахождения ускорений тел механической системы.
Так же было получено ускорение центра масс данной системы, которые равно 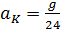 , количество движения системы,
равное:
, количество движения системы,
равное: 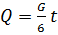 , а также главный вектор внешних сил,
действующих на систему:
, а также главный вектор внешних сил,
действующих на систему: 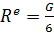
Заключение
В ходе выполнения курсового проекта выполнены поставленные задачи:
определены реакции связей плоской составной и пространственной
конструкции;
определены усилия в стержнях плоской фермы;
проведено исследование кинематики кривошипно-ползунного механизма
компрессора;
исследована динамика механической системы с помощью:
дифференциальных уравнений движения;
теоремы об изменении кинетической энергии в интегральном виде;
общего уравнения динамики;
уравнения Лагранжа II
рода;
теоремы о движении центра масс механической системы;
теоремы об изменении количества движения.
В результате расчетов получены следующие параметры движения механической
системы:
Таблица 13- Сравнительная таблица
|
Метод или теорема
|
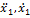
|
|
Общее уравнение динамики
|
1.67м/с2
|
|
Теорема об изменении
кинетической энергии механической системы (интегральный вид)
|
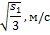
|
|
Уравнения Лагранжа II
рода
|
1.67м/с2
|
В результате проведенного исследования, было доказано, что независимо от
метода исследования механической системы, результат расчётов одинаков, поэтому,
любой метод исследования динамики механической системы пригоден для нахождения
параметров механической системы. Максимальная погрешность составила
Таблица 14 - Сравнительная таблица погрешностей
|
Раздел курсового проекта
|
%
|
|
Статика
|
0,12
|
|
Кинематика
|
0
|
|
Динамика
|
0
|
В курсовом проекте показан путь перехода от абстрактных научных положений
к практической деятельности инженера.
В процессе работы над курсовым проектом ознакомились с действующими
стандартами, нормами, научной и справочной литературой.
Библиографический список
1. Бутенин Н.В. и др. Курс теоретической механики:
учеб.пособие: В 2 т:. Рек. Мин. обр. РФ - СПб.: Лань, 2014. -730 с.
. Тарг С.М. Краткий курс теоретической механики: Учебник.
Рек. Мин. обр. РФ - М.: Высшая школа, 2006. - 416с.
. Яблонский А.А. и др. Курс теоретической механики:
учеб.пособие: Рек. Мин. обр. РФ - СПб.: Лань, 2004. -765 с.
. Диевский В.А. Теоретическая механика: учеб.пособие: Рек.
УМО/ - СПб.: Лань, 2005. -320 с.
. Луганцева Т.А. Плоскопараллельное движение: учеб.пособие.
АмГУ, Эн.ф. - Благовещенск: Изд-во АмГУ, 2012. - 105 с.
Режимдоступаfile://10.4.1.254/DigitalLibrary/AmurSU_Edition/3122.pdf
. Луганцева Т.А., Ларченко Н.М. Введение в статику:
учеб.пособие. /Т.А.Луганцева, Н.М.Ларченко.; АмГУ, Эн.ф. - Благовещенск: Изд-во
АмГУ, 2010. - 88с.
Режимдоступаfile://10.4.1.254/DigitalLibrary/AmurSU_Edition/3121.pdf.
. Луганцева Т.А., Труфанова Т.В. Динамика.учеб. пособие /Т.А.Луганцева, Т.В.Труфанова. - АмГУ, - Благовещенск: Изд-во АмГУ, 2011. - 144 с.
Режимдоступаfile://10.4.1.254/DigitalLibrary/AmurSU_Edition/3120.pdf.
8. Сборник заданий для курсовых работ по теоретической
механике: Учеб.пособие: Доп. Мин.обр. СССР / Ред. А.А. Яблонский/. - М.:
Интеграл-Пресс, 2004. - 382 с.
. Сборник курсовых заданий по теоретической механике
[Электронный ресурс] : учебное пособие / : Московский государственный горный
университет, 2003. - 194 с. - 5-7418-0277-Х. Режим доступа:
http://www.biblioclub.ru/index.php?page=book&id=83708
10. Электронный ресурс библиотеки АмГУ: http://www.biblioclub.ru -Электронная библиотечная система
«Университетская библиотека - online».