Магнитные характеристики материалов
Содержание
Введение
1. Классификация магнитных материалов
1.1 Общая характеристика магнитных материалов
1.2 Магнитомягкие материалы для постоянных и низкочастотных
магнитных полей
1.3 Ферриты и магнитодиэлектрики
1.4 Магнитные материалы специального назначения
2. Цепи магнитного тока и их характеристика
2.1 Общая характеристика магнитного поля
2.2 Порядок расчета магнитной цепи электромагнитного реле
2.3 Анализ магнитных цепей постоянного тока
2.4 Практический расчет магнитной цепи
Заключение
Список использованной литературы
Введение
Как известно из курса физики, вокруг проводника с током появляется
магнитное поле. Интенсивность магнитного поля характеризуется векторной
величиной: напряженностью магнитного поля 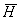 , измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором
магнитной индукции
, измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором
магнитной индукции 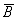 , измеряемой в теслах (Тл). Напряженность
магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей
среды. Магнитная цепь - последовательность взаимосвязанных магнетиков, по
которым проходит магнитный поток. То есть магнитной цепью или магнитопроводом
называется путь, по которому замыкается магнитный поток. Этот путь может
проходить целиком по воздуху.
, измеряемой в теслах (Тл). Напряженность
магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей
среды. Магнитная цепь - последовательность взаимосвязанных магнетиков, по
которым проходит магнитный поток. То есть магнитной цепью или магнитопроводом
называется путь, по которому замыкается магнитный поток. Этот путь может
проходить целиком по воздуху.
Магнитные цепи по своей конфигурации могут быть подразделены на
неразветвленные и разветвленные. В неразветвленной магнитной цепи на всех ее
участках имеет место один и тот же поток, т.е. различные участки цепи соединены
между собой последовательно. Разветвленные магнитные цепи содержат два и более
контура.
Актуальность темы заключается в том, что магнитная цепь и
сопутствующий математический аппарат используется для расчётов трансформаторов,
электрических машин, магнитных усилителей и т.п.
Целью данной работы является рассмотрение и анализ магнитных
характеристик материалов, магнитных цепей и направлений их применения.
Основными задачами, выделяемыми в рамках данной цели, являются:
- классификация наиболее применяемых на
практике магнитных материалов;
- описание основных принципов существования
магнитного поля;
- рассмотрение методики расчета
разветвленных и неразветвленных магнитных цепей постоянного и переменного тока;
- решение
практической задачи.
1.
Классификация магнитных материалов
1.1 Общая
характеристика магнитных материалов
Магнитные материалы подразделяют на магнитомягкие,
магнитотвердые и материалы специализированного назначения.
К магнитомягким относят материалы с малой коэрцетивной силой
(Нс < 800 А/м) и высокой магнитной проницаемостью. Они
намагничиваются до насыщения в любых магнитных полях, обладают узкой петлей
гистерезиса и малыми потерями на перемагничивание. Их используют в качестве
сердечников дросселей, трансформаторов, электромагнитов и т.п.
К магнитотвердым относят материалы с большой коэрцитивной
силой (Нс > 4кА/м). Они
перемагничиваются в очень сильных магнитных полях и служат в основном для
изготовления постоянных магнитов.
Среди материалов специализированного назначения в
радиоэлектронике применяются материалы с прямоугольной петлей гистерезиса
(ППГ), ферриты для устройств сверхвысокочастотного диапазона и
магнитострикционные материалы [3].
1.2
Магнитомягкие материалы для постоянных и низкочастотных магнитных полей
Магнитомягкие материалы должны обладать высокой магнитной
проницаемостью, малой коэрцитивной силой, большой индукцией насыщения, малыми
потерями на перемагничивание. Магнитные свойства материалов должны мало
зависеть от механических напряжений, в результате действия которых сильно
меняется mнач, mмакс, Нс. Магнитные
свойства после механической обработки восстанавливают термообработкой
(обжигом). В некоторых случаях важными являются температурная и временная
стабильность, линейность кривой намагничивания и др.
Этим требованием наиболее полно удовлетворяют железо и его
сплавы. Железо - это типичный магнитомягкий материал, магнитные свойства
которого существенно зависят от содержания примесей, структуры (особенно
величины зерна - чем крупнее зерна, тем выше магнитные свойства).
Вследствие низкого удельного сопротивления железо используют
для изготовления изделий, которые работают в постоянных магнитных полях.
Технически чистое железо применяется для получения почти всех ферромагнитных
сплавов [3, 5].
Сталь электротехническая является основным магнитомягким
материалом и представляет собой сплавы железа и кремния (до 4,5%). Добавки
кремния повышают удельное сопротивление, увеличивают mн и mmax, уменьшают Нс, потери на гистерезис, константы
магнитной анизотропии и магнитострикции, повышают стабильность магнитных свойств
во времени, но вместе с тем увеличивают хрупкость и твердость стали. Свойства
стали значительно улучшаются в результате образования магнитной текстуры при ее
холодной прокатке и последующем отжиге в водороде. Вдоль направления прокатки
наблюдается более высокое значение магнитной проницаемости и меньше потери на
гистерезис. Текстурированные стали используются при изготовлении ленточных
сердечников. В этом случае магнитный поток полностью проходит вдоль направления
легкого намагничивания. Сталь выпускается в виде рулонов, листов и резанной
ленты толщиной 0,05 - 1 мкм. Тонкий прокат применяется в полях повышенной
частоты (до 1 кГц). С уменьшением толщины уменьшаются потери на вихревые токи,
однако возрастает коэрцитивная сила и увеличиваются потери на гистерезис.
Пермаллои - железоникелевые сплавы, обладающие большой
магнитной проницаемостью в области слабых полей и очень маленькой коэрцитивной
силой. Высоконикелевые пермаллои содержат 72 - 80% никеля, а низконикелевые -
40 - 50% никеля. С увеличением содержания никеля возрастает магнитная
проницаемость, однако повышаются удельные потери и уменьшается индукция
насыщения. Низконикелевые пермаллои имеют mн = (1.5 - 4) ×103, mмакс = (15 - 40) ×103, Hc = 8 - 32 A/м, Bm = 1 - 1.5 Tл, а высоконикелевые - mн = (1 - 4) ×104, mмакс = (7 - 35) ×104, Hc = 0.4 - 4.8 A/м, Bm = 0.5 - 1 Tл.
Большие значения mн и mмакс пермаллоя объясняются небольшими величинами магнитной апизотропии
и магнитострикции. Это облегчает поворот магнитных моментов из направления
легкого намагничивания в направлении поля и не вызывает механических
напряжений, которые затрудняют смещение доменных границ под воздействием
слабого поля. Магнитная проницаемость пермаллоев сильно снижается с увеличением
частоты (из-за влияния вихревых токов) и напряженности подмагничивающего
(постоянного) поля. Для увеличения удельного сопротивления, улучшения магнитных
характеристик и их стабильности в диапазоне напряженностей магнитного поля и
температур, повышения механической прочности и обрабатываемости в пермаллой
добавляют легирующие элементы - молибден, хром, кремний, марганец, медь [3, 5].
Пермаллой очень чувствителен к механическим воздействиям,
поэтому при изготовлении деталей из него необходимо избегать ударов, рихтовки и
т.п. После всех механических операций производят термообработку в вакууме или в
атмосфере водорода.
Пермаллой используется для изготовления магнитных экранов,
сердечников малогабаритных и импульсных трансформаторов, сердечников катушек
индуктивности, головок аппаратуры магнитной записи.
Альсиферы - тройные сплавы железа с кремнием и алюминием.
Оптимальный состав альсифера 9.5% Si, 5.6 % Al, остальное Fe. Такой сплав отличается
твердостью и хрупкостью.
Свойства альсифера (mн = 3500, mмакс = 117000, Hc = 1.8 A/м) не уступают свойствам высоконикелевого
пермаллоя. Изделия из альсифера - магнитные экраны, корпуса приборов и т.п.
изготавливаются методом литья с толщиной стенок не менее 2-3 мм в виду
хрупкости сплава. Его можно размалывать в порошок и использовать для
изготовления высокочастотных прессованных сердечников.
1.3 Ферриты и
магнитодиэлектрики
Ферриты - химические соединения окиси железа Fe2О3 с оксидами
одного или нескольких двухвалентных металлов, имеющих общую формулу МеО×Fe2O3, где Ме - двухвалентный металл. Феррит может быть магнитным, если
на месте Ме стоит ион марганца, никеля, магния, меди и некоторые другие
металлы, и немагнитным - если стоит ион цинка.
Ферриты получают в виде керамики и монокристаллов. Ферритовая
керамика не содержит стекловидной фазы. Изделия из ферритов получают методом
спекания спрессованной массы порошкообразных окислов металлов. Ферриты являются
твердыми и хрупкими материалами и допускают только шлифовку и поліровку [9, c.167 - 169].
Технические ферриты представляют собой раствор магнитного и
немагнитного ферритов. Ферриты для радиочастот делятся на две группы:
никель-цинковые (NiO-ZnO-Fe2O3) и марганец-цинковый (MnO-ZnO-Fe2O3). Цинковые ферриты добавляют в магнитные ферриты
для увеличения магнитной проницаемости и уменьшения коэрцитивной силы, но это
приводит к снижению температурной стабильности магнитных свойств.
Значения величин mн и Hc определяется составом и
структурой материала. Микроскопические поры, участки с дефектной
кристаллической решеткой и др. мешают свободному перемещению доменных границ и являются
причиной уменьшения магнитной проницаемости. С увеличением размера
кристаллических зерен возрастает mн.
В слабых переменных магнитных полях ферриты обладают
незначительными потерями на вихревые токи и гистерезис. Поэтому значение
тангенса угла потерь tgd на высоких частотах в
основном определяется магнитными потерями, обусловленными релаксационными и
резонансными явлениями. Частота, при которой начинается резкое возрастание tgd
называется критической fкр. Обычно fкр - это частота, при
которой tgd = 0.1.
Инерционность смещения доменных границ, которая проявляется
на высоких частотах приводит также к снижению магнитной проницаемости ферритов.
Частоту fгр, при которой mн уменьшается до 0.7 от ее
значения в постоянном магнитном поле называют граничной. Как правило, fкр < fгр.
Марганец - цинковые ферриты в области частот до 1 МГц
обладают лучшими магнитными свойствами, чем никель - цинковые. У них меньший
относительный тангенс угла потерь - tgd/mн, более высокая индукция
насыщения и температура Кюри. Однако никель-цинковые ферриты обладают более
высоким удельным сопротивлением и лучшими частотными свойствами. Чем больше mн, тем при более низких частотах наблюдается ее снижение. Ферриты с
большим значением mэфф обладают большим значением tgd
и меньшим fкр [3, 9].
Во избежание ухудшения магнитных характеристик, ферриты
следует оберегать от механических нагрузок.
Маркировка магнито-мягких ферритов следующая. На первом месте
стоит численное значение mн, следующее за ним буквы
Н и В означают соответственно низкочастотный (fкр = 0.1-50МГц) или
высокочастотный (fкр = 50 - 600МГц) материал, стоящая далее буква М означает
марганец-цинковый, большая Н - никель-цинковый, литий - цинковый и т.д.
ферриты. Буква С означает, что феррит применяется в области сильных полей, Н -
контурах, перестраиваемых подмагничиванием.
По электрическим свойствам ферриты относятся к
полупроводникам с электронной проводимостью. Их электропроводность обусловлена
слабосвязанными электронами, которые принадлежат ионам железа или другим
катионам переменной валентности. Такие электроны под влиянием теплового
движения могут переходить от иона Fe2+ к иону Fe3+, который превращается в двухвалентный ион Fe2+ и сохраняет это свойство
некоторое время. С увеличением концентрации ионов Fe2+ возрастает удельная
проводимость и уменьшается энергия активации Э0. Рост температуры
сопровождается резким повышением проводимости из-за увеличения числа
перемещающихся электронов [9, c.171].
s=s0 exp [-Э0/кТ],
где s0 - постоянная величина для данного
материала;
Э0 - энергия активации электропроводности (Э0 =
0.1 - 0.5 ЭВ).
Концентрация двухвалентных ионов Fe2+ зависит
от состава феррита и режима его обжига. Для снижения концентрации Fe2+ вводят различные добавки. Процессы поляризации ферритов и
диэлектрические потери определяются дрейфом слабосвязанных электронов под
действием электрического поля. С ростом частоты поля уменьшается число
электронов, которые участвует в дрейфе, и уменьшается расстояние, на которое
они смещаются, и соответственно снижается поляризованность. Например на
частотах ниже 1000 Гц у марганец-цинковых ферритов величина e ~ 100000, а с увеличением частоты e резко падает до значения порядка 100.
Частотные характеристики диэлектрических потерь имеют максимум.
Магнитомягкие ферриты применяются в качестве сердечников контурных
катушек постоянной и переменной индуктивности, сердечников импульсных
трансформаторов, трансформаторов развертки телевизоров, магнитных модуляторов и
усилителей. Из них изготавливают стержневые магнитные антенны, индуктивные линии
задержки и др. Монокристаллы магнитомягких ферритов применяются при
изготовлении магнитных головок записи и воспроизведения сигнала звукового и
видеодиапазонов в магнитофонах, т.к. они обладают высоким удельным
сопротивлением (что важно для уменьшения потерь) и большей твердостью по
сравнению с металлическими.
Магнитодиэлектрики - это композиционные магнитомягкие материалы,
состоящие из ферромагнетика и диэлектрика, применяемого в качестве связующего
электроизоляционного материала. Основа должна обладать высокими магнитными
свойствами, а связка - способностью образовывать между зернами сплошную
электроизоляционную пленку одинаковой толщины. В качестве основы применяют
карбонильное железо, альсифер, молибденовый пермаллой. Изолирующей связкой
служат фенолформоальдегидные смолы, полистирол, стекло и др.
Суммарные потери мощности в магнитодиэлектрике определяются
потерями на вихревые токи, последействие, гистерезис и диэлектрическими
потерями. С уменьшением размера частиц ферромагнетика потери снижаются, особенно
обусловленные вихревыми токами. Магнитная проницаемость магнитодиэлектриков (mн = 10 - 250) ниже магнитной проницаемости монолитных
ферромагнетиков. Это связанно с тем, что изолированные друг от друга
ферромагнитные частицы создают внутреннее поле, направленное навстречу
внешнему, и слабо выражен механизм намагничивания за счет смещения доменных
границ, определяющий значение mн [3, 9].
Из-за сильного влияния размагничивающего фактора
магнитодиэлектрики имеют близкую к линейной зависимость индукции от напряженности
магнитного поля и характеризуются незначительными потерями на гистерезис.
Достоинства магнитодиэлектриков: малые удельные потери энергии,
слабая зависимость параметров от температуры, времени и напряженности
магнитного поля, постоянство магнитной проницаемости в диапазоне частот, а
недостаток - сравнительно малая начальная магнитная проницаемость.
Прессованные сердечники из магнитодиэлектриков применяются в
катушках индуктивности контуров радиоприемных устройств, генераторов, фильтров
и т.д.
магнитный материал магнитомягкий феррит
Сердечники на основе карбонильного железа обладают высокой
стабильностью, малыми потерями, положительным температурным коэффициентом
магнитной проницаемости и могут использоваться в широком диапазоне частот.
Карбонильное железо получается посредством термического разложения
пентакарбоната железа в виде тонкого порошка, что удобно для изготовления
прессованных магнитных сердечников. В карбонильном железе отсутствует кремний,
фосфор, сера, но содержится углерод.
Промышленность выпускает два класса карбонильного железа: Р
(марки Р-10, Р-20, Р-100) - для радиоаппаратуры и Пс - для проводной
связи. Цифры указывают максимальную рабочую частоту в МГц.
Альсифер обладает невысокой стоимостью. Его температурный
коэффициент магнитной проницаемости зависит от содержания алюминия и кремния и
может быть положительным, отрицательным или равным нулю [5].
1.4 Магнитные
материалы специального назначения
К магнитным материалам специального назначения относят
магнитные материалы с прямоугольной петлей гистерезиса, СВЧ ферриты,
магнитострикционные материалы. Магнитные материалы с прямоугольной петлей
гистерезиса (ППГ) находят широкое применение в устройствах автоматики,
аппаратуре связи. Сердечники из материала с ППГ имеют два устойчивых магнитных
состояния, которые соответствуют различным направлениям магнитной индукции. Это
свойство используется для хранения и переработки двоичной информации. Материалы
с ППГ характеризуются коэффициентом прямоугольности kпу петли гистерезиса.
kпу = Br/Bmax
Большим значением kпу обладают железоникелевые и
железокобальтовые сплавы, легированные медью и некоторыми другими металлами.
Эти сплавы обладают кристаллографической или магнитной текстурой. Наиболее
высокую прямоугольность (до 0,98) имеют железоникелькобальтовые сердечники из
лент микронной толщины.
Более широко распространены ферриты с ППГ, сердечники из которых
более технологичны и дешевле. Прямоугольность петли гистерезиса достигается
выбором определенного химического состава и условиями спекания феррита. Для
сердечников с ППГ чаще применяются магний-марганцевые и литиевые ферриты [5,
9].
Ферромагниты для устройств СВЧ используются в диапазоне длин волн
от 1м до 1 мм. Электромагнитная энергия на таких частотах передается по
волноводам, коаксиальным и полосковым линиям передачи. Ферритовый сердечник -
вкладыш, помещенный внутрь волновода, изменяет структуру поля и скорость
распространения волны. На этих частотах в ферритах используется
магнитооптический эффект Фарадея, эффект ферромагнитного резонанса и
зависимость магнитной проницаемости от величины внешнего поля.
Магнитооптический эффект Фарадея заключается в повороте плоскости
поляризации высокочастотных колебаний в феррите за счет внешнего поля. Это
позволяет изменять угол поворота плоскости поляризации и направлять энергию в
разные каналы.
Ферромагнитный резонанс наблюдается при совпадении частоты
внешнего поля с собственно частотой прецессии электронов, которой можно
управлять с помощью постоянного подмагничивающего поля. При резонансе, волна
распространяющаяся в прямом направлении, проходит без затухания, а в обратном -
с затуханием. В результате получается высокочастотный вентиль. Это явление
используется в антенных переключателях, в фазовращателях, модуляторах и т.д.
Для каждого диапазона длин волн используется определенная
разновидность феррита. Например, для диапазона длин волн 0,8 - 2 см
используются некоторые никель-цинковые ферриты, для диапазона 5 см и более
используют ферриты с добавками хрома (феррохроматы) или алюминия
(ферроалюмиты); феррогранат используется в диапазоне волн несколько десятков
сантиметров. Ферриты СВЧ маркируются буквами СЧ, впереди которых стоит цифра,
указывающая длину волны в см. Цифра после букв СЧ указывает различие по
свойствам. В магнитострикционных материалах используется явление
магнитострикции и магнитоупругий эффект - изменение магнитных свойств материала
под влиянием механических воздействий. К магнитострикционным материалам
относится никель, пермендюр (сплавы FeCo),
альферы (сплавы FeAl), никелевый и никель-кобальтовые ферриты
и др. Магнитострикционные ферриты имеют малые потери на вихревые токи по
сравнению с никелем и металлическими сплавами, не подвержены действию
химических агрессивных сред.
С помощью керамической технологии можно изготовить преобразователи
любых форм и размеров. Магнитострикционные материалы применяются для
изготовления сердечников электромеханических преобразователей для
электроакустической и ультразвуковой технике, сердечника электромеханических и
магнитострикционных фильтров, резонаторов и линий задержек [9].
2. Цепи магнитного
тока и их характеристика
2.1 Общая
характеристика магнитного поля
Электромагнитное поле, которое лежит в основе всех
многообразных явлений и процессов, исследуемых в электротехнике, имеет две
равнозначные стороны - электрическую и магнитную. Как известно, в электрической
цепи под воздействием источников энергии возникают электрические токи, которые
протекают по электрическим проводам. Подобно электрическим цепям существуют
также магнитные цепи, состоящие из магнитных проводов или кратко магнитопроводов,
в которых под воздействием магнитодвижущих сил (МДС) возникают и замыкаются
магнитные потоки Ф. Формальную схожесть или аналогию между электрическими и
магнитными цепями в дальнейшем будем именовать принципом двойственности.
Следует помнить, что при формальной схожести электрические и магнитные явления
физически различны [1, 2].
Магнитные цепи применяются в электрических машинах,
трансформаторах, электромагнитных аппаратах, реле, приборах и т.д. Их
назначением является создание заданной величины и формы магнитного потока Ф (t)
и проведение его по заданному пути.
Как известно, магнитное поле характеризуется векторными величинами
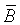 и
и 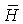 , между которыми существует связь
, между которыми существует связь 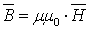 , где
, где 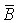 вектор индукции (или плотности)
магнитного поля [Тл],
вектор индукции (или плотности)
магнитного поля [Тл], 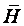 вектор напряженности магнитного
поля [А/м], который создается электрическим током и является первопричиной
магнитного поля,
вектор напряженности магнитного
поля [А/м], который создается электрическим током и является первопричиной
магнитного поля,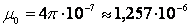 [Гн/м] магнитная проницаемость
пустоты,
[Гн/м] магнитная проницаемость
пустоты, 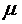 относительная магнитная
проницаемость, характеризующая способность материала к намагничиванию.
относительная магнитная
проницаемость, характеризующая способность материала к намагничиванию.
Способы составления системы операторных уравнений. При расчете
переходных процессов операторным методом на практике применяется два способа составления
системы операторных уравнений. Сущность 1-го способа состоит в том, что для
исходной электрической схемы составляется система дифференциальных уравнений по
законам Кирхгофа. Затем каждое слагаемое в этих уравнениях непосредственно
подвергается преобразованию Лапласа и таким образом система дифференциальных
уравнений преобразуется в соответствующую ей систему операторных уравнений.
Составление операторной схемы при этом не требуется.
Все материалы по способности их к намагничиванию условно разделяют
на две группы: ферромагнитные и неферромагнитные. Для ферромагнитных материалов
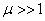 . К ним относятся железо (Fe), никель
(Ni), кобальт (Co) и их сплавы. Ферромагнитные материалы способны к
намагничиванию и создают малое магнитное сопротивление для магнитного потока,
поэтому применяются в технике для изготовления магнитопроводов. Для
неферромагнитных материалов
. К ним относятся железо (Fe), никель
(Ni), кобальт (Co) и их сплавы. Ферромагнитные материалы способны к
намагничиванию и создают малое магнитное сопротивление для магнитного потока,
поэтому применяются в технике для изготовления магнитопроводов. Для
неферромагнитных материалов 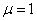 , они создают большое сопротивление магнитному потоку и в
магнитной цепи выполняют роль магнитных изоляторов.
, они создают большое сопротивление магнитному потоку и в
магнитной цепи выполняют роль магнитных изоляторов.
Следует отметить, что если в электрической цепи соотношение между
удельной проводимостью металла (провода) и диэлектрика (изоляция) составляет 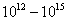 , то для магнитной цепи это соотношение
составляет всего около
, то для магнитной цепи это соотношение
составляет всего около 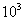 . Это означает, что изоляция в магнитных
цепях очень несовершенна, что в таких цепях существенная часть магнитного
потока рассеивается, т.е. замыкается через участки с несовершенной магнитной
изоляцией.
. Это означает, что изоляция в магнитных
цепях очень несовершенна, что в таких цепях существенная часть магнитного
потока рассеивается, т.е. замыкается через участки с несовершенной магнитной
изоляцией.
Зависимость между векторами 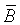 и
и 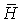 для ферромагнитных материалов не имеет
точного аналитического выражения, на графической диаграмме эта зависимость B=f
(H), имеет форму петли и называется петлей гистерезиса (рис. 1) [4, c.52 - 54].
для ферромагнитных материалов не имеет
точного аналитического выражения, на графической диаграмме эта зависимость B=f
(H), имеет форму петли и называется петлей гистерезиса (рис. 1) [4, c.52 - 54].
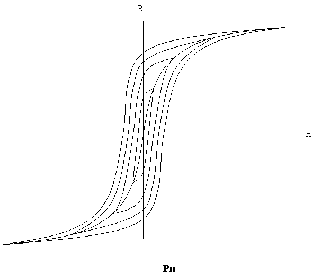
Рис. 1. - Характеристика магнитного поля
При периодическом перемагничивании материала с увеличением
амплитуды индукции Bm площадь петли гистерезиса увеличивается, а ее вершина все
больше смещается в область насыщения материала.
Кривая, проходящая через вершины симметричных петель гистерезиса,
называется основной кривой намагничивания B=f (H) для данного материала.
Сведения об основных кривых намагничивания B=f (H) для
ферромагнитных материалов, которые применяются в технике для изготовления
магнитопроводов, приводятся в справочной литературе в виде таблиц или
графических диаграмм и используются в инженерной практике для расчета магнитных
цепей [4, 10].
2.2 Порядок
расчета магнитной цепи электромагнитного реле
Пусть требуется выполнить расчет магнитной цепи
электромагнитного реле, состоящей из катушки с w витками, ярма (неподвижная
часть магнитопровода), якоря (подвижная часть магнитопровода) и воздушного
зазора между ярмом и якорем (рис.2а).
Геометрические размеры магнитной цепи заданы.
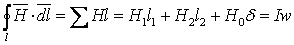
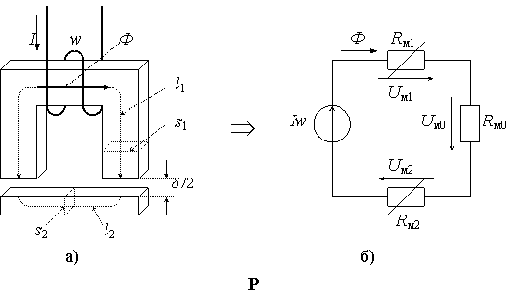
Рис. 2. - Схема магнитной цепи
В основе расчета магнитных цепей лежит известный из физики закон
полного тока:
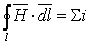
При применении закона полного тока к магнитной цепи ее разбивают
на отдельные однородные участки, для которых H=const, а контур интегрирования
выбирают вдоль магнитных линий. При выполнении этих условий интеграл по
замкнутому контуру заменяется суммой простых произведений 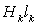 , а
, а 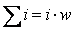 . Для рассматриваемого примера получим:
. Для рассматриваемого примера получим:
Здесь произведение 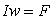 называется магнитодвижущей силой (МДС) или намагничивающей силой
(НС), является источником магнитного потока Ф.
называется магнитодвижущей силой (МДС) или намагничивающей силой
(НС), является источником магнитного потока Ф.
Слагаемые типа Hk·lk называются магнитным напряжением: 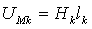 [A], а полученное выше уравнение
представляет собой второй закон Кирхгофа для магнитной цепи:
[A], а полученное выше уравнение
представляет собой второй закон Кирхгофа для магнитной цепи:
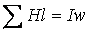 или
или 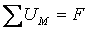
Из курса физики известно, что магнитные линии поля непрерывны. Из
этого следует, что магнитный поток Ф на всех участках неразветвленной магнитной
цепи имеем одно и то же значение 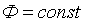 . Индукция поля
. Индукция поля 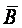 и напряженность поля
и напряженность поля 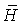 на отдельных участках будут различны:
на отдельных участках будут различны:
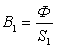 ;
; 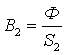 ;
; 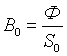
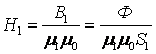 ;
;
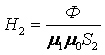 ;
;
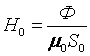 .
.
Сделаем подстановку в уравнение 2-го закона Кирхгофа:
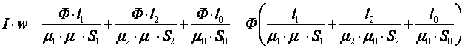
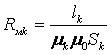
где R магнитное сопротивление к-го участка магнитной
цепи [6, 10].
Для сравнения: формула электрического сопротивления проводника
имеет аналогичную структуру:
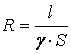 ,
,
В магнитной цепи электрической проводимости 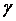 соответствует магнитная проницаемости
материала
соответствует магнитная проницаемости
материала 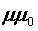 . Магнитные сопротивления для участков
магнитопровода зависят от магнитной проницаемости
. Магнитные сопротивления для участков
магнитопровода зависят от магнитной проницаемости 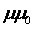 , которая является функцией магнитного
состояния (
, которая является функцией магнитного
состояния (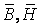 ). Следовательно, магнитные сопротивления
отдельных участков магнитопровода являются нелинейными и на схеме
представляются нелинейными элементами.
). Следовательно, магнитные сопротивления
отдельных участков магнитопровода являются нелинейными и на схеме
представляются нелинейными элементами.
Магнитное сопротивление зазора:
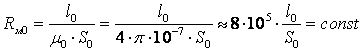
И, следовательно, является линейным элементом.
С учетом сказанного выше, рассматриваемая магнитная цепь может
быть представлена эквивалентной схемой с нелинейными элементами.
Для сложных магнитных цепей, имеющих разветвления и содержащих
несколько источников МДС, в полной мере соблюдаются оба закона Кирхгофа:
) 1-й закон Кирхгофа: 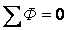 алгебраическая сумма магнитных потоков в узле магнитной
цепи равна нулю;
алгебраическая сумма магнитных потоков в узле магнитной
цепи равна нулю;
) 2-й закон Кирхгофа: 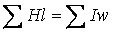 алгебраическая сумма падений магнитных напряжений в
замкнутом контуре магнитной цепи равна алгебраическая сумма МДС.
алгебраическая сумма падений магнитных напряжений в
замкнутом контуре магнитной цепи равна алгебраическая сумма МДС.
Магнитные цепи постоянного потока относятся к классу нелинейных
цепей. В силу принципа двойственности к их расчету применимы все методы расчета
нелинейных электрических цепей постоянного тока.
Следует отметить, что магнитные цепи обладают своими характерными
особенностями, которые вносят некоторые отличия в методы их расчета.
Аппроксимация вебер-амперных характеристик Uм=f (Ф)
нелинейных элементов магнитных цепей.
Как было уже сказано, в справочной литературе для каждого
типа ферромагнитного материала, применяемого для изготовления магнитопроводов,
приводятся сведения об основной кривой намагничивания B=f (H) в виде таблицы
координат точек или в виде графической диаграммы этой функции (рис.3).
Вебер-амперные характеристики (ВАХ) Uм=f (Ф) отдельных однородных
участков магнитной цепи рассчитывается через их геометрические размеры по
основной кривой намагничивания: 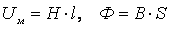 . Вследствие пропорциональной зависимости
. Вследствие пропорциональной зависимости 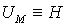 и
и 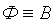 графические диаграммы ВАХ отдельных участков магнитной цепи будут
в некотором линейном масштабе подобны диаграмме кривой намагничивания B=f (H)
(рис.3) [6,c.44-46].
графические диаграммы ВАХ отдельных участков магнитной цепи будут
в некотором линейном масштабе подобны диаграмме кривой намагничивания B=f (H)
(рис.3) [6,c.44-46].
В аналитических методах расчета магнитных цепей применяется
аппроксимация Uм=f (Ф) для отдельных участков. Рассмотрим эту процедуру на
примере аппроксимации основной кривой намагничивания B=f (H) (рис. 3).
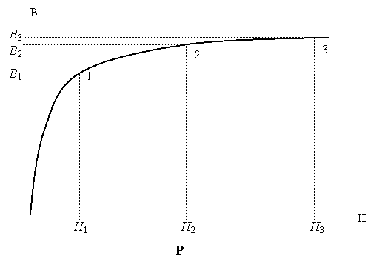
Рис. 3. - Кривая намагничивания B=f (H)
Для аппроксимации ВАХ, симметричных относительно начала координат,
используют нечетные математические функции, например, степенной полином с
нечетными степенями или уравнение гиперболического синуса: 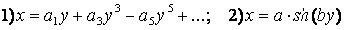 .
.
Выберем для аппроксимации основной кривой намагничивания степенной
полином усеченного вида: 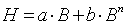 . Коэффициенты аппроксимации a, b, n можно
определить по методу выбранных точек. Для этой цели на графической диаграмме
(или в таблице координат) функции B=f (H) выбираются три точки 1, 2, 3 (по
числу определяемых коэффициентов), как показано на рис.3. и определяются их
координаты, например: 1 (1,0 Тл, 100 А/м), 2 (1,4 Тл, 500А/м), 3 (1,5 Тл, 800
А/м). Так как функция B=f (H) в области насыщения описывается в основном вторым
слагаемым bBn, то для точек 2 и 3 можно приближенно принять:
. Коэффициенты аппроксимации a, b, n можно
определить по методу выбранных точек. Для этой цели на графической диаграмме
(или в таблице координат) функции B=f (H) выбираются три точки 1, 2, 3 (по
числу определяемых коэффициентов), как показано на рис.3. и определяются их
координаты, например: 1 (1,0 Тл, 100 А/м), 2 (1,4 Тл, 500А/м), 3 (1,5 Тл, 800
А/м). Так как функция B=f (H) в области насыщения описывается в основном вторым
слагаемым bBn, то для точек 2 и 3 можно приближенно принять:

Так как показатель степени n должен быть целым нечетным числом, то
принимаем n=7 [6, 8].
Коэффициенты a и b определяются из совместного решения системы
уравнений для точек 1 и 2:
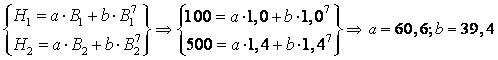
Уравнение аппроксимации примет окончательный вид:
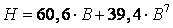 .
.
При аппроксимации основной кривой намагничивания уравнением
гиперболического синуса 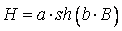 коэффициенты аппроксимации определяются
также по методу выбранных точек. Используем для этой цели координаты точек 1 и
2:
коэффициенты аппроксимации определяются
также по методу выбранных точек. Используем для этой цели координаты точек 1 и
2:

Совместное решение этих уравнений позволяет определить
коэффициенты a и b:
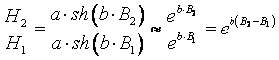 ,
,
откуда следует
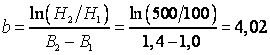 ;
;
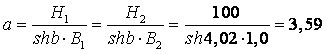 .
.
Уравнение аппроксимации примет окончательный вид:
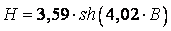 .
.
Уравнения аппроксимации используются в аналитических методах
расчета магнитных цепей.
2.3 Анализ
магнитных цепей постоянного тока
Суть анализа сводится к определению основных параметров
магнитных цепей: Н, Ф, В, I, S.
При этом пользуются понятиями магнитодвижущей силы, закона полного
тока, магнитного напряжения 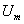 и магнитного сопротивления
и магнитного сопротивления 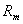 .
.
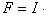 v
v
Связь между магнитодвижущей силой F и напряженностью магнитного
поля Н устанавливает закон полного тока [7, 10]:
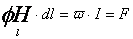
При анализе магнитных цепей пользуются значением средней линии
магнитопровода, поэтому
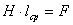
Произведение:
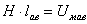
называют магнитным напряжением участка цепи длиной ав.
Если магнитная цепь содержит два неоднородных участка длиной 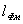 и
и 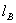 , то справедливо:
, то справедливо:
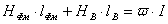
или имеет вид:
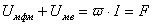
Таким образом алгебраическая сумма магнитных напряжений на
участках цепи равна магнитодвижущей силе обмотки. Выражение (8.11) представляет
собой второй закон Кирхгофа для магнитной цепи.
Аналогично первого закона Кирхгофа является теорема Гауса: поток
вектора магнитной индукции через любую замкнутую поверхность равен нулю:
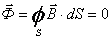
Рассмотрим выражение для магнитногонапряжения:
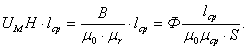
Обозначим выражение:
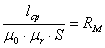
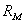 называется магнитным сопротивлением.
называется магнитным сопротивлением.
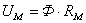
Равенство (2.29) представляет собой закон Ома для магнитной цепи.
Если основной характеристикой электрической цепи является
вольт-амперная характеристика, то для магнитной цепи - это ампер-веберная
характеристика - зависимость между магнитным потоком и намагничивающим током 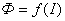 (рис. 4).
(рис. 4).
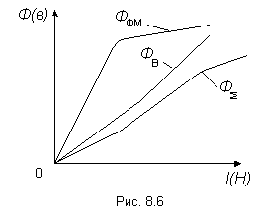
Рис. 4. - Зависимость между магнитным потоком и намагничивающим
током
На рис.4 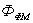 - поток в ферромагнитном материале,
- поток в ферромагнитном материале, 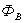 - поток в воздушном зазоре,
- поток в воздушном зазоре, 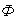 å - результирующий поток. На практике
используется зависимость
å - результирующий поток. На практике
используется зависимость 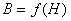 , так как Н пропорциональна
намагничивающему току I, а В пропорциональна магнитному потоку Ф.
, так как Н пропорциональна
намагничивающему току I, а В пропорциональна магнитному потоку Ф.
Особенности физических процессов в магнитных цепях переменного
тока
При анализе магнитных цепей переменного тока вводят следующие
допущения, что магнитное поле рассеяния отсутствует, а активное сопротивление
обмотки равно нулю [8].
При таких допущениях можно записать

где 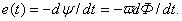
Отсюда следует, что магнитный поток в магнитопроводе переменный и
определяется напряжением (воздействием):
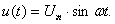
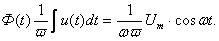
Таким образом, закон изменения магнитного потока Ф (t) не зависит
от параметров цепи. Это первая особенность магнитных цепей переменного тока.
Чтобы определить вторую особенность обратимся к известному выражению
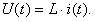
Из него следует, что
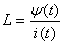
Но для простейшей магнитной цепи справедливы уравнения:
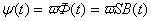
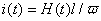 .
.
Переменные В (t) и Н (t) связаны по закону динамической петли
гистерезиса. Эта связь нелинейна. Значит зависимость (2.37) тоже нелинейна, а
индуктивность переменна. Это вторая особенность.
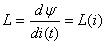
Индуктивность обмотки магнитопровода непостоянна и зависит от тока
цепи, а уравнение 2.39 нелинейно.
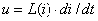 .
.
Отсюда третья особенность: магнитные цепи являются нелинейными
цепями, поэтому при синусоидальном напряжении на обмотке ток в ней оказывается
несинусоидальным.
Изменение магнитного потока Ф (t) c частотой w приводит к нагреву магнитопровода из-за
гистерезиса. Следовательно, в магнитопроводе возникают потери электроэнергии.
Их называют магнитными потерями. Это четвертая особенность.
Теоремы об источниках тока и напряжения и их применение для
расчета цепей. Принцип суперпозиции и его применение для расчета цепей. Расчет
цепей методами наложения и эквивалентного генератора. Примеры и особенности
расчета цепей данными методами. Расчет цепей методом преобразования
треугольника сопротивлений в звезду сопротивлений и наоборот. Потенциальная
диаграмма. Способы решения систем алгебраических уравнений [8, 10].
2.4
Практический расчет магнитной цепи
Пусть задано:
) геометрические размеры магнитной цепи;
) характеристика B = f (H) (кривая намагничивания) ферромагнитных материалов, из которых
выполнена магнитная цепь;
) магнитный поток Ф, который надо создать в магнитной цепи.
Требуется найти намагничивающую силу обмотки F = IW.
Решение задачи рассматривается применительно к
магнитопроводу, представленному на рис. 5.
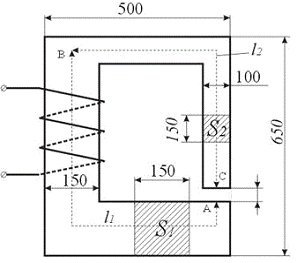
Рис. 5. Магнитная цепь
. Магнитная цепь разбивается на ряд участков с одинаковым
поперечным сечением S, выполненном из однородного материала.
. Намечается путь прохождения средней магнитной линии (на рис.4.7
показано пунктиром).
. Т.к. магнитный поток на всех участках цепи остается постоянным,
то магнитная индукция B = Ф / S на каждом из участков и напряженность магнитного поля Н
неизменны. Это позволяет сравнительно просто определить значение 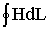 для контура, образованного средней
магнитной линией, а следовательно, найти искомую величину намагничивающей силы,
поскольку
для контура, образованного средней
магнитной линией, а следовательно, найти искомую величину намагничивающей силы,
поскольку 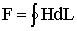 .
.
Запишем интеграл 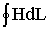 в виде суммы интегралов с границами интегрирования, совпадающими
с началом и концом каждого участка цепи. Тогда
в виде суммы интегралов с границами интегрирования, совпадающими
с началом и концом каждого участка цепи. Тогда
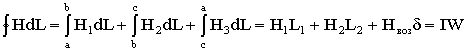 .
.
где: L1 и L2 - длины ферромагнитных участков цепи [м].
δ - ширина воздушного зазора, [м].
. Значения Н1 и Н2 определяют по известным
величинам магнитной индукции В с помощью кривых намагничивания, соответствующих
ферромагнитных материалов.
А для воздушного зазора
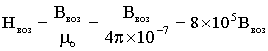 А/м.
А/м.
Обратная задача
Задано:
1. Геометрические размеры магнитной цепи;
2. Характеристики ферромагнитных
материалов;
. Намагничивающая сила обмотки F.
Непосредственное использование формулы:
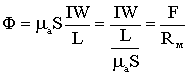
для определения магнитного потока Ф оказывается невозможным,
поскольку магнитное сопротивление цепи переменное и само зависит от величины
магнитного потока. Такие задачи решаются методом последовательного приближения
в следующем порядке. Задаются рядом произвольных значений магнитного потока в
цепи и для каждого из этих значений определяют необходимую намагничивающую силу
обмотки так, как это делается при решении прямой задачи.
По полученным данным строят кривую Ф (F) - вебер-амперную характеристику. Имея эту зависимость, нетрудно
для заданного значения намагничивающей силы найти величину магнитного потока.
Для оценки необходимого значения Ф можно пренебречь сопротивлением
ферромагнитного участка и посчитать поток, который получится под действием
намагничивающей силы F при
сопротивлении воздушного участка. Это значение Ф заведомо больше расчетного.
Остальные значения можно давать меньше.
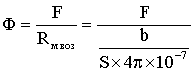
Заключение
Формальная аналогия между электрическими и магнитными цепями
позволяет распространить все методы и технику расчета нелинейных резистивных
цепей постоянного тока на нелинейные магнитные цепи. При этом для наглядности
можно составить эквивалентную электрическую схему замещения исходной магнитной
цепи, с использованием которой выполняется расчет. Нелинейность магнитных цепей
определяется нелинейным характером зависимости 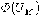 , являющейся аналогом ВАХ
, являющейся аналогом ВАХ 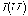 и определяемой характеристикой ферромагнитного материала
и определяемой характеристикой ферромагнитного материала 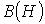 . При расчете магнитных цепей при
постоянных потоках обычно используют основную кривую намагничивания.
Петлеобразный характер зависимости
. При расчете магнитных цепей при
постоянных потоках обычно используют основную кривую намагничивания.
Петлеобразный характер зависимости 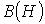 учитывается при расчете постоянных магнитов и электротехнических
устройств на их основе.
учитывается при расчете постоянных магнитов и электротехнических
устройств на их основе.
При расчете магнитных цепей на практике встречаются типичные
задачи:
- задача определения величины
намагничивающей силы (НС), необходимой для создания заданного магнитного потока
(заданной магнитной индукции) на каком - либо участке магнитопровода
("прямая" задача);
- задача нахождения потоков (магнитных
индукций) на отдельных участках цепи по заданным значениям НС (задача анализа
или "обратная” задача).
Следует отметить, что задачи второго типа являются обычно
более сложными и трудоемкими в решении. В общем случае в зависимости от типа
решаемой задачи ("прямой" или "обратной") решение может
быть осуществлено регулярными, графическими и итерационными методами.
При этом при использовании каждого из этих методов
первоначально необходимо указать на схеме направления НС, если известны
направления токов в обмотках, или задаться их положительными направлениями,
если их нужно определить. Затем задаются положительными направлениями магнитных
потоков, после чего можно переходить к составлению эквивалентной схемы
замещения и расчетам.
Список
использованной литературы
1. Волынский
В.А. и др. Электротехника /Б.А. Волынский, Е.Н. Зейн, В.Е. Шатерников: Учеб.
пособие для вузов. - М.: Энергоатомиздат, 2007. - 528с.
2. Касаткин
А.С., Немцов М.В. Электротехника: Учеб. пособие для вузов. - 4-е изд., перераб.
- М.: Энергоатомиздат, 2007. - 440 с.
. Материалы
в приборостроении и автоматике: Справочник / Под ред. Ю.М. Пятина. - М.:
Машиностроение, 1992. - 528 с.
. Матханов
П.А. Основы анализа электрических цепей. - М.: Высш. шк., 1990. - 400 с.
. Мишин
Д.Д. Магнитные материалы. Учеб. пособие для вузов. - 2-е изд., перераб. и доп.
- М.: Высш. шк., 1991. - 384 с.
. Основы
промышленной электроники: Учебник для неэлектротехн. спец. вузов /В.Г.
Герасимов, О М. Князьков, А Е. Краснопольский, В.В. Сухоруков; под ред.В.Г.
Герасимова. - 3-е изд., перераб. и доп. - М.: Высш. шк., 2008. - 336 с.
. Основы
теории цепей: Учебник для вузов/ Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В.
Страхов. - 5-е изд., перераб. - М.: Энергоатомиздат, 2007. - 528 с.
. Теоретические
основы электротехники. В 3-х ч. - Ч.I. Атабеков Г.И. Линейные электрические
цепи: Учебник для вузов. - 5-е изд., испр. и доп. - М.: Энергия, 2008. - 592 с.
. Шихин
А.Я. Испытание магнитных материалов и систем. - М.: ЭнергоАтомИздат, 1984. -
376 с.
. Электротехника
и электроника в 3-х кн. Под ред.В.Г. Герасимова Кн.1. Электрические и магнитные
цепи. - М.: Высшая шк. - 2009. - 386 с.