Прохождение сигнала сложной формы через линейную цепь
МИНОБРНАУКИ
РОССИИ
федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
«Балтийский
государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова»
(БГТУ
«ВОЕНМЕХ» им. Д.Ф. Устинова»)
Факультет
И «Информационные и управляющие системы»
Кафедра
И4 «Радиоэлектронные системы управления»
Дисциплина
(модуль) «Радиотехнические цепи и сигналы»
КУРСОВАЯ
РАБОТА
Прохождение
сигнала сложной формы через линейную цепь
Выполнила студент
группы И443
Сивова В.М.
Научный
руководитель
Аникин С.Н.
САНКТ-ПЕТЕРБУРГ
2016г
Введение
сигнал цепь спектральный импульс
Сигнал - физический процесс (или явление),
несущий информацию о состоянии какого-либо объекта наблюдения. Сигнал позволяет
переносить информацию в пространстве и времени. По своей физической природе
сигналы бывают электрическими, световыми, звуковыми и др. В радиотехнике
используются электрические или магнитные сигналы.Основная задача радиотехники
состоит в передаче информации на расстояние с помощью электромагнитных
колебаний. В более широком смысле современная радиотехника - область науки и
техники, связанная с генерацией, усилением, преобразованием, обработкой,
хранением, передачей и приемом электромагнитных колебаний радиочастотного
диапазона, используемых для передачи информации на расстояние.
Информация, наряду с материей и энергией,
относится к фундаментальным категориям естествознания и является одной из
движущих сил современного развития науки и техники. Но информация не относится
к числу материальных объектов и не существует в явной физической форме.
Данная курсовая работа направлена на закрепление
материала по курсу «Радиотехнические цепи и сигналы», который раскрывает
разновидности сигналов, их характеристики и свойства. Основной целью данного курса
является усвоение закономерностей обработки, передачи, преобразования, хранения
и приёма радиотехнических сигналов.
Аналитическое и графическое представления
исходного сигнала
Заданный сигнал можно разделить на отрезки и
записать в виде системы:
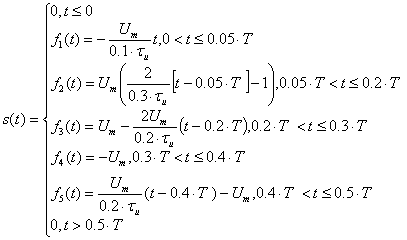
где:  ,
, ,
,
Используя функцию Хевисайда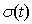 , выражение
, выражение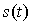 можно
представить следующим образом[1]:
можно
представить следующим образом[1]:
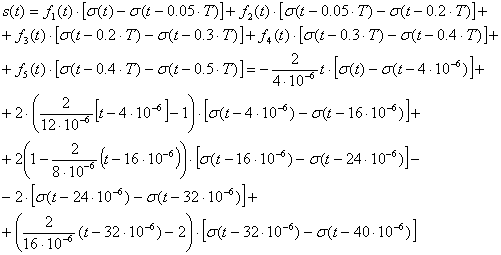
Графическое изображение сигнала
изображено на рисунке 1:
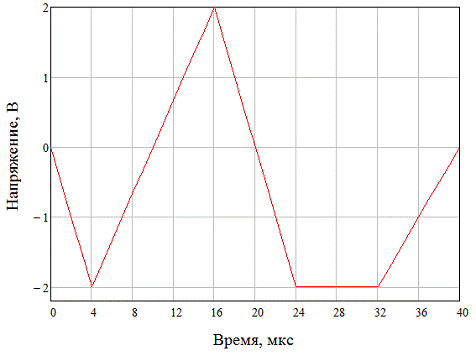
Рисунок 1. Исходный импульсный
сигнал
Спектральный анализ непериодического сигнала
Аналитическое выражение спектральной плотности
Спектральная плотность сигнала
находится путём подстановки выражения 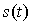 , в прямое преобразование Фурье и
вычислением интеграла вида:
, в прямое преобразование Фурье и
вычислением интеграла вида:
|
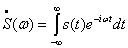 (2.1) (2.1)
|
|
Аналитическое представление заданного сигнала:

Графическое представление модуля и
аргумента спектральной плотности
Модуль спектральной плотности 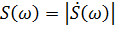 определяет
АЧХ сигнала, а ее аргумент
определяет
АЧХ сигнала, а ее аргумент 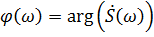 называют ФЧХ сигнала. Смысл модуля
называют ФЧХ сигнала. Смысл модуля определяется как амплитуда сигнала, приходящаяся на 1 Гц в бесконечно узкой
полосе частот, которая включает в себя рассматриваемую частоту
определяется как амплитуда сигнала, приходящаяся на 1 Гц в бесконечно узкой
полосе частот, которая включает в себя рассматриваемую частоту  .
.
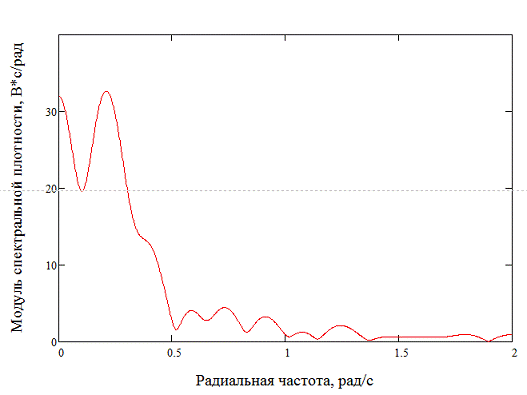
Рисунок 2. Модуль спектральной
плотности
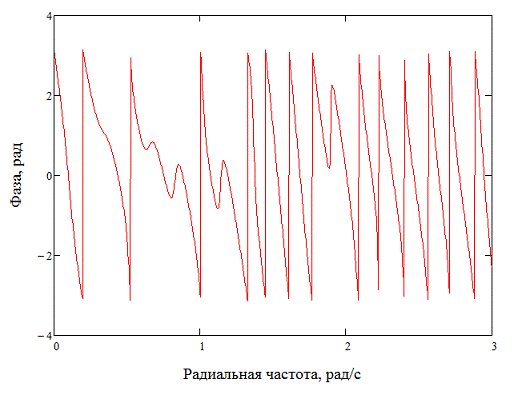
Рисунок 3. Аргумент спектральной
плотности
Эффективная ширина спектра
Эффективная ширина спектра
определяется как ширина спектральной плотности, при которой ее значение больше
или равно 10% от максимального значения. По рисунку 2 эффективная ширина
спектра примерно равна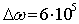 рад/с.
рад/с.
Эффективная длительность сигнала
Эффективную длительность сигнала
можно определить из формулы:
|
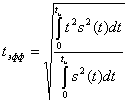 (2.2) (2.2)
|
|
Для заданного сигнала эффективная
длительность 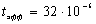 с.
с.
Энергия сигнала
Энергия сигнала определяется по
формуле:
|
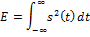
|
(2.3)
|
Для заданного сигнала:
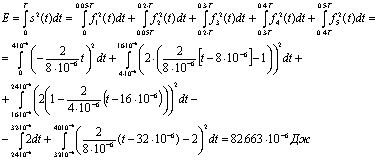
Спектрограмма сигнала, задержанного на половину
длительности импульса
Исходный сигнал сдвигается на:
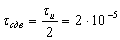 с.
с.
Спектральная плотность сдвинутого
сигнала:
|
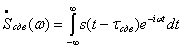 (2.4) (2.4)
|
|
Для данного сигнала его аналитическое
представление имеет вид:
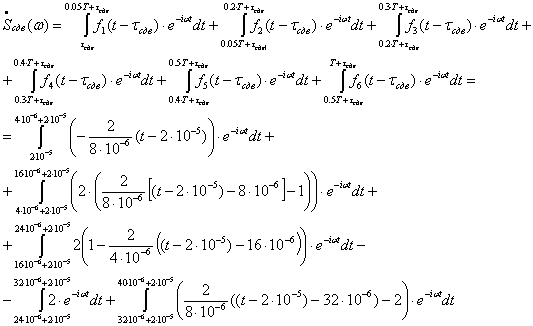
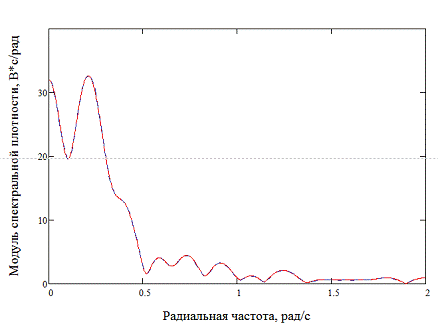
Рисунок 4. Модули спектральной
плотности заданного и сдвинутого сигналов
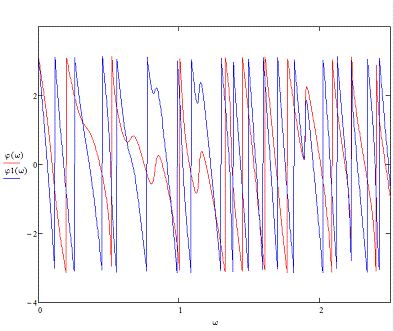
Рисунок 5. Аргументы спектральной
плотности заданного и сдвинутого сигналов
Из графиков видно, что при сдвиге
сигнала фазовая характеристика изменяется, амплитудная остается неизменной.
Спектральный анализ периодического
сигнала
Представление сигнала рядом Фурье
(амплитудный и фазовый спектры)
Сигнал представляется рядом Фурье
формулой:
|
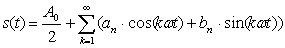 (3.1) (3.1)
|
|
где:
Круговая частота сигнала
определяется по формуле:
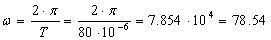 рад\с
рад\с
Амплитудный спектр сигнала (рисунок
5) представляется следующим выражением:
|
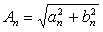 (3.2) (3.2)
|
|
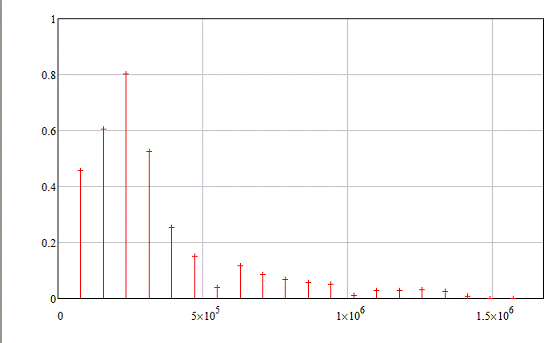
Рисунок 5. Амплитудный спектр периодического
сигнала
Фазовый спектр сигнала (рисунок 6)
представляется следующим выражением
|
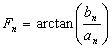 (3.3) (3.3)
|
|
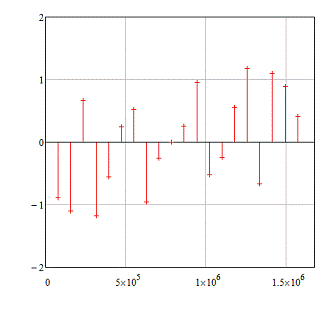
Рисунок 6. Фазовый спектр периодического сигнала
Сигнал, представленный рядом Фурье:
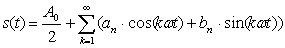
Полученный сигнал (из 70 гармоник)
изображен на рисунке 7.
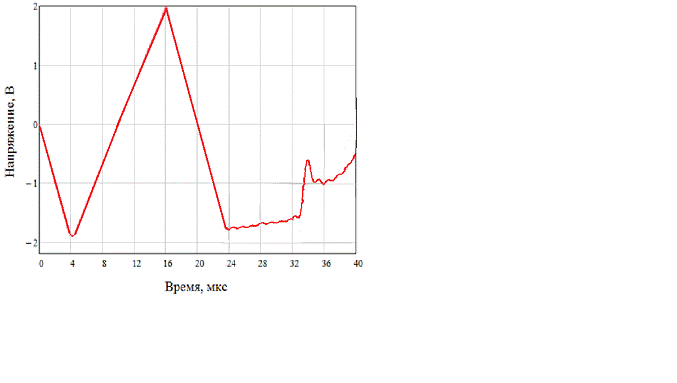
Рисунок 7. Полученный импульсный
сигнал
Данный рисунок, полученный после
обратного преобразования Фурье, совпадает с рисунком 1. Для большей точности
совпадения полученного сигнала с исходным сигналом можно увеличить число
гармоник.
Средняя мощность периодического
сигнала
Средняя мощность сигнала
определяется как отношение энергии сигнала к его периоду
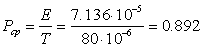 Вт.
Вт.
Анализ характеристик исходной
линейной цепи
Аналитическое выражение коэффициента
передачи цепи
Исходная схема выглядит следующим
образом:
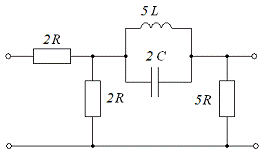
Рисунок 8. Исходная схема
электрической цепи
Преобразуем участок цепи типа
«треугольник» к типу «звезда», и преобразуем всю цепь к виду:

Рисунок 9. Преобразованная схема электрической
цепи
В результате преобразования получим следующие
сопротивления участков цепи:
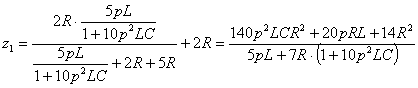 ,
,
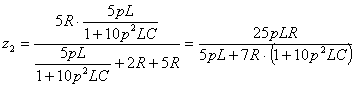 ,
,
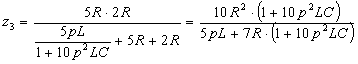 .
.
Из системы уравнения
четырехполюсников
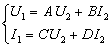
в режиме холостого хода коэффициент
передачи по напряжению 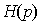 равен:
равен:
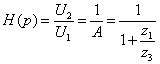
Коэффициент передачи заданной
линейной цепи будет равен:
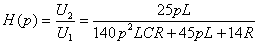
Передаточная характеристика
определяется из коэффициента передачи путем подстановки 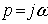 :
:
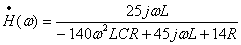
Графики АЧХ и ФЧХ цепи
Амплитудно-частотная характеристика (рисунок 10)
определяется по формуле:
|
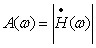 (4.1) (4.1)
|
|
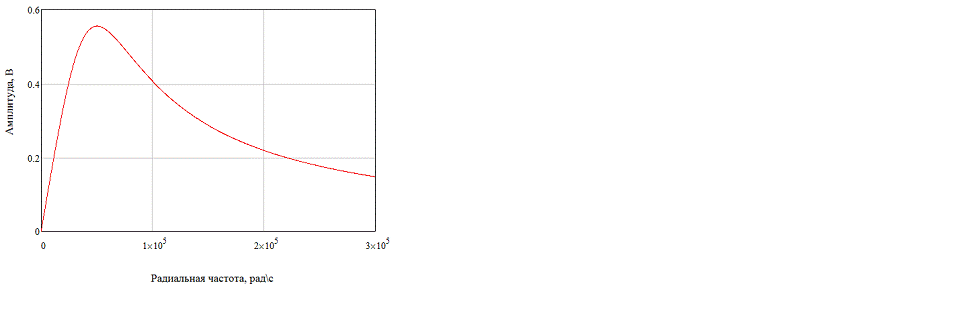
Рисунок 10. АЧХ цепи
Фазо-частотная характеристика (рисунок 11)
определяется по формуле:
|
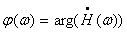 (4.2) (4.2)
|
|
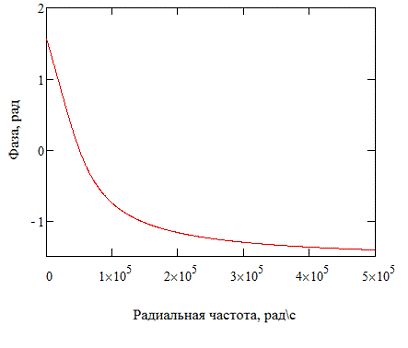
Рисунок 11. ФЧХ цепи
Аналитическое выражение и график импульсной
характеристики цепи
Расчет импульсной характеристики
цепи h(t) выполняется с помощью обратного преобразования Лапласа от
коэффициента передачи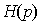 .
.
Представим коэффициент передачи как 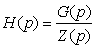 .
.
С этой целью найдем полюсы 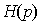 ,
соответствующие корням уравнения
,
соответствующие корням уравнения
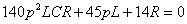 .
.
Корни этого уравнения 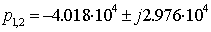 .Подставим
их в формулу для импульсной характеристики:
.Подставим
их в формулу для импульсной характеристики:
|
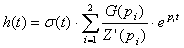 (4.3) (4.3)
|
|
График импульсной характеристики представлен на
рисунке 12.
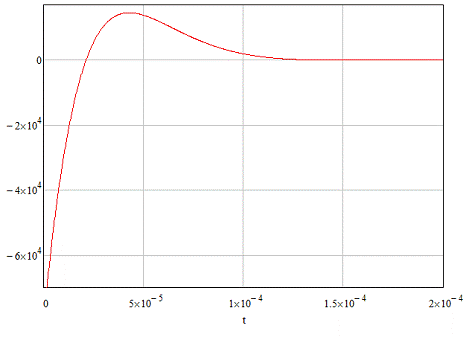
Рисунок 12. Импульсная характеристика
Аналитическое выражение и график переходной
характеристики цепи
Переходная характеристика связана с импульсной
характеристикой следующей формулой:
|
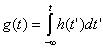 (4.4) (4.4)
|
|
График переходной характеристики представлен на
рисунке 13.
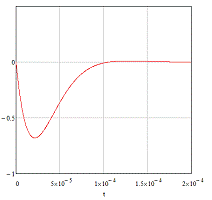
Рисунок 13. Переходная характеристика
Анализ сигналов, полученных на выходе исходной
линейной цепи
Сигнал на выходе цепи определяется с помощью
следующего интеграла:
|
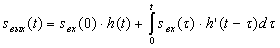 (5.1) (5.1)
|
|
Сигналы на выходе цепи получены с помощью САПР
OrCAD 9.2 для моделирования прохождения заданных сигналов через заданную цепь.
Графическое представление непериодического
сигнала на выходе цепи
При подаче на вход цепи непериодического
заданного сигнала, на выходе получится сигнал, показанный на рисунке 14.
Рисунок 14. Сигнал на выходе цепи при подаче
непериодического сигнала
Графическое представление периодического сигнала
на выходе цепи
При подаче на вход цепи периодического заданного
сигнала, на выходе получится сигнал, показанный на рисунке 15.
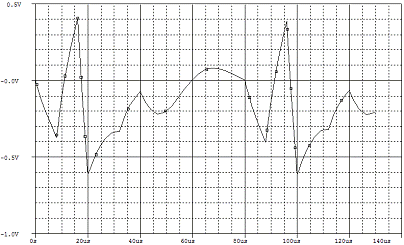
Рисунок 15. Сигнал на выходе цепи при подаче
периодического сигнала
Корреляционный анализ сигналов
Аналитическое и графическое представление
корреляционной функции исходного непериодического сигнала
Рассчитаем автокорреляционную функцию сигнала по
формуле:
|
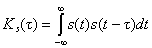 (6.1) (6.1)
|
|
Примем следующие условные обозначения:
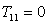 ,
, 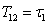 ;
;
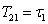 ,
, 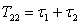 ;
;
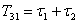 ,
, 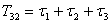 ;
;
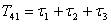 ,
, 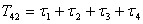 ;
;
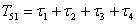 ,
, 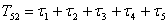 .
.
где 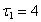 мкс,
мкс,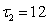 мкс,
мкс, 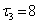 мкс,
мкс, 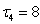 мкс,
мкс, 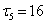 мкс.
мкс.
Расчет автокорреляционной функции
заданного сигнала сводится к вычислению интегралов на следующих интервалах
значений сдвига:
а) 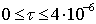

б) 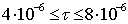
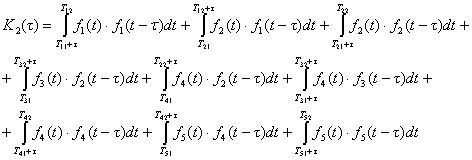
в)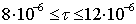
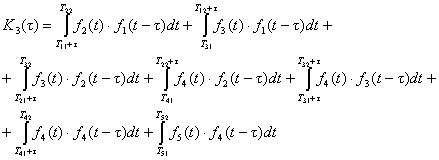
г) 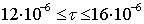
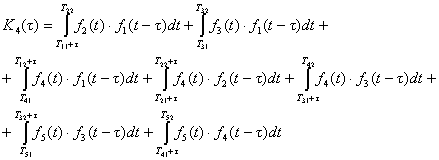
д) 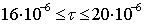
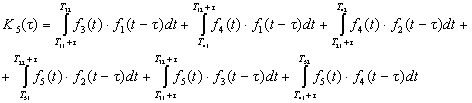
е) 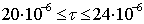
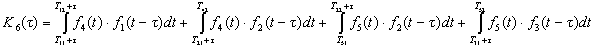 ж)
ж) 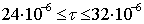
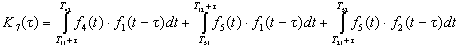
з) 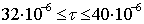
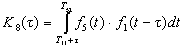
С учетом четной симметрии
автокорреляционной функции общее её выражение примет, следующий вид:
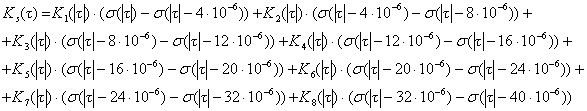
График 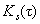 приведен на
рисунке 16.
приведен на
рисунке 16.
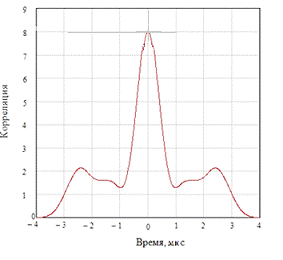
Рисунок 16. Корреляционная функция
исходного непериодического сигнала
Из графика видно, что корреляционная
функция, как и исходный сигнал, является непериодической.
Аналитическое и графическое представление
корреляционной функции исходного периодического сигнала
Расчет автокорреляционной функции периодического
сигнала производится по формуле
|
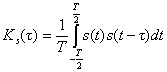 (6.2) (6.2)
|
|
График 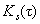 приведен на
рисунке 17.
приведен на
рисунке 17.

Рисунок 17. Корреляционная функция
исходного периодического сигнала
Аналогично предыдущему случаю,
корреляционная функция является периодической.
Влияние параметров цепи на АЧХ и ФЧХ
Рассмотрим влияние параметров
линейной цепи на её амплитудно- и фазочастотные характеристики.
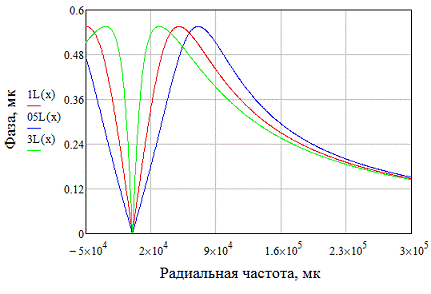
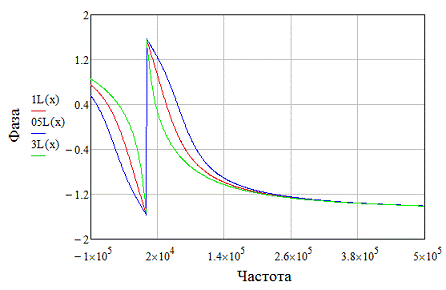
Рисунок 18. АЧХ и ФЧХ при изменении
индуктивности
При уменьшении сопротивления, АЧХ в
районе резонанса становится более пологой, что уменьшает добротность фильтра и
увеличивает его полосу подавления; ФЧХ также зависит от параметров цепи - чем
шире полоса подавления, тем более плавный спад фазы на частотах в полосе
подавления(рисунок 18).
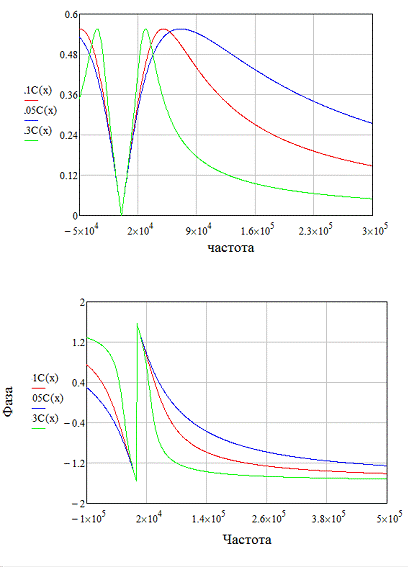
Рисунок 19. АЧХ и ФЧХ при изменении
емкости
При изменении емкости (рисунок 19),
минимум АЧХ и положение скачка на ℼ в ФЧХ смещаются по оси частот из-за
изменения центральной частоты подавления полосно-заграждающего или режекторного
фильтра; кроме того, изменяется ширина полоса заграждения из-за изменения
добротности колебательного контура, входящего в данный фильтр.
Аналогичные изменения происходят при
изменении сопротивления (рисунок 20).
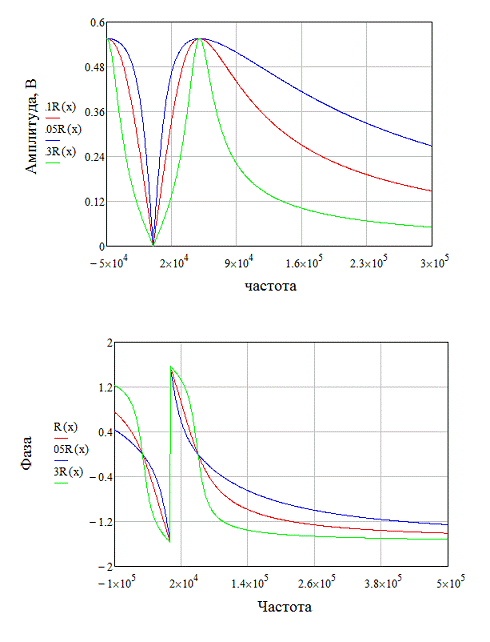
Рисунок 20. АЧХ и ФЧХ при изменении
сопротивления
Заключение
При выполнении курсовой работы был описан
исходный сигнал с помощью функции Хевисайда, определены спектральная плотность,
амплитудный и фазовый спектры сигнала. При вычислении спектральной плотности
были применены свойства преобразования Фурье. Автокорреляционная функция
сигнала имеела вид сглаженной кривой и максимум при τ=0.
Также
была проанализирована заданная линейная RC-цепь, определена комплексная передаточная
функция, из которой затем вычисляется амплитудно-частотная и фазо-частотная
характеристики. Виды АЧХ и ФЧХ были смоделированы в программной системе
компьютерной алгебры из класса систем автоматизированного
проектированияMathCAD, в дальнейшем подтвердившийся при моделировании в
программе Multisim 11. Далее была определена импульсная характеристика цепи,
которая при применении в интеграле Дюамеля выдает выходной сигнал при любом
заданном входном сигнале. Этот процесс был смоделирован в программе OrCAD 9.2,
что показано в пункте 5 курсовой работы. В результате были приобретены знания
фундаментальных закономерностей, связанных с описанием заданных сигналов,
получения их характеристик, обработкой и преобразованием в радиотехнических
цепях, описания заданной цепи, получения важных характеристик цепи. Закреплены
ранее полученные знания и навыки выполнения поставленных задач.
Список литературы
Гоноровский
И. С. Радиотехнические цепи и сигналы: Учебник для вузов. - 4-е изд., перераб.
и доп. - М: Радио и связь, 1986. - 512 с.: ил.
Л.
Б. Кочин, В. К. Соколов. Радиотехнические цепи и сигналы. Методические указания
по выполнению курсовой работы. СПб, 2002.
.
Е.Ф. Березкин Основы теории информации и кодирования. Лабораторный практикум.
Учебно-методическое пособиеМИФИ, 2-е издание. Москва 2009.
.
[Электронный ресурс] /Основы радиоэлектроники и связи; ред. Андреевская Т.М..-
Режим доступа http://jstonline.narod.ru/rsw/, свободный. (Дата обращения:
02.11.2016 г.)
.
В.Г. Патюков, Е.В. Патюков, В.Б. Кашкин Радиотехнические цепи и сигналы,
конспект лекций- Красноярск 2007: СФУ. -200 с.