Дискретизация и частотное разрешение
Реферат
Дискретизация и частотное разрешение
Содержание
1. Число параметров или степеней свободы сигнала
2. Комплексный ряд Фурье для дискретизированного сигнала
3. Метод дискретизации Шеннона
4. Метод дискретизации и интеграл Фурье
5. Частотное разрешение сигналов. Приложение к анализу
рентгеновских спектров поглощения атома в соединении
Литература
1. Число
параметров или степеней свободы сигнала
Рассмотрим математические методы анализа дискретизированных
сигналов и связь этих методов.
Рассмотрим теперь следующую задачу: пусть функция времени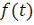
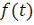 имеет спектр, не содержащий частот выше предельной верхней границы
имеет спектр, не содержащий частот выше предельной верхней границы
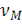
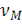 , а сама функция отлична от нуля на промежутке от 0 до
, а сама функция отлична от нуля на промежутке от 0 до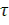
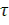 . Возникает вопрос - какое число параметров (или число степеней
свободы) требуется для определения такой функции?
. Возникает вопрос - какое число параметров (или число степеней
свободы) требуется для определения такой функции?
Докажем, что имеется только независимых параметров для такой
функции, и обсудим различные возможные способы выбора этих параметров, а также
некоторые общие свойства таких функций.
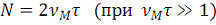 (1)
(1)
Прежде всего, следует отметить, что функция не является полностью
определенной, если мы ограничиваемся заданием её значений только на интервале 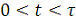
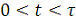 .
.
Существуют два различных способа доопределения функции, не
вносящих дополнительной информации в функцию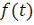
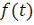 :
:
A. Периодическая функция, поведение которой на промежутке от 0 до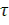
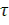 повторяется за пределами этого промежутка бесконечное число раз:
повторяется за пределами этого промежутка бесконечное число раз:
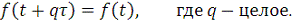 (2)
(2)
B. Функция одиночного сообщения, поведение которой
удовлетворяет условию:
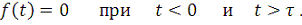 (3)
(3)
Последний случай был рассмотрен Шенноном в методе
дискретизации.
Начнем рассмотрение с первого случая и исследуем периодическую
функцию с периодом 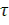
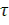 . Разложение такой периодической функции в ряде Фурье имеет вид:
. Разложение такой периодической функции в ряде Фурье имеет вид:
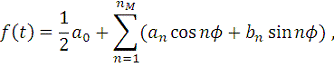 (4)
(4)
где
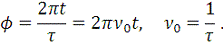 (5)
(5)
Будем полагать, что максимум частоты 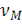
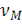 точно соответствует одной из гармоник
точно соответствует одной из гармоник 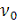
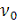 :
:
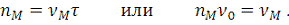 (6)
(6)
Ряд Фурье содержит конечное число слагаемых до целого 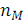
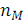 . Для каждой определенной частоты мы имеем две компоненты
. Для каждой определенной частоты мы имеем две компоненты 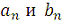
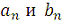 и следовательно полное число компонент определяется равенством:
и следовательно полное число компонент определяется равенством:
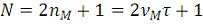 (7)
(7)
включая постоянное слагаемое 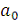
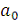 . Если продолжительность
. Если продолжительность 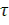
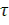 сигнала достаточно велика, то формула (7) практически сводится к
(1). При этом коэффициенты
сигнала достаточно велика, то формула (7) практически сводится к
(1). При этом коэффициенты 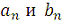
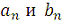 представляют один из возможных вариантов выбора параметров.
представляют один из возможных вариантов выбора параметров.
Вместо действительного ряда Фурье (4) можно использовать
комплексный ряд Фурье, как в уравнениях (1) и (2):
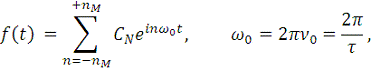 (8)
(8)

где звездочка снова означает комплексно-сопряженное.
Вместо рядов Фурье, можно воспользоваться методом дискретизации
периодической функции
 . Выберем
. Выберем 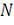
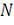 эквидистантных точек дискретизации в пределах одного периода
эквидистантных точек дискретизации в пределах одного периода 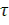
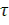 , например:
, например:
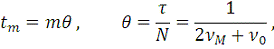 (9)
(9)
где
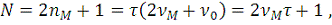
Введем обозначения для дискретных значений 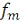
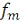 функции f:
функции f:
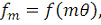 (10)
(10)
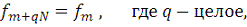
в соответствии с условием периодичности (2).
дискретизация частотное разрешение сигнал
Исходную функцию 
 можно восстановить если известны
можно восстановить если известны 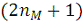
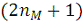 её дискретных значений в пределах одного периода
её дискретных значений в пределах одного периода 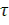
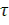 . Представим
. Представим
 в виде:
в виде:
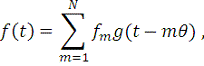 (11)
(11)
где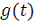
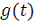 является импульсной функцией времени, центрированной на моменте
времени
является импульсной функцией времени, центрированной на моменте
времени 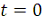
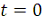 и повторяющейся с периодичностью
и повторяющейся с периодичностью 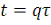
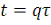 . Для такой импульсной функции выберем следующее определение:
. Для такой импульсной функции выберем следующее определение:

Используемая импульсная функция является нулевой для всех других
точек дискретизации в пределах одного периода 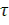
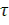 . Такую функцию с ограниченным частотным спектром, не превышающим
. Такую функцию с ограниченным частотным спектром, не превышающим 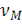
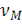 , можнопостроитьвоспользовавшись тождеством Лагранжа:
, можнопостроитьвоспользовавшись тождеством Лагранжа:
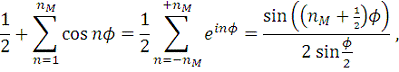 (12)
(12)
где 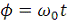
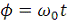 .
.
Эта функция равна 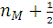
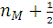 при
при 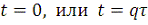
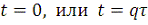 , когда знаменатель равен нулю. Она осциллирует и обращается в
нуль в точках
, когда знаменатель равен нулю. Она осциллирует и обращается в
нуль в точках
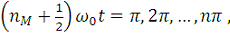
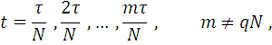
пока 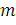
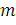 не является кратным
не является кратным 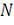
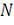 .
.
Для импульсной функции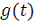
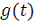 воспользуемся выражением:
воспользуемся выражением:
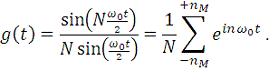 (13)
(13)
Сравнивая теперь выражения (11), (13) и (8) мы получаем:
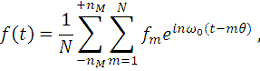
и следовательно
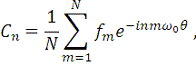 (14)
(14)
т.е. выражение, которое напрямую связывает коэффициенты Фурье с
дискретными значениями 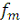
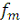 . Обратное соотношение получается из (8) и имеет вид:
. Обратное соотношение получается из (8) и имеет вид:
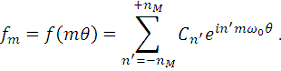 (15)
(15)
2.
Комплексный ряд Фурье для дискретизированного сигнала
В комплексных рядах Фурье имеется 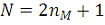
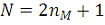 комплексных амплитуд
комплексных амплитуд 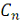
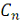 , являющихся сопряженными для
, являющихся сопряженными для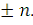
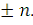 Вместе это дает
Вместе это дает 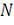
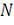 независимых вещественных переменных, и имеющиеся
независимых вещественных переменных, и имеющиеся 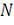
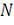 дискретных точек сигнала обеспечивают такое же числостепеней
свободы. Легко получить прямую проверку выражений (14) и (15):
дискретных точек сигнала обеспечивают такое же числостепеней
свободы. Легко получить прямую проверку выражений (14) и (15):
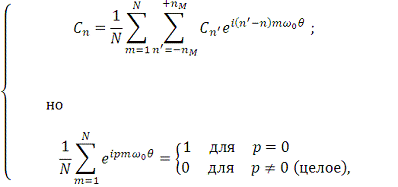 (16)
(16)
поскольку при 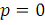
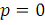 мы имеем
мы имеем 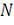
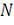 слагаемых, дающих в сумме 1, тогда как при
слагаемых, дающих в сумме 1, тогда как при 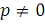
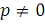 получаем
получаем 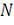
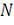 гармоник с частотами, равномерно распределенными от 0 до
гармоник с частотами, равномерно распределенными от 0 до 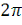
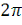 , дающих в результате 0.
, дающих в результате 0.
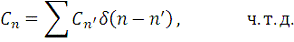
Вместо дискретизации в точках времени 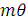
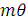 можно брать точки
можно брать точки 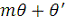
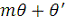 , добавляя константу времени
, добавляя константу времени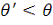
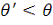 . Такая процедура даст набор новых дискретных значений
. Такая процедура даст набор новых дискретных значений 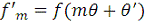
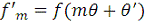 , которые можно использовать вместо
, которые можно использовать вместо 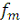
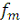 . Уравнения (14) и (15) будут заменены на:
. Уравнения (14) и (15) будут заменены на:
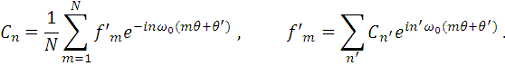
При этом, между 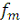
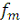 и
и 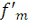
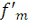 существует набор
существует набор 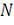
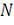 линейных соотношений.
линейных соотношений.
3. Метод
дискретизации Шеннона
Шеннон использовал метод дискретизации применительно к упомянутому
выше доопределению B вида (3) функции одиночного сообщения f (t),
которая считается нулевой для 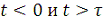
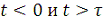 . Проблема решается в рамках следующего подхода.
. Проблема решается в рамках следующего подхода.
Возьмем периодическую функциюf (t) с большим периодом 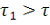
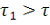 и будем считать, что
и будем считать, что 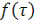
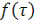 принимает свои значения на интервале от 0 до
принимает свои значения на интервале от 0 до 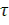
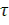 и обращается в ноль на интервалеот
и обращается в ноль на интервалеот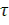
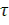 до
до 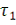
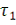 .
.
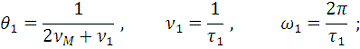 (17)
(17)
Если 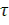
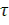 и
и 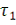
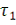 являются большими, то соответствующие частоты
являются большими, то соответствующие частоты 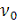
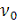 и
и 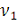
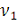 пренебрежимо малы по сравнению с максимальной частотой
пренебрежимо малы по сравнению с максимальной частотой 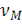
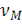 , и мы получаем
, и мы получаем
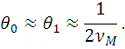
Полное число точек дискретизации определяется теперь формулой
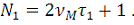 (18)
(18)
Из этих 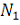
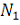 дискретных точек,
дискретных точек, 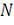
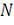 точек попадают в интервал
точек попадают в интервал 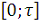
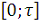 , а оставшиеся
, а оставшиеся 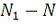
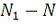 точек - в интервал
точек - в интервал 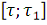
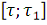 . Первый набор точек дает ненулевые дискретные значения:
. Первый набор точек дает ненулевые дискретные значения:
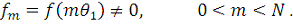 (19)
(19)
Тогда как другие точки дают ноль:

Импульсная функция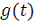
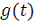 уравнения (13) принимает вид
уравнения (13) принимает вид
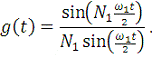 (20)
(20)
Устремляя теперь 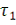
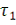 к бесконечности и, соответственно
к бесконечности и, соответственно 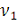
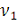 к нулю, мы получаем предельное значение для шага дискретизации:
к нулю, мы получаем предельное значение для шага дискретизации:
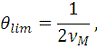
А также имеем бесконечное число дискретных значений 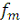
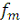 равных нулю. Единственные ненулевые значения соответствуют
интервалу
равных нулю. Единственные ненулевые значения соответствуют
интервалу
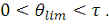
Их число определяется выражением
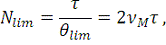 (21)
(21)
что соответствует формуле (1), в то время как импульсная функция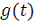
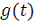 упрощается и принимает вид
упрощается и принимает вид
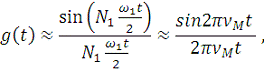 (22)
(22)
поскольку
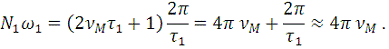
В результате функция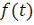
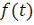 , дискретизированная согласно (11), принимает в данном предельном
случае вид:
, дискретизированная согласно (11), принимает в данном предельном
случае вид:
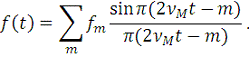 (23)
(23)
Легко доказать, что разложение (23) принимает значение 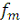
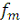 во всех точках дискретизации. Рассмотрим, например точку с
номером
во всех точках дискретизации. Рассмотрим, например точку с
номером 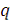
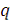 :
:
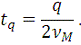
Слагаемое 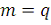
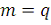 в сумме (23) дает вклад
в сумме (23) дает вклад 
 , тогда как все остальные слагаемые обращаются в ноль:
, тогда как все остальные слагаемые обращаются в ноль:
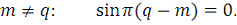
Сумма (23) не дает точных нулевых значений 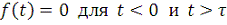
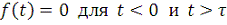 , но получаемая функция быстро обращается в ноль на обеих
границах, имея малые осцилляции частоты
, но получаемая функция быстро обращается в ноль на обеих
границах, имея малые осцилляции частоты 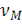
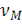 . Такой тип представления функции и рассматривался Шенноном.
. Такой тип представления функции и рассматривался Шенноном.
4. Метод
дискретизации и интеграл Фурье
Функция 
 , доопределенная с помощью условий (3), имеет только
, доопределенная с помощью условий (3), имеет только 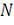
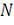 степеней свободы, как это следует из метода дискретизации. Если
эта функция анализируется с помощью метода Фурье, то мы вместо рядов приходим к
интегралам Фурье. Число членов в Фурье-анализе становится бесконечным, но они
снова содержат только
степеней свободы, как это следует из метода дискретизации. Если
эта функция анализируется с помощью метода Фурье, то мы вместо рядов приходим к
интегралам Фурье. Число членов в Фурье-анализе становится бесконечным, но они
снова содержат только 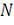
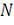 независимых переменных
независимых переменных 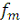
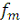 . Этот результат можно проверить, поскольку используемая функция
. Этот результат можно проверить, поскольку используемая функция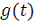
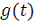 идентична рассмотренному выше колоколообразному импульсу (26) и
имеет спектр:
идентична рассмотренному выше колоколообразному импульсу (26) и
имеет спектр:
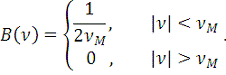 (24)
(24)
следовательно
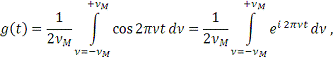 (25)
(25)
и
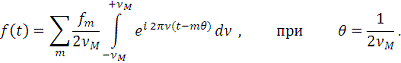 (26)
(26)
Следует отметить, что главные принципы метода дискретизации были
разработаны независимо рядом ученых.
5. Частотное
разрешение сигналов. Приложение к анализу рентгеновских спектров поглощения
атома в соединении
В разделе 2 установлен результат, согласно которому заданная
функция времени f (t), существующая на интервале длительности τ, удовлетворяющая условиям f (t) =0 при t<0, t>τ, и имеющая спектр, ограниченный максимальной частотой ωmax, определяется числом независимых параметров или степеней свободы
(Nidp), которое, (если не ограничиваться большими τ) находится с помощью выражения:
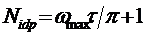 (27)
(27)
Как мы видели, такой результат следует из представления функции f
(t) в виде ряда или интеграла Фурье, а также является следствием применения
метода дискретизации сигнала, когда f (t) представляется в виде
дискретизированной функции f (tm), задаваемой в точках tm
с m=1,2,…,Nidp.
При этом шаг дискретизации δt в шкале t составляет δt = τ/Nidp, а частотное разрешение δω в шкале ω, характеризующее число различаемых частот
в спектре, определяется выражением:
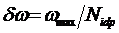 (28)
(28)
Следует отметить, что число точек дискретизации функции f (t), и
как следствие, значения δt и δω, определяются величиной Nidp, а
не общим числом экспериментальных точек N, в которых выполнено измерение f (t)
поскольку, несмотря на независимый характер всех N измерений, они не являются
независимыми для сигналов ограниченных по времени и частоте.
Применительно к теории рентгеновских спектров поглощения
(X-rayabsorptionspectra или XAS) представленные результаты могут быть
переписаны путем замены переменных: длительность сигнала τ → Δk = (kmax - kmin) -
протяженность XAS сигнала в прямом или k-пространстве (kmin,kmax
- соответственно нижняя и верхняя границы сигнала), и частота ω → 2R - частота в пространстве
межатомных расстояний. В результате такой замены соотношение (27) принимает
вид:
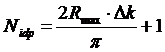 (29)
(29)
В представленном соотношении можно выделить величину разрешения δR межатомных расстояний, определяемую в
соответствии с (28) как δR=Rmax/Nidp, и записать для нее
выражение:
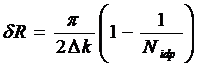 (30)
(30)
При проведении структурных исследований с помощью протяженной
области рентгеновских спектров поглощения (ExtendedAbsorptionFineStructure или
EXAFS), протяженность сигнала χ (k) в шкале k составляет Δk ~ 10-15 Å-1, что в соответствии с (29) дает величину Nidp ~
10. При столь большом числе независимых параметров Nidp изучаемого
сигнала χ (k)
вторым слагаемым (~ 1/Nidp) в (30) можно пренебречь, после чего (30)
приобретает вид:
δR = π / (2 Δk) (31)
Полученное оценочное соотношение устанавливает широко
распространенный в теории EXAFS предел разрешения двух межатомных расстояний,
согласно которому два расстояния R1 иR2 от поглощающего
центра до атомов окружения, разность которых удовлетворяет неравенству ΔR = |R2 - R1| <δR = π/ (2Δk), не могут быть разрешены с помощью
Фурье-анализа сигнала χ (k) по
имеющемуся интервалу волновых чиселΔk. Оценки с помощью формулы (31) дают для
предела разрешения двух межатомных расстояний величину ~ 0.15 Å, если Δk ~ 10 Å-1. При использовании ограниченных по протяженности
интервалов Δk (~ 3, 4 Å-1), соответствующих околопороговой области спектра,
определяемое из (29) число независимых параметров сигнала χ (k) оказывается небольшим Nidp
~ 4, и для оценки δR
воспользуемся (30), что дает величину ~ 0.4 Å.
Представленные оценки предела разрешения двух межатомных
расстояний с помощью (31) для EXAFS области спектра или с помощью (30) для
околопороговой области, приближенно соответствуют критерию, при котором имеет
место "визуальное” разрешение Фурье-пиков, обусловленных расстояниями R1
иR2. Такое разрешение иллюстрируется на рисунке 1, где
показаны результаты Фурье-преобразования по интервалам a) Δk = 10.0 Å-1 и б) Δk = 3.0 Å-1 теоретической функции χ (k) вида:
χ (k) = {N1 sin (2kR1)
+ N2 sin (2kR2) } exp ( - 2σ2k2) (32)
В выражении (32): N1 - амплитуда первого слагаемого,
рассчитываемого с использованием величины R1 = 2.0 Å; N2 - амплитуда второго
слагаемого, которое рассчитывается с величиной R2 = 2.15 Å (обеспечивающей ΔR =│R2 - R1│=
0.15 Å) для
Фурье-анализа по интервалу Δk = 10.0 Å-1, и с величиной R2 = 2.4 Å (обеспечивающей ΔR = 0.4 Å) для Фурье-анализа по интервалу Δk = 3.0 Å-1. Фактор exp (-2σ2k2) включен для приближения формы сигнала к
используемой в теории XAS и соответствует учету теплового движения атомов в
гармоническом приближении с характерной для металлов при комнатной температуре
величиной параметра Дебая-Валлера (ДВ) σ2 = 0.005 Å2. Такой модельный сигнал (32) может быть
использован для установления адекватности применения к ним критериев типа (30),
(31), имеющих достаточно общий характер.
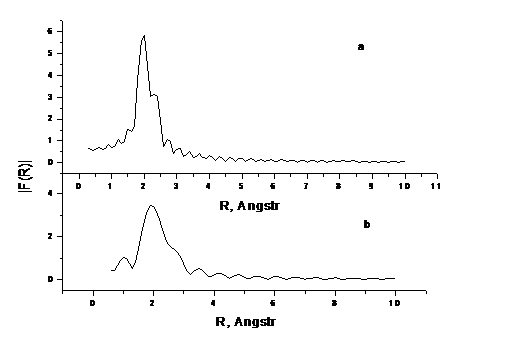
Рисунок 1. Модули Фурье-образов F (R) функций χ (k), рассчитанных по формуле (32) для ΔR = 0.15 Å - (a) и ΔR = 0.4 Å - (b). Фурье-преобразование χ (k) в случае (a) выполнено по интервалу Δk = 10.0 Å-1, а в случае (b) - по Δk = 3.0 Å-1.
Соотношения (30), (31) носят оценочный характер, поскольку в
отличие от используемых при их выводе общих положений метода дискретизации и
Фурье-анализа, формулируемых для сигналов произвольной формы и удовлетворяющих
граничным условиям, а также условиям A или B доопределения функции в разделе
2.1, плохо соответствующим XAS сигналу. На практике предел разрешении двух
межатомных расстояний с помощью Фурье-преобразования функции χ (k) по рассмотренным интервалам Δk во многих случаях оказывается гораздо
выше оценок, получаемых по формулам (30), (31). Причиной этого может также
служить конечность ширины Фурье-пика, соответствующего каждому из расстояний Ri,
вследствие чего на ширине результирующего Фурье-пика, отвечающего двум
расстояниям R1 и R2, может укладываться более одного δR-интервала (минимум две различаемые
частоты). В этом случае, несмотря на отсутствие "визуального"
разделения Фурье-пиков, обусловленных R1 и R2, решение
задачи определения близких межатомных расстояний может быть получено путем
численного сопоставления, при одинаковых Δk-интервалах, ширины и асимметрии Фурье-пика
координирующих атомов в экспериментальной функции χ (k) с соответствующими характеристиками
Фурье-пика пробной функции, моделирующей распределение атомов относительно
поглощающего центра.
Литература
1.
Боккуцци, Д. Обработка сигналов для беспроводной связи / Д. Боккуцци; Пер. с
англ. Ю.Л. Цвирко; Под ред.В.И. Борисова. - М.: Техносфера, 2012. - 672 c.
.
Воробьев, С.Н. Цифровая обработка сигналов: Учебник для студентов учреждений
высшего профессионального образования / С.Н. Воробьев. - М.: ИЦ Академия, 2013.
- 320 c.
.
Лайонс, Р. Цифровая обработка сигналов: Пер. с англ. / Р. Лайонс. - М.:
Бином-Пресс, 2013. - 656 c.
.
Оппенгейм, А. Цифровая обработка сигналов / А. Оппенгейм, Р. Шафер; Пер. с
англ. С.А. Кулешов; Пер. с англ. С.Ф. Боев. - М.: Техносфера, 2012. - 1048 c.
.
Солонина, А.И. Цифровая обработка сигналов и MATLAB: Учебное пособие / А.И.
Солонина, Д.М. Клионский, Т.В. Меркучева. - СПб.: БХВ-Петербург, 2013. - 512 c.
.
Хименко, В.И. Статистическая акустооптика и обработка сигналов / В.И. Хименко,
Д.В. Тигин. - СПб.: СПбГУ, 2012. - 292 c.
.
Чан, Т.Т. Высокоскоростная цифровая обработка сигналов и проектирование
аналоговых систем / Т.Т. Чан; Пер. с англ. К.В. Юдинцев. - М.: Техносфера,
2013. - 192 c.