Економіко-математичне моделювання діяльності страхових компаній
АНОТАЦІЯ
Дипломна робота на
тему: "Економіко-математичне моделювання діяльності страхових
компаній"
Текстова частина
включає: вступ, три розділи, висновки, список використаної літератури.
Обсяг роботи
становить 91 сторінку.
Основний зміст
роботи: Проаналізовано історію страхування життя та виникнення наукових
підходів щодо обчислення тарифних ставок по страхуванню життя.
Наведені основи
фінансової математики, зокрема поняття процентних ставок, приведеної вартості,
детермінованих рент, які широко використовуються для побудови довгострокових
моделей страхування життя. Здійснено аналіз побудови короткотермінових та
довготермінових моделей страхування життя, страхових резервів, періодичних
премій.
Розв’язано декілька
задач знаходження тарифних ставок для змішаного страхування життя, приведено
числові приклади побудови короткотермінових і довготермінових моделей
страхування життя які мають практичне спрямування.
Ключові слова:
брутто-ставка, нетто-ставка, навантаження, страхувальник, страховик, принцип
еквівалентності страхових зобов’язань
ВСТУП
Найважливіша
проблема страхового бізнесу - це обчислення вартості премії за страхування
(страхового тарифу). З одного боку, вона повинна забезпечувати страховій
компанії не тільки захист від збитків, а й хороший прибуток, з іншого -
конкурувати з преміями інших страхових компаній.
У нашій країна з
огляду на погане становище страхового бізнесу в цілому відшукання оптимальної
премії є особливо важливим. Але сьогодні страхові компанії України переважно не
рахують тарифи самостійно, а беруть їх з російського страхового ринку. Однак
зрозуміло, що становище українського ринку значно відрізняється від
російського. Крім того, одна з проблем, які постають на шляху обчислення премій
за страхування, полягає у тому, що дуже важко знайти статистичні дані, які б
реально описували становище українського страхового ринку. Часто беруть дані
європейських страхових ринків, оскільки такої статистики немає і в Росії. І як
наслідок знову неправильна оцінка премії, а неправильна оцінка премій за
страхування в багатьох випадках призводить до банкрутства страхових компаній. І
ще одна перешкода для правильної оцінки страхових премій - це нестабільність
нашого ринку на законодавчому рівні. Швидкі зміни законодавства в галузі
страхування зумовлюють коливання страхового ринку, зміни економічного
становища. Оскільки змінюється ситуація на ринку, то повинна змінюватися і
стратегія поведінки страхової компанії.
Загальноприйнята
назва наукового напряму, що займається вивченням математичних моделей і методів
страхової справи - актуарна математика (aktuarial mathematics) яка походить від
actuary - актуарій, статистик страхового товариства. Разом з відповідними
економічними і юридичними дисциплінами актуарна математика утворює більш широку
область знань - актуарну науку (actuerial science), яка є теоретичною основою
страхового бізнесу.
Актуарна освіта у
світі має вікові традиції. Однак у нашій країні з майже 70-річною відсутністю
вільних ринкових відносин актуарна освіта у актуарна наука практично були
відсутніми до 90-х років ХХ століття. У теперішній час з’явився великий інтерес
до цієї сфери діяльності, що пов’язано з великою потребою у
спеціалістах-актуаріях зі сторони страхових компаній.
Дослідження,
виконані в Україні в останнє десятиліття в області актуарной математики носять
фрагментарний й епізодичний характер, відносяться в першу чергу до прикладних
робіт. Відсутність статистичних даних (часто вони є комерційною таємницею) і
недостатнє цільове фінансування, очевидно, є основними причинами цього, крім зазначеної
вище «молодості» і нерозвиненості цієї області в цілому, що виражається в
недостачі інформаційного забезпечення й кваліфікованих кадрів. Основною рисою
сучасного стану актуарної науки в Україні можна назвати воістину величезний
розрив, що існує між теорією й практикою. Украй мало таких робіт, де досить
передові теоретичні розробки були б доведені до практичної реалізації; навіть
демонстрації їхнього застосування одиничні, не говорячи вже про систематичне
використання.
Розрізняють
актуарну математику у майновому і особистому страхуванні. Під майновим
страхуванням (non-life insurance) розуміють всі види страхової діяльності, не
пов’язані з особистим страхуванням (страхування житла, автомобілів, підприємств
і т.д.). У найзагальнішому плані особисте страхування можна визначити як галузь
страхової діяльності, яка забезпечує страховий захист громадян або зміцнення
досягнутого ними сімейного добробуту.
Особисте
страхування включає:
страхування
життя;
страхування
від нещасних випадків;
страхування
додаткової пенсії;
добровільне
медичне страхування;
страхування
від нещасних випадків на транспорті.
Особисте
страхування має багато спільного з соціальним, насамперед у об'єктах страхового
захисту громадян. Головна відмінність між ними - в джерелах формування
страхових фондів: для соціального - це в основному кошти підприємств, установ,
організацій, і лише незначною мірою - індивідуальні доходи, тоді як для
особистого індивідуальні доходи є головним джерелом, а кошти підприємств,
установ і організацій - тією мірою, якою особисте страхування є обов'язковим.
Необхідність
особистого добровільного страхування зумовлюється як ризиковим характером
відтворення робочої сили, так і підвищенням ступеня ризику життя у зв'язку з
урбанізацією, погіршенням довкілля, а також зростанням частки людей похилого
віку у загальній чисельності населення. Це ускладнює захист особистих інтересів
громадян з боку держави та за її рахунок і передбачає формування захисних
механізмів за рахунок перерозподілу індивідуальних доходів.
Особисте
страхування регламентується Законом України "Про страхування". У
даній дипломній роботі зосередимо увагу на добровільному особистому
страхуванні.
У дипломній роботі
викладаються основні математичні моделі й методи, які використаються для
розрахунків характеристик тривалості життя, разових і періодичних премій,
страхових надбавок, резервів і т.д. для різних видів страхування життя й
пенсійних схем.
Даний поглиблений
виклад основних математичних моделей і методів, необхідних для визначення
характеристик тривалості життя, разових і періодичних премій, страхових
надбавок, резервів і т.д. для різних видів страхування й пенсійних схем.
Задачі, які
розв’язані у дипломній роботі мають яскраво виражену практичну спрямованість і
дозволяють одержати певне уявлення не тільки про актуарні розрахунки, але й про
розробку страхових продуктів, андеррайтингу й т.д.
При актуарних
розрахунках у довгостроковому страхуванні життя широко використовується теорія
складних відсотків. Тому, у дипломну роботу включено розділ „Основи фінансової
математики та її застосування до актуарних розрахунків”.
РОЗДІЛ
1. ТЕОРЕТИЧНІ ОСНОВИ СТРАХУВАННЯ ЖИТТЯ
тарифний ставка
страхування життя
1.1
Історія страхування життя і виникнення наукових методів обчислення розмірів
тарифних ставок
Історія страхування
життя налічує приблизно 20 століть. Зародковими формами страхування життя були
[1] грошові фонди для благодійних цілей у древній Індії, комунальні установи
древніх іудеїв, колегії Римської імперії. Організації, подібні до римських
колегій, існували в епоху середніх віків у цехах і гільдіях. Надаючи
матеріальну підтримку своїм членам у скрутних випадках, вони піклувалися також
про забезпечення близьких померлого.
У докапіталістичних
формаціях страхування знаходилося в зародку. Господарство тієї епохи мало
натуральний характер. Кожен рабовласник чи феодал у натуральній, а іноді й у
грошовій формі зберігав у себе спеціальний "страховий фонд".
Страхування
засноване на участі окремих господарств та осіб у створенні єдиного страхового
фонду. За самою своєю природою воно несумісне з замкнутістю натурального
господарства. Поява страхування в докапіталістичних формаціях припускає
порушення цієї замкнутості. А порушувалася вона насамперед у сфері торгівлі й
ремесла, простого товарного виробництва. Але оскільки товарне виробництво і
торгівля в економіці тієї епохи відігравали другорядну роль, страхування не
одержало широкого поширення.
У рабовласницькому
суспільстві та при феодалізмі визначилися лише найбільш загальні риси страхової
справи. Не існувало ще ні страхових премій, що регулярно вносилися б членами
цехів і гільдій у загальну касу, не було й заздалегідь створених страхових
фондів. Страхування не відокремилося ще від ремесла і торгівлі, не виділилося в
особливі спеціалізовані страхові організації. Те саме об'єднання ремісників і
торговців виступало одночасно у ролі страхувальника й у ролі страховика.
Слідом за розвитком
товарного виробництва розвивається і страхування. Поступово уточнюється перелік
страхових випадків, при настанні яких виплачується допомога, форми і розміри
виплат. Збір коштів для виплати допомоги після настання страхового випадку
змінюється попередньою акумуляцією страхового фонду, розкладка збитку -
системою регулярних внесків. Призначення регулярних внесків і утвореного ними
фонду поступово здобуває стійкий характер.
При капіталізмі
страхування поступово перетворюється в особливу галузь економіки, здобуває
загальне поширення як необхідний її елемент.
У 1706 р. в Англії
виникло перше товариство страхування життя - "Емікебл". Система тарифних
ставок у нього була недосконалою, вони ще не диференціювалися за віком.
Через деякий час
з'являються товариства "Рефьюдж іксчендж" і "Лондон іншуренс
корпорейшен". Вони вперше застосували поліси з фіксованими страховими
сумами.
У 1762 р. було
створено товариство "Еквітебл". Для розрахунку тарифних ставок воно
використовувало відомості про смертність населення, зібрані й оброблені відомим
ученим Р. Прайсом. Більш точні дані про смертність, а також диференціація
тарифних ставок за віковими групами дозволили їх істотно знизити. Зниження
тарифів сприяло інтенсивному розширенню операцій "Еквітебла" і разом
з тим зростанню його капіталу. Такий успіх звернув на себе увагу і викликав
появу нових товариств.
Трохи пізніше ніж в
Англії товариства страхування життя комерційного типу виникають і в інших
країнах. Так, у Франції перше товариство з'явилося у 1829р., у Німеччині - у
1827р., у СШ А - у 1830 р., у Росії - у 1835 р. До кінця XIX ст. операції по
страхуванню життя одержали широке поширення у всіх країнах світу.
Значно вплинули на
розвиток страхування життя статистика і математика.
Виникла статистика
у так званій школі "політичних арифметиків". Один із засновників цієї
школи англійський учений Д. Граунт у 1662 р. опублікував роботу "Природні
і політичні спостереження, виконані над бюлетенями смертності", яка
поклала початок страховій математиці - теорії актуарних розрахунків.
Майже одночасно з
Д. Граунтом питання залежності страхування життя від смертності людей
досліджував голландець Я. де-Вітт, який написав роботу про ціну довічної ренти,
де розробив метод розрахунку страхових внесків у залежності від віку
застрахованого і норми зростання грошей.
Своє продовження
теорія актуарних розрахунків знайшла в працях англійського вченого Е. Галлея.
Він склав таблицю смертності на основі матеріалів про смертність населення
Бреславля за період 1687-1691 рр., дав визначення основних функцій таблиці
смертності, обчислював ймовірності дожити і вмерти, увів у науку поняття
ймовірної тривалості життя, застосував принцип розрахунку середньої тривалості
життя при обчисленні щорічної ренти в залежності від віку, показав, що таблиця
смертності дозволяє регулювати розміри страхових внесків. Форма таблиці Галлея
застосовується в страхуванні життя дотепер.
Потім англійський
математик А. Муавр, вивчивши таблицю смертності Е.Галлея, зумів спростити
актуарні розрахунки. Він склав три інші таблиці на основі даних про смертність
застрахованих у Голландії і Франції, а також про смертність населення Лондона
за 1728-1737 рр.
До кінця XVII - початку
XVIII ст. були сформульовані основні положення математичної теорії ймовірностей
і нагромадилися статистичні дані про смертність населення. Страхування життя
було поставлено на наукову основу.
Розвиток страхової
справи у свою чергу стимулює розширення наукових досліджень. У середині XVIII
ст. починається новий підйом у статистиці. Кілька праць ("Про довічні
ренти", "Про овдовілі каси", "Про страхування сиріт"
та ін.) присвячує страхуванню життя один з найвідоміших математиків світу
Леонард Ейлер. Виходять друком роботи французького вченого Е. Дювильяра
"Дослідження про ренти, позики і платежі", "План страхової
асоціації".
Проблемами,
пов'язаними з актуарними розрахунками, займалися майже усі великі математики
того часу: Л. Ейлер, Н. Фус, С. Лакруа та ін. В ці роки були складені таблиці
смертності В. Керсебума, А. Депарс'є. У цей час у теорії актуарних розрахунків
застосовуються новітні досягнення математики і статистики. Страхові товариства
одними з перших стали використовувати обчислювальну техніку [2].
1.2
Особливості побудови тарифної ставки по страхуванню життя і її структура
Тарифна ставка [4]
- ціна страхового ризику та інших витрат, необхідних для виконання зобов'язань
страховика перед страхувальником за підписаним договором страхування.
Тарифна ставка, за
якою укладається страховий договір, називається брутто-ставкою. Вона
складається з двох частин: нетто-ставки і навантаження.
Нетто-ставка - ціна
страхового ризику (вибуху, пожежі і т.д.).
Навантаження -
вартість, яка покриває витрати страховика з організації та ведення страхової
справи, а також містить елементи прибутку.
Для розрахунку
тарифів можуть бути використані кілька методів [8]:
· на
основі теорії імовірності та методів математичної статистики з використанням
часових рядів;
· на
базі експертних оцінок;
· за
аналогією до інших об'єктів або компаній;
· з
використанням математичної статистики і розрахунку дохідності.
У даній дипломній
роботі наведені основи розрахунків тарифної ставки на основі теорії
ймовірностей та методів математичної статистики.
Страхування життя
пов'язане з наступними ризиками: смерть страхувальника (застрахованої особи);
тимчасова і постійна втрата працездатності; закінчення трудової діяльності у
зв'язку з виходом на пенсію за віком, дожиття страхувальника до закінчення терміну
страхування або обумовленого договором віку. Настання цих подій, крім
останньої, може суттєво знизити сімейний дохід страхувальника, і в зв'язку з
цим виплата страхових винагород за договорами страхування життя є матеріальною
підтримкою для людини і її сім'ї у важкі періоди часу.
Імовірність
настання страхових випадків в житті сприяє розвитку відповідних видів
страхування.
Страхування дітей
дозволяє забезпечити інтереси дитини (застрахованої особи). При цьому виді
страхування страхувальниками виступають батьки або інші родичі дитини, а
застрахованими - діти від дня їх народження до 18 років. Термін страхування
визначається як різниця між віком 18 років та віком (у повних роках)
застрахованого при укладанні договору.
Страхова сума
виплачується застрахованому у разі нещасного випадку, що стався в період дії
договору (певний відсоток), та при дожитті дитини до 18 років.
Страхування до
шлюбу. Договір може бути укладено на користь дітей, котрі постійно проживають в
Україні. Вік дитини на день підписання договору не може перевищувати 15 повних
років.
Страхова сума
виплачується застрахованому при його вступі до законного шлюбу в період з дня
укладання договору страхування до досягнення 21 року. При не вступі до шлюбу
страхова сума виплачується по дожитті застрахованого до 21 року.
Пенсійне
страхування проводиться для осіб похилого віку з метою забезпечення громадян
додатковим доходом при виході на пенсію.
Страхування на
випадок смерті гарантує виплату відповідної суми у випадку смерті
страхувальника.
Змішане страхування
життя - вид страхування, який об'єднує в одному договорі кілька самостійних
договорів страхування, зокрема три випадки:
дожиття
до закінчення строку страхування;
смерть
застрахованого;
втрата
здоров'я від нещасних випадків.
Страхувальниками в
цьому виді страхування є тільки фізичні особи.
Договори змішаного
страхування життя укладаються з громадянами віком від 16 до 75 років строком на
3, 5, 10, 15 або 20 років. Розмір страхової суми визначає страхувальник.
При страхуванні на
дожиття до закінчення договору страхування страхувальник отримує повну страхову
суму, на яку було укладено договір, незалежно від того, отримував він страхові
суми у зв'язку з нещасними випадками впродовж дії договору, чи ні.
У разі смерті
застрахованого в період дії страхового договору страхова сума в розмірі 100%
виплачується правонаступнику, зазначеному в договорі страхування. Природна
смерть як наслідок хвороби, старості і т. ін. не є страховим випадком.
При страхуванні від
нещасних випадків з настанням страхової події застрахований отримує певний
відсоток від страхової суми залежно від ступеня втрати здоров'я. Отримання
страхової суми за страховим договором від нещасних випадків не залежить від
виплат, на які має право страхувальник з державного соціального та пенсійного
забезпечення.
Нещасними випадками
за цим видом страхування вважаються:
утоплення;
опіки,
ураження блискавкою або електричним струмом;
обмороження;
гострі
отруєння газами або парами, отруйними та хімічними речовинами, ліками,
харчовими продуктами.
Побудова тарифів по
страхуванню життя має свої особливості:
1
розрахунки проводяться з
використанням демографічної статистики і теорії ймовірності;
2
при розрахунках застосовуються
способи довгострокових фінансових розрахунків;
3
тарифні нетто-ставки складаються з
кількох частин, кожна з яких покликана сформувати страховий фонд за одним з
видів страхової відповідальності, який включений в умови страхування.
Тарифна ставка
визначає, скільки грошей кожний із страхувальників повинен внести в загальний
страховий фонд з одиниці страхової суми. Тому тарифи повинні бути розраховані
так, щоб сума зібраних внесків виявилася достатньою для виплат, передбачених
умовами страхування. Таким чином, тарифна ставка - це ціна послуги, що
надається страховиком населенню, тобто своєрідна ціна страхового захисту. Від
чого ж залежать її розміри, як установити ціну на той чи інший вид страхування
життя?
Отже, для
розрахунку обсягу страхового фонду потрібно мати відомості про те, скільки осіб
з числа застрахованих доживе до закінчення терміну дії їх договорів страхування
і скільки з них щороку може вмерти; у скількох і в якому ступені настане втрата
здоров'я. Кількість виплат, помножена на відповідні страхові суми, дозволить
визначити розміри майбутніх виплат, тобто з'явиться можливість дізнатися, у
яких розмірах потрібно буде акумулювати страховий фонд.
Тривалість життя
окремих людей коливається в широких межах. Вона відноситься до категорії
випадкових величин. Теорія ймовірності і статистика досліджують випадкові
явища, що мають масовий характер, у тому числі смертність населення.
Установлено, що демографічний процес зміни поколінь, що виражається в зміні
рівня повікової смертності, підпорядкований закону великих чисел, настільки
одноманітному у своїх проявах і настільки достовірному в результатах, що він
може бути основою фінансових розрахунків у страхуванні.
Демографічною
статистикою виявлена і виражена за допомогою математичних формул залежність
смертності від віку людей. Розроблено спеціальну методику складання так званих
таблиць смертності, де на конкретних цифрах показується послідовна зміна
смертності слідом за віком. Цими таблицями страхові компанії користуються для
розрахунку тарифів.
Крім
закономірностей, пов'язаних із процесом дожиття і смертності, при побудові
тарифів враховується довгостроковий характер операцій страхування життя,
оскільки ці договори укладаються на тривалі терміни від трьох і більше років.
Протягом усього часу їхньої дії (чи на самому початку терміну страхування при
одноразовій сплаті) страхові компанії одержують внески. Виплати ж страхових сум
проводяться протягом терміну страхування чи після закінчення визначеного
періоду від початку дії договору, якщо настане смерть застрахованого чи він
втратить здоров'я.
Тимчасово вільні
кошти акумулюються страховою компанією і використовуються як кредитні ресурси.
За користування ними сплачується позичковий відсоток. Але якщо при ощадній
операції дохід від відсотків приєднується до внеску, то в страхуванні на суму
цього доходу заздалегідь зменшуються (дисконтуються) внески страхувальника, що
підлягають сплаті. Для того щоб заздалегідь понизити тарифні ставки на той
дохід, що буде утворюватись протягом ряду років, використовуються методи теорії
довгострокових фінансових розрахунків.
Тарифні ставки в
страхуванні життя складаються з кількох частин. Візьмемо для прикладу змішане
страхування життя. У ньому поєднуються кілька видів страхування, що могли б
бути і самостійними:
страхування
на дожиття;
страхування
на випадок смерті;
страхування
від нещасних випадків.
По кожному з них за
допомогою тарифу створюється страховий фонд, тому тарифна ставка в змішаному
страхуванні складається з трьох частин, що входять у нетто-ставку, і четвертої
частини - навантаження.
Аналогічно
складається структура тарифних ставок і по інших видах страхування життя.
Структура тарифної
ставки наведена на рис. 1.
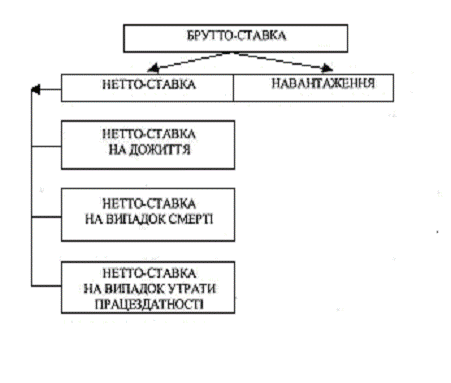
Рис. 1. Структура
тарифної ставки змішаного страхування життя
РОЗДІЛ 2. ОСНОВИ
ФІНАНСОВОЇ МАТЕМАТИКИ ТА ЇЇ ЗАСТОСУВАННЯ ДО АКТУАРНИХ РОЗРАХУНКІВ
2.1
Основи фінансової математики
.1.1
Процентні ставки
Ефективна процентна
ставка
Поняття відсотків
на капітал виникає в наступній найпростішій ситуації.
Припустимо, що в момент t ми
позичаємо суму C (наприклад, кладемо на свій рахунок у банку, вносимо плату за
страховку, перераховуємо пенсійний внесок у пенсійний фонд і т.д.). Через час h
ми можемо розраховувати на певний прибуток 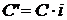 від інвестування нашого капіталу С.
Сума
від інвестування нашого капіталу С.
Сума 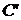 є винагородою
за те, що наші засоби використовувалися іншою людиною. Звичайно її вимірюють у
відносних одиницях; величина
є винагородою
за те, що наші засоби використовувалися іншою людиною. Звичайно її вимірюють у
відносних одиницях; величина 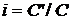 називається ефективною процентною
ставкою (effective rate of interest) або нормою прибутковості за розглянутий
проміжок часу (t, t+h).
називається ефективною процентною
ставкою (effective rate of interest) або нормою прибутковості за розглянутий
проміжок часу (t, t+h).
Прості й складні відсотки
Припустимо тепер, що сума C
може інвестуватися на два послідовних проміжки часу; нехай 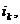 k = 1, 2, -
ефективна процентна ставка на k-му проміжку. Існують дві схеми обчислення
доходу
k = 1, 2, -
ефективна процентна ставка на k-му проміжку. Існують дві схеми обчислення
доходу 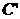 на
об'єднаному інтервалі:
на
об'єднаному інтервалі:
. Принцип простих
відсотків (simple interest) припускає, що відсотки нараховуються тільки на
основний капітал. Тому 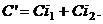 Відповідно,
підсумкова процентна ставка
Відповідно,
підсумкова процентна ставка 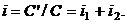
. Принцип складних
відсотків (compound interest) припускає, що відсотки нараховуються не тільки на
основний капітал, але й на вже зароблені відсотки. Тому наприкінці другого
інтервалу часу основний капітал C виросте до величини
 (2.1.1)
(2.1.1)
Відповідно, підсумкова
процентна ставка i визначається з умови 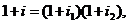 тобто
тобто 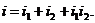
Принцип складних відсотків
фактично означає, що інвестор може вільно розпоряджатися своїми засобами. Тому
в актуарной математиці прийнято використовувати принцип складних відсотків при
визначенні доходу від вкладення засобів.
Процентні ставки, які
використовуються в більшості розрахунків в актуарній математиці, визначаються,
виходячи з консервативних оцінок прибутковості реальних майбутніх інвестицій
страховика. Вони набагато нижчі від реальних процентних ставок, які є на ринку
для різних видів інвестиційних проектів. Їхнє призначення полягає в тому, щоб
хоч як-небудь урахувати збільшення об’єму грошей, внесених як плату за страхове
покриття. Тому їх називають технічними процентними ставками [6]. Насправді
страхова компанія заробляє набагато більші відсотки; більше того, це одине із
самих головних (якщо не саме головне) джерело доходу страховика.
Накопичення
Виберемо деякий проміжок часу
в якості одиничного (як правило, це буде один рік) і припустимо, що процентна
ставка за цей проміжок дорівнює i. Припустимо, що в момент 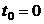 сума
сума 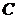 інвестується
на t одиниць часу. З принципу складних відсотків слідує, що в момент
інвестується
на t одиниць часу. З принципу складних відсотків слідує, що в момент 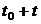 капітал C
перетвориться в суму
капітал C
перетвориться в суму 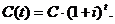 Величину
Величину 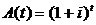 деколи
називають коефіцієнтом нагромадження або відсотковим множником за час t (див.
Додаток 2).
деколи
називають коефіцієнтом нагромадження або відсотковим множником за час t (див.
Додаток 2).
Інтенсивність відсотків
Інтенсивність відсотків
(force of interest) 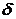 - це
миттєва відносна швидкість нагромадження засобів
- це
миттєва відносна швидкість нагромадження засобів
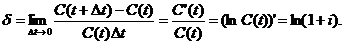 (2.1.2)
(2.1.2)
Оскільки 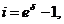 коефіцієнт
нагромадження за час t задається формулою
коефіцієнт
нагромадження за час t задається формулою
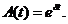
Інтенсивність відсотків
зручно використати для вивчення нагромаджень у випадку, коли процентні ставки
змінюються. У цьому випадку
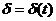 і
і
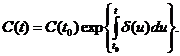
Номінальні
процентні ставки
Розглянемо проміжок
часу довжиною 1/р. Якщо за одиницю виміру прийняти один рік, та найцікавішими є
випадки: р = 12 (розглянутий проміжок часу дорівнює одному місяцю), р = 4
(розглянутий проміжок часу дорівнює одному кварталу), р = 2 (розглянутий
проміжок часу дорівнює півріччю).
Ефективна процентна ставка 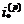 за цей
проміжок часу рівна
за цей
проміжок часу рівна
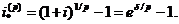 (2.1.3)
(2.1.3)
Однак у фінансовій математиці
прийнято характеризувати прибутковість вкладення засобів на проміжку 1/р не
ефективною (тобто реальною) процентною ставкою 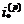 , а так званою номінальною
процентною ставкою (nominal rate of interest)
, а так званою номінальною
процентною ставкою (nominal rate of interest)
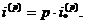 (2.1.4)
(2.1.4)
Іноді величину 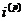 називають
номінальною процентною ставкою, виплачуваною ( нараховуваною) із частотою р
(nominal rate of interest payable (convertible) p thly).
називають
номінальною процентною ставкою, виплачуваною ( нараховуваною) із частотою р
(nominal rate of interest payable (convertible) p thly).
.1.2
Приведена вартість
Припустимо, що в момент 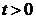 у
майбутньому ми повинні будемо виплатити деяку суму С. Щоб до моменту t мати
точно необхідну суму C, у даний час
у
майбутньому ми повинні будемо виплатити деяку суму С. Щоб до моменту t мати
точно необхідну суму C, у даний час 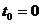 потрібно мати у своєму
розпорядженні суму
потрібно мати у своєму
розпорядженні суму 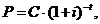 тому що
після інвестування на час t сума Р перетвориться в суму
тому що
після інвестування на час t сума Р перетвориться в суму 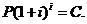 Величина Р
називається сучасною вартістю (present value) суми С у момент t. Іноді
вживається термін сучасна цінність, приведена вартість і т.д.
Величина Р
називається сучасною вартістю (present value) суми С у момент t. Іноді
вживається термін сучасна цінність, приведена вартість і т.д.
Величину 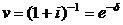 називають
коефіцієнтом дисконтування (обліку) (discount factor). З її допомогою формулу
для приведеної вартості можна записати у вигляді
називають
коефіцієнтом дисконтування (обліку) (discount factor). З її допомогою формулу
для приведеної вартості можна записати у вигляді
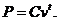
Облікова ставка
Припустимо, що в момент 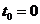 ми
позичаємо суму С. Тоді в момент
ми
позичаємо суму С. Тоді в момент 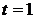 нам повинні повернути суму
нам повинні повернути суму 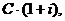 що
складається із двох частин: повернення основного капіталу С и відсотків на
капітал
що
складається із двох частин: повернення основного капіталу С и відсотків на
капітал 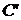 .
.
Якщо суму 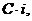 що повинна
бути виплачена в момент t=1, привести до моменту
що повинна
бути виплачена в момент t=1, привести до моменту 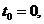 то ми одержимо суму
то ми одержимо суму 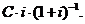 Тому, якщо
відсотки на капітал можуть бути виплачені заздалегідь, у момент
Тому, якщо
відсотки на капітал можуть бути виплачені заздалегідь, у момент 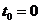 одержання
позики, то ці відсотки, виплачувані наперед, становлять
одержання
позики, то ці відсотки, виплачувані наперед, становлять 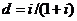 від суми
позики С. Величина d називається ефективною обліковою ставкою [6] (effective
rate of discount) за одиницю часу.
від суми
позики С. Величина d називається ефективною обліковою ставкою [6] (effective
rate of discount) за одиницю часу.
Облікова ставка d може бути
виражена й через інтенсивність відсотків 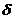 і коефіцієнт дисконтування v.
і коефіцієнт дисконтування v.
Припустимо тепер, що сума C=1
дається в борг на час 1/р із завчасною виплатою відсотків. Як ми бачили,
ефективна процентна ставка рівна 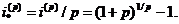 Саме ця сума повинна бути виплачена
в момент t = 1/р у вигляді відсотків. Якщо її привести до моменту
Саме ця сума повинна бути виплачена
в момент t = 1/р у вигляді відсотків. Якщо її привести до моменту 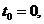 то вона перетвориться
в суму
то вона перетвориться
в суму 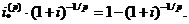 Оскільки
Оскільки 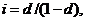 для
ефективної облікової ставки
для
ефективної облікової ставки 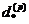 за час 1/р одержимо формулу
за час 1/р одержимо формулу
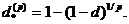 (2.1.5)
(2.1.5)
Однак у фінансовій математиці
прийнято працювати не з ефективними (тобто реальними) дисконтними ставками за
час 1/р, а з так званими номінальними (тобто умовними, що не існують реально)
обліковими ставками (nominal rate of discount)
Величину 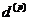 називають
номінальною обліковою ставкою, що нараховується із частотою р (nominal rate of
discount convertible p thly).
називають
номінальною обліковою ставкою, що нараховується із частотою р (nominal rate of
discount convertible p thly).
2.1.3
Оцінювання серії платежів. Детерміновані ренти
Якщо ми хочемо оцінити серію
виплат, які повинні бути здійснені в різні моменти часу, то всі ці виплати
повинні бути приведені до деякого фіксованого моменту 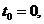 після чого
ці виплати можна додавати, порівнювати й т.д. З погляду застосування до
страхування й пенсійних схем найбільш важливою є задача визначення сучасної
вартості а серії з п виплат величиною
після чого
ці виплати можна додавати, порівнювати й т.д. З погляду застосування до
страхування й пенсійних схем найбільш важливою є задача визначення сучасної
вартості а серії з п виплат величиною 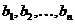 відповідно, які будуть зроблені в
деякі моменти
відповідно, які будуть зроблені в
деякі моменти  у майбутньому.
Величина а може розглядатися, наприклад, як сума, яку людина повинен внести в
пенсійний фонд у момент укладання договору (цей момент звичайно приймають за
початковий) для того, щоб у майбутньому, у моменти
у майбутньому.
Величина а може розглядатися, наприклад, як сума, яку людина повинен внести в
пенсійний фонд у момент укладання договору (цей момент звичайно приймають за
початковий) для того, щоб у майбутньому, у моменти  , одержувати
пенсію величиною
, одержувати
пенсію величиною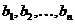 .
.
Як слідує з вищесказаного
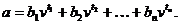
Якщо плата за пенсії
відбувається у вигляді декількох платежів величиною 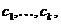 зроблених у
моменти
зроблених у
моменти  то
справедливе співвідношення між внесками
то
справедливе співвідношення між внесками 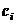 і пенсійними виплатами
і пенсійними виплатами 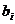 знаходиться
із принципу еквівалентності зобов'язань:
знаходиться
із принципу еквівалентності зобов'язань:
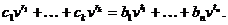
Ліва частина цієї формули
виражає сучасну цінність всіх внесків у пенсійний фонд або страхову компанію, а
права - сучасну вартість всіх пенсійних виплат.
Описана вище загальна модель
детермінованої пенсійної схеми на практиці як правило не застосовується.
Реально використовуються схеми, що мають ту чи іншу форму регулярності як за величиною
внесків і виплат, так і за моментами здійснення цих платежів. Особливо важливим
є випадок серії платежів фіксованої величини, які здійснюються через рівні
проміжки часу фіксовану кількість разів. Такі серії платежів звичайно називають
постійними рентами (level annuity). Часто, якщо немає небезпеки плутанини з
термінами, слово «постійні» опускають.
Детерміновані постійні ренти
Розглянемо п послідовних
одиничних проміжків часу 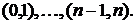 Під
моментом
Під
моментом  ми звичайно
будемо мати на увазі теперішній момент, а за одиничний проміжок часу приймемо
один рік (цей вибір, звичайно, умовний, тому нижченаведені формули можна
застосовувати й у випадку, якщо за одиничний проміжок часу обраний один
тиждень, один місяць, один квартал і т.д.).
ми звичайно
будемо мати на увазі теперішній момент, а за одиничний проміжок часу приймемо
один рік (цей вибір, звичайно, умовний, тому нижченаведені формули можна
застосовувати й у випадку, якщо за одиничний проміжок часу обраний один
тиждень, один місяць, один квартал і т.д.).
Серія з п виплат, кожна
величиною 1, зроблених наприкінці цих проміжків, тобто в моменти 1, 2, ..., n,
називається рентою із запізненням (annuity payable in advance чи annuity-due).
Серія з п виплат, кожна
величиною 1, зроблених на початку цих проміжків, тобто в моменти 0, 1, 2, ...,
п-1, називається рентою із випередженням (annuity payable in advance чи
annuity-due).
Відмінність між рентою із
запізненням і рентою із випередженням умовна й пов'язана з вибором початку
відліку. Зрозуміло, що якщо за початковий момент вибрати момент 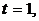 то рента із
запізненням може розглядатися як рента із випередженням.
то рента із
запізненням може розглядатися як рента із випередженням.
Приведена цінність ренти із
випередженням у фінансовій математиці позначається 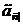 . Це -
цінність серії з п платежів величиною 1, здійснених через одиничні інтервали
часу. Вартість цієї серії розраховується в момент здійснення першого платежу.
. Це -
цінність серії з п платежів величиною 1, здійснених через одиничні інтервали
часу. Вартість цієї серії розраховується в момент здійснення першого платежу.
У випадку, коли цінність
даної серії платежів розраховується не на момент першого платежу, а на одиницю
часу раніше (умовний нуль), то приведена цінність називається приведеною
цінністю із запізненням і позначається 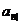 .
.
Щоб підрахувати ці величини,
потрібно привести кожний з п платежів до початкового моменту часу 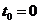 , а потім
додати отримані значення:
, а потім
додати отримані значення:
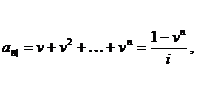 (2.1.6)
(2.1.6)
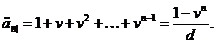 (2.1.7)
(2.1.7)
Величини 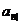 і
і 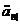 дозволяють
підрахувати розмір суми, яку потрібно інвестувати в даний момент для того, щоб
одержувати фіксований регулярний дохід у майбутньому. З їхньою допомогою також
можна визначити величину регулярних виплат у випадку, коли борг повертається не
одним платежем, а серією однакових платежів.
дозволяють
підрахувати розмір суми, яку потрібно інвестувати в даний момент для того, щоб
одержувати фіксований регулярний дохід у майбутньому. З їхньою допомогою також
можна визначити величину регулярних виплат у випадку, коли борг повертається не
одним платежем, а серією однакових платежів.
Розглянуті вище рентні
платежі починалися на першому ж проміжку (0, 1) (на його початку, тобто в
момент 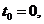 для ренти з
випередженням, і наприкінці, тобто в момент
для ренти з
випередженням, і наприкінці, тобто в момент 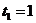 , для ренти із запізненням). Для
застосування на практиці важливі також так звані відтерміновані ренти (defferred
annuities). Щоб дати означення таких рент, розглянемо послідовні одиничні
проміжки часу (0,1), (1, 2), … , (m-1, m), (m, m+1), … , (m+п-1, m+п). Як і
раніше, під моментом
, для ренти із запізненням). Для
застосування на практиці важливі також так звані відтерміновані ренти (defferred
annuities). Щоб дати означення таких рент, розглянемо послідовні одиничні
проміжки часу (0,1), (1, 2), … , (m-1, m), (m, m+1), … , (m+п-1, m+п). Як і
раніше, під моментом  ми будемо
мати на увазі дійсний момент часу.
ми будемо
мати на увазі дійсний момент часу.
Серія з п виплат, кожна
величиною 1, зроблених наприкінці проміжків (m, m+1), …, (m+n-1, m+n), тобто в
моменти m+1, ..., m+n, називається відтермінованою рентою із запізненням
(deferred immediate annuity). Її цінність у даний момент 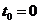 позначається
позначається
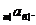 Щоб
підрахувати цю величину, приведемо кожний з п платежів у моменти m+1, …, m+n до
початкового моменту часу, після чого додамо одержані значення:
Щоб
підрахувати цю величину, приведемо кожний з п платежів у моменти m+1, …, m+n до
початкового моменту часу, після чого додамо одержані значення:
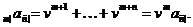
Серія із n виплат, кожна
величиною 1, зроблених на початку проміжків (m, m+1), …, (m+n-1, т+п), тобто в
моменти m, … m+n-1, називається відтермінованою рентою із випередженням
(deferred annuity-due). Її вартість у теперішній момент 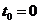 позначається
позначається
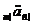 . Щоб
підрахувати цю величину, приведемо кожний з п платежів у моменти m,. . . ,
m+n-1 до теперішнього моменту часу, а потім додамо отримані значення:
. Щоб
підрахувати цю величину, приведемо кожний з п платежів у моменти m,. . . ,
m+n-1 до теперішнього моменту часу, а потім додамо отримані значення:
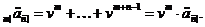
Часто корисно знати цінність
ренти не в початковий момент часу, а наприкінці останнього платіжного періоду.
Цю цінність можна інтерпретувати як загальну суму, накопичену на банківському
рахунку після серії регулярних внесків. Її позначають так само, як і відповідну
приведену цінність у початковий момент, але із заміною букви а на букву s.
Отже, 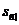 - це
приведена вартість ренти із запізненням в момент
- це
приведена вартість ренти із запізненням в момент 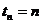 останнього платежу, а
останнього платежу, а 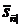 - це
приведена цінність ренти з випередженням, у момент
- це
приведена цінність ренти з випередженням, у момент 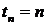 , тобто
через одиницю часу після останнього платежу.
, тобто
через одиницю часу після останнього платежу.
Формули для нагромаджень 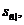
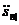 можна
одержати безпосередньо, привівши кожний з п платежів до моменту
можна
одержати безпосередньо, привівши кожний з п платежів до моменту 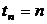 і потім
додавши отримані значення:
і потім
додавши отримані значення:
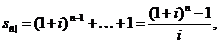 (2.1.8)
(2.1.8)
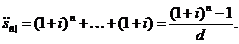 (2.1.9)
(2.1.9)
Детерміновані постійні ренти,
виплачувані із частотою р
Розглянемо п послідовних
одиничних проміжків часу (0,1), (1, 2), … , (п-1, п). Під моментом 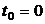 ми, як
правило, будемо мати на увазі дійсний момент, а як одиничний проміжок часу
будемо розглядати один рік.
ми, як
правило, будемо мати на увазі дійсний момент, а як одиничний проміжок часу
будемо розглядати один рік.
Розіб’ємо кожний з п
одиничних проміжків на р рівних частин довжиною 1/р кожна. Якщо, як ми
відзначали, за одиниця часу прийнято один рік, то найцікавішими є випадки:
1)
р = 12 (проміжок часу 1/р відповідає
одному місяцю),
2)
р = 4 (проміжок часу 1/р відповідає
одному кварталу),
3)
р = 2 (проміжок часу 1/р відповідає
одному півріччю).
Серія з np виплат,
кожна величиною 1/р, зроблених наприкінці цих підпроміжків, тобто в моменти
1/р, ..., р/р = 1;
… ; п-1+1/р, …, п-1+р/р=п,
називається рентою із
запізненням, виплачуваною із частотою р (annuity payable p thly in arrear чи
immediate annuity payable p thly). Її цінність у даний момент 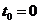 позначається
позначається
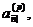 а цінність
у момент
а цінність
у момент 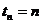 останнього
платіжного періоду називається нагромадженням і позначається
останнього
платіжного періоду називається нагромадженням і позначається 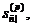
Зазначимо, що кожна виплата
має величину 1/р, так що як одиниця виміру грошових сум розглядається
алгебраїчна сума всіх виплат за одиничний проміжок часу (у типовому випадку -
за рік).
Серія з np виплат, кожна
величиною 1/р, зроблених на початку підпроміжків, тобто в момент
; 1/p; …; (p-1)/p; …; n-1,
n-1+1/p; …; n-1+(p-1)/p,
називається рентою з
випередженням, виплачуваною із частотою p (annuity payable p thly in advance чи
p thly annuity-due). Її цінність у даний момент 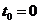 позначається
позначається 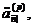 а цінність
у момент
а цінність
у момент 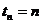 закінчення
останнього платіжного періоду називається нагромадженням і позначається
закінчення
останнього платіжного періоду називається нагромадженням і позначається 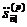 .
.
Величини 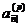 і
і 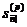 , так само
як і величини
, так само
як і величини 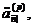
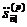 , оцінюють ту саму серію платежів,
але в різні моменти часу. Тому між ними негайно може бути встановлений простий
зв'язок:
, оцінюють ту саму серію платежів,
але в різні моменти часу. Тому між ними негайно може бути встановлений простий
зв'язок:
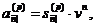
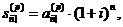
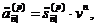
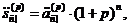
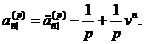
Отже, нам досить мати формулу
для величини 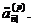 Із цією
метою візьмемо за одиничний відрізок часу р-у частку початкового одиничного
відрізка (наприклад, якщо р=12 і вихідний одиничний проміжок часу був один рік,
то новим одиничним відрізком часу буде один місяць). Ефективна процентна ставка
для цього нового одиничного відрізка дорівнює
Із цією
метою візьмемо за одиничний відрізок часу р-у частку початкового одиничного
відрізка (наприклад, якщо р=12 і вихідний одиничний проміжок часу був один рік,
то новим одиничним відрізком часу буде один місяць). Ефективна процентна ставка
для цього нового одиничного відрізка дорівнює
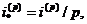
де 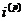 -
номінальна процентна ставка для основного одиничного проміжку, що нараховується
із частотою р. Відповідно, нова облікова ставка дорівнює
-
номінальна процентна ставка для основного одиничного проміжку, що нараховується
із частотою р. Відповідно, нова облікова ставка дорівнює 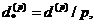 а нове
значення коефіцієнта дисконтування рівне
а нове
значення коефіцієнта дисконтування рівне 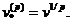
Тепер на ренту з
випередженням, виплачувану із частотою р на проміжку (0, n), можна дивитися як
на звичайну ренту з випередженням, виплачувану на проміжку (0, np). Оскільки
кожна виплата дорівнює 1/р, ми маємо:
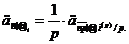 (2.1.10)
(2.1.10)
де символом 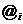 позначено
ефективну процентну ставку на проміжку, що розглядається в якості одиничного.
Звідси випливає, що:
позначено
ефективну процентну ставку на проміжку, що розглядається в якості одиничного.
Звідси випливає, що:
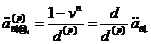 (2.1.11)
(2.1.11)
Для 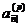 вірна
аналогічна формула:
вірна
аналогічна формула:
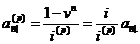 (2.1.12)
(2.1.12)
Неперервні ренти
Розглянемо тепер ренти із
запізненням і з випередженням, які виплачуються із частотою р на проміжку [0,
п], і припустимо, що 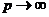 . Неважко
показати, що
. Неважко
показати, що
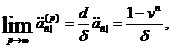
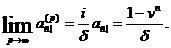
Той факт, що ці границі
співпадають, легко пояснити інтуїтивно.
Якщо 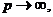 то ми маємо
справу з більшою кількістю малих платежів (величиною 1/р кожний), які
здійснюються через малі проміжки часу 1/р. При
то ми маємо
справу з більшою кількістю малих платежів (величиною 1/р кожний), які
здійснюються через малі проміжки часу 1/р. При 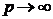 можна розглядати надходження
засобів як неперервний процес, подібний до плину рідини. При цьому на
нескінченності різниця між платежами на початку й наприкінці проміжків зникне.
Неперервний потік платежів, який з’явився у цьому міркуванні, називається
неперервно виплачуваною рентою [7] (continuously payable annuity). Приведена
вартість неперервного потоку платежів у момент
можна розглядати надходження
засобів як неперервний процес, подібний до плину рідини. При цьому на
нескінченності різниця між платежами на початку й наприкінці проміжків зникне.
Неперервний потік платежів, який з’явився у цьому міркуванні, називається
неперервно виплачуваною рентою [7] (continuously payable annuity). Приведена
вартість неперервного потоку платежів у момент 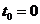 позначається
позначається 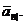
Розглядаючи надходження
засобів у граничному випадку 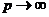 як неперервний потік, легко
безпосередньо визначити величину
як неперервний потік, легко
безпосередньо визначити величину 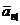 як інтеграл
як інтеграл
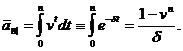
Можна ввести й довільну
неперервну ренту на проміжку [0, n], що характеризується довільною швидкістю
р(t) надходження засобів у момент t. Для такої ренти приведена вартість у
момент 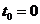 рівна
інтегралу
рівна
інтегралу
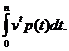
Неперервні ренти часто
використаються як наближення для рент, які виплачуються достатньо часто:
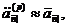
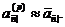
Можна одержати і більш точні
формули:
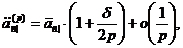
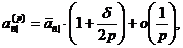
Сума, накопичена до моменту t
при неперервному надходженні засобів зі швидкістю 1, позначається 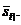 Вона може
бути підрахована приведенням суми
Вона може
бути підрахована приведенням суми 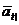 до моменту t:
до моменту t:
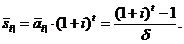
Детерміновані зростаючі ренти
Розглянемо п послідовних
одиничних проміжків часу (0,1), (1, 2), …, (п-1, п). Під моментом 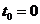 ми будемо
мати на увазі поточний момент, а за одиничний проміжок часу приймемо один рік.
Серія з п виплат величиною 1, 2, . . . , n, зроблених наприкінці цих проміжків,
тобто в моменти
ми будемо
мати на увазі поточний момент, а за одиничний проміжок часу приймемо один рік.
Серія з п виплат величиною 1, 2, . . . , n, зроблених наприкінці цих проміжків,
тобто в моменти 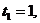
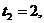 …,
…, 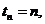 називається
зростаючою рентою із запізненням (increasing immediate annuity). Її приведена
цінність у момент
називається
зростаючою рентою із запізненням (increasing immediate annuity). Її приведена
цінність у момент 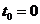 у
фінансовій математиці позначається
у
фінансовій математиці позначається 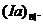 Для підрахунку цієї величини
потрібно всі платежі привести до початкового моменту, а потім додати:
Для підрахунку цієї величини
потрібно всі платежі привести до початкового моменту, а потім додати:
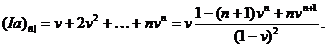 (2.1.13)
(2.1.13)
Серія з п виплат величиною 1,
2, …, n, зроблених на початку проміжків (0,1),.. ., (п-1, n), тобто в моменти 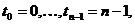 називається
зростаючою рентою з випередженням (increasing immediate annuity). Її приведена
цінність у момент
називається
зростаючою рентою з випередженням (increasing immediate annuity). Її приведена
цінність у момент 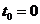 позначається
позначається
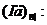
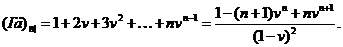 (2.1.14)
(2.1.14)
2.1.4
Прибутковість інвестиційних проектів
Інвестиційний проект - це
угода, згідно якої інвестор у певні моменти часу 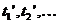 вкладає кошти в розмірі
вкладає кошти в розмірі 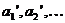 відповідно,
а потім у моменти
відповідно,
а потім у моменти 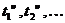 одержує
дохід у розмірі
одержує
дохід у розмірі 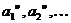 відповідно.
відповідно.
Моменти 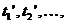 коли
інвестор вкладає кошти, не зобов'язані передувати моментам
коли
інвестор вкладає кошти, не зобов'язані передувати моментам 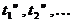 , коли
інвестор одержує дохід (хоча для застосувань до страхування це, як правило, має
місце), а можуть чергуватися.
, коли
інвестор одержує дохід (хоча для застосувань до страхування це, як правило, має
місце), а можуть чергуватися.
Для спрощення теоретичних
міркувань зручно розглядати об'єднану послідовність моментів часу 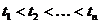 і вважати,
що
і вважати,
що
. якщо 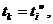 то в момент
то в момент
 проект
приносить прибуток у розмірі
проект
приносить прибуток у розмірі 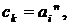
. якщо 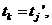 то в момент
то в момент
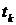 проект приносить
негативний дохід у розмірі
проект приносить
негативний дохід у розмірі 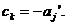
Послідовність 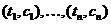 називається
чистим грошовим потоком.
називається
чистим грошовим потоком.
Найпростішою мірою
прибутковості інвестиційного проекту є внутрішня ставка прибутковості (internal
rate of return - IRR). Ця величина задовольняє наступне рівняння прибутковості
(yield equation):
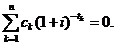
Загалом кажучи, рівняння
прибутковості має декілька дійсних коренів. Інтерпретувати як процентну ставку
можна лише корінь, що більше, ніж -1; при цьому лише позитивний корінь означає
власне дохід. Зрозуміло, що якщо не робити ніяких припущень про структуру
інвестиційного проекту, то рівняння прибутковості може мати кілька таких
коренів. У цьому випадку вважають, що внутрішня ставка прибутковості не
визначена.
У застосуваннях до
страхування життя доводиться мати справу із проектами, у яких всі негативні
платежі передують позитивним. Для таких проектів рівняння прибутковості має
єдиний корінь 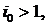 який
приймають у якості IRR. Якщо, крім того, сума абсолютних величин всіх
негативних платежів менша, ніж сума всіх позитивних, то цей корінь рівняння
прибутковості позитивний.
який
приймають у якості IRR. Якщо, крім того, сума абсолютних величин всіх
негативних платежів менша, ніж сума всіх позитивних, то цей корінь рівняння
прибутковості позитивний.
2.2
Характеристики тривалості життя
2.2.1 Час
життя як випадкова величина
Невизначеність моменту смерті є
основним фактором ризику для страхування життя. Тому, створення адекватної
теорії для страхування життя повинне починатися з розробки системи понять і
означення величин, які дозволяють висловлювати об’єктивне твердження про
тривалість життя. Основним є наступний висновок.
Відносно моменту смерті окремої
людини неможливо сказати нічого визначеного. Однак, якщо ми маємо справу з
великою однорідною групою людей і не цікавимося долею окремих людей з цієї
групи, то ми знаходимося в рамках теорії ймовірностей як науки про масові
випадкові явища, які володіють властивістю стійкості частот. Відповідно, ми
можемо говорити про тривалість життя як про випадкову величину T.
Функція виживання
В теорії ймовірностей
описують стохастичну природу будь-якої випадкової величини T функцією розподілу
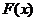 , яка
визначається як ймовірність того, що випадкова величина T менша, ніж число x:
, яка
визначається як ймовірність того, що випадкова величина T менша, ніж число x:
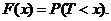
В актуарій математиці
прийнято працювати не з функцією розподілу, а з додатковою функцією розподілу
[9] 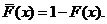 Застосовуючи
до тривалості життя
Застосовуючи
до тривалості життя 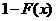 - це ймовірність
того, що людина доживе до віку x років. Функція
- це ймовірність
того, що людина доживе до віку x років. Функція
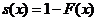
називається функцією
виживання (survival function):
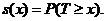
Функція виживання володіє
наступними характеристичними властивостями:
. 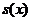 спадає (при
спадає (при
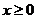 );
);
. 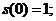
. 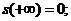
. 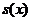 неперервна.
неперервна.
В таблицях тривалості життя
як правило вважають, що існує деякий граничний вік (limiting age) 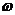 (переважно,
(переважно,
 =100-120
років) і відповідно
=100-120
років) і відповідно 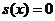 при
при 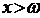 . При
описанні смертності аналітичними законами переважно вважають, що час життя
необмежений, однак підбирають вид і параметри законів так, щоб ймовірність
життя понад деякий вік була б нескінечно мала.
. При
описанні смертності аналітичними законами переважно вважають, що час життя
необмежений, однак підбирають вид і параметри законів так, щоб ймовірність
життя понад деякий вік була б нескінечно мала.
Функція виживання має простий
статистичний зміст. Припустимо, що ми спостерігаємо за групою з 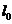 новонароджених
(як правило,
новонароджених
(як правило, 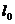 =100000) і
можемо фіксувати моменти їх смерті. Позначимо кількість живих представників
цієї групи у віці x через
=100000) і
можемо фіксувати моменти їх смерті. Позначимо кількість живих представників
цієї групи у віці x через 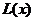 . Тоді:
. Тоді:
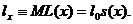
Символ M тут і нижче
використовується для позначення математичного сподівання. Отже, функція
виживання 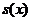 рівна
середній частці доживших до віку x з деякої фіксованої групи новонароджених.
рівна
середній частці доживших до віку x з деякої фіксованої групи новонароджених.
В актуарій математиці часто
працюють не з функцією виживання 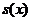 , а з тільки що введеною величиною
, а з тільки що введеною величиною 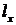 (зафіксувавши
початковий розмір групи
(зафіксувавши
початковий розмір групи 
Крива смертей
В теорії ймовірностей
прийнято описувати стохастичну природу неперервних випадкових величин щільністю
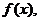 яка може
бути визначена як похідна від функції розподілу. В актуарій математиці графік
щільності тривалості життя
яка може
бути визначена як похідна від функції розподілу. В актуарій математиці графік
щільності тривалості життя 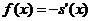 (чи, що практично одне і те ж,
графік функції
(чи, що практично одне і те ж,
графік функції 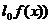 називають
кривою смертей (the curve of deaths). Величина
називають
кривою смертей (the curve of deaths). Величина 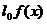 має простий статистичний зміст.
Розглянемо середню кількість представників вихідної групи з
має простий статистичний зміст.
Розглянемо середню кількість представників вихідної групи з 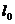 новонароджених,
які померли у віці x років; ця величина позначається
новонароджених,
які померли у віці x років; ця величина позначається 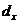 і рівна
і рівна 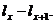 Тоді
Тоді 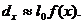
Функція виживання 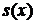 може бути
відновлено по щільності
може бути
відновлено по щільності
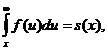
тому крива смертей може бути
використана у якості первісної характеристики тривалості життя.
Інтенсивність смертності
Величина
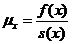
називається інтенсивністю
смертності (the force of montality). Для людини, яка дожила до x років при
малих t величина 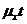 наближено
виражає ймовірність смерті у інтервалі (x, x+t).
наближено
виражає ймовірність смерті у інтервалі (x, x+t).
Оскільки функція виживання 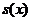 може бути
відновлена по інтенсивності смертності:
може бути
відновлена по інтенсивності смертності:
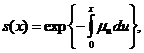
інтенсивність смертності може
бути використана у якості первинної характеристики тривалості життя.
Макрохарактеристики
тривалості життя
З практичної точки зору
важливими є наступні макрохарактеристики смертності:
) середній час життя
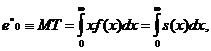
2) дисперсія часу життя
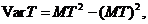
де
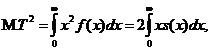
) медіана часу життя 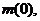 яка
визначається як корінь рівняння
яка
визначається як корінь рівняння 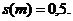
Медіана часу життя - це вік,
до якого доживає рівно половина представників вихідної групи новонароджених.
Аналітичні закони смертності
Для спрощення розрахунків,
теоретичного аналізу і т.д. природно спробувати описати одержувані емпіричним
шляхом дані про функцію виживання чи інтенсивності смертності за допомогою
простих аналітичних формул.
Просте наближення було
введено у 1729 році де Муавром (de Moivre), який запропонував рахувати, що час
життя рівномірно розподілений на інтервалі 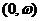 , де
, де  - граничний вік. В моделі де Мавра
при
- граничний вік. В моделі де Мавра
при 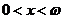
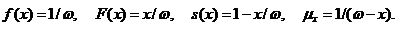
Порівняння графіків цих
функцій з реальними графіками функції виживання 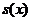 , функції смертей f(x),
інтенсивності смертності
, функції смертей f(x),
інтенсивності смертності 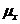 показує, що
закон де Мавра є не дуже хорошим наближенням. Наприклад, перши формула означає,
що крива смертей f(x) є горизонтальною лінією, у той час як емпіричні дані
вказують на пік у районі 80 років.
показує, що
закон де Мавра є не дуже хорошим наближенням. Наприклад, перши формула означає,
що крива смертей f(x) є горизонтальною лінією, у той час як емпіричні дані
вказують на пік у районі 80 років.
В моделі, яку запропонував у
1825 році п. Гомпертць (Gompertz), інтенсивність смертності 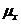 наближається
показниковою функцією виду
наближається
показниковою функцією виду 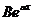 , де
, де 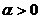 і
і 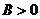 - деякі параметри. Відповідна
функція виживання s(x) має вигляд
- деякі параметри. Відповідна
функція виживання s(x) має вигляд
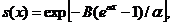 (2.2.1)
(2.2.1)
а крива смертей
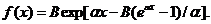
Мейкхам (Makeham) у 1860 році
узагальнив попередню модель, наблизивши інтенсивність смертності 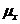 функцією
виду
функцією
виду  Постійний
доданок A дозволяє врахувати ризики для життя, пов’язані з нещасними випадками
(які мало залежать від віку), у той час як доданок
Постійний
доданок A дозволяє врахувати ризики для життя, пов’язані з нещасними випадками
(які мало залежать від віку), у той час як доданок 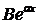 враховує
вплив віку на смертність. У цій моделі
враховує
вплив віку на смертність. У цій моделі
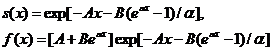 (2.2.2)
(2.2.2)
Другий закон Мейкхама,
введений у 1889 році, наближає інтенсивність смертності 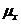 функцією
виду
функцією
виду 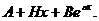 У цій
моделі
У цій
моделі
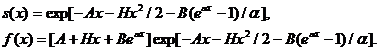 (2.2.3)
(2.2.3)
Вейбулл (Weibull) у 1939 році
запропонував наближати інтенсивність смертності 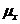 більш простою функцією виду
більш простою функцією виду 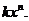 У цій
моделі
У цій
моделі
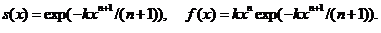 (2.2.4)
(2.2.4)
2.2.2
Залишковий час життя
Страхова компанія має справу
з конкретними людьми, які дожили до певного віку. Статистичні властивості часу
життя таких людей суттєво відрізняються від властивостей часу життя
новонароджених. Якщо людина у віці x років звернулася у страхову компанію (в
актуарій математиці таку людину позначають через (x)), то відомо, що вона
дожила до віку x років, і тому усі випадкові події, пов’язані з цією людиною,
повинні розглядатися при умові, що 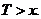
Для людини у віці x років
переважно розглядають не тривалість життя Т, а залишковий час життя 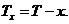 Розподіл
випадкової величини
Розподіл
випадкової величини 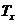 - це
умовний розподіл величини
- це
умовний розподіл величини 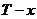 при умові,
що
при умові,
що 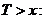
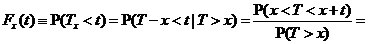

Відповідна функція виживання 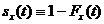 задається
формулою:
задається
формулою:
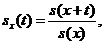
тому щільність 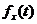 випадкової
величини
випадкової
величини 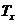 може бути
підрахована за формулою:
може бути
підрахована за формулою:
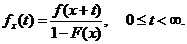
Інтенсивність смертності,
пов’язана з величиною 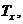 якщо
якщо
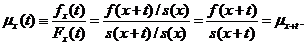
Це співвідношення означає, що
інтенсивність смертності через час t для людини, якій зараз x років, рівна
інтенсивності смертності у віці x+t для новонародженого. Іншими словами,
інтенсивність смертності у даному віці x+t не залежить від вже прожитих років.
Основні величини, пов’язані з
залишковим часом життя
Ймовірність 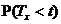 (тобто
ймовірність смерті людини віку x років на протязі найближчих t років) в
актуарій науці позначається символом
(тобто
ймовірність смерті людини віку x років на протязі найближчих t років) в
актуарій науці позначається символом 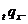 З наведених вище формул для
З наведених вище формул для 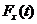 випливає,
що
випливає,
що
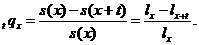
Додаткова ймовірність 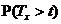 (тобто
ймовірність того, що людина у віці x років проживе як мінімум t років) в
актуарій науці позначається символом
(тобто
ймовірність того, що людина у віці x років проживе як мінімум t років) в
актуарій науці позначається символом 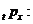
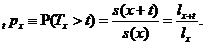
Випадок 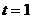 відіграє
особливу практичну роль і зустрічається найбільш часто. Для нього прийнято
опускати передній індекс у змінних
відіграє
особливу практичну роль і зустрічається найбільш часто. Для нього прийнято
опускати передній індекс у змінних 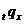 і
і 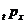 . Таким чином символ
. Таким чином символ 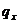 позначає
ймовірність того, що людина у віці x років помре на протязі найближчого року, а
символ
позначає
ймовірність того, що людина у віці x років помре на протязі найближчого року, а
символ 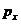 позначає
ймовірність того, що людина у віці x років проживе ще як мінімум один рік. З
наведених вище загальних формул маємо:
позначає
ймовірність того, що людина у віці x років проживе ще як мінімум один рік. З
наведених вище загальних формул маємо:
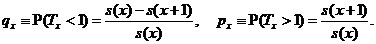
За допомогою ймовірностей 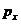 можна
підрахувати і більш загальні ймовірності
можна
підрахувати і більш загальні ймовірності 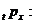

Розглянемо тепер більш
загальну подію, яка полягає у тому, що людина віку x проживе ще t років, але
помре на протязі u наступних років.
В термінах залишкового часу
життя 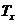 цю подію
можна виразити подвійною нерівністю:
цю подію
можна виразити подвійною нерівністю: 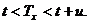 Ця ймовірність позначається
Ця ймовірність позначається 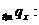
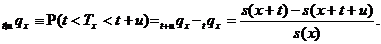
Випадок 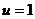 цікавий для
застосування до страхування життя. Як і в попередньому випадку, відповідний
індекс прийнято упускати. Отже,
цікавий для
застосування до страхування життя. Як і в попередньому випадку, відповідний
індекс прийнято упускати. Отже, 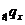 - це ймовірність того, що людина у
віці x років проживе ще t років, але помре на протязі наступного року. Наведені
вище загальні формули дають:
- це ймовірність того, що людина у
віці x років проживе ще t років, але помре на протязі наступного року. Наведені
вище загальні формули дають:
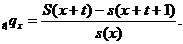
Макрохарактеристики
залишкового часу життя
Середнє значення залишкового
часу життя людини у віці x років 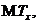 позначається
позначається 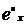 і
називається повною сподіваною тривалістю життя (the
complete-expectation-of-life):
і
називається повною сподіваною тривалістю життя (the
complete-expectation-of-life):
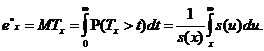 (2.2.5)
(2.2.5)
Для другого моменту 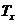 вірна
аналогічна формула:
вірна
аналогічна формула:
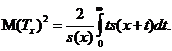 (2.2.6)
(2.2.6)
Середній залишковий час життя
можна виразити і через інші характеристики часу життя. З цією ціллю розглянемо
групу з 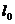 новонароджених
і позначимо через
новонароджених
і позначимо через 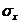 сумарну
кількість років, які були прожиті представниками цієї групи після віку x років.
Таким чином, якщо час життя і-го представника групи
сумарну
кількість років, які були прожиті представниками цієї групи після віку x років.
Таким чином, якщо час життя і-го представника групи 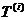 менший від
x, його вклад у суму
менший від
x, його вклад у суму 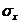 рівний 0.
Якщо ж
рівний 0.
Якщо ж 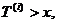 то вклад у
суму рівний
то вклад у
суму рівний 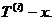
Тоді
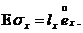
Середнє значення величини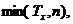 де n -
деяка додатна константа, називають частковою середньою тривалістю життя і
позначають
де n -
деяка додатна константа, називають частковою середньою тривалістю життя і
позначають 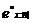 . Для неї
вірна формула
. Для неї
вірна формула
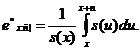
2.2.3
Заокруглена тривалість життя
Зазвичай люди ведуть рахунок
прожитих років цілими роками, а страхові компанії зазвичай заключають договори
страхування життя на 1, 3, 5 і т.д. цілу кількість років. У зв’язку з цим
природно розглянути поряд із звичайною тривалістю життя 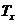 її цілу
частину
її цілу
частину 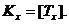 Таким
чином, якщо наприклад,
Таким
чином, якщо наприклад, 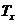 =18 років 9
місяців=18,75 років, то
=18 років 9
місяців=18,75 років, то 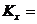 18 років.
Величина
18 років.
Величина 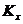 називається
округленою залишковою тривалістю життя (curtate-future-lifetime). Слід
відзначити, що заокруглення здійснюється не до найближчого цілого, а завжди з
недостачею (тобто до найближчого цілого, яке менше, ніж дане дробове число). В
цьому розумінні англійський термін curtate („урізана”) - точніший, ніж
прийнятий термін „заокруглена”.
називається
округленою залишковою тривалістю життя (curtate-future-lifetime). Слід
відзначити, що заокруглення здійснюється не до найближчого цілого, а завжди з
недостачею (тобто до найближчого цілого, яке менше, ніж дане дробове число). В
цьому розумінні англійський термін curtate („урізана”) - точніший, ніж
прийнятий термін „заокруглена”.
Розподіл заокругленого часу
життя
Оскільки випадкова величина 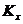 приймає
тільки цілі значення, її стохастична природа характеризується (як це прийнято в
теорії ймовірностей) не функцією розподілу, а розподілом, тобто набором ймовірностей
приймає
тільки цілі значення, її стохастична природа характеризується (як це прийнято в
теорії ймовірностей) не функцією розподілу, а розподілом, тобто набором ймовірностей
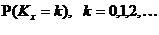 . Оскільки
подія
. Оскільки
подія 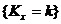 еквівалентна
тому, що
еквівалентна
тому, що 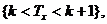 є істинними
рівності:
є істинними
рівності:
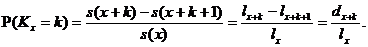
Середня заокруглена
тривалість життя і її дисперсія
Математичне сподівання
випадкової величини 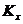 називається
середньою заокругленою тривалістю життя (curtate-expectation-of-life) і
позначається
називається
середньою заокругленою тривалістю життя (curtate-expectation-of-life) і
позначається 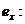
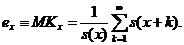 (2.2.7)
(2.2.7)
Подібним чином для другого
моменту 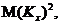 який є
необхідним для розрахунку
який є
необхідним для розрахунку 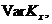 ми маємо:
ми маємо:
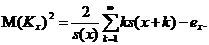 (2.2.8)
(2.2.8)
Більш цікавою є рекурентна
формула
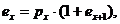
звідки випливають наступні
співвідношення, які пов’язують середню заокруглену тривалість життя і
ймовірність смерті на протязі найближчого року
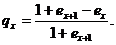
.2.4
Таблиці тривалості життя
Статистичні дані про
тривалість життя, як ми уже зазначали, підсумовуються у таблицях тривалості
життя (life tables) (див. Додаток 1); іноді їх називають таблицями смертності
(mortality tables). Найпростішим видом таблиць є таблиці, які містять
інформацію про статистичні властивості тривалості життя випадково вибраної
людини, про якого відомим є тільки його вік. Такі таблиці називають загальними
чи спрощеними [4] (aggregate tables). Вони дозволяють одержати загальну
наближену картину смертності. Прикладом таких таблиць можуть служити популярні
таблиці, які містять дані про смертність населення. В принципі для
розв’язування будь-якої задачі достатнім є знання функції виживання 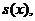 однак для
наочності в таблиці як правило включають введені раніше величини:
однак для
наочності в таблиці як правило включають введені раніше величини:
) 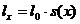 - середня
кількість живих представників деякої групи з
- середня
кількість живих представників деякої групи з 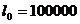 новонароджених у віці x років;
новонароджених у віці x років;
) 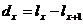 - кількість
представників групи, які померли у віці від x до x+1 років;
- кількість
представників групи, які померли у віці від x до x+1 років;
) 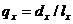 -
ймовірність смерті протягом року для людини у віці x років;
-
ймовірність смерті протягом року для людини у віці x років;
) 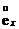 - середній залишковий
час життя.
- середній залишковий
час життя.
У якості кроку таблиці як
правило розглядають 1 рік, тобто табулюють значення функції від x для x =0, 1,
2, … років.
Таблиці відбору ризику
Очевидно, що статистичні
властивості тривалості життя цілком різні у жителя високорозвиненої країни
Заходу і жителя бідної африканської держави, тому абсолютно загальна таблиця
взагалі не має реального інтересу.
Однак, зрозуміло, що і серед
жителів однієї країни існують різноманітні групи людей з різними
характеристиками тривалості життя. Перш за все, важливо відзначити, що
смертність серед мужчин є у декілька разів вищою ніж смертність серед жінок.
Ймовірно, смертність серед домогосподарок є меншою, ніж серед шахтарів;
смертність серед людей, які пройшли медичну комісію перед укладанням договору страхування,
є меншою, ніж у середньому по країні ; смертність серед людей, які вийшли на
пенсію через хворобу, навпаки, є вищою (звичайно, у всіх випадках ми повинні
порівнювати людей у одному віці x). Однак, страхова компанія має справу не з
абстрактними людьми, а з цілком конкретними, відносно яких відома деяка
інформація (стать, професія, перенесені хвороби і т.д.). Тому зрозуміло, що
компанія повинна мати цілий спектр таблиць тривалості життя для різних груп
населення. Такі таблиці називаються таблицями з відбором (select tables) чи
таблицями відбору ризику. Як правило створюється декілька базових таблиць, а
багаточисельні додаткові ризики враховуються за допомогою вказівок по
андеррайтингу, які дають відповідні коефіцієнти (чи адитивні надбавки) до базових
тарифів. Моральні небезпеки переважно враховують юридичними обмеженнями і
зменшенням страхової суми.
У зв’язку з цим величини,
включені у таблиці з відбором, мають два аргументи: один показує момент відбору
x, а другий - час t, який пройшов з моменту відбору. Щоб вказати цю залежність,
в актуарій математиці не пишуть 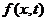 чи
чи 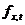 (як ми це зробили б у загальному
курсі математики), а застосовують наступне позначення:
(як ми це зробили б у загальному
курсі математики), а застосовують наступне позначення: 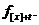
При фіксованому віці 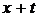 і моменті
відбору
і моменті
відбору 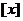 (чи, що те
ж саме, проміжку часу t, який пройшов з моменту відбору) величина виду
(чи, що те
ж саме, проміжку часу t, який пройшов з моменту відбору) величина виду 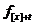 нічим
принципово не відрізняється від величини
нічим
принципово не відрізняється від величини 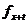 (ми лише явно вказуємо деяку
додаткову умову, при якій вона розглядається). Тому, для характеристик
тривалості життя «відібраних» людей справедливі усі наведені вище результати,
включаючи введені там позначення (так само, як для умовних ймовірностей в
класичному курсі теорії ймовірностей справедливі всі теореми, доведені для
звичайних ймовірностей). Наприклад,
(ми лише явно вказуємо деяку
додаткову умову, при якій вона розглядається). Тому, для характеристик
тривалості життя «відібраних» людей справедливі усі наведені вище результати,
включаючи введені там позначення (так само, як для умовних ймовірностей в
класичному курсі теорії ймовірностей справедливі всі теореми, доведені для
звичайних ймовірностей). Наприклад,
) 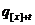 позначає
умовну ймовірність смерті на протязі року людини у віці x+t років, яка t років
назад (тобто у віці x років) була відібрана у групу;
позначає
умовну ймовірність смерті на протязі року людини у віці x+t років, яка t років
назад (тобто у віці x років) була відібрана у групу;
) 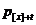 - це
ймовірність того, що людина у віці x+t років, яка була t років тому назад
(тобто у віці x років) відібрана у групу, проживе ще як мінімум рік;
- це
ймовірність того, що людина у віці x+t років, яка була t років тому назад
(тобто у віці x років) відібрана у групу, проживе ще як мінімум рік;
) 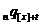 -
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
помре на протязі найближчих n років;
-
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
помре на протязі найближчих n років;
) 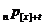 -
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще як мінімум n років;
-
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще як мінімум n років;
) 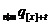 -
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще n років, але помре на протязі m наступних років;
-
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще n років, але помре на протязі m наступних років;
) 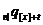 -
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще n років, але помре на протязі наступного року.
-
ймовірність того, що людина у віці x+t років, яка відібрана t років назад,
проживе ще n років, але помре на протязі наступного року.
Всі ці ймовірності можуть
бути виражені через ймовірності 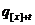 ; наприклад,
; наприклад,

Таблиці з відбором обмеженої
дії
Тонкий статистичний аналіз
показує, що як правило вплив відбору продовжується необмежено довго. Однак, у
більшості випадків, залежність характеристик смертності від часу, який пройшов
з моменту відбору, швидко зменшується і через деякий час (з тим чи іншим
ступенем точності) ці характеристики залежать тільки від досягнутого віку. Слід
відзначити, що сам вплив відбору зберігається, у тому розумінні, що ці
характеристики відрізняються від популяційних.
Проміжок часу r, після якого
залежністю від моменту відбору можна знехтувати і розглядати всі характеристики
тривалості життя тільки як функції досягнутого віку, називається (хоча цей
термін не дуже правильно передає суть справи) періодом дії відбору (select
period).
Відповідна таблиця
називається таблицею з відбором обмеженої дії (select-and-ultimate table).
Граничні значення 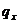 (які
заміняють
(які
заміняють 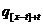 при
при 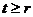 ) утворюють
так звану граничну таблицю (ultimate table). По своїй структурі вона є таблицею
найпростішого виду.
) утворюють
так звану граничну таблицю (ultimate table). По своїй структурі вона є таблицею
найпростішого виду.
Розрахунок характеристик
смертності серед представників виділеної групи може бути значно спрощений, якщо
замість ймовірностей 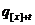 ввести у
розгляд спеціальні величини
ввести у
розгляд спеціальні величини 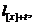 які є аналогічними до величин
які є аналогічними до величин 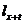 із
загальних таблиць смертності.
із
загальних таблиць смертності.
Розглянемо деяку таблицю з відбором,
який діє на протязі r років, і визначимо величини 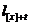 за
допомогою наступної формули:
за
допомогою наступної формули:
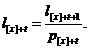
Оскільки період дії відбору
рівний r, ми покладаємо
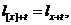 якщо
якщо 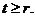
Тоді
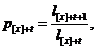
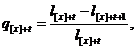
і тому величини 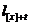 можуть
використовуватися у якості первинних характеристик смертності представників
виділеної групи. Однак важливішим є те, що більш складні характеристики
смертності, такі як
можуть
використовуватися у якості первинних характеристик смертності представників
виділеної групи. Однак важливішим є те, що більш складні характеристики
смертності, такі як 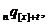
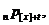
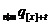 ,
, 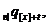 можуть бути
простіше виражені через величини
можуть бути
простіше виражені через величини 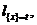 ніж через величини
ніж через величини 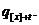 Наприклад,
Наприклад,
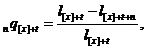
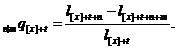
Для подальшого спрощення
формул можна ввести величини
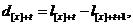
так що, наприклад,
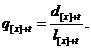
Тому, часто у таблиці з
відбором обмеженої дії включають тільки величини 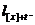
.2.5
Наближення для дробового віку
Реальні статистичні дані про
смертність доступні у виді таблиць, у які входять ймовірності 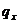 , величини
, величини 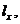
 і т.д. для
цілочисельних значень віку x. Це означає, що всі формули в актуарій математиці
повинні бути приведені до вигляду, коли в них включаються тільки ці величини.
Однак всі основні формули для розрахунку премій, резервів і інших величин,
необхідних для ведення страхового бізнесу, містять інтеграли (з підінтегральною
функцією, яка включає функцію виживання
і т.д. для
цілочисельних значень віку x. Це означає, що всі формули в актуарій математиці
повинні бути приведені до вигляду, коли в них включаються тільки ці величини.
Однак всі основні формули для розрахунку премій, резервів і інших величин,
необхідних для ведення страхового бізнесу, містять інтеграли (з підінтегральною
функцією, яка включає функцію виживання 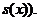 Таким чином, ми повинні знати
функцію виживання для всіх дійсних значень аргументу x, а не тільки для цілих.
Таким чином, ми повинні знати
функцію виживання для всіх дійсних значень аргументу x, а не тільки для цілих.
Ця задача може розглядатися
як задача інтерполяції. В актуарій математиці як правило вирішують цю задачу,
постулюючи той чи інший вид функції s(x) між вузлами інтерполяції, тобто
отримують шукану функцію s(x), склеюючи в цілочисельних точках більш прості
функції. Основними є три наступних постулати.
Рівномірний розподіл смертей
Самою простою є інтерполяція
лінійними функціями:
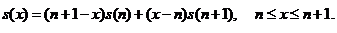
Записуючи x у вигляді
=n+t
де 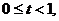 цій формулі
можна надати вигляду:
цій формулі
можна надати вигляду:
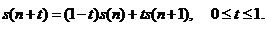
Для щільності f(x) це
наближення дає:
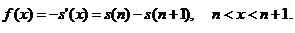
Відповідно для інтенсивності
смертності 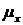 ми маємо
наступне наближення:
ми маємо
наступне наближення:
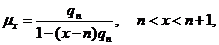
чи, що те саме,
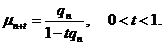
Зазначимо, що в цілочисельних
точках щільність f(x) і інтенсивність смертності 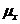 не визначені.
не визначені.
Один з найбільш важливих
наслідків припущення про лінійну інтерполяцію функції виживання полягає у
наступному. Розглянемо величину 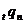 (n - ціле,
(n - ціле, 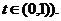 Для неї
маємо:
Для неї
маємо:
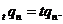
Отже, в припущенні про
лінійну інтерполяцію функції виживання ймовірність смерті на протязі частини
року пропорційна величині цієї частини.
Правильним є і обернене
твердження, якщо ймовірність смерті на протязі (початкової) частини року
пропорційна величині цієї частини (тобто 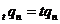 ), то для дробових значень змінної x
(між двома сусідніми цілими значеннями) функція виживання є лінійною.
), то для дробових значень змінної x
(між двома сусідніми цілими значеннями) функція виживання є лінійною.
Введемо тепер наступну
величину 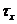 , яка рівна
дробовій частині величини
, яка рівна
дробовій частині величини
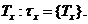
Таким чином
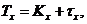
де 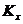 -
заокруглений час життя. Величина
-
заокруглений час життя. Величина 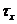 описує момент смерті серед року.
описує момент смерті серед року.
Для інтерполяції, яка розглядається
) випадкова величина 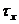 рівномірно
розподілена на (0, 1);
рівномірно
розподілена на (0, 1);
) випадкові величини 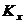 і
і 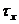 -
незалежні.
-
незалежні.
Правильним є і зворотне
твердження, якщо випадкова величина 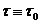 рівномірно розподілена на (0, 1) і
не залежить від
рівномірно розподілена на (0, 1) і
не залежить від 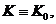 то для
дробових значень x (між двома сусідніми цілими) функція виживання є лінійною.
то для
дробових значень x (між двома сусідніми цілими) функція виживання є лінійною.
Постійна інтенсивність
смертності
Якщо наближати функцію
виживання s(x) на відрізку 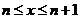 показниковою функцією
показниковою функцією 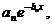 то
то
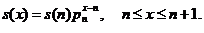
Записуючи x у вигляді
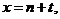
де 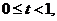 цій формулі
можна надати вигляду
цій формулі
можна надати вигляду
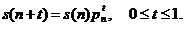
Для щільності f(x) це
наближення дасть
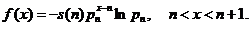
Звідси для інтенсивності
смертності 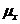 ми маємо
наступне наближення:
ми маємо
наступне наближення:
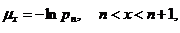
тобто даній інтерполяції
відповідає припущення про постійну інтенсивність смертності між двома днями
народження.
Припущення Балдуччі
(Balducci) [9]
Припущення Балдуччі зовні
подібне на припущення про рівномірний розподіл смертей, однак, на відміну від
останнього, лінійними функціями інтерполюється 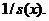 Це приводить до наступних формул
(нижче
Це приводить до наступних формул
(нижче 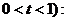
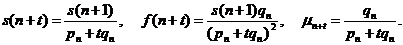 (2.2.7)
(2.2.7)
Один з найбільш важливих
наслідків припущення Балдуччі полягає у наступному. Розглянемо величину 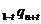 (ймовірність
такого виду з’являється при оцінці для дробових моментів часу). Для неї маємо:
(ймовірність
такого виду з’являється при оцінці для дробових моментів часу). Для неї маємо:

Отже, в припущенні Балдуччі
ймовірність смерті до чергового дня народження пропорційна часу, який залишився
до цього дня народження.
Правильним є і зворотне
твердження: якщо ймовірність смерті до чергового дня народження пропорційна
часу до цього дня народження (тобто 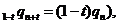 то для виду функції виживання для
дробових значень x (між двома сусідніми цілими) істинне припущення Балдуччі.
то для виду функції виживання для
дробових значень x (між двома сусідніми цілими) істинне припущення Балдуччі.
РОЗДІЛ 3.
ЕКОНОМІКО-МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ СТРАХУВАННЯ ЖИТТЯ
.1
Моделі короткострокового страхування
В актуарній
математиці моделі страхування життя умовно ділять на дві великі групи залежно
від того, приймається чи ні в розрахунок дохід від інвестування зібраних
премій. Якщо ні, то ми говоримо про короткострокове страхування (short-term
insurance); в якості такого “короткого” інтервалу ми будемо розглядати інтервал
в 1 рік. Якщо ж так, то ми говоримо про довгострокове страхування (long-term
insurance). Звичайно, цей поділ умовний і, крім того, довгострокове страхування
пов'язане з рядом інших обставин, наприклад, андеррайтингом.
Найпростіший вид
страхування життя полягає в наступному.
Страхувальник
платить страховій компанії р грн (ця сума, як уже зазначалося, називається
страховою премією - premium); страхувальником може бути сам застрахований або
інша особа (наприклад, його роботодавець).
У свою чергу
страхова компанія зобов'язується виплатити особі, на користь якої укладений
договір, страхову суму (sum assured) b грн у випадку смерті застрахованого
протягом року із причин, перерахованих у договорі (і не платити нічого, якщо
він не помре протягом року або помре через причину, що не покривається
договором).
Страховая сума
часто приймається рівної 1 або 1000. Це означає, що премія виражається як
частка від страхової суми або на 1000 страхової суми відповідно.
Нетто-премія
Величина страхової
виплати (benefit), звичайно, набагато більша, ніж страхова премія, і
знаходження «правильного» співвідношення між ними - одна з найважливіших задач
актуарной математики.
Питання про те, яку
плату страхова компанія повинна призначати за прийняття на себе того чи іншого
ризику, украй складне. При його вирішенні враховується велика кількість
різнорідних факторів: імовірність настання страхового випадку, його очікувана
величина й можливі флуктуації, зв'язок з іншими ризиками, які вже прийняті
компанією, організаційні витрати компанії на ведення справи, співвідношення між
попитом та пропозицією по даному виду ризиків на ринку страхових послуг і т.д.
Однак основним звичайно є принцип еквівалентності фінансових зобов'язань
страхової компанії й застрахованого.
В розглянутій вище
найпростішій схемі страхування, коли плата за страховку повністю вноситься в
момент укладання договору, зобов'язання застрахованого виражається в сплаті
премії р. Зобов'язання компанії полягає у виплаті страхової суми, якщо
наступить страховий випадок. Таким чином, грошовий еквівалент зобов'язань
страховика, X, є випадковою величиною:
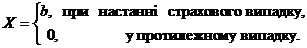
У найпростішій формі принцип
еквівалентності зобов'язань виражається рівністю р = МХ, тобто, як плата за
страховку призначається очікувана величина збитку. Ця премія, як уже
зазначалося, називається нетто-премією (net premium).
Ризикова надбавка
Купивши за фіксовану премію р
грн. страховий поліс, страховик позбавив укладача договору страхування від
ризику фінансових втрат, пов'язаних з невизначеністю моменту смерті
застрахованого. Однак сам ризик не зник; його прийняла на себе страхова
компанія.
Тому рівність р = MX
насправді не виражає еквівалентності зобов'язань страхувальника й страховика.
Хоча в середньому й страховик, і страхувальник платять ту саму суму, страхова
компанія має ризик, пов'язаний з тим, що в силу випадкових обставин їй,
можливо, прийдеться виплатити набагато більшу суму, ніж МХ. Страхувальник же
такого ризику не має. Тому було б справедливо, щоб плата за страховку включала
деяку надбавку l, яка б служила еквівалентом випадковості, що впливає на
компанію. Цю надбавку називають ризиковою (або захисною) надбавкою (security
loading), а 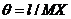 - відносною
ризиковою надбавкою (relative security loading). Розмір ризикової надбавки
береться таким, щоб імовірність того, що компанія буде мати втрати по деякому
портфелю договорів («розориться»), була досить малою величиною.
- відносною
ризиковою надбавкою (relative security loading). Розмір ризикової надбавки
береться таким, щоб імовірність того, що компанія буде мати втрати по деякому
портфелю договорів («розориться»), була досить малою величиною.
Слід зазначити, що реальна
плата за страховку (брутто-премія або офісна премія) - більша нетто-премії з
ризиковою надбавкою (часто в кілька разів). Різниця між ними дозволяє страховій
компанії покрити адміністративні витрати, забезпечити доход і т.д.
Модель індивідуальних втрат
Точний розрахунок ризикової
надбавки може бути здійснений у рамках теорії ризику.
Найпростішою моделлю
функціонування страхової компанії, призначеної для розрахунку ймовірності
банкрутства, є модель індивідуального ризику. Вона базується на наступних
спрощених припущеннях:
1)
аналізується фіксований відносно
короткий проміжок часу (так що можна знехтувати інфляцією й не враховувати
прибуток від інвестування активів) - як правило це один рік;
2)
кількість договорів страхування N
фіксована й невипадкова;
3)
премія повністю вноситься на початку
аналізованого періоду; ніяких надходжень протягом цього періоду немає;
4)
ми спостерігаємо кожен окремий
договір страхування й знаємо статистичні властивості пов'язаних з ним
індивідуальних втрат X.
Як правило припускається, що
в моделі індивідуального ризику випадкові величини 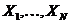 - незалежні
(зокрема, виключаються катастрофи, коли одночасно по декількох договорах
наступають страхові випадки).
- незалежні
(зокрема, виключаються катастрофи, коли одночасно по декількох договорах
наступають страхові випадки).
У рамках цієї моделі
«банкрутство» визначається сумарними втратами по портфелю 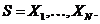 . Якщо ці
сумарні виплати більші, ніж активи компанії, призначені для виплат по цьому
блоці бізнесу, u, то компанія не зможе виконати всі свої зобов'язання (без
залучення додаткових засобів); у цьому випадку говорять про «розорення».
. Якщо ці
сумарні виплати більші, ніж активи компанії, призначені для виплат по цьому
блоці бізнесу, u, то компанія не зможе виконати всі свої зобов'язання (без
залучення додаткових засобів); у цьому випадку говорять про «розорення».
Отже, імовірність «розорення»
компанії дорівнює
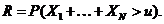
Іншими словами, імовірність
«розорення» - це додаткова функція розподілу величини сумарних втрат компанії
за розглянутий проміжок часу.
Оскільки сумарні виплати S
являють собою суму незалежних випадкових величин, розподіл випадкової величини
S може бути підрахований за допомогою класичних теорем і методів теорії
ймовірностей.
Насамперед - це використання
згорток. Нагадаємо, що якщо 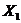 і
і 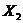 - дві незалежні невід’ємні
випадкові величини з функціями розподілу
- дві незалежні невід’ємні
випадкові величини з функціями розподілу 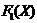 і
і 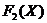 відповідно, то функція розподілу їх
суми
відповідно, то функція розподілу їх
суми 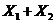 може бути
підрахована по формулі
може бути
підрахована по формулі
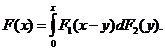
Застосовуючи цю формулу
декілька разів, можна підрахувати функцію розподілу суми будь-якої кількості
доданків.
Якщо випадкові величини 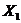 і
і 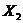 -
неперервні, то працюють із щільностями
-
неперервні, то працюють із щільностями 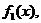
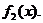 Щільність суми може бути
підрахована по формулі
Щільність суми може бути
підрахована по формулі
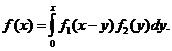
Якщо випадкові величини 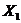 і
і 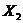 -
целочисельні, то замість функцій розподілу як правило працюють із розподілами
-
целочисельні, то замість функцій розподілу як правило працюють із розподілами
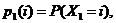
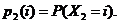
Розподіл суми 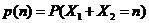 може бути
визначений за формулою
може бути
визначений за формулою
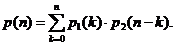
Підрахунок імовірності
розорення часто спрощується, якщо використовувати похідні функції й/або
перетворення Лапласа.
Як правило кількість
застрахованих у страховій компанії дуже велика. Тому для підрахунку імовірності
розорення потрібно здійснити розрахунок функції розподілу суми великої
кількості доданків. У цьому випадку точний безпосередній чисельний розрахунок
може привести до проблем, пов'язаних з малою величиною ймовірностей. Однак
обставина, що утрудняє точний розрахунок, відкриває можливість швидкого й
простого наближеного розрахунку. Це пов'язано з тим, що при збільшенні N
імовірність 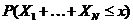 часто має
визначену границю (переважно потрібно, щоб х певним чином змінювалося разом з
N), яку можна прийняти як наближене значення цієї ймовірності. Точність
подібних наближень звичайно дуже велика й задовольняє практичні потреби.
Основним є нормальне (гауссівське) наближення.
часто має
визначену границю (переважно потрібно, щоб х певним чином змінювалося разом з
N), яку можна прийняти як наближене значення цієї ймовірності. Точність
подібних наближень звичайно дуже велика й задовольняє практичні потреби.
Основним є нормальне (гауссівське) наближення.
Гауссівське наближення
грунтується на центральній граничній теоремі теорії ймовірностей. У
найпростішому формулюванні ця теорема виглядає в такий спосіб: якщо випадкові
величини 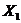 , …,
, …, 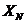 незалежні й
однаково розподілені із середнім а й дисперсією
незалежні й
однаково розподілені із середнім а й дисперсією  , то при
, то при 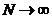 функція
розподілу центрованої й нормованої суми
функція
розподілу центрованої й нормованої суми
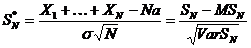
має границю, яка рівна
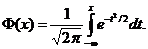 (3.1.1)
(3.1.1)
Існують численні узагальнення
центральної граничної теореми на випадки, коли доданки 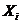 мають різні
розподіли, є залежними й т.д. В даній роботі ми обмежимося твердженням, що якщо
кількість доданків велика (звичайно досить, щоб N мало б порядок декількох
десятків), а доданки не дуже малі й не дуже різнорідні, те можна застосувати
гауссівське наближення для
мають різні
розподіли, є залежними й т.д. В даній роботі ми обмежимося твердженням, що якщо
кількість доданків велика (звичайно досить, щоб N мало б порядок декількох
десятків), а доданки не дуже малі й не дуже різнорідні, те можна застосувати
гауссівське наближення для
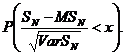
Звичайно, це твердження дуже
невизначене, але й класична центральна гранична теорема без точних оцінок
похибки не дає точної вказівки про сферу застосування. Стандартна гауссівська
фунція розподілу 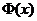 детально
вивчена в теорії ймовірностей. Існують детальні таблиці як для самої функції
розподілу
детально
вивчена в теорії ймовірностей. Існують детальні таблиці як для самої функції
розподілу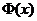 , так і для
щільності
, так і для
щільності
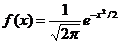
Значення 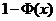 у найбільш
цікавому діапазоні
у найбільш
цікавому діапазоні 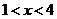 наведені в
таблиці 1.
наведені в
таблиці 1.
Таблиця 1 Значення 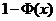
|
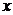 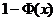 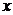 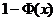 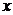 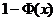
|
|
|
|
|
|
|
1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9
|
15,87% 13,57% 11,51% 9,68% 8,08% 6,68% 5,48%
4,46% 3,59% 2,87%
|
2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9
|
2,28% 1,79% 1,39% 1,07% 0,82% 0,62% 0,47%
0,35% 0,26% 0,19%
|
3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9
|
0,14% 0,10% 0,069% 0,048% 0,034% 0,023% 0,020%
0,011% 0,007% 0,005%
|
Корисно також мати таблицю
квантилів 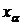 , (
, (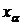 - це корінь
рівняння
- це корінь
рівняння 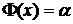 ) що
відповідають досить малій ймовірності розорення
) що
відповідають досить малій ймовірності розорення 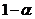 ; вони наведені в таблиці 2.
; вони наведені в таблиці 2.
Таблиця 2. Таблиця квантилів
|
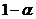 0,1%0,5%1%2% 0,1%0,5%1%2%
|
|
|
|
|
|
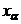 3,0902,5762,3262,054 3,0902,5762,3262,054
|
|
|
|
|
|
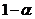 3%4%5%10% 3%4%5%10%
|
|
|
|
|
|
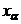 1,8811,7511,6451,282 1,8811,7511,6451,282
|
|
|
|
|
.2
Моделі довгострокового страхування життя
.2.1
Основні види довгострокового страхування життя
Довічне страхування
(whole life insurance)
При цьому виді
страхування фіксована страхова сума виплачується в момент смерті.
Оскільки людина
рано чи пізно помре, страхова компанія гарантовано виплатить страхову суму
(якщо тільки причина смерті не покривається умовами договору, наприклад, якщо
смерть наступила в результаті протиправних дій застрахованого). Якщо плата за
це покриття повністю вноситься в момент укладання договору, то мова йде про
досить велику суму, співмірну зі страховою сумою. Тому звичайно премії
виплачуються періодично протягом всього життя або аж до досягнення
застрахованим певного віку (скажімо, пенсійного, коли його доходи різко
знижуються).
У цьому розділі ми
для простоти розрахунків будемо припускати, що по всіх видах страхування, які
розглядаються премія повністю вноситься в момент укладання договору.річне
тимчасове страхування життя (п-year term life insurance)
При цьому виді
страхування виплата фіксованої страхової суми здійснюється в момент смерті,
якщо застрахований помер протягом терміну дії договору, тобто протягом п років
з моменту укладання договору. Якщо ж застрахований прожив ці п років, то
компанія не платить нічого.
У типових випадках
імовірність смерті застрахованого протягом терміну дії договору мала, так що премія
по цьому виду страхування відносно невелика. Тому тимчасове страхування часто
використовують у випадках, коли потрібне покриття на більшу суму.
Страхування зі
змінною страховою виплатою (varying benefit insurance)
У розглянутих вище прикладах
величина страхової виплати була фіксована й не залежала від моменту виплати.
Існують численні види страхування, коли страхове відшкодування може
змінюватися. Як приклад можна привести довічне страхування зі страховим
відшкодуванням, що безупинно збільшується (continuously increasing whole life
insurance). При цьому виді страхування компанія виплачує в момент смерті суму,
рівну 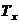 (ми
вважаємо, що грошові суми вимірюються в нас деякою умовною одиницею).
Страхування зі страховою виплатою, що зменшується виникає в кредитному
страхуванні життя.
(ми
вважаємо, що грошові суми вимірюються в нас деякою умовною одиницею).
Страхування зі страховою виплатою, що зменшується виникає в кредитному
страхуванні життя.
Пожиттєве страхування,
відтерміноване на т років (т-year deferred whole life insurance)
При цьому виді страхування
виплата фіксованої страхової суми проводиться в момент смерті застрахованого, але
тільки якщо вона настала після закінчення m-річного терміну з моменту укладання
договору. Якщо застрахований помре раніше, ніж через т років після укладання
договору, страхове відшкодування не виплачується зовсім.
За аналогією з довічним
страхуванням, відтермінованим на т років, можна ввести й інші види
відтермінованого страхування, що узагальнюють раніше введені види звичайного
страхування.
Дискретні договори
У всіх описаних вище
прикладах страхове відшкодування (benefit) виплачується у вигляді разової суми
(lump sum) у момент смерті застрахованого (звичайно, у реальності як укладачу
договору, так і компанії потрібен певний час для підготовки документів) - такі
види страхування часто називають неперервними. Однак можливі виплати й в інші
моменти часу. Найбільш важливий (з теоретичної точки зору) випадок, коли
виплата здійснюється не в момент смерті, а в наступний за ним день народження
застрахованого - такі види страхування часто називають дискретними. Якщо
вважати (як це звичайно робиться при актуарних розрахунках), що вік
застрахованого в момент укладання договору - ціле число, то дискретні договори
можна описати як договори з виплатою страхової суми в чергову, після моменту
смерті, річницю укладання договору.
Наприклад, при довічному
страхуванні з виплатою страхової суми наприкінці року смерті страхове
відшкодування виплачується в момент
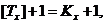
де 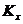 -
заокруглений час життя. Для кожного з розглянутих раніше неперервних видів
страхування існує дискретний аналог з виплатою страхової суми наприкінці року
смерті.
-
заокруглений час життя. Для кожного з розглянутих раніше неперервних видів
страхування існує дискретний аналог з виплатою страхової суми наприкінці року
смерті.
У пенсійних схемах центральну
роль відіграють договори іншого типу, коли виплата страхової суми здійснюється
не у випадку смерті, а у випадку дожиття до певного моменту. Як приклади можна
привестирічне чисто накопичувальне страхування (п-year pure endowment
insurance)
При цьому виді страхування
виплата страхової суми фіксованої величини здійснюється в момент n, якщо
застрахований дожив до цього моменту. У випадку смерті застрахованого до
моменту п страхова сума не виплачується (однак, як правило таке покриття
передбачає повернення всіх внесених премій у випадку смерті застрахованого до
закінчення терміну дії договору).річне змішане страхування (п-year endowment
insurance)
При цьому виді страхування
виплата фіксованої страхової суми здійснюється на наступних умовах. Якщо смерть
застрахованого наступить до закінчення терміну дії договору, то страхова сума
виплачується в момент смерті. Якщо ж застрахований дожив до закінчення терміну
дії договору, то страхова сума виплачується в момент п закінчення терміну дії
договору. Неважко зрозуміти, що цей вид страхування виконує функції як власне
страхування (тобто забезпечує дохід родині застрахованого у випадку його
смерті), так і нагромадження коштів (тобто забезпечує самого застрахованого).
Іноді при змішаному страхуванні страхові суми, виплачувані у випадку смерті й у
випадку дожиття, відрізняються.
3.2.2
Актуарна сучасна вартість зобов'язань
З математичної точки зору
довгострокове страхування (long-term insurance) характеризується тим, що при
розрахунках враховується зміна цінності грошей із часом. Тому теорія
довгострокового страхування істотно опирається на теорію складних відсотків.
Зокрема, зпівставляючи
зобов'язання страхувальника й страховика, ми повинні приводити їх до одного
моменту часу. Скажімо, для того, щоб сформулювати принцип еквівалентності
зобов'язань у момент укладання договору, ми повинні привести зобов'язання
страхувальника й страховика саме до цього моменту. Їхні середні значення
називаються актуарними сучасними вартостями зобов'язань.
Нижче ми будемо припускати,
що інтенсивність відсотків 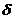 не змінюється із часом;
не змінюється із часом; 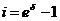 буде
позначати ефективну річну процентну ставку,
буде
позначати ефективну річну процентну ставку, 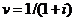 коефіцієнт дисконтування й т.д.
коефіцієнт дисконтування й т.д.
Крім того, оскільки величина
страхової суми, як правило, фіксована, в актуарних розрахунках ми будемо
приймати її за одиницю виміру грошових сум.
Величина зобов'язань
страхової компанії по договорах страхування життя з разовою виплатою одиничної
страхової суми, приведена на момент укладання договору, позначається буквою Z з
додатковими індексами, що описують структуру покриття. У всіх випадках вік
застрахованого на момент укладання договору вказується у вигляді індекса внизу
ліворуч. Якщо страхова сума виплачується в момент смерті («неперервний»
договір), то зверху ставиться риска; відсутність верхньої риски означає, що
договір - «дискретний», тобто страхове відшкодування виплачується наприкінці
року смерті. Термін дії договору вказується через двокрапку після віку
застрахованого й обрамлений прямим кутом (зверху й праворуч).
Математичне сподівання
приведеної вартості зобов'язань називається їх актуарною сучасною вартістю й
позначається буквою A з тими ж індексами, що й змінна Z.
Наприклад, для довічного
страхування
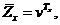
для тимчасового страхування
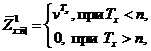
для змішаного страхування
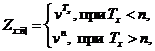
для відкладеного страхування
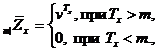
3.3
Довічні ренти
.3.1
Основні види рент
Повна довічна рента (whole
life annuity)
Найпростіша довічна рента
може бути описана в такий спосіб. Починаючи з деякого моменту 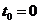 людина раз
у рік починає одержувати певну суму (яку звичайно приймають у якості умовної
грошової одиниці). Виплати здійснюються тільки під час життя людини.
людина раз
у рік починає одержувати певну суму (яку звичайно приймають у якості умовної
грошової одиниці). Виплати здійснюються тільки під час життя людини.
Рента може розглядатися як
регулярний дохід для одержувача ренти (переважно в старості). З іншого боку,
періодичні премії, виплачувані страхувальником за звичайним договором
страхування життя, можна розглядати як ренту, одержувану страховою компанією.
Тому теорія рент важлива не тільки для розрахунку пенсійних схем, але й для
розрахунку періодичних премій.
Тимчасова довічна рента
Нехай, як і раніше, 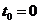 -
теперішній момент, а вік людини, якій виплачується рента - х років. N-річна
тимчасова довічна рента (n-year temporary life annuity) визначається як серія
виплат одиничної суми, здійснених раз у рік довічно, починаючи з моменту
-
теперішній момент, а вік людини, якій виплачується рента - х років. N-річна
тимчасова довічна рента (n-year temporary life annuity) визначається як серія
виплат одиничної суми, здійснених раз у рік довічно, починаючи з моменту 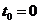 , але не
більш, ніж п років. Таким чином, якщо людина проживе ще п років (тобто якщо
, але не
більш, ніж п років. Таким чином, якщо людина проживе ще п років (тобто якщо 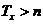 ), то
здійснюється рівно п виплат з випередженням; якщо ж
), то
здійснюється рівно п виплат з випередженням; якщо ж 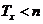 , то
здійснюється
, то
здійснюється 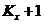 виплата.
виплата.
Відтермінована довічна рента
Нехай, як і раніше, 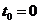 - дійсний
момент, а вік людини, якій виплачується рента - x років. Відтермінована на т
років довічна рента (deferred life annuity) визначається як серія виплат
одиничної суми, здійснених раз у рік, починаючи з моменту
- дійсний
момент, а вік людини, якій виплачується рента - x років. Відтермінована на т
років довічна рента (deferred life annuity) визначається як серія виплат
одиничної суми, здійснених раз у рік, починаючи з моменту 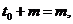 доти, поки
людина жива. Однак якщо людина помре до моменту m, то ні однієї виплати не
здійснюється.
доти, поки
людина жива. Однак якщо людина помре до моменту m, то ні однієї виплати не
здійснюється.
Довічні ренти виплачувані із
частотою р
У розглянутих вище прикладах
передбачалося, що виплати здійснюються один раз у рік (на початку року). Для
застосувань до пенсійних схем набагато цікавішим є випадок, коли виплати
здійснюються раз на місяць (р = 12), раз у квартал (р = 4), раз у тиждень (р =
52). У стандартних рентах такого виду в якості умовної грошової одиниці
розглядається алгебраїчна сума всіх виплат протягом року. Інакше кажучи, кожна
окрема виплата має величину 1/р.
Неперервні ренти
Неперервні ренти можна
розглядати як граничний випадок рент, виплачуваних із частотою р при 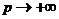 . Їх можна
представляти як неперервний грошовий потік, що тече зі швидкістю 1.
. Їх можна
представляти як неперервний грошовий потік, що тече зі швидкістю 1.
3.3.2.
Оцінювання рент
Метод сумарної виплати
Вартість ренти в початковий
момент часу 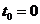 позначають
символом Y з відповідними індексами. Її можна підрахувати двома основними
способами. При використанні методу сумарної виплати (aggregate payment
technique) довічна рента розглядається як звичайна рента, але з випадковим
числом виплат. Це дозволяє одержати явну формулу для сучасної вартості ренти за
допомогою формул для детермінованих рент і пов'язати її із сучасною вартістю
відповідного виду страхування. Наприклад, для довічної ренти
позначають
символом Y з відповідними індексами. Її можна підрахувати двома основними
способами. При використанні методу сумарної виплати (aggregate payment
technique) довічна рента розглядається як звичайна рента, але з випадковим
числом виплат. Це дозволяє одержати явну формулу для сучасної вартості ренти за
допомогою формул для детермінованих рент і пов'язати її із сучасною вартістю
відповідного виду страхування. Наприклад, для довічної ренти
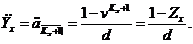 (3.1.2)
(3.1.2)
для тимчасової довічної ренти
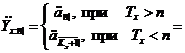
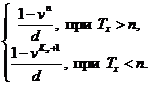 (3.1.3)
(3.1.3)
для відкладеної довічної
ренти
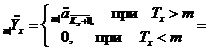
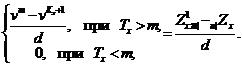 (3.1.4)
(3.1.4)
Актуарна сучасна вартість
ренти - це просто математичне очікування (випадкової) сучасної вартості. Вона
позначається символом а з відповідними індексами. Тому метод сумарного платежу
негайно дає наступні формули для актуарних сучасних вартостей базових рент:
для довічної ренти
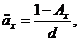
для тимчасової довічної ренти
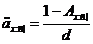 (3.1.5)
(3.1.5)
для відкладеної довічної
ренти
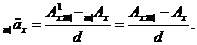 (3.1.6)
(3.1.6)
Метод поточного платежу
На відміну від методу
сумарної виплати, що розглядає довічну ренту як суму випадкової кількості
детермінованих доданків, метод поточної виплати (current payment technique)
розглядає довічну ренту як суму детермінованої (можливо, нескінченної)
кількості випадкових доданків.
Наприклад, для довічної ренти
це означає наступне. У принципі виплати можливі в будь-який момент часу  Виплата в
момент k здійснюється, якщо людина ще жива, тобто якщо
Виплата в
момент k здійснюється, якщо людина ще жива, тобто якщо 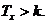 Тому величина
виплати в момент k - це індикатор події
Тому величина
виплати в момент k - це індикатор події 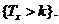 Відповідно, приведена цінність цієї
виплати в момент
Відповідно, приведена цінність цієї
виплати в момент 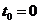 - це
випадкова величина
- це
випадкова величина 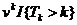 і, отже,
і, отже,
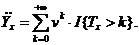 (3.1.7)
(3.1.7)
Тому для середнього значення
маємо:
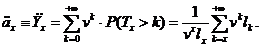 (3.1.8)
(3.1.8)
Для тимчасової довічної ренти
відповідна формула виглядає в такий спосіб:
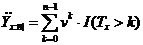
і, виходить,
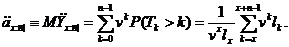 (3.1.9)
(3.1.9)
Для відкладеної на m років
довічної ренти відповідна формула має вигляд:
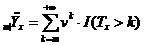
і, отже,
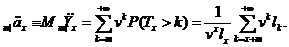 (3.1.10)
(3.1.10)
3.3.3.
Актуарне нагромадження
Розглянемо пенсійний фонд, у
який N людей у віці х років кожна внесли по одиничній сумі в момент 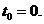 До моменту
t ця сума збільшиться до
До моменту
t ця сума збільшиться до 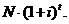 Одночасно
скоротиться й кількість учасників фонду - у живих залишиться в середньому
Одночасно
скоротиться й кількість учасників фонду - у живих залишиться в середньому 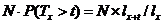 людей. Якщо
на кошти фонду можуть претендувати тільки живі учасники фонду, то на кожного з
них буде припадати сума
людей. Якщо
на кошти фонду можуть претендувати тільки живі учасники фонду, то на кожного з
них буде припадати сума

Це актуарне нагромадження є
більшим, ніж звичайне нагромадження 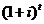 у теорії складних відсотків, тому що
пенсійний рахунок учасника збільшується не тільки за рахунок доходів від
відсотків, але й за рахунок коштів померлих учасників фонду.
у теорії складних відсотків, тому що
пенсійний рахунок учасника збільшується не тільки за рахунок доходів від
відсотків, але й за рахунок коштів померлих учасників фонду.
Актуарний коефіцієнт
дисконтувания 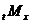 - це
середня сума, яку потрібно мати в момент
- це
середня сума, яку потрібно мати в момент 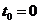 людині у віці x, щоб у момент t
одержати, якщо вона ще жива, одиничну суму:
людині у віці x, щоб у момент t
одержати, якщо вона ще жива, одиничну суму:
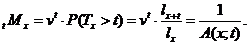 (3.1.11)
(3.1.11)
Використовуючи
поняття актуарного дисконтування, можна записати нові версії формул для
введених вище актуарних вартостей рент:
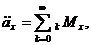
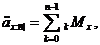
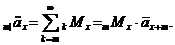 (3.1.12)
(3.1.12)
3.4
Періодичні премії
.4.1
Періодичні нетто-премії
Дотепер ми припускали, що
придбання страховки або довічної пенсії здійснюється у вигляді одиночної премії
в момент укладання договору. Однак звичайно премія виплачується у вигляді серії
платежів протягом деякого зазначеному у договорі терміну.
Як і у найпростіших випадках,
що обговорювалися раніше, повна періодична премія складається з декількох
частин. Найважливіша складова частина премії - це нетто-премія, що визначається
із принципу еквівалентності фінансових зобов'язань страхової компанії
(пенсійного фонду) і страхувальника (учасника фонду).
Якщо символ А (або а, у
випадку довічних рент), можливо з деякими індексами, використовується для
позначення разової нетто-премії, то символ Р(А) використовується для позначення
періодичної нетто-премії, яка вноситься на протязі всього часу дії договору.
Крім того, буква Р може мати свої індекси, які характеризують процес
надходження премій. Наприклад, якщо премії вносяться із частотою m, то вгорі
праворуч ставиться індекс (m); якщо премії платяться неперервно, то над буквою
Р ставиться риска й т.д. Якщо, крім того, період платежів обмежений строком t,
то відповідна періодична премія позначається 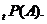 Для дискретних видів страхування
часто букву А опускають і використають тільки символ Р, але з усіма індексами,
які були у символа А.
Для дискретних видів страхування
часто букву А опускають і використають тільки символ Р, але з усіма індексами,
які були у символа А.
В загальному виді схема
розрахунку нетто-премій може бути представлена в такий спосіб.
Нехай 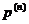 - шукана
нетто-премія.
- шукана
нетто-премія.
Визначимо сучасну актуарну
вартість фінансових зобов’язань страхувальника 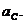 Ця величина, очевидно, є функцією
від шуканої премії
Ця величина, очевидно, є функцією
від шуканої премії
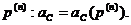
Потім підрахуємо сучасну
актуарну вартість фінансових зобов'язань компанії 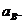
Величина 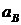 , загалом
кажучи, також залежить від шуканої премії
, загалом
кажучи, також залежить від шуканої премії
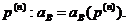
Принцип еквівалентності
фінансових зобов'язань страхової компанії (пенсійного фонду) і страхувальника
(учасника фонду) означає, що
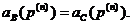
Корінь цього рівняння і є
шуканою нетто-премією.
Для регулярних видів
страховок і довічних пенсій величина періодичних премій визначається в термінах
відповідних довічних рент.
.4.2
Премії, що враховують витрати
Заключення і підтримка
договорів страхування й договорів пенсійного забезпечення пов'язані з певними
витратами: комісійні агентам, за підготовку документації, сплата податків,
аналіз страхових випадків перед виплатою страхових відшкодувань, оплата судових
витрат у спірних випадках і т.д. Деякі із цих витрат фіксовані (наприклад,
оформлення документації), деякі становлять певний відсоток від величини премії
(наприклад, комісійні агентам або податки), деякі становлять певний відсоток
від величини страхового відшкодування (наприклад, судові витрати в спірних
випадках). Крім того, частина витрат пов'язана тільки з моментом укладання
договору, а частина з'являється періодично при одержанні чергових премій. Деякі
витрати виникають тільки при настанні страхових випадків.
Всі ці витрати оплачуються
страхувальниками за рахунок певного збільшення нетто-премій. Дуже важливо, щоб
це збільшення не було довільним, а розраховувалося належним чином. Занадто
велике збільшення премій зачіпає інтереси страхувальників і неприйнятно з
погляду суспільства; занадто малі надбавки до премії можуть викликати фінансові
проблеми в компанії (що також не в інтересах її клієнтів).
Витрати на ведення справи
можна розглядати як специфічну форму фінансових зобов'язань компанії. Тому
премії, що враховують витрати, визначаються із принципу еквівалентності
фінансових зобов'язань страхової компанії або пенсійного фонду й застрахованого
(учасника фонду).
Самі значні витрати виникають
при укладанні договору; часто вони перевищують першу премію, виплачену
страхувальником. Різницю компанія покриває із власних коштів (або за допомогою
перестрахування), а потім поступово відшкодовує свої витрати за рахунок
збільшених премій. Якщо ж страхувальник вирішить розірвати (lapse) договір
протягом декількох перших років дії договору, то компанія зазнає збитків (хоча
частково вони можуть бути зменшені, якщо зажадати від агентів повернути
комісійні, або зменшити викупну суму, виплачувану страхувальникові).
.4.3
Розрахунок захисної надбавки
Для захисту від випадкових
флуктуації тривалості життя нетто-премія 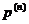 повинна бути певним чином
«навантажена», тобто повна премія
повинна бути певним чином
«навантажена», тобто повна премія
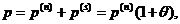
де 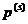 - захисна
(ризикова) надбавка, а
- захисна
(ризикова) надбавка, а 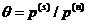 - відносна
ризикова надбавка [3].
- відносна
ризикова надбавка [3].
Найпростіший метод розрахунку
страхової надбавки до нетто-премії у випадку періодичних виплат премій полягає
у наступному. Приймемо до розгляду сучасну величину збитку 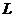 , пов'язану
з одним договором. Цей збиток визначається як різниця між сучасною величиною
, пов'язану
з одним договором. Цей збиток визначається як різниця між сучасною величиною 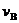 у страхового
відшкодування або пенсії й сучасною величиною
у страхового
відшкодування або пенсії й сучасною величиною 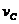 потоку премій. У загальному випадку
як
потоку премій. У загальному випадку
як 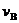 , так і
, так і 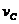 залежать
від навантаженої премії
залежать
від навантаженої премії
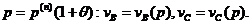
Відповідно, збиток 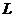 також
залежить від р:
також
залежить від р:
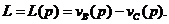
Для кожного конкретного
договору збиток L може бути як позитивний, так і негативний. Нам звичайно хотілося
б, щоб весь портфель договорів, розглянутий як єдине ціле, не приносив би
збитків (однак, в окремі моменти часу можливий негативний баланс). Іншими
словами, ми б хотіли, щоб з великою ймовірністю 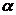 сумарний збиток
сумарний збиток
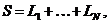
де N - кількість договорів, а
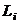 збиток від
i-го договору, був би недодатнім:
збиток від
i-го договору, був би недодатнім:
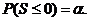
Переписуючи цю умову у
вигляді (ми вважаємо ризики, пов'язані з різними договорами незалежними)
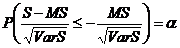
і застосовуючи гауссівське
наближення, ми одержимо:
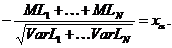 (3.1.13)
(3.1.13)
Для основних принципів
призначення страхових надбавок можливе введення єдиного параметра k. Тому
насправді це рівняння є рівнянням щодо однієї невідомої величини k і може бути
легко розв’язане.
3.5
Резерви
.5.1
Поняття резерву
Розглянемо деякий договір
страхування й приймемо момент його підписання за початковий момент часу.
Припустимо, що через час t договір усе ще зберігає чинність (так що
застрахований ще живий) і позначимо актуарну приведену вартість зобов'язань
компанії (застрахованого) у цей момент через  (відповідно,
(відповідно, 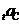 ). Величина
). Величина  визначає
середню суму, що має бути виплачена у майбутньому страховій компанії за
розглянутим договором. Тільки частина коштів (у середньому
визначає
середню суму, що має бути виплачена у майбутньому страховій компанії за
розглянутим договором. Тільки частина коштів (у середньому 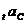 ) надійде
від застрахованого. Відсутню суму (у середньому
) надійде
від застрахованого. Відсутню суму (у середньому 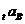 -
-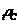 ) компанія повинна покрити з інших
джерел. Однак, оскільки необхідність цієї додаткової суми зрозуміла уже в
момент t, компанія повинна передбачити резерв (reserve)
) компанія повинна покрити з інших
джерел. Однак, оскільки необхідність цієї додаткової суми зрозуміла уже в
момент t, компанія повинна передбачити резерв (reserve) 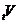 величиною
величиною  -
-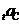 в цей
момент:
в цей
момент:
Підкреслимо, що резерв, що
визначається цією формулою, не враховує випадкові флуктуації виплат і
надходжень, пов'язаних з випадковістю часу життя.
Визначення резерву, подане
вище, пов'язане з аналізом майбутнього (перспективного) розвитку подій. Тому
метод розрахунку резерву безпосередньо за визначенням називають перспективним
методом (prospective method).
Для конкретного договору
страхування з разовою нетто-премією, що позначена буквою А (або, у випадку
довічних рент, буквою а) з відповідними індексами, резерв через час t після
укладання договору позначається 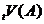 . Крім того, буква V може мати свої
індекси, які характеризують процес надходження премій. Ці індекси аналогічні
індексам, які використовуються для позначення періодичних нетто-премій.
Наприклад, якщо премії вносяться із частотою т, то вгорі праворуч ставиться
індекс (т); якщо премії виплачуються неперервно, то над буквою V ставиться
риска й т.д. Якщо період виплат премій обмежений деяким числом h, то його
ставлять ліворуч угорі (а не ліворуч унизу як при позначенні нетто-премій, тому
що це місце вже зайняте для вказівки моменту t). Для дискретних видів
страхування букву А часто опускають і використають тільки символ V, але з усіма
індексами, які були у символа А.
. Крім того, буква V може мати свої
індекси, які характеризують процес надходження премій. Ці індекси аналогічні
індексам, які використовуються для позначення періодичних нетто-премій.
Наприклад, якщо премії вносяться із частотою т, то вгорі праворуч ставиться
індекс (т); якщо премії виплачуються неперервно, то над буквою V ставиться
риска й т.д. Якщо період виплат премій обмежений деяким числом h, то його
ставлять ліворуч угорі (а не ліворуч унизу як при позначенні нетто-премій, тому
що це місце вже зайняте для вказівки моменту t). Для дискретних видів
страхування букву А часто опускають і використають тільки символ V, але з усіма
індексами, які були у символа А.
Особливо звернемо увагу на
наступну обставину. Звичайно термін «резерв» вживається для позначення якихось
запасів. Наприклад, теплова електростанція створює резервний запас вугілля для
того, щоб забезпечити безперебійне функціонування агрегатів у випадку збоїв у
регулярних поставках палива із шахт. Страховик (як і будь-яка інша компанія або
фізична особа) може мати певний резерв фінансових коштів для того, щоб без
затримок фінансувати які-небудь непередбачені витрати. Однак ми вживаємо термін
«резерв» зовсім в іншому значенні. Резерв у страхуванні -це виміряна в грошових
одиницях вартість майбутніх зобов'язань компанії. Оскільки величина цих
зобов'язань залежить від випадкових факторів, які відносяться до далекого
майбутнього, строго кажучи, виміряти їх у сьогоденні взагалі неможливо. Тому
резерв - це деяка розумна й, як правило, консервативна оцінка балансу майбутніх
витрат і доходів. Відповідно, немає й не може бути однозначного визначення
резерву. Визначення, наведене вище, є одним з найпростіших і найпоширеніших.
Маючи на увазі ці обставини,
було б розумно використати при оцінці резерву завищену смертність (у
страхуванні, і занижену смертність - при оцінці рент і пенсій), занижену
процентну ставку й т.д. Інакше кажучи, оцінюючи майбутній розвиток подій,
потрібно бути трохи песимістом (рівень цього песимізму звичайно приписується
страховим компаніям регулювальними органами).
Якщо при оцінці резерву
використовується нетто-премія й ті ж таблиця смертності й технічна процентна
ставка, що й при розрахунку нетто-премій, то резерв називають нетто-резервом
або резервом нетто-премій (net premium reserve). Якщо ж премія, яка використовується
при розрахунку резерву, враховує витрати, і/або при розрахунку резерву
використовується особлива таблиця смертності (valuation table) і/або змінена
технічна процентна ставка, то резерв називається спеціальним або модифікованим.
3.5.2
Додаткові методи розрахунку резервів
Рекурентна формула для
резервів
Розглянемо наступну загальну
схему страхування:
договір страхування укладений
у момент 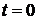 на термін п
років;
на термін п
років;
1)
вік застрахованого в момент
укладання договору - х років;
премія вноситься в кожну
річницю укладання договору й на k-й рік, дорівнює 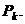
зобов'язання страховика на
k-й рік дії договору полягають у виплаті наприкінці року страхової суми 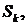 якщо
застрахований помер протягом цього року, і суми
якщо
застрахований помер протягом цього року, і суми 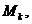 якщо застрахований дожив до кінця
цього року.
якщо застрахований дожив до кінця
цього року.
Припустимо, що наприкінці
k-го року (тобто в момент 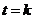 ) договір
усе ще зберігає чинність (так що застрахований ще живий і його вік рівний
) договір
усе ще зберігає чинність (так що застрахований ще живий і його вік рівний 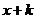 ). Цей
договір
). Цей
договір
• негайно принесе у вигляді
премії суму 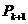 (індекс
(індекс 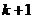 вказує, що
почався
вказує, що
почався 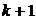 -й рік дії
договору)
-й рік дії
договору)
і, крім того,
• з імовірністю 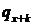 приведе до
виплати страхової суми
приведе до
виплати страхової суми 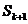 у момент
у момент 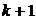 (її
приведена вартість у момент k дорівнює
(її
приведена вартість у момент k дорівнює 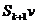 ),
),
• а з імовірністю 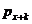 буде діяти
й у момент
буде діяти
й у момент 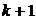 , що буде
вимагати
, що буде
вимагати
виплати суми 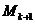 (її
приведена вартість у момент k дорівнює
(її
приведена вартість у момент k дорівнює 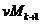 );
);
і (у середньому) наявності
суми 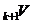 для
виконання страховиком своїх зобов'язань після моменту
для
виконання страховиком своїх зобов'язань після моменту 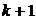 (її
приведена вартість у момент k дорівнює
(її
приведена вартість у момент k дорівнює 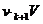 ).
).
Тому середня сума, необхідна
страховикові в момент k для виконання своїх зобов'язань за договором (тобто
нетто-резерв 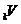 ) дорівнює
) дорівнює
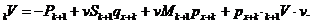 (3.1.14)
(3.1.14)
Це і є рекурентна формула для
резервів наприкінці послідовних років дії договору.
Ретроспективна формула для
нетто-резерву
Якщо премія з деякого виду
страхування або пенсійної схеми визначена із принципу еквівалентності, то в
середньому компанія не повинна залучати власні кошти для виконання фінансових
зобов'язань перед клієнтами. Це означає, що резерв у момент t, необхідний для
виконання майбутніх фінансових зобов'язань по кожному ще діючому договору,
повинен бути рівним сумі, яка накопичена до моменту t на кожен діючий договір.
Тому ми можемо оцінювати
резерви, виходячи з минулого (ретроспективного) розвитку подій:
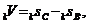
де 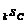 - актуарне
накопичення до моменту k за рахунок премій, а
- актуарне
накопичення до моменту k за рахунок премій, а 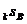 - актуарна накопичена вартість у
момент k всіх виплат на проміжку (0, k).
- актуарна накопичена вартість у
момент k всіх виплат на проміжку (0, k).
Цей метод розрахунку резервів
називається ретроспективним (retrospective).
Ретроспективна формула зручна
при розрахунку резервів для відтермінованих видів страхування й рент до
настання періоду страхових виплат. У цьому випадку резерв - це просто актуарна
накопичена вартість всіх внесених премій.
3.6
Приклади знаходження тарифних ставок для різних видів страхування життя
.6.1
Побудова тарифних ставок по змішаному страхуванню життя
Уклавши договір страхування життя,
страхувальник і страховик починають виконувати свої фінансові зобов'язання.
Фінансові зобов'язання полягають у
сплаті страхових внесків. Якщо страхувальник сплачує їх одразу при укладанні
договору, то такий внесок називається одноразовим. Якщо ж він виконує свої
зобов'язання протягом усього терміну страхування, застосовуються річні внески,
які потім можуть сплачуватися у розстрочку - щомісяця.
Для виплат за кожним видом страхової
відповідальності страховик повинен створити у себе страховий фонд. Крім того,
йому необхідні кошти для компенсації витрат на проведення страхових операцій.
Тому тарифна ставка по змішаному страхуванню життя складається з:
- нетто-ставки на дожиття;
- нетто-ставки на випадок
смерті;
нетто-ставки на випадок
утрати працездатності;
навантаження.
Розглянемо послідовно процес
побудови тарифних ставок.
) Одноразова нетто-ставка на
дожиття.
Припустимо, що особа у віці 40 років
(x=40) укладає договір страхування на дожиття терміном на 5 років на суму
100грн. Яка повинна бути для нього величина одноразового страхового внеску?
Уявимо, що такі договори страхування
уклали всі сорокарічні особи з наведеної у додатку 1 таблиці смертності. Після
закінчення п'яти років страховій компанії необхідно буде виплатити певну
кількість страхових сум тим, хто доживе до закінчення терміну дії договору. З
таблиці смертності знаходимо, що до 45 років доживе 91631 чол. Виходить, і
виплат буде 91631. Страхова сума кожного договору - 100грн. Отже, страховий
фонд, призначений для цих виплат, повинен становити
грн∙91631=9163100грн.
Однак на початку страхування він
може мати меншу величину, враховуючи, що щороку на ній буде наростати 3
складних відсотки доходу. Щоб відповідно зменшити цей фонд, тобто знайти його
сучасну вартість, застосуємо дисконтуючий множник за 5 років, рівний при 3%-й
нормі прибутковості 0,86261.
грн∙0,86261=7904182грн.
Отже, щоб через 5 років мати кошти
для виплати страхових сум по дожиттю, страхова компанія на початку страхування
повинна мати у своєму розпорядженні фонд у 7904182грн. Цю суму і потрібно
одноразово зібрати зі страхувальників. Різниця між сумою збору і сумою виплат
буде покрита за рахунок 3%-го доходу на зібрані кошти. 7904182грн є сучасною
вартістю 9163100грн, що будуть виплачені через 5 років.
Щоб визначити розмір внеску кожного
із застрахованих у цей загальний фонд, розділимо отриману суму на кількість
осіб на початку страхування (див. Додаток 1, x=40). Одержимо:
грн / 93597=84грн 45коп.
Це і буде одноразова нетто-ставка на
дожиття.
Розмір тарифної ставки був,
відповідно, обчислений таким чином:
∙0,86261 / 93597∙100=84,45.
91631 - це кількість осіб, що
доживають до 45 років. Воно позначається символом 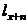 , де x - вік
на початку страхування, n - термін страхування.
, де x - вік
на початку страхування, n - термін страхування.
,86261 - дисконтуючий множник
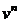 ;
;
- кількість осіб на початку
страхування 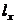 ;
;
- страхова сума S.
Звідси отримаємо формулу
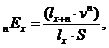
де 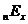 -
одноразова нетто-ставка по страхуванню на дожиття для осіб у віці x років
терміном на n років.
-
одноразова нетто-ставка по страхуванню на дожиття для осіб у віці x років
терміном на n років.
Підставляючи в цю формулу
відповідні значення, можна обчислити розмір тарифної ставки на дожиття для
будь-якого віку і терміну.
) Одноразова нетто-ставка на
випадок смерті.
Припустимо, що особа у віці
40 років укладає договір страхування на випадок смерті терміном на 5 років на
100грн. Якщо, обчислюючи нетто-ставку на дожиття, необхідно було знайти
кількість осіб, що доживають до 45 років, то тепер варто визначити кількість
застрахованих, які не доживуть до 45 років.
По таблиці смертності (див.
Додаток 1) знаходимо, що у віці 40 років звичайно помирає 335 чол., у віці 41
року - 360, 42 років - 390, 43 років -422, 44 років - 459 чол. Отже, страховій
компанії необхідно виплатити у зв'язку з випадками смерті на першому році
страхування 33500грн, на другому 36000грн тощо. Перемноживши ці суми на
відповідні (для одного року, для двох років і т. ін.) дисконтуючі множники,
знайдемо сумарну вартість майбутніх п'ятирічних виплат у випадку смерті:
∙0,97087+36000∙0,94260+39000∙0,91514+42200∙0,88849+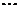 +45900∙0,86261=179237грн.
+45900∙0,86261=179237грн.
Розділимо отриману суму на
кількість осіб, що вступають у страхування:
/93597=1грн 91коп.
Таким чином, особи у віці 40
років, уклавши договір страхування на випадок смерті на страхову суму 100грн,
повинні при укладанні договору внести у загальний страховий фонд 1грн 91 коп.
Розмір тарифної ставки був
обчислений за допомогою таких дій:
(335∙0/97087+360∙0,94260+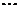 +459∙0,86261)/93597∙100=1,91,
+459∙0,86261)/93597∙100=1,91,
де
- кількість осіб, що
помирають у віці 40 років, або 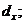
- кількість осіб, що
помирають у віці 41 року, або 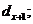 і т.д.;
і т.д.;
- кількість осіб, що
помирають на останньому році страхування, або 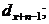
,97087; 0,94260, 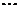 і т.д. -
множники, що дисконтують, для відповідних років страхування:
і т.д. -
множники, що дисконтують, для відповідних років страхування: 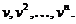
- кількість осіб при вступі у
страхування 
- страхова сума, або S.
Одноразова нетто-ставка по
страхуванню на випадок смерті для осіб у віці x років при терміні страхування n
років позначається символом 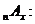
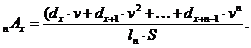
Користуючись цією формулою,
можна обчислити розмір тарифної ставки по страхуванню на випадок смерті для
осіб будь-якого віку на будь-який термін.
3) Річна
нетто-ставка.
Більшості
страхувальників зручніше робити внески протягом усього періоду страхування. Для
цього обчислюються річні нетто-ставки.
Визначаючи розмір
річної нетто-ставки, не можна механічно ділити одноразову ставку на число років
страхування. Необхідний особливий розрахунок, що враховує як втрату доходу на
відсотках, так і зменшення числа застрахованих внаслідок смертності.
Для обчислення
річних ставок застосовуються спеціальні коефіцієнти розстрочки (ануїтети).
Розглянемо
конкретний приклад. Уявімо: всі 93597 осіб 40-річного віку, що значаться в
таблиці смертності, зобов'язалися протягом п'яти років наприкінці кожного року
вносити страховій компанії по 1 грн. Але оскільки протягом п'яти років частина
застрахованих може померти, страхова компанія одержить відповідно до таблиці
смертності: наприкінці
-го року - 93262
грн;
-го року - 92902
грн;
-го року - 92512
грн;
-го року - 92090
грн;
-го року -
91631грн.
Сучасна вартість
суми, внесеної в першому році, дорівнює 93262 ∙ 0,97087 (0,97087 -
дисконтуючий множник за один рік). Сучасна вартість внесків другого року
дорівнює 92902 ∙ 0,94260 (0,94260 - дисконтуючий множник за 2 роки) і
т.д. Перемноживши суми внесків кожного року на відповідні дисконтуючи множники,
знайдемо сучасну вартість загальної суми внесків усіх застрахованих. Розділивши
отриману величину на 93597 (кількість осіб, що вступили в страхування),
розраховуємо сучасну вартість річних внесків у розмірі 1грн, сплачених протягом
п'яти років кожним із 40-річних застрахованих. У результаті підрахунку
отримаємо 4грн 53 коп. Це значить, що протягом п'яти років страхувальник буде
вносити страховій компанії по 1грн і усього він внесе 5 грн. Сучасна вартість
цих 5грн у момент укладання договору страхування дорівнює 4грн 53 коп.
Сучасна вартість річних
внесків у розмірі 1грн називається коефіцієнтам розстрочки (ануїтетом) і
позначається символом 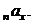 .
.
Якщо в наведеному розрахунку
замінити цифрові значення літерними позначеннями, отримаємо формулу:
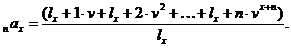
У ній враховується і норма
прибутковості, і природне зменшення внаслідок смертності числа застрахованих
осіб протягом терміну страхування.
Деякі значення ануїтетів
наведені у таблиці 3.
Таблиця 3. Деякі значення
ануїтетів
|
20
|
30
|
40
|
50
|
60
|
|
5 10 15 20
|
4,56 8,45 11,77 14,60
|
4,55 8,42 11,70 14,46
|
4,53 8,34 11,51 14,11
|
4,47 8,13 11,04 13,25
|
4,34 7,64 9,98 11,49
|
Як відомо,
одноразова нетто-ставка дорівнює сучасній вартості взаємних фінансових
зобов'язань страховика і страхувальника. Якщо страхувальник погашає свої
фінансові зобов'язання річними внесками, одноразова ставка дорівнює сучасній
вартості суми річних внесків.
Коефіцієнт
розстрочки дорівнює сучасній вартості річних внесків у розмірі 1грн. Отже,
одноразова ставка так відноситься до річної, як коефіцієнт розстрочки до 1грн.
Складемо пропорцію
Одноразова ставка: пах =
річна ставка / 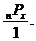 .
.
Звідси річна ставка дорівнює
одноразовій, помноженій на 1грн і поділеній на коефіцієнт розстрочки, або 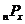 = одноразова
ставка /
= одноразова
ставка /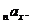 .
.
Абсолютні значення коефіцієнтів
розстрочки близькі до значення п - терміну страхування, але трохи нижчі за
нього (див. табл. 3). У результаті розміри річних ставок виходять більш
високими, ніж при механічному діленні одноразової ставки на число років
страхування. Так відшкодовуються втрати на відсотках і враховується зменшення
протягом терміну страхування кількості осіб, що роблять внески.
Застосувавши коефіцієнт
розстрочки у розмірі 4,53; обчислимо річні ставки для особи у віці 40 років при
терміні страхування 5 років.
Річна нетто-ставка по дожиттю
дорівнює 18грн 64коп (84грн 45 коп. / 4,53); річна нетто-ставка по страхуванню
на випадок смерті складе 42 коп. (1грн 91 коп./4,53), а по змішаному
страхуванню (без відповідальності за втрату працездатності) - 19грн 06коп.
Таким чином, договір
змішаного страхування життя терміном на 5 років для сорокарічної особи
характеризується такими даними: 100 грн - страхова сума; 95грн 30 коп. - сума
річних внесків - нетто; 86грн 36 коп - одноразовий внесок - нетто.
) Нетто-ставки на випадок
утрати працездатності.
Нетто-ставку по страхуванню
на випадок утрати працездатності прийнято включати в усі річні тарифні ставки в
єдиному розмірі, незалежно від віку застрахованого. ЇЇ розмір установлюється на
основі практичних даних страхових компаній про виплати страхових сум у зв'язку
з утратою застрахованими працездатності від нещасного випадку.
Остаточний розмір річної
нетто-ставки по змішаному страхуванню життя із 100грн страхової суми, що
передбачає відповідальність страхових компаній по дожиттю, на випадок смерті і
втрати працездатності для особи у віці 40 років при терміні страхування 5 років
складе 19грн 38коп, у тому числі:
грн 64 коп - нетто-ставка по
страхуванню на дожиття;
коп - нетто-ставка по
страхуванню на випадок смерті;
коп - нетто-ставка по страхуванню
на випадок утрати працездатності.
Переважну питому вагу займає
нетто-ставка на дожиття.
Величина нетто-ставки
залежить, таким чином, від рівня смертності застрахованих, ймовірності втрати
працездатності від нещасного випадку і норми прибутковості. Оскільки ця
залежність носить об'єктивний характер, розміри нетто-ставок не можна довільно
змінювати.
) Брутто-ставки.
Одержуючи внески в розмірі
нетто-ставок, страховик акумулює у своїх руках стільки коштів, скільки йому
знадобиться для виплати страхових сум. Але він несе витрати, пов'язані з
витратами на проведення страхування, тобто повинен оплатити працю всіх
працівників по укладанню договорів страхування та інші витрати.
Оскільки страхування
проводиться, в основному, за рахунок самих страхувальників, кошти на покриття
цих витрат також передбачаються у тарифній ставці. Тому до нетто-ставки
приєднується навантаження.
У тарифних ставках по
змішаному страхуванню життя у навантаження включені лише чисті витрати
страхових компаній по проведенню страхових операцій. Річна брутто-ставка по
змішаному страхуванню життя на 100 грн для особи у віці 40 років і терміном на
5 років складає 21 грн 11 коп.
Брутто-ставки обчислюються за
формулою

де 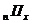 -
брутто-ставка;
-
брутто-ставка;
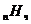 - нетто-ставка;
- нетто-ставка;
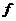 - питома вага навантаження у
брутто-ставці.
- питома вага навантаження у
брутто-ставці.
Тут нетто-ставка позначається
символом 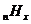 , тому що за
цією формулою обчислюються одноразові і річні ставки. У процесі розрахунків
замість
, тому що за
цією формулою обчислюються одноразові і річні ставки. У процесі розрахунків
замість 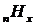 підставляється
відповідна нетто-ставка, наприклад,
підставляється
відповідна нетто-ставка, наприклад, 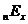 ,
, 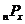 тощо. Якщо йдеться про одноразові
внески, вживаються символи
тощо. Якщо йдеться про одноразові
внески, вживаються символи 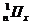 і
і 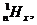 , якщо про
річні -
, якщо про
річні - 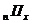 і
і 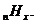
Правилами змішаного
страхування життя надається можливість щомісячної чи одноразової сплати
внесків. Щомісячні внески за своїм розміром дорівнюють 1/12 частині річних
брутто-ставок.
Аналізуючи брутто-ставки,
можна зробити такі висновки: розмір тарифів збільшується слідом за віком особи,
що укладає договір страхування; чим довший термін страхування, тим нижча
тарифна ставка; одноразовий внесок менший страхової суми і нижчий суми місячних
внесків; перевищення загальної суми сплачених у розстрочку внесків буде тим
меншим або його зовсім не буде, чим довший термін страхування і молодша особа,
що укладає договір.
.6.2
Приклад короткострокової моделі страхування життя
Припустимо, що страхова
компанія уклала N = 10000 договорів страхування життя терміном на один рік на
наступних умовах: у випадку смерті застрахованого протягом року від нещасного
випадку компанія виплачує укладачу договору 400 000 грн., а у випадку смерті
від природних причин - 100 000 грн. Компанія не платить нічого, якщо
застрахований не помре протягом року. Імовірність смерті від нещасного випадку
одна й та сама для всіх застрахованих і дорівнює 0,0005. Імовірність смерті від
природних причин залежить від віку. Застрахованих можна розбити на дві вікові
групи, що містять 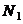 = 4000 і
= 4000 і 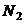 = 6000
людей, з імовірністю смерті протягом року
= 6000
людей, з імовірністю смерті протягом року 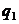 = 0,0040 і
= 0,0040 і 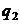 = 0,0020
відповідно.
= 0,0020
відповідно.
Потрібно підрахувати премію,
достатню для виконання компанією своїх зобов'язань із імовірністю 95% без
залучення додаткових засобів. Захисна надбавка для індивідуального договору
береться пропорційною
1)
нетто-премії
2)
дисперсії виплат за договором;
3)
середньому квадратичному відхиленню
виплат за договором.
Для розв’язання
задачі приймемо суму 100 000 грн за одиницю виміру грошових сум.
Тоді для першої
групи договорів індивідуальний збиток приймає три значення: 0, 1 й 4 з
імовірностями 0,9955, 0,0040 й 0,0005 відповідно. Середнє значення й дисперсія
величини індивідуального збитку рівні
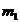 = 1 · 0,0040 + 4 · 0,0005 = 0,0060,
= 1 · 0,0040 + 4 · 0,0005 = 0,0060,
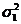 =
= 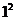 · 0,0040 +
· 0,0040 + 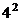 · 0,0005 -
· 0,0005 - 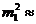 0,0120.
0,0120.
Для другої групи договорів
індивідуальний збиток приймає ті ж три значення 0, 1 й 4, але з іншими
ймовірностями: 0,9975, 0,0020 й 0,0005. У цій групі середнє значення й
дисперсія індивідуального збитку є
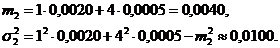
Таким чином, для договорів
першої групи нетто-премія рівна 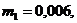 а для договорів другої групи
нетто-премія рівна
а для договорів другої групи
нетто-премія рівна 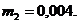
Займемося тепер ризиковими
надбавками.
Середнє значення й дисперсія
сумарних виплат по всьому портфелю рівні:
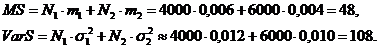
Припустимо, що сумарна премія
дорівнює u. Використовуючи гауссівське наближення для центрованої й нормованої
величини сумарних виплат, ми можемо представити ймовірність нерозорення
компанії в наступному виді:
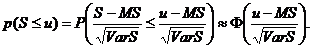
Якщо ми хочемо, щоб
імовірність банкрутства була 5 %, величина 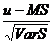 повинна бути рівною
повинна бути рівною 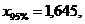 тобто
сумарна премія повинна бути рівною
тобто
сумарна премія повинна бути рівною 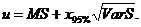 Перший доданок,
Перший доданок, 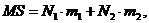 є сумарною
нетто-премією (як ми бачили, вона дорівнює 48), а другий дає загальну ризикову
надбавку l:
є сумарною
нетто-премією (як ми бачили, вона дорівнює 48), а другий дає загальну ризикову
надбавку l:
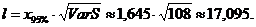
Щодо індивідуальних ризикових
надбавок 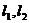 для
договорів з першої й другої груп відповідно ми знаємо поки лише те, що
для
договорів з першої й другої груп відповідно ми знаємо поки лише те, що
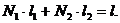
1. Якщо
індивідуальні захисні надбавки пропорційні до нетто-премій:
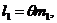
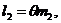
то відносна страхова надбавка
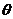 одна і та
сама для всіх договорів і дорівнює
одна і та
сама для всіх договорів і дорівнює
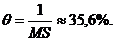
Тому для договорів з першої
групи премія рівна
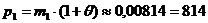 грн.
грн.
Для договорів із другої групи
премія рівна
 грн.
грн.
2. Якщо
додаткова сума l ділиться пропорційно до дисперсій, то коефіцієнт
пропорційності k дорівнює
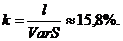
Тому для договорів
з першої групи страхова надбавка дорівнює
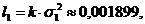
так що премія рівна
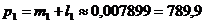 грн,
грн,
а відносна ризикова надбавка
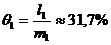
Для договорів із другої групи
ризикова надбавка дорівнює
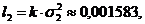
так що премія рівна
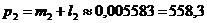 грн,
грн,
а відносна ризикова надбавка
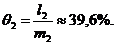
. Якщо додаткова сума
ділиться пропорційна середнім квадратичним відхиленням (вони рівні 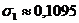 для
договорів першої групи і
для
договорів першої групи і 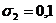 для
договорів другої групи), то коефіцієнт пропорційності k дорівнює
для
договорів другої групи), то коефіцієнт пропорційності k дорівнює
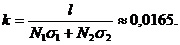
Тому для договорів із першої
групи ризикова надбавка рівна
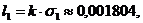
так що премія рівна
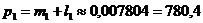 грн.,
грн.,
а відносна ризикова надбавка
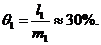
Для договорів із другої групи
ризикова надбавка дорівнює
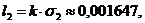
так що премія рівна
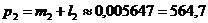 грн,
грн,
а відносна ризикова надбавка
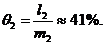
Зауваження. Зміна принципу
призначення індивідуальних премій приводить до зменшення відносної ризикової
надбавки для договорів першої групи:
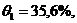
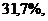
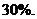
Відповідно для договорів
другої групи відносна ризикова надбавка збільшується:
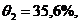
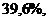
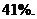
Це пов'язане з тим, що
коефіцієнт розсіювання сумарного збитку рівний
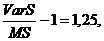
у той час як для договорів
першої (другої) групи він дорівнює 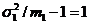 - (відповідно,
- (відповідно, 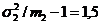 ).
Коефіцієнт варіації величини індивідуального збитку для договорів першої групи
рівний
).
Коефіцієнт варіації величини індивідуального збитку для договорів першої групи
рівний
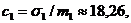
а для договорів другої групи
він дорівнює
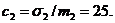
Середній коефіцієнт варіації,
усереднений по всьому портфелю з вагами 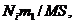
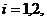 рівний
рівний
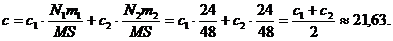
Таким чином, хоч дисперсія
величини індивідуального збитку для договорів другої групи менша, ніж для
договорів першої групи, флуктуації індивідуальних збитків для договорів другої
групи (виміряні як коефіцієнтом розсіювання, так і коефіцієнтом варіації)
перевищують середні флуктуації по всьому портфелю. Тому було б виправданим
прийняти один із принципів 2 або 3 за основу для призначення індивідуальних
премій.
Маючи на увазі тільки небанкрутство
компанії, зовсім неважливо, як загальна ризикова надбавка розподіляється по
індивідуальних договорах (рівною мірою не грає ролі розподіл сумарної
нетто-премії на індивідуальні нетто-премії). Однак маючи на увазі маркетингові
міркування, важливо зробити це «справедливим» чином. Насамперед, зрозуміло, що
в силу статистичної однорідності договорів у межах однієї групи (із двох
розглянутих), захисна надбавка повинна бути однією й тією ж для договорів з
однієї групи. Однак одного рівняння 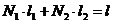 недостатньо для однозначного
визначення індивідуальних надбавок
недостатньо для однозначного
визначення індивідуальних надбавок 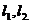 Необхідно прийняти деяке принципове
рішення про “справедливе” співвідношенні між ними.
Необхідно прийняти деяке принципове
рішення про “справедливе” співвідношенні між ними.
.6.3
Приклад обчислення нетто-премії при довгостроковому страхуванні життя
Страхова компанія уклала N =
10000 договорів довічного страхування зі страховою сумою 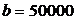 грн кожний.
Припустимо, що залишковий час життя кожного із застрахованих характеризується
інтенсивністю смертності
грн кожний.
Припустимо, що залишковий час життя кожного із застрахованих характеризується
інтенсивністю смертності 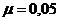 , що не
змінюється із часом, а інтенсивність відсотків
, що не
змінюється із часом, а інтенсивність відсотків 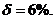
Підрахуємо величину премії,
що гарантувала б 95% імовірність виконання компанією своїх зобов'язань без
залучення додаткових коштів.
Приймемо страхову суму за
одиниця виміру грошових сум.
Підрахуємо спочатку
нетто-премію:
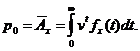
де 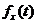 - щільність
залишкового часу життя. Оскільки інтенсивність смертності відома, ми можемо
знайти функцію виживання:
- щільність
залишкового часу життя. Оскільки інтенсивність смертності відома, ми можемо
знайти функцію виживання:
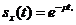 ,
,
що, у свою чергу, дає
наступну формулу для 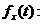
Тепер ми можемо підрахувати
нетто-премію:
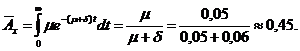
Другий момент сучасної
величини виплат за індивідуальним договором може бути отриманий із цієї формули
заміною 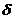 на 2
на 2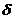 :
:
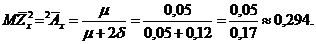
Отже,
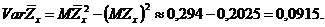
Тепер можна підрахувати
відносну ризикову надбавку:
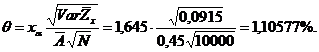
Відповідно, премія рівна
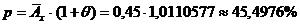
Нагадаємо, що величина
страхової суми b використовується нами як одиниця виміру грошових сум, так що в
абсолютних цифрах р = 2274880 грн.
.6.4
Приклад обчислення величини періодичних премій
Розглянемо N = 2500 договорів
3-х річного змішаного дискретного страхування життя зі страховим відшкодуванням
b = 1000 грн. Премії вносяться в кожну річницю укладання договору протягом
усього терміну його дії, вік всіх застрахованих - 30 років. Компанія
використовує наступну таблицю смертності:
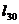 = 96307,
= 96307,  = 96117,
= 96117, 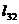 = 95918,
= 95918,
і технічну процентну ставку i
= 25%.
Визначимо величину
періодичної премії Р, що гарантувала б відсутність втрат по всьому портфелю з
імовірністю 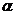 = 99%.
= 99%.
Зобов'язання застрахованого
полягає у виплаті 3-х річної тимчасової довічної ренти. Приведена вартість
цього зобов'язання в момент укладання договору рівна 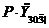 з середнім
значенням
з середнім
значенням 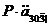 . Величина
. Величина 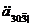 може бути
легко підрахована:
може бути
легко підрахована:
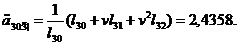
Відзначимо, крім того, що для
подвоєної інтенсивності відсотків
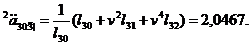
Зобов'язання страхової
компанії полягають у виплаті страхової суми b = 1000 грн. наприкінці року
смерті, якщо вона наступить не пізніше, ніж через 3 роки після укладання
договору, або в момент закінчення терміну дії договору, якщо застрахований
проживе ці 3 роки. Приведена вартість цього зобов'язання в момент укладання
договору рівна 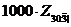 з середнім
значенням
з середнім
значенням 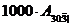 . Як відомо,
. Як відомо,
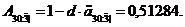
Відзначимо, крім того, що
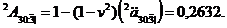
і тому
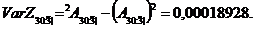
Сучасна величина збитку,
пов'язаного з одним договором, може бути записана у вигляді:
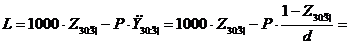
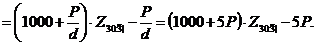
Ми хотіли б, щоб
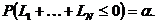
Переписуючи цю умову у
вигляді
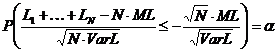
і використовуючи гауссівске
наближення, ми одержимо:
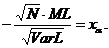
Але
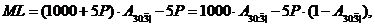
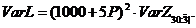
Тому
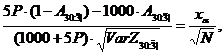
звідки
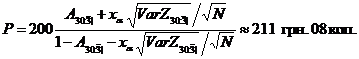
Нетто-премія за
розглянутим договором рівна
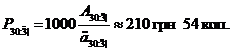
Таким чином, відносна
ризикова надбавка 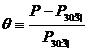 приблизно
дорівнює 0,26%. Настільки мала величина відносної ризикової надбавки пов'язана
з тим, що при змішаному страхуванні з імовірністю близькою до 1 виплата
здійснюється по закінченні терміну дії договору. Відповідно відхилення,
пов'язані зі смертністю, украй малі.
приблизно
дорівнює 0,26%. Настільки мала величина відносної ризикової надбавки пов'язана
з тим, що при змішаному страхуванні з імовірністю близькою до 1 виплата
здійснюється по закінченні терміну дії договору. Відповідно відхилення,
пов'язані зі смертністю, украй малі.
ВИСНОВКИ
У даній дипломній роботі
висвітлюється таке питання актуарних розрахунків, як побудова тарифних ставок
по страхуванню життя, яке є особливо важливим для діяльності страхових компаній
в ринкових умовах. Неправильний розрахунок тарифних ставок може привести до
банкрутства страхової компанії. Тому, не дивно, що актуарій (фахівець, який за
допомогою методів математичної статистики розраховує страхові тарифи) - одна з
найбільш престижних професій у західних країнах, про що свідчать проведені
газетами "Нью-Йорк Таймс" і "Крисчиен Сайенс Монітор"
опитування молоді США про найбільш привабливі з їхнього погляду професії.
У дипломній роботі наведена
методика розрахунків тарифних ставок по страхуванню життя. Показано, що
величина нетто-ставки залежить від рівня смертності застрахованих, ймовірності
втрати працездатності від нещасного випадку і норми прибутковості. Оскільки ця
залежність носить об'єктивний характер, розміри нетто-ставок не можна довільно
змінювати. Також, узагальнюючи розрахунки тарифних ставок, наведена методика
побудови математичних моделей страхування життя, які ґрунтуються на принципі
еквівалентності страхових відносин сторін, тобто нетто-ставки повинні
максимально відповідати ймовірності збитку. Також розв’язано декілька задач по
знаходженню тарифний ставок, які мають практичне спрямування і їх результати
можуть бути використані пенсійним фондом і страховими компаніями.
СПИСОК ВИКОРИСТАНОЇ
ЛІТЕРАТУРИ
1. В.Д.Базилевич,
К.С.Базилевич, Страхова справа. - 5-те вид., стер. - Знання, 2006. - 351с.
. Брагинский М.И. Договор
страхования. - М.: Статут, 2000. - 174 с.
3. Боровков А.А. Математическая
статистика. Новосибирск: Наука; Изд-во Института математики. 1997, 772 с.
. Виленкин С.Я. Статистическая
обработка результатов исследования случайных функций. М.: Энергия, 1979. - 320
с.
. Гербер Х. Математика
страхования жизни. М. Мир, 1995, 154 с.
6. Залєтов О.М., Страхування.
Навчальний посібник. - К.: Міжнародна агенція "BeeZone", 2003. - 320
с.
. Закон України “ Про
внесення змін до Закону України “ Про страхування” // Урядовий кур’єр. - 2001.
- 7 листопада.
8. Крамер Г. Математические
методы статистики М.: Мир. 1975. - 648 с.
. Колемаев В.А., Калинина
В.Н. Теория вероятностей и математическая статистика. М.: Инфра-М, 1997, 302 с.
. Кошкин Г.М., Основы
актуарной математики. - Учебное пособие / Томск: Томский государственный
университет, 2002. 116 с.
11. С.М.Лаптєв, В.І.Грушко,
М.П.Денисенко, В.Г.Кабанов, І.О.Ковтун, О.С.Любунь. Основи актуарних розрахунків:
Навчально-методичний посібник. К.: Алерта, 2004. - 328с.
12. Е.Марецька, Математичні
моделі страхування життя - Вісник Львів. ун-ту, сер. прикл. матем. інформ.,
2002, Вип. 5, С. 112-117.
13. А.Я.Оленко. Збірник задач з
актуарної математики - К.: ВПЦ “Київський університет”, 2005.-67с.
14. Програма розвитку страхового
ринку України 2001-2004 р. //Страхова справа № 1. 2001. - с. 48-55.
15. Самойловский А.Л. Моделі
державного регулювання страхової діяльності: досвід західноєвропейських країн
// Нацыональна безпека ы оборона. - 2000. - № 4. - с. 40-42.
. Страховий ринок в Україні
стан, проблеми, перспективи. - Національна оборона і безпека, № 6 (42) 2003. -
56 с.
. Страхування. Підручник //
Керівник авт. колективу і наук. Редактор С.С.Осадець. - Вид. 2-ге, перероб, і
доп. - К.: КНЕУ, 2002. - 599 с.
18. Філонюк О.Ф. Сучасні
тенденції розвитку страхування // Страхова справа. - 2002. - №3. - с. 6-9.
19. Фалин Г. И., Фалин А. И.
Актуарная математика в задачах. - 2-е изд., перераб. и доп. - М.: ФИЗМАТЛИТ,
2003. - 192 с.
20. Фалин Г. И., Фалин А. И.
Введение в атуарную математику. М.: Изд-во МГУ, 1994, 86 с.
21. Фалин Г.И. Математический
анализ рисков в страховании. М.: Российский юридический издательский дом, 1994,
130 с.
. Філонюк О.Ф. Кроки
становлення страхового ринку України або 10 років життя єдиної страхової сім’ї
// Страхова справа. - 2002. - № 1. - с. 2-5.
. Філонюк О.Ф. Сучасні
тенденції розвитку страхування // Страхова справа. - 2002/ - № 3/ - c. 6-9.
. Філонюк О.Ф. Чинники, що
стримують розвиток страхового ринку // Страхова справа. - 2001. - № 3. - с.
32-35.
Додаток 1
Зразок таблиці
смертності
|
Вік у роках
|
Кількість доживаючих до віку x років
|
Кількість помираючих при переході від віку x
до x+1 років
|
Ймовірність померти на протязі майбутнього
року життя
|
Ймовірність дожити до віку x+1 років
|
|
X
|
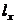 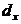 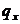 
|
|
|
|
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 … 30 … 40 41 42 43 44 45 …
|
100000 98719 98547 98454 98385 98326 98273
98225 98180 98138 98099 98062 98026 97988 97945 97894 97833 97760 97674 97575
97464 … 95982 … 93597 93262 92902 92512 92090 91631 …
|
1281 172 93 69 59 53 48 45 42 39 37 36 38 43
51 61 73 86 99 111 122 … 179 … 335 360 390 422 459 498 …
|
0,01281 0,00174 0,00094 0,00070 0,00060
0,00054 0,00049 0,00046 0,00043 0,00040 0,00038 0,00037 0,00039 0,00044
0,00052 0,00062 0,00075 0,00088 0,00101 0,00114 0,00125 … 0,00186 … 0,00358
0,00386 0,00420 0,00456 0,00498 0,00543 …
|
0,98719 0,99826 0,99906 0,99930 0,99940
0,99946 0,99951 0,99954 0,99957 0,99960 0,99962 0,99963 0,99961 0,99956
0,99948 0,99938 0,99925 0,99912 0,99899 0,99886 0,99875 … 0,99814 … 0,99642
0,99614 0,99580 0,99544 0,99502 0,99457 …
|
Додаток
2
Таблиця відсоткових
множників
|
Кількість років, n
|
Значення чисел 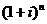 при: при:
|
|
i=0,03
|
i=0,04
|
i=0,05
|
|
1 2 3 4 5 10 14 15 18 20 23 30 50
|
1,03000 1,06090 1,09273 1,12551 1,15927 1,34392
1,51259 1,55797 1,70243 1,80611 1,97359 2,42726 4,38391
|
1,04000 1,08160 1,12486 1,16986 1,21665
1,48824 1,73168 1,80094 2,02582 2,19112 2,46472 3,24340 7,10668
|
1,05000 1,10250 1,15763 1,21551 1,27628
1,62889 1,97993 2,07893 2,40662 2,65330 3,07152 4,32194 11,46740
|
Додаток 3
Таблиця дисконтуючих множників
|
Кількість років, n
|
Дисконтуючі множники при:
|
|
і=0,03
|
і=0,04
|
і=0,05
|
|
1 2 3 4 5 10 14 15 18 20 23 30 40 50
|
0,97087 0,94260 0,91514 0,88849 0,86261
0,74409 0,66112 0,64186 0,58739 0,55368 0,50669 0,41199 0,30656 0,22811
|
0,96154 0,92456 0,83900 0,85480 0,82193
0,67556 0,57748 0,55526 0,49363 0,45639 0,40573 0,30832 0,20829 0,14071
|
0,95238 0,90703 0,86384 0,82270 0,78353
0,61391 0,50507 0,48102 0,41552 0,37689 0,32557 0,23138 0,14205 0,08720
|
Доповід
Слайд 1. Шановний
голово, шановні члени державної кваліфікаційної комісії. До Вашої уваги
виноситься дипломна робота на тему «Економіко-математичне моделювання страхування
життя», яка складається з вступу, трьох розділів, висновків, списку
використаної літератури. Слайд 2.
Найважливіша
проблема страхового бізнесу - це обчислення вартості премії за страхування
(страхового тарифу). З одного боку, вона повинна забезпечувати страховій
компанії не тільки захист від збитків, а й хороший прибуток, з іншого -
конкурувати з преміями інших страхових компаній.
У нашій країна з
огляду на погане становище страхового бізнесу в цілому відшукання оптимальної
премії є особливо важливим. Але сьогодні страхові компанії України переважно не
рахують тарифи самостійно, а беруть їх з російського страхового ринку. Однак
зрозуміло, що становище українського ринку значно відрізняється від
російського. Крім того, одна з проблем, які постають на шляху обчислення премій
за страхування, полягає у тому, що дуже важко знайти статистичні дані, які б
реально описували становище українського страхового ринку. Часто беруть дані
європейських страхових ринків, оскільки такої статистики немає і в Росії. І як
наслідок знову неправильна оцінка премії, а неправильна оцінка премій за
страхування в багатьох випадках призводить до банкрутства страхових компаній. І
ще одна перешкода для правильної оцінки страхових премій - це нестабільність
нашого ринку на законодавчому рівні. Швидкі зміни законодавства в галузі
страхування зумовлюють коливання страхового ринку, зміни економічного
становища. Оскільки змінюється ситуація на ринку, то повинна змінюватися і
стратегія поведінки страхової компанії.
Загальноприйнята
назва наукового напряму, що займається вивченням математичних моделей і методів
страхової справи - актуарна математика (aktuarial mathematics) яка походить від
actuary - актуарій, статистик страхового товариства. Разом з відповідними
економічними і юридичними дисциплінами актуарна математика утворює більш широку
область знань - актуарну науку (actuerial science), яка є теоретичною основою
страхового бізнесу.
Дослідження,
виконані в Україні в останнє десятиліття в області актуарной математики носять
фрагментарний й епізодичний характер, відносяться в першу чергу до прикладних
робіт. Відсутність статистичних даних (часто вони є комерційною таємницею) і
недостатнє цільове фінансування, очевидно, є основними причинами цього, крім
зазначеної вище «молодості» і нерозвиненості цієї області в цілому, що
виражається в недостачі інформаційного забезпечення й кваліфікованих кадрів.
Основною рисою сучасного стану актуарної науки в Україні можна назвати воістину
величезний розрив, що існує між теорією й практикою. Украй мало таких робіт, де
досить передові теоретичні розробки були б доведені до практичної реалізації;
навіть демонстрації їхнього застосування одиничні, не говорячи вже про
систематичне використання.
Розрізняють
актуарну математику у майновому і особистому страхуванні. Під майновим
страхуванням (non-life insurance) розуміють всі види страхової діяльності, не
пов’язані з особистим страхуванням (страхування житла, автомобілів, підприємств
і т.д.). У найзагальнішому плані особисте страхування можна визначити як галузь
страхової діяльності, яка забезпечує страховий захист громадян або зміцнення
досягнутого ними сімейного добробуту.
Особисте
страхування включає:
страхування
життя;
страхування
від нещасних випадків;
страхування
додаткової пенсії;
добровільне
медичне страхування;
страхування
від нещасних випадків на транспорті.
Особисте
страхування має багато спільного з соціальним, насамперед у об'єктах страхового
захисту громадян. Головна відмінність між ними - в джерелах формування
страхових фондів: для соціального - це в основному кошти підприємств, установ,
організацій, і лише незначною мірою - індивідуальні доходи, тоді як для
особистого індивідуальні доходи є головним джерелом, а кошти підприємств,
установ і організацій - тією мірою, якою особисте страхування є обов'язковим.
Необхідність
особистого добровільного страхування зумовлюється як ризиковим характером
відтворення робочої сили, так і підвищенням ступеня ризику життя у зв'язку з
урбанізацією, погіршенням довкілля, а також зростанням частки людей похилого
віку у загальній чисельності населення. Це ускладнює захист особистих інтересів
громадян з боку держави та за її рахунок і передбачає формування захисних
механізмів за рахунок перерозподілу індивідуальних доходів.
Історія страхування
життя налічує приблизно 20 століть. Зародковими формами страхування життя були
[1] грошові фонди для благодійних цілей у древній Індії, комунальні установи
древніх іудеїв, колегії Римської імперії. Організації, подібні до римських
колегій, існували в епоху середніх віків у цехах і гільдіях. Надаючи
матеріальну підтримку своїм членам у скрутних випадках, вони піклувалися також
про забезпечення близьких померлого.
При капіталізмі
страхування поступово перетворюється в особливу галузь економіки, здобуває
загальне поширення як необхідний її елемент.
У 1706 р. в Англії
виникло перше товариство страхування життя - "Емікебл". Система
тарифних ставок у нього була недосконалою, вони ще не диференціювалися за
віком.
Значно вплинули на
розвиток страхування життя статистика і математика.
Виникла статистика
у так званій школі "політичних арифметиків". Один із засновників цієї
школи англійський учений Д. Граунт у 1662 р. опублікував роботу "Природні
і політичні спостереження, виконані над бюлетенями смертності", яка поклала
початок страховій математиці - теорії актуарних розрахунків.
Майже одночасно з
Д. Граунтом питання залежності страхування життя від смертності людей
досліджував голландець Я. де-Вітт, який написав роботу про ціну довічної ренти,
де розробив метод розрахунку страхових внесків у залежності від віку
застрахованого і норми зростання грошей.
Своє продовження
теорія актуарних розрахунків знайшла в працях англійського вченого Е. Галлея.
Він склав таблицю смертності на основі матеріалів про смертність населення
Бреславля за період 1687-1691 рр., дав визначення основних функцій таблиці
смертності, обчислював ймовірності дожити і вмерти, увів у науку поняття
ймовірної тривалості життя, застосував принцип розрахунку середньої тривалості
життя при обчисленні щорічної ренти в залежності від віку, показав, що таблиця
смертності дозволяє регулювати розміри страхових внесків. Форма таблиці Галлея
застосовується в страхуванні життя дотепер.
Потім англійський
математик А. Муавр, вивчивши таблицю смертності Е.Галлея, зумів спростити
актуарні розрахунки. Він склав три інші таблиці на основі даних про смертність
застрахованих у Голландії і Франції, а також про смертність населення Лондона
за 1728-1737 рр.
Проблемами,
пов'язаними з актуарними розрахунками, займалися майже такі великі математики
як Л. Ейлер, Н. Фус, С. Лакруа та ін. Були складені таблиці смертності В.
Керсебума, А. Депарс'є. У теорії актуарних розрахунків застосовуються новітні
досягнення математики і статистики. Страхові товариства одними з перших стали
використовувати обчислювальну техніку.
Тарифна ставка -
ціна страхового ризику та інших витрат, необхідних для виконання зобов'язань
страховика перед страхувальником за підписаним договором страхування.
Нетто-ставка - ціна
страхового ризику, тобто гроші, зібрані з нетто-ставок підуть виключно на
виплати клієнтам страхової компанії у разі настання страхового випадку.
Навантаження -
вартість, яка покриває витрати страховика з організації та ведення страхової
справи, а також містить елементи прибутку.
Для розрахунку
тарифів можуть бути використані кілька методів [8]:
· на
основі теорії імовірності та методів математичної статистики з використанням
часових рядів;
· на
базі експертних оцінок;
· за
аналогією до інших об'єктів або компаній;
· з
використанням математичної статистики і розрахунку дохідності.
Слайд 3. (Наведено
структуру тарифної ставки по змішаному страхуванню життя).
Тарифна ставка визначає, скільки
грошей кожний із страхувальників повинен внести в загальний страховий фонд з
одиниці страхової суми. Тому тарифи повинні бути розраховані так, щоб сума
зібраних внесків виявилася достатньою для виплат, передбачених умовами
страхування. Таким чином, тарифна ставка - це ціна послуги, що надається
страховиком населенню, тобто своєрідна ціна страхового захисту.
Від чого ж залежать
її розміри, як установити ціну на той чи інший вид страхування життя?
Для розрахунку
обсягу страхового фонду при страхуванні життя потрібно мати відомості про те,
скільки осіб з числа застрахованих доживе до закінчення терміну дії їх
договорів страхування і скільки з них щороку може померти; у скількох і в якому
ступені настане втрата здоров'я. Кількість виплат, помножена на відповідні
страхові суми, дозволить визначити розміри майбутніх виплат, тобто з'явиться
можливість дізнатися, у яких розмірах потрібно буде акумулювати страховий фонд.
Тривалість життя
окремих людей коливається в широких межах. Вона відноситься до категорії
випадкових величин. Теорія ймовірності і статистика досліджують випадкові
явища, що мають масовий характер, у тому числі смертність населення.
Установлено, що демографічний процес зміни поколінь, що виражається в зміні
рівня повікової смертності, підпорядкований закону великих чисел, настільки
одноманітному у своїх проявах і настільки достовірному в результатах, що він
може бути основою фінансових розрахунків у страхуванні.
Демографічною
статистикою виявлена і виражена за допомогою математичних формул залежність
смертності від віку людей. Розроблено спеціальну методику складання так званих
таблиць смертності, де на конкретних цифрах показується послідовна зміна
смертності слідом за віком. Цими таблицями страхові компанії користуються для
розрахунку тарифів.
Крім
закономірностей, пов'язаних із процесом дожиття і смертності, при побудові
тарифів враховується довгостроковий характер операцій страхування життя,
оскільки ці договори укладаються на тривалі терміни від трьох і більше років.
Протягом усього часу їхньої дії (чи на самому початку терміну страхування при
одноразовій сплаті) страхові компанії одержують внески. Виплати ж страхових сум
проводяться протягом терміну страхування чи після закінчення визначеного
періоду від початку дії договору, якщо настане смерть застрахованого чи він
втратить здоров'я.
Тимчасово вільні
кошти акумулюються страховою компанією і використовуються як кредитні ресурси. За
користування ними сплачується позичковий відсоток. Але якщо при ощадній
операції дохід від відсотків приєднується до внеску, то в страхуванні на суму
цього доходу заздалегідь зменшуються (дисконтуються) внески страхувальника, що
підлягають сплаті. Для того щоб заздалегідь понизити тарифні ставки на той
дохід, що буде утворюватись протягом ряду років, використовуються методи теорії
довгострокових фінансових розрахунків.
Слайд 4. В
актуарній математиці моделі страхування життя умовно ділять на дві великі групи
залежно від того, приймається чи ні в розрахунок дохід від інвестування
зібраних премій. Якщо ні, то ми говоримо про короткострокове страхування
(short-term insurance); в якості такого “короткого” інтервалу ми будемо
розглядати інтервал в 1 рік. Якщо ж так, то ми говоримо про довгострокове
страхування (long-term insurance). Звичайно, цей поділ умовний і, крім того,
довгострокове страхування пов'язане з рядом інших обставин, наприклад,
андеррайтингом.
Слайд 5.
Найпростіший вид страхування життя полягає в наступному.
Страхувальник
платить страховій компанії р грн (ця сума, як уже зазначалося, називається
страховою премією - premium); страхувальником може бути сам застрахований або
інша особа (наприклад, його роботодавець).
У свою чергу
страхова компанія зобов'язується виплатити особі, на користь якої укладений
договір, страхову суму (sum assured) b грн у випадку смерті застрахованого
протягом року із причин, перерахованих у договорі (і не платити нічого, якщо
він не помре протягом року або помре через причину, що не покривається
договором).
Страховая сума
часто приймається рівної 1 або 1000. Це означає, що премія виражається як
частка від страхової суми або на 1000 страхової суми відповідно.
Величина страхової
виплати (benefit), звичайно, набагато більша, ніж страхова премія, і
знаходження «правильного» співвідношення між ними - одна з найважливіших задач
актуарной математики.
Питання про те, яку
плату страхова компанія повинна призначати за прийняття на себе того чи іншого
ризику, украй складне. При його вирішенні враховується велика кількість
різнорідних факторів: імовірність настання страхового випадку, його очікувана
величина й можливі флуктуації, зв'язок з іншими ризиками, які вже прийняті
компанією, організаційні витрати компанії на ведення справи, співвідношення між
попитом та пропозицією по даному виду ризиків на ринку страхових послуг і т.д.
Однак основним звичайно є принцип еквівалентності фінансових зобов'язань
страхової компанії й застрахованого.
В розглянутій вище
найпростішій схемі страхування, коли плата за страховку повністю вноситься в
момент укладання договору, зобов'язання застрахованого виражається в сплаті
премії р. Зобов'язання компанії полягає у виплаті страхової суми, якщо
наступить страховий випадок. Таким чином, грошовий еквівалент зобов'язань
страховика, X, є випадковою величиною:
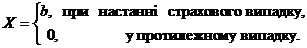
У найпростішій формі принцип
еквівалентності зобов'язань виражається рівністю р = МХ, тобто, як плата за
страховку призначається очікувана величина збитку. Ця премія, як уже
зазначалося, називається нетто-премією (net premium).
Купивши за фіксовану премію р
грн. страховий поліс, страховик позбавив укладача договору страхування від
ризику фінансових втрат, пов'язаних з невизначеністю моменту смерті
застрахованого. Однак сам ризик не зник; його прийняла на себе страхова компанія.
Тому рівність р = MX
насправді не виражає еквівалентності зобов'язань страхувальника й страховика.
Хоча в середньому й страховик, і страхувальник платять ту саму суму, страхова
компанія має ризик, пов'язаний з тим, що в силу випадкових обставин їй,
можливо, прийдеться виплатити набагато більшу суму, ніж МХ. Страхувальник же
такого ризику не має. Тому було б справедливо, щоб плата за страховку включала
деяку надбавку l, яка б служила еквівалентом випадковості, що впливає на
компанію. Ризикову надбавку часто розраховують, як середньоквадратичне
відхилення реальних виплат на одиницю страхової суми за останні роки від
сподіваного значення виплат, тобто, від математичного сподівання. Цю надбавку
називають ризиковою (або захисною) надбавкою (security loading), а 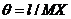 - відносною
ризиковою надбавкою (relative security loading). Розмір ризикової надбавки
береться таким, щоб імовірність того, що компанія буде мати втрати по деякому
портфелю договорів («розориться»), була досить малою величиною.
- відносною
ризиковою надбавкою (relative security loading). Розмір ризикової надбавки
береться таким, щоб імовірність того, що компанія буде мати втрати по деякому
портфелю договорів («розориться»), була досить малою величиною.
Слід зазначити, що реальна
плата за страховку (брутто-премія або офісна премія) - більша нетто-премії з
ризиковою надбавкою (часто в кілька разів). Різниця між ними дозволяє страховій
компанії покрити адміністративні витрати, забезпечити доход і т.д.
Точний розрахунок ризикової
надбавки може бути здійснений у рамках теорії ризику.
Слайд 6, 7. Найпростішою
моделлю функціонування страхової компанії, призначеної для розрахунку
ймовірності банкрутства, є модель індивідуального ризику. Вона базується на
наступних спрощених припущеннях:
1)
аналізується фіксований відносно
короткий проміжок часу (так що можна знехтувати інфляцією й не враховувати
прибуток від інвестування активів) - як правило це один рік;
2)
кількість договорів страхування N
фіксована й невипадкова;
3)
премія повністю вноситься на початку
аналізованого періоду; ніяких надходжень протягом цього періоду немає;
4)
ми спостерігаємо кожен окремий
договір страхування й знаємо статистичні властивості пов'язаних з ним
індивідуальних втрат X.
Як правило припускається, що
в моделі індивідуального ризику випадкові величини 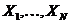 - незалежні
(зокрема, виключаються катастрофи, коли одночасно по декількох договорах
наступають страхові випадки).
- незалежні
(зокрема, виключаються катастрофи, коли одночасно по декількох договорах
наступають страхові випадки).
У рамках цієї моделі «банкрутство»
визначається сумарними втратами по портфелю 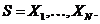 . Якщо ці сумарні виплати більші,
ніж активи компанії, призначені для виплат по цьому блоці бізнесу, u, то
компанія не зможе виконати всі свої зобов'язання (без залучення додаткових
засобів); у цьому випадку говорять про «розорення».
. Якщо ці сумарні виплати більші,
ніж активи компанії, призначені для виплат по цьому блоці бізнесу, u, то
компанія не зможе виконати всі свої зобов'язання (без залучення додаткових
засобів); у цьому випадку говорять про «розорення».
Отже, імовірність «розорення»
компанії дорівнює
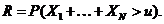
Іншими словами, імовірність
«розорення» - це додаткова функція розподілу величини сумарних втрат компанії
за розглянутий проміжок часу.
Оскільки сумарні виплати S
являють собою суму незалежних випадкових величин, розподіл випадкової величини
S може бути підрахований за допомогою класичних теорем і методів теорії
ймовірностей.
Слайд 8. З математичної точки
зору довгострокове страхування (long-term insurance) характеризується тим, що
при розрахунках враховується зміна цінності грошей із часом. Тому теорія
довгострокового страхування істотно опирається на теорію складних відсотків.
Зокрема, зпівставляючи
зобов'язання страхувальника й страховика, ми повинні приводити їх до одного
моменту часу. Скажімо, для того, щоб сформулювати принцип еквівалентності
зобов'язань у момент укладання договору, ми повинні привести зобов'язання
страхувальника й страховика саме до цього моменту. Їхні середні значення
називаються актуарними сучасними вартостями зобов'язань.
У дипломній роботі наведено приклади
знаходження тарифних ставок для різних випадків. Зокрема, розв’язана наступна
задача, яка стосується короткострокового страхування життя:
Слайд 9-15 (Задача)
Припустимо, що страхова
компанія уклала N = 10000 договорів страхування життя терміном на один рік на
наступних умовах: у випадку смерті застрахованого протягом року від нещасного
випадку компанія виплачує укладачу договору 400 000 грн., а у випадку смерті
від природних причин - 100 000 грн. Компанія не платить нічого, якщо
застрахований не помре протягом року. Імовірність смерті від нещасного випадку
одна й та сама для всіх застрахованих і дорівнює 0,0005. Імовірність смерті від
природних причин залежить від віку. Застрахованих можна розбити на дві вікові
групи, що містять 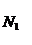 = 4000 і
= 4000 і 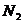 = 6000
людей, з імовірністю смерті протягом року
= 6000
людей, з імовірністю смерті протягом року 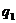 = 0,0040 і
= 0,0040 і 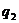 = 0,0020
відповідно.
= 0,0020
відповідно.
Потрібно підрахувати премію,
достатню для виконання компанією своїх зобов'язань із імовірністю 95% без
залучення додаткових засобів. Захисна надбавка для індивідуального договору
береться пропорційною
1)
нетто-премії
2)
дисперсії виплат за договором;
3)
середньому квадратичному відхиленню виплат
за договором.
Також розв’язана задача по
довгостроковому страхуванні життя:
Слайд 16.
Страхова компанія уклала N =
10000 договорів довічного страхування зі страховою сумою 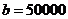 грн кожний.
Припустимо, що залишковий час життя кожного із застрахованих характеризується
інтенсивністю смертності
грн кожний.
Припустимо, що залишковий час життя кожного із застрахованих характеризується
інтенсивністю смертності 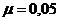 , що не
змінюється із часом, а інтенсивність відсотків
, що не
змінюється із часом, а інтенсивність відсотків 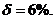
Підрахуємо величину премії,
що гарантувала б 95% імовірність виконання компанією своїх зобов'язань без
залучення додаткових коштів.
Обчислена величина періодичних
премій Слайд 17.
У дипломній роботі
викладаються основні математичні моделі й методи, які використаються для
розрахунків характеристик тривалості життя, разових і періодичних премій,
страхових надбавок, резервів і т.д. для різних видів страхування життя й
пенсійних схем.
Даний поглиблений
виклад основних математичних моделей і методів, необхідних для визначення
характеристик тривалості життя, разових і періодичних премій, страхових
надбавок, резервів і т.д. для різних видів страхування й пенсійних схем.
Задачі, які
розв’язані у дипломній роботі мають яскраво виражену практичну спрямованість і
дозволяють одержати певне уявлення не тільки про актуарні розрахунки, але й про
розробку страхових продуктів, андеррайтингу й т.д. При актуарних розрахунках у
довгостроковому страхуванні життя широко використовується теорія складних відсотків.
Тому, у дипломну роботу включено розділ „Основи фінансової математики”.