Двухшаговый метод наименьших квадратов для решения систем эконометрических уравнений
"Двухшаговый
метод наименьших квадратов для решения систем эконометрических уравнений"
Введение
В области естественных наук важной задачей является исследование
взаимосвязи различных величин, то есть поиск ответа на вопрос: как влияет изменение
одной величины (или, в общем случае, нескольких) на значение, принимаемые
другой. Подбор удачного вида функциональной зависимости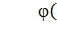 
- искусство, а определение наилучших
(в требуемом смысле) параметров формулы делается стандартными методами [13, c.
27]. Этим вопросом и занимается регрессионный анализ. Одним из наиболее
разработанных и часто используемых алгоритмов регрессионного анализа является
метод наименьших квадратов. [1].
При использовании отдельных уравнений регрессии в большинстве случаев
предполагается, что аргументы можно изменять независимо друг от друга. Однако
это предположение является очень грубым: практически изменение одной
переменной, как правило, не может происходить при абсолютной неизменности других.
Ее изменение повлечет за собой изменения во всей системе взаимосвязанных
признаков. Следовательно, отдельно взятое уравнение множественной регрессии не
может характеризовать истинные влияния отдельных признаков на вариацию
результирующей переменной. [4, c.
246]. При моделировании часто приходится вводить не одно, а несколько связанных
между собой уравнений, т. е. описывать модель системой уравнений. Например,
простейшая макроэкономическая кейнсианская модель потребления может быть
представлена в следующем виде:
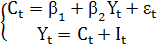
где 
- агрегированное потребление, 
- национальный доход, 
- инвестиции в период времени t, 
- автономное потребление, 
- случайная величина (возмущение).
Коэффициент носит название склонность к потреблению.
Наличие связи между переменными и , определяемой вторым уравнением,
требует корректировки метода наименьших квадратов для оценивания параметров
модели и . Вообще, оценивание систем уравнений
требует введения новых понятий и разработки новых методов [2, с. 220], чему и
посвящена данная работа.
Данная работа рассматривает решение систем взаимозависимых уравнений. В
ходе работы произведено исследование численных методов решения систем эконометрических
уравнений, приведен пример решения двухшаговым методом наименьших квадратов.
Под системой эконометрических уравнений обычно понимается система
одновременных, совместных уравнений.
Целью работы является углубление знаний в области численных методов, в
частности исследование различных вариаций метода наименьших квадратов, который
используется для оценки неизвестных параметров регрессионных моделей по
выборочным данным.
1.
Теоретическая часть
1.1
Система эконометрических уравнений
эконометрический
двухшаговый уравнение
При исследовании сложных явлений приходится
учитывать, как правило, несколько взаимосвязей и, вводить в модель несколько
зависимых переменных, которые могут влиять друг на друга. В таких ситуациях
эконометрические модели строятся в виде систем уравнений. [3, c. 48]
Система уравнений может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная
у рассматривается как функция одного и того же набора факторов х:
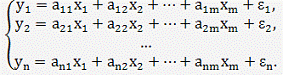
Если зависимая переменная у одного уравнения выступает в виде фактора х в
другом, то исследователь может строить модель в виде системы рекурсивных
уравнений:
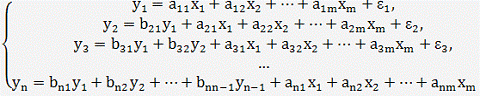
Наибольшее распространение в эконометрических исследованиях получила
система взаимозависимых уравнений. В ней одни и те же зависимые переменные в
одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы:
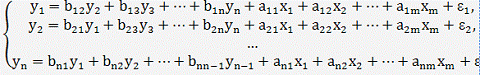
Система взаимозависимых уравнений получила название система совместных,
одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же
переменные у одновременно рассматриваются как зависимые в одних уравнениях и
как независимые в других. Эта система уравнений называется также структурной
формой модели. В отличие от предыдущих систем каждое уравнение системы
одновременных уравнений не может рассматриваться самостоятельно, и для
нахождения его параметров традиционный МНК неприменим. C этой целью используются специальные приемы оценивания. [4, c. 247].
Если с помощью преобразований исключить зависимые переменные из правых
частей уравнений (1.3), то полученная система уравнений называется приведенной
формой модели:
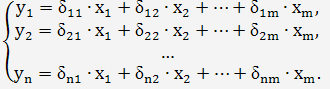
Параметры 
приведенной
формой модели являются алгебраическими функциями от структурных коэффициентов аij и bij и называются приведенными коэффициентами.
1.2
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь
сталкивается с проблемой идентификации. Идентификация - это единственность
соответствия между приведенной и структурной формами модели. [4, c. 255].
С позиции идентифицируемости структурные модели можно подразделить на три
вида: а) идентифицируемые, б) неидентифицируемые, в) сверхидентифицируемые.
Модель идентифицируема, если все ее структурные
коэффициенты определяются однозначно, единственным образом по коэффициентам
приведенной формы модели, т. е. если число параметров структурной модели равно
числу параметров приведенной формы модели. В этом случае структурные
коэффициенты модели оцениваются через параметры приведенной формы модели.
Модель неидентифицируема, если число приведенных коэффициентов меньше
числа структурных коэффициентов, и в результате структурные коэффициенты не
могут быть оценены через коэффициенты приведенной формы модели.
Модель сверхидентифицируема, если число приведенных коэффициентов больше
числа структурных. В этом случае на основе коэффициентов приведенной формы
можно получить два или более значений одного структурного коэффициента. В этой
модели число структурных коэффициентов меньше числа коэффициентов приведенной
формы.[4, c. 257].
Структурная модель всегда представляет собой систему совместных
уравнений, каждое из которых необходимо проверять на идентификацию. Модель
считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если
хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается
неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно
сверхидентифицируемое уравнение. [4, c. 258].
Необходимое условие идентификации - выполнение счетного правила:
D + 1
= H - уравнение идентифицируемо;
D + 1
< H - уравнение неидентифицируемо;
D + 1
> H - уравнение сверхидентифицируемо,
где H - число эндогенных (зависимых)
переменных в уравнении,
D -
число предопределенных (независимых) переменных, отсутствующих в уравнении, но
присутствующих в системе.
Достаточное условие идентификации - определитель матрицы, составленной из
коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен
нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без
единицы.
Для решения идентифицируемого уравнения применяется косвенный метод
наименьших квадратов, для решения сверхидентифицированных - двухшаговый МНК.
[5, c. 107].
Для оценки параметров структурной модели система должна быть
идентифицируема или сверхидентифицируема. [4, c. 260].
1.3 Методы
оценивания параметров структурной модели
Коэффициенты структурной модели могут быть оценены разными способами в
зависимости от вида системы одновременных уравнений. Наибольшее распространение
в литературе получили следующие методы оценивания коэффициентов структурной модели:
• косвенный метод наименьших квадратов (КМНК);
• двухшаговый метод наименьших квадратов (ДМНК);
• трехшаговый метод наименьших квадратов (ТМНК). [4, c. 264].
Косвенный и двухшаговый МНК подробно описаны в литературе и
рассматриваются как традиционные методы оценки коэффициентов структурной
модели.[4, c. 264].
1.4
Косвенный метод наименьших квадратов
Косвенный МНК предназначен для оценивания структурных параметров
отдельного уравнения системы и может дать результат только в применении к точно
идентифицируемому уравнению. [6, c.
353].
Применение косвенного МНК включает в себя следующие этапы:
. преобразование структурной модели в приведенную форму модели;
. оценивание коэффициентов приведенной формы 
при помощи обычного МНК;
. трансформация коэффициентов 
в параметры структурной модели.
1.5
Двухшаговый метод наименьших квадратов
Если система сверхидентифицируема, то КМНК не
используется, ибо он не дает однозначных оценок для параметров структурной
модели. В этом случае могут применяться разные методы оценивания, среди которых
двухшаговый метод наименьших квадратов. [4, c. 271].
Двухшаговый МНК является одним из наиболее «популярных» методов оценки
параметров моделей структурной формы. Причем обычно он используется в случае
изолированного рассмотрения каждой из моделей системы. [7, c. 330].
Основная идея ДМНК - на основе приведенной формы модели получить для
сверхидентифицируемого уравнения теоретические значения эндогенных переменных,
содержащихся в правой части уравнения. Далее, подставив их вместо фактических
значений, можно применить обычный МНК к структурной форме
сверхидентифицируемого уравнения. Метод получил название «двухшаговый МНК», ибо
МНК используется дважды: на I шаге
при определении приведенной формы модели и нахождении на ее основе оценок
теоретических значений эндогенной переменной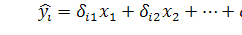 
и на II шаге применительно к структурному сверхидентифицируемому
уравнению при определении структурных коэффициентов по данным теоретических
(расчетных) значений эндогенных переменных.
Если все уравнения системы сверхидентифицируемые, то для оценки
структурных коэффициентов каждого уравнения используется ДМНК. Если в системе
есть точно идентифицируемые уравнения, то структурные коэффициенты по ним
находятся из системы приведенных уравнений. [4, c. 271].
2.
Практическая часть
2.1 Пример
решения системы двухшаговым методом наименьших квадратов
.1.1
Постановка задачи
Изучается простейшая макроэкономическая кейнсианская модель потребления
вида:
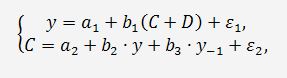
где y - валовой национальный доход;
y-1
- валовой
национальный доход предшествующего года;
C -
личное потребление;
D -
конечный спрос (помимо личного потребления);
и 
- случайные составляющие;
- неучтенный доход;
- автономное потребление;
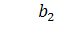- склонность к потребления текущего и предшествующего периода.
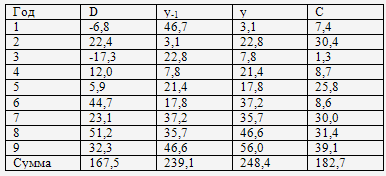
Информация за девять лет о приростах всех показателей дана в таблице 2.1.
Таблица 2.1 - Данные для примера
Задание:
. Трансформировать систему к приведенному виду.
. Провести идентификацию модели.
. Рассчитать параметры уравнений структурной модели. [5, c. 113].
2.1.2
Решение
1. Приведенная форма модели составит:
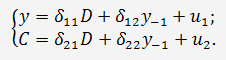
где и - случайные ошибки приведенной формы модели.
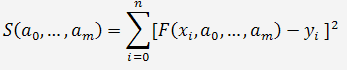
где - коэф-ты, - аппроксимирующая функция, 
- независимые и зависимые переменные.
который геометрически представляет собой сумму квадратов отклонений
значений от значений аппроксимирующей функции
в точках (рис. 2.1). [12, c. 75].
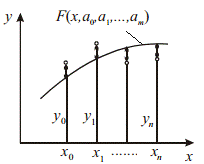
Рисунок 2.1 - Аппроксимирующая функция
Необходимым условием минимума функции многих переменных является
равенство нулю ее частных производных первого порядка по независимым переменным.
В функционале (2.1) такими независимыми переменными являются коэффициенты , которые до их определения являются
не постоянными, а варьируемыми переменными.
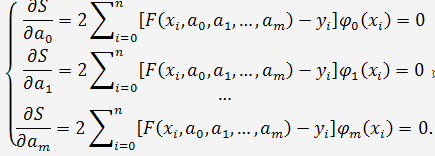
где - базисные функции.
Для определения минимума данного функционала можно использовать только
необходимое условие минимума, так как существует всего лишь одна точка, в
которой все частные производные равны нулю. Также нетрудно проверить, что данный
функционал удовлетворяет достаточному условию минимума.
Система (2.2) представляет собой систему линейных алгебраических
уравнений порядка m+1 относительно неизвестных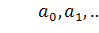 
. Она называется системой нормальных
уравнений. Решения 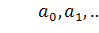доставляют минимум функционалу (2.1). [11, c. 75].
Для I уравнения приведенной формы система
нормальных уравнений составит:
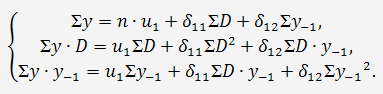
Применительно к рассматриваемому примеру, имеем:
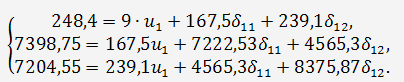
Решив данную систему, получим следующее I уравнение приведенной формы модели:
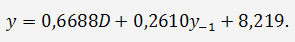
Аналогично применяем МНК для второго уравнения приведенной формы модели.
Система нормальных уравнений составит:
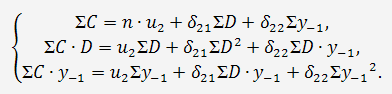
В соответствии с нашим примером имеем:
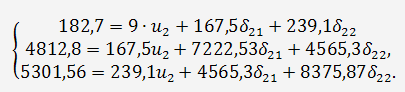
Откуда второе приведенное уравнение составит:
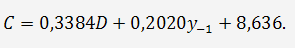
Таким образом, приведенная форма модели имеет вид:
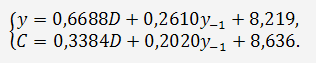
2. В данной модели две эндогенные переменные (y и C) и
две экзогенные переменные (D и y-1). Второе уравнение точно
идентифицировано, так как содержит две эндогенные переменные и не содержит одну
экзогенную переменную из системы. Иными словами, для второго уравнения имеем по
счетному правилу идентификации равенство: 2 = 1 + 1.
Первое уравнение сверхидентифицировано. В этом уравнении содержится одна
эндогенная переменная у. Переменная С в данном уравнении не рассматривается как
эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с
переменной D. В данном уравнении отсутствует одна
экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации
получаем: 1 + 1 = 2: D + 1
> H. Это больше, чем число эндогенных
переменных в данном уравнении, следовательно, система сверхидентифицирована.
[5, c. 113].
. Для определения параметров
сверхидентифицированной модели используется ДМНК.
Шаг 1. На основе системы приведенных уравнений по
точно идентифицированному II уравнению определим теоретические
значения эндогенной переменной С. В приведенное уравнение
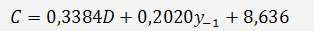
подставим значения D и y-1, имеющиеся в условии задачи. Получим:
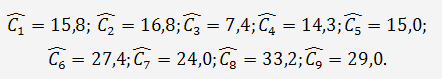
Шаг 2. По сверхидентифицированному уравнению
структурной формы модели заменяем фактические значения С на теоретические 
и рассчитываем
новую переменную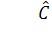 
(табл. 2.2).
Таблица 2.2 - Расчетные данные для второго шага ДМНК
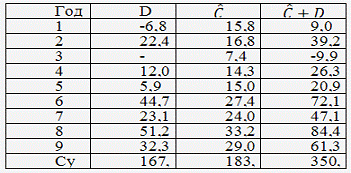
Далее к сверхидентифицированному уравнению применяется метод наименьших
квадратов. Обозначим новую переменную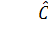 
через Z. Решаем уравнение
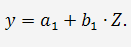
Система нормальных уравнений составит:
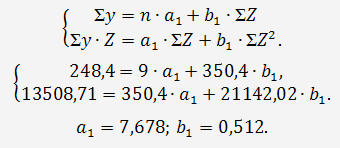
Итак, первое уравнение структурной модели будет таким: [5, c. 114].
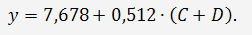
Так как второе уравнение точно идентифицировано, то его коэффициенты
определяются по приведенной форме. В связи с этим рассматриваемая
система примет вид:
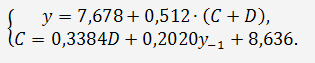
2.2
Пример, для решения которого не применяется двухшаговый метод наименьших
квадратов
Если система идентифицируема, то оценки структурных коэффициентов,
полученные косвенным методом наименьших квадратов и оценки, полученные
двухшаговым методом наименьших квадратов будут одинаковыми [8], это говорит о
том, что двухшаговый метод наименьших квадратов применим к любой (кроме
неидентифицируемой) системе одновременных эконометрических уравнений. Несмотря
на это, все же для решения идентифицированной системы применяется косвенный
МНК, а для решения сверхидентифицированных - двухшаговый МНК. Это связано,
прежде всего, с тем, что косвенный МНК проще в реализации и не требует
нахождения теоретических значений эндогенных переменных. Поэтому в какой-то
степени «плохим примером» для двухшагового МНК можно считать любую точно
идентифицируемую систему одновременных уравнений.
2.2.1
Постановка задачи
Имеются данные за 1990-1994 гг. (табл. 2.3)
Таблица 2.3 - Данные для примера
Задание:
Построить модель вида
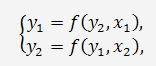
рассчитав соответствующие структурные коэффициенты.
2.2.2
Решение
Система одновременных уравнений с двумя эндогенными (зависимыми) и двумя
экзогенными (независимыми) переменными имеет вид
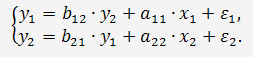
В каждом уравнении две эндогенные и одна отсутствующая экзогенная
переменная из имеющихся в системе. Для каждого уравнения данной системы
действует счетное правило 2 = 1 + 1. Это означает, что каждое уравнение и
система в целом идентифицированы. для определения параметров такой системы
применяется косвенный МНК.
С этой целью структурная форма модели преобразуется в приведенную форму:
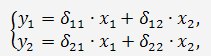
в которой коэффициенты при х определяются методом наименьших квадратов.
Для нахождения значений 
и запишем систему нормальных уравнений:
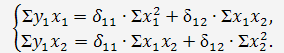
При ее решении предполагается, что х и у выражены через отклонения от
средних уровней, т.е. матрица исходных данных составит:
Таблица
Применительно к ней необходимые суммы оказываются следующими:
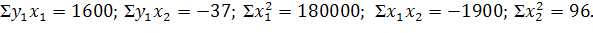
Система нормальных уравнений составит:
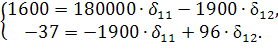
Решая ее, получим: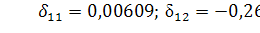 
Итак, имеем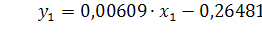 
Аналогично строим систему норм. уравнений для определения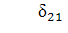 
:
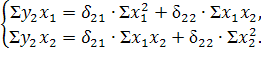
Следовательно,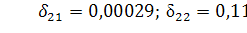 
Приведенная форма модели имеет вид:
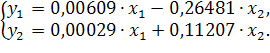
Из приведенной формы модели определяем коэффициенты структурной модели:
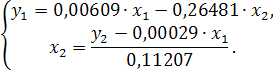
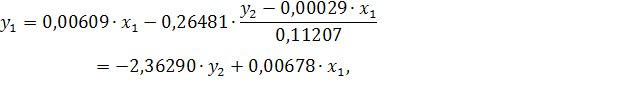
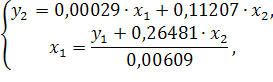
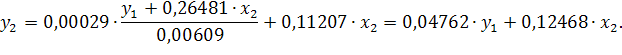
Итак, структурная форма модели имеет вид:
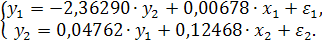
Заключение
В результате проведенной работы были углублены знания в области
эконометрики и численных методов, изучены модификации метода наименьших
квадратов, в частности, косвенный, двухшаговый и трехшаговый методы наименьших
квадратов. Подробно рассмотрен двухшаговый метод наименьших квадратов и
приведен пример для этого метода.
По типу построения системы эконометрических уравнений могут быть трех
видов: системы независимых уравнений, системы рекурсивных уравнений и системы
взаимозависимых уравнений. Последние наиболее часто встречаются на практике, и
их решению была посвящена данная работа.
В ходе работы рассмотрены основные проблемы в решении систем
эконометрических уравнений, такие как проблема идентификации и проблема
перехода от структурной формы модели к приведенной форме. Установлено, что
системы одновременных уравнений могут быть точно идентифицируемыми, для которых
коэффициенты приведенной формы модели могут быть определены однозначно,
сверхидентифицируемыми и неидентифицируемыми, коэффициенты структурной модели
которых нельзя однозначно оценить.
Для оценки коэффициентов структурной модели точно идентифицируемой
системы одновременных уравнений применяется косвенный метод наименьших
квадратов, для сверхидентифицируемой - двухшаговый МНК, трехшаговый и другие.
Список
используемой литературы
1. Регрессионный анализ. [Электронный ресурс] URL:
http://ru.wikipedia.org/wiki/ Регрессионный_анализ (Дата обращения: 02.05.14)
. Магнус Я.Р., Катышев П.К., Пересецкий А.А. / Эконометрика.
Начальный курс: Учеб. - 6-е изд., перераб. и доп. - М.: Дело, 2004. - 576 с.
. Шанченко, Н. И. / Эконометрика: лабораторный практикум: учебное
пособие - Ульяновск: УлГТУ, 2011. - 117 с.
. Эконометрика: учебник / И.И. Елисеева, СВ. Курышева, Т.В.
Костеева и др; под ред. И.И. Елисеевой. - 2-е изд., перераб. и доп. - М.:
Финансы и статистика, 2007. - 576 с: ил.
. Практикум по эконометрике: Учеб. пособие / И. И. Елисеева, С.
В. Курышева, Н. М. Гордеенко и др.; Под ред. И. И. Елисеевой. - М.: Финансы и
статистика, 2004. - 192 с.: ил.
. Прикладная статистика. Основы эконометрики: Учебник для вузов:
В 2 т. 2-е изд., испр. - Т. 2: Айвазян С А. Основы эконометрики. - М.:
ЮНИТИ-ДАНА, 2001. - 432 с.
. Эконометрика: Учебник / Н.П.Тихомиров, Е.Ю.Дорохина - М.:
Издательство «Экзамен», 2003. - 512 с.
. Структурная и приведённая формы системы одновременных
уравнений. Идентификация модели. [Электронный ресурс] URL:
http://www.e-reading.ws/chapter.php/1002275/88/
Yakovleva_Angelina_-_Otvety_na_ekzamenacionnye_bilety_po_ekonometrike.html
(Дата обращения: 05.05.14).
. Эконометрика: Учебник для вузов / Под ред. проф.Н.Ш. Кремера. -
М.: ЮНИТИ-ДАНА, 2002. - 311 с.
. Доугерти К. / Введение в эконометрику: Пер. с англ. - М.:
ИНФРА-М, 1999. - XIV, 400 с.
. Волков Е. А. Численные методы: Учеб. пособие для вузов.- 2-е
изд., испр. - М: Наука. Гл. ред. физ.-мат. лит., 1987.- 248 с.
. Метод наименьших квадратов. [Электронный ресурс] URL:
http://www.uchites.ru/ files/nummethod_book_chapter3-3.pdf (Дата обращения:
11.05.14).
. Калиткин Н.Н. / Численные методы: учебник для вузов - М.:
Наука, 1978. - 512 с.
14.