Теория электромагнитного поля
Контрольная
работа
Теория
электромагнитного поля
Москва
2015
1. Задача 1
Определить частичные емкости С11, С22, С12 на
метр длины двухпроводной бортовой проводки. Расположение проводов показано на
рис. 1. Относительная диэлектрическая проницаемость среды, окружающей провод, e=
1, l1= 10 см=10*10-2 м, l2=15 см= 15*10-2м, h=4см=4*10-2 м, d1=0,4 см=4*10-3 м
d2=0,3 см=3*10-3 м.
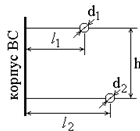
Рис. 1
Данную задачу необходимо рассматривать, как
электростатическое поле системы заряженных тел, расположенных вблизи проводящей
плоскости, используя систему уравнений первой группой формул Максвелла, т.е.
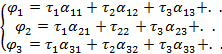
Где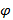 
потенциал
провода, 
-
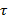количество заряда на проводе,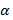 
- потенциальный
коэффициент, который находиться по формуле
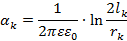
Где l - расстояние между бортовым проводом и
корпусом воздушного судна, r-радиус провода.
Так как в рассматриваемом случае используется
двухпроводная линия, то система уравнений будет выглядить следующим образом.
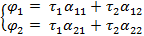
Далее
, 
,
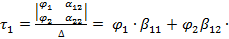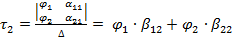где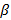 
емкостной
коэффициент, имеющий обратную размерность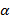 
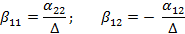
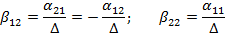
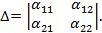
Таким образом,
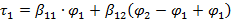
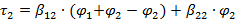
при условии что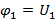 
,
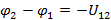получаем
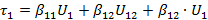
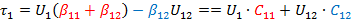
при условии что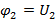 
,
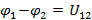
получаем
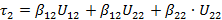
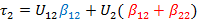
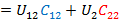
Следовательно, для двухпроводной линии
;
;
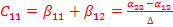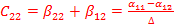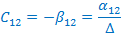
Найдем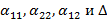 
.
При этом учитываем, что электрическая постоянная 
.
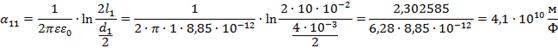
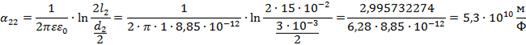
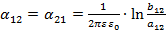Чтобы определить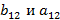 
воспользуемся
рисунком 2.
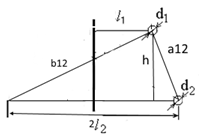
Рис 2.
Определим расстояние между проводами:
,
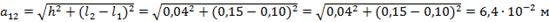а также расстояние первого провода до
зеркального изображения второго провода.
.
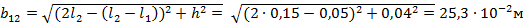Подставляем полученные результаты
;
;
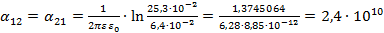
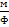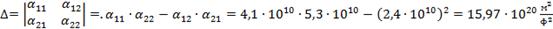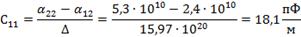
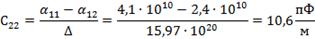
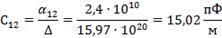
. Задача 2
Цилиндрический конденсатор заполнен двухслойным
диэлектриком. Относительные диэлектрические проницаемости слоев eа=1
и eb=2.
Геометрические размеры конденсатора r1=3мм=3*10-3 м, r2=6 мм=6*10-3 м, r3=9
мм=9*10-3 м показаны на рис. 3. Определить емкость конденсатора на один метр
длины.
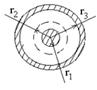
Рис. 3
Для решения задачи воспользуемся теоремой
Гаусса. В качестве поверхности интегрирования возьмем замкнутую цилиндрическую
поверхность длиной l, линейная плотность заряда 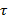и
радиусом r.
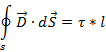
Из-за цилиндрической симметрии, т.к. вектор
электрического смещения на этой поверхности не изменяется по величине и
направлен по радиусу, то уравнение представленное выше можно представить
следующим образом:
Откуда
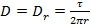
Напряженность поля будет при этом равна:
) В первом слое:
;
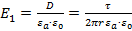) Во втором слое:
;
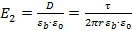электростатический поле конденсатор
напряженность
Разность потенциалов между электродами
определяется при помощи выражений напряженности, которое в общем виде будет
иметь следующий вид:
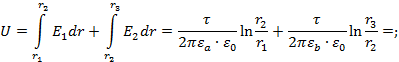
Емкость конденсатора на единицу его длины будет
равна
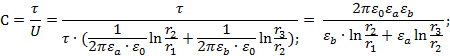
Проверка:
Отметим, что емкость цилиндрического
конденсатора с двухслойным диэлектриком можно определить и по такой формуле
;
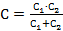Где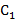 
-
емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами
обкладок 
и
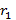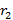и
диэлектрической проницаемостью диэлектрика, равной диэлектрической
проницаемости первого слоя;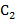 
- емкость
цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок 
и
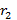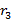и
диэлектрической проницаемостью диэлектрика, равной диэлектрической
проницаемости второго слоя;
;
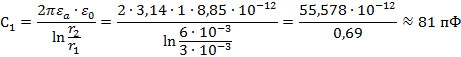
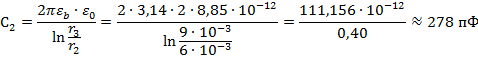
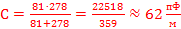. Задача 3
Построить зависимость потенциала и напряженности
в электрическом поле, образованном заряженным облаком над землей, если задана
объемная плотность зарядов облака r, высота облака над
землей h, толщина облака b. Землю считать проводящей средой, воздух и облако
имеют диэлектрическую проницаемость e=1. Выше облака
электрическая напряженность E=0.
r=1,5*10-11 Кл/м3, b=150 м, h=2000 м
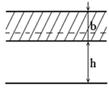
Данная задача представляется как решение
соединения двух плоских конденсаторов.
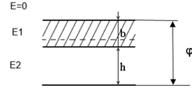
Положим, что разность потенциалов между верхней
частью облака и землей равна U. При этом условии в каждом слое поле будет
равномерным. В силу того, что нормальная составляющая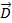 
,
непрерывна имеем 
.
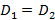Следовательно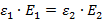 
,
т.к по условию задачи 
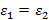, то 
=
.
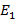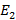Разность потенциалов будем искать из следующего
уравнения:
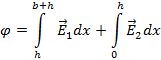
Теперь определим напряженность электрического
поля внутри облачного слоя, равномерно заряженного по объему плотностью r.
Данная система обладает зеркальной симметрией относительно плоскости,
параллельной образующим слоя, а точки любой плоскости слоя, параллельной
плоскости симметрии, находятся в одинаковых физических условиях. Следовательно,
напряженность электрического поля должна быть одинакова в этих точках как по
величине, так и по направлению. Согласно этим утверждениям можно сделать вывод,
что поток вектора напряженности электрического поля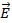 
через
замкнутую поверхность (S ) произвольной формы пропорционален суммарному
алгебраическому заряду (qs), находящемуся внутри данной поверхности, т.е.
используем теорему Гаусса
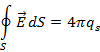
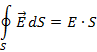
Следовательно, заряд, содержащийся внутри
облака, будет определяться выражением
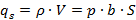
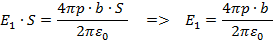
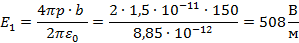
Учитывая, что напряженность выше облака равна
нулю, то потенциал в толще облака будет прирастать до величины
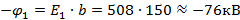
Значит, потенциал в облаке от верхней границе к
нижней будет изменяться;
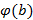- 0 В÷
-76 кВ
Площади взаимодействия поверхности земли и
облака, как аналог плоского конденсатора одинаковы, поэтому сам воздух
представляется как однородный диэлектрический слой, с одинаковой площадью
пластин, а значит земля, по условию задачи являясь проводящей средой, под облаком
имеет положительный заряд с потенциалом
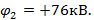
Соответственно потенциал между облаком и землей
буде прирастать на U=152кВ.
Построим графики
(l) E=0 l>b+h=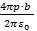
b+h >l ≥ h=
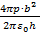h> l>0
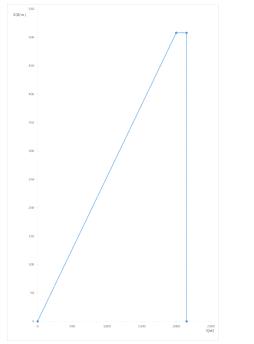
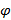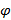(l) =0
l>b+h
=
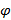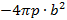b+h >l ≥ h
h> l>0
