Статистический анализ рисковых активов. Нелинейные модели
Контрольная
работа
Статистический
анализ рисковых активов. Нелинейные модели
Содержание
1.
Условно-гауссовские модели финансовых индексов
.
Авторегрессионая модель условной неоднородности (ARCH)
. Модель
GARCH
. Модели
EGARCH, TGARCH, HARCH
. Модель
стохастической волатильности
. Оценка
волатильности
. Устойчивые
распределения
.
Условно-устойчивые распределения
. Безгранично
делимые распределения
. Нелинейные
хаотические модели
Литература
1. Условно-гауссовские модели финансовых индексов
Рассмотрим следующую модель эволюции стоимости рискового актива (акции).
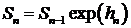 ,
, 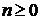 . (1)
. (1)
Величины 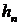 принято считать случайными. Наиболее привлекательным с точки
зрения анализа и развитой статистики является гауссовский закон совместного
распределения величин
принято считать случайными. Наиболее привлекательным с точки
зрения анализа и развитой статистики является гауссовский закон совместного
распределения величин 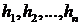 . Гауссовский закон совместного распределения приводит к
линейным моделям временных рядов таких как скользящее среднее авто-регрессия,
которые подробно рассмотрены в [1]. Однако реальные данные для многих
финансовых временных рядов показывают, что линейные модели не всегда адекватно
отражают истинную картину поведения цен.
. Гауссовский закон совместного распределения приводит к
линейным моделям временных рядов таких как скользящее среднее авто-регрессия,
которые подробно рассмотрены в [1]. Однако реальные данные для многих
финансовых временных рядов показывают, что линейные модели не всегда адекватно
отражают истинную картину поведения цен.
Если иметь ввиду разложение Дуба [2], в котором привлекаются условные
математические ожидания 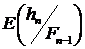 , вполне естественным является предположение о том, что
условные распределения являются гауссовскими:
, вполне естественным является предположение о том, что
условные распределения являются гауссовскими:
финансовый рисковый актив цена
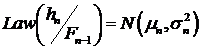 . (2)
. (2)
В (2) 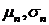 - предсказуемые случайные величины. Из представления (2)
следует, что существует условное математическое ожидание и условная дисперсия
- предсказуемые случайные величины. Из представления (2)
следует, что существует условное математическое ожидание и условная дисперсия
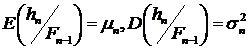 . (3)
. (3)
Безусловный закон распределения 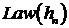 является смесью гауссовских законов
и получается интегрированием по распределению
является смесью гауссовских законов
и получается интегрированием по распределению 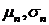 , что позволяет говорить о
разнообразии этого класса распределений.
, что позволяет говорить о
разнообразии этого класса распределений.
Рассмотрим последовательность
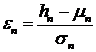 . (4)
. (4)
Эта последовательность также является условно-гауссовской
последовательностью со стандартным нормальным распределением  . Отсюда следует, что
. Отсюда следует, что 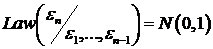 , поэтому последовательность
, поэтому последовательность 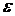 - последовательность независимых
стандартных нормальных случайных величин. Из этого рассуждения следует, что
условно-гауссовская последовательность
- последовательность независимых
стандартных нормальных случайных величин. Из этого рассуждения следует, что
условно-гауссовская последовательность  представима в виде
представима в виде
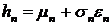 , (5)
, (5)
где 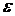 последовательность независимых стандартных нормальных
случайных величин - белый шум.
последовательность независимых стандартных нормальных
случайных величин - белый шум.
Условно-гауссовские последовательности позволяют достаточно просто решать
задачи прогноза цены. Так условный точечный прогноз с минимальной дисперсией
ошибки для 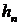 -
- 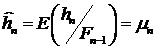 . Условный доверительный интервал для
. Условный доверительный интервал для 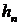 -
- 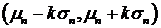 , где
, где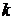 - решение уравнения
- решение уравнения 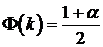 ,
,  - условная доверительная вероятность,
а
- условная доверительная вероятность,
а 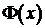 - функция стандартного нормального
распределения. Отсюда для цены условный точечный прогноз
- функция стандартного нормального
распределения. Отсюда для цены условный точечный прогноз
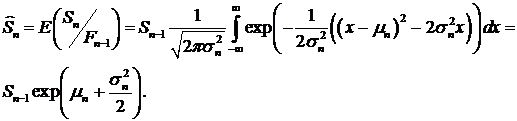 (6)
(6)
Условный доверительный интервал с условной доверительной вероятностью 
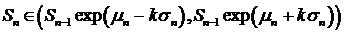 . (7)
. (7)
Ясно, что более подробное описание условно-гауссовских
последовательностей зависит от конкретизации структуры величин 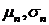 . Именно этому и посвящено изложение,
причем внимание уделяется нелинейным моделям.
. Именно этому и посвящено изложение,
причем внимание уделяется нелинейным моделям.
. Авторегрессионая модель условной неоднородности (ARCH)
Здесь и далее мы будем предполагать, что белый шум 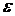 является единственным источником
случайности, то есть фильтрация
является единственным источником
случайности, то есть фильтрация 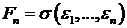 ,
, 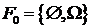 . Модель ARCH была впервые введена в работе Р.Энгля [3],
который поставил перед собой цель объяснить возникновение кластерности
(группировки) больших или малых значений
. Модель ARCH была впервые введена в работе Р.Энгля [3],
который поставил перед собой цель объяснить возникновение кластерности
(группировки) больших или малых значений  . В этой модели
. В этой модели
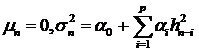 , (8)
, (8)
с 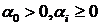 , и начальными значениями
, и начальными значениями 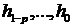 , которые могут быть случайными
величинами, независящими от
, которые могут быть случайными
величинами, независящими от 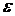 , но обычно считают их постоянными. Из (8) видим, что
волатильность
, но обычно считают их постоянными. Из (8) видим, что
волатильность 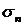 является (предсказуемой) функцией от
является (предсказуемой) функцией от 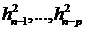 . При этом в силу особенности модели
если
. При этом в силу особенности модели
если 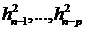 были большими, то это приводит к
большому значению
были большими, то это приводит к
большому значению 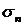 , что в свою очередь приводит к большому значению
, что в свою очередь приводит к большому значению 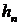 . Если
. Если 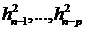 были малыми, то большое значение
были малыми, то большое значение 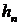 может появиться только за счет
большого значения
может появиться только за счет
большого значения 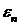 . Таким образом, становится понятным, почему ARCH-модель
объясняет явления кластерности. Это в свою очередь оправдывает название модели
- Авторегрессионая модель условной неоднородности, в которой волатильность
ведет себя весьма неоднородно в зависимости от прошлых значений
. Таким образом, становится понятным, почему ARCH-модель
объясняет явления кластерности. Это в свою очередь оправдывает название модели
- Авторегрессионая модель условной неоднородности, в которой волатильность
ведет себя весьма неоднородно в зависимости от прошлых значений  .
.
Отметим, что модель (8) может быть переписана в виде
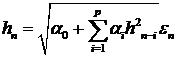 . (9)
. (9)
На рисунке 1. представлена машинная реализация ARCH-модели второго
порядка.
Остановимся на рассмотрении ряда статистических свойств
последовательности  , которая описывается ARCH-моделью первого порядка.
Использование модели первого порядка, обусловлено желанием упростить изложение.
, которая описывается ARCH-моделью первого порядка.
Использование модели первого порядка, обусловлено желанием упростить изложение.
Для модели первого порядка формула (9) приобретает вид
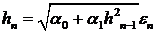 . (10)
. (10)
Прежде всего, определим математическое ожидание и дисперсию 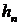 . Математическое ожидание
. Математическое ожидание
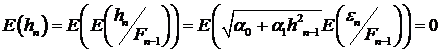 , (11)
, (11)
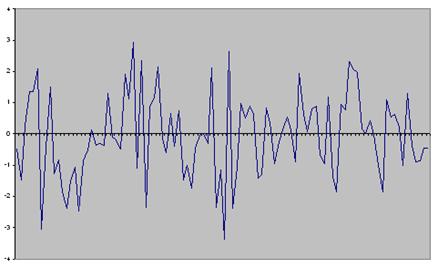
Рис. 1. График компьютерной реализации последовательности  , подчиняющейся ARCH-модели второго
порядка с
, подчиняющейся ARCH-модели второго
порядка с  .
.
Дисперсия
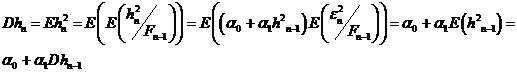 ((12)
((12)
В предположении 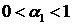 рекуррентное уравнение (12) имеет единственное стационарное
решение (решение независящее от
рекуррентное уравнение (12) имеет единственное стационарное
решение (решение независящее от 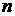 )
)
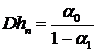 . (13)
. (13)
Вычислим ковариацию - 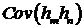 . Пусть
. Пусть 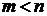 . Ковариация
. Ковариация
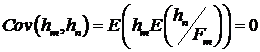 . (14)
. (14)
Однако свойство (14) не означает, что случайные величины независимы,
поскольку совместный закон распределения 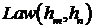 не является гауссовским. Чтобы
установить факт зависимости рассмотрим корреляционную зависимость между
не является гауссовским. Чтобы
установить факт зависимости рассмотрим корреляционную зависимость между 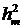 и
и 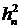 . В стационарном случае ковариация
. В стационарном случае ковариация
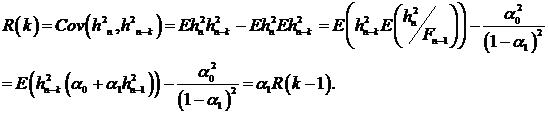
Отсюда 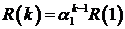 . Вычислим
. Вычислим 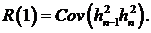 Непосредственно вычисляем
Непосредственно вычисляем
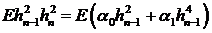 .
.
Далее
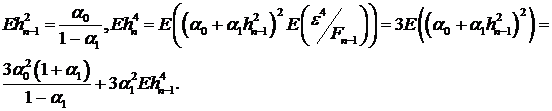
При условии, что 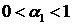 и
и 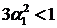 , единственное стационарное решение последнего рекуррентного
уравнения -
, единственное стационарное решение последнего рекуррентного
уравнения - 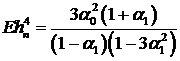 . Отсюда
. Отсюда 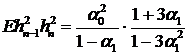 . Следовательно
. Следовательно 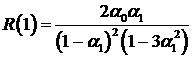 . Отсюда
. Отсюда
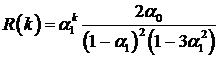 . (15)
. (15)
Нетрудно показать, что дисперсия 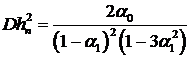 . Теперь можно определить
автокорреляционную функцию
. Теперь можно определить
автокорреляционную функцию 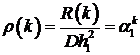
Покажем, что ARCH - модель тесным образом связана с авторегрессионной
моделью. Действительно, пусть имеется ARCH - модель (9), из которой следует,
что 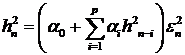 . Обозначим через
. Обозначим через 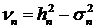 . Поскольку
. Поскольку 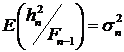 , то последовательность
, то последовательность 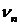 является мартингал-разностью. Тогда
является мартингал-разностью. Тогда
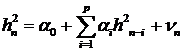 . (16)
. (16)
Таким образом, величины 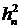 удовлетворяют авторегрессионной модели с шумом
удовлетворяют авторегрессионной модели с шумом 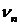 , являющимся мартингал-разностью.
, являющимся мартингал-разностью.
Для модели первого порядка
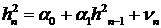 . (17)
. (17)
Рассмотрим авторегрессионную модель первого порядка со случайными
коэффициентами
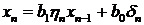 , (18)
, (18)
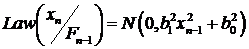 . (19)
. (19)
Напомним, что для ARCH - модели 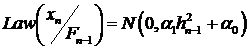 . Сопоставив с
. Сопоставив с 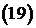 , получим, что
, получим, что 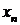 устроены точно также, что и
устроены точно также, что и 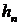 при условии, что
при условии, что 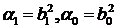 .
.
Для ARCH - модели 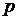 -го порядка эквивалентная с точки зрения распределения
авторегрессионная модель со случайными коэффициентами модель:
-го порядка эквивалентная с точки зрения распределения
авторегрессионная модель со случайными коэффициентами модель:
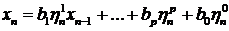 , (20)
, (20)
где 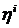 - независимые стандартные гауссовские последовательности,
при
- независимые стандартные гауссовские последовательности,
при 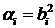 .
.
Рассмотрим несколько более сложную модель:
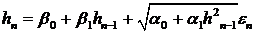 , (21)
, (21)
в которой сочетается ARCH и AR - модели.
На рисунке 2. представлена компьютерная реализация модели.
Условно-гауссовский характер модели позволяет представить плотность
совместного распределения 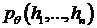 величин
величин  при
при 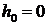
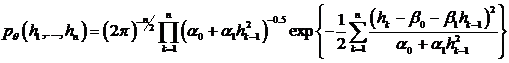 . (22)
. (22)
Применим метод максимального правдоподобия для получения оценок
параметров аторегрессионной составляющей модели.
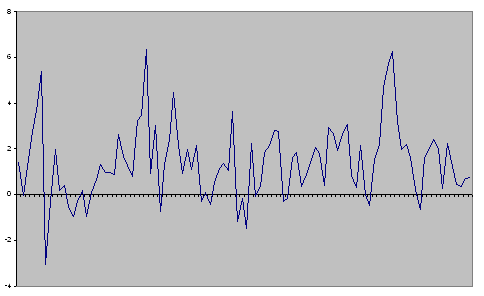
Рис. 2. График компьютерной реализации последовательности  , подчиняющейся ARCH, AR - модели
второго порядка с
, подчиняющейся ARCH, AR - модели
второго порядка с 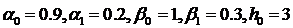 .
.
Не вдаваясь подробно в сущность метода максимального правдоподобия,
отметим, что в нашем случае для получения оценок максимального правдоподобия
требуется найти
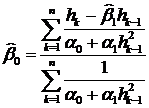 ,
, 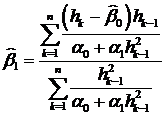 . (23)
. (23)
Рассмотрим вопрос о предсказании будущего движения цен, считая, что
последовательность  подчинена ARCH - модели.
подчинена ARCH - модели.
Поскольку последовательность  является мартингал разностью, то
оптимальная в среднеквадратическом смысле оценка
является мартингал разностью, то
оптимальная в среднеквадратическом смысле оценка 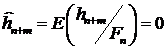 . Тривиальность этой оценки говорит о
том, что ARCH - модель непригодна для получения точечных оценок. Поэтому
целесообразно говорить об оценках нелинейных функций от
. Тривиальность этой оценки говорит о
том, что ARCH - модель непригодна для получения точечных оценок. Поэтому
целесообразно говорить об оценках нелинейных функций от  -
- 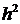 или
или 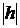 .
.
Рассмотрим оценку 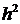 с целью в дальнейшем получить доверительный интервал для
цены. Вычислим
с целью в дальнейшем получить доверительный интервал для
цены. Вычислим
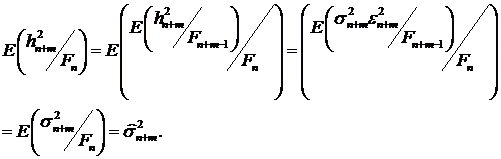
Отсюда следует, что оценка 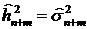 . По индукции получаем
. По индукции получаем
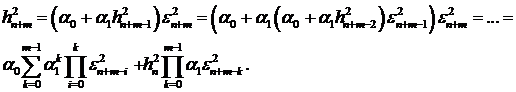
Отсюда
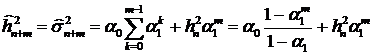 . (24)
. (24)
Если 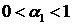 , то при
, то при 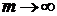 оценки сходятся с вероятностью единица к значению
оценки сходятся с вероятностью единица к значению 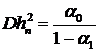 .
.
Остановимся на прогнозировании цены. Если  подчиняется ARCH - модели, то
одношаговый точечный прогноз для цены:
подчиняется ARCH - модели, то
одношаговый точечный прогноз для цены:
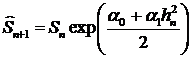 . (25)
. (25)
Парадоксальность ситуации заключается в том, что при любых
обстоятельствах точеный одношаговый прогноз предвещает рост цены.
Одношаговый доверительный интервал
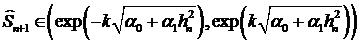 . (26)
. (26)
Рассмотрим многошаговый прогноз цены, а именно рассмотрим построение
доверительного интервала в первом приближении.
Поскольку
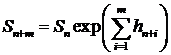 , (27)
, (27)
то нам необходимо найти условное математическое ожидание
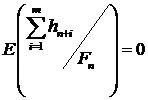 (28)
(28)
и условную дисперсию
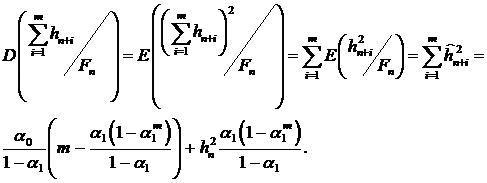 (29)
(29)
При вычислении дисперсии использовалось некоррелированность 
Таким
образом, условный доверительный интервал:
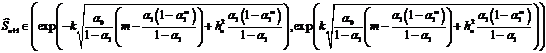 (30)
(30)
Отметим, что использование гауссовского закона при выборе 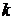 для заданной доверительной
вероятности необоснованно, поскольку
для заданной доверительной
вероятности необоснованно, поскольку 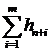 не является нормально распределенной
случайной величиной, и вопрос о том, насколько истинные уровни надежности
согласуются с расчетами, использующими гауссовский закон распределения, требует
дополнительного исследования относительности точности нормальной аппроксимации
суммы
не является нормально распределенной
случайной величиной, и вопрос о том, насколько истинные уровни надежности
согласуются с расчетами, использующими гауссовский закон распределения, требует
дополнительного исследования относительности точности нормальной аппроксимации
суммы 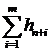 .
.
. Модель GARCH
Успех условно-гауссовской модели ARCH при описании таких эффектов
поведения плотности распределения индексов, как кластерность, вытянутость,
тяжелые хвосты, породил много ее обобщений, преследующих цель описать другие
эффекты, которые обнаруживается при статистическом анализе реальных данных.
Одним из первых обобщений модели ARCH была модель, предложенная в 1986
Т.Боллерслевом [4] - модель GARCH:
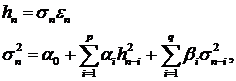 (31)
(31)
где 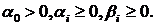
На рисунке 3 представлена компьютерная реализация модели. Как видно из
(31) в модели волатильность зависит предсказуемым образом не только от  но и от
но и от 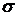 .
.
Основное достоинство модели (экспериментальный факт) заключается в том,
что при небольших значениях 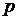 и
и 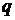 удается хорошо "подогнать модель".
удается хорошо "подогнать модель".
Так же как и в предыдущем параграфе рассмотрим простейший вариант модели
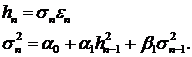 (32)
(32)
Приведем ряд простых формул.
Прежде всего 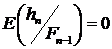 , то есть по-прежнему
, то есть по-прежнему  - квадратично интегрируемый
мартингал-разность. Далее, так как
- квадратично интегрируемый
мартингал-разность. Далее, так как 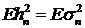 , то для дисперсии получается
рекуррентное уравнение
, то для дисперсии получается
рекуррентное уравнение
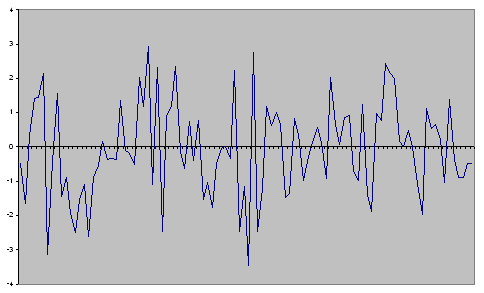
Рис.3 График машинной реализации модели GARCH (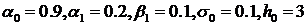 ).
).
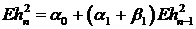 , которое при
, которое при 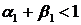 имеет единственное стационарное решение:
имеет единственное стационарное решение:
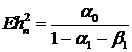 . (33)
. (33)
Для
автокорреляционной функции справедлива формула:
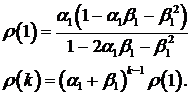 (34)
(34)
Для модели GARCH формула (24) приобретает вид:
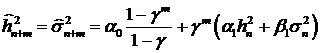 , (35)
, (35)
где 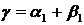 .
.
Одношаговый прогноз цены (формулы (25) и (26)) обобщаются следующим
образом
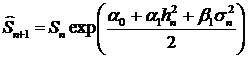 , (36)
, (36)
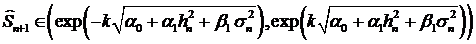 . (37)
. (37)
Интервальный прогноз цены на 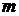 шагов приобретает вид:
шагов приобретает вид:
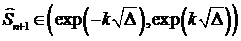 , (38)
, (38)
где 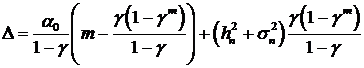 .
.
. Модели EGARCH, TGARCH, HARCH
Ф. Блэк в 1976 отметил отрицательную коррелированность между финансовым
индексом 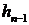 и волатильностью
и волатильностью 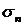 :
: 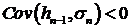 . Этот эффект, получивший название
эффекта рычага, приводит к тому, что волатильность рынка стремится к
возрастанию после падения цен. Это явление невозможно объяснить в рамках
моделей ARCH и GARCH, поскольку в этих моделях волатильность зависит от
квадратов, предшествующих финансовых индексов и не зависит от их знака. Так
финансовый индекс
. Этот эффект, получивший название
эффекта рычага, приводит к тому, что волатильность рынка стремится к
возрастанию после падения цен. Это явление невозможно объяснить в рамках
моделей ARCH и GARCH, поскольку в этих моделях волатильность зависит от
квадратов, предшествующих финансовых индексов и не зависит от их знака. Так
финансовый индекс 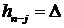 вносит тот же вклад в волатильность, что
вносит тот же вклад в волатильность, что 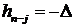 . Для объяснения этого эффекта Д.
Нельсон в 1990 году предложил модель (экспоненциальную ARCH), в которой эффект
рычага реализовался в том, что вместо
. Для объяснения этого эффекта Д.
Нельсон в 1990 году предложил модель (экспоненциальную ARCH), в которой эффект
рычага реализовался в том, что вместо 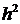 использовалась линейная комбинация
использовалась линейная комбинация 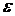 и
и 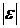 . Следовало также учесть, что в этом
случае регрессия может принимать отрицательные значения.
. Следовало также учесть, что в этом
случае регрессия может принимать отрицательные значения.
Модель EGARCH описывается уравнениями:
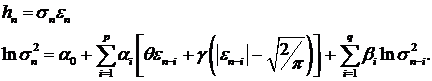 (39)
(39)
Компьютерная реализация модели представлена на рисунке 4. Отметим, что 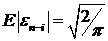 . Поскольку знаки у
. Поскольку знаки у  и
и 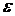 совпадают, то если
совпадают, то если 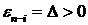 , то соответствующий вклад в
, то соответствующий вклад в 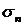 определяется величиной
определяется величиной 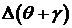 . Если
. Если 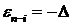 , то соответствующий вклад в
, то соответствующий вклад в 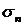 определяется величиной
определяется величиной 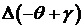 .
.
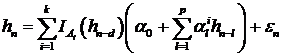 , (40)
, (40)
где 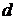 - параметр запаздывания,
- параметр запаздывания, 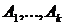 образуют разбиение
образуют разбиение  .
.
Например,
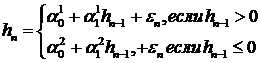 (41)
(41)
Таким образом, по определению последовательность  описывается TGARCH - моделью, если
описывается TGARCH - моделью, если
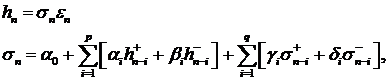 (42)
(42)
где, как обычно, 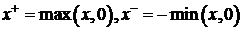 . Отметим, что в этой модели не предполагается
неотрицательность волатильностей, однако
. Отметим, что в этой модели не предполагается
неотрицательность волатильностей, однако  - условная дисперсия по-прежнему -
положительна.
- условная дисперсия по-прежнему -
положительна.
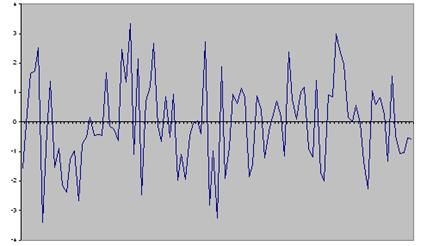
Рис. 4. График компьютерной реализации модели EGARCH c параметрами 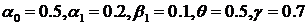
Поскольку
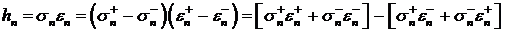 , то
, то 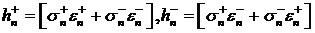 ,
,
то Последние соотношения позволяют представить (42) в несколько другом
виде
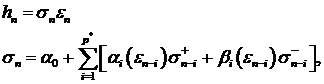 (43)
(43)
где 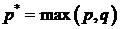 ,
, 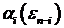 и
и 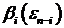 - линейные комбинации величин
- линейные комбинации величин 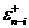 и
и 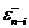 .
.
При 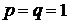 модель (43) приобретает вид:
модель (43) приобретает вид:
 (44)
(44)
где
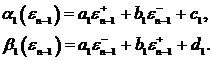 (45)
(45)
График машинной реализации модели (44),(45) представлен на рисунке 5.
Отметим, что при изучении модели (43) возникает техническая сложность,
поскольку последовательность 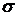 не обладает марковским свойством. В модели (44), (45), если
не обладает марковским свойством. В модели (44), (45), если 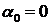 , то возможна факторизация:
, то возможна факторизация:
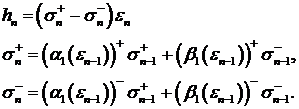 (46)
(46)
В модели (46) последовательность 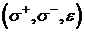 является марковской и для ее анализа
можно применять стандартные марковские методы.
является марковской и для ее анализа
можно применять стандартные марковские методы.
Пусть  . Рассмотрим вычисление
. Рассмотрим вычисление 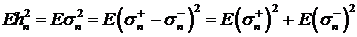 . Так как
. Так как
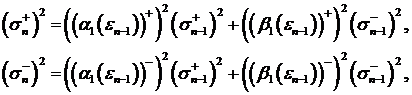 (47)
(47)
то
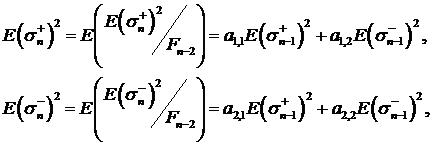 (48)
(48)
где 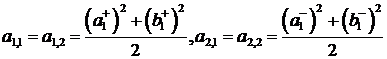 .
.
Отсюда и из (48)
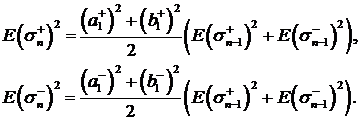 (49)
(49)
Тогда
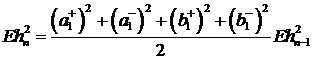 (50)
(50)
или
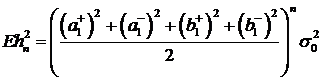 (51)
(51)
Рис. 5. График компьютерной реализации TGARCH - модели ( ).
).
В работе [5] изучалась новая модель HARCH в которой по сравнению с
моделями рассмотренными ранее характер убывания автокорреляционной функции
более медленный. То есть в модели HARCH присутствует эффект "долгой
памяти".
Согласно определению, модель HARCH описывается уравнениями:
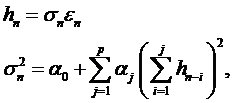 (52)
(52)
с 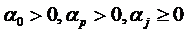 . В частности, для
. В частности, для 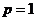
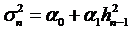 и HARCH совпадает с ARCH.
и HARCH совпадает с ARCH.
В случае 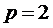
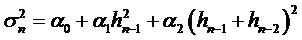 . (53)
. (53)
На рисунке 6 приведен график компьютерной реализации HARCH - модели.
Рис. 6. График машинной реализации модели HARCH (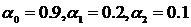 ).
).
Приведем некоторые свойства этой модели. Прежде всего отметим, что
наличие 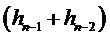 позволяет описать эффект рычага, о
котором упоминалась ранее. Отметим, что
позволяет описать эффект рычага, о
котором упоминалась ранее. Отметим, что 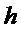 - мартингал разность. Вычислим
дисперсию
- мартингал разность. Вычислим
дисперсию 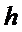
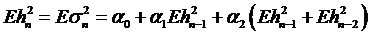 . (54)
. (54)
При условии 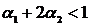 уравнение (54) имеет единственное стационарное решение:
уравнение (54) имеет единственное стационарное решение:
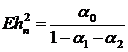 . (55)
. (55)
Найдем значение автокорреляционной функции 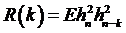 . Для
. Для 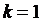
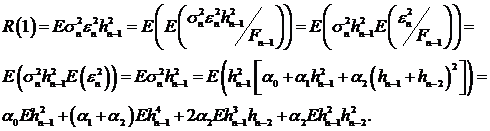
Далее
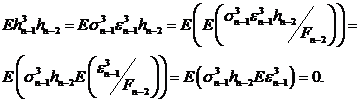
Отсюда
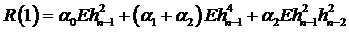 . (56)
. (56)
При условии, что 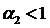 уравнение (56) имеет единственное стационарное решение:
уравнение (56) имеет единственное стационарное решение:
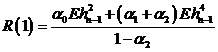 . (57)
. (57)
Вычислим
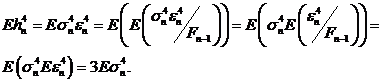
Далее из (53), используя 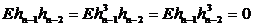 , находим стационарное решение при условии
, находим стационарное решение при условии 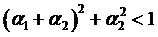
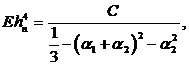 (58)
(58)
где
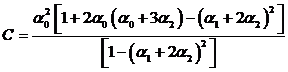 . (59)
. (59)
Далее,
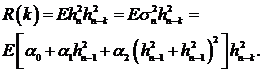
Отсюда
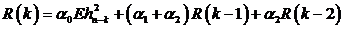 , (60)
, (60)
где 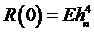 , а
, а 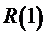 вычисляется по формуле (57).
вычисляется по формуле (57).
. Модель стохастической волатильности
Основным отличием этих моделей является наличие двух источников
случайности 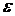 и
и 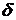 , определяющих поведение последовательности
, определяющих поведение последовательности 
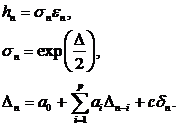 (61)
(61)
Обе последовательности будем предполагать независимыми стандартными
гауссовскимм. Выразив 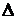 , мы можем представить модель (61) в виде
, мы можем представить модель (61) в виде
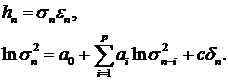 (62)
(62)
На рисунке 6 представлена компьютерная реализация модели.
Рис. 6. График компьютерной реализации модели стохастической
волатильности (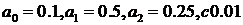 )
)
Обозначим через 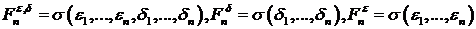 .
.
Ясно, что 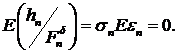 Далее
Далее 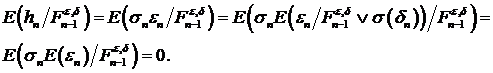
Отсюда следует, что величины  образуют мартингал разность
относительно потока
образуют мартингал разность
относительно потока 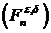 .
.
Далее
рассмотрим модель первого порядка
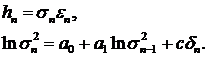 (63)
(63)
В предположении, что 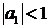 .
.
Вычислим 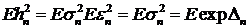 . Пусть величина
. Пусть величина 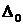 распределена по нормальному закону
распределена по нормальному закону 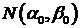 , тогда из (63) следует, что величина
, тогда из (63) следует, что величина
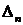 - распределена по нормальному закону
- распределена по нормальному закону
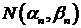 с параметрами, удовлетворяющими
разностным уравнениям
с параметрами, удовлетворяющими
разностным уравнениям
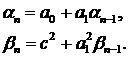 (64)
(64)
При 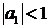 уравнения (64) имеют единственные стационарные решения:
уравнения (64) имеют единственные стационарные решения:
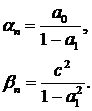 (65)
(65)
Пусть 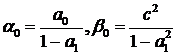 , тогда
, тогда 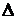 - стационарная последовательность и величина
- стационарная последовательность и величина 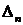 распределена по нормальному закону
распределена по нормальному закону 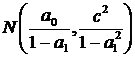 . Отсюда
. Отсюда
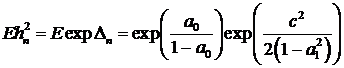 . (66)
. (66)
Вычислим 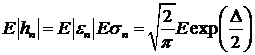 . Отсюда
. Отсюда
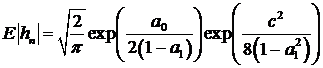 (67)
(67)
Рассмотрим теперь ковариационные свойства последовательностей  и
и 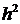 . Поскольку
. Поскольку  - квадратично интегрируемый
мартингал разность, то
- квадратично интегрируемый
мартингал разность, то
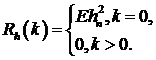 (68)
(68)
Вычислим
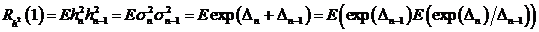 ,
,
Далее
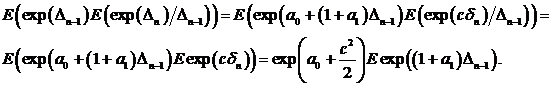
Далее
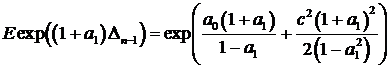 .
.
Отсюда
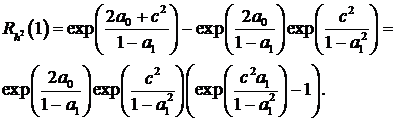 (68)
(68)
Отметим, в связи с формулой (68), что если 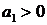 , то
, то 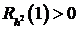 , если
, если 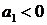 , то
, то 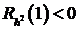 .
.
. Оценка волатильности
Во всех рассмотренных моделях ключевое место занимает волатильность.
Поэтому остановимся на оценках волатильности по результатам наблюдений
последовательности  . Допустим, что
. Допустим, что 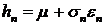 , тогда
, тогда 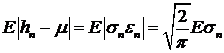 . Это равенство можно положить в
основу несмещенной оценки волатильности
. Это равенство можно положить в
основу несмещенной оценки волатильности
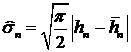 , (69)
, (69)
где 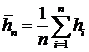 , если
, если 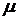 неизвестно и
неизвестно и
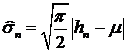 , (70)
, (70)
если 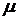 известно. Если
известно. Если 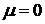 , то
, то
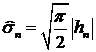 . (71)
. (71)
При 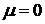 в качестве оценки можно было бы взять
в качестве оценки можно было бы взять
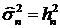 , (72)
, (72)
использовав то факт, что 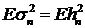 . Эта оценка будет несмещенной, однако, дисперсия ошибки
может быть большой. Действительно, для модели стохастической волатильности
. Эта оценка будет несмещенной, однако, дисперсия ошибки
может быть большой. Действительно, для модели стохастической волатильности
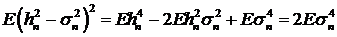 .
.
Для модели первого порядка
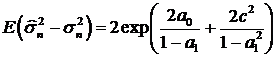 . (73)
. (73)
Естественно, использовать тот факт, что величины 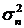 - коррелированны. Этот факт можно
использовать, применив технологию
- коррелированны. Этот факт можно
использовать, применив технологию 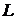 - статистик [6]
- статистик [6]
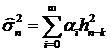 , (74)
, (74)
где 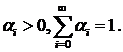 Отметим, что из
Отметим, что из 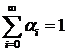 следует сходимость ряда в среднем
квадратичном.
следует сходимость ряда в среднем
квадратичном.
В частности при 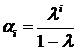 получается експоненциально-взвешенная оценка:
получается експоненциально-взвешенная оценка:
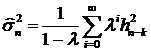 . (75)
. (75)
Отметим, что
формула (75) эквивалентна рекуррентной оценке
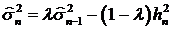 . (76)
. (76)
Основная задача заключается в оптимальном выборе весов.
Оперируя конкретной моделью наиболее естественным было бы получение
оптимальной в средне квадратичном смысле оценки волатильности или какой либо
функции от волатильности. Так, оперируя моделью стохастической волатильности
первого порядка, естественно попытаться найти оптимальную оценку 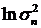 , исходя из уравнений:
, исходя из уравнений:
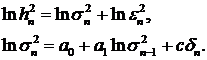 (77)
(77)
Введем обозначения 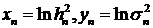 . В этих обозначениях система (77) приобретает вид
. В этих обозначениях система (77) приобретает вид
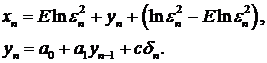 (78)
(78)
Рассмотрим случайную величину 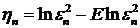 . Математическое ожидание и дисперсия
. Математическое ожидание и дисперсия
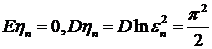 . Представим уравнения (78) в виде
. Представим уравнения (78) в виде
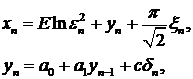 (79)
(79)
где 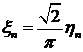 . Математическое ожидание и дисперсия
. Математическое ожидание и дисперсия 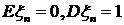 . Таким образом, уравнения (79)
задают линейную стохастическую систему, в которой величины
. Таким образом, уравнения (79)
задают линейную стохастическую систему, в которой величины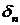 распределены по нормальному закону
распределены по нормальному закону 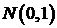 , а величины
, а величины 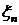 не являются гауссовскими. Это
обстоятельство препятствует непосредственному использованию теории линейной
фильтрации Калмана-Бьюси [7].
не являются гауссовскими. Это
обстоятельство препятствует непосредственному использованию теории линейной
фильтрации Калмана-Бьюси [7].
Тем не менее, чтобы получить линейный фильтр рассмотрим фильтр
Калмана-Бьюси, который будет оптимальным при условии гауссовости величин 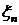 . Обозначим через
. Обозначим через 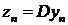 ,
, 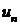 - наилучшая в среднеквадратичном
смысле линейная оценка
- наилучшая в среднеквадратичном
смысле линейная оценка 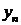 по наблюдаемым
по наблюдаемым 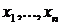 . В этих обозначениях фильтр
Калмана-Бьюси реализуется в уравнениях:
. В этих обозначениях фильтр
Калмана-Бьюси реализуется в уравнениях:
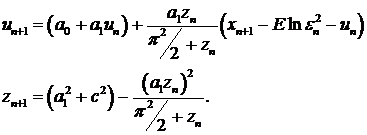 (80)
(80)
В (80) 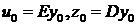
На рисунках 7 изображен график 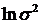 и
и  . Как видно из рисунка прогноз с
помощью линейного фильтра Калма-Бьюси является удовлетворительным прогнозом.
Отметим, что прогноз волатильности позволяет найти одношаговый интервальный
прогноз цены.
. Как видно из рисунка прогноз с
помощью линейного фильтра Калма-Бьюси является удовлетворительным прогнозом.
Отметим, что прогноз волатильности позволяет найти одношаговый интервальный
прогноз цены.
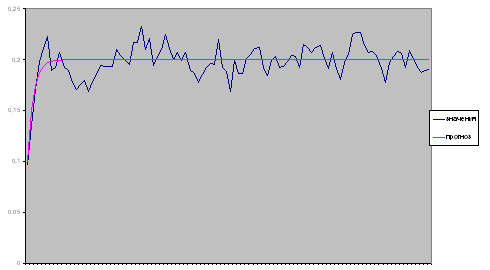
Рис. 7. График компьютерной реализации значений  и прогноза
и прогноза 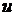 для модели стохастической
волатильности (
для модели стохастической
волатильности (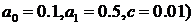 .
.
Отметим, что в том случае, когда в исходной модели известны априорные
распределения вероятностей для параметров, при оценке более эффективным
является байесовский подход, в котором используется апостериорное распределение
параметров модели.
До сих пор мы использовали в качестве исходного гауссовское
распределение. Однако тематика нелинейных моделей далеко не исчерпывается этим.
Интерес представляют также и другие распределения, обладающие свойствами
устойчивости и безграничной делимости.
. Устойчивые распределения
Устойчивым и безгранично делимым распределениям уделяется большое
внимание в литературе, посвященной моделированию поведения обменных курсов
валют и финансовых индексов.
Устойчивые и безгранично делимые распределения изучались в работах
П.Леви, Дж. Пойа, А.Я. Хинчина.
Остановимся на определении устойчивых распределений. Существует два
равносильных определения. Приведем одно из них
Определение. Случайная величина называется устойчивой, если для всякого 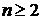 найдутся
найдутся 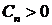 и
и 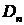 такие, что
такие, что
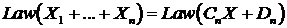 , (81)
, (81)
где 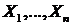 - независимые копии случайной величины
- независимые копии случайной величины 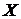 . Если в (81)
. Если в (81) 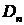 =0, т.е.
=0, т.е.
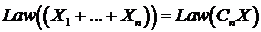 , (82)
, (82)
то случайная величина 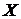 называется строго устойчивой.
называется строго устойчивой.
Замечательно,
что доказывается следующий факт
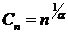 (83)
(83)
Приведем пример. Рассмотрим нормальный закон 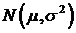 , тогда сумма
, тогда сумма 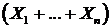 распределена по нормальному закону
распределена по нормальному закону 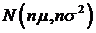 , точно также распределена случайная
величина
, точно также распределена случайная
величина 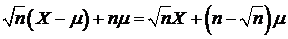 . Здесь
. Здесь 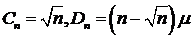 . Откуда следует, что гауссовский
закон является устойчивым законом с индексом устойчивости
. Откуда следует, что гауссовский
закон является устойчивым законом с индексом устойчивости 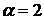 . Причем строго устойчивым, если
. Причем строго устойчивым, если 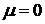 .
.
Для полноты картины следует отметить факт, характеризующий устойчивое
распределение как распределение бесконечных сумм независимых и одинаково
распределенных случайных величин.
Устойчивое распределение имеет область притяжения в том смысле, что
найдется последовательность независимых одинаково распределенных случайных
величин  , и последовательности положительных
чисел
, и последовательности положительных
чисел 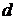 и вещественных чисел
и вещественных чисел 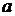 такие, что
такие, что
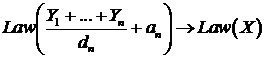 . (84)
. (84)
Рассмотрим характеристическую функцию распределения случайной величины 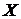
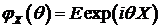 . (85)
. (85)
Характеристическая функция суммы 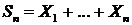 независимых копий
независимых копий 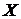
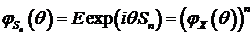 . (86)
. (86)
Сопоставим
(86) и (82) получим, что для строго устойчивого распределения
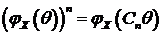 . (87)
. (87)
Таким образом, на языке характеристических функций распределение
называется строго устойчивым, если для любого 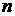 существует такое положительное число
существует такое положительное число
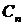 , что выполняется (87). Поскольку
, что выполняется (87). Поскольку 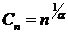 , то (87) приобретает вид:
, то (87) приобретает вид:
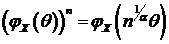 . (88)
. (88)
Рассмотрим
распределение Пуассона
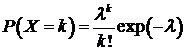 . (89)
. (89)
Характеристическая функция распределения Пуассона:
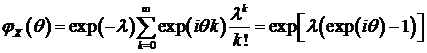 . (90)
. (90)
Отсюда 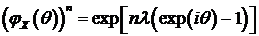 и распределение Пуассона не является устойчивым
распределением. Свойство строгой устойчивости связано еще с одним свойством
закона распределения. Напомним, что сверткой функций распределения называется
функция распределения
и распределение Пуассона не является устойчивым
распределением. Свойство строгой устойчивости связано еще с одним свойством
закона распределения. Напомним, что сверткой функций распределения называется
функция распределения 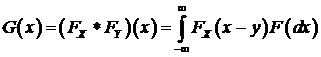 . Если функции распределения
. Если функции распределения 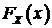 и
и 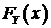 обладают плотностями
обладают плотностями 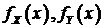 , то функция распределения
, то функция распределения 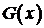 также обладает плотностью
также обладает плотностью 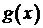 , причем
, причем 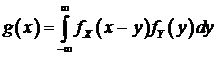 . При этом, если случайные величины
. При этом, если случайные величины 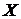 и
и 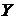 - независимые, то
- независимые, то 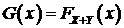 . Введем обозначение
. Введем обозначение 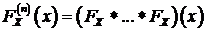 . В этом обозначении функция
распределения суммы
. В этом обозначении функция
распределения суммы 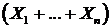 -
- 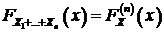 . Следовательно, функция распределения строго устойчивого
закона должна обладать свойством:
. Следовательно, функция распределения строго устойчивого
закона должна обладать свойством:
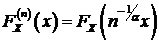 . (91)
. (91)
Если
существует плотность, то
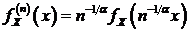 . (92)
. (92)
В этой связи рассмотрим распределение Коши:
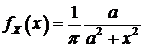 . (93)
. (93)
Непосредственным
интегрированием и индукцией нетрудно убедиться, что
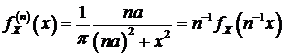 . (94)
. (94)
Отсюда следует, что распределение Коши строго устойчиво с индексом
устойчивости 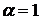 .
.
Отметим, что замечательный результат теории вероятностей (П. Леви, А.Я.
Хинчин) дает следующее представление характеристической функции устойчивой
случайной величины:
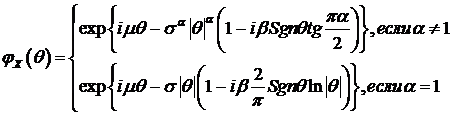 , (95)
, (95)
где 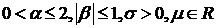 . Смысл параметров
. Смысл параметров 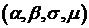 следующий:
следующий:
 - индекс устойчивости,
- индекс устойчивости,
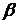 - параметр скошенности плотности распределения,
- параметр скошенности плотности распределения,
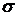 - параметр масштаба,
- параметр масштаба,
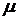 - параметр положения.
- параметр положения.
Параметр  определяет скорость убывания хвостов распределения.
определяет скорость убывания хвостов распределения.
Если 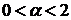 , то
, то
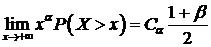 , (95)
, (95)
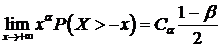 , (96)
, (96)
где
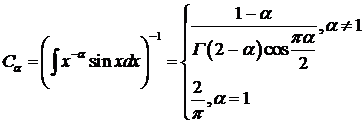 ,
,
а 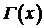 - гамма функция.
- гамма функция.
Рассмотрим случай 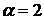 . Из (95) следует, что
. Из (95) следует, что
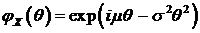 , (97)
, (97)
которая является характеристической функцией нормального закона 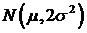 . Об устойчивости нормального закона
с индексом устойчивости
. Об устойчивости нормального закона
с индексом устойчивости 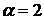 уже упоминалось выше. Отметим, что произведение
уже упоминалось выше. Отметим, что произведение 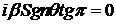 , поэтому
, поэтому 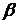 не определяется однозначно. Принято
считать, что
не определяется однозначно. Принято
считать, что 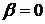 .
.
С точки зрения поведения хвостов распределения случаи 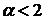 и
и 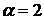 существенно отличаются.
Действительно, пусть
существенно отличаются.
Действительно, пусть 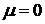 , тогда
, тогда
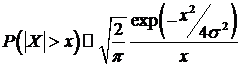 при
при 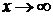 . (98)
. (98)
Сопоставление (98) с (95) и (96) позволяет сделать вывод, что стремление
к нулю хвостов распределения в случае, когда 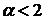 более медленное. Поэтому такие
распределения принято называть распределениями с тяжелыми хвостами. Как
показывают статистические исследования многие финансовые инструменты имеют
логарифмические возвраты
более медленное. Поэтому такие
распределения принято называть распределениями с тяжелыми хвостами. Как
показывают статистические исследования многие финансовые инструменты имеют
логарифмические возвраты 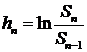 , у которых распределения обладают тяжелыми хвостами. Этот
статистический факт делает устойчивые распределения привлекательными для
описания поведения логарифмических возвратов.
, у которых распределения обладают тяжелыми хвостами. Этот
статистический факт делает устойчивые распределения привлекательными для
описания поведения логарифмических возвратов.
Отметим, что 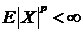 в том и только в том случае, когда
в том и только в том случае, когда 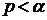 . Действительно, если
. Действительно, если 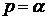 , то из (95) и (96) следует, что
, то из (95) и (96) следует, что 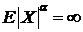 . Если
. Если 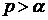 , то из неравенства
, то из неравенства 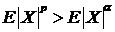 , следует
, следует 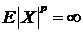 . Пусть
. Пусть 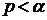 , тогда из неравенства
, тогда из неравенства 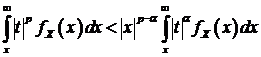 следует, что
следует, что 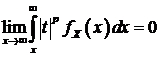 .
.
В связи с показательной асимптотикой остановимся на распределении Парето,
плотность которого
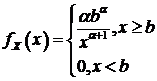 . (99)
. (99)
С параметрами 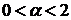 (индекс устойчивости) и
(индекс устойчивости) и 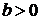 . График плотности распределения
Парето представлен на рисунке 8.
. График плотности распределения
Парето представлен на рисунке 8.
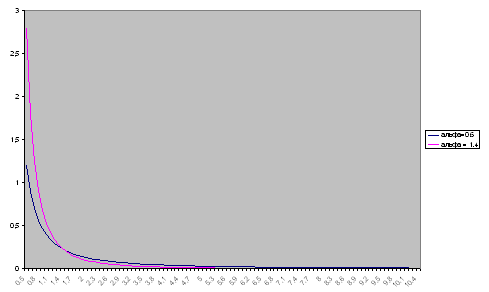
Рис. 8. Графикт плотности распределения Парето 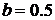 ,
, 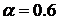 и
и 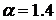 соответственно.
соответственно.
Функция распределения 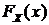
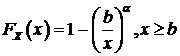 , (100)
, (100)
а вероятность 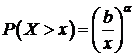 . Сравнение с (95) показывает, что на бесконечности
устойчивые распределения ведут себя так же, как и распределение Парето. Поэтому
хвостовая часть устойчивых распределений относится к паретовскому типу.
. Сравнение с (95) показывает, что на бесконечности
устойчивые распределения ведут себя так же, как и распределение Парето. Поэтому
хвостовая часть устойчивых распределений относится к паретовскому типу.
Можно рассмотреть симметричное распределение Парето:
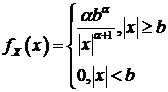 , (101)
, (101)
которое выглядит более естественным при моделировании последовательности  . Параметр скошенности (асимметрии)
. Параметр скошенности (асимметрии) 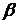 определяет насколько распределение
асимметрично. Если
определяет насколько распределение
асимметрично. Если 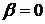 , то есть
, то есть
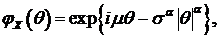 (102)
(102)
то распределение симметрично относительно 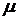 . Чем ближе
. Чем ближе 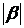 к единице, тем сильнее выражена
асимметрия распределения. Причем если
к единице, тем сильнее выражена
асимметрия распределения. Причем если 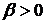 , то распределение скошено сильнее
слева, при
, то распределение скошено сильнее
слева, при 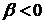 - справа.
- справа.
Параметр 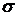 является масштабным параметром.
является масштабным параметром.
При 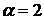 , случай нормального распределения
, случай нормального распределения 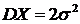 . При
. При 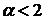 - дисперсии не существует. Поэтому
параметр
- дисперсии не существует. Поэтому
параметр 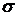 отличается от среднего
квадратического отклонения.
отличается от среднего
квадратического отклонения.
Параметр 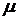 - параметр положения при
- параметр положения при 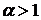 , как уже отмечалось выше,
, как уже отмечалось выше, 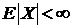 и существует математическое ожидание
и существует математическое ожидание
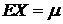 . При
. При 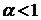 математическое ожидание может быть
не определено, поэтому
математическое ожидание может быть
не определено, поэтому 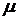 не следует интерпретировать как математическое ожидание.
не следует интерпретировать как математическое ожидание.
Традиционным обозначением для устойчивых распределений является
обозначение 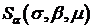 . Отметим, что при
. Отметим, что при 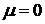
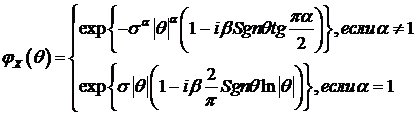 . (103)
. (103)
Отсюда
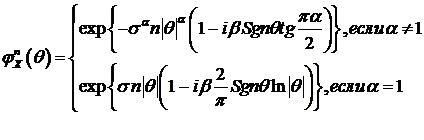 . (104)
. (104)
Пусть 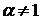 , тогда
, тогда 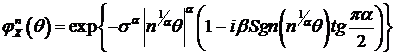 , и из (88) следует, что распределение является строго
устойчивым. Если
, и из (88) следует, что распределение является строго
устойчивым. Если 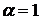 , то при
, то при 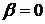
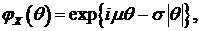 , и поскольку
, и поскольку 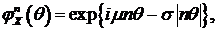 то распределение в этом случае также является строго
устойчивым. Симметричное распределение -
то распределение в этом случае также является строго
устойчивым. Симметричное распределение - 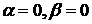 - является строго устойчивым. В этом
случае характеристическая функция
- является строго устойчивым. В этом
случае характеристическая функция
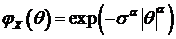 . (105)
. (105)
Явный вид плотностей устойчивых распределений известен только при
некоторых значениях параметров. Этими распределениями являются:
нормальное распределение 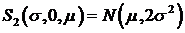 ;
;
распределение Коши 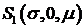 с плотностью
с плотностью
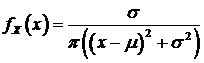 ; (106)
; (106)
распределение Леви 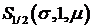 с плотностью
с плотностью
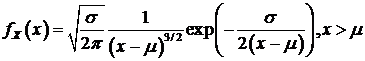 (107)
(107)
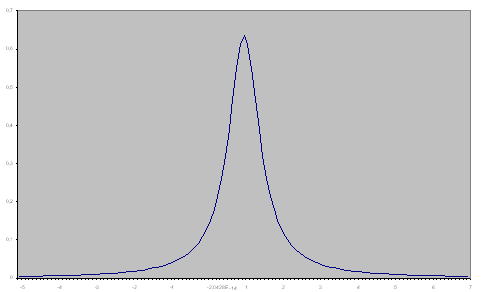
Рис. 9. График плотности распределения Коши (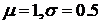 ).
).
Рис. 10. График плотности распределения Леви (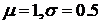 ).
).
Пусть 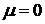 , если
, если 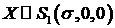 , то
, то
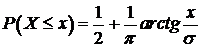 ; (108)
; (108)
если 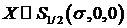 , то для
, то для 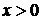
 . (109)
. (109)
Рассмотрим эволюцию цены акции 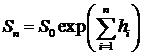 . Используем стохастическую
последовательность
. Используем стохастическую
последовательность 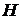 :
:
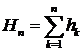 . (110)
. (110)
Пусть 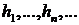 - независимые случайные величины такие, что
- независимые случайные величины такие, что
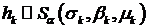 . (111)
. (111)
Из (110) и
(111) следует, что характеристическая функция
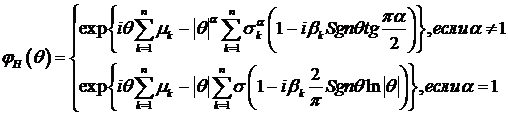 . (112)
. (112)
Из (112)
следует, что
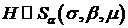 , (113)
, (113)
где
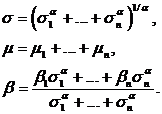 (114)
(114)
В частности, если  независимые и одинаково распределены
независимые и одинаково распределены 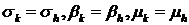 , то
, то
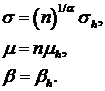 (115)
(115)
8. Условно-устойчивые распределения
Рассмотрим последовательность сигма-алгебр 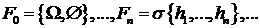 .
.
По аналогии с условно-гауссовскими моделями рассмотрим последовательности
предсказуемых случайных величин  и
и 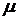 .
.
Будем говорить, что случайная величина 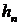 условно-устойчива с индесом
устойчивости
условно-устойчива с индесом
устойчивости  , если условный закон распределения случайной величины
, если условный закон распределения случайной величины
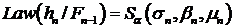 . (116)
. (116)
Рассмотрим пример модели аналогичной модели 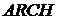 с использованием распределения Коши:
с использованием распределения Коши:
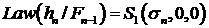 ,
,
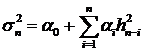 . (117)
. (117)
На рисунке 10 представлен график машинной реализации модели (111) при
этом рассматривается модель первого порядка 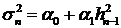 .
.
. Безгранично делимые распределения
Перейдем к рассмотрению класса распределений, который включает в себя
устойчивые распределения.
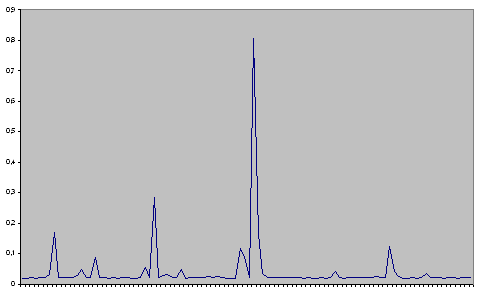
Рис. 10. График машинной реализации модели (111) (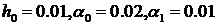 )
)
Распределение 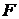 называется безгранично делимым, если для каждого
называется безгранично делимым, если для каждого 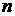 существует такое распределение
существует такое распределение 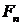 , что
, что
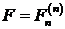 . (118)
. (118)
Другими словами для каждого 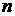 существуют
существуют 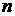 независимых случайных величин с
независимых случайных величин с 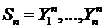 одним и тем же распределением
одним и тем же распределением 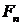 , что сумма
, что сумма 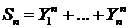 имеет распределение
имеет распределение 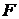 . Как уже отмечалось выше, класс
устойчивых распределений включен в класс безгранично делимых распределений.
. Как уже отмечалось выше, класс
устойчивых распределений включен в класс безгранично делимых распределений.
Действительно, пусть 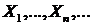 - независимые копии
- независимые копии 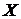 и распределение
и распределение 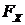 - устойчиво с индексом устойчивости
- устойчиво с индексом устойчивости  . Определим
. Определим
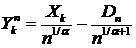 , (119)
, (119)
Тогда сумма 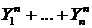 имеет распределение
имеет распределение  .
.
В качестве первого примера рассмотрим распределение Пуассона.
Характеристическая функция распределения Пуассона, как уже показывалось ранее, 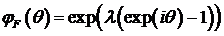 . Поскольку характеристическая
функция свертки
. Поскольку характеристическая
функция свертки 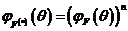 , то распределение
, то распределение 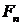 в (118) - распределение Пуассона с
параметром
в (118) - распределение Пуассона с
параметром 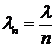 . Следовательно, распределение Пуассона безгранично делимое
распределение.
. Следовательно, распределение Пуассона безгранично делимое
распределение.
Рассмотрим гамма-распределение с плотностью:
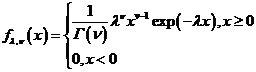 . (120)
. (120)
где  - параметры распределения. В частности при
- параметры распределения. В частности при 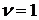 получается показательное
распределение
получается показательное
распределение
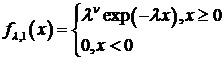 (121)
(121)
Рассмотрим свертку гамма распределений:
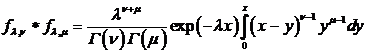 (122)
(122)
Сделаем подстановку в интеграле 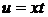 , в результате получим
, в результате получим
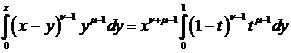 . (123)
. (123)
Интеграл в (123) - бета функция
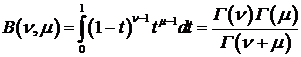 . (124)
. (124)
В результате
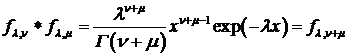 . (125)
. (125)
Замкнутость свертки для гамма-распределений позволяет утверждать, что
гамма-распределение безгранично делимо. Действительно для гамма-распределения 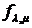 -
- 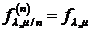 . В частности для показательного
распределения
. В частности для показательного
распределения 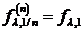 .
.
Рассмотрим вырожденную случайную величину, сидящую в одной точке 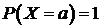 .Характеристическая функция распределения:
.Характеристическая функция распределения:
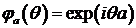 . Поскольку
. Поскольку 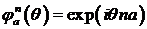 , то
, то 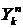 - вырожденные случайные величины,
сидящие в точке
- вырожденные случайные величины,
сидящие в точке 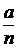 .
.
В результате работ Б. де Финнети, А.Н. Колмогорова, П. Леви и А.Я.
Хинчина получена формула для характеристических функций безгранично делимых
распределений
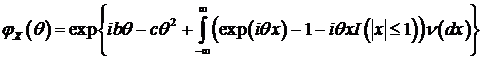 , (126)
, (126)
где  ,
, 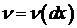 - положительная мера (называемая мерой Леви),
удовлетворяющая условиям:
- положительная мера (называемая мерой Леви),
удовлетворяющая условиям:
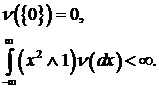 (127)
(127)
Таким образом, безгранично делимое распределение описывается триплетом 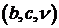 , который определяется единственным
образом.
, который определяется единственным
образом.
В качестве примера вернемся к распределению Пуассона с характеристической
функцией 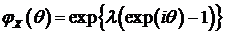 для которой триплет -
для которой триплет - 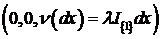 .
.
. Нелинейные хаотические модели
До сих пор при описании поведения цен мы исходили из стохастической
природы цен. Однако, достаточно хорошо известно, что детерминированные системы:
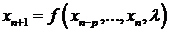 , (128)
, (128)
где 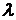 - параметр, порождают последовательности, поведение которых
весьма схоже с поведением стохастических последовательностей. Этот факт делает
привлекательным использование моделей вида (128) для моделирования поведения
цен, поскольку эти модели позволяют описывать ряд свойств (например, типа
кластерности) наблюдаемых при статистическом анализе финансовых данных.
- параметр, порождают последовательности, поведение которых
весьма схоже с поведением стохастических последовательностей. Этот факт делает
привлекательным использование моделей вида (128) для моделирования поведения
цен, поскольку эти модели позволяют описывать ряд свойств (например, типа
кластерности) наблюдаемых при статистическом анализе финансовых данных.
Приведем ряд примеров таких моделей.
Рассмотрим модель, порождаемую логистической функцией 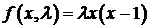 ,
, 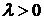 - параметр:
- параметр:
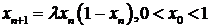 . (129)
. (129)
На рисунках 11 - 15 приведены компьютерные реализации модели (129) при
различных значениях 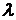 .
.
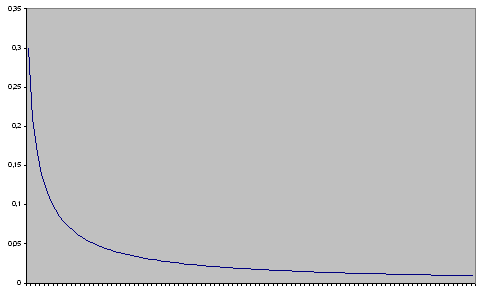
Рис. 11. Случай  .
.
Для значений 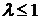 и
и 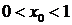 получаем, что
получаем, что 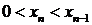 . У стационарного уравнения для
логистической функции
. У стационарного уравнения для
логистической функции
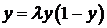 (130)
(130)
два решения
При 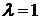 эти решения совпадают. Так как ограниченная снизу убывающая
последовательность имеет предел, то
эти решения совпадают. Так как ограниченная снизу убывающая
последовательность имеет предел, то 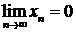 .
.
Смотри рис. 11.
При 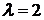 (рис. 12) решения стационарного уравнения (130) -
(рис. 12) решения стационарного уравнения (130) - 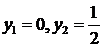 .
.
Пусть 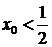 , тогда
, тогда 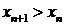 . По индукции можно показать, что
. По индукции можно показать, что 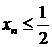 .
.
Отсюда
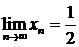 .
.
Пусть 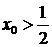 , тогда
, тогда 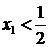 , поэтому и в этом случае
, поэтому и в этом случае 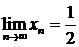 . См рис. 12.
. См рис. 12.

Рис. 12. Случай 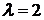 .
.
В этих двух случаях система имеет единственное устойчивое состояние, к
которому притягиваются 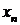 при
при 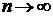 .
.
Будем увеличивать 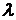 . При
. При 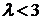 у системы сохраняется единственное устойчивое состояние.
Однако, при
у системы сохраняется единственное устойчивое состояние.
Однако, при 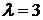 у системы появляются два устойчивых состояния, в которых
система находится попеременно при
у системы появляются два устойчивых состояния, в которых
система находится попеременно при 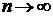 . См. рис.13.
. См. рис.13.
Такой же характер поведения системы будет сохраняться при увеличении 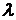 . Но затем, при
. Но затем, при 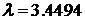 у системы появляются четыре
состояния устойчивости. См. рис.14. Далее с ростом
у системы появляются четыре
состояния устойчивости. См. рис.14. Далее с ростом 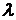 число состояний увеличивается, их
становится 16, затем 64. По своей структуре этот процесс совпадает с бинарным
дроблением атомов (бифуркацией). Для
число состояний увеличивается, их
становится 16, затем 64. По своей структуре этот процесс совпадает с бинарным
дроблением атомов (бифуркацией). Для 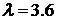 , число состояний, по которым
блуждает система, становится равным бесконечности. См. рис. 15. При этом
исчезает периодичность в поведении системы, что означает потерю устойчивости.
Отметим, что, не смотря на детерминированность системы, отсутствует возможность
какого-либо прогноза за счет погрешности вычислений. Пусть
, число состояний, по которым
блуждает система, становится равным бесконечности. См. рис. 15. При этом
исчезает периодичность в поведении системы, что означает потерю устойчивости.
Отметим, что, не смотря на детерминированность системы, отсутствует возможность
какого-либо прогноза за счет погрешности вычислений. Пусть 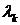 - последовательность точек дробления
атомов. Понятно, что значения
- последовательность точек дробления
атомов. Понятно, что значения 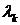 должны становится все ближе. В этой связи интересен
результат, предсказанный М.Фейгенбаумом и доказанный О. Ландфордом [8]:
должны становится все ближе. В этой связи интересен
результат, предсказанный М.Фейгенбаумом и доказанный О. Ландфордом [8]:
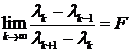 , (132)
, (132)
где 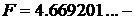 универсальная константа, называемая числом Фейгенбаума.
универсальная константа, называемая числом Фейгенбаума.
При значении параметра 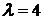 возникает последовательность, напоминающая реализацию белого
шума.
возникает последовательность, напоминающая реализацию белого
шума.
Действительно, зададим начальное значение 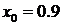 и вычислим по формуле
и вычислим по формуле 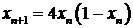 тысячу значений. Подсчитанные
значения среднего
тысячу значений. Подсчитанные
значения среднего 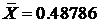 ,стандартного отклонения
,стандартного отклонения 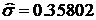 и выборочной корреляционной функции
и выборочной корреляционной функции 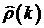 для тысячи значений
для тысячи значений
Таблица 1.
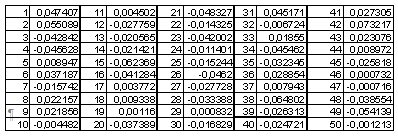
Из таблицы 1. видно что случайные величины 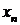 можно считать некоррелированными. В
этом смысле можно говорить, что уравнение
можно считать некоррелированными. В
этом смысле можно говорить, что уравнение 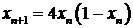 порождает белый шум. Отметим, что
для последовательности
порождает белый шум. Отметим, что
для последовательности 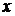 существует инвариантное распределение
существует инвариантное распределение 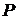 , то есть для любого борелевского
подмножества интервала
, то есть для любого борелевского
подмножества интервала 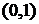 -
- 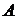
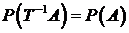 , (133)
, (133)
где 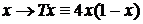 . Распределение обладает плотностью
. Распределение обладает плотностью
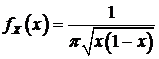 . (134)
. (134)
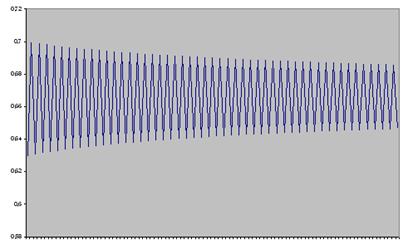
Рис. 13. Случай  .
.
Тем самым если считать, что  - случайная величина с плотностью
распределения (134), то для всех
- случайная величина с плотностью
распределения (134), то для всех  случайная величина
случайная величина 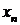 распределена с той же плотностью. То
есть у стохастической динамической системы вся случайность определяется
случайным начальным значением, все остальные переходы
распределена с той же плотностью. То
есть у стохастической динамической системы вся случайность определяется
случайным начальным значением, все остальные переходы 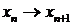 детерминированы. Нетрудно найти
детерминированы. Нетрудно найти 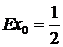 , дисперсию
, дисперсию 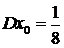 и среднее квадратическое отклонение
и среднее квадратическое отклонение 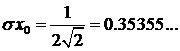 (полезно сравнить с выборочным
средним
(полезно сравнить с выборочным
средним  и стандартным отклонением
и стандартным отклонением 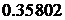 ).
).
Приведем еще три примера.
Преобразование Бернулли:
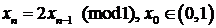 . (135)
. (135)
Инвариантным здесь является равномерное на интервале  распределение с корреляционной функцией
распределение с корреляционной функцией
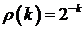 .
.
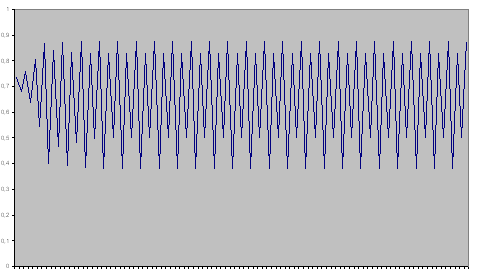
Рис.14. Случай 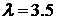 .
.
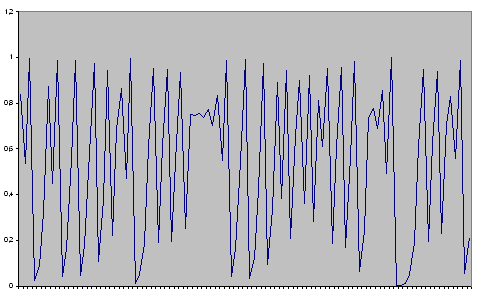
Рис. 15. Случай  .
.
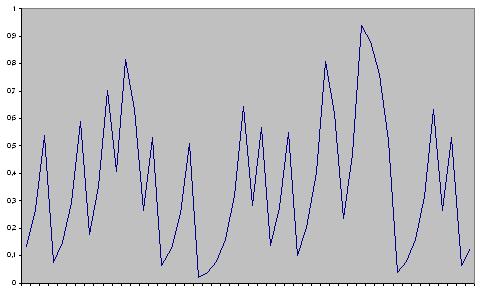
Рис. 16. График машинной реализации преобразования Бернулли (модель 135)
Палаточное преобразование:
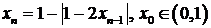 . (136)
. (136)
Инвариантным является равномерное распределение с 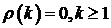 . График машинной реализации приведен
на рисунке 17.
. График машинной реализации приведен
на рисунке 17.
Следующая
модель
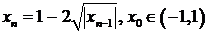 . (137)
. (137)
Инвариантное распределение на интервале 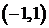 определяется плотностью
определяется плотностью
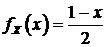 (138)
(138)
с 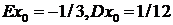 . График компьютерной реализации
модели представлен на рисунке 18.
. График компьютерной реализации
модели представлен на рисунке 18.
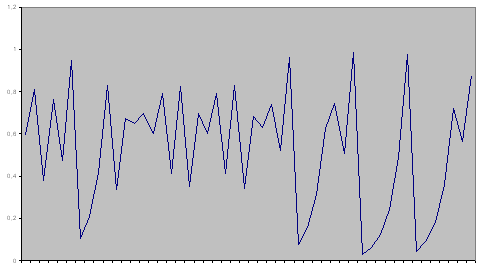
Рис. 17. График компьютерной реализации палаточного преобразования
(модель (136)).
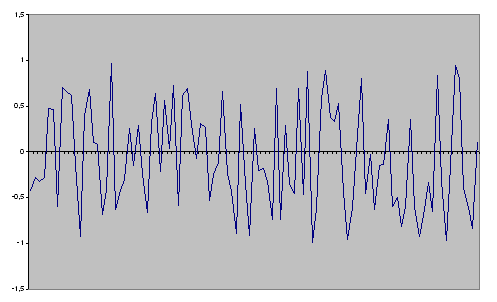
Рис. 18. График машинной реализации модели (137).
Модели динамического хаоса представляют интерес с нескольких точек
зрения. Во-первых, как средство имитационного моделирования поведения цен в
периоды кризиса, когда наблюдается скорее хаотичное поведение, чем
стохастическое. Во-вторых, например, логистическая модель, которая развивается
за счет бинарного дробления атомов, непосредственно приводит к идее
фрактальности. В-третьих, возможность рассмотрения инвариантных распределений,
за счет чего случайность стохастических динамических моделей связана со
случайностью только начального значения.
Литература
1. Белявский
Г.И. Статистический анализ рисковых активов. Часть первая. ЮФУ. 2007.
. Ширяев
А.Н. Основы стохастической финансовой математики. Факты. Модели. ФАЗИС. 2008.
3. Engle
R.F. Autoregressive conditional heteroscedasticity with estimates of the
variance of United Kingdom inflation. Econometrica 2012, V. 50, №4.
. Bollerslev
T. Generalized autoregressive conditional heteroscedasticity. Journal of
econometrics. 2006, V. 31.
. Dacorogna
M.M., Muller U.A., Embrechts P., Samorodnitsky G. Moment condition for the
HARCH(k) models. Preprint Zurich, "Olsen and Associates", May, 2005.
. Леман
Э., Теория точечного оценивания, М., Наука, 2011.
. Балакришнан
А.В. Теория фильтрации Калмана. Мир, 2008.
8. Lanford
O.A computer-assisted proof of the Feigenbaum conjectures. American Mathematical society.
Bulletin. 2012.V. 6. №3.