Функции дискретного преобразования
Задание 1
Доказать, что множество функций 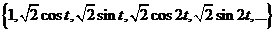 на отрезке [-π; π] образуют систему ортонормированных
функций.
на отрезке [-π; π] образуют систему ортонормированных
функций.
Решение:
Систему функций 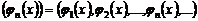 (конечную или бесконечную) называют ортогональной на отрезке
(конечную или бесконечную) называют ортогональной на отрезке 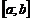 , если все функции этой системы являются
попарно ортогональными на данном отрезке, т.е.
, если все функции этой системы являются
попарно ортогональными на данном отрезке, т.е.
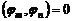 ,
,  ,
, 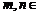 .
.
Ортогональную система функций (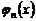 ) на отрезке
) на отрезке 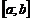 называют ортонормированной системой, если
называют ортонормированной системой, если
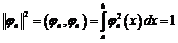
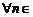 .
.
Любая ортогональная на 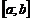 система функций (
система функций (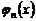 ) с
) с 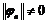
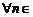 ℕ может
быть нормирована. Для этого следует разделить каждую функцию системы (
ℕ может
быть нормирована. Для этого следует разделить каждую функцию системы (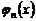 ) на ее норму. В результате будет получена
ортонормированная система функций
) на ее норму. В результате будет получена
ортонормированная система функций 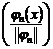 .
.
Проверим условие ортогональности для заданной системы.
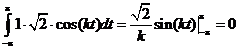
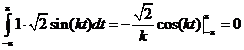
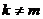
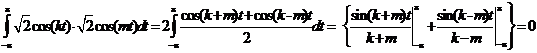
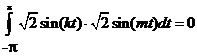
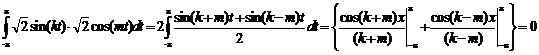
и так далее.
Значит, все функции данной системы попарно ортогональны.
Проверим условие нормированности функций системы
Найдем вадраты норм всех функций:
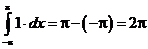
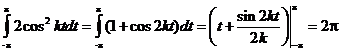
Следовательно, данная система функций является ортогональной, но
не является нормированной.
функция дискретный фурье сигнал
Задание 2
Разложить в тригонометрический и комплексный ряды Фурье
пилообразный сигнал на отрезке [-π;
π], показанный
на рисунке.
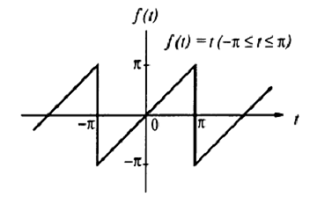
Решение:
Ряд Фурье периодической функции 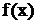 с периодом
с периодом 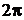 , которая определена на сегменте
, которая определена на сегменте 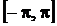 , это ряд вида:
, это ряд вида:
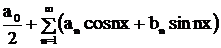 ,
,
где
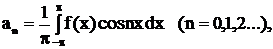
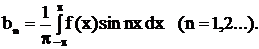
Если данный ряд является сходящим, то его суммой 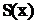 является периодическая функция с периодом
является периодическая функция с периодом
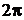 , т.е.
, т.е. 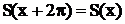 .
.
Когда 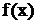 является нечетной функцией, ее ряд Фурье
содержит только синусы, т.е.
является нечетной функцией, ее ряд Фурье
содержит только синусы, т.е.
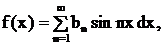
где 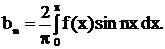
Заданная функция имеет период 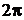 и задана на интервале
и задана на интервале 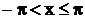 формулой:
формулой: 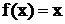
Данная функция удовлетворяет условиям Дирихле и, следовательно, её
можно разложить в ряд Фурье. Функция является нечетной.
Находим коэффициенты Фурье:
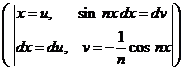 :
:
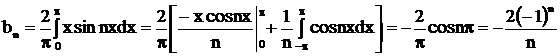 ,
,
т.к. 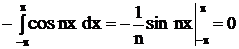 .
.
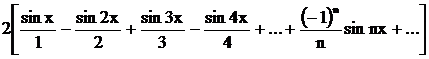 .
.
Так как функция 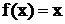 удовлетворяет условиям Дирихле, то в любой точке непрерывности
удовлетворяет условиям Дирихле, то в любой точке непрерывности 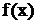 сумма ряда равна значению функции. В
точках
сумма ряда равна значению функции. В
точках 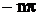 и
и 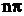 сумма ряда равна нулю. Покажем графики: функции
сумма ряда равна нулю. Покажем графики: функции 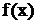 и частичных сумм ряда, содержащие 1, 2 и
3 члена на рисунке. График частичных сумм ряда приближается к графику функции
и частичных сумм ряда, содержащие 1, 2 и
3 члена на рисунке. График частичных сумм ряда приближается к графику функции  при увеличении членов суммы.
при увеличении членов суммы.

y 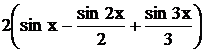
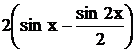
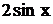
Для функций с произвольным периодом 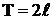 ряд Фурье в комплексной форме имеет вид
ряд Фурье в комплексной форме имеет вид
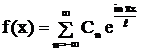 ,
,
где
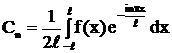 .
.
Находим комплексную форму ряда Фурье заданной функции. По формуле:
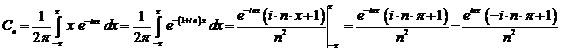
По формулам Эйлера
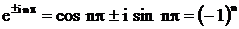 .
.
Следовательно:
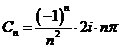 .
.
Задание 3
Используя специализированные программные средства (Matlab,
LabVIEW и т.д.), нужно:
Сгенерировать программно произвольный сигнал, состоящий из
определенного количества выборок. Построить график сигнала.
Выполнить дискретное преобразование Фурье данного сигнала,
используя функции из специальных библиотек.
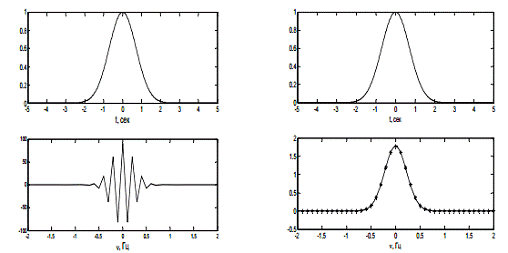
Построить графики действительных частей коэффициентов Фурье,
мнимых частей коэффициентов Фурье, спектра амплитуд. Считая, что исходный
цифровой сигнал был дискретизирован с определенной частотой выборки fs,
подписать на графиках частоты в Гц. Частота выборки fs выбирается
самостоятельно.
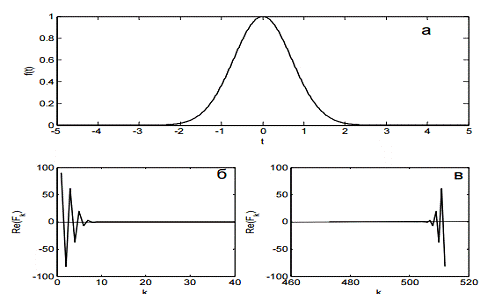
Дискретное преобразование Фурье. а) Исходная функция -
Действительная часть преобразованной функции, построенная как функция номера
=512;%Число точек T=10;
%Интервал времени =T/(N-1); =linspace(-5,5,N);%Задание
вектора времени=exp(-t.^2);%Вычисление дискретной функции =fft(f);%Вычисление
преобразования Фурье (211); plot(t,f);%Отрисовка исходной функции
=F(1:N/2+1);%Выделение первых N/2+1 (положительные частоты)
=F(N/2+1:N);%Выделение спектра отрицательных частот =[F2,F1];%Объединение
спектра
%Вычисление вектора частот = (N-1)/(N*T);
%Шаг частоты =1/(2*dt);
%Частота = -nuNyq+dnu*(0:N); (212); (nu
(N/2+1-20:N/2+1+20),real (F(N/2+1-20:N/2+1+20)))
Литература
1. Гоноровский И.С. Радиотехнические цепи и
сигналы. - М.: Радио и связь, 1986. - 512 с.
. Колобов А.М. Избранные главы высшей математики.
- Ч. 1. Ряд Фурье. Интеграл Фурье. Операционные исчисления. - Минск: Высшая
школа, 1985. - 220 с.
. Ефимов А.В. Математический анализ (специальные
разделы) - Ч. 1. Общие функциональные ряды и их приложение. - М.: Высшая школа,
1980. - 279 с.