Рівняння з параметрами, що містять знак модуля
Рівняння
з параметрами, що містять знак модуля
Донецьк
- 2014
АНОТАЦІЯ (ТЕЗИ)
Учнівська науково-дослідна робота на тему:
РІВНЯННЯ З ПАРАМЕТРАМИ, ЩО МІСТЯТЬ ЗНАК МОДУЛЯ
Актуальність теми роботи полягає в тому, що
залучення до навчального процесу задач із параметрами дозволяє імітувати повний
процес прикладного математичного дослідження або окремих його етапів, що сприяє
розвитку глибокого стійкого інтересу до досліджень з великою кількістю
евристичних прийомів загального і спеціального характеру .
Об'єкт дослідження - процес навчання математики
учнів класів з поглибленим теоретичним і практичним вивченням математики.
Предмет дослідження - система задач із
параметрами, що містять знак модуля, як засіб розвитку дослідницьких умінь учнів.
Мета дослідження - доведення доцільності
впровадження в дослідженнях системи задач із параметрами русифікованого
програмно -графічного комплексу Microsoft Mathematics 4.0 з метою реалізації
розвиваючого навчання, ідей моделювання і прикладної спрямованості курсу
математики.
В проведеному дослідженні в якості новітнього
програмно-технічного засобу розвиваючого навчання запропоноване застосування
російськомовного програмно-графічного калькулятора Microsoft Mathemаtics 4.0 з
„дружнім” інтерфейсом, який з 2011 року вільно розповсюджується корпорацією
Microsoft та призначений для використання як на звичайних комп’ютерах, так і на
новітніх інтерактивно-тактильних планшетах та „електронних класних дошках” під
керуванням операційних систем Windows 7/8.
Практичне значення результатів дослідження
полягає в тому, що на прикладах розв’язання рівнянь та нерівностей з
параметрами, що містять модулі, графо-аналітичним способом доведена
ефективність застосування програмно-графічного калькулятора Microsoft
Mathemаtics 4.0 при побудові на одному масштабному полі систем паралельних,
гомотетичних та поворотних функцій при зміні параметра, що дає яскраву
наочність викладення курсу задач з параметрами вчителем математики в школі та
можливість самостійних досліджень учнем задач з параметрами на класному та
домашньому компьютерах.
ВСТУП
рівняння параметр модуль калькулятор
Залучення до навчального процесу задач із
параметрами дозволяє імітувати повний процес прикладного математичного
дослідження або окремих його етапів, що сприяє розвитку глибокого стійкого
інтересу до дослідження. В процесі розв’язування задач із параметрами
учні-дослідники знайомляться з великою кількістю евристичних прийомів
загального і спеціального характеру .
Об'єкт дослідження - процес навчання математики
учнів класів з поглибленим теоретичним і практичним вивченням математики.
Предмет дослідження - система задач із
параметрами, що містять знак модуля, як засіб розвитку дослідницьких умінь
учнів.
Мета дослідження - доведення доцільності
впровадження в дослідженнях системи задач із параметрами русифікованого
програмно -графічного комплексу Microsoft Mathematics 4.0 з метою реалізації
розвиваючого навчання, ідей моделювання і прикладної спрямованості курсу
математики.
У методичній літературі зустрічається ряд робіт,
пов'язаних із задачами з параметрами, автори яких П.І.Горнштейн, О.М.Гольдман,
Г.В.Дорофєєв, Л.С.Заслонкіна, К.С.Кочарова, О.А.Корміхін, В.С.Крамор,
В.В.Лікоть, Т.С.Рогівська, С.І.Мещерякова, Г.Ф.Олійник, Н.О.Тарасенкова,
І.І.Чучаєв, І.Ф.Шаригін та ін., але тестування (ЗНО) учнів 11-х класів
показало, що задачам з параметрами, навіть у класах із поглибленим теоретичним
і практичним вивченням математики, не надається належної уваги, оскільки їх
розв’язання має специфічний інструментарій дослідницького характеру, який не
застосовується в процесі навчання.
Практичне значення результатів дослідження
полягає в тому, що в ньому запропонована методика розв’язання системи задач з
параметрами на основі методології математичного моделювання, розвитку інтелектуальних
і дослідницьких умінь і навичок, оволодінню корисними прийомами евристики та
прикладного застосування комп’ютерних систем професійного рівня.
РОЗДІЛ 1. АНАЛІТИЧНІ
МЕТОДИ
РОЗВ’ЯЗАННЯ
РІВНЯНЬ
З
ПАРАМЕТРАМИ,
ЩО
МІСТЯТЬ
ЗМІННІ
ПІД
ЗНАКОМ
МОДУЛЯ
1.1 Способи розв’язання рівнянь з параметрами,
що містять змінні під знаком модуля
Загальних методів рішення задач, у яких присутні
числові параметри, не існує. У кожному конкретному випадку підхід до їхнього
рішення вибирається виходячи зі структури завдання. У всіх випадках необхідний
аналіз отриманого рішення залежно від конкретного значення параметра.
В основу рішення задач із параметром може бути
покладений наступний принцип: значення параметра вважається довільно
фіксованим, а потім шука-ється рішення задачі так, як рішення рівняння з одним
невідомим (або системи рівнянь із двома невідомими). Відповіддю повинне бути
перерахування всіх рішень для кожного припустимого значення параметра, що
вимагає проведення дослідження [1].
Для проведення дослідження множину значень
параметра розбивають на підмножини тими значеннями параметра, при яких або при
переході через які відбувається якісна зміна рівняння.
Існують різні способи рішення задач із
параметрами, серед яких найбільш часто використовують алгебраїчний,
функціонально-аналітичний і графо-ана-літичний способи.
При алгебраїчному способі деякі рівняння з
параметрами, що містять змінні під знаком модуля, розв’язуються з урахуванням
певних умов, при виконанні яких задані типи рівнянь мають певну кількість коренів,
або не мають їх зовсім [5].
Основними функціонально-аналітичними способами
розв’язання рівнянь з параметрами, що містять змінні під знаком модуля, є
методи інтервалів та методи областей [2].
1. Метод інтервалів ( для рівнянь
типу 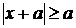 ):
):
Визначаємо область допустимих
значень рівняння, позначаємо її на числовій прямій;
Прирівнюємо до нуля вирази, які
стоять під знаком модуля, знаходи-мо відповідні значення невідомих;
Нулі виразів, що стоять під знаком
модуля, і область допустимих значень рівняння визначають на числовій прямі
систему інтервалів, на кожному з яких функції, що стоять під знаком модуля, є
неперервними;
Розв’язуємо рівняння на кожному з
інтервалів;
Знаходимо остаточний розв’язок
рівняння як об’єднання множин розв’язків на кожному інтервалі.
. Метод областей ( для рівнянь типу 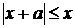 ):
):
Знаходимо і будуємо на площині
область допустимих значень рівняння з параметром;
Прирівнюємо до нуля вирази, які
стоять під знаком модуля. Будуємо множину точок (графіки) на координатній
площині xOa (x - змінна, a - параметр), які задовольняють цим рівностям;
Визначаємо систему областей, на які
область допустимих значень виявилась розбитою побудованими графіками;
Розв’язуємо рівняння у кожній з областей;
Знаходимо остаточний розв’язок
рівняння як об’єднання множин розв’язків кожної області.
При розв’язуванні рівнянь, що
містять змінну під знаком модуля, найчастіше застосовують такі аналітичні
методи, як [3]: ) розкриття модуля за визначенням;) метод інтервалів.
За визначенням модуля [4]:
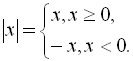
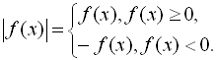
Відзначимо такі властивості модуля,
які нерідко використовуються на практиці [4]:
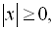
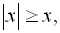
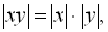
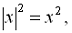
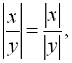
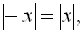
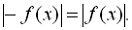
Для найпростіших рівнянь з модулем
слід пам’ятати, що рівняння
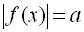
рівносильне сукупності рівнянь
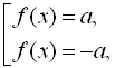 якщо
якщо 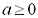 .
.
Якщо ж 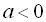 , то
рівняння
, то
рівняння 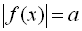 розв’язків
не має.
розв’язків
не має.
Основними графо-аналітичними
способами розв’язання рівнянь з пара-метрами, що містять змінні під знаком
модуля, є [4]:
методи паралельного переносу;
методи повороту;
методи гомотетії,
при яких на координатній площині
будується система графіків функцій f(x, f(a)), де а - параметр, дослідження
яких дозволяє знайти розв’язки.
Для застосування графо-аналітичними
способів розв’язання рівнянь з па-раметрами, що містять змінні під знаком
модуля, в дійсній роботі використову-ється програмно-графічний калькулятор
Мicrosoft Mathematics 4.0 на ПЕОМ під управлінням 32-розрядної операційної
системи Windows XP,7,8 [7].
.2 Приклади застосування
аналітичного способу розв’язання рівнянь з параметрами, що містять змінні під
знаком модуля
Приклад № 1.1
Знайти всі значення параметра  , для
кожного з яких існує тільки одне значення
, для
кожного з яких існує тільки одне значення 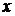 , яке задовольняє систему рівнянь
, яке задовольняє систему рівнянь
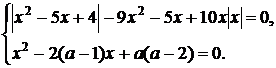 (1.1.1)
(1.1.1)
Розв’язання:
Розв’яжемо перше рівняння системи
(1.1). Для цього спочатку звіль-нимося від знака модуля. Оскільки 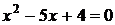 при
при 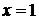 і
і 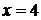 , то
розіб’ємо числову пряму на проміжки
, то
розіб’ємо числову пряму на проміжки 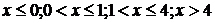 і знайдемо розв’язки рівняння у
кожному із цих проміжків
і знайдемо розв’язки рівняння у
кожному із цих проміжків
Нехай 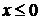 ; тоді
; тоді 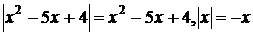 , а рівняння
(1) в системі (1.1.1) запишеться у вигляді
, а рівняння
(1) в системі (1.1.1) запишеться у вигляді
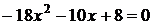 (1.1.2)
(1.1.2)
Рівняння (1.1.2) має корені 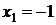 і
і 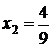 . У
розглянутий проміжок входить тільки
. У
розглянутий проміжок входить тільки 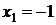 . Отже, у проміжку
. Отже, у проміжку 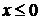 рівняння
(1) системи (1.1.1) має один корінь
рівняння
(1) системи (1.1.1) має один корінь 
Нехай 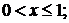 тоді
тоді 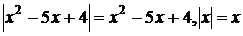 , а рівняння (1) в системі (1.1.1)
буде мати вигляд
, а рівняння (1) в системі (1.1.1)
буде мати вигляд
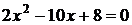 (1.1.3)
(1.1.3)
Рівняння (1.1.3) має корені 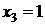 і
і 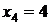 , з яких у
розглянутий проміжок входить тільки
, з яких у
розглянутий проміжок входить тільки 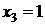 . Отже, у проміжку
. Отже, у проміжку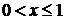 рівняння
(1) системи (1.1.1) має один корінь
рівняння
(1) системи (1.1.1) має один корінь 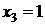 .
.
Нехай 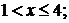 тоді
тоді 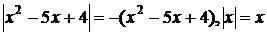 , а рівняння (1) в системі (1.1.1)
рівносильне тотожності 0=0, тобто задовольняється при будь-якому значення
, а рівняння (1) в системі (1.1.1)
рівносильне тотожності 0=0, тобто задовольняється при будь-якому значення 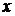 із проміжку
із проміжку
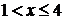 . Тому
будь-яке значення
. Тому
будь-яке значення 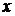 із проміжку
із проміжку
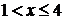 є
розв’язком рівняння.
є
розв’язком рівняння.
Нехай 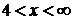 ;
; 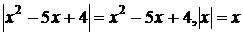 , а рівняння (1) в системі (1.1.1)
запишеться у вигляді
, а рівняння (1) в системі (1.1.1)
запишеться у вигляді
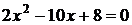 (1.1.4)
(1.1.4)
Рівняння (1.1.4) має корені 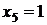 і
і 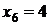 , жоден з
яких не входить у розглянутий проміжок. Отже, у проміжку
, жоден з
яких не входить у розглянутий проміжок. Отже, у проміжку 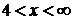 рівняння
(1) системи (1.1.1) не має розв’язків.
рівняння
(1) системи (1.1.1) не має розв’язків.
Зібравши разом усі знайдені вище
розв’язки, одержуємо, що розв’язками рівняння (1) в системі (1.1.1) є  і всі
і всі 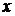 з проміжку
з проміжку 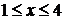 . На
числовій прямій відзначимо розв’язки рівняння (1) системи (1.1.1).
. На
числовій прямій відзначимо розв’язки рівняння (1) системи (1.1.1).
Друге рівняння системи (1.1.1) має
два корені: 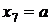 і
і 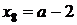 . Вочевидь,
що при будь-якому
. Вочевидь,
що при будь-якому  розв’язки
рівняння (2) системи (1.1.1) пов’язані співвідношенням
розв’язки
рівняння (2) системи (1.1.1) пов’язані співвідношенням 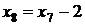 .
.
З’ясуємо тепер, при яких значеннях  система
рівнянь (1.1.1) сумісна; для цього будемо розглядати різні значення
система
рівнянь (1.1.1) сумісна; для цього будемо розглядати різні значення  , рухаючись
вздовж числової прямої зліва направо.
, рухаючись
вздовж числової прямої зліва направо.
Для будь-якого 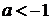 обидва
корені рівняння (2) системи (1.1.1) лежать лівіше від будь-якого кореня
рівняння (1) системи (1.1.1), а тому система (1.1.1) - несумісна.
обидва
корені рівняння (2) системи (1.1.1) лежать лівіше від будь-якого кореня
рівняння (1) системи (1.1.1), а тому система (1.1.1) - несумісна.
Якщо 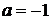 , то, оскільки
, то, оскільки 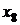 лежить
лівіше від точки
лежить
лівіше від точки 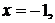 система
(1.1.1) має єдиний розвязок
система
(1.1.1) має єдиний розвязок 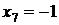 .
.
Для будь-якого  із проміжку
із проміжку
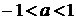 число
число 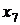 лежить між
коренями рівняння (1) системи (1.1.1), а
лежить між
коренями рівняння (1) системи (1.1.1), а 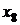 лежить лівіше від кореня рівняння
(1) системи (1.1.1), який дорівнює -1. Отже, система (1.1.1) -несумісна.
лежить лівіше від кореня рівняння
(1) системи (1.1.1), який дорівнює -1. Отже, система (1.1.1) -несумісна.
Якщо 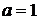 , то, вочевидь, система (1.1.1) має
два розвязки
, то, вочевидь, система (1.1.1) має
два розвязки 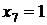 і
і 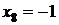 .
.
Для будь-якого  із проміжку
із проміжку
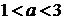 система
(1.1.1) -сумісна. Її розв’язком є тільки
система
(1.1.1) -сумісна. Її розв’язком є тільки 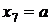 , оскільки
, оскільки 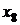 буде лежати
між числами -1 і 1 .
буде лежати
між числами -1 і 1 .
Для будь-якого  з проміжку
з проміжку 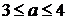 система
(1.1.1) має два розв’язки
система
(1.1.1) має два розв’язки 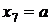 і
і 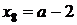 , оскільки
обидва ці числа лежать на проміжку
, оскільки
обидва ці числа лежать на проміжку 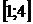 .
.
Для будь-якого  з проміжку
з проміжку 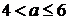 система
(1.1.1) - сумісна, її розв’язком є
система
(1.1.1) - сумісна, її розв’язком є 
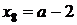 , оскільки
, оскільки 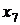 буде
знаходитися правіше від відрізка
буде
знаходитися правіше від відрізка 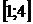 .
.
Для будь-якого 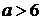 система
(1.1.1) несумісна, оскільки
система
(1.1.1) несумісна, оскільки 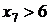 і
і 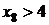 .
.
Оскільки нас цікавлять лише ті
значення  , для
кожного з яких система (1.1.1) має єдиний розв’язок , то з попереднього
випливає, що умову задачі задовольняють
, для
кожного з яких система (1.1.1) має єдиний розв’язок , то з попереднього
випливає, що умову задачі задовольняють 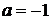 , а також будь-які
, а також будь-які  з двох
проміжків
з двох
проміжків 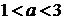 і
і 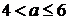 .
.
Відповідь: 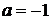 ,
, 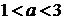 ,
, 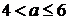
Приклад № 1.2
При яких значеннях параметра  всі
розв’язки рівняння
всі
розв’язки рівняння
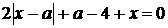 (1.2.1)
(1.2.1)
задольняють нерівність 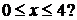
Розв’язання:
Дане рівняння рівносильне до
сукупності двох змішаних систем
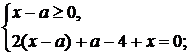 (1.2.2)
(1.2.2)
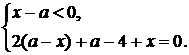 (1.2.3)
(1.2.3)
Рівняння (2) системи (1.2.2) має
розв’язок  . Щоб цей
розв’язок задовольняв умову
. Щоб цей
розв’язок задовольняв умову 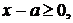 повинна виконуватися нерівність
повинна виконуватися нерівність 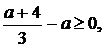 звідки
звідки 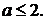
Рівняння (2) системи (1.2.3) має
розв’язок 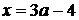 . Щоб цей
розв’язок задовольняв умову
. Щоб цей
розв’язок задовольняв умову 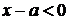 , повинна виконуватися нерівність
, повинна виконуватися нерівність 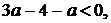 звідки
звідки 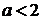 .
.
Якщо 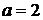 , то початкове рівняння має один
розв’язок
, то початкове рівняння має один
розв’язок 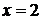 , який
задовольняє нерівність
, який
задовольняє нерівність 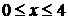 .
.
Якщо ж 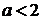 , то
початкове рівняння має два розв’язки, які задовольняють нерівність
, то
початкове рівняння має два розв’язки, які задовольняють нерівність 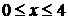 при
значеннях
при
значеннях  , які є
розв’язками системи нерівностей
, які є
розв’язками системи нерівностей
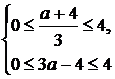
тобто при 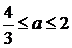 .
.
Відповідь : 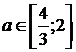
Приклад № 1.3
Для кожного значення параметра  знайти всі
значення
знайти всі
значення 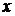 , які
задовольняють рівняння
, які
задовольняють рівняння
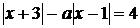 (1.3.1)
(1.3.1)
Розв’язання:
Розіб’ємо числову пряму на три
проміжки: 1) 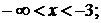
2) 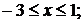 3)
3) 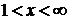 .
.
Розв’яжемо рівняння (1.3.1) на
кожному з проміжків.
Розглянемо проміжок 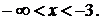 На цьому
проміжку рівняння (1.3.1) набуде вигляду
На цьому
проміжку рівняння (1.3.1) набуде вигляду
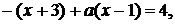 або
або 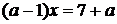 . (1.3.2)
. (1.3.2)
Звідси видно, що при 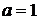 рівняння
(1.3.2) не має розв’язків.
рівняння
(1.3.2) не має розв’язків.
Якщо ж 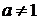 , то
рівняння (1.3.2) має один корінь
, то
рівняння (1.3.2) має один корінь
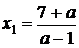 (1.3.3)
(1.3.3)
Тепер варто з’ясувати, при яких
значеннях  цей корінь
задоволь-няє нерівність
цей корінь
задоволь-няє нерівність 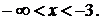
а) Для цього потрібно розв’язати
нерівність
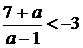 (1.3.4)
(1.3.4)
б) Запишемо нерівність (1.3.4) у
вигляді
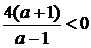 (1.3.5)
(1.3.5)
в) Розв’язком нерівності (1.3.5) є
проміжок 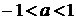 . Отже, на
множині
. Отже, на
множині 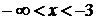 початкове
рівняння (1.3.1) має 1 корень (1.3.3) при будь- якому значенні
початкове
рівняння (1.3.1) має 1 корень (1.3.3) при будь- якому значенні  з проміжку
з проміжку 
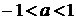 і не має коренів при будь-якому
значенні
і не має коренів при будь-якому
значенні  , що не
належать цьому проміжку
, що не
належать цьому проміжку
. Розглянемо проміжок 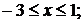 У цьому
проміжку рівняння (1.3.1) набуває вигляду
У цьому
проміжку рівняння (1.3.1) набуває вигляду
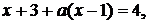 або
або 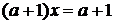 . (1.3.6)
. (1.3.6)
Звідси видно, що при 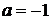 розв’язком
рівняння (1.3.6) є будь-яке дійсне число, оскільки
розв’язком
рівняння (1.3.6) є будь-яке дійсне число, оскільки 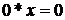 .
.
Якщо ж 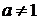 , то
рівняння (1.3.6) має один корінь
, то
рівняння (1.3.6) має один корінь 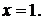 Отже, в розглянутому проміжку
рівняння (1.3.1) має єдиний корінь
Отже, в розглянутому проміжку
рівняння (1.3.1) має єдиний корінь 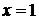 при будь-якому
при будь-якому 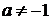 , а при
, а при 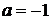 його
розв’язком буде будь-яке число з проміжку
його
розв’язком буде будь-яке число з проміжку 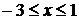 .
.
5. Розглянемо проміжок 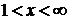 . У цьому
проміжку рівняння (1.3.1) набуде вигляду
. У цьому
проміжку рівняння (1.3.1) набуде вигляду
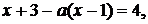 або
або 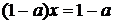 . (1.3.7)
. (1.3.7)
Звідси видно, що при 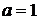 розв’язком
рівняння (1.3.7) є будь-яке дійсне число.
розв’язком
рівняння (1.3.7) є будь-яке дійсне число.
Якщо ж 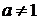 , то
рівняння (1.3.7) має єдиний корінь
, то
рівняння (1.3.7) має єдиний корінь 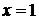 , який не лежить у розглянутому
проміжку. Отже, в інтервалі
, який не лежить у розглянутому
проміжку. Отже, в інтервалі 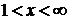 початкове рівняння (1.3.1) не має
коренів при будь-якому
початкове рівняння (1.3.1) не має
коренів при будь-якому 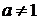 , а при
, а при 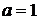 його
розв’язком є будь-яке число з проміжку
його
розв’язком є будь-яке число з проміжку 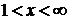 .
.
. Підбиваючи підсумок, одержуємо, що
при 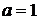 розв’язком
початкового рівняння (1.3.1) є всі значення
розв’язком
початкового рівняння (1.3.1) є всі значення 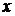 із проміжку
із проміжку 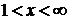 , при
, при 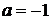 - всі
значення
- всі
значення 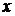 із проміжку
із проміжку
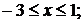 при
будь-якому значенні
при
будь-якому значенні  такому, що
такому, що 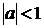 , початкове
рівняння має два корені
, початкове
рівняння має два корені 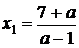 і
і 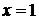 ; при
будь-якому значенні
; при
будь-якому значенні  такому , що
такому , що
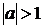 , початкове
рівняння має один корінь
, початкове
рівняння має один корінь 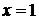 .
.
Відповідь:
якщо 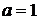 , то всі значення
, то всі значення 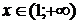 ;
;
якщо 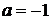 , то всі значення
, то всі значення 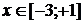 ;
;
якщо 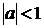 , то
, то 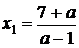 і
і 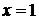 ;
;
якщо 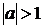 , то
, то 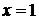 .
.
Приклад № 1.4
Розв’язати рівняння
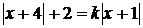 (1.4.1)
(1.4.1)
Розв’яжемо дане рівняння на трьох
проміжках:
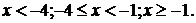
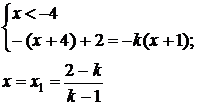
Корінь 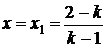 повинен
задовольняти нерівність
повинен
задовольняти нерівність 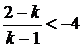 Розв’язавши
її, знаходимо
Розв’язавши
її, знаходимо 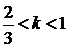 . Отже, якщо
. Отже, якщо
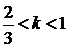 , то
, то 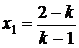
. 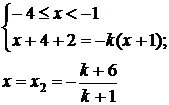
Розв’язавши подвійну нерівність 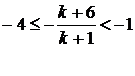 , що
рівносильна системі
, що
рівносильна системі
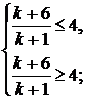
одержуємо 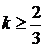
. 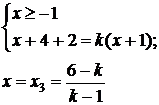
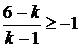 виконується при
виконується при 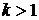 .
.
Для запису відповіді побудуємо схему
(рис. 1.4.1), на якій зазначено які корені отримуємо при тих чи інших значеннях
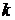 .
.
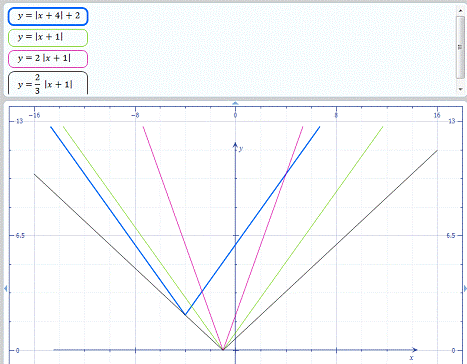
Рис. 1.4.1 Схема коренів в
залежності від значення параметру k
Відповідь:
Якщо 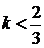 , то рівняння не має розвязків;
, то рівняння не має розвязків;
Якщо 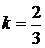 , то
, то 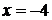 ;
;
Якщо 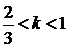 , то
, то 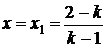 і
і 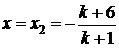 ;
;
Якщо 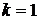 , то
, то 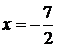 ; Якщо
; Якщо 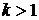
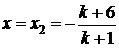 і
і 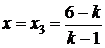 .
.
Приклад № 1.5
Для кожного значення параметра  знайти всі
розв’язки рівняння
знайти всі
розв’язки рівняння
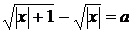 (1.5.1)
(1.5.1)
Розв’язання:
Оскільки 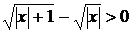 при всіх
значеннях
при всіх
значеннях 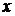 , то
рівняння (1.5.1) не має розв’язків, якщо
, то
рівняння (1.5.1) не має розв’язків, якщо 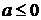 . Надалі вважатимемо, що
. Надалі вважатимемо, що 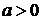 .
.
Перепишемо рівняння (1.5.1) у
вигляді
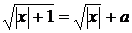 (1.5.2)
(1.5.2)
З огляду на те, що при будь-якому
значенні 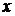 ліва і
права частини рівняння (1.5.2) додатні, їх можна піднести до квадрата
ліва і
права частини рівняння (1.5.2) додатні, їх можна піднести до квадрата
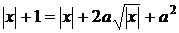
Або
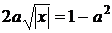 (1.5.3)
(1.5.3)
При будь-якому значенні 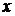 ліва
частина рівняння (1.5.3) невід’ємна, тому рівняння не має розв’язків, якщо
ліва
частина рівняння (1.5.3) невід’ємна, тому рівняння не має розв’язків, якщо 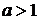 .
Вважатимемо, що
.
Вважатимемо, що 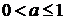 . Тоді
рівняння (1.5.3) рівносильне рівнянню
. Тоді
рівняння (1.5.3) рівносильне рівнянню
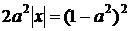
тобто 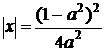
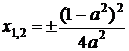
Відповідь: якщо 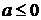 або
або 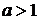 , то коренів
немає;
, то коренів
немає;
якщо 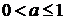 , то два кореня
, то два кореня 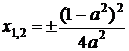 ;
;
якщо 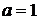 , то один корінь
, то один корінь 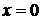 .
.
РОЗДІЛ 2. ГРАФО-АНАЛІТИЧНІ МЕТОДИ
РОЗВ’ЯЗАННЯ РІВНЯНЬ З МОДУЛЯМИ ТА ПАРАМЕТРАМИ З ЗАСТОСУВАННЯМ
ПРОГРАМНО-ГРАФІЧНОГО КАЛЬКУЛЯТОРА MICROSOFT MATHEMATICS 4.0
.1 Застосування графічних методів
паралельного переносу в розв’язанні задач з параметрами
Російськомовна версія графічного
комп’ютерного калькулятора Microsoft Mathematics 4.0 автоматично будує в
масштабі графіки модулів функцій будь-якої складності, що дозволяє оцінити ОДЗ
функцій та характерні інтервали зростання і падіння. Одночасно, калькулятор
Microsoft Mathematics 4.0 дозволяє будувати декілька функцій 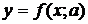 на одному
графіку різними кольорами, що дає змогу моделювати декілька графіків
аналізуємих функцій при зміні значення параметра а.
на одному
графіку різними кольорами, що дає змогу моделювати декілька графіків
аналізуємих функцій при зміні значення параметра а.
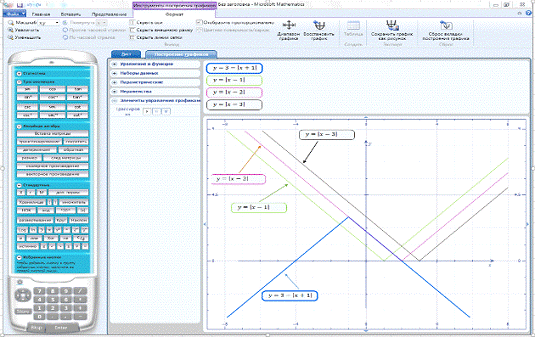
Рис. 1. Загальний вигляд інтерфейсу
калькулятора Microsoft Mathematics 4.0 при графічному розв’язанні рівняння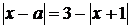 варіацією
параметра аПриклад 2.1.1. Для кожного значення параметра а визначити число
розв’язків рівняння
варіацією
параметра аПриклад 2.1.1. Для кожного значення параметра а визначити число
розв’язків рівняння 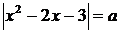 .
.
Розв’язання. Побудуємо графіки
функцій 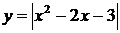 та
та 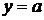 .
.
На рис. 2.1.1 побудована множина
паралельних прямих 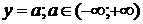 , при цьому
вибір зроблений так, щоб кількість точок перетинання була різною.
, при цьому
вибір зроблений так, щоб кількість точок перетинання була різною.
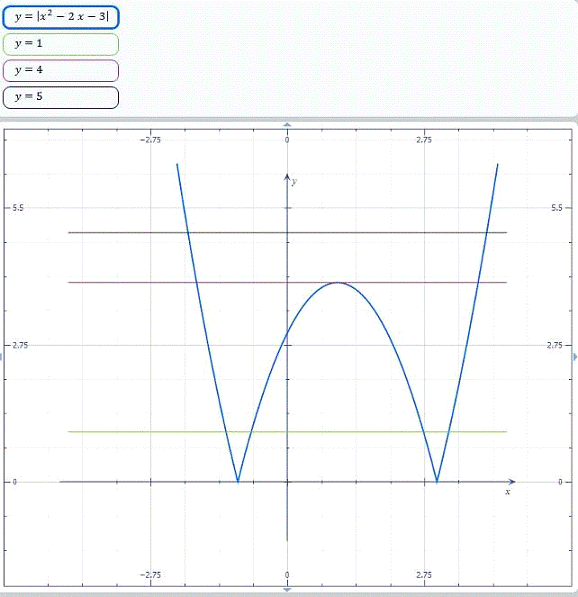
Рис. 2.1.1. Графіки функцій 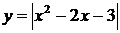 та
та 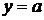 (при різних
значеннях параметра а)
(при різних
значеннях параметра а)
З рисунка 2.1.1 випливає, що при 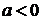 - розв’язків
немає, при
- розв’язків
немає, при 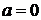 - 2
розв’язки, при
- 2
розв’язки, при 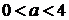 - 4
розв’язки, при
- 4
розв’язки, при 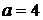 - 3
розв’язки, при
- 3
розв’язки, при 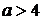 - 2
розв’язки.
- 2
розв’язки.
Пакет Microsoft Mathematics 4.0
дозволяє знайти корні в типових проміжках параметру а, задаючи значення 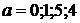 та
вирішуючи рівняння
та
вирішуючи рівняння
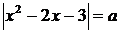 . Нижче наведені чисельні рішення.
Одночасно пакет Microsoft Mathematics 4.0 дозволяє навести алгебраїчні рішення
рівняння з параметрами, які характеризують наявність при
. Нижче наведені чисельні рішення.
Одночасно пакет Microsoft Mathematics 4.0 дозволяє навести алгебраїчні рішення
рівняння з параметрами, які характеризують наявність при 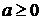 двох
коренів (зовнішня гілка параболи) та наявність на проміжку
двох
коренів (зовнішня гілка параболи) та наявність на проміжку 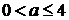 ще другої
пари коренів (внутрішня гілка параболи до вершини).
ще другої
пари коренів (внутрішня гілка параболи до вершини).

Відповідь: при 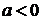 - розв’язків
немає,
- розв’язків
немає,
при 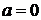 - 2 розв’язки,
- 2 розв’язки,
при 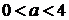 - 4 розв’язки,
- 4 розв’язки,
при 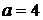 - 3 розв’язки,
- 3 розв’язки,
при 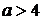 - 2 розв’язки.
- 2 розв’язки.
Приклад 2.1.2. Для кожного значення
параметра  визначити
число розв’язків рівняння
визначити
число розв’язків рівняння 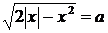 .
.
Розв’язання.
. Отримуємо рішення рівняння з
параметрами 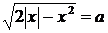 в пакеті
Microsoft Mathematics 4.0.
в пакеті
Microsoft Mathematics 4.0.
Як показує аналіз розв’язків,
параметр а знаходиться в проміжку
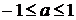 (при цьому вирішується рівняння з
знаком
(при цьому вирішується рівняння з
знаком 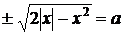 .
.
Як показує аналіз рішення рівняння
має 4 корені на проміжку 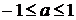
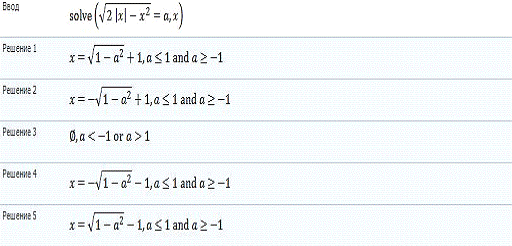
З аналізу машинного рішення випливає
відповідь:
при 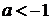 та
та 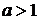 - розв’язків немає,
- розв’язків немає,
при 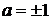 - 2 розв’язки,
- 2 розв’язки,
при 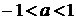 - 4 розв’язки.
- 4 розв’язки.
. Побудуємо графік функції 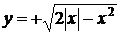 та
та 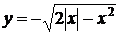 При цьому
врахуємо ОДЗ функції під коренем
При цьому
врахуємо ОДЗ функції під коренем 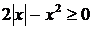 , тобто
, тобто 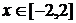 .
.
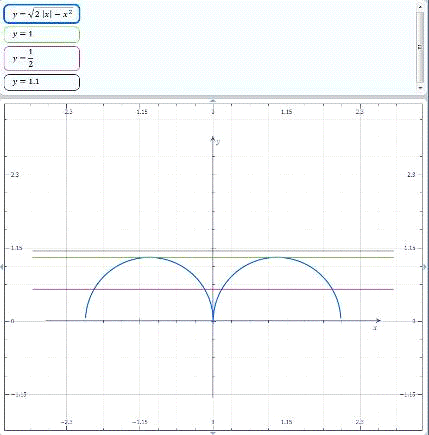
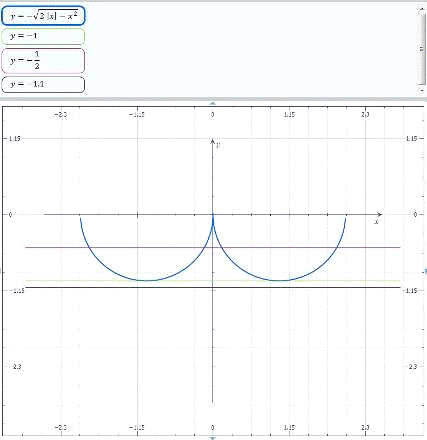
Рис. 2.1.2. Графіки функцій 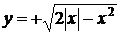 та
та 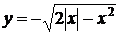
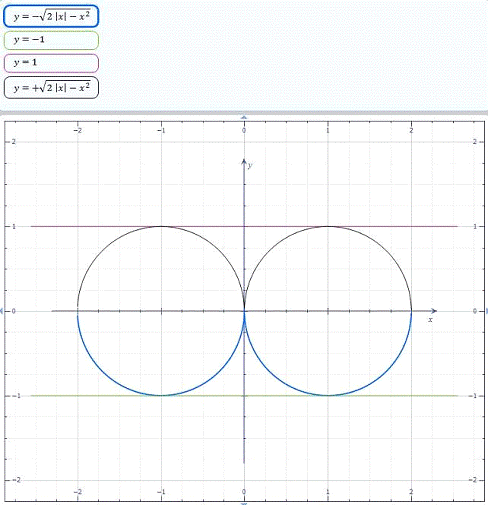
З аналізу графікі рис. 2.1.2 та
2.1.2а випливає відповідь, що підтверджує машинний розрахунок:
при 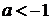 та
та 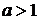 - розв’язків немає,
- розв’язків немає,
при 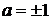 - 2 розв’язки,
- 2 розв’язки,
при 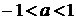 - 4 розв’язки.
- 4 розв’язки.
.2 Застосування графічних методів
повороту в розв’язанні задач з параметрами
В цьому параграфі вибір сім’ї кривих
не є різноманітним, а точніше він одноваріантний: члени сім’ї кривих 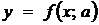 - прямі.
Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося
сім’єю виду
- прямі.
Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося
сім’єю виду 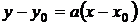 , де
, де 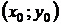 - центр
повороту.
- центр
повороту.
Такий вибір обумовлено тим, що в
рівності 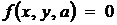 складно
побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому
про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
складно
побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому
про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
Приклад 2.2.1. При яких  рівняння
рівняння 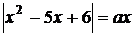 має три
розв’язки?
має три
розв’язки?
Розв’язання.
. Побудуємо графіки функцій 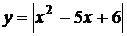 та
та 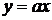 . Прямі
. Прямі 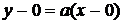 переходять
друг в друга шляхом перетворення повороту з центром в точці О(0; 0).
переходять
друг в друга шляхом перетворення повороту з центром в точці О(0; 0).
. Аналіз варіантів перетинання
графіки функцій 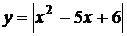 та
та 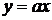 (рис.
3.2.1) показує, що вихідне рівняння буде мати три розв’язки, коли пряма
(рис.
3.2.1) показує, що вихідне рівняння буде мати три розв’язки, коли пряма 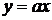 перетинає
параболу в двох точках і дотикається до вершини, тобто коли
перетинає
параболу в двох точках і дотикається до вершини, тобто коли 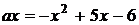 .
.
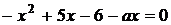
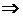
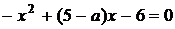
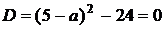
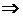
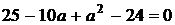
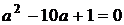
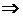
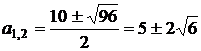
Обираємо 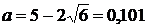 , так як при
, так як при
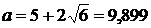 пряма
пряма 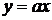 перетинає
тільки 2 вітки гіперболи (рис. 3.2.1) нижче вісі абсцис.
перетинає
тільки 2 вітки гіперболи (рис. 3.2.1) нижче вісі абсцис.
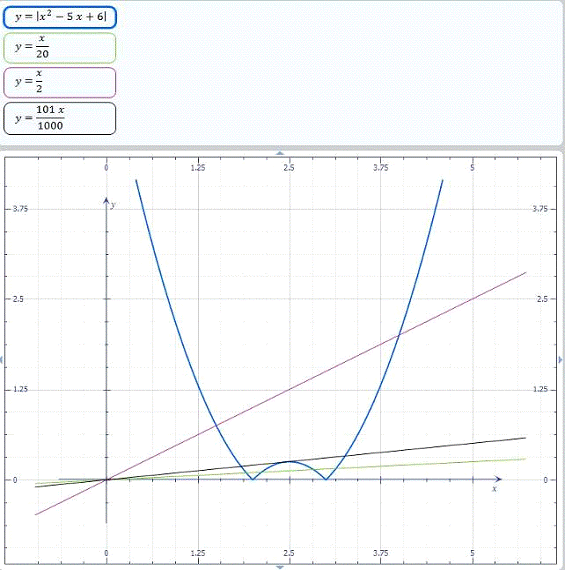
Рис. 2.2.1. Графіки функцій 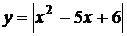 та
та 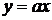 (поворот
прямої при довільному
(поворот
прямої при довільному  )
)
Відповідь: 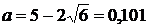
Приклад 2.2.2. При яких значеннях 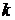 рівняння
рівняння 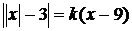 має одно,
два, три, чотири розв’язки?
має одно,
два, три, чотири розв’язки?
Розв’язання. Побудуємо графіки
функцій 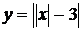 та
та 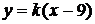 . Прямі
. Прямі 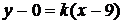 переходять
друг в друга шляхом перетворення повороту з центром в точці О(9; 0).
переходять
друг в друга шляхом перетворення повороту з центром в точці О(9; 0).
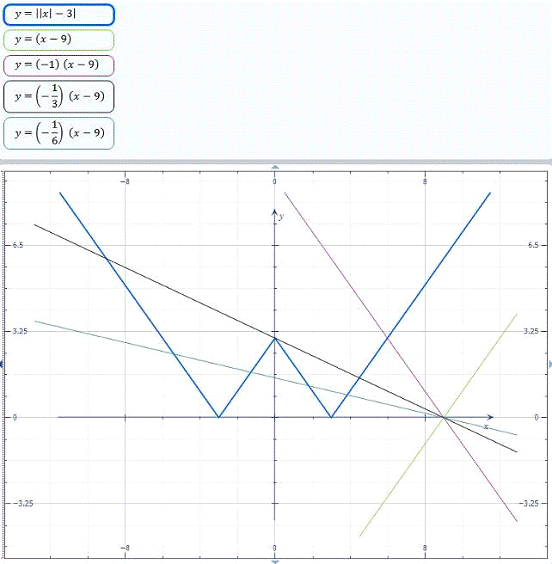
Рис. 2.2.2. Графіки функцій 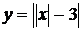 та
та 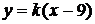 при змінному
при змінному
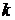 ( поворот
прямих відносно точки (9; 0))
( поворот
прямих відносно точки (9; 0))
З рис. 2.2.2 видно, що:
а) при 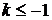 рівняння
має 1 розв’язок;
рівняння
має 1 розв’язок;
б) при 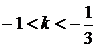 - 2
розв’язки;
- 2
розв’язки;
в) при 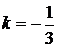 - 3
розв’язки;
- 3
розв’язки;
г) при 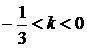 - 4
розв’язки;
- 4
розв’язки;
д) при 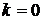 - 2
розв’язки;
- 2
розв’язки;
е) при 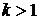 - 1
розв’язок;
- 1
розв’язок;
ж) при 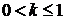 - розв’язки
відсутні.
- розв’язки
відсутні.
Відповідь:
при 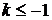 - 1 розв’язок,
- 1 розв’язок,
при 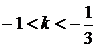 - 2 розв’язки,
- 2 розв’язки,
при 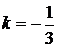 - 3 розв’язки,
- 3 розв’язки,
при 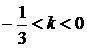 - 4 розв’язки,
- 4 розв’язки,
при 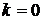 - 2 розв’язки,
- 2 розв’язки,
при 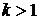 - 1 розв’язок.
- 1 розв’язок.
.3 Застосування графічних методів
гомотетії в розв’язанні задач з параметрами
Приклад 2.3.1. Знайти число
розв’язків системи рівнянь (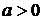 )
)
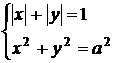
Розв’язання. Побудуємо в пакеті
Microsoft Matematics графіки функцій 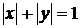 (квадрат зі стороною
(квадрат зі стороною 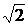 ) та
) та 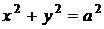 . Члени
сім’ї функцій
. Члени
сім’ї функцій 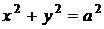 -
гомотетичні кола (з центром гомотетії (0,0)) - рис.3.3.1.
-
гомотетичні кола (з центром гомотетії (0,0)) - рис.3.3.1.
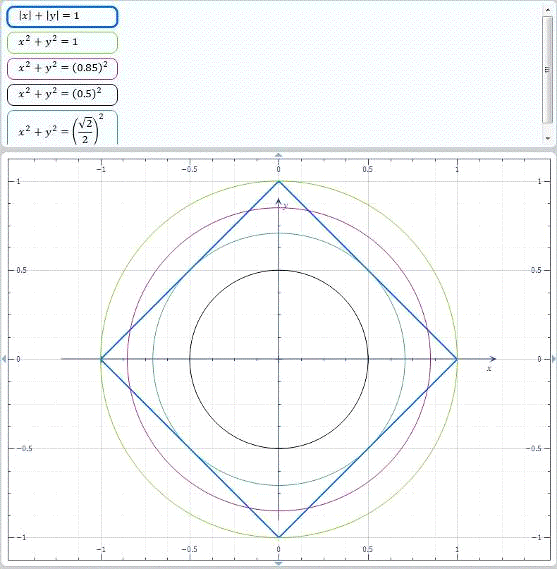
Рис. 2.3.1. Графіки функцій 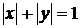 (квадрат зі
стороною
(квадрат зі
стороною 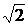 ) та
гомотетичні кола
) та
гомотетичні кола 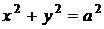 з центром в
точці (0;0)
з центром в
точці (0;0)
Якщо коло лежить всередині квадрата,
то розв’язків немає.
Якщо коло вписане в квадрат, то
з’являються розв’язки. В цьому випадку з теореми Піфагора: 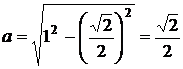 . При
. При 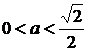 система
немає розв’язків, при
система
немає розв’язків, при 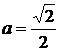 система має
4 розв’язки. Далі зі збільшенням
система має
4 розв’язки. Далі зі збільшенням  (
(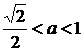 ) кожна сторона квадрата має дві
спільні точки перетину з колом (всього 8 розв’язків).
) кожна сторона квадрата має дві
спільні точки перетину з колом (всього 8 розв’язків).
При 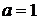 квадрат вписаний в коло, маємо 4
розв’язки. При
квадрат вписаний в коло, маємо 4
розв’язки. При 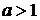 розв’язків
немає.
розв’язків
немає.
Відповідь: при 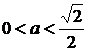 розв’язків
немає, при
розв’язків
немає, при 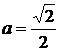 - 4
розв’язки, при
- 4
розв’язки, при 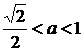 - 8
розв’язків, при
- 8
розв’язків, при 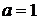 - 4
розв’язки, при
- 4
розв’язки, при  розв’язків
немає.
розв’язків
немає.
ВИСНОВКИ
В проведеному дослідженні в якості
новітнього програмно-технічного засобу розвиваючого навчання запропоноване
застосування російськомовного програмно-графічного калькулятора Microsoft
Mathemаtics 4.0 з „дружнім” інтерфейсом, який з 2011 року вільно
розповсюджується корпорацією Microsoft та призначений для використання як на
звичайних комп’ютерах, так і на новітніх інтерактивно-тактильних планшетах та
„електронних класних дошках” під керуванням операційних систем Windows 7/8.
На прикладах розв’язання рівнянь та
нерівностей з параметрами, що містять модулі, графічним способом доведена
ефективність застосування програмно-графічного калькулятора Microsoft
Mathemаtics 4.0 при побудові на одному масштабному полі систем паралельних,
гомотетичних та поворотних функцій при зміні параметра, що дає яскраву
наочність викладення курсу задач з параметрами вчителем математики в школі та
можливість самостійних досліджень учнем задач з параметрами на класному та
домашньому компьютерах.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1.
Горнштейн П.І. Задачі з параметрами / П.І.Горнштейн, В.Б.Полонський, М.С.Якір.
- Тернопіль, 2004. - 186 с.
.
Заслонкіна Л. С. Задачі з параметрами. - Х. : Вид. група «Основа», 2012. - 108
с.
.
Козко А.И. ЕГЭ 2011. Математика. Задаса С5. Задачи с параметром / А.И.Козко,
В.С.Панферов, И.Н. Сергеев, В.Г. Чирский. - под ред. А.Л.Семенова и И.В.Ященко.
- М.: МЦНМО, 2011. - 144 с.
.
Крамор В.С. Задачі з параметрами і методи їх розв’язання /В.С.Крамор: пер. з
рос. А.Кравчука. - Тернопіль:Навчальна книга. - Богдан, 2012. - 416 с.
.
Лікоть В.В. Задачі з параметрами / В.В.Лікоть - К., «Знання», 2003. -135 с.
.
Рогівська Т. С. Рівняння з параметрами. Розробки занять елективного курсу для 8
класу. - Х. : Вид. група «Основа», 2012. - 140 с.
7.
http://www.microsoft.com/education/ Mathem4tics-guide.aspx - Microsoft Математика
4.0 в
классе
- Microsoft Matematics, 2012